Errors of Probability in Historical Context

PRAKASH GORROOCHURN

1. Introduction

This article outlines some of the mistakes made in the calculus of probability, especially when the discipline was being developed. Such is the character of the doctrine of chances that simple-looking problems can deceive even the sharpest minds. In his celebrated Essai Philosophique sur les Probabilités (Laplace 1814, p. 273), the eminent French mathematician Pierre-Simon Laplace (1749–1827) said,

… the theory of probabilities is at bottom only common sense reduced to calculus.

There is no doubt that Laplace was right, but the fact remains that blunders and fallacies persist even today in the field of probability, often when “common sense” is applied to problems.

The errors I describe here can be broken down into three main categories: (i) use of “reasoning on the mean” (ROTM), (ii) incorrect enumeration of sample points, and (iii) confusion regarding the use of statistical independence.

2. Use of “Reasoning on the Mean” (ROTM)

In the history of probability, the physician and mathematician Gerolamo Cardano (1501–1575) was among the first to attempt a systematic study of the calculus of probabilities. Like those of his contemporaries, Cardano’s studies were primarily driven by games of chance. Concerning his 25 years of gambling, he famously said in his autobiography (Cardano 1935, p. 146),

… and I do not mean to say only from time to time during those years, but I am ashamed to say it, everyday.

Cardano’s works on probability were published posthumously in the famous 15-page Liber de Ludo Aleae,¹ consisting of 32 small chapters (Cardano 1564). Cardano was undoubtedly a great mathematician of his time but stumbled on several questions, and this one in particular: “How many throws of a fair die do we need in order to have a fair chance of at least one six?” In this case, he thought the number of throws should be three.² In Chapter 9 of his book, Cardano says of a die:

One-half of the total number of faces always represents equality³; thus the chances are equal that a given point will turn up in three throws …

Cardano’s mistake stems from a prevalent general confusion between the concepts of probability and expectation. Let us dig deeper into Cardano’s reasoning. In the De Ludo Aleae, Cardano frequently makes use of an erroneous principle, which Ore called a “reasoning on the mean” (ROTM) (Ore 1953, p. 150; Williams 2005), to deal with various probability problems. According to the ROTM, if an event has a probability p in one trial of an experiment, then in n trials the event will occur np times on average, which is then wrongly taken to represent the probability that the event will occur in n trials. In our case, we have p = 1/6 so that, with n = 3 throws, the event “at least a six” is wrongly taken to occur an average np = 3(1/6) = 1/2 of the time. But if X is the number of sixes in three throws, then X ˜ B(3,1/6), the probability of one six in three throws is 0.347, and the probability of at least one six is 0.421. On the other hand, the expected value of X is 0.5. Thus, although the expected number of sixes in three throws is 1/2, neither the probability of one six or at least one six is 1/2.

We now move to about a century later when the Chevalier de Méré⁴ (1607–1684) used the Old Gambler’s Rule, leading to fallacious results. As we shall see, the Old Gambler’s Rule is an offshoot of ROTM. The Chevalier de Méré had been winning consistently by betting even money that a six would come up at least once in four rolls with a single die. However, he had now been losing on a new bet, when in 1654 he met his friend, the amateur mathematician Pierre de Carcavi (1600–1684). De Méré had thought that the odds were favorable on betting that he could throw at least one sonnez (i.e., double six) with 24 throws of a pair of dice. However, his own experiences indicated that 25 throws were required.⁵ Unable to resolve the issue, the two men consulted their mutual friend, the great mathematician, physicist, and philosopher Blaise Pascal (1623–1662).⁶ Pascal himself had previously been interested in the games of chance (Groothuis 2003, p. 10). Pascal must have been intrigued by this problem and, through the intermediary of Carcavi,⁷ contacted the eminent mathematician, Pierre de Fermat (1601–1665),⁸ who was a lawyer in Toulouse. In a letter Pascal addressed to Fermat, dated July 29, 1654, Pascal says (Smith 1929, p. 552),

He [De Méré] tells me that he has found an error in the numbers for this reason:

If one undertakes to throw a six with a die, the advantage of undertaking to do it in 4 is as 671 is to 625.

If one undertakes to throw double sixes with two dice the disadvantage of the undertaking is 24.

But nonetheless, 24 is to 36 (which is the number of faces of two dice) as 4 is to 6 (which is the number of faces of one die).

This is what was his great scandal which made him say haughtily that the theorems were not consistent and that arithmetic was demented. But you can easily see the reason by the principles which you have.

De Méré was thus distressed that his observations were in contradiction with his mathematical calculations. His erroneous mathematical reasoning was based on the erroneous Old Gambler’s Rule (Weaver 1982, p. 47), which uses the concept of the critical value of a game. The critical value C of a game is the smallest number of plays such that the probability the gambler will win at least one play is 1/2 or more. Let us now explain how the Old Gambler’s Rule is derived. Recall Cardano’s “reasoning on the mean” (ROTM): If a gambler has a probability p of winning one play of a game, then in n plays the gambler will win an average of np times, which is then wrongly equated to the probability of winning in n plays. Then, by setting the latter probability to be half, we have

Moreover, given a first game with (p₁, C₁), then a second game which has probability of winning p₂ in each play must have critical value C₂, where

That is, the Old Gambler’s Rule states that the critical values of two games are in inverse proportion as their respective probabilities of winning. Using C₁ = 4, p₁ = 1/6, and p₂ = 1/36, we get C₂ = 24. However, with 24 throws, the probability of at least one double six is 0.491, which is less than 1/2. So C₂ = 24 cannot be a critical value (the correct critical value is shown below to be 25), and the Old Gambler’s Rule cannot be correct. It was thus the belief in the validity of the Old Gambler’s Rule that made de Méré wrongly think that, with 24 throws, he should have had a probability of 1/2 for at least one double six.

Let us see how the erroneous Old Gambler’s Rule should be corrected. By definition, C₁ = [x₁], the smallest integer greater or equal to x₁, such that (− p₂)^x1 = 0.5, that is, x _l = ln(0.5)/ln(1 − p₁). With obvious notation, for the second game, C₂ = [x₂], where x₂ = ln(0.5)/ln(1 − p₂). Thus the true relationship should be

We see that Equations (1) and (2) are quite different from each other. Even if p₁ and p₂ were very small, so that ln(1 − p₁) ≈ −p₁ and ln(1 − p₂) ≈ −p₂, we would get x₂ = x₁p₁/p₂ approximately. This is still different from Equation (1) because the latter uses the integers C₁ and C₂, instead of the real numbers x₁ and x₂.

The Old Gambler’s Rule was later investigated by the French mathematician Abraham de Moivre (1667–1754), who was a close friend to Isaac Newton. Thus, in the Doctrine of Chances (de Moivre 1718, p. 14), Problem V, we read,

To find in how many Trials an Event will Probably Happen or how many Trials will be required to make it indifferent to lay on its Happening or Failing; supposing that a is the number of Chances for its Happening in any one Trial, and b the number of chances for its Failing.

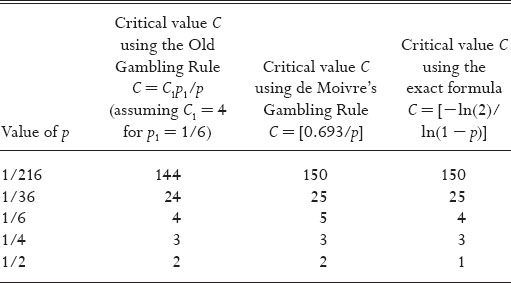
TABLE 1.
Critical values obtained using the Old Gambling Rule, de Moivre’s Gambling Rule, and the exact formula for different values of p, the probability of the event of interest

De Moivre solves (1 − p)^x = 1/2 and obtains x = −ln(2)/ln(1 − p). For small p,

Let us see if we obtain the correct answer when we apply de Moivre’s Gambling Rule for the two-dice problem. Using x ≈ 0.693/p with p = 1/36 gives x ≈ 24.95, and we obtain the correct critical value C = 25. The formula works only because p is small enough and is valid only for such cases.⁹ The other formula that could be used, and that is valid for all values of p, is x = −ln(2)/ln(1 − p). For the two-dice problem, this exact formula gives x = −ln(2)/ln(35/36) = 24.60, so that C = 25. Table 1 compares critical values obtained using the Old Gambler’s Rule, de Moivre’s Gambling Rule, and the exact formula.

3. Incorrect Enumeration of Sample Points

The Problem of Points¹⁰ was another problem about which de Méré asked Pascal in 1654 and was the question that really launched the theory of probability in the hands of Pascal and Fermat. It goes as follows: “Two players A and B play a fair game such that the player who wins a total of 6 rounds first wins a prize. Suppose the game unexpectedly stops when A has won a total of 5 rounds and B has won a total of 3 rounds. How should the prize be divided between A and B?” To solve the Problem of Points, we need to determine how likely A and B are to win the prize if they had continued the game, based on the number of rounds they have already won. The relative probabilities of A and B winning thus determine the division of the prize. Player A is one round short, and player B three rounds short, of winning the prize. The maximum number of hypothetical remaining rounds is (1 + 3) − 1 = 3, each of which could be equally won by A or B. The sample space for the game is

Here B₁A₂, for example, denotes the event that B would win the first remaining round and A would win the second (and then the game would have to stop since A is only one round short). However, the four sample points in Ω are not equally likely.

For example, event A₁ occurs if any one of the following four equally likely events occurs: A₁A₂A₃, A₁A₂B₃, A₁B₂A₃, and A₁B₂B₃. In terms of equally likely sample points, the sample space is thus

There are in all eight equally likely outcomes, only one of which (B₁B₂B₃) results in B hypothetically winning the game. Player A thus has a probability of 7/8 of winning. The prize should therefore be divided between A and B in the ratio 7:1.

The Problem of Points had already been known hundreds of years before the times of these mathematicians.¹¹ It had appeared in Italian manuscripts as early as 1380 (Burton 2006, p. 445). However, it first came in print in Fra Luca Pacioli’s Summa de Arithmetica, Geometrica, Proportioni, et Proportionalita (1494).¹² Pacioli’s incorrect answer was that the prize should be divided in the same ratio as the total number of games the players had won. Thus, for our problem, the ratio is 5:3. A simple counterexample shows why Pacioli’s reasoning cannot be correct. Suppose players A and B need to win 100 rounds to win a game, and when they stop Player A has won one round and Player B has won none. Then Pacioli’s rule would give the whole prize to A even though she is a single round ahead of B and would have needed to win 99 more rounds had the game continued!¹³

Cardano had also considered the Problem of Points in the Practica arithmetice (Cardano 1539). His major insight was that the division of stakes should depend on how many rounds each player had yet to win, not on how many rounds they had already won. However, in spite of this, Cardano was unable to give the correct division ratio: He concluded that, if players A and B are a and b rounds short of winning, respectively, then the division ratio between A and B should be b(b + 1): a(a + 1). In our case, a = 1, b = 3, giving a division ratio of 6:1.

Pascal was at first unsure of his own solution to the problem and turned to a friend, the mathematician Gilles Personne de Roberval (1602–1675). Roberval was not of much help, and Pascal then asked for the opinion of Fermat, who was immediately intrigued by the problem. A beautiful account of the ensuing correspondence between Pascal and Fermat can be found in a recent book by Keith Devlin, The Unfinished Game: Pascal, Fermat and the Seventeenth Century Letter That Made the World Modern (2008). An English translation of the extant letters can be found in Smith (1929, pp. 546–565).

Fermat made use of the fact that the solution depended not on how many rounds each player had already won but on how many each player must still win to win the prize. This is the same observation Cardano had previously made, although he had been unable to solve the problem correctly. The solution we provided earlier is based on Fermat’s idea of extending the unfinished game. Fermat also enumerated the different sample points as in our solution and reached the correct division ratio of 7:1.

Pascal seems to have been aware of Fermat’s method of enumeration (Edwards 1982), at least for two players. However, when he received Fermat’s method, Pascal made two important observations in his August 24, 1654, letter. First, he stated that his friend Roberval believed that there was a fault in Fermat’s reasoning and that he had tried to convince Roberval that Fermat’ s method was indeed correct. Roberval’s argument was that, in our example, it made no sense to consider three hypothetical additional rounds, because in fact the game could end in one, two, or perhaps three rounds. The difficulty with Roberval’s reasoning is that it leads us to write the sample space as in (5). Since there are three ways out of four for A to win, a naïve application of the classical definition of probability results in the wrong division ratio of 3:1 for A and B (instead of the correct 7:1). The problem here is that the sample points in Ω above are not all equally likely, so that the classical definition cannot be applied. It is thus important to consider the maximum number of hypothetical rounds, namely three, for us to be able to write the sample space in terms of equally likely sample points, as in Equation (5), from which the correct division ratio of 7:1 can deduced.

Pascal’s second observation concerns his own belief that Fermat’s method was not applicable to a game with three players. In a letter dated August 24, 1654, Pascal says (Smith 1929, p. 554),

When there are but two players, your theory which proceeds by combinations is very just. But when there are three, I believe I have a proof that it is unjust that you should proceed in any other manner than the one I have.

Let us explain how Pascal made a slip when dealing with the Problem of Points with three players. Pascal considers the case of three players A, B, and C, who were respectively 1, 2, and 2 rounds short of winning. In this case, the maximum of further rounds before the game has to finish is (1 + 2 + 2) − 2 = 3.¹⁴ With three maximum rounds, there are 3³ = 27 possible combinations in which the three players can win each round. Pascal correctly enumerates all the 27 ways but now makes a mistake: He counts the number of favorable combinations which lead to A winning the game as 19. As can be seen in Table 2, there are 19 combinations (denoted by check marks and Xs) for which A wins at least one round. But out of these, only 17 lead to A winning the game (the check marks) because in the remaining two (the Xs), either B or C wins the game first. Similarly, Pascal incorrectly counts the number of favorable combinations leading to B and C winning as 7 and 7, respectively, instead of 5 and 5. Pascal thus reaches an incorrect division ratio of 19:7:7.

Now Pascal again reasons incorrectly and argues that out of the 19 favorable cases for A winning the game, six of these (namely A₁B₂B₃, A₁C₂C₃, B₁A₂B₃, B₁B₂A₃, C₁A₂C₃, and C₁C₂A₃) result in either both A and B winning the game or both A and C winning the game. So he argues the net number of favorable combinations for A should be 13 + (6/2) = 16. Likewise, he changes the number of favorable combinations for B and C, finally reaching a division ratio of 16 : 5 : 5. But he correctly notes

TABLE 2.
The possible combinations when A, B, and C are 1, 2, and 2 rounds short of winning the game, respectively. The check marks and Xs indicate the combinations that Pascal incorrectly chose to correspond to A winning the game. However, the Xs cannot be winning combinations for A because B₁B₂A₃ results in B winning and C₁C₂A₃ results in C winning

that the answer cannot be right, for his own recursive method gives the correct ratio of 17:5:5. Thus, Pascal at first wrongly believed Fermat’s method of enumeration was not generalizable to more than two players. Fermat was quick to point out the error in Pascal’s reasoning. In his letter dated September 25, 1654, Fermat explains (Smith 1929, p. 562),

In taking the example of the three gamblers of whom the first lacks one point, and each of the others lack two, which is the case in which you oppose, I find here only 17 combinations for the first and 5 for each of the others; for when you say that the combination acc is good for the first, recollect that everything that is done after one of the players has won is worth nothing. But this combination having made the first win on the first die, what does it matter that the third gains two afterwards, since even when he gains thirty all this is superfluous? The consequence, as you have well called it “this fiction,” of extending the game to a certain number of plays serves only to make the rule easy and (according to my opinion) to make all the chances equal; or better, more intelligibly to reduce all the fractions to the same denomination.

We next move to the renowned German mathematician and philosopher Gottfried Wilhelm Leibniz (1646–1716), who is usually remembered as the coinventor of differential calculus, with archrival Isaac Newton. However, he was also interested in probability and famously made a similar mistake of incorrectly enumerating sample points. When confronted with the question “With two dice, is a throw of twelve as likely as a throw of eleven?” Leibniz states in the Opera Omnia (Leibniz 1768, p. 217),

… for example, with two dice, it is equally likely to throw twelve points, than to throw eleven; because one or the other can be done in only one manner.

Thus, Leibniz believed the two throws to be equally likely, arguing that in each case the throw could be obtained in a single way. Although it is true that a throw of 11 can be realized only with a five and a six, there are two ways in which it could happen: the first die could be a five and the second a six, or vice versa. On the other hand, a throw of 12 can be realized in only one way: a six on each die. Thus the first probability is twice the second. Commenting on Leibniz’s error, Todhunter states (Todhunter 1865, p. 48),

Leibniz however furnishes an example of the liability to error which seems peculiarly characteristic of our subject.

Nonetheless, this should not in any way undermine some of the contributions Leibniz made to probability theory. For one thing, he was one of the very first to give an explicit definition of classical probability, except phrased in terms of an expectation (Leibniz 1969, p. 161),

If a situation can lead to different advantageous results ruling out each other, the estimation of the expectation will be the sum of the possible advantages for the set of all these results, divided into the total number of results.

In spite of being conversant with the classical definition, Leibniz was interested in establishing a logical theory for different degrees of certainty. He may rightly be regarded as a precursor to later developments in the logical foundations of probability by Keynes, Jeffreys, Carnap, and others. Since Jacob Bernoulli had similar interests, Leibniz started a communication with him in 1703. He undoubtedly had some influence in Bernoulli’s Ars Conjectandi (Bernoulli 1713). When Bernoulli communicated to Leibniz about his law of large numbers, the latter reacted critically. As Schneider explains (2005, p. 90),

Leibniz’s main criticisms were that the probability of contingent events, which he identified with dependence on infinitely many conditions, could not be determined by a finite number of observations and that the appearance of new circumstances could change the probability of an event. Bernoulli agreed that only a finite number of trials can be undertaken; but he differed from Leibniz in being convinced by the urn model that a reasonably great number of trials yielded estimates of the sought-after probabilities that were sufficient for all practical purposes.

Thus, in spite of Leibniz’s criticism, Bernoulli was convinced of the authenticity of his theorem. This situation is fortunate because Bernoulli’s law was nothing less than a watershed moment in the history of probability.

A few years after Leibniz’s death, Jean le Rond d’Alembert (1717– 1783), who was one of the foremost intellectuals of his times, infamously considered the following problem: “In two tosses of a fair coin, what is the probability that heads will appear at least once?” For this problem, d’Alembert denied that 3/4 could be the correct answer. He reasoned as follows: once a head occurs, there is no need for a second throw; the possible outcomes are thus H, T H, T T, and the required probability is 2/3. Of course, d’Alembert’s reasoning is wrong because he failed to realize that each of H, T H, T T is not equally likely. The erroneous answer was even included in his article Croix ou Pile¹⁵ of the Encyclopédie (d’Alembert 1754, Vol. IV, pp. 512–513). Bertrand (1889, pp. ix–x) did not mince his words about d’Alembert’s various faux pas in the games of chance:

When it comes to the calculus of probability, D’Alembert’s astute mind slips completely.

Similarly, in his History of Statistics, Karl Pearson writes (Pearson 1978, p. 535),

What then did D’Alembert contribute to our subject? I think the answer to that question must be that he contributed absolutely nothing.

In spite of Bertrand’s and Pearson’s somewhat harsh words, it would be misleading for us to think that d’Alembert, a man of immense mathematical prowess, was so naïve that he would have no strong basis for his probabilistic reasoning. In the Croix ou Pile article, a sample space of {H H, H T, T H, T T} made no sense to d’Alembert because it did not correspond to reality. In real life, no person would ever observe H H, because once an initial H was observed the game would end. By proposing an alternative model for the calculus of probabilities, namely that of equiprobability on observable events, d’Alembert was effectively asking why his model could not be right, given the absence of an existing theoretical framework for the calculus of probabilities. D’Alembert’s skepticism was partly responsible for later mathematicians seeking a solid theoretical foundation for probability, culminating in its axiomatization by Kolmogorov (1933).

4. Confusion Regarding the Use of Statistical Independence

D’Alembert also famously considered the following problem: “When a fair coin is tossed, given that heads have occurred three times in a row, what is the probability that the next toss is a tail?” When presented with the problem, d’Alembert insisted that the probability of a tail must “obviously” be greater than 1/2,¹⁶ thus rejecting the concept of independence between the tosses. The claim was made in d’Alembert’s Opuscules Mathématiques (d’Alembert 1761, pp. 13–14). In his own words,

Let’s look at other examples which I promised in the previous Article, which show the lack of exactitude in the ordinary calculus of probabilities.

In this calculus, by combining all possible events, we make two assumptions which can, it seems to me, be contested. The first of these assumptions is that, if an event has occurred several times successively, for example, if in the game of heads and tails, heads has occurred three times in a row, it is equally likely that head or tail will occur on the fourth time? However I ask if this assumption is really true, and if the number of times that heads has already successively occurred by the hypothesis, does not make it more likely the occurrence of tails on the fourth time? Because after all it is not possible, it is even physically impossible that tails never occurs. Therefore the more heads occurs successively, the more it is likely tail will occur the next time. If this is the case, as it seems to me one will not disagree, the rule of combination of possible events is thus still deficient in this respect.

D’Alembert states that it is physically impossible for tails never to occur in a long series of tosses of a coin, and thus used his concepts of physical and metaphysical probabilities¹⁷ to support his erroneous argument.

D’Alembert’s remarks need some clarification because the misconceptions are still widely believed. Consider the following two sequences when a fair coin is tossed four times:

sequence 1 : H H H H

sequence 2 : H H H T

Many would believe that the first sequence is less likely than the second one. After all, it seems highly improbable to obtain four heads in a row. However, it is equally unlikely to obtain the second sequence in that specific order. Although it is less likely to obtain four heads than to obtain a total of three heads and one tail,¹⁸ H H H T is as likely as any other of the same length, even if it contains all heads or all tails.

A more subtle “mistake” concerning the issue of independence was made by Laplace. Pierre-Simon Laplace (1749–1827) was a real giant in mathematics. His works on inverse probability were fundamental in bringing the Bayesian paradigm to the forefront of the calculus of probability and of statistical inference. Hogben says (1957, p. 133),

The fons et irigo of inverse probability is Laplace. For good or ill, the ideas commonly identified with the name of Bayes are largely his.

Indeed, the form of Bayes’ theorem as it usually appears in textbooks, namely

is due to Laplace. In Equation (6), A₁, A₂, …, A_n is a sequence of mutually exclusive and exhaustive events, Pr{A_j} is the prior probability of A_j, and Pr{A_j|B} is the posterior probability of A_j given B. The continuous version of Equation (6) can be written as

where f(i) is the prior density of i, f(x|i) is the likelihood of the data x, and f(i|x) is the posterior density of i.

Before commenting on a specific example of Laplace’s work on inverse probability, let us recall that it is with him that the classical definition of probability is usually associated, for he was the first to have given it in its clearest terms. Indeed, Laplace’s classical definition of probability is the one that is still used today. In his very first paper on probability, Mémoire sur les suites récurro-recurrentes et sur leurs usages dans la théorie des hasards (Laplace 1774b), Laplace writes,

… if each case is equally probable, the probability of the event is equal to the number of favorable cases divided by the number of all possible cases.

This definition was repeated both in Laplace’s Théorie Analytique and Essai Philosophique (1814).

The rule in Equation (6) was first enunciated by Laplace in his 1774 Mémoire de la Probabilité des Causes par les Evènements (Laplace 1774a). This is how Laplace phrases it:

If an event can be produced by a number n of different causes, the probabilities of the existence of these causes, calculated from the event, are to each other as the probabilities of the event, calculated from the causes; and the probability of each cause is equal to the probability of the event, calculated from that cause, divided by the sum of all the probabilities of the event, calculated from each of the causes.

It is very likely that Laplace was unaware of Bayes’ previous work on inverse probability (Bayes 1764) when he enunciated the rule in 1774. However, the 1778 volume of the Histoire de l’Académie Royale des Sciences, which appeared in 1781, contains an interesting summary by the Marquis de Condorcet¹⁹ (1743–1794) of Laplace’s article Sur les Probabilités, which also appeared in that volume (Laplace 1781). Although Laplace’s article itself makes mention of neither Bayes nor Price,²⁰ Condorcet’s summary explicitly acknowledges the two Englishmen²¹ (Laplace 1781, p. 43):

These questions [on inverse probability] about which it seems that Messrs. Bernoulli and Moivre had thought, have been since then examined by Messrs. Bayes and Price; but they have limited themselves to exposing the principles that can be used to solve them. M. de Laplace has expanded on them …

Coming back to the 1774 paper, after having enunciated his principle on inverse probability, Laplace is famous for discussing the following problem: “A box contains a large number of black and white balls. We sample n balls with replacement, of which b turn out to be black and n − b turn out to be white. What is the conditional probability that the next ball drawn will be black?” Laplace’s solution to this problem essentially boils down to the following, in modern notation. Let X_n be the number of black balls out of the sample of size n, and let the probability that a ball is black be p. Also, let B* be the event that the next ball is black. From Bayes’ theorem, we have

Then the required probability is

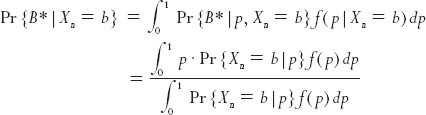
In the above, it is assumed that Pr{B* | p, X_n = b} = p, that is, each ball is drawn independently of the other. Laplace also assumes that p is uniform in [0,1], so that

In particular, if all of the n balls turn out to be black, then the probability that the next ball is also black is (n + 1)/(n + 2). The above problem has been much discussed in the literature and is known as Laplace’s rule of succession.²² Using the rule of succession, Laplace considered the following question: “Given that the sun has risen every day for the past 5,000 years, what is the probability that it will rise tomorrow?” Substituting n = 5,000 × 365.2426 = 1,826,213 in the above formula, Laplace obtained the probability 1,826,214/1,826,215 (0.9999994). Thus, in his Essai Philosophique sur les Probabilités²³ (1814) English edition, p. 19, Laplace says,

Thus we find that an event having occurred successively any number of times, the probability that it will happen again the next time is equal to this number increased by unity divided by the same number, increased by two units. Placing the most ancient epoch of history at five thousand years ago, or at 1,826,213 days, and the sun having risen constantly in the interval at each revolution of 24 hours, it is a bet of 1,826,214 to one that it will rise again tomorrow.

Laplace’s calculation was meant to be an answer to Hume’s problem of induction. Fifteen years before the publication of Bayes’ Essay, the eminent Scottish philosopher David Hume (1711–1776) wrote his groundbreaking book An Enquiry Concerning Human Understanding (Hume 1748). In this work, Hume formulated his famous problem of induction, which we now explain. Suppose out of a large number n of occurrences of an event A, an event B occurs m times. Based on these observations, an inductive inference would lead us to believe that approximately m/n of all events of type A is also of type B, that is, the probability of B given A is approximately m/n. Hume’s problem of induction states that such an inference has no rational justification but arises only as a consequence of custom and habit. Earlier in his book, Hume gave the famous “rise-of-the sun” example, which was meant to illustrate the shaky ground on which “matters of fact” or inductive reasoning rested (Hume 1748):

Matters of fact, which are the second objects of human reason, are not ascertained in the same manner; nor is our evidence of their truth, however great, of a like nature with the foregoing. The contrary of every matter of fact is still possible; because it can never imply a contradiction, and is conceived by the mind with the same facility and distinctness, as if ever so conformable to reality. That the sun will not rise to-morrow is no less intelligible a proposition, and implies no more contradiction, than the affirmation, that it will rise. We should in vain, therefore, attempt to demonstrate its falsehood. Were it demonstratively false, it would imply a contradiction, and could never be distinctly conceived by the mind.

Laplace thus thought that his calculations provided a possible solution to Hume’s problem of induction. However, Laplace, who so often has been called France’s Newton, was harshly criticized for his calculations. Zabell says (2005, p. 47),

Laplace has perhaps received more ridicule for this statement than for any other.

Somehow, Laplace must have felt that there was something amiss with his calculations. For his very next sentence reads,

But this number is incomparably greater for him who, recognizing in the totality of phenomena the principal regulator of days and seasons, sees that nothing at the present moment can arrest the course of it.

Laplace here seems to warn the reader that his method is correct when based only on the information from the sample, but his statement is too timid. To understand the criticism leveled against Laplace’s calculation, consider the following example given by the Austro-British philosopher Karl Popper (1902–1994) (Popper 1957; Gillies 2000, p. 73): Suppose that the sun rises for 1,826,213 days (5,000 years), but then suddenly the Earth stops rotating on day 1,826,214. Then, for parts of the globe (say Part A), the sun does not rise on that day, whereas for other parts (say Part B), the sun will appear fixed in the sky. What then is the probability that the sun will rise again in Part A of the globe? Applying the generalized form of the rule of succession with n = 1,826,214 and B = 1,826,213 gives a probability of 0.9999989, which is almost as high as the original probability of 0.9999994! The answer is preposterous since it does not give enough weight to the recent failure.

The rule of succession is perfectly valid as long as the assumptions it makes are all tenable. Applying the rule of succession to the rising of the sun, however, should be viewed with skepticism for several reasons (see, e.g., Schay 2007, p. 65). A major criticism lies in the assumption of independence. Moreover, it is also dubious that the rising of the sun on a given day can be considered a random event at all. Finally, the solution relies on the principle of indifference: The probability of the sun rising is equally likely to take any of the values in [0,1] because there is no reason to favor any particular value for the probability. To many, this is not a reasonable assumption.

5. Conclusion

We have outlined some of the more well-known errors that were made during the early development of the theory of probability. The solution to the problems we considered would seem quite elementary nowadays. It must be borne in mind, however, that in the times of those considered here and even afterwards, notions about probability, sample spaces, and sample points were quite abstruse. It took a while before the proper notion of a mathematical model was developed, and a proper axiomatic model of probability was developed only as late as 1933 by Kolmogorov (1933). Perhaps, then, the personalities and their errors discussed in this article should not be judged too harshly.

Notes

1. The Book on Games of Chance. An English translation of the book and a thorough analysis of Cardano’s connections with games of chance can be found in Ore’s Cardano: The Gambling Scholar (Ore 1953). More bibliographic details can be found in Gliozzi (1980, pp. 64–67) and Scardovi (2004, pp. 754–758).

2. The correct answer is four and can be obtained by solving for the smallest N integer such that 1 − (5/6)ⁿ = 1/2.

3. Cardano frequently uses the term “equality” in the Liber to denote half of the total number of sample points in the sample space. See Ore (1953, p. 149).

4. Real name Antoine Gombaud. Leibniz describes the Chevalier de Méré as “a man of penetrating mind who was both a player and a philosopher” (Leibniz 1896, p. 539). Pascal biographer Tulloch also notes (1878, p. 66): “Among the men whom Pascal evidently met at the hotel of the Duc de Roannez [Pascal’s younger friend], and with whom he formed something of a friendship, was the well-known Chevalier de Méré, whom we know best as a tutor of Madame de Maintenon, and whose graceful but flippant letters still survive as a picture of the time. He was a gambler and libertine, yet with some tincture of science and professed interest in its progress.” Pascal himself was less flattering. In a letter to Fermat, Pascal says (Smith 1929, p. 552): “… he [de Méré] has ability but he is not a geometer (which is, as you know, a great defect) and he does not even comprehend that a mathematical line is infinitely divisible and he is firmly convinced that it is composed of a finite number of points. I have never been able to get him out of it. If you could do so, it would make him perfect.” The book by Chamaillard (1921) is completely devoted to the Chevalier de Méré.

5. Ore (1960) believes that the difference in the probabilities for 24 and 25 throws is so small that it is unlikely that de Méré could have detected this difference through observations.

6. Of the several books that have been written on Pascal, the biographies by Groothuis (2003) and Hammond (2003) are good introductions to his life and works.

7. Carcavi had been an old friend of Pascal’s father and was very close to Pascal.

8. Fermat is today mostly remembered for the so-called “Fermat’s Last Theorem,” which he conjectured in 1637 and which was not proved until 1995 by Andrew Wiles (1995). The theorem states that no three positive integers a, b, c can satisfy the equation aⁿ + bⁿ = cⁿ for any integer n greater than 2. A good introduction to Fermat’s Last Theorem can be found in Aczel (1996). The book by Mahoney (1994) is an excellent biography of Fermat, whose probability work appears on pp. 402–410 of the book.

9. For example, if we apply de Moivre’s Gambling Rule to the one-die problem, we obtain x = 0.693/(1/6) = 4.158 so that C = 5. This answer cannot be correct because we showed in the solution that we need only four tosses.

10. The Problem of Points is also discussed by Todhunter (1865, Chap. II), Hald (2003, pp. 56–63), Petkovic (2009, pp. 212–214), Paolella (2006, pp. 97– 99), Montucla (1802, pp. 383–390), Marques de Sá (2007, pp. 61–62), Kaplan and Kaplan (2006, pp. 25–30), and Isaac (1995, p. 55).

11. For a full discussion of the Problem of Points before Pascal, see Coumet (1965).

12. Everything about Arithmetic, Geometry, and Proportion.

13. The correct division ratio for A and B here is approximately 53:47.

14. The general formula is: Maximum number of remaining rounds = (sum of the number of rounds each player is short of winning) − (number of players − 1).

15. Heads or Tails.

16. The correct answer is, of course, 1/2.

17. According to d’Alembert, an event is metaphysically possible if its probability is greater than zero and is physically possible if it is not so rare that its probability is very close to zero.

18. Remember that the specific sequence H H H T is one of four possible ways of obtaining a total of three heads and one tail.

19. Condorcet was assistant secretary in the Académie des Sciences and was in charge of editing Laplace’s papers for the transactions of the academy.

20. Upon Bayes’ death, his friend Richard Price (1723–1791) decided to publish some of his papers with the Royal Society. Bayes’ Essay (1764) was augmented by an introduction and an appendix written by Price.

21. Laplace’s acknowledgment of Bayes appears in his Essai Philosophique (Laplace 1814) English edition, p. 189.

22. Laplace’s rule of succession is also discussed by Pitman (1993, p. 421), Sarkar and Pfeifer (2006, p. 47), Pearson (1900, pp. 140–150), Zabell (2005,Chap. 2), Jackman (2009, p. 57), Keynes (1921, p. 376), Chatterjee (2003, pp. 216–218), Good (1983, p. 67), Gelman et al. (2003, p. 36), Blom et al. (1994, p. 58), Isaac (1995, p. 36), and Chung and AitSahlia (2003, p. 129).

23. Philosophical Essay on Probabilities.

References

Aczel, A. D. (1996), Fermat’s Last Theorem: Unlocking the Secret of an Ancient Mathematical Problem, Delta Trade Paperbacks.

Bayes, T. (1764), “An Essay Towards Solving a Problem in the Doctrine of Chances,” Philosophical Transactions of the Royal Society of London, 53, 370–418. Reprinted in Studies in the History of Statistics and Probability, Vol. 1, eds. E. S. Pearson and M. G. Kendall, London: Charles Griffin, 1970, pp. 134–153.

Bernoulli, J. (1713), Ars Conjectandi, Basel.

Bertrand, J. (1889), Calcul des Probabilités, Gauthier-Villars et fils, Paris.

Blom, G., Holst, L., and Sandell, D. (1994), Problems and Snapshots from the World of Probability, Berlin: Springer-Verlag.

Burton, D. M. (2006), The History of Mathematics: An Introduction (6th ed.), New York: McGraw-Hill.

Cardano, G. (1539), Practica Arithmetice, & Mensurandi Singularis. In qua que preter alias cõtinentur, versa pagina demonstrabit, Io. Antonins Castellioneus medidani imprimebat, impensis Bernardini calusci., Milan (Appears as Practica Arithmeticae Generalis Omnium Copiosissima & Utilissima, in the 1663 ed.).

——— (1564), Liber de Ludo Aleae, first printed in Opera Omnia, Vol. 1, 1663 Edition (pp. 262–276).

——— (1935), Ma Vie, Paris (translated by Jean Dayre).

Chamaillard, E. (1921), Le Chevalier de Méré, G. Clouzot, Niort.

Chatterjee, S. K. (2003), Statistical Thought: A Perspective and History, Oxford: Oxford University Press.

Chung, K. L., and AitSahlia, F. (2003), Elementary Probability Theory (4th ed.), Berlin: Springer-Verlag.

Coumet, E. (1965), “Le Problème des Partis avant Pascal,” Archives Internationales d’Histoire des Sciences, 18, 245–272.

d’Alembert, J. L. R. (1754), “Croix ou Pile,” in Encyclopédie ou Dictionnaire Raisonné des Sciences, des Arts et des Métiers (Vol. 4), eds. D. Diderot and J. L. R. d’Alembert, Stuttgart.

——— (1761), Opuscules Mathématiques (Vol. 2), Paris: David.

de Moivre, A. (1718), The Doctrine of Chances, or a Method of Calculating the Probability of Events in Play (1st Ed.), London: Millar.

Devlin, K. (2008), The Unfinished Game: Pascal, Fermat, and the Seventeenth-Century Letter That Made the World Modern, New York: Basic Books.

Edwards, A. W. F. (1982), “Pascal and the Problem of Points,” International Statistical Review, 50, 259–266.

Gelman, A., Carlin, J. B., Stern, H. S., and Rubin, D. (2003), Bayesian Data Analysis (2nd Ed.), Boca Raton, Fl.: Chapman & Hall/CRC.

Gillies, D. A. (2000), Philosophical Theories of Probability, London: Routledge.

Gliozzi, M. (1980), “Cardano, Girolamo,” in Dictionary of Scientific Biography (Vol. 3), ed. C. C. Gillispie, New York: Charles Scribner’s Sons.

Good, I. J. (1983), Good Thinking: The Foundations of Probability and Its Applications, Minneapolis: University of Minnesota Press.

Groothuis, D. (2003), On Pascal, Belmont, Calif.: Thomson Wadsworth.

Hald, A. (2003), A History of Probability and Statistics and Their Applications Before 1750, New York: Wiley.

Hammond, N. (ed.) (2003), The Cambridge Companion to Pascal, Cambridge: Cambridge University Press.

Hogben, L. (1957), Statistical Theory: The Relationship of Probability, Credibility and Error, New York: W.W. Norton & Co.

Hume, D. (1748), An Enquiry Concerning Human Understanding, ed. P. Millican. London (2007 edition edited by P. Millican, Oxford University Press, Oxford).

Isaac, R. (1995), The Pleasures of Probability, New York: Springer-Verlag.

Jackman, S. (2009), Bayesian Modelling in the Social Sciences, New York: Wiley.

Kaplan, M., and Kaplan, E. (2006), Chances Are: Adventures in Probability, Baltimore: Penguin Books.

Keynes, J. M. (1921), A Treatise on Probability, London: Macmillan & Co.

Kolmogorov, A. (1933), Grundbegriffe der Wahrscheinlichkeitsrechnung, Berlin: Springer.

Laplace, P.-S. (1774a), “Mémoire de la Probabilité des Causes par les Evènements,” Memoire de l’Académie Royale des Sciences de Paris (savants étrangers), Tome VI: 621–656.

——— (1774b), “Mémoire sur les Suites Récurro-récurrentes et sur leurs usages dans la théorie des hasards,” Mémoire de l’Académie Royale des Sciences de Paris (savants étrangers) Tome VI: 353–371.

——— (1781), “Sur les probabilités,” Histoire de l’Académie Royale des Sciences, année 1778, Tome VI: 227–323.

——— (1814), Essai Philosophique sur les Probabilités, Paris: Courcier: Paris (6th ed. 1840, translated 1902 as A Philosophical Essay on Probabilities, translated by F. W. Truscott & F. L. Emory. Reprinted, Dover, New York, 1951).

Leibniz, G. W. (1768), Opera Omnia, Geneva.

——— (1896), New Essays Concerning Human Understanding, New York: Macmillan (original work written in 1704 and published in 1765).

——— (1969), Théodicée, Paris: Garnier-Flammarion (original work published in 1710).

Mahoney, M. S. (1994), The Mathematical Career of Pierre de Fermat, 1601–1665 (2nd Ed.), Princeton, N.J.: Princeton University Press.

Marques de Sá, J. P. (2007), Chance: The Life of Games & the Game of Life, Berlin: Springer-Verlag.

Montucla, J. F. (1802), Histoire des Mathématiques (Tome III), Paris: Henri Agasse.

Ore, O. (1953), Cardano: The Gambling Scholar, Princeton, N.J.: Princeton University Press.

——— (1960), “Pascal and the Invention of Probability Theory,” American Mathematical Monthly, 67, 409–419.

Pacioli, L. (1494), Summa de Arithmetica, Geometrica, Proportioni, et Proportionalita, Venice.

Paolella, M. S. (2006), Fundamental Probability: A Computational Approach, New York: Wiley.

Pearson, E. S. (ed.) (1978), The History of Statistics in the 17th and 18th Centuries, Against the Changing Background of Intellectual, Scientific and Religious Thought. Lectures by Karl Pearson Given at University College London During Academic Sessions 1921–1933, London: Griffin.

Pearson, K. (1900), The Grammar of Science, (2nd Ed.), London: Adam and Charles Black.

Petkovic, M. S. (2009), Famous Puzzles of Great Mathematicians, American Mathematical Society. Pitman, J. (1993), Probability, New York: Springer.

Popper, K. R. (1957), “Probability Magic or Knowledge out of Ignorance,” Dialectica, 11, 354–374.

Sarkar, S., and Pfeifer, J. (2006), The Philosophy of Science: An Encyclopedia, London: Routledge.

Scardovi, I. (2004), “Cardano, Gerolamo,” in Encyclopedia of Statistical Sciences (2nd ed.), eds. S. Kotz, C. B. Read, N. Balakrishnan, and B. Vidakovic, New York: Wiley.

Schay, G. (2007), Introduction to Probability with Statistical Applications, Boston: Birkhauser.

Schneider, I. (2005), “Jakob Bernoulli, Ars Conjectandi (1713),” in Landmark Writings in Western Mathematics 1640–1940, ed. I. Grattan-Guinness, Amsterdam: Elsevier.

Smith, D. E. (1929), A Source Book in Mathematics, New York: McGraw-Hill.

Todhunter, I. (1865), A History of the Mathematical Theory of Probability From the Time of Pascal to That of Laplace, London: Macmillan (Reprinted by Chelsea, New York, 1949, 1965).

Tulloch, P. (1878), Pascal, London: William Blackwood and Sons.

Weaver, W. (1982), Lady Luck: The Theory of Probability, New York: Dover (originally published by Anchor Books, Doubleday & Company, Inc., Garden City, N.Y., 1963).

Wiles, A. (1995), “Modular Elliptic Curves and Fermat’s Last Theorem,” The Annals of Mathematics, 141, 443–551.

Williams, L. (2005), “Cardano and the Gambler’s Habitus,” Studies in History and Philosophy of Science, 36, 23–41.

Zabell, S. L. (2005), Symmetry and its Discontents, Cambridge: Cambridge University Press.