Chapter 15
Keeping in Step: Coordinate Geometry
IN THIS CHAPTER
![]() Taking off on the coordinate plane
Taking off on the coordinate plane
![]() Using formulas to find slope, graph lines, and determine midpoints and distances
Using formulas to find slope, graph lines, and determine midpoints and distances
![]() Evaluating functions
Evaluating functions
Coordinate geometry involves working with points on a graph that’s officially known as the Cartesian coordinate plane. This perfectly flat surface has a system that allows you to identify the position of points by using pairs of numbers. In this chapter, you figure out how equations and numbers relate to geometric forms and shapes, such as a straight line or a parabola, and review the formulas you need to know to fly high on questions about the coordinate plane.
Taking Flight: The Coordinate Plane
The coordinate plane doesn’t have wings, but it does have points that spread out infinitely. You may not have encountered the coordinate plane in a while (it isn’t something most people deal with in everyday life), so take just a minute to refresh your memory about a few relevant terms that may pop up on the GMAT. Although you won’t be asked to define the terms in the following sections, knowing what they mean is absolutely essential to answering GMAT math questions.
Line dancing: Understanding coordinate geometry
Before you get too engrossed in the study of coordinate geometry, ground yourself with an understanding of these essential terms:
- Coordinate plane: The coordinate plane is a perfectly flat surface where points can be identified by their positions, using ordered pairs of numbers. These pairs of numbers represent the points’ distances from an origin on perpendicular axes. The coordinate of any particular point is the set of numbers that identifies the location of the point, such as (3, 4) or (x, y).
- x-axis: The x-axis is the horizontal axis (number line) on a coordinate plane. The values start at the origin, which has a value of 0. Numbers increase in value to the right of the origin and decrease in value to the left. The x value of a point’s coordinate is listed first in its ordered pair.
- y-axis: The y-axis is the vertical axis (number line) on a coordinate plane. Its values start at the origin, which has a value of 0. Numbers increase in value going up from the origin and decrease in value going down. The y value of a point’s coordinate is listed second in its ordered pair.
- Origin: The origin is the point (0, 0) on the coordinate plane. It’s where the x- and y-axes intersect.
- Ordered pair: Also known as a coordinate pair, this duo is the set of two values that expresses the distance a point lies from the origin. The horizontal (x) coordinate is always listed first, and the vertical (y) coordinate is listed second.
- x-intercept: The value of x where a line, curve, or some other function crosses the x-axis. The value of y is 0 at the x-intercept. The x-intercept is often the solution or root of an equation.
- y-intercept: The value of y where a line, curve, or some other function crosses the y-axis. The value of x is 0 at the y-intercept.
- Slope: Slope measures how steep a line is and is commonly referred to as the rise over the run.
What’s the point? Finding the coordinates
You can identify any point on the coordinate plane by its coordinates, which designate the point’s location along the x- and y-axes. For example, the ordered pair (2, 3) has a coordinate point located two units to the right of the origin along the horizontal (x) number line and three units up on the vertical (y) number line. In Figure 15-1, point A is at (2, 3). The x-coordinate appears first, and the y-coordinate shows up second. Pretty simple so far, huh?

© John Wiley & Sons, Inc.
FIGURE 15-1: Points on the coordinate plane.
On all fours: Identifying quadrants
The intersection of the x- and y-axes forms four quadrants on the coordinate plane, which just so happen to be named Quadrants I, II, III, and IV (see Figure 15-1). Here’s what you can assume about points based on the quadrants they’re in:
- All points in Quadrant I have a positive x value and a positive y value.
- All points in Quadrant II have a negative x value and a positive y value.
- All points in Quadrant III have a negative x value and a negative y value.
- All points in Quadrant IV have a positive x value and a negative y value.
- All points along the x-axis have a y value of 0.
- All points along the y-axis have an x value of 0.
Quadrant I starts to the right of the y-axis and above the x-axis. It’s the upper-right portion of the coordinate plane. As shown in Figure 15-1, the other quadrants move counterclockwise around the origin. Figure 15-1 also shows the location of coordinate points A, B, C, and D:
- Point A is in Quadrant I and has coordinates (2, 3).
- Point B is in Quadrant II and has coordinates (–1, 4).
- Point C is in Quadrant III and has coordinates (–5, –2).
- Point D is in Quadrant IV and has coordinates (7, –6).
The GMAT won’t ask you to pick your favorite quadrant, but you may be asked to identify which quadrant a particular point belongs in.
Slip-Sliding Away: Slope and Linear Equations
One of the handiest things about the coordinate plane is that it graphs the locations of lines and linear equations. In fact, questions that expect you to know how to graph lines and equations are some of the most common GMAT coordinate geometry questions. You should know the formulas for finding the slope and the slope-intercept equation and for determining the midpoint and the distance between two points on the plane. Lucky for you, we discuss all those formulas in the following sections.
Taking a peak: Defining the slope of a line
If a line isn’t parallel to one of the coordinate axes, it either rises or falls from the left-hand side of the coordinate plane to the right-hand side. The measure of the steepness of the line’s rising or falling is its slope. In the following sections, we explain how to find the slope of a line and explore the different types of slopes on a coordinate plane.
The formula for slope
You can think of the slope as the value of the rise over the value of the run. In more mathematical terms, the slope formula looks like this:
The x and y values in the equation stand for the coordinates of two points on the line. The formula is just the ratio of the vertical distance between two points and the horizontal distance between those same two points. You subtract the y-coordinate of one point from the y-coordinate of the other point to get the numerator. Then you subtract the x-coordinate of one point from the x-coordinate of the other point to get the denominator.
The graph in Figure 15-2 shows how important it is to perform these operations in the right order.

© John Wiley & Sons, Inc.
FIGURE 15-2: Finding slope.
Figure 15-2 shows coordinate point (0, 2) as ![]() , and the coordinate point (4, 0) as
, and the coordinate point (4, 0) as ![]() . You may be tempted to subtract the 0 in each coordinate point from the corresponding greater number in the other coordinate point, but doing that switches the order of how you subtract the x and y values in the two coordinate points.
. You may be tempted to subtract the 0 in each coordinate point from the corresponding greater number in the other coordinate point, but doing that switches the order of how you subtract the x and y values in the two coordinate points.
For the slope formula to work, you calculate 0 – 2 for your ![]() operation (which gives you –2), and then you take 4 – 0 for your
operation (which gives you –2), and then you take 4 – 0 for your ![]() (which gives you 4). The resulting ratio, or fraction, is
(which gives you 4). The resulting ratio, or fraction, is ![]() , or
, or ![]() . This gives you a slope of
. This gives you a slope of ![]() .
.
Types of slope
The line in Figure 15-2 falls from left to right. This nice ski-slope image is your visual clue that the line has a negative slope. Figure 15-3 shows how you can quickly eyeball a line to get a good idea of what kind of slope a line has.

© John Wiley & Sons, Inc.
FIGURE 15-3: Types of slope.
In Figure 15-3, line m has a negative slope; line n has a positive slope; a line on the horizontal x-axis has a slope of 0; and a line on the vertical y-axis has an undefined slope.
 A line with a negative slope falls from left to right (its left side is higher than its right), and its slope is less than 0.
A line with a negative slope falls from left to right (its left side is higher than its right), and its slope is less than 0.- A line with a positive slope rises from left to right (its right side is higher than its left), and its slope is greater than 0.
- A horizontal line has a slope of 0; it neither rises nor falls and is parallel to the x-axis.
- The slope of a vertical line is undefined because you don’t know whether it’s rising or falling; it has no slope and is parallel to the y-axis.
Using the slope-intercept form to graph lines
The characteristics of a line can be conveyed through a mathematical formula. The equation of a line (also known as the slope-intercept form) generally shows y as a function of x, like this:
In the slope-intercept form, the coefficient m is a constant that indicates the slope of the line, and the constant b is the y-intercept (that is, the point where the line crosses the y-axis). The equation of the line in Figure 15-2 is ![]() , because the slope is
, because the slope is ![]() and the y-intercept is 2. The equation
and the y-intercept is 2. The equation ![]() indicates a horizontal line that intersects the y-axis at point (0, 2). The equation
indicates a horizontal line that intersects the y-axis at point (0, 2). The equation ![]() indicates a vertical line that intersects the x-axis at point (3, 0). A line with the formula
indicates a vertical line that intersects the x-axis at point (3, 0). A line with the formula ![]() has a slope of 4 (which is a rise of 4 and run of 1) and a y-intercept of 1. The line is graphed in Figure 15-4.
has a slope of 4 (which is a rise of 4 and run of 1) and a y-intercept of 1. The line is graphed in Figure 15-4.

© John Wiley & Sons, Inc.
FIGURE 15-4: The graph of y = 4x + 1.
The GMAT may give you an equation of a line and ask you to choose the graph that correctly grids it. You can figure out how the line should look when it’s graphed by starting with the value of the y-intercept, marking points that fit the value of the slope, and then connecting these points with a line.

The new equation gives you the slope of the line, 3, as well as the y-intercept, 9. Pretty handy! Here’s a sample question to give you a taste of how the slope-intercept form may be tested on the GMAT.
(A) ![]()
(B) ![]()
(C) ![]()
(D) ![]()
(E) ![]()
 In the slope-intercept form,
In the slope-intercept form, ![]() , m is the slope, and b is the y-intercept. Plug the values the problem gives you into the equation:
, m is the slope, and b is the y-intercept. Plug the values the problem gives you into the equation:
This isn’t an answer choice, but all options have the same format of ![]() . So you need to convert your equation to that format. Move the terms around by multiplying all terms on both sides by 4 and adding 3x to both sides, like this:
. So you need to convert your equation to that format. Move the terms around by multiplying all terms on both sides by 4 and adding 3x to both sides, like this:

Choice (E) is the correct answer.
Graphing a linear inequality is almost exactly the same as graphing the equation of a line, except a linear inequality covers a lot more ground on the coordinate plane. While the graph of an equation for a line simply shows the actual line on the coordinate plane, the graph of a linear inequality shows everything either above or below the line on the plane. The graph appears as a shaded area to one side of the line. Figure 15-5 shows the graphs of several inequalities.

© John Wiley & Sons, Inc.
FIGURE 15-5: Graphing lines and inequalities.
Meeting in the middle
If the GMAT asks you for the midpoint coordinates of a line segment on the coordinate plane, you simply apply the midpoint formula:
M stands for midpoint and the x and y variables are the x and y coordinates of the line’s two endpoints. So, to figure out the midpoint of a line segment that ends at points A (2, 3) and B (–1, 4), use the formula:

Going the distance
Some of the questions on the GMAT may ask you to calculate the distance between two points on a line. You can solve these problems with coordinate geometry.
To answer these questions, use the distance formula. Assume you have two points, A ![]() and B
and B ![]() , on a line. The formula to find the distance between A and B is this:
, on a line. The formula to find the distance between A and B is this:
Look at the graph in Figure 15-6 to see how the distance formula actually works.

© John Wiley & Sons, Inc.
FIGURE 15-6: Finding the distance between two points.
Notice that Point A has coordinates (2, 1) and Point B has coordinates (6, 4). To find the distance between these two points, you plug these numbers into the distance formula:

If you’re thinking this formula looks familiar, you’re absolutely right. It’s another use for the good old Pythagorean theorem: ![]() . (If this theorem is only vaguely familiar to you, check out Chapter 14.) Connecting points A and B to a third point, C, as shown in Figure 15-5, gives you a right triangle, which in this case happens to be your tried-and-true 3:4:5 right triangle.
. (If this theorem is only vaguely familiar to you, check out Chapter 14.) Connecting points A and B to a third point, C, as shown in Figure 15-5, gives you a right triangle, which in this case happens to be your tried-and-true 3:4:5 right triangle.
Here’s a sample problem that asks you to find the distance between two points.
(A) ![]()
(B) ![]()
(C) 5
(D) 8.94
(E) 13.42
Use the distance formula to figure out the distance between the coordinates of the origin (0, 0) and the endpoint (–2, –3):

Choice (B) is the answer. If you chose Choice (C), you simply took the coordinates for the endpoint, (–2, –3), and added them together to get distance, which, of course, isn’t the proper method. Choice (A) results from failing to square the differences of the coordinates. You can guess that Choices (D) and (E) are probably incorrect because uncovering their values requires using a calculator, which you won’t have available on the GMAT quantitative section.
Considering other shapes on the coordinate plane
Occasionally, the GMAT may ask you coordinate geometry questions that deal with shapes other than straight lines.
- Circles: The equation of a circle is
 , where the center of the circle is point (h, k) and r is the circle’s radius. If the origin is the center of the circle, the equation would be
, where the center of the circle is point (h, k) and r is the circle’s radius. If the origin is the center of the circle, the equation would be  .
. Parabolas: When you graph a quadratic equation, it appears as a parabola, a curve shape that opens either upward or downward. Two important properties of parabolas are
- The axis of symmetry: This is the vertical line that bisects the parabola so that each side is a mirror image of the other.
- The vertex: This is the rounded end of the parabola, which is the lowest point on a curve that opens upward and the highest point on a curve that opens downward. It’s where the parabola crosses the axis of symmetry.
The equation for a parabola is
 , where the coordinate point (h, k) is the vertex. The vertical line x = h is the axis of symmetry. If a is a positive number, the parabola opens upward. If a is negative, it opens downward. Figure 15-7 shows the graph of
, where the coordinate point (h, k) is the vertex. The vertical line x = h is the axis of symmetry. If a is a positive number, the parabola opens upward. If a is negative, it opens downward. Figure 15-7 shows the graph of  . The values for h and k are 0, so the vertex is at the origin. The parabola opens upward because a is 1, a positive number.
. The values for h and k are 0, so the vertex is at the origin. The parabola opens upward because a is 1, a positive number.

© John Wiley & Sons, Inc.
FIGURE 15-7: A parabola with its vertex on the origin.
Here’s a sample question that requires to you apply the parabola formula.
(A) (–3, –4)
(B) (3, 4)
(C) (3, –4)
(D) (–3, 4)
(E) (–6, –4)
Remember the equation of a parabola: ![]() . The vertex of the parabola is (h, k). The h value in the equation is 3, and the k value is –4. So the vertex of the graph of the equation in the question is (3, –4). The correct answer is Choice (C).
. The vertex of the parabola is (h, k). The h value in the equation is 3, and the k value is –4. So the vertex of the graph of the equation in the question is (3, –4). The correct answer is Choice (C).
 Choice (D) is a trap answer. Note that the value of h is 3 and not –3. The only way that the value of h could be –3 is if the original equation were
Choice (D) is a trap answer. Note that the value of h is 3 and not –3. The only way that the value of h could be –3 is if the original equation were ![]() . Then you’d have to switch the sign to put the equation into the correct form for the equation of a parabola.
. Then you’d have to switch the sign to put the equation into the correct form for the equation of a parabola.
Fully Functioning: Graphing Functions
Coordinate geometry and functions are connected. You can actually evaluate functions on the coordinate plane. By looking at a graph of a function, you can tell something about the function and its domain and range. The GMAT may give you a graph of a function and ask you to determine whether a statement about the function is true or false. In the following sections, we give you the info you need to know to get these questions right.
When you graph a function f(x) on the coordinate plane, the x value of the function (the input, or the domain, of the function) goes along the horizontal (x) axis, and the f(x) value of the function goes along the vertical (y) axis. Anytime you see a coordinate pair that represents a function, for example (x, y), the x value is the domain, or input, of the function and the y value is the output, or range, of the function. (For more info on functions, see Chapter 13.)
Passing the vertical line test
A function is a distinct relationship between the x (input) value and the y or f(x) (output) value. For every x value, there’s a distinct y value, and only one y value, that corresponds to the x value. The vertical line test is one way to look at a graph and tell whether it’s a graph of a function. This test states that no vertical line intersects the graph of a function at more than one point.
For example, the graphs in Figure 15-8 show two straight lines that pass the vertical line test and, therefore, represent functions.

© John Wiley & Sons, Inc.
FIGURE 15-8: Straight lines that pass the vertical line test.
The two lines in Figure 15-8 go on infinitely in both directions. Any vertical line you draw on the graph intersects the graphed line at only one point. For every x value along the line in each of these graphs, a separate and distinct y value corresponds to it. These lines pass the vertical line test, which means they represent functions.
Not all lines are straight. Sometimes you see graphs of curved lines. Take a look at the two graphs in Figure 15-9 and determine which of them graphs a function.

© John Wiley & Sons, Inc.
FIGURE 15-9: Graphs of curved lines (parabolas).
The curves in Figure 15-9 are parabolas, a shape we discuss in more detail in the upcoming section about graphing domain and range. The curve in the left graph opens downward, so it goes on infinitely downward and outward. For every x value on that curve, there’s a separate and distinct y value. This curve passes the vertical line test and, therefore, graphs a function. The curve in the right graph is almost like the first one, except that it opens sideways. One vertical line can cross the path of this curve in more than one place. Therefore, this curve isn’t the graph of a function.
Questions that ask you to recognize the graph of a function appear rarely on the GMAT, but if you see one, you’ll know what to do.

 This question is easy when you’re familiar with the vertical line test. Choice (E) has to be the correct answer because it’s a curve that sort of doubles back from right to left. A vertical line can intersect that curve at more than one point. The other graphs in this question show curves, lines, or some other shape that a vertical line wouldn’t pass through at more than one point. All the graphs except Choice (E) pass the test and are graphs of functions.
This question is easy when you’re familiar with the vertical line test. Choice (E) has to be the correct answer because it’s a curve that sort of doubles back from right to left. A vertical line can intersect that curve at more than one point. The other graphs in this question show curves, lines, or some other shape that a vertical line wouldn’t pass through at more than one point. All the graphs except Choice (E) pass the test and are graphs of functions.
Feeling at home with domain and range
The GMAT expects you to be able to look at a graph of a function and have a pretty good idea of what the domain and the range of that particular function are. Figures 15-10, 15-11, and 15-12 are examples of what some of these graphs may look like.
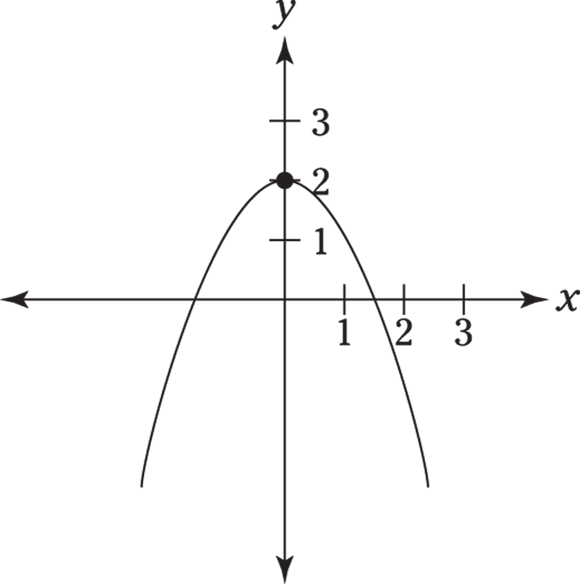
© John Wiley & Sons, Inc.
FIGURE 15-10: Domain and range demonstrated by a parabola.

© John Wiley & Sons, Inc.
FIGURE 15-11: Domain and range demonstrated by a sloping straight line.

© John Wiley & Sons, Inc.
FIGURE 15-12: Domain and range demonstrated by a horizontal line.
Figure 15-10 shows you a parabola. Its vertex is the coordinate point (0, 2). The graph extends outward infinitely from side to side, so this function contains all possible values of x, which means its domain is all real numbers. The graph also extends downward infinitely, but because the y value in this function is limited on the upward side and doesn’t extend above the point (0, 2), its range is ![]() .
.
In Figure 15-11, you see a straight line that goes on forever from left to right. This line also extends infinitely upward on the left side and infinitely downward on the right side. The domain and range of this linear function are also all real numbers. There’s no artificial limit to the x and y values in this graph.
In Figure 15-12, the horizontal line extends infinitely from right to left, but it has only one value on the y-axis. Its y value is limited to –3, so the equation for this line is y = –3, and the range is limited to simply ![]() . Because the line goes on forever from left to right, it includes every possible x value, which means the domain of this linear function is all real numbers.
. Because the line goes on forever from left to right, it includes every possible x value, which means the domain of this linear function is all real numbers.
That’s really all there is to it. See how easy determining domain can be with the following question.

(A) ![]()
(B) ![]()
(C) ![]()
(D) ![]()
(E) ![]()
 This question asks for the domain, not the range, so don’t let the fact that the upper limit of the y value is just shy of 3 distract you from looking for all the possible x values that make up the domain. You should toss out any answer choice that refers to the value 3, so get rid of Choices (B) and (D) right away.
This question asks for the domain, not the range, so don’t let the fact that the upper limit of the y value is just shy of 3 distract you from looking for all the possible x values that make up the domain. You should toss out any answer choice that refers to the value 3, so get rid of Choices (B) and (D) right away.
The empty circle point (0, 3) means that you don’t count that point in your answer. So Choice (C) is exactly the opposite of what you’re looking for. Also, Choice (C) limits your domain to only one value: 0. Because the value of 0 is actually excluded from the function, Choice (C) simply can’t be right. The way Choice (E) is formatted doesn’t make sense at all. Set your sights on Choice (A) as the answer of the hour. The domain, or x value, isn’t equal to 0.

 What is the equation of a line with a slope
What is the equation of a line with a slope