CHAPTER 8
Manual Adjoint Differentiation
In this first introductory chapter to AAD, we introduce adjoint differentiation (AD) through simple examples. We explain how AD may compute many derivative sensitivities in constant time and show how this can be achieved by coding AD by hand.
In the next chapter, we will generalize and formalize adjoint mathematics, and show how adjoint calculations can be executed automatically through autogenerated calculation graphs without the need to code any form of differentiation manually.
In Chapter 10, we will turn these ideas into a general-purpose AAD library in C++, and, in subsequent chapters, we will apply this AAD library to differentiate serial and parallel Monte-Carlo simulations in constant time.
8.1 INTRODUCTION TO ADJOINT DIFFERENTIATION
We start with a simple example where we differentiate a well-known analytic function with respect to all its inputs and introduce adjoint calculations as a means to compute all those derivatives from one another in constant time. From the example, we abstract and illustrate a general methodology for the manual computation of adjoints and the production of corresponding code.
Example: The Black and Scholes formula
The well known Black and Scholes formula, derived in 1973 in [22], gives the price of a call option in the absence of arbitrage, under the assumption that the volatility of the underlying asset is a known constant, as a function of a small number of observable variables and the constant volatility. Under this simple model, the value of the option may be expressed in closed-form, as demonstrated on page 165:
The function has 6 inputs:
- The current spot price

- The interest rate

- The dividend yield

- The volatility

- The strike
 and maturity
and maturity  of the option
of the option
and carries the following calculations:
- The discount factor

- The forward

- The standard deviation
 of the return to maturity
of the return to maturity - The log-moneyness

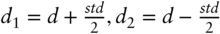
- The probabilities to end in the money under the spot measure
 and under the risk-neutral measure
and under the risk-neutral measure  where
where  is the cumulative normal distribution
is the cumulative normal distribution - Finally the call option price

Note ![]() has no analytic form but precise (if somewhat expensive) approximations exist, such as the function
has no analytic form but precise (if somewhat expensive) approximations exist, such as the function ![]() in the file gaussians.h in our repository.
in the file gaussians.h in our repository.
To implement Black and Scholes' formula in C++ code is trivial:

where the function was purposely written in a form that highlights and stores the intermediate calculations.
It follows that, despite its closed form, the evaluation of Black-Scholes is not especially cheap: it takes two evaluations of the normal distribution, two exponentials, a square root, and 10 multiplications and divisions.
In what follows, we call “operation” a piece of the calculation that produces an intermediate result out of previously available numbers and for which partial derivatives are known analytically. Our function has nine such operations, labeled accordingly in the code.
Differentiation
We now investigate different means of computing the six differentials of the formula to its inputs as efficiently as possible.
One solution is finite difference:

Besides the lack of accuracy, such differentiation through one-sided finite differences performs six additional evaluations of the function, once per input. The benefit of finite differences is that they are easily automated. The drawback is that the computation of differentials is expensive, linear in the number of desired sensitivities.
In our simple example, the differentials of Black and Scholes' formula are derived in closed form without difficulty, and are actually well known:

where ![]() is the normal density:
is the normal density: ![]() .
.
Perhaps surprisingly, the closed-form derivatives don't help performance: to compute the six sensitivities, we must still conduct six additional calculations, each of a complexity similar to the Black and Scholes formula.
But we note that all those derivatives share many common factors, so if we compute all the sensitivities together, we can calculate those common factors once and achieve a much better performance. In particular, the expensive ![]() and
and ![]() may be calculated once and reused six times. Besides, these quantities are known from the initial evaluation of the formula. We have other common factors, like
may be calculated once and reused six times. Besides, these quantities are known from the initial evaluation of the formula. We have other common factors, like ![]() , which is shared between theta and vega.1
, which is shared between theta and vega.1
It turns out that this is not a coincidence: the different sensitivities of a given calculation always share common factors as a consequence of the chain rule for derivatives:

from which it follows that, when a calculation with inputs ![]() and
and ![]() computes an intermediate result
computes an intermediate result ![]() and uses it to produce a final result
and uses it to produce a final result ![]() , we have:
, we have:

so the two sensitivities share the common factor ![]() . In Black and Scholes,
. In Black and Scholes, ![]() is a function of
is a function of ![]() and
and ![]() is a function of
is a function of ![]() and
and ![]() (and
(and ![]() and
and ![]() ).
). ![]() and
and ![]() don't contribute to the result besides affecting the forward, so it follows from the chain rule that:
don't contribute to the result besides affecting the forward, so it follows from the chain rule that:
The two sensitivities share the common factor ![]() , as seen in their analytic expression.2 We can produce them together cheaply by computing
, as seen in their analytic expression.2 We can produce them together cheaply by computing ![]() first, and then multiply it respectively by
first, and then multiply it respectively by ![]() and
and ![]() . We note that in the evaluation of the function,
. We note that in the evaluation of the function, ![]() is computed first out of
is computed first out of ![]() , and
, and ![]() is computed next as a function of
is computed next as a function of ![]() . We reversed that order to compute sensitivities: we computed the common factor
. We reversed that order to compute sensitivities: we computed the common factor ![]() first, then
first, then ![]() and
and ![]() as a function of the common factor.
as a function of the common factor.
In order to compute all the sensitivities with maximum performance, we must identify all the factors common to multiple derivatives and compute them once. In general, we don't know the derivatives analytically and we can't inspect their formula to identify the common factors by the eye. We must find a systematic way to identify all those common factors and compute them first. This is where adjoint differentiation comes into play. AD builds on the chain rule to find an order of computation for the derivatives that maximizes factoring and guarantees that all derivatives are computed in a time proportional to the number of operations, but independent of the number of inputs. We will see that this is achieved by systematically reversing the calculation order for the computation of differentials.
Adjoint differentiation
We identify the computation order for differentials that optimally reuses common factors with the help of two fundamental notions: the adjoints and the calculation graph. We illustrate these notions here and formalize them in the next chapter.
We call “adjoint of ![]() ” and denote
” and denote ![]() the derivative of the final result to
the derivative of the final result to ![]() . In Black and Scholes, for instance:
. In Black and Scholes, for instance:
To compute all the derivative sensitivities of a calculation means to calculate the adjoints of all its inputs. We will see that we can compute the adjoints of all the operations, including those of inputs, in constant time. It helps to draw a visual representation of all the operations involved and their dependencies. This is something we can easily infer from the code:

The figure shows the sequence of the nine operations involved in Black and Scholes, top to bottom. The arrows represent the dependencies between them. This is called a calculation graph. In the next chapter, we will learn to generate such graphs automatically from the code. For now, we note that every calculation defines a graph, which can be drawn by hand from an inspection of the code, without major difficulty. The graph offers a visual glimpse of the dependencies between the operations, which, in conjunction with the chain rule, provides the means to compute sensitivities in a way that reuses all the common factors at best.
Starting with ![]() , we have only one branch out of
, we have only one branch out of ![]() that connects to
that connects to ![]() ; hence, by an immediate application of the chain rule:
; hence, by an immediate application of the chain rule:
or, using adjoint notations:
Hence, we can compute ![]() after we know
after we know ![]() . We note once again that the adjoint relationship is reversed:
. We note once again that the adjoint relationship is reversed: ![]() is a function of
is a function of ![]() , but it is
, but it is ![]() that is a function of
that is a function of ![]() .
.
Two branches connect from ![]() , respectively to
, respectively to ![]() and
and ![]() , hence (again, from an immediate application of the chain rule):
, hence (again, from an immediate application of the chain rule):

That the adjoint of ![]() is 1 is evident from the definition: the adjoint of the final result is the sensitivity of the result to itself. The adjoint of the final result of any calculation is always 1. We can compute
is 1 is evident from the definition: the adjoint of the final result is the sensitivity of the result to itself. The adjoint of the final result of any calculation is always 1. We can compute ![]() as a function of
as a function of ![]() , once again, in the reverse order from the evaluation of the function where
, once again, in the reverse order from the evaluation of the function where ![]() is a function of
is a function of ![]() . Further, we see two branches out of
. Further, we see two branches out of ![]() connecting to
connecting to ![]() and
and ![]() , hence:
, hence:

Further, ![]() and
and ![]() depend on
depend on ![]() and
and ![]() ; hence,
; hence, ![]() and
and ![]() depend on
depend on ![]() and
and ![]() :
:

and ![]() and
and ![]() both depend on
both depend on ![]() :
:

With those equations, we compute ![]() and
and ![]() , then
, then ![]() and
and ![]() , then
, then ![]() , then
, then ![]() , and eventually
, and eventually ![]() , in the exact reverse order from the evaluation of the function. This is a general rule: adjoints are always computed from one another, in the reverse order from the calculation, starting with the adjoint of the final result, which is always 1:
, in the exact reverse order from the evaluation of the function. This is a general rule: adjoints are always computed from one another, in the reverse order from the calculation, starting with the adjoint of the final result, which is always 1:

as expected, since a simple calculation shows that ![]() .
.
Moving on to the adjoint of ![]() , we can compute it in the exact same manner. From the graph,
, we can compute it in the exact same manner. From the graph, ![]() affects
affects ![]() and
and ![]() , hence:
, hence:
since ![]() . So, we can also compute
. So, we can also compute ![]() as a function of
as a function of ![]() , which we already know from our decomposition of
, which we already know from our decomposition of ![]() , and the result follows. The details are left as an exercise.
, and the result follows. The details are left as an exercise.
Moving on to ![]() , the graph shows one connection to
, the graph shows one connection to ![]() , hence:
, hence:
where ![]() affects
affects ![]() ,
, ![]() , and
, and ![]() , hence:
, hence:

where we already know that ![]() , hence:
, hence:

and ![]() and
and ![]() are known from the previous computation of
are known from the previous computation of ![]() , so we can compute
, so we can compute ![]() with a few multiplications (which details are also left as an exercise).
with a few multiplications (which details are also left as an exercise).
The equations just above illustrate two general properties of adjoints:
 is the sum of the three terms corresponding to the three operations that directly depend on
is the sum of the three terms corresponding to the three operations that directly depend on  on the graph. More generally, an adjoint
on the graph. More generally, an adjoint  is always the sum, over all the subsequent operations that use
is always the sum, over all the subsequent operations that use  as an argument, of the adjoints of those operations, weighted by their partial derivatives to
as an argument, of the adjoints of those operations, weighted by their partial derivatives to  . We will formalize this in the next chapter; for now, we note that this is an immediate consequence of the chain rule.
. We will formalize this in the next chapter; for now, we note that this is an immediate consequence of the chain rule. , in addition to its dependency on
, in addition to its dependency on  and
and  , also depends on
, also depends on  . The partial derivatives that intervene in adjoint equations of the form:
generally depend on the values of the arguments. Therefore, the values of all the intermediate results, computed in the direct evaluation order, must be accessible when we compute the adjoints in the reverse order.
. The partial derivatives that intervene in adjoint equations of the form:
generally depend on the values of the arguments. Therefore, the values of all the intermediate results, computed in the direct evaluation order, must be accessible when we compute the adjoints in the reverse order.
We compute ![]() ,
, ![]() and
and ![]() in the same manner. We noted that
in the same manner. We noted that ![]() and
and ![]() are computed very quickly once the common factors
are computed very quickly once the common factors ![]() ,
, ![]() , and
, and ![]() are known, and the same applies to
are known, and the same applies to ![]() ,
, ![]() , and
, and ![]() . We already dealt with
. We already dealt with ![]() earlier and noted that:
earlier and noted that:
since the only contribution of ![]() to
to ![]() is through the forward; hence,
is through the forward; hence, ![]() is immediately deduced from
is immediately deduced from ![]() , which we already know from our computation of
, which we already know from our computation of ![]() . Similar reasoning applies to
. Similar reasoning applies to ![]() and
and ![]() , left as an exercise.
, left as an exercise.
Back-propagation
It follows from the rules we extracted from our example that:
- Adjoints are computed from one another in the reverse order of the calculation.
- The adjoint
 of an operation resulting in
of an operation resulting in  is the sum of the adjoints of the future operations that use
is the sum of the adjoints of the future operations that use  , weighted by the partial derivatives of the future operations to
, weighted by the partial derivatives of the future operations to  .
. - The adjoint of the final result is 1.
It follows that we can always calculate all adjoints with the following algorithm, called adjoint differentiation:
- Evaluate the calculation, that is, the sequence of all the operations of the form:
keeping track of all the intermediate
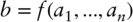
 s and
s and  s so that we can later compute the partial derivatives
s so that we can later compute the partial derivatives  .
. - Start with the adjoint of the final result
 and zero all the other adjoints. This is called seeding the back-propagation algorithm.
and zero all the other adjoints. This is called seeding the back-propagation algorithm. - For every operation in the evaluation, of the form:
conduct the

 adjoint operations:
(where the C style “+=” means “add the right-hand side to the value of the left-hand side”) in the reverse order from the evaluation, last operation first, first operation last. This is the back-propagation phase, where all adjoints are computed from one another. Note that the entire adjoint differentiation algorithm is often called “back-propagation,” especially in machine learning.
adjoint operations:
(where the C style “+=” means “add the right-hand side to the value of the left-hand side”) in the reverse order from the evaluation, last operation first, first operation last. This is the back-propagation phase, where all adjoints are computed from one another. Note that the entire adjoint differentiation algorithm is often called “back-propagation,” especially in machine learning.
That this algorithm correctly computes all the adjoints, hence, all the derivatives sensitivities, of any calculation, is a direct consequence of the chain rule. The adjoints are zeroed first and accumulated during the back-propagation phase. For this reason, this algorithm is sometimes also called “adjoint accumulation.”
The back-propagation algorithm has a number of important properties.
Analytic differentiation First, it is apparent that back-propagation produces analytic differentials, as long as the partial derivatives in the adjoint equations:

are themselves analytic.
An important comment is that the partial derivatives of the operations involved in a calculation are always known analytically, provided that the calculation is broken down into sufficiently small pieces. In the limit, any calculation may be broken down to additions, subtractions, multiplications, divisions, powers, and a few mathematical functions like ![]() ,
, ![]() ,
, ![]() , or the cumulative Normal distribution
, or the cumulative Normal distribution ![]() , for which analytic partial derivatives are obviously known. This is exactly what the automatic algorithm in the next chapter does with the overloading of arithmetic operators and mathematical functions. We don't have to go that far when we apply AD manually, but we must break the calculation down to pieces small enough so their partial derivatives are known, explicit and easily derived.
, for which analytic partial derivatives are obviously known. This is exactly what the automatic algorithm in the next chapter does with the overloading of arithmetic operators and mathematical functions. We don't have to go that far when we apply AD manually, but we must break the calculation down to pieces small enough so their partial derivatives are known, explicit and easily derived.
Linear memory consumption We made the observation that, in order to compute the partial derivatives involved in the adjoint operations during the back-propagation phase, we must store the results of all the operations involved in the calculation as we evaluate it.
Therefore, manual AD requires (re-)writing the calculation code such that all intermediate results are stored and not overwritten. We coded our Black and Scholes function this way to start with, but in real life, to manually differentiate existing calculation code may take a lot of rewriting.
Automatic AD (AAD), as described from the next chapter onwards, does not require any rewriting. It is, however, subject, as any form of AD, to a vast memory consumption proportional to the number of operations. Memory consumption is the principal challenge of AD. If not addressed correctly, memory requirements make AD impractical and inefficient.4
Memory management is addressed in much detail in Chapters 10 and up. For now, we note that a linear (in the number of operations) memory consumption is a defining characteristic of back-propagation.
Constant time Finally, the most remarkable property of back-propagation, the unique property that differentiates it from all other differentiation methods, and the whole point of implementing it, is that it computes all the differentials of a calculation code in constant time in the number of inputs.
To see this, recall that for every operation in the evaluation of the form:
back-propagation conducts the ![]() adjoint operations:
adjoint operations:

Hence, the whole differentiation is conducted in less than ![]() operations, where
operations, where ![]() is the number of operations involved in the calculation and
is the number of operations involved in the calculation and ![]() is the maximum number of arguments to an operation. The complexity of the adjoint accumulation is therefore proportional to the complexity of the calculation (with coefficient
is the maximum number of arguments to an operation. The complexity of the adjoint accumulation is therefore proportional to the complexity of the calculation (with coefficient ![]() ), but independent from the number of inputs or required differentials.
), but independent from the number of inputs or required differentials.
Provided that the calculation was broken down to elementary pieces like addition, multiplication, logarithm, square root, or Gaussian density, ![]() since all the elementary operations are either unary or binary. In this case, the adjoint algorithm computes the result together with all sensitivities in less than three times the complexity of the evaluation alone.
since all the elementary operations are either unary or binary. In this case, the adjoint algorithm computes the result together with all sensitivities in less than three times the complexity of the evaluation alone.
In our Black and Scholes code, we did not break the calculation down to elementary pieces: for instance, the ninth operation “v = df * (F * nd1 - K * nd2)” conducts four computations out of five arguments. This operation can be further broken down into elementary pieces as follows:

When we construct calculation graphs automatically in the next chapter, we always break calculations down to elementary operations. With manual adjoint differentiation, this is unnecessary and to group operations may help clarify the code.
A graphical illustration of back-propagation
The following chart shows the application of back-propagation to Black and Scholes: it displays all the direct operations conducted top to bottom, with the corresponding adjoint operations conducted bottom to top.

In the next chapter, we will learn to apply back-propagation automatically to any calculation code. For now, we apply it manually to the Black and Scholes code to earn a more intimate experience with the algorithm, and identify some programming rules for the differentiation of C++ calculation code.
8.2 ADJOINT DIFFERENTIATION BY HAND
We identified a general adjoint differentiation methodology, which for now we apply by hand, to compute all the derivatives of any calculation code in constant time.
First, conduct the evaluation step, that is, the usual sequence of operations to produce the result of the calculation, keeping track of all intermediate results. This means that the calculation must be (re-)coded in functional terms, where variables are immutable and memory is not overwritten. Otherwise, intermediate results are no longer accessible next, when we carry the adjoint operations, in the reverse order, where we must compute the partial derivatives of every operation, which derivatives depend on the arguments of the operation. Automatic AD is resilient to overwriting, because it stores intermediate results in a special area of memory called the “tape,” independently of variables. For this reason, AAD is noninvasive and, contrary to manual AD, does not require the calculation code to be (re-)written in a special manner (other than templating on the number type, see next chapter).
In a second adjoint propagation step, conduct the adjoint computations for every operation in the sequence, in the reverse order:
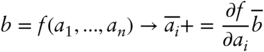
As seen in the previous section, this methodology is guaranteed to produce all the differentials of a given calculation code, analytically and in constant time.
We can now complete the differentiation code for Black-Scholes. Note that we don't hard code the adjoint of ![]() to 1, which would assume that
to 1, which would assume that ![]() is the final result being differentiated. The call to Black-Scholes may well be an intermediate step in a wider calculation (for example, the value of a portfolio of options); hence we let the client code pass the adjoint of
is the final result being differentiated. The call to Black-Scholes may well be an intermediate step in a wider calculation (for example, the value of a portfolio of options); hence we let the client code pass the adjoint of ![]() as an argument. For the same reason (the inputs to Black-Scholes may contribute to the final result not only as arguments to Black-Scholes, but also through other means), we don't initialize the adjoints of the arguments to zero in the code, leaving that to the caller.
as an argument. For the same reason (the inputs to Black-Scholes may contribute to the final result not only as arguments to Black-Scholes, but also through other means), we don't initialize the adjoints of the arguments to zero in the code, leaving that to the caller.


What we did not yet cover are some practical technicalities: how to deal with nested function calls and control flow. The automatic, noninvasive algorithm of the next chapter correctly deals with nested function calls and control flow, behind the scenes. For now, we discuss solutions in the context of manual AD.
Nested function calls
Suppose that the call to our function ![]() is part of a wider computation, for instance, the value and risk of a portfolio of options. We call
is part of a wider computation, for instance, the value and risk of a portfolio of options. We call ![]() the top-level function that computes the value of the portfolio, and suppose that
the top-level function that computes the value of the portfolio, and suppose that ![]() involves a number of nested calls to
involves a number of nested calls to ![]() , as in:
, as in:

To differentiate ![]() with respect to its inputs, we apply adjoint differentiation rules and perform the adjoint calculations in the reverse order:
with respect to its inputs, we apply adjoint differentiation rules and perform the adjoint calculations in the reverse order:

In the evaluation step, we call ![]() in evaluation mode to compute the value of the call option from the inputs. In the adjoint step, we call
in evaluation mode to compute the value of the call option from the inputs. In the adjoint step, we call ![]() in adjoint mode, passing the adjoint
in adjoint mode, passing the adjoint ![]() of the result of
of the result of ![]() . We programmed
. We programmed ![]() so that this call correctly back-propagates c_ to S0_, r_, y_, sig_, K_, and T_, and the outer back-propagation process for
so that this call correctly back-propagates c_ to S0_, r_, y_, sig_, K_, and T_, and the outer back-propagation process for ![]() can continue from there.
can continue from there.
When we write the adjoint code for a function, we must also write adjoint code for all the inner functions called from the function. This is, however, impossible when the function calls third-party libraries, for which the source may not be available or easily modifiable. In this case, we can wrap the third-party function in a function that satisfies the API of adjoint code, but conducts finite differences internally. Of course, we don't get the speed of adjoint differentiation for this part of the code, but adjoints do get propagated so the rest of the code can benefit from the acceleration. Concretely, if we have a function ![]() from a third-party library, we wrap it as follows:
from a third-party library, we wrap it as follows:

Then, the wrapper function can be used in adjoint code in the same way we used our Black-Scholes adjoint code to differentiate a higher level calculation.
Conditional code and smoothing
Conditional code (“if this then that”) is a more delicate subject. It must be understood that conditional code is discontinuous by nature, and not differentiable, with AD or otherwise. When AD deals with conditional code, it computes the differentials of the calculation over the same branch as the evaluation, but it does not differentiate through the condition itself. Concretely, the adjoint for the code:

is:

The adjoint code simply repeats the conditions, and the adjoints are back-propagated along the same branch where the calculation effectively took place. The condition itself, and the alternative calculations, are ignored in the differentiation. Note that this is the desired behavior in some cases. Where this is not, and it is desired to differentiate through the condition, the code must be modified and the condition smoothed so as to remove the discontinuity. Note that this is not particular to AD. All types of differentiation algorithms, including finite differences, are at best unstable when differentiating through control flow. Therefore, the algorithms that make control flow differentiable, collectively known as smoothing algorithms, are not related to AD, although a code can be easily differentiated with AD after it is smoothed. It also follows that smoothing is out of the scope of this text; we refer interested readers to Bergomi's [78] and our dedicated talk [77] and publication [11].
Loops and linear algebra
Finally, operations made in a loop are no different than others. For instance, a loop like:

conducts ![]() operations. In accordance with the rules of AD, we should separately store the result of each operation so we can back-propagate adjoints through the
operations. In accordance with the rules of AD, we should separately store the result of each operation so we can back-propagate adjoints through the ![]() additions and the
additions and the ![]() multiplications, last to first. Our automatic algorithm in the next chapter deals with loops in this manner exactly. When differentiating manually, however, we may indulge in shortcuts to improve both the clarity and the performance of the code. The loop above evidently implements:
multiplications, last to first. Our automatic algorithm in the next chapter deals with loops in this manner exactly. When differentiating manually, however, we may indulge in shortcuts to improve both the clarity and the performance of the code. The loop above evidently implements:

so the adjoint operations are:

in a loop on ![]() , or, using vector notations, we write the operation under the compact form:
, or, using vector notations, we write the operation under the compact form:
and using a basic matrix differentiation result, we can write the adjoint operations in a compact vector form, too:

which is evidently the same result as before, just with more compact notations.
More generally, with calculations involving matrix algebra, we have two options for the adjoint code: we can break all the matrix operations down to scalar operations and deal with the sequence of those as usual; or, we can use matrix differentiation results to derive and code the adjoint equations in matrix form, which is cleaner and sometimes more efficient, matrix operations often being optimized compared to hand-crafted loops.
For matrix differentiation results, we refer, for example, to [91] or [92]. For adjoint matrix calculus and applications to otherwise non-differentiable routines like singular value decomposition (SVD), we refer to [93]. For applications to calibration and FDM, we refer to [94].
8.3 APPLICATIONS IN MACHINE LEARNING AND FINANCE
Adjoint differentiation is known in the field of machine learning under the name “backpropagation,” or simply “backprop.” Backprop is what allows large, deep neural networks to learn their parameters in a reasonable time. In quantitative finance, in addition to risk sensitivities covered in detail in the following chapters, adjoint differentiation substantially accelerates calibration. Deep learning and calibration are both high-dimensional fitting problems that benefit from the quick computation of the sensitivities of error parameters.
We briefly introduce these applications and conclude before moving on to the automation of AD.
Deep learning and backpropagation

In the context of deep learning, multilayer artificial neural networks learn their weights (represented by the many edges in the chart above) by minimization of errors (difference between the targets and their predictors obtained by forward-feeding the corresponding inputs through the network) over a learning set, similarly to a regression problem, of which deep learning may be seen as an extension. Contrary to linear regression problems, however, deep learning has no closed-form solution, and an iterative procedure must be invoked to minimize the loss function (generally, the sum of squared errors).
The most widely used optimization algorithm in the field of machine learning 5 is the stochastic gradient descent (SGD), described in vast amounts of literature like [65] and online tutorials. SGD starts with a guess for the weights and updates them in the direction of the gradient of the error, iterating over the learning set. Hence, SGD requires the computation, at every step of the gradient, of the derivatives of the error function to the many weights in the network.
The derivatives of the error in a deep learning problem are generally analytic, and yet, the evaluation cost of all those closed-form derivatives at each step of the SGD would be prohibitive. Deep learning software computes all these derivatives in constant time with what they call backprop. Backprop equations are listed in Bishop [65], chapter 5.3, together with the feedforward equations that define the network. These equations are not reproduced here. What we see there is that the backprop equations are exactly the adjoints of the feedforward equations. Backprop steps are therefore the adjoints to the feedforward steps, conducted in reverse order. Backprop is a direct application of adjoint differentiation to the errors of a deep network as functions of its weights. Hence, it is an application of AD (or AAD when adjoint differentiation is performed automatically) to the feedforward equations that define the neural network. AD is what ultimately powers deep learning and allows it to learn a vast amount of weights in constant time. Without AD, the recent and spectacular successes of deep learning would not have been possible, due to the prohibitive amount of time it would take to calibrate a deep network without constant time differentiation.
Calibration
A similar problem in the context of financial derivatives is calibration, where the parameters of a model are set to fit the market prices of a number of liquid instruments. Dynamic models are typically dependent on curves and surfaces of parameters, like Dupire's local volatility or Hull and White's short rate volatility and mean-reversion. The parameters are generally time-dependent and their number is typically large. Perhaps against intuition, it is not customary to set those parameters through statistical estimates. For reasons explained for instance in [46], it is best practice to calibrate them to the market prices of traded instruments. The parameters of dynamic models are typically set to fit the market prices of European options, before the model is applied to produce the value and risk of more complex, less liquid exotics. Calibration is the process where a model learns its parameters on a sample consisting in a number of simple, standardized, actively traded instruments.
With the very notable exception of Dupire's model, calibration doesn't generally have an analytic solution in the form of a closed-form expression for the parameters as a function of option prices. A numerical optimization must be conducted to find the model parameters that minimize the errors. Derivatives practitioners generally favor the very effective Levenberg-Marquardt algorithm explained in Numerical Recipes [20], chapter 15.5. Like SGD, this is an iterative algorithm that starts with a guess for the parameters and updates them at each step from the gradient of the objective function (the sum of squared errors) and an internal approximation of its Hessian matrix.
Levenberg-Marquardt requires the computation, at each step, of the model prices of all the target instruments, along with their sensitivities to the model parameters. Model prices of European options are generally a closed form, either exact (Hull and White) or approximate (Libor Market Models or Multi-Factor Cheyette). The derivatives to parameters are therefore also analytic. However, the evaluation of a large number of sensitivities on each iteration is too expensive for a global calibration to converge fast enough. For this reason, it is common practice to localize calibrations (sequentially conduct “small” calibrations, where a small number of parameters is set to match a small number of market prices) or apply slower, less efficient alternatives to Levenberg-Marquardt that don't require derivative sensitivities, like the downhill simplex algorithm described in [20], chapter 10.4.
The performance of a global calibration can therefore considerably improve with the computation of the derivatives of the model prices to all the parameters in constant time with the adjoint method, with the added benefit that the recourse to less precise, less stable algorithms is no longer necessary. A possible implementation is by the manual adjoint differentiation of the pricing function for European options in the model, as we illustrated in the particularly simple case of Black and Scholes: code the adjoints of the sequence of all the operations in the evaluation in the reverse order. The process must be repeated for the multitude of pricing functions for various models across a changing library where new models are added and the implementation of existing models is typically improved over time. For this reason, hand-coded adjoint differentiation may not be the best option for calibration. Like market risks, the production of sensitivities for calibration is best conducted automatically.
Calibration is not limited to dynamic models. The construction of continuous interest rate curves and surfaces from a discrete number of market-traded swap and basis swap rates, deposits, and futures is also a calibration.6 The construction of rate surfaces is a delicate, specialized field of quantitative finance and a prerequisite for trading any kind of interest rate derivative, including vanilla swaps, caps and swaptions, interest rate exotics and hybrids, or the calculation of xVA.
Swap markets are moving fast in near-continuous time; hence, swap traders need a reliable, near-instantaneous rate surface calibration, despite the complexities involved (see [39] for an introduction). Rate surfaces are subject to a vast number of parameters; hence, AD accelerates their calibration by orders of magnitude, as demonstrated in Scavenius' pioneering work [95].
Manual and automatic adjoint differentiation
It is apparent from our examples that manual adjoint differentiation is tedious, time consuming, and error prone. In addition, the maintenance of libraries with handwritten adjoint code may turn into a nightmare: every modification in the calculation code must be correctly reflected in the adjoint code in a manual process.
This is why our text focuses on automatic adjoint differentiation, whereby the adjoint calculations are conducted automatically and correctly, behind the scenes. Developers only write the calculation code. The adjoint “code” is generated at run time.
This being said, maximum performance is obtained with a manual differentiation. A naive implementation of AAD, like the play tool in the next chapter, carries a prohibitive overhead. The techniques explained in Chapters 10 and 13 mitigate the overhead and substantially accelerate AAD, but they still fall short of the performance of hand-coded AD. Only the advanced implementation of AAD in Chapter 15 approaches the performance of manual AD thanks to expression templates. It is still worth hand coding the derivatives of some short, unary, or binary low-level functions that are frequently called in the calculation code. We will demonstrate how to do this in the context of our AAD library.
In this chapter, we covered manual adjoint differentiation mainly for a pedagogical purpose, in order to gently introduce readers to adjoint calculations before we delve into algorithms that automate them. Readers are encouraged to try hand-coded adjoint differentiation for various examples involving nested function calls, conditions, and loops to earn some experience and an intimate knowledge of the concepts covered here. They will also find a more complete coverage of manual adjoint differentiation in [88].
