CHAPTER 8
Reducing Uncertainty with Bayesian Methods
We are now in possession of proven theorems and masses of worked‐out numerical examples. As a result, the superiority of Bayesian methods is now a thoroughly demonstrated fact in a hundred different areas.
—E. T. Jaynes, Probability Theory: The Logic of Science
The previous chapter showed how the performance of subjective probabilities is objectively measurable—and they have been measured thoroughly in published scientific literature. These subjective “prior probabilities” (“priors” for short) are the starting point of all our analyses. This is the best way to both preserve the special knowledge and experience of the cybersecurity expert and produce results that are mathematically meaningful and useful in simulations. Stating our current uncertainty in a quantitative manner allows us to update our probabilities with new observations using some powerful mathematical methods.
The tools we are introducing in this chapter are part of Bayesian methods in probability and statistics, named after the original eighteenth‐century developer of the idea, Reverend Thomas Bayes. These have multiple advantages that are particularly well suited to the problems the cybersecurity expert faces. First, Bayesian methods exploit existing knowledge of experts. This is in contrast to conventional methods the reader may have been exposed to in first‐semester statistics, which assume that literally nothing else is known about a measurement before the sample data was acquired. Second, because Bayesian methods use this prior knowledge we can make inferences from very little data. These inferences may be just slight reductions in the cybersecurity expert's uncertainty, but they can still have a big impact on risk mitigation decisions. If you do have a lot of data, the Bayesian solution and the measurements from basic sampling methods that ignore prior knowledge will converge.
In this chapter we will introduce some of the basic Bayesian reasoning and how it might apply to cybersecurity. We will, for now, focus on fundamental mechanics to lay a foundation. The basics we are covering will be trivial for some. We assume nothing more than that the reader is familiar with basic algebra. But there is a lot of detail to cover, so, if you find this trivial, feel free to skim quickly. If you find it overwhelming, bear in mind that you still, as always, have access to the calculations done for you in our downloadable spreadsheet (www.howtomeasureanything.com/cybersecurity). If you can make it through this chapter, the reward is access to some very powerful tools in the next chapter.
A Brief Introduction to Bayes and Probability Theory
The claim has often been correctly made that Einstein's equation E = mc2 is of supreme importance because it underlies so much of physics… . I would claim that Bayes equation, or rule, is equally important because it describes how we ought to react to the acquisition of new information.
—Dennis V. Lindley 1
We mentioned back in Chapter 2 that you probably have a lot more data than you think, but you probably also need less data than you think. This chapter is more about the latter. In cybersecurity, as in many areas, we have some idea of what a probability might be, but we could modify or update that probability if we had a little more data. For example, you will need to estimate the probability of a data breach and the probability of a breach given a new control. And you often need to do that with very little data.
It often surprises managers and technicians that we can make any progress at all with just a few data points. However, Bayesian methods demonstrate that sometimes we can just incrementally change our uncertainty even with a single observation. How a single observation reduces uncertainty is obvious in some extreme examples—such as the chance that bypassing a particular control is even possible is informed by observing just one such event. In more subtle situations, we start with a state of uncertainty (from a calibrated SME, of course), and we want to know how much that changes with very limited observations. To understand how that works, we first need to review some very basic rules of probability.
The Language of Probabilities: A Basic Vocabulary
If we give you a little notation now, we can avoid longer and potentially more confusing verbal expressions. This may be trivial to some readers, but if you are the least bit rusty, look this over to get back up to speed on how to write in the language of probabilities. For now, we will just mention a few handy rules from probability theory. This is not the complete list of fundamental axioms from probability theory, and it's definitely not a comprehensive list of all theorems that might be useful. But it is enough to get through this chapter.
- How to write “Probability.”


If P(MDB) is the probability of a major data breach in a given year, then P(∼MDB) is the probability there won't be a major data breach.
- The “Something has to be true but contradictory things can't both be true” rule.
The probabilities of all mutually exclusive and collectively exhaustive events or states must add up to 1. In probability theory, this is known as the Complement Rule. If there are just two possible outcomes, say A or not A, then:

For example, either there will be a major data breach or not. If we defined this term unambiguously (which we assume we have in this specific case), it has to be one or the other, and it can't be both (i.e., we can't have MDB happen and not happen).
- How to write the probability of “More than one thing happens.”
P(A,B) means both A and B are true. If A and B are “independent,” meaning the probability of one does not depend on the other, then P(A,B) = P(A)P(B). It must also be the case that P(A,B) = P(B,A). This is the “commutative property.”
- How to write, and compute, probability when “It depends” (conditional probability).
P(A|B) = conditional probability of A given B.
- How to decompose “More than one thing happens” into a series of “It depends.”
We can use rule 4 to turn a larger joint probability of two things into P(A,B) = P(A|B)P(B) and, if we have a joint probability of three things, we can write P(A,B,C) = P(A|B,C)P(B|C)P(C) and so on. This is called the “chain rule.”
- How to add up “It can happen different ways” rule.
We can extend rule 4 to working out the probability based on all the conditions under which it could happen and the probabilities of each of those conditions. This is known as “the law of total probability.”

- How to “flip” a conditional probability: Bayes's Rule.
We will often want to “flip” a conditional probability. That is, we might start out with P(A|B) but what we really want is P(B|A). These two things are only equal if P(A) = P(B), which is often not the case. So in order to flip them we have to apply Bayes's rule, which is written as:

Sometimes the form of this is referred to as the “general” form of Bayes by computing P(B) according to rule 3. If we consider just two conditions for P(B), then rule 4 allows us to substitute P(B) so that:
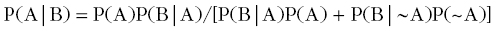
The Proof of Bayes
If you've absorbed all of that to the point of its being intuitive, there are some more concepts you can pick up if you understand where Bayes's rule comes from. In each of the steps below, we will refer to how it comes from rules 1 through 6 above or previous steps.
Prove P(A|B) = P(A)P(B|A)/P(B):
- Step 1. P(A,B) = P(B,A)—rule 3, the commutative property.
- Step 2. P(A,B) = P(A)P(B|A)—rule 5, the chain rule.
- Step 3. P(B,A) = P(B)P(A|B)—from steps 1 and 2.
- Step 4. P(A)P(B|A) = P(B)P(A|B)—true because of 1, 2, and 3.
- Step 5. P(A|B) = P(A)P(B|A)P(B)—divide #4 by P(B).
Please don't feel you need to memorize these; just understand them as subrules. We reference these throughout our analysis. But let's pause to consider the consequences of these rules so far. We often want to work out the probability some hypothesis is true given some observation. Sometimes it is easier to work out the probability that we will observe something given some hypothesis is true. If we know the latter and we have a prior for the probability of an observation, we can compute the former.
We can refer to the law of total probability (rule 6) to compute probability of a given observation.
P(B) = P(B|A)P(A) + P(B|~A)(1 − P(A))
If we substitute P(B) with the right‐hand side of the equation above, we get what is called the “general form” of Bayes’s theorem.

An Example from Little Data: Does Multifactor Authentication Work?
Now let's use all of these tools in an example. The authors have run into many claims by cybersecurity vendors and others, which you might be interested in testing. In one case, we find a source that states that multifactor authentication (MFA) should reduce material data breaches by 90%.2 But you are also reading a lot of information about how to bypass MFA.3 So, is MFA just a lot of hype? It seems like it should reduce risk just because it makes access much more difficult.
Suppose you haven't implemented MFA yet, but you conducted a previous assessment of other industry data or calibrated estimates. Knowing that your firm's size makes major breaches more likely and knowing what your insurer quoted you for coverage, you estimated that your chance of a breach was somewhere between 4% and 16% per year. Since for this example you are just going to use a single discrete probability, you go with a mean of 10% per year. You are considering a major investment in MFA to reduce risk, but to justify the cost you have to determine how much risk would be reduced.
Objective independent data is sparse. However, suppose you know of a firm similar to yours that implemented MFA across all platforms a year ago, and they say they haven't had a material breach since then. Is this evidence that MFA is working? It's certainly not proof it is working because, given our estimate above, there was a 90% chance of not having a significant breach, anyway. But it turns out it is evidence in the sense that the information from one year of no observed breaches at one organization does reduce our uncertainty, even if just incrementally.
The Solution
Let's keep our current example simple and assume a simple binary outcome: either MFA works as advertised or it does not. The articles you were reading raise some doubts about whether there is a chink in the MFA armor, but suppose you still think there is a 60% chance the claims are true. After your colleague in the other firm reveals their experience with this MFA solution, you compute the updated probability that MFA really does reduce the chance of a material breach by 90%.
- The probability that MFA works (W) as advertised: P(W) = 0.6.
- Based on the research you performed with your own firm, independent articles, and other data about firms that had not yet implemented MFA, you estimated a chance that a material breach (B) would be realized without MFA. This is the same as implementing MFA that doesn't work (~W): P(B|~W) = 0.1.
- The advertised probability of a material breach given MFA works—that is, it reduces the chance of a breach by 90% (i.e., just one‐tenth of probability without MFA): P(B|W) = (1 − 0.9)(0.1) = 0.01.
- The probability there would be no breach observed in that time period for that firm given MFA worked: P(~B|W) = 1 − P(B|W) = 1 − 0.01 = 0.99.
- The total probability of a material breach using the law of total probability: P(B) = P(B|W)P(W) + P(B|~W)(1 − P(W)) = (0.01)(0.6) + (0.1)(1 − 0.6) = 0.046.
- The probability of no breach would be observed: P(~B) = 1 − P(B) = 1 − 0.046 = 0.954.
- The chance MFA is working given that there was no breach after one year of observation at one firm: P(W|~B) = P(W)P(~B|W)/P(~B) = (0.6)(0.99)/(0.954) = 0.622642.
So just one year of observations updates our belief that MFA works from 60% to 62.2642%. That's not much of a change, but we did move the needle. How much did it change the probability of a material breach if you implemented MFA? To keep the notation simple, we'll call your updated belief in the chance MFA works P(W|~B) by adding an apostrophe P(W)’ = 0.622642. Then let's apply the same procedure above with P(W)’ instead of P(W). You just need to compute P(B) = P(B|W)P(W)’ + P(B|~W)(1 − P(W)’). You should get 0.043962. That's not much less than our previous estimate of a data breach given we implemented MFA (previously 0.046), but it is definitely a lot less than our current probability 0.1 of a breach without MFA [remember, P(B|~W) is the same as not implementing MFA].
Adding More Observations
Now suppose you checked around further, and you found more similar firms that implemented MFA but did not yet observe a breach after implementing MFA, some two or three years ago. Let's further suppose this adds up to 11 more company‐years of observations, 12 including the first company you talked to with just one year of observations. Let's treat each year of observations for each firm as a separate random outcomes and as if they are equivalent in all other respects.
In that case, the probability that no breach is observed in a total of 12 company‐years of data is, according to rule 3, the product of all of those individual probabilities. Our original probability of no breach we get from the law of total probability was 0.954. Getting 12 random samples where there are no observed breaches, the updated probability is (0.954)12 = 0.568.
Given all this new data for breaches in firms that implemented MFA, how does this update our belief about whether MFA works as advertised? How does it change the probability of a breach if we implement MFA? If you work through the example with the probability of seeing no breaches in 12 observed company‐years, you should get a probability that MFA works equal to 9.358% and a probability of a data breach after implementing MFA equal to 1.5776%. If you go to the website at www.howtomeasureanything.com/cybersecurity, you can see this example worked out in detail. We also provided the assumptions behind the example in Chapter 4, where we worked out how long we would have to observe a single firm to get to various levels of confidence about a control working.
Now, keep in mind that after you implement MFA, more data is gathered with each year of observations. If you went another year and none of the 12 firms observed a data breach yet, then you have 12 more company‐years of data for a total of 24 company‐years. In that case, you would have updated your prior so that you now have a 93.66% probability MFA works as advertised, and your estimate for the probability of a breach the next year is down to 1.57%. See the same spreadsheet above for this example as well.
A Brief Note on Priors
All the operations just described require some source of an input. In this example, we will be using the calibrated estimates of the CISO. Since the CISO is using his previous experience and his calibrated probability‐assessment skill to generate the inputs, we call them an “informative prior.” Again, “prior” is short for “what you already believe about something.” An informative prior is a fancy way for saying that your prior is generated by a subject matter expert who knows something, is well calibrated, and is willing to state how some things are more likely than others.
We could also start with an “uninformative prior.” The idea here is to have a prior that assumes a maximum possible level of uncertainty at first; any changes to that will be informed by the data. It is considered a more conservative starting point since it can't be influenced by the mistaken beliefs of the expert—on the other hand, it can't take into account perfectly legitimate beliefs, either.
It could be argued that an uninformative prior on a discrete binary event is 50%. There is actually a philosophical debate about this, which we won't get into, but, mathematically speaking, that is the most uncertainty we can have in a system with only two possible states. Of course, the selection of a prior in either case is subjective. The uninformative prior is considered more conservative by some people, but it is probably also less realistic than the informative (i.e., you usually don't really have zero prior information). Whatever the mix you have on the subjective‐to‐objective scale, probability theory can help make your reasoning far more consistent.
Other Ways Bayes Applies
Bayes and the other basic probability rules used above apply to much more than the one simplified problem we discussed. For many of the questions we need to answer, it is easier to work out the probability of a given observation given a hypothesis is true than it is to work out the probability the hypothesis is true given the observation. Consider the following questions.
- “What is the probability of a breach in my firm next year given that two of 20 firms in my industry reported a material breach in the last three years?”
Written: P(Breach|Industry Observations = 2 of 60 company years).
- “What is the probability of that number of breaches in my industry if the true frequency was 3% per firm per year?”
Written: P(Industry Observations = 2 of 60 company years|Breach rate=0.03).
Do you see how these are different? The first led with asking, “What is the probability of the event (Breach) given the evidence?” The second is asking, “What is the probability of observing the evidence given the fact that the event has occurred?” (Getting these two confused is also known as the “Prosecutor's fallacy” if you want to study this further.)
This “flip” is what Bayes's rule is all about, and we will find it becomes a very important foundation of reasoning under uncertainty. Bayesian probability becomes a “consistency” yardstick for measuring your beliefs about some uncertain event as you get more data. In particular, it makes the process of updating those beliefs reasonable.
Questions such as these are a particularly useful variation on a conditional probability because it starts with an easier question. Specifically, if we knew, for example, that the chance of one random draw being a “hit” was 0.03 per draw, then what is the chance of seeing exactly 2 “hits” out of 60 draws? This can be easily worked out and, thanks to Bayes, we can work out the probability that the underlying frequency is 0.03 given those observations. Now we will get into how to work out the solution to that problem and a few more in the next chapter. We will discuss:
- How can we have uncertainty about the frequency itself?
- How we can update beliefs where there may be multiple events in the same company each year?
- How does this relate to Laplace's rule of succession?
- How can we use this to combine—and improve—the estimates from multiple experts?
It may not be obvious now how the answers to all these questions come from the six rules of probability we discussed, but they do.
Notes
- 1. Dennis V. Lindley, Understanding Uncertainty (Hoboken, NJ: John Wiley & Sons, 2006).
- 2. Phil Muncaster, “Tech CEOs: Multi‐Factor Authentication Can Prevent 90% of Attacks,” Info Security, Sept. 2021, https://www.infosecurity-magazine.com/news/tech-execs-mfa-prevent-90-of/.
- 3. Hitesh Sheth, “Top 5 Techniques Attackers Use to Bypass MFA,” Dark Reading, Aug. 2021, https://www.darkreading.com/endpoint/top-5-techniques-attackers-use-to-bypass-mfa.
