![]()
Vector and Matrix Functions of Complex Variables
5.1 Complex Numbers
MATLAB implements a simple way to work with complex numbers in binary form a+bi or a+bj, representing the imaginary unit by means of the symbol i or j. Note that it is not necessary to include the product symbol (asterisk) before the imaginary unit, but if it is included, everything still works correctly. It is important, however, that spaces are not introduced between the imaginary unit i and its coefficient.
Complex numbers can have symbolic or numeric real or imaginary parts. Operations are carried out with a precision that is set by the command format. Thus, it is possible to work with complex numbers in exact rational format via the command format rat.
The common arithmetical operations with complex numbers (sum, difference, product, division and exponentiation) are carried out in the usual way. Examples are shown in Figure 5-1.
Obviously, as the real numbers are a subset of the complex numbers, any function of complex variables will also be valid for real variables.
5.2 General Functions of a Complex Variable
MATLAB has a range of preset general functions of a complex variable, which of course will also be valid for real, rational and integer variables. The following sections present the most important examples.
5.2.1 Trigonometric Functions of a Complex Variable
Below is a table summarizing the trigonometric functions of a complex variable and their inverses that are incorporated in MATLAB, illustrated with examples.
Function | Inverse |
|---|---|
sin (z) sine >> sin(5-6i) | asin (z) arc sine >> asin(1-i) |
cos (z) cosine >> cos (3 + 4i) | acos (z) arc cosine >> acos (-i) |
tan (z) tangent >> tan(pi/4i) | atan(z) and atan2(imag(z),real(z)) arc tangent >> atan(-pi*i) |
csc (z) cosecant >> csc(1-i) | acsc (z) arc cosecant >> acsc(2i) |
sec (z) secant >> sec(-i) | asec (z) arc secant >> asec(0.6481+0i) |
cot (z) cotangent >> cot(-j) | acot (z) arc cotangent >> acot(1-6j) |
5.2.2 Hyperbolic Functions of a Complex Variable
Below is a table of hyperbolic functions of a complex variable and their inverses that are incorporated in MATLAB, illustrated with examples.
Function | Inverse |
|---|---|
sinh(z) hyperbolic sine >> sinh(1+i) | asinh(z) arc hyperbolic sine >> asinh(0.6350 + 1.2985i) |
cosh(z) hyperbolic cosine >> cosh(1-i) | acosh(z) arc hyperbolic cosine >> acosh(0.8337 - 0.9889i) |
tanh(z) hyperbolic tangent >> tanh(3-5i) | atanh(z) arc hyperbolic tangent >> atanh(3-41) |
csch(z) hyperbolic cosecant >> csch(i) | acsch(z) arc hyperbolic cosecant >> acsch(-1.1884i) |
sech(z) hyperbolic secant >> sech(i^i) | asech(z) arc hyperbolic secant >> asech(5-0i) |
coth(z) hyperbolic cotangent >> coth(9+i) | acoth(z) arc hyperbolic cotangent >> acoth(1-i) |
5.2.3 Exponential and Logarithmic Functions of a Complex Variable
Below is a table summarizing the exponential and logarithmic functions that are incorporated in MATLAB, illustrated with examples.
Function | Meaning |
|---|---|
exp (z) | Exponential function to base e (e ^ x) >> exp(1-i) |
log (x) | Base e logarithm of x >> log(1.4687-2.2874i) |
log10 (x) | Base 10 logarithm of x >> log10(100 + 100i) |
log2 (x) | Base 2 logarithm of x >> log2(4-6i) |
pow2 (x) | Base 2 power function (2^x) >> pow2(2.8502-1.4179i) |
sqrt (x) | Square root of x >> sqrt(1+i) |
5.2.4 Specific Functions of a Complex Variable
MATLAB incorporates a specific group of functions of a complex variable which allow you to work with moduli, arguments, and real and imaginary parts. Among these features are the following:
Function | Meaning |
|---|---|
abs (z) | The modulus (absolute value) of z >> abs(12.425-8.263i) |
angle (z) | The argument of z >> angle(12.425-8.263i) |
conj (z) | The complex conjugate of z >> conj(12.425-8.263i) |
real (z) | The real part of z >> real(12.425-8.263i) |
imag (z) | The imaginary part of z >> imag(12.425-8.263i) |
floor (z) | Applies the floor function to real(z) and imag(z) >> floor(12.425-8.263i) |
ceil (z) | Applies the ceiling function to real(z) and imag(z) >> ceil(12.425-8.263i) |
round (z) | Applies the round function to real(z) and imag(z) >> round(12.425-8.263i) |
fix (z) | Applies the fix function to real(z) and imag(z) >> fix(12.425-8.263i) |
5.3 Basic Functions with Complex Vector Arguments
MATLAB enables you to work with functions of a complex matrix or vector. Of course, these functions are also valid for real variables since the real numbers are included in the complex numbers. Below is a table summarizing the functions of complex vector variables that are incorporated in MATLAB. Later, when the functions of complex matrix variables are tabulated, we will observe that all of them are also valid for vector variables, a vector being a particular case of a matrix.
max (V) | The maximum component of V. (max is calculated for complex vectors as the complex number with the largest complex modulus (magnitude), computed with max(abs(V)). Then it computes the largest phase angle with max(angle(V)), if necessary.) >> max([1-i 1+i 3-5i 6i]) >> max ([1, 0, -23, 12, 16]) |
min (V) | The minimum component of V. (min is calculated for complex vectors as the complex number with the smallest complex modulus (magnitude), computed with min(abs(V)). Then it computes the smallest phase angle with min(angle(V)), if necessary.) >> min([1-i 1+i 3-5i 6i]) >> min ([1, 0, -23, 12, 16]) |
mean (V) | Average of the components of V. >> mean([1-i 1+i 3-5i 6i]) >> mean ([1, 0, -23, 12, 16]) |
median (V) | Median of the components of V. >> median([1-i 1+i 3-5i 6i]) >> median ([1, 0, -23, 12, 16]) |
std (V) | Standard deviation of the components of V. >> std([1-i 1+i 3-5i 6i]) >> std ([1, 0, -23, 12, 16]) |
sort (V) | Sorts the components of V in ascending order. For complex entries the order is by absolute value and argument. >> sort([1-i 1+i 3-5i 6i]) >> sort ([1, 0, -23, 12, 16]) |
sum (V) | Returns the sum of the components of V. >> sum([1-i 1+i 3-5i 6i]) >> sum ([1, 0, -23, 12, 16]) |
prod (V) | Returns the product of the components of V, so, for example, n! = prod(1:n). >> prod([1-i 1+i 3-5i 6i]) >> prod ([1, 0, -23, 12, 16]) |
cumsum (V) | Gives the cumulative sums of the components of V. >> cumsum([1-i 1+i 3-5i 6i]) >> cumsum ([1, 0, -23, 12, 16]) |
cumprod (V) | Gives the cumulative products of the components of V. >> cumprod([1-i 1+i 3-5i 6i]) >> cumprod ([1, 0, -23, 12, 16]) |
diff (V) | Gives the vector of first differences of V (Vt - V-t-1). >> diff([1-i 1+i 3-5i 6i]) >> diff([1, 0, -23, 12, 16]) |
gradient (V) | Gives the gradient of V. >> gradient([1-i 1+i 3-5i 6i]) >> gradient ([1, 0, -23, 12, 16]) |
del2 (V) | Gives the Laplacian of V (5-point discrete). >> del2([1-i 1+i 3-5i 6i]) >> del2 ([1, 0, -23, 12, 16]) |
fft (V) | Gives the discrete Fourier transform of V. >> fft([1-i 1+i 3-5i 6i]) >> fft([1, 0, -23, 12, 16]) |
fft2 (V) | Gives the two-dimensional discrete Fourier transform of V. >> fft2([1-i 1+i 3-5i 6i]) >> fft2([1, 0, -23, 12, 16]) |
ifft (V) | Gives the inverse discrete Fourier transform of V. >> ifft([1-i 1+i 3-5i 6i]) >> ifft([1, 0, -23, 12, 16]) |
ifft2 (V) | Gives the inverse two-dimensional discrete Fourier transform of V. >> ifft2([1-i 1+i 3-5i 6i]) >> ifft2([1, 0, -23, 12, 16]) |
5.4 Basic Functions with Complex Matrix Arguments
The functions given in the above table also support complex matrices as arguments, in which case the result is a row vector whose components are the results of applying the function to each column of the matrix. Let us not forget that these functions are also valid for real variables, since the set of real numbers is a subset of the set of complex numbers.
max (Z) | Returns a row vector indicating the maximum component of each column of the matrix Z. (max is calculated for complex vectors V as the complex number with the largest complex modulus (magnitude), computed with max(abs(V)). Then it computes the largest phase angle with max(angle(V)), if necessary.) >> Z = [1-i 3i 5;-1+i 0 2i;6-5i 8i -7] |
min (Z) | Returns a row vector indicating the minimum component of each column of the matrix Z. (min is calculated for complex vectors V as the complex number with the smallest complex modulus (magnitude), computed with min(abs(V)). Then it computes the smallest phase angle with min(angle(V)), if necessary.) >> min(Z) >> min(Z1) |
mean (Z) | Returns a row vector indicating the mean of the components of each column of Z. >> mean(Z) >> mean(Z1) |
median (Z) | Returns a row vector indicating the median of the components of each column of Z. >> median(Z) >> median(Z1) |
std (Z) | Returns a row vector indicating the standard deviation of the components of each column of Z. >> std(Z) >> std(Z1) |
sort (Z) | Sorts the components of the columns of Z in ascending order. For complex entries the order is by absolute value and argument. >> sort(Z) |
sum (Z) | Returns a row vector indicating the sum of the components of each column of Z. |
prod (Z) | Returns a row vector indicating the product of the components of each column of Z. >> prod(Z) >> prod(Z1) |
cumsum (Z) | Returns a matrix indicating the cumulative sums of the elements in the columns of Z. >> cumsum(Z) >> cumsum(Z1) |
cumprod(V) | Returns a matrix indicating the cumulative products of the elements in the columns of Z. >> cumprod(Z) |
diff (Z) | Returns the matrix of first differences of the components of the columns of Z. >> diff(Z) |
gradient (Z) | Returns the matrix of gradients for the columns of Z. >> gradient(Z) |
del2 (Z) | Returns the matrix indicating the Laplacian of the columns of Z (5-point discrete). >> del2(Z) |
fft (Z) | Returns the matrix with discrete Fourier transforms of the columns of Z. >> fft(Z) |
fft2 (Z) | Returns the matrix with the two-dimensional discrete Fourier transforms of the columns of the matrix Z. >> fft2(Z) |
ifft (Z) | Returns the matrix with the inverse inverse discrete Fourier transform of the columns of the matrix Z. >> ifft(Z) |
ifft2 (Z) | Returns the matrix with the inverse two-dimensional discrete Fourier transform of the columns of Z. >> ifft2(Z) |
5.5 General Functions with Complex Matrix Arguments
MATLAB incorporates a broad group of hyperbolic, trigonometric, exponential and logarithmic functions that support a complex matrix as an argument. Obviously, all these functions also accept a complex vector as the argument, since a vector is a particular case of matrix. All functions are applied elementwise in the matrix.
5.5.1 Trigonometric Functions of a Complex Matrix Variable
Below is a table summarizing the trigonometric functions of a complex variable and their inverses which are incorporated in MATLAB, illustrated with examples. All the examples use as arguments the matrices Z and Z1 introduced at the beginning of the table in the description of the sine function.
Direct Trigonometric Functions |
|---|
sin(Z) sine function >> Z = [1-i, 1+i, 2i;3-6i, 2+4i, -i;i,2i,3i] |
cos (Z) cosine function >> cos(Z) >> cos(Z1) |
tan (Z) tangent function >> tan(Z) >> tan(Z1) |
csc (Z) cosecant function >> csc(Z) >> csc(Z1) |
sec (Z) secant function >> sec(Z) >> sec(Z1) |
cot (Z) cotangent function >> cot(Z) >> cot(Z1) |
Inverse Trigonometric Functions |
|---|
asin (Z) arc sine function >> asin(Z) >> asin(Z1) |
acos (Z) arc cosine function >> acos(Z) >> acos(Z1) |
atan(Z) and atan2 (real(Z),imag(Z)) arc tangent function >> atan(Z) >> atan(Z1) |
acsc (Z) arc cosecant function >> acsc(Z) >> acsc(Z1) |
asec (Z) arc secant function >> asec(Z) >> asec(Z1) |
acot (Z) arc cotangent function >> acot(Z) >> acot(Z1) |
5.5.2 Hyperbolic Functions of a Complex Matrix Variable
Below is a table summarizing the hyperbolic functions of complex matrix variables and their inverses which are incorporated in MATLAB, illustrated with examples.
Direct Hyperbolic Functions |
|---|
sinh (Z) hyperbolic sine function >> sinh (Z) >> sinh(Z1) |
cosh (Z) hyperbolic cosine function >> cosh(Z) >> cosh(Z1) |
tanh (Z) hyperbolic tangent function >> tanh(Z) >> tanh(Z1) |
csch (z) hyperbolic cosecant function >> csch (Z) >> csch(Z1) |
sech (Z) hyperbolic secant function >> sech (Z) >> sech(Z1) |
coth (Z) hyperbolic cotangent function >> coth (Z) >> coth(Z1) |
Inverse Hyperbolic Functions |
|---|
asinh (Z) hyperbolic arc sine function >> asinh(Z) >> asinh(Z1) |
acosh (Z) hyperbolic arc cosine function >> acosh(Z) >> acosh(Z1) |
atanh (Z) hyperbolic arc tangent function >> atanh(Z) >> atanh(Z1) |
acsch (Z) hyperbolic arc cosecant function >> acsch(Z) >> acsch(Z1) |
asech (Z) hyperbolic arc secant function >> asech(Z) >> asech(Z1) |
acoth (Z) hyperbolic arc cotangent function >> acoth(Z) >> acoth(Z1) |
5.5.3 Exponential and Logarithmic Functions of Complex Matrix Variables
Below is a table summarizing the exponential and logarithmic functions which are incorporated in MATLAB, illustrated with examples. The matrices Z1 and Z are the same as those in the previous examples.
Function | Meaning |
|---|---|
exp (Z) | Base e exponential function (e ^ x) >> exp(Z) >> exp(Z1) |
log (Z) | Base e logarithm of Z. >> log(Z) >> log(Z1) |
log10 (Z) | Base 10 logarithm of Z. >> log10(Z) >> log10(Z1) |
log2 (Z) | Base 2 logarithm of Z. >> log2(Z) >> log2(Z1) |
pow2 (Z) | Base 2 exponential function (2^Z). >> pow2(Z) >> pow2(Z1) |
sqrt (Z) | Square root of Z. >> sqrt (Z) >> sqrt(Z1) |
5.5.4 Specific Features of Complex Matrices
MATLAB incorporates a specific group of functions of a complex variable allowing you to work with moduli, arguments, and real and imaginary parts. Among these functions are the following:
Function | Meaning |
|---|---|
abs (Z) | The complex modulus (absolute value). >> abs (Z) >> abs(Z1) |
angle (Z) | Argument function. >> angle (Z) >> angle(Z1) |
conj (Z) | Complex conjugate. >> conj (Z) >> conj(Z1) |
real (Z) | Real part. >> real (Z) >> real(Z1) |
imag (Z) | Imaginary part. >> imag (Z) >> imag (Z1) |
floor (Z) | Floor function applied to real and imaginary parts. >> floor(12.357*Z) >> floor(12.357*Z1) |
ceil (Z) | Ceiling function applied to real and imaginary parts. >> ceil(12.357*Z) >> ceil(12.357*Z1) |
round (Z) | Round function applied to real and imaginary parts. >> round(12.357*Z) >> round(12.357*Z1) |
fix (Z) | Fix applied to real and imaginary parts. >> fix(12.357*Z) >> fix(12.357*Z1) |
5.6 Operations with Real and Complex Variables
MATLAB includes the usual matrix operations of sum, difference, product, exponentiation and inversion. Obviously all these operations will also be valid for real matrices. The following table summarizes those operations that are valid both for numerical and algebraic real and complex matrices.
A + B | Sum of matrices. >> A=[1+i, 1-i, 2i; -i,-3i,6-5i; 2+3i, 2-3i, i] >> B=[i, -i, 2i; 1-i,7-3i,2-5i; 8-6i, 5-i, 1+i] >> A1=[1 6 2; 3 5 0; 2 4 -1] >> B1=[-3 -6 1; -3 -5 2; 12 14 -10] >> A+B >> A1+B1 |
A-B | Difference of matrices. >> A-B >> A1-B1 |
A * B | Product of matrices. >> A * B >> A1*B1 |
A^n | nth power of the matrix A. >> A^3 >> A1^3 >> cumprod ([1, 0, -23, 12, 16]) |
P^A | Scalar p raised to the power of the matrix A. >> 3^A >> 3^A1 |
A' | Transpose of the matrix A. >> A' >> A1' |
A^-1 | Inverse of A . >> A^-1 >> A1^-1 >> A*A^-1 >> A1*A1^-1 |
AB | If A is square AB= (A-1) * B and if A is not square AB is the solution in the sense of least-squares of the system AX = B. >> AB >> A1B1 |
B/A | Equivalent to A'B' >> B/A >> A'B' >> B1/A1 >> A1'B1' |
EXERCISE 5-1
Given the complex numbers z1= 1-i, and z2= 5i, calculate: z13 z12/z24, z11/2, z23/2, ln(z1+z2), sin(z1-z2), and tanh (z1/z2).
>> Z1=1-i
Z1 =
1.0000 - 1.0000i
>> Z2=5i
Z2 =
0 + 5.0000i
>> Z1^3
ans =
-2.0000 - 2.0000i
>> Z1^2/Z2^4
ans =
0 - 0.0032i
>> sqrt(Z1)
ans =
1.0987 - 0.4551i
>> sqrt(Z2^3)
ans =
7.9057 - 7.9057i
>> log(Z1+Z2)
ans =
1.4166 + 1.3258i
>> sin(Z1-Z2)
ans =
1.6974e+002 -1.0899e+002i
>> tanh(Z1/Z2)
ans =
-0.2052 - 0.1945i
EXERCISE 5-2
Perform the following operations with complex numbers:

>> (i^8-i^(-8))/(3-4*i) + 1
ans =
1
>> i^(sin(1+i))
ans =
-0.16665202215166 + 0.32904139450307i
>> (2+log(i))^(1/i)
ans =
1.15809185259777 - 1.56388053989023i
>> (1+i)^i
ans =
0.42882900629437 + 0.15487175246425i
>> i^(log(1+i))
ans =
0.24911518828716 + 0.15081974484717i
>> (1+sqrt(3)*i)^(1-i)
ans =
5.34581479196611 + 1.97594883452873i
EXERCISE 5-3
Find the real part, imaginary part, modulus and argument of the following expressions:
![]()
>> Z1=i^3*i; Z2=(1+sqrt(3)*i)^(1-i); Z3=(i^i)^i;Z4=i^i;
>> format short
>> real([Z1 Z2 Z3 Z4])
ans =
1.0000 5.3458 0.0000 0.2079
>> imag([Z1 Z2 Z3 Z4])
ans =
0 1.9759 -1.0000 0
>> abs([Z1 Z2 Z3 Z4])
ans =
1.0000 5.6993 1.0000 0.2079
>> angle([Z1 Z2 Z3 Z4])
ans =
0 0.3541 -1.5708 0
EXERCISE 5-4
Consider the 3×3 matrix M whose elements are the squares of the first nine positive integers, multiplied by the imaginary unit (reading from left to right and top to bottom).
Find the square, the square root and the exponential to base 2 and – 2 of M.
Find the elementwise Naperian logarithm and base e exponential of M.
Find eMand log(M).
>> M=i*[1 2 3;4 5 6;7 8 9]
M =
0 + 1.0000i 0 + 2.0000i 0 + 3.0000i
0 + 4.0000i 0 + 5.0000i 0 + 6.0000i
0 + 7.0000i 0 + 8.0000i 0 + 9.0000i
>> C=M^2
C =
-30 -36 -42
-66 -81 -96
-102 -126 -150
>> D=M^(1/2)
D =
0.8570 - 0.2210i 0.5370 + 0.2445i 0.2169 + 0.7101i
0.7797 + 0.6607i 0.9011 + 0.8688i 1.0224 + 1.0769i
0.7024 + 1.5424i 1.2651 + 1.4930i 1.8279 + 1.4437i
>> 2^M
ans =
0.7020 - 0.6146i -0.1693 - 0.2723i -0.0407 + 0.0699i
-0.2320 - 0.3055i 0.7366 - 0.3220i -0.2947 - 0.3386i
-0.1661 + 0.0036i -0.3574 - 0.3717i 0.4513 - 0.7471i
>> (-2)^M
ans =
17.3946 - 16.8443i 4.3404 - 4.5696i -7.7139 + 7.7050i
1.5685 - 1.8595i 1.1826 - 0.5045i -1.2033 + 0.8506i
-13.2575 + 13.1252i -3.9751 + 3.5607i 6.3073 - 6.0038i
>> log(M)
ans =
0 + 1.5708i 0.6931 + 1.5708i 1.0986 + 1.5708i
1.3863 + 1.5708i 1.6094 + 1.5708i 1.7918 + 1.5708i
1.9459 + 1.5708i 2.0794 + 1.5708i 2.1972 + 1.5708i
>> exp(M)
ans =
0.5403 + 0.8415i -0.4161 + 0.9093i -0.9900 + 0.1411i
-0.6536 - 0.7568i 0.2837 - 0.9589i 0.9602 - 0.2794i
0.7539 + 0.6570i -0.1455 + 0.9894i -0.9111 + 0.4121i
>> logm(M)
ans =
-5.4033 - 0.8472i 11.9931 - 0.3109i -5.3770 + 0.8846i
12.3029 + 0.0537i -22.3087 + 0.8953i 12.6127 + 0.4183i
-4.7574 + 1.6138i 12.9225 + 0.7828i -4.1641 + 0.6112i
>> expm(M)
ans =
0.3802 - 0.6928i -0.3738 - 0.2306i -0.1278 + 0.2316i
-0.5312 - 0.1724i 0.3901 - 0.1434i -0.6886 - 0.1143i
-0.4426 + 0.3479i -0.8460 - 0.0561i -0.2493 - 0.4602i
EXERCISE 5-5
Consider the vector sum Z of the complex vector V = (i,-i, i) and the real vector R = (0,1,1). Find the mean, median, standard deviation, variance, sum, product, maximum and minimum of the elements of V, as well as its gradient, the discrete Fourier transform and its inverse.
>> Z=[i,-i,i]
Z =
0 + 1.0000i 0 - 1.0000i 0 + 1.0000i
>> R=[0,1,1]
R =
0 1 1
>> V=Z+R
V =
0 + 1.0000i 1.0000 - 1.0000i 1.0000 + 1.0000i
>> [mean(V),median(V),std(V),var(V),sum(V),prod(V),max(V),min(V)]'
ans =
0.6667 - 0.3333i
1.0000 + 1.0000i
1.2910
1.6667
2.0000 - 1.0000i
0 - 2.0000i
1.0000 + 1.0000i
0 - 1.0000i
>> gradient(V)
ans =
1.0000 - 2.0000i 0.5000 0 + 2.0000i
>> fft(V)
ans =
2.0000 + 1.0000i -2.7321 + 1.0000i 0.7321 + 1.0000i
>> ifft(V)
ans =
0.6667 + 0.3333i 0.2440 + 0.3333i -0.9107 + 0.3333i
EXERCISE 5-6
Given the following matrices:
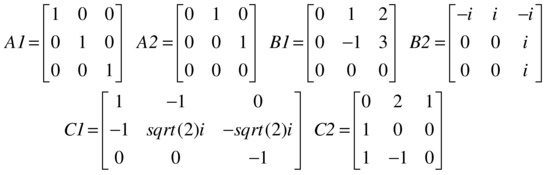
First calculate A1 + A2, B1-B2 and C1 + C2.
Then calculate AB - BA, A2 + B2 + C2, ABC, sqrt (A) + sqrt (B) - sqrt(C), (eB+ eC), their transposes and their inverses.
Finally check that any matrix multiplied by its inverse yields the identity matrix
>> A1=eye(3)
A1 =
1 0 0
0 1 0
0 0 1
>> A2=[0 1 0; 0 0 1;0 0 0]
A2 =
0 1 0
0 0 1
0 0 0
>> A= A1+A2
A =
1 1 0
0 1 1
0 0 1
>> B1=[0 1 2;0 -1 3;0 0 0]
B1 =
0 1 2
0 -1 3
0 0 0
>> B2=[-i i -i;0 0 i;0 0 i]
B2 =
0 - 1.0000i 0 + 1.0000i 0 - 1.0000i
0 0 0 + 1.0000i
0 0 0 + 1.0000i
>> B=B1-B2
B =
0 + 1.0000i 1.0000 - 1.0000i 2.0000 + 1.0000i
0 -1.0000 3.0000 - 1.0000i
0 0 0 - 1.0000i
>> C1=[1, -1, 0;-1,sqrt(2)*i,-sqrt(2)*i;0,0,-1]
C1 =
1.0000 -1.0000 0
-1.0000 0 + 1.4142i 0 - 1.4142i
0 0 -1.0000
>> C2=[0 2 1;1 0 0;1 -1 0]
C2 =
0 2 1
1 0 0
1 -1 0
>> C=C1+C2
C =
1.0000 1.0000 1.0000
0 0 + 1.4142i 0 - 1.4142i
1.0000 -1.0000 -1.0000
>> M1=A*B-B*A
M1 =
0 -1.0000 - 1.0000i 2.0000
0 0 1.0000 - 1.0000i
0 0 0
>> M2=A^2+B^2+C^2
M2 =
2.0000 2.0000 + 3.4142i 3.0000 - 5.4142i
0 - 1.4142i -0.0000 + 1.4142i 0.0000 - 0.5858i
0 2.0000 - 1.4142i 2.0000 + 1.4142i
>> M3=A*B*C
M3 =
5.0000 + 1.0000i -3.5858 + 1.0000i -6.4142 + 1.0000i
3.0000 - 2.0000i -3.0000 + 0.5858i -3.0000 + 3.4142i
0 - 1.0000i 0 + 1.0000i 0 + 1.0000i
>> M4=sqrtm(A)+sqrtm(B)-sqrtm(C)
M4 =
0.6356 + 0.8361i -0.3250 - 0.8204i 3.0734 + 1.2896i
0.1582 - 0.1521i 0.0896 + 0.5702i 3.3029 - 1.8025i
-0.3740 - 0.2654i 0.7472 + 0.3370i 1.2255 + 0.1048i
>> M5=expm(A)*(expm(B)+expm(C))
M5 =
14.1906 - 0.0822i 5.4400 + 4.2724i 17.9169 - 9.5842i
4.5854 - 1.4972i 0.6830 + 2.1575i 8.5597 - 7.6573i
3.5528 + 0.3560i 0.1008 - 0.7488i 3.2433 - 1.8406i
>> inv(A)
ans =
1 -1 1
0 1 -1
0 0 1
>> inv(B)
ans =
0 - 1.0000i -1.0000 - 1.0000i -4.0000 + 3.0000i
0 -1.0000 1.0000 + 3.0000i
0 0 0 + 1.0000i
>> inv(C)
ans =
0.5000 0 0.5000
0.2500 0 - 0.3536i -0.2500
0.2500 0 + 0.3536i -0.2500
>> [A*inv(A) B*inv(B) C*inv(C)]
ans =
1 0 0 1 0 0 1 0 0
0 1 0 0 1 0 0 1 0
0 0 1 0 0 1 0 0 1
>> A'
ans =
1 0 0
1 1 0
0 1 1
>> B'
ans =
0 - 1.0000i 0 0
1.0000 + 1.0000i -1.0000 0
2.0000 - 1.0000i 3.0000 + 1.0000i 0 + 1.0000i
>> C'
ans =
1.0000 0 1.0000
1.0000 0 - 1.4142i -1.0000
1.0000 0 + 1.4142i -1.0000
EXERCISE 5-7
Apply the sine, base e exponential, logarithm, square root, modulus, argument and rounding functions to each of the following matrices:

Calculate eBand ln(A)
>> A=[1 2 3; 4 5 6; 7 8 9]
A =
1 2 3
4 5 6
7 8 9
>> sin(A)
ans =
0.8415 0.9093 0.1411
-0.7568 -0.9589 -0.2794
0.6570 0.9894 0.4121
>> B=[1+i 2+i;3+i,4+i]
B =
1.0000 + 1.0000i 2.0000 + 1.0000i
3.0000 + 1.0000i 4.0000 + 1.0000i
>> sin(B)
ans =
1.2985 + 0.6350i 1.4031 - 0.4891i
0.2178 - 1.1634i -1.1678 - 0.7682i
>> exp(A)
ans =
1.0e+003 *
0.0027 0.0074 0.0201
0.0546 0.1484 0.4034
1.0966 2.9810 8.1031
>> exp(B)
ans =
1.4687 + 2.2874i 3.9923 + 6.2177i
10.8523 + 16.9014i 29.4995 + 45.9428i
>> log(B)
ans =
0.3466 + 0.7854i 0.8047 + 0.4636i
1.1513 + 0.3218i 1.4166 + 0.2450i
>> sqrt(B)
ans =
1.0987 + 0.4551i 1.4553 + 0.3436i
1.7553 + 0.2848i 2.0153 + 0.2481i
>> abs(B)
ans =
1.4142 2.2361
3.1623 4.1231
>> imag(B)
ans =
1 1
1 1
>> fix(sin(B))
ans =
1.0000 1.0000
0 - 1.0000i - 1.0000
>> ceil(log(A))
ans =
0 1 2
2 2 2
2 3 3
>> sign(B)
ans =
0.7071 + 0.7071i 0.8944 + 0.4472i
0.9487 + 0.3162i 0.9701 + 0.2425i
The exponential functions, square root and logarithm used above apply element to element to the array, and have nothing to do with the matrix exponential and logarithmic functions that are used below.
>> expm(B)
ans =
1.0e+002 *
-0.3071 + 0.4625i -0.3583 + 0.6939i
-0.3629 + 1.0431i -0.3207 + 1.5102i
>> logm(A)
ans =
-5.6588 + 2.7896i 12.5041 - 0.4325i -5.6325 - 0.5129i
12.8139 - 0.7970i -23.3307 + 2.1623i 13.1237 - 1.1616i
-5.0129 - 1.2421i 13.4334 - 1.5262i -4.4196 + 1.3313i
EXERCISE 5-8
Solve the following equation in the complex field:
sin (z) = 2.
>> vpa (solve ('sin (z) = 2'))
ans =
1.316957896924816708625046347308 * i + 1.5707963267948966192313216916398
1.5707963267948966192313216916398 1.316957896924816708625046347308 * i
EXERCISE 5-9
Solve the following equations:
a. 1+x+x2 +x3 +x4 +x5 = 0
b. x2 +(6-i)x+8-4i = 0
c. tan (Z) = 3i/5
>> solve('1+x+x^2+x^3+x^4+x^5 = 0')
ans =
-1
-1/2 - (3-^(1/2) * i) / 2
1/2 - (3-^(1/2) * i) / 2
-1/2 + (3 ^(1/2) * i) / 2
1/2 + (3 ^(1/2) * i) / 2
>> solve ('x ^ 2 +(6-i) * x + 8-4 * i = 0')
ans =
-4
i 2
>> vpa (solve ('tan (Z) = 3 * i/5 '))
ans =
0.69314718055994530941723212145818 * i
EXERCISE 5-10
Find the results of the following operations:
a. the fourth root of - 1 and 1;
b. the fifth roots of 2 + 2i and - 1 + i√3;
c. the real part of tan (iLn ((a+ib) / (a-ib)));
d. the imaginary part of (2 + i)cos(4+i) .
>> solve('x^4+1=0')
ans =
2 ^(1/2) *(-i/2-1/2)
2 ^(1/2) *(i/2-1/2)
2 ^(1/2) *(1/2-i/2)
2 ^(1/2) *(i/2 + 1/2)
>> pretty (solve('x^4+1=0'))
+- -+
| 1/2 / i 1 |
| 2 | - - - - | |
| 2 2 / |
| |
| 1/2 / i 1 |
| 2 | - - - | |
| 2 2 / |
| |
| 1/2 / 1 i |
| 2 | - - - | |
| 2 2 / |
| |
| 1/2 / i 1 |
| 2 | - + - | |
| 2 2 / |
+- -+
>> solve('x^4-1=0')
ans =
-1
1
-i
i
>> vpa(solve('x^5-2-2*i=0'))
ans =
0.19259341768888084906125263406469 * i + 1.2159869826496146992458377919696
-0.87055056329612413913627001747975 * i - 0.87055056329612413913627001747975
0.55892786746600970394985946846702 * i - 1.0969577045083811131206798770216
0.55892786746600970394985946846702 1.0969577045083811131206798770216 * i
1.2159869826496146992458377919696 * i + 0.19259341768888084906125263406469
>> vpa(solve('x^5+1-sqrt(3)*i=0'))
ans =
0.46721771281818786757419290603946 * i + 1.0493881644090691705137652947201
1.1424056652180689506550734259384 * i - 0.1200716738059215411240904754285
0.76862922680258900220179378744147 0.85364923855044142809268986292246 * i
-0.99480195671282768870147766609475 * i - 0.57434917749851750339931347338896
0.23882781722701229856490119703938 * i - 1.1235965399072191281921551333441
>> simplify (vpa (real (tan (i * log ((a+i*b) /(a-i*b))))))
ans =
-0.5 * tanh (conj (log ((a^2 + 2.0*a*b*i-1.0*b^2) /(a^2 + b^2))) * i + (0.5 * ((a^2 + 2.0*a*b*i-1.0*b^2) ^ 2 /(a^2 + b^2) ^ 2 - 1) * i) / ((a^2 + 2.0*a*b*i-1.0*b^2) ^ 2 /(a^2 + b^2) ^ 2 + 1))
>> simplify(vpa(imag((2+i)^cos(4-i))))
ans =
-0.62107490808037524310236676683417

