6
Tension–Compression in a Cylindrical Rod
6.1. Tension–compression without transverse deformation
Consider a cylindrical rod of length L, radius R, density ρ and Young’s modulus E; assume that it is vibrating longitudinally and at first only its longitudinal deformation εx is considered, and the corresponding displacement u, at any point x (-L/2≤x≤+L/2). Then the following relation can be written:
The energies corresponding to deformation T and displacement V can be written as:
The vibration resonance is characterized by a harmonic function of displacement whose general form is f(x,y,z,t)=f(x,y,z)sin(2πFLt), where FL is the resonance frequency. The integration over a period T=1/FL therefore yields:
In what follows, this relation is systematically used at any speed in the displacement energy. The spatial Lagrangian can be written in a timeindependent form:
Hamilton’s principle or Lagrange’s least action principle yields:
The integration by parts of the first integral term first yields a boundary condition (in L/2 and –L/2):
Then, the new minimization is:
This yields the general equation of vibration that is valid along the whole cylinder:
It is a dimensionless differential equation whose mathematical solution takes the form u(x)=sin(nπx/L), where n is an integer greater than or equal to 1. This makes it possible to establish the analytical relation between the resonance frequency and Young’s modulus:
This elementary example is an illustration of the formalism for a very simple case.
6.2. Tension–compression with transverse deformation
More realistically, transverse radial deformation is added to the previous problem:
Since εx does not depend on r, the integration with respect to r yields:
Potential and kinetic energies then become:
The writing grows in complexity, being two-dimensional. After integration with respect to r, the Lagrangian becomes one-dimensional, which can be written as:
The Lagrangian is minimized and u(x) is determined in exactly the same way as for the transverse deformation:
The integration by parts yields the same boundary condition. However, the new equation of vibration of harmonic k becomes:
If R<<L, then equation [5.2] is obtained, and E and ν can be deduced from equations [5.3] and [5.4].
6.3. Determination of E and ν of isotropic and anisotropic materials
As an example, an isotropic titanium alloy was studied as a function of temperature using this method, and the evolution of elasticity data is represented in Figure 6.1.
The evolution of Young’s modulus with temperature presents no scattering. While a clear increase in Poisson’s ratio with temperature can be noted (as described in section 2.1 of Chapter 2), a certain scattering due to the problems presented in section 5.1 of Chapter 5 can be observed. The same scattering is found with the AM1 superalloy whose evolution with temperature (Figure 6.2) was already mentioned in Chapter 5, but with bending and torsion measurements.
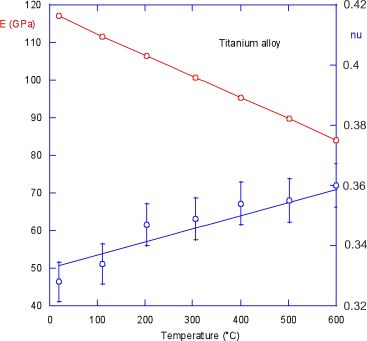
Figure 6.1. Elasticity as a function of temperature for an isotropic titanium alloy. Tension–compression test. For a color version of this figure, see www.iste.co.uk/gadaud/elasticity.zip

Figure 6.2. Elasticity as a function of temperature for an anisotropic superalloy. Tension–compression test along a <100> direction. For a color version of this figure, see www.iste.co.uk/gadaud/elasticity.zip
Honestly speaking, it is a tedious task for the experimenter to reach a given temperature, stabilize at this temperature in order to detect the fundamental resonance frequency and its harmonics, repeat the operation throughout the temperature range of the study and finally face the difficulty of detecting the harmonics. This task is increasingly burdensome with temperature.
These are the reasons why this historical measurement technique was abandoned, which was replaced by the torsion tests described in Chapter 8 in addition to bending.
