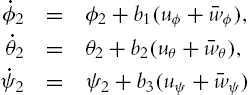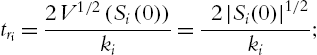Search in book...
Toggle Font Controls
Create new playlist

Name your new playlist

Playlist description (optional)
Sign In

Email address

Password

Forgot Password?

or

Continue with Facebook

Continue with Google
Sign Up

Full Name

Email address

Confirm Email Address

Password

or

Continue with Facebook

Continue with Google

Chapter 7

Sliding Mode Control^*

Abstract

The sliding controllers are becoming popular when working with aerial vehicles. They are generally used for their good performance and robustness properties in the presence of unknown perturbations. They are often used in nonlinear systems despite their greatest weakness to produce chattering in the control inputs. In this chapter two results are presented: on the one hand, a methodology is described to represent the nonlinear and perturbed attitude dynamics of a quadcopter in a linear and perturbed attitude system as mostly used in several works, and, on the other hand, a robust sliding mode algorithm with an integral component is conceived and validated to stabilize this system. Graphs obtained from simulation and experimental results introduce good performance of the closed-loop system even in the presence of several disturbances and noise in the states.

Keywords

Sliding mode control; Nonlinear MIMO system; Attitude dynamics; Quadcopter vehicle; Real-time validation

Controlling the attitude dynamics of a drone is an essential task when working with aerial vehicles. This dynamics has a nonlinear nature included in the Coriolis matrix, see Chap. 2. It was demonstrated in previous chapters that generally this dynamics is used to conceive control algorithms in its linear or simplified nonlinear mode. Nevertheless, it is also possible to represent these nonlinear equations as linear and perturbed equations, implying the design of controllers in an easy way. Nonlinear controllers are becoming popular when working with UAVs because they can be robust with respect to unknown perturbations such as wind present in the environment. Several researchers have proposed countless algorithms to stabilize the attitude of the aerial vehicle. The sliding mode approach becomes an essential tool due to its robustness and quick dynamics to converge the states. This methodology has been extensively studied in many works, see [1–5].

In this chapter the sliding mode and singular optimal control methodologies are used to design nonlinear controllers to stabilize the nonlinear attitude of a quadcopter vehicle. Two results are introduced here: first, a new form to represent the nonlinear equations for the orientation of a VTOL¹ vehicle in the presence of unknown disturbances as a linear MIMO and perturbed system is presented, and second, a control law is proposed and validated in simulations and in real time to stabilize the attitude of a quadcopter.

7.1 From the Nonlinear Attitude Representation to Linear MIMO Expression

The simplest form to represent the orientation of a quadcopter or VTOL vehicle is to consider two integrators in cascade with external perturbations as follows:

$\ddot{η} = u_{η} + w_{η},$

(7.1)

$\dot{x} = \bar{A} x + {\bar{B}}_{1} u_{η} + {\bar{B}}_{2} w_{η} with x = [η_{1} η_{2}],$

(7.2)

where η represents the attitude vector with η being ϕ, θ, or ψ, i.e., the Euler angles, roll, pitch, and yaw, respectively, $u_{η}$ defines the control input, and $w_{η}$ the unknown and external perturbation. Even if this representation is experimentally valid for small angles, it does not represent the Coriolis and aerodynamic effects that the aerial vehicle experiences and can generate undesirable dynamics in flight when the vehicle moves quickly.

Studying the complete nonlinear attitude equations to design the controller can be an arduous task; nevertheless, some authors prefer to consider the strongest terms in the orientation to represent their model. These equations are described in the following and, considering our experience with quadcopters, they closely represent the attitude of a quadrotor vehicle:

$\begin{matrix} \ddot{ϕ} = \dot{θ} \dot{ψ} (\frac{I_{y} - I_{z}}{I_{x}}) - \frac{I_{r}}{I_{x}} \dot{θ} Ω + \frac{l}{I_{x}} u_{ϕ} + w_{ϕ}, \\ \ddot{θ} = \dot{ϕ} \dot{ψ} (\frac{I_{z} - I_{x}}{I_{y}}) - \frac{I_{r}}{I_{y}} \dot{ϕ} Ω + \frac{l}{I_{y}} u_{θ} + w_{θ}, \\ \ddot{ψ} = \dot{θ} \dot{ϕ} (\frac{I_{x} - I_{y}}{I_{z}}) + \frac{l}{I_{z}} u_{ψ} + w_{ψ}, \end{matrix}$

(7.3)

where the distance from each motor to the gravity center of the vehicle is denoted by l. The inertia of the vehicle in each axis is defined by $I_{x}$ , $I_{y}$ , and $I_{z}$ while the inertia of the motor is represented by $I_{r}$ , and the speed of the rotor is defined by Ω.

Notice that system (7.3) is quite different from (7.1) even if the unknown disturbances or uncertainties, $w_{η}$ , are also considered in the model. We study the system with bounded perturbations because it is obvious that the physical characteristics of the vehicle (power motors, etc.) are not unlimited, and, as a consequence, the perturbations need to be bounded, i.e., $| w_{η} | ≦ L_{η}$ , where $L_{η}$ is a constant that defines the amplitude of each perturbation.

Theorem 7.1

System (7.3) is equivalent to system

$\dot{x} = A x + B (u + \bar{w})$

(7.4)

with $x = {(ϕ_{1} θ_{1} ψ_{1} ϕ_{2} θ_{2} ψ_{2})}^{T}$ , $u = {(u_{ϕ} u_{θ} u_{ψ})}^{T}$ ,

$\bar{w} = (\begin{matrix} \frac{θ_{2} (ψ_{2} (\frac{I_{y} - I_{z}}{I_{x}}) - \frac{I_{r}}{I_{x}} Ω) - ϕ_{2} + w_{ϕ}}{\frac{l}{I_{x}}} \\ \frac{ϕ_{2} (ψ_{2} (\frac{I_{z} - I_{x}}{I_{y}}) - \frac{I_{r}}{I_{y}} Ω) - θ_{2} + w_{θ}}{\frac{l}{I_{y}}} \\ \frac{θ_{2} ϕ_{2} (\frac{I_{x} - I_{y}}{I_{z}}) - ψ_{2} + w_{ψ}}{\frac{l}{I_{z}}} \end{matrix}), \begin{matrix} A = (\begin{matrix} 0_{3 \times 3} \\ 0_{3 \times 3} \end{matrix} \begin{matrix} I_{3 \times 3} \\ I_{3 \times 3} \end{matrix}), \\ B = (\begin{matrix} 0_{3 \times 3} \\ B_{2} \end{matrix}), \\ B_{2} = (\begin{matrix} \frac{l}{I_{x}} & 0 & 0 \\ 0 & \frac{l}{I_{y}} & 0 \\ 0 & 0 & \frac{l}{I_{z}} \end{matrix}) . \end{matrix}$

Proof

Consider $γ_{1} = (\frac{I_{y} - I_{z}}{I_{x}})$ , $γ_{2} = (\frac{I_{z} - I_{x}}{I_{y}})$ , $γ_{3} = (\frac{I_{x} - I_{y}}{I_{z}})$ , $β_{1} = \frac{I_{r}}{I_{x}} Ω$ , $β_{2} = \frac{I_{r}}{I_{y}} Ω$ , $b_{1} = \frac{l}{I_{x}}$ , $b_{2} = \frac{l}{I_{y}}$ , and $b_{3} = \frac{l}{I_{z}}$ . Define $ϕ_{1} = ϕ$ , $θ_{1} = θ$ , $ψ_{1} = ψ$ , ${\dot{ϕ}}_{1} = ϕ_{2}$ , ${\dot{θ}}_{1} = θ_{2}$ , and ${\dot{ψ}}_{1} = ψ_{2}$ .

Then, rewriting (7.3) it follows that

$\begin{matrix} {\dot{ϕ}}_{1} & = ϕ_{2}, & {\dot{ϕ}}_{2} & = θ_{2} (ψ_{2} γ_{1} - β_{1}) + b_{1} u_{ϕ} + w_{ϕ}, \\ {\dot{θ}}_{1} & = θ_{2}, & {\dot{θ}}_{2} & = ϕ_{2} (ψ_{2} γ_{2} - β_{2}) + b_{2} u_{θ} + w_{θ}, \\ {\dot{ψ}}_{1} & = ψ_{2}, & {\dot{ψ}}_{2} & = θ_{2} ϕ_{2} γ_{3} + b_{3} u_{ψ} + w_{ψ} . \end{matrix}$

(7.5)

To simplify the analysis, define $f_{1} = θ_{2} (ψ_{2} γ_{1} - β_{1})$ , $f_{2} = ϕ_{2} (ψ_{2} γ_{2} - β_{2})$ , and $f_{3} = θ_{2} ϕ_{2} γ_{3}$ . Taking the three right equations of (7.5), we obtain

$\begin{matrix} {\dot{ϕ}}_{2} & = & ϕ_{2} - ϕ_{2} + f_{1} + b_{1} u_{ϕ} + w_{ϕ}, \\ {\dot{θ}}_{2} & = & θ_{2} - θ_{2} + f_{2} + b_{2} u_{θ} + w_{θ}, \\ {\dot{ψ}}_{2} & = & ψ_{2} - ψ_{2} + f_{3} + b_{3} u_{ψ} + w_{ψ} . \end{matrix}$

Define $Φ_{1} = f_{1} - ϕ_{2}$ , $Φ_{2} = f_{2} - θ_{2}$ , and $Φ_{3} = f_{3} - ψ_{2}$ . Then

$\begin{matrix} {\dot{ϕ}}_{2} & = & ϕ_{2} + b_{1} (u_{ϕ} + {\bar{w}}_{ϕ}), \\ {\dot{θ}}_{2} & = & θ_{2} + b_{2} (u_{θ} + {\bar{w}}_{θ}), \\ {\dot{ψ}}_{2} & = & ψ_{2} + b_{3} (u_{ψ} + {\bar{w}}_{ψ}) \end{matrix}$

with ${\bar{w}}_{i} = (Φ_{i} + w_{η}) / b_{i}$ . Finally, define $η_{i} = {(ϕ_{i} θ_{i} ψ_{i})}^{T}$ , $i = 1, 2$ . Then we can write

$\begin{matrix} {\dot{η}}_{1} & = & η_{2}, \\ {\dot{η}}_{2} & = & η_{2} + B_{2} (u + \bar{w}), \end{matrix}$

which is equivalent to system (7.4).

7.2 Nonlinear Optimal Controller with Integral Sliding Mode Design

The goal is to stabilize the quadcopter attitude using an optimal control u that is robust with respect to perturbations and parameter variations. For this it is necessary to minimize the following singular quadratic cost:

$J (x (t)) = \frac{1}{2} \int_{t_{1}}^{\infty} [x {(t)}^{T} Q x (t)] d t,$

(7.6)

with $Q = Q^{T} > 0$ . The minimization of (7.6) is subject to

$\dot{η_{1}} = η_{2} .$

(7.7)

Developing (7.6), it follows that

$J = \frac{1}{2} \int_{t_{1}}^{\infty} ({η_{1}}^{T} Q_{11} η_{1} + 2 {η_{1}}^{T} Q_{12} η_{2} + {η_{2}}^{T} Q_{22} η_{2}) d t .$

(7.8)

To eliminate the cross terms, the Utkin variable $υ = η_{2} + Q_{22}^{- 1} Q_{12}^{T} η_{1}$ is used. Then

$J = \frac{1}{2} \int_{t_{1}}^{\infty} (η_{1}^{T} Q_{1} η_{1} + υ^{T} Q_{22} υ) d t$

(7.9)

with $Q_{1} = Q_{11} - Q_{12} Q_{22}^{- 1} Q_{12}^{T}$ . Rewriting (7.7) with the Utkin variable yields

$\dot{η_{1}} = A_{1} η_{1} + υ,$

(7.10)

where $A_{1} = - Q_{22}^{- 1} Q_{12}^{T}$ . Then (7.9) is not singular with respect to the variable υ, so that υ is taken as an optimal virtual control variable and is given by

$υ = - Q_{22}^{- 1} P η_{1},$

(7.11)

where $P \in R^{3 \times 3}$ is the solution to the Riccati equation $P A_{1} + A_{1}^{T} P - P Q_{22}^{- 1} P + Q_{1} = 0$ . Introducing the Utkin variable into (7.11), we have

$η_{2} + Q_{22}^{- 1} (Q_{12}^{T} + P) η_{1} = 0 .$

(7.12)

Notice that (7.11) and (7.12) are only true if (7.9) is minimized for all $t_{1} ⩾ 0$ .

Observe that (7.12) is an optimal vector that can be used for designing the vector $S \in R^{3}$ given by

$S = η_{2} + Q_{22}^{- 1} (Q_{12}^{T} + P) η_{1},$

(7.13)

where (7.13) represents the sliding surface vector. Taking the derivative of the previous equation with respect to time gives

$\dot{S} = [I_{3 \times 3} + Q_{22}^{- 1} (Q_{12}^{T} + P)] η_{2} + B_{2} (u + \bar{w}) .$

(7.14)

To remove the linear parts, take u as

$u = B_{2}^{- 1} {\bar{u} - [I_{3 \times 3} + Q_{22}^{- 1} (Q_{12}^{T} + P)] η_{2}} .$

(7.15)

Thus

$\dot{S} = \bar{u} + B_{2} w,$

(7.16)

where $\bar{u}$ is the new controller to assure the convergence of the system. Developing the above, it follows that

$\begin{matrix} (\begin{matrix} {\dot{S}}_{1} \\ {\dot{S}}_{2} \\ {\dot{S}}_{3} \end{matrix}) = (\begin{matrix} {\bar{u}}_{1} + f_{1} - ϕ_{2} + w_{ϕ} \\ {\bar{u}}_{2} + f_{2} - θ_{2} + w_{θ} \\ {\bar{u}}_{3} + f_{3} - ψ_{2} + w_{ψ} \end{matrix}) . \end{matrix}$

To remove the linearities $η_{2}$ , we propose $\bar{u}$ as

$\bar{u} = \begin{matrix} (\begin{matrix} {\bar{u}}_{1} \\ {\bar{u}}_{2} \\ {\bar{u}}_{3} \end{matrix}) = (\begin{matrix} {\bar{v}}_{1} + ϕ_{2} \\ {\bar{v}}_{2} + θ_{2} \\ {\bar{v}}_{3} + ψ_{2} \end{matrix}) . \end{matrix}$

Then, rewrite $\dot{S}$ as

$\dot{S} = (\begin{matrix} {\bar{v}}_{1} + f_{1} + w_{ϕ} \\ {\bar{v}}_{2} + f_{2} + w_{θ} \\ {\bar{v}}_{3} + f_{3} + w_{ψ} \end{matrix}),$

where each ${\dot{S}}_{i} \in \dot{S}$ is represented as

${\dot{S}}_{i} = {\bar{v}}_{i} + f_{i} (η_{1}, η_{2}, t) + w_{η} .$

(7.17)

7.2.1 Convergence of the Sliding Surfaces

In the conventional sliding mode control the robustness property is not guaranteed from the first time instant because the robustness is only guaranteed when the sliding surface reaches zero.

With the integral sliding mode we will be able to compensate nonlinear terms and bounded uncertainties, also the robustness will be guaranteed from the initial time instance. In the following, we introduce variable ${\bar{v}}_{i}$ to stabilize the sliding surfaces.

Then, we propose

${\bar{v}}_{i} = {\bar{v}}_{i 1} + {\bar{v}}_{i 2} .$

(7.18)

• Part ${\bar{v}}_{i 1}$ will be responsible of compensating the nonlinear terms $f_{i}$ and the bounded disturbance $w_{η}$ from the beginning.

• Component ${\bar{v}}_{i 2}$ will make sure that each sliding surface $S_{i}$ reaches the optimal surface $S_{i} = 0$ at a defined finite time $t_{1}$ taking in consideration that the perturbations $f_{i}$ and $w_{η}$ have been compensated from the initial time instance $t = 0$ .

Design of ${\bar{v}}_{i 1}$

For ${\bar{v}}_{i 1}$ we propose a new auxiliary surface $σ_{i}$ with $i = 1, 2, 3$ given by²

${\begin{matrix} σ_{i} = S_{i} - Z_{i}, \\ {\dot{Z}}_{i} = {\bar{v}}_{i 2} . \end{matrix}$

(7.19)

It should be mentioned that ${\bar{v}}_{i 1}$ is designed as a conventional sliding mode control. This means that for the stability analysis a candidate Lyapunov function could be used. Therefore

$V (σ_{i}) = \frac{1}{2} σ_{i}^{2} > 0 .$

(7.20)

The asymptotic stability of (7.19) at the equilibrium point 0 can be proved if the following conditions are satisfied:

$(a) \lim_{| σ_{i} | \to \infty} V = \infty,$

(7.21)

$(b) \dot{V} < 0 for σ_{i} \neq 0 .$

(7.22)

Condition (a) is obviously satisfied by V in (7.20). Nevertheless, the finite-time convergence (global finite-time stability) could be achieved if condition (b) is modified as

$\dot{V} ⩽ - α_{i} V^{1 / 2}, α_{i} > 0 .$

(7.23)

Indeed, separating variables and integrating inequality (7.23) over the time interval $0 ⩽ τ ⩽ t$ , we obtain

$V^{1 / 2} (σ_{i} (t)) ⩽ - \frac{1}{2} α_{i} t + V^{1 / 2} (σ_{i} (0)),$

(7.24)

and, considering that $V (σ_{i} (t))$ reaches zero in finite time $t_{r}$ , get

$t_{r} ⩽ \frac{2 V^{1 / 2} (σ_{i} (0))}{α_{i}} .$

(7.25)

Therefore control ${\bar{v}}_{i 1}$ that satisfies (7.23) will drive $σ_{i}$ to zero in finite time $t_{r}$ and will keep it at zero $\forall t ⩾ t_{r}$ .

Now notice that (7.23) can be written as

$σ_{i} {\dot{σ}}_{i} ⩽ - {\bar{α}}_{i} | σ_{i} |, {\bar{α}}_{i} = \frac{α_{i}}{\sqrt{2}}, {\bar{α}}_{i} > 0 .$

(7.26)

Consequently, from the above and with (7.17), (7.18) and (7.19) we have

$\begin{matrix} σ_{i} ⁎ (\dot{S_{i}} - {\dot{Z}}_{i}) & = σ_{i} ⁎ ({\bar{v}}_{i 1} + {\bar{v}}_{i 2} + f_{i} (η_{1}, η_{2}, t) + w_{η} - {\bar{v}}_{i 2}) \\ = σ_{i} ⁎ ({\bar{v}}_{i 1} + f_{i} (η_{1}, η_{2}, t) + w_{η}), \end{matrix}$

and, selecting ${\bar{v}}_{i 1} = - ρ_{i} sgn (σ_{i})$ , condition (7.26) is fulfilled if and only if

$ρ_{i} = {\bar{α}}_{i} + | f_{i} (η_{1}, η_{2}, t) | + L_{η} .$

(7.27)

Notice that (7.27) represents the necessary gains for ensuring the finite time stability in a bounded finite time $t_{r}$ , which means

$t_{r} ⩽ \frac{2 V^{1 / 2} (σ_{i} (0))}{α_{i}} = \frac{| σ_{i} (0) |}{\bar{α}} .$

(7.28)

The above implies that $σ_{i} = {\dot{σ}}_{i} = 0$ for all $t ⩾ t_{r}$ , then the condition ${\dot{σ}}_{i} = 0$ produces

${\dot{σ}}_{i} = \underset{{\bar{v}}_{i 1}}{\underset{︸}{- ρ_{i} sgn (σ_{i})}} + f_{i} (η_{1}, η_{2}, t) + w_{η} = 0 \forall t ⩾ t_{r},$

meaning that $- ρ_{1} sgn (σ_{i})$ will compensate the perturbative terms $f_{i} (η_{1}, η_{2}, t) + w_{η}$ only during the reaching phase.

In the following, to eliminate the reaching phase, we observe in (7.28) that proposing $σ_{i} (0) = 0$ will imply $t_{r} = 0$ and as a result $σ_{i} = {\dot{σ}}_{i} = 0$ for all $t ⩾ 0$ .

Based on the above considerations, we present the next result

${\bar{v}}_{i 1} = - ρ_{i} sgn (σ_{i}) = - (f_{i} (η_{1}, η_{2}, t) + w_{η}), \forall t ⩾ 0$

if and only if $σ_{i} (0) = 0$ .

Therefore control ${\bar{v}}_{i 1} = - ρ_{i} sgn (σ_{i})$ compensates $f_{i} (η_{1}, η_{2}, t) + w_{η}$ for all $t ⩾ 0$ if and only if $σ_{i} (0) = 0$ .

Now considering that control ${\bar{v}}_{i 1}$ accomplishes $σ_{i} (t) = 0$ for all $t ⩾ 0$ and due to (7.19), it follows that $S_{i} (t) = Z_{i} (t)$ for all $t ⩾ 0$ . Therefore (7.19) can be rewritten as

${\begin{matrix} S_{i} = Z_{i}, \\ {\dot{Z}}_{i} = {\bar{v}}_{i 2}, \end{matrix} with Z_{i} (0) = S_{i} (0) .$

(7.29)

Then considering (7.29) we have

${\dot{S}}_{i} = {\bar{v}}_{i 2} .$

The next step is to design ${\bar{v}}_{i 2}$ such that $S_{i}$ converges to zero in finite time.

Design of ${\bar{v}}_{i 2}$

In order to achieve global finite-time stability at the optimal sliding surfaces $S_{i} = 0$ , we introduce ${\bar{v}}_{i 2} = - k_{i} {| S_{i} |}^{1 / 2} sgn (S_{i})$ ; then ${\dot{S}}_{i}$ is written as

${\dot{S}}_{i} = - k_{i} {| S_{i} |}^{1 / 2} sgn (S_{i}) .$

(7.30)

The following Lyapunov function is proposed to prove that (7.30) converges to zero in finite time:

$V (S_{i}) = | S_{i} | > 0 .$

(7.31)

The previous equations must satisfy conditions (7.22). Observe that, by definition (7.31), condition (a) is achieved; to fulfill condition (b), we use (7.23). Notice that when introducing (7.31) into (7.23) an equivalent modified condition is obtained, which is given by

$\frac{S_{i} {\dot{S}}_{i}}{| S_{i} |} ⩽ - α_{i} {| S_{i} |}^{1 / 2} .$

(7.32)

Introducing (7.30) into (7.32), the previous inequality becomes

$- k_{i} {| S_{i} |}^{1 / 2} ⩽ - α_{i} {| S_{i} |}^{1 / 2} .$

(7.33)

Therefore to satisfy (7.33) each gain $k_{i}$ must be equal to $α_{i}$ , meaning that $k_{i} > 0$ , and this implies that

$\dot{V} = - α_{i} V^{1 / 2} if k_{i} = α_{i} > 0 .$

Observe that the finite-time convergence time $t_{r_{i}}$ will not be bounded, it will be exactly equal to

$t_{r_{i}} = \frac{2 V^{1 / 2} (S_{i} (0))}{k_{i}} = \frac{2 {| S_{i} (0) |}^{1 / 2}}{k_{i}};$

(7.34)

consequently, $S_{i} = 0$ in a finite time $t_{r_{i}}$ . Observe that (7.34) represents the finite-time convergence of each $S_{i}$ to the optimal sliding surface $S_{i} = 0$ . With the purpose that each $S_{i}$ has the same finite time convergence, we fix $t_{r_{i}} = t_{1} = cte$ ,³ then we will be able to design the gains $k_{i}$ in order to have $S_{1} (t_{1}) = S_{2} (t_{1}) = \dots = S_{n} (t_{1}) = 0$ .

Fixing $t_{r_{i}} = t_{1} = cte$ , the necessary gains for getting $S_{i} (t_{1}) = 0$ can be obtained with $k_{i} = \frac{2 {| S_{i} (0) |}^{1 / 2}}{t_{1}}$ .

Summarizing the methodology, it follows that when considering (7.17) and the fact that ${\bar{v}}_{i} = {\bar{v}}_{i 1} + {\bar{v}}_{i 2}$ , we have

${\dot{S}}_{i} = \underset{{\bar{v}}_{i 1}}{\underset{︸}{- ρ_{i} sgn (S_{i} - Z_{i})}} + \underset{{\bar{v}}_{i 2}}{\underset{︸}{(- k_{i} {| S_{i} |}^{1 / 2} sgn (S_{i}))}} + f_{i} + w_{η}$

with gains

$ρ_{i} = {\bar{α}}_{i} + | f_{i} (η_{1}, η_{2}, t) | + L_{η} and k_{i} = \frac{2 {| S_{i} (0) |}^{1 / 2}}{t_{1}} .$

(7.35)

• Component ${\bar{v}}_{i 1}$ will compensate the perturbative terms $f_{i} (η_{1}, η_{2}, t) + w_{η}$ for all $t ⩾ 0$ if and only if $Z_{i} (0) = S_{i} (0)$ .

• Considering that the perturbative terms have been compensated from the initial time, control ${\bar{v}}_{i 2}$ will ensure that every $S_{i}$ will converge to the optimal sliding surface $S_{i} = 0$ in a fixed reaching time $t_{1}$ .

Therefore, component ${\bar{u}}_{i}$ from (7.15) is given by

$\begin{matrix} {\bar{u}}_{i} = - ρ_{i} sgn (S_{i} - Z_{i}) - k_{i} {| S_{i} |}^{1 / 2} sgn (S_{i}) + η_{2_{i}}, \\ Z_{i} = - k_{i} \int {| S_{i} |}^{1 / 2} sgn (S_{i}) d t with Z_{i} (0) = S_{i} (0), \end{matrix}$

(7.36)

and gains $t_{1} = cte$ and ${\bar{α}}_{i} = \frac{α_{i}}{\sqrt{2}}$ in (7.35).

7.3 Numerical Validation

Simulations are realized to validate the proposed controllers. From section 7.1 notice that (7.3) can be expressed in regular form as

$\begin{matrix} {\dot{η}}_{1} & = & η_{2}, \\ {\dot{η}}_{2} & = & η_{2} + B_{2} (u + \bar{w}), \end{matrix}$

where $η_{1} = {(ϕ_{1}, θ_{1}, ψ_{1})}^{T}$ and $η_{2} = {(ϕ_{2}, θ_{2}, ψ_{2})}^{T}$ .

Following the previous control procedure, some matrices are necessary to compute u. These matrices are proposed as follows:

$Q = Q^{T} = (\begin{matrix} 17 & 8 & 7 & - 6 & - 4 & 2 \\ 8 & 26 & 6 & 4 & 4 & 13 \\ 7 & 6 & 11 & 9 & 1 & 2 \\ - 6 & 4 & 9 & 23 & 9 & 4 \\ - 4 & 4 & 1 & 9 & 9 & 3 \\ 2 & 13 & 2 & 4 & 3 & 8 \end{matrix}) > 0,$

thus

$\begin{matrix} Q_{11} = (\begin{matrix} 17 & 8 & 7 \\ 8 & 26 & 6 \\ 7 & 6 & 11 \end{matrix}), Q_{12} = Q_{12}^{T} = (\begin{matrix} - 6 & - 4 & 2 \\ 4 & 4 & 13 \\ 9 & 1 & 2 \end{matrix}), \\ Q_{22} = (\begin{matrix} 23 & 9 & 4 \\ 9 & 9 & 3 \\ 4 & 3 & 8 \end{matrix}) . \end{matrix}$

Therefore, from (7.9) and (7.10),

$Q_{1} = (\begin{matrix} 13.1924 & 3.9244 & 8.0378 \\ 3.9244 & 4.5773 & 3.7113 \\ 8.0378 & 3.7113 & 6.1443 \end{matrix}),$

$A_{1} = (\begin{matrix} 0.1787 & 0.1203 & - 0.5601 \\ 0.4330 & - 0.0034 & 0.5017 \\ - 0.5017 & - 1.6838 & - 0.1581 \end{matrix}) .$

Solving the Riccati equation, it follows that

$P = (\begin{matrix} 25.3132 & 9.9395 & - 0.5181 \\ 9.9395 & 8.9679 & - 1.5217 \\ - 0.5181 & - 1.5217 & 4.4597 \end{matrix}),$

and finally S can be written as

$S = η_{2} + \underset{M}{\underset{︸}{Q_{22}^{- 1} (Q_{12}^{T} + P)}} η_{1},$

(7.37)

where

$\begin{matrix} M = (\begin{matrix} M_{11} & M_{12} & M_{13} \\ M_{21} & M_{22} & M_{23} \\ M_{31} & M_{32} & M_{33} \end{matrix}) = (\begin{matrix} 0.9702 & - 0.0036 & 0.5814 \\ - 0.2404 & 1.1036 & - 0.9275 \\ - 0.2097 & 1.0228 & 0.8646 \end{matrix}) . \end{matrix}$

Then, the sliding surfaces are given by

$\begin{matrix} S_{1} & = ϕ_{2} + M_{11} ϕ_{1} + M_{12} θ_{1} + M_{13} ψ_{1}, \\ S_{2} & = θ_{2} + M_{21} ϕ_{1} + M_{22} θ_{1} + M_{23} ψ_{1}, \\ S_{3} & = ψ_{2} + M_{31} ϕ_{1} + M_{32} θ_{1} + M_{33} ψ_{1} . \end{matrix}$

Rewriting $u \in R^{3}$ , it follows that

$\begin{matrix} u_{ϕ} & = (I_{x} / l) ({\bar{u}}_{1} - M_{13} ψ_{2} - M_{12} θ_{2} - (M_{11} + 1) ϕ_{2}), \\ u_{θ} & = (I_{y} / l) ({\bar{u}}_{2} - M_{21} ϕ_{2} - M_{23} ψ_{2} - (M_{22} + 1) θ_{2}), \\ u_{ψ} & = (I_{z} / l) ({\bar{u}}_{3} - M_{31} ϕ_{2} - M_{32} θ_{2} - (M_{33} + 1) ψ_{2}), \end{matrix}$

with

$\begin{matrix} {\bar{u}}_{1} & = & - ρ_{1} sgn (S_{1} - Z_{1}) - k_{1} {| S_{1} |}^{1 / 2} sgn (S_{1}) + ϕ_{2}, \\ Z_{1} & = & - k_{1} \int {| S_{1} |}^{1 / 2} sgn (S_{1}) d t with Z_{1} (0) = S_{1} (0), \\ {\bar{u}}_{2} & = & - ρ_{2} sgn (S_{2} - Z_{2}) - k_{2} {| S_{2} |}^{1 / 2} sgn (S_{2}) + θ_{2}, \\ Z_{2} & = & - k_{2} \int {| S_{2} |}^{1 / 2} sgn (S_{2}) d t with Z_{2} (0) = S_{2} (0), \\ {\bar{u}}_{3} & = & - ρ_{3} sgn (S_{3} - Z_{3}) - k_{3} {| S_{3} |}^{1 / 2} sgn (S_{3}) + ψ_{2}, \\ Z_{3} & = & - k_{3} \int {| S_{3} |}^{1 / 2} sgn (S_{3}) d t with Z_{3} (0) = S_{3} (0), \end{matrix}$

and gains given by

$\begin{matrix} ρ_{1} = (\frac{α_{1}}{\sqrt{2}} + | θ_{2} (ψ_{2} γ_{1} - β_{1}) | + L_{1}), \\ ρ_{2} = (\frac{α_{2}}{\sqrt{2}} + | ϕ_{2} (ψ_{2} γ_{2} - β_{2}) | + L_{2}), \\ ρ_{3} = (\frac{α_{3}}{\sqrt{2}} + | θ_{2} ϕ_{2} γ_{3} | + L_{3}) . \end{matrix}$

$\begin{matrix} k_{1} = \frac{2 {| S_{1} (0) |}^{1 / 2}}{t_{1}} \\ k_{2} = \frac{2 {| S_{2} (0) |}^{1 / 2}}{t_{1}} \\ k_{3} = \frac{2 {| S_{3} (0) |}^{1 / 2}}{t_{1}} \end{matrix} |, \begin{matrix} t_{1} = cte \end{matrix}$

(7.38)

The initial conditions were set as $ϕ_{1} (0) = - 5$ , $θ_{1} (0) = 2$ , $ψ_{1} (0) = - 3$ , all in grad, $ϕ_{2} (0) = 6$ , $θ_{2} (0) = 4$ , $ψ_{2} (0) = 6$ in grad/s. These conditions imply $S_{1} (0) = - 0.6026$ , $S_{2} (0) = 10.1917$ , and $S_{3} (0) = 6.5004$ . We can also define $t_{1} = 1 s$ as a finite-time convergence instance for the sliding surfaces $S_{1}$ , $S_{2}$ , and $S_{3}$ . Thus, from (7.38) we obtained $k_{1} = 1.5525$ , $k_{2} = 6.3849$ , and $k_{3} = 5.0992$ . Furthermore, for simulation purposes we assumed $α_{1} = 0.12$ , $α_{2} = 0.14$ , and $α_{3} = 0.2$ . The bounded disturbances were selected as follows:

$\begin{matrix} w_{ϕ} & = 2 \sin (t) sgn (S_{1}), & | w_{ϕ} | & ≦ L_{ϕ} = 2, \\ w_{θ} & = - 1.5 \cos (2 t) sgn (S_{2}), & | w_{θ} | & ≦ L_{θ} = 1.5, \\ w_{ψ} & = - 0.5 \exp (\cos (t)) sgn (S_{3}), & | w_{ψ} | & ≦ L_{ψ} = 0.5 \exp (1) . \end{matrix}$

The above disturbances were considered multiplied by $sgn (S_{i})$ for the following reasons:

1. To observe that the effect chattering produced by $sgn (S_{i})$ is not relevant for the compensation of such disturbances. We are only interested in the knowledge of the maximum amplitude that each perturbation can reach, and not in the high frequency that it can produce.

2. To graphically validate the theory. It is expected to observe an evident chattering effect in $w_{ϕ}$ , $w_{θ}$ , and $w_{ψ}$ when $S_{i} = 0$ at the desired finite time $t_{1} = 1$ .

The following graphs were obtained when applying the proposed control scheme. From Fig. 7.1 observe that the auxiliary sliding surfaces $σ_{1}$ , $σ_{2}$ , and $σ_{3}$ are zero from the initial time instance, meaning that the robustness is guaranteed with respect to bounded uncertainties all the time. Besides, $S_{1}$ , $S_{2}$ , and $S_{3}$ converge to zero in a desired finite time $t_{1} = 1$ ; this means that the vector of sliding surface $S = η_{2} + Q_{22}^{- 1} (Q_{12}^{T} + P) η_{1}$ converges to the optimal vector of sliding surfaces $S = 0$ in finite time $t_{1} = 1$ , and with this fact every solution $η_{1} = {(ϕ, θ, ψ)}^{T}$ and $η_{2} = {(\dot{ϕ}, \dot{θ}, \dot{ψ})}^{T}$ that belongs to $S = 0$ will be called an optimal sliding mode because it will be able to minimize the cost function (7.9) for all $t ⩾ t_{1}$ and in this manner solve the LQR problem.⁴

Figure 7.1 Convergence of auxiliary surfaces σ_i and sliding surfaces S_i.

In Fig. 7.2 an asymptotic stabilization is clearly visible for the dynamics of $ϕ, θ, ψ$ and $\dot{ϕ}, \dot{θ}, \dot{ψ}$ due to the convergence of the vector S to the optimal sliding vector $S = 0$ in finite time $t_{1} = 1$ .

Figure 7.2 Stabilization of the dynamics of ϕ, θ, ψ and $\dot{ϕ}$ , $\dot{θ}$ , $\dot{ψ}$ .

In Fig. 7.3 it can be observed that the bounded uncertainties $w_{ϕ}$ , $w_{θ}$ , and $w_{ψ}$ present an evident chattering effect by considering the factor $sgn (S_{i})$ , and also that this chattering effect appears at time $t_{1} = 1$ . However, although these uncertainties present a high frequency, the control signal responses $u_{ϕ}$ , $u_{θ}$ , and $u_{ψ}$ shown in Fig. 7.4 compensate such perturbations from the initial time instance $t = 0$ .

Figure 7.3 Bounded uncertainties w_ϕ, w_θ, and w_ψ.

Figure 7.4 Control signals u_ϕ, u_θ, and u_ψ.

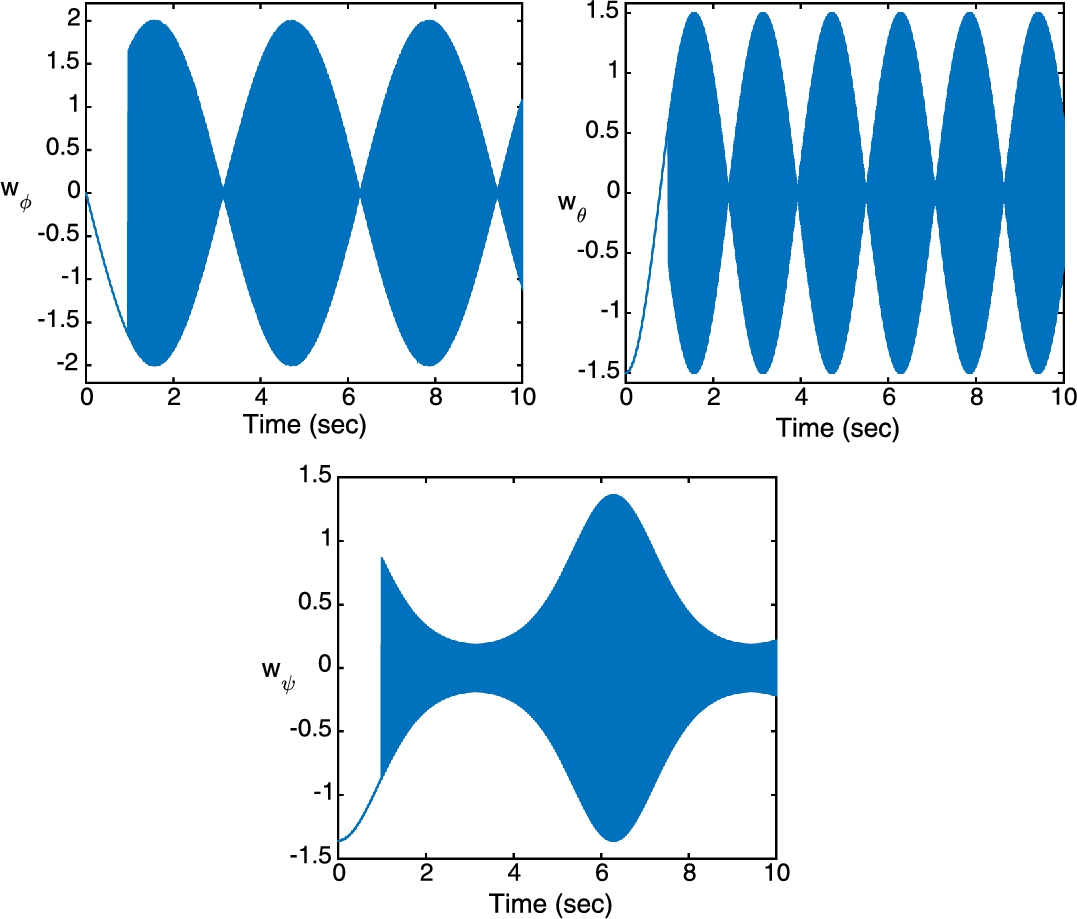
In Fig. 7.4 it is shown that the control signal responses $u_{ϕ}$ , $u_{θ}$ , and $u_{ψ}$ have a chattering effect from the beginning, meaning that such controllers are compensating the proposed bounded uncertainties $w_{ϕ}$ , $w_{θ}$ , and $w_{ψ}$ for all $t ⩾ 0$ .

7.3.1 Emulation Results

One of the problems existing today is due to the discontinuity produced by the sgn function. This discontinuity produces a high frequency, normally called the chattering effect, which in practical applications is not convenient because it could produce unwanted vibrations that could damage the instruments in real-time implementations. Nevertheless, there exists extensive literature on techniques that help diminish the chattering effect.

Notice the chattering effect produced by the sgn function in Fig. 7.4. If we want to improve the performance of the control inputs, several tricks could be used. One technique used frequently is to approximate the sgn function; see, for example, [6, Chap. 1]. This approximation can be applied as

$sgn (σ) \approx \frac{σ}{| σ | + ϵ} .$

(7.39)

For our simulations purposes we consider $ϵ = 0.0007$ .

The idea when validating the proposed algorithm is to have similar results in simulations and/or experiments. For this we consider that all states ϕ, θ, ψ, $\dot{ϕ}$ , $\dot{θ}$ , and $\dot{ψ}$ are affected by some kind of white noise (that it is true when using inertial sensors). Under these assumptions the following graphs are obtained.

In Fig. 7.5 we observe that the sliding surfaces $S_{1}$ , $S_{2}$ , and $S_{3}$ converge to zero in finite time $t_{1}$ , although the nonlinear system is being affected by white noise. In Fig. 7.6 asymptotic convergence is observed for the dynamics of $ϕ, θ, ψ$ and $\dot{ϕ}, \dot{θ}, \dot{ψ}$ in spite of having white noise in the internal dynamics of the system. Due to this, the controls shown in Fig. 7.7 achieve the convergence of the vector S to the optimal sliding vector $S = 0$ in finite time. In Fig. 7.7 a representation of the controllers $u_{ϕ}$ , $u_{θ}$ , and $u_{ψ}$ is shown; they drive S to zero in finite time in the presence of white noise and bounded uncertainties.

Figure 7.5 Convergence of the sliding surfaces S₁, S₂, and S₃.

Figure 7.6 Dynamic stabilization of ϕ, θ, ψ and $\dot{ϕ}$ , $\dot{θ}$ , $\dot{ψ}$ with sensor noise.

Figure 7.7 Control signals u_ϕ, u_θ, and u_ψ.

7.4 Real-Time Validation

The previous controller was validated on our platform (see Sect. 4.1.5 of Chap. 4) to analyze the attitude performance of a quadcopter. Manual and aggressive references were given to test the behavior of the controller. The following main graphs illustrate the results.

Applying the controller as obtained in Sect. 7.3 in real time is very difficult, and the system is very sensible to small changes. This effect appears because even if the sliding surfaces go to zero, the cross terms of other variables are present in these surfaces, e.g., recall that surface $S_{1}$ is for assuring the roll angle convergence and notice that pitch and yaw terms are also included. In addition, if the terms $M_{i j}$ of these variables (pitch and yaw) are bigger then they will strongly influence the controller performance. Therefore, in this part we will include a theoretical–practical tune up that could be used for sliding controllers.

Observe that $S = v_{q} + M q$ . Then we can choose M not only to assure convergence of the sliding surfaces but also to facilitate the implementation in real time. Therefore the goal will be to weigh the main diagonal of M to assure good convergence of each state. Remember that M is given by $M = Q_{22}^{- 1} (Q_{12}^{T} + P)$ and Q is given by

$Q = Q^{T} = (\begin{matrix} Q_{11} & Q_{12} \\ Q_{12}^{T} & Q_{22} \end{matrix}) > 0, Q_{11}, Q_{12}, Q_{22} \in R^{3 \times 3} .$

For a practical tune up we can consider $Q_{12} = 0_{3 \times 3}$ and $Q_{22}$ as

$Q_{22} = (\begin{matrix} r & 0 & 0 \\ 0 & s & 0 \\ 0 & 0 & g \end{matrix})$

with r, s, and g being positive numbers to guarantee $Q_{22} = Q_{22}^{T} > 0$ . Hence M becomes

$M = (\begin{matrix} P_{11} / r & 0 & 0 \\ 0 & P_{22} / s & 0 \\ 0 & 0 & P_{33 / g} \end{matrix}) = (\begin{matrix} M_{11} & 0 & 0 \\ 0 & M_{22} & 0 \\ 0 & 0 & M_{33} \end{matrix}),$

and this implies that each $S_{i}$ is given by

$\begin{matrix} S_{1} & = ϕ_{2} + M_{11} ϕ_{1}, \\ S_{2} & = θ_{2} + M_{22} θ_{1}, \\ S_{3} & = ψ_{2} + M_{33} ψ_{1} . \end{matrix}$

Then $u \in R^{3}$ for practical validation is given as

$\begin{matrix} u_{ϕ} & = (I_{x} / l) ({\bar{u}}_{1} - (M_{11} + 1) ϕ_{2}), \\ u_{θ} & = (I_{y} / l) ({\bar{u}}_{2} - (M_{22} + 1) θ_{2}), \\ u_{ψ} & = (I_{z} / l) ({\bar{u}}_{3} - (M_{33} + 1) ψ_{2}), \end{matrix}$

with

The new gains are given by

$\begin{matrix} ρ_{1} & = & (\frac{α_{1}}{\sqrt{2}} + | θ_{2} (ψ_{2} γ_{1} - β_{1}) | + L_{1}), \\ ρ_{2} & = & (\frac{α_{2}}{\sqrt{2}} + | ϕ_{2} (ψ_{2} γ_{2} - β_{2}) | + L_{2}), \\ ρ_{3} & = & (\frac{α_{3}}{\sqrt{2}} + | θ_{2} ϕ_{2} γ_{3} | + L_{3}), \end{matrix}$

and other parameters are

$\begin{matrix} k_{1} = \frac{2 {| S_{1} (0) |}^{1 / 2}}{t_{1}} \\ k_{2} = \frac{2 {| S_{2} (0) |}^{1 / 2}}{t_{1}} \\ k_{3} = \frac{2 {| S_{3} (0) |}^{1 / 2}}{t_{1}} \end{matrix} | \begin{matrix} t_{1} = cte, \end{matrix}$

$\begin{matrix} β_{1} & = β_{2} (γ_{1} + 1), & γ_{3} & = - γ_{1} (\frac{1}{γ_{2} (γ_{1} + 1) + 1}), \\ b_{2} & = \frac{b_{1}}{(γ_{1} + 1)}, & b_{3} & = \frac{b_{1}}{[γ_{2} (γ_{1} + 1) + 1]}, \\ b_{2}^{- 1} & = \frac{(γ_{1} + 1)}{b_{1}}, & b_{3}^{- 1} & = \frac{[γ_{2} (γ_{1} + 1) + 1]}{b_{1}} . \end{matrix}$

Analyzing the previous gains, we can observe that the gains for heuristic tune up are $β_{2}, γ_{1}, γ_{2}$ , and $b_{1}$ . Thus, the gains can be proposed as

$\begin{matrix} ρ_{1} = (| θ_{2} (ψ_{2} γ_{1} - β_{1}) | + L_{x}), \\ ρ_{2} = (| ϕ_{2} (ψ_{2} γ_{2} - β_{2}) | + L_{y}), \\ ρ_{3} = (| θ_{2} ϕ_{2} γ_{3} | + L_{z}), \end{matrix}$

and if we want and then for the tune up we can use the following expressions:

$γ_{3} = - \frac{γ_{1}}{γ_{1} + 1}, γ_{1}, b_{1} = any number, b_{2} = b_{3} = \frac{b_{1}}{(γ_{1} + 1)},$

and then the gains become $ρ_{1} = (L_{x}), ρ_{2} = (L_{y})$ , and $ρ_{3} = (| θ_{2} ϕ_{2} γ_{3} | + L_{z})$ .

Fig. 7.8 introduces the behavior of the controllers when they are applied in a quadcopter prototype. Observe in this figure that the controller performs well in practice and that the closed-loop system is guaranteed even in the presence of aggressive maneuvers. Also notice that the procedure to tune the gains in the controller works pretty well and can be applied to others sliding controllers. Desired references were given manually by the pilot. Notice that several changes were produced to observe the performance of the controller.

Figure 7.8 Attitude response when applying the controller in real time.

7.5 Discussion

Sliding mode control is becoming a popular tool when working with UAVs since robustness and quick convergence properties make such controllers very interesting to apply in autonomous vehicles. On the negative side, the main problem is the chattering effect produced in the control responses. This effect could damage the physical parts of the system and could require lots of energy for good efficiency. New controllers as proposed in this chapter try to reduce these drawbacks and improve the performance of such algorithms. Nevertheless, many issues still need to be solved and remain an open research topic.

The controller presented in this chapter was designed to be robust with respect to unknown and bounded perturbations and to guarantee convergence in finite time. This fact is not typical in controllers. From emulation results we could observe good performance of the algorithms. The next step for this controller will be to reduce the chattering effect in its design. In addition, a methodology to theoretically tune sliding algorithms was also presented in this chapter. It is very useful when applying the controller in real time. The graphs obtained when implementing the proposed controller demonstrated good performance in closed-loop system.

..................Content has been hidden....................

You can't read the all page of ebook, please click here login for view all page.

Table of Contents for Chapter 7: Sliding Mode Control

Create new playlist

Sign In

Sign Up