CHAPTER 1
BASIC CONCEPTS
During the early development of probability theory, the evolution was based more on intuition rather than mathematical axioms. The axiomatic basis for probability theory was provided by A. N. Kolmogorov in 1933 and his approach conserved the theoretical ideas of all other approaches. This chapter is based on the axiomatic approach and starts with this notion.
1.1 PROBABILITY SPACE
In this section we develop the notion of probability measure and present its basic properties.
When an ordinary die is rolled once, the outcome cannot be accurately predicted; we know, however, that the set of all possible outcomes is {1,2,3,4,5,6}. An experiment like this is called a random experiment.
Definition 1.1 (Random Experiment) An experiment is said to be random if its result cannot be determined beforehand.
It is assumed that the set of possible results of a random experiment is known. This set is called a sample space.
Definition 1.2 (Sample Space) The set Ω of all possible results of a random experiment is called a sample space. An element 
Ω is called an outcome or a sample point.
Experiment: Flipping a fair coin. The possible results in this case are “head” = H and “tail” = T. That is, Ω = {H,T}. 
Experiment: Rolling an ordinary die three consecutive times. In this case the possible results are triplets of the form (a, b, c) with a, b, c {1,2,3,4,5,6}. That is:
Ω = {(a, b, c) : a, b, c {1,2,3,4,5,6}}.
Experiment: Items coming off a production line are marked defective (D) or nondefective (N). Items are observed and their condition noted. This is continued until two consecutive defectives are produced or four items have been checked, which ever occurs first. In this case:
Experiment: Observe the number of ongoing calls in a particular telephone exchange switch. In this case Ω = {0,1,2, . . .}.
We notice that the elements of a sample space can be numbers, vectors, symbols, etc. and they are determined by the experiment being considered.
Definition 1.3 (Discrete Sample Space) A sample space Ω is called discrete if it is either finite or countable. A random experiment is called finite (discrete) if its sample space is finite (discrete).
Going back to Example 1.2, a question that arises naturally is: what’s the “chance” of a given “event” such as “the sum of the results obtained is greater than or equal to 2”? In other words, what is the “chance” of
A := {(a, b, c) Ω : a + b + c ≥ 2}
happening?
Now, what is an event? Following the aforementioned idea, we can expect an event merely to be a subset of the sample space, but in this case, can we say that all subsets of the sample space are events? The answer is no. The class of subsets of the sample space for which the “chance” of happening is defined must have a σ-algebra structure, a concept we will further explain:
Definition 1.4 (σ-Algebra) Let Ω ≠ 
. A collection 
of subsets of Ω is called a σ-algebra (or a σ-field) over Ω:
(i) If Ω .
(ii) If A , then Ac .
(iii) If A1, A2, . . . , then 
The elements of are called events.
Consider Example 1.1. Ω = {H,T}. Then 
= {, Ω} is a trivial σ-algebra over Ω, whereas 
= {, {H}} is not a σ-algebra over Ω.
Consider a random experiment of flipping two fair coins.
Ω = {HH, HT, TH, TT}. Then = {, {HH, HT}, {TH, TT}, Ω} is a σ-algebra over Ω.
Consider Example 1.2. Ω = {(a, b, c) : a, b, c {1,2,3,4,5,6}}. Then = {, {(1, 2, 3)}, Ω {(1,2,3)}, Ω} is a σ-algebra over Ω whereas = {(1,2,3), (1,1,1)} is not a σ-algebra over Ω.
Let Ω ≠ . Then 0 = {, Ω} and 
(Ω) := {A : A 
Ω} are σ-algebras over Ω. 0 is called the trivial σ-algebra over Ω while (Ω) is known as the total σ-algebra over Ω.
Let Ω = {1,2,3}. Then = {, {1}, {2,3}, Ω} is a σ-algebra over Ω but the collection = {, {1}, {2}, {3}, Ω} is not a σ-algebra over Ω.
Let Ω ≠ be finite or countable, and let be a σ-algebra over Ω containing all subsets of the form {} with Ω. Then = (Ω).
Theorem 1.1 If Ω ≠ and 1, 2, · · · are σ-algebras over Ω, then 
is also a σ-algebra over Ω.
Proof: Since Ω j for every j, this implies that Ω 
. Let A , then A j for all j, this means that Ac j for all j. Hence Ac . Finally, let A1, A2, · · · . Then Ai j, for all i and j, hence 
for all j. Thus we conclude that 
. 
Note that, in general, the union of σ-algebras over Ω is not a σ-algebra over Ω. For example, Ω = {1,2,3}, 1 = {, Ω, {1}, {2,3}} and 2 = {, Ω {1, 2}, {3}}. Clearly 1 and 2 are σ-algebras over Ω, but 1 ⋃ 2 is not a σ-algebra over Ω.
Definition 1.5 (Generated σ-Algebra) Let Ω ≠ and let 
be a collection of subsets of Ω. Let 
= { : is a σ-algebra over Ω containing }. Then, the preceding example implies that 
is the smallest σ-algebra over Ω containing . σ() is called the σ-algebra generated by .
The smallest σ-algebra over 
containing all intervals of the form (–∞, a] with a is called the Borel σ-algebra and is usually written as 
. If A , then A is called a Borel subset of . Since is a σ-algebra, if we take a, b with a < b, then the following are Borel subsets of :
Can we say, then, that all subsets of are Borel subsets? The answer to this question is no; see Royden (1968) for an example on this regard.
EXAMPLE 1.12 Borel σ-algebra over n
Let a = (a1,· · · ,an) and b = (b1, · · · , bn) be elements of n with a ≤ b, that is, ai ≤ bi for all i = 1,· · ·, n. The σ-algebra, denoted by n, generated by all intervals of the form
(a, b] := {x = (x1,· · ·, xn) n : ai < xi ≤ bi, i = 1, · · ·, n}
is called the Borel σ-algebra over n.
Definition 1.6 (Measurable Space) Let Ω ≠ and let be a σ-algebra over Ω. The couple (Ω, ) is called a measurable space.
It is clear from the definition that both Ω and belong to any σ-algebra defined over Ω. is called the impossible event, Ω is called the sure event. An event of the form {} with Ω is called a simple event.
We say that the event A happens if after carrying out the random experiment we obtain an outcome in A, that is, A happens if the result is a certain with A. Therefore, if A and B are two events, then:
(i) The event A ⋃ B happens if and only if either A or B or both happen.
(ii) The event A ⋂ B happens if and only if both A and B happen.
(iii) The event Ac happens if and only if A doesn’t happen.
(iv) The event A B happens if and only if A happens but B doesn’t.
If in Example 1.2 we consider the events: A = “the result of the first toss is a prime number” and B = “the sum of all results is less than or equal to 4”. Then
A ⋃ B = {(a, b, c) Ω : a {2,3,5} or (a + b + c) ≤ 4},
so (2,1,1), (5,3,4), (1,1,1) are all elements of A ⋃ B. In addition:
A ⋂ B = {(a, b, c) : a {2,3,5} and (a + b + c) ≤ 4} = {(2,1,1)}.
The reader is advised to see what the events AB and Ac are equal to.
Definition 1.7 (Mutually Exclusive Events) Two events A and B are said to be mutually exclusive if A ⋂ B = .
A coin is flipped once. Let A = “the result obtained is a head” and B = “the result obtained is a tail”. Clearly the events A and B are mutually exclusive.
A coin is flipped as many times as needed to obtain a head for the first time, and the number of tosses required is being counted. If
A := “no heads that are obtained before the third toss” = {3,4,5,· · ·} and
B := “no heads that are obtained before the second toss” = {2,3,4,· · ·} then A and B are not mutually exclusive.
Our goal now is to assign to each event A a nonnegative real number indicating its “chance” of happening. Suppose that a random experiment is carried out n times keeping its conditions stable throughout the different repetitions.
Definition 1.8 (Relative Frequency) For each event A, the number 
is called the relative frequency of A, where n(A) indicates the number of times the event A happened in the n repetitions of the experiment.
Suppose a coin is flipped 100 times and 60 of the tosses produced a “head” as a result; then the relative frequencies of the events A := “the result is head” and B := “the result is tail” are respectively 
and 
.
A fair die is rolled 500 times and in 83 of those tosses the number 3 was obtained. In this case the relative frequency of the event
A := “the result obtained is 3”
equals 
.
Unfortunately for each fixed A, fr(A) is not constant: its value depends on n; it has been observed, however, that when a random experiment is repeated under almost the same conditions for a large number of times, the relative frequency fr(A) stabilizes around a specific value between 0 and 1.
Suppose a die is tossed n times and let:
A := “the result obtained is 3”.
The following table summarizes the values obtained:
The stabilization of the relative frequency is known as “statistic regularity” and this is what allows us to make predictions that eliminate, though partially, the uncertainty present in unforeseeable phenomena.
The value P(A) around which the relative frequency of an event stabilizes indicates its “chance” of happening. We are interested now in describing the properties that such a number should have. First, we observe that since n(A) ≥ 0 then P(A) must be greater than or equal to zero, and because n(Ω) = n, fr(Ω) = 1 and therefore P(Ω) = 1. Furthermore, if A and B are mutually exclusive events, then n(A ⋃ B) = n(A) + n(B) and therefore fr(A ⋃ B) = fr(A) + fr(B), which in turn implies that whenever A ⋂ B = then P(A ⋃ B) = P(A) + P(B). These considerations lead us to state the following definition:
Definition 1.9 (Probability Space) Let (Ω,) be a measurable space. A real-valued function P defined over satisfying the conditions
(i) P(A) ≥ 0 for all A (nonnegative property)
(ii) P(Ω) = 1 (normed property)
(iii) if A1, A2,· · · are mutually exclusive events in , that is,
Ai ⋂ Aj = for all i ≠ j,
then
is called a probability measure over (Ω, ). The triplet (Ω, , P) is called a probability space.
Consider Example 1.9. Let Ω = {1,2,3}, = {, {1}, {2,3}, Ω} and P be the following map over for any A :
It is easy to verify that P is indeed a probability measure over (Ω, ).
Consider Example 1.4. Let Ω = {0,1,· · ·}, = (Ω) and P be defined on {i}:
P({i}) = (1 − q)qi, i = 0,1,· · ·, 0 < q < 1.
Since all three properties of Definition 1.9 are satisfied, P is a probability measure over (Ω, ).
Let Ω = {1, 2}, = (Ω) and let P be the map over defined by:
P is a probability measure.
Next we establish the most important properties of a probability measure P.
Theorem 1.2 Let (Ω, , P) be a probability space. Then:
1. P() = 0.
2. If A, B and A ⋂ B = , then P (A ⋃ B) = P(A) + P(B).
3. For any A , P(Ac) = 1 — P(A).
4. If A B, then P(A) ≤ P(B) and P(B A) = P(B) − P(A). In particular P(A) ≤ 1 for all A .
5. For any A, B , P(A ⋃ B) = P(A) + P(B) − P(A ⋂ B).
6. Let (An)n be an increasing sequence of elements in , that is, An and An An+1 for all n = 1,2,· · ·; then
where 
7. Let (An)n be a decreasing sequence of elements in , that is, An and An 
An+1 for all n = 1,2,· · ·; then
where 
Proof:
1. 1 = P(Ω) = P(Ω ⋃ ⋃ ⋃ · · ·) = P(Ω) + P() + P() + · · ·. Then 0 ≥ P() ≥ 0 and therefore P() = 0.
2. A ⋃ B = A ⋃ B ⋃ ⋃ ⋃ · · ·. Thus, the proof follows from property iii from the definition of probability measure and the previous result.
3. P(A) + P(Ac) = P(A ⋃ Ac) = P(Ω) = 1.
4. B = A ⋃ (B A). We obtain P(B) = P(A) + P(B A) ≥ P(A) by applying 2.
5. As an exercise for the reader.
6. Let C1 = A1, C2 = A2 A1,· · · , Cn = An An−1. It is clear that:
Furthermore, since Ci ⋂ Cj = for all i ≠ j, it follows from property iii of probability measures that:
7. Left as an exercise for the reader.
Note 1.1 Let A, B and C be events. Applying the previous theorem:
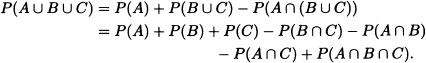
An inductive argument can be used to see that if A1, A2,· · ·, An are events, then
P(A1 ⋃ A2 ⋃ · · · ⋃ An)
is taken over all possible subsets of size r of the set {1,2,· · · , n}.
Note 1.2 Let (Ω, , P) be a probability space with finite or countable Ω and = (Ω). Let ≠ A . It is clear that
and therefore
where P() := P({}). That is, P is completely determined by pj := P(j), where j with j = 1,2, · · · denote the different elements of Ω.
Clearly, the |Ω|-dimensional vector p := (p1,p2,· · ·) (where |Ω| is the number of elements of Ω) satisfies the following conditions:
(i) pj ≥ 0.
A vector p satisfying the above conditions is called a probability vector.
Note 1.3 Let Ω = {1, 2 · · ·} be a (nonempty) finite or countable set, (Ω) the total σ-algebra over Ω and p a |Ω|-dimensional probability vector. It is easy to verify that the mapping P defined over (Ω) by
is a probability measure. The probability space (Ω, (Ω), P) obtained in this fashion is called a discrete probability space.
Let (Ω, , P) be a probability space with:
Let (Ω, (Ω), P) be a discrete probability space with Ω = {a, b, c} and P given by the probability vector 
Then:
Let (Ω, , P) be a probability space. If A and B are events such that P(A) = p, P(B) = q and P(A ⋃ B) = r, then:
Consider three wireless service providers Vodafone, Aircel, and Reliance mobile in Delhi. For a randomly chosen location in this city, the probability of coverage for the Vodafone (V), Aircel(A), and Reliance mobile (R) are P(V) = 0.52, P(A) = 0.51, P(R) = 0.36, respectively. We also know that P(V ⋃ A) = 0.84, P(A ⋃ R) = 0.76 and P(A ⋂ R ⋂ V) = 0.02. What is the probability of not having coverage from Reliance mobile? Aircel claims it has better coverage than Vodafone. Can you verify this? If you own two cell phones, one from Vodafone and one from Aircel, what is your worst case coverage?
Using the above information, the probability of not having coverage from Reliance mobile is:
Aircel’s claim is incorrect as P(A) < P(V). The worst case coverage is:
Let (Ω, , P) be a probability space, and let A and B be elements of with P(A) = 
and P(B) = 
. Then
since P(A ⋂ B) ≤ P(A) = and P(A ⋃ B) ≤ 1.
A biased die is tossed once. Suppose that:
Then, the probability of obtaining a number not divisible by 3 and whose square is smaller than 20 equals 
, while the probability of getting a number i such that |i − 5| ≤ 3 equals 
.
1.2 LAPLACE PROBABILITY SPACE
Among random experiments, the easiest to analyze are those with a finite number of possible results with each of them having the same likelihood. These experiments are called Laplace experiments. The tossing of a fair coin or a fair die a finite number of times is a classic example of Laplace experiments.
Definition 1.10 (Laplace Probability Space) A probability space (Ω, , P) with finite Ω, = (Ω) and 
for all Ω is called a Laplace probability space. The probability measure P is called the uniform or classic distribution on Ω.
Note 1.4 If (Ω, , P) is a Laplace probability space and A 
Ω, then:
In other words:
This last expression is in no way a definition of probability, but only a consequence of assuming every outcome of the experiment to be equally likely and a finite number of possible results.
Thereby, in a Laplace probability space we have that probability calculus is reduced to counting the elements of a finite set, that is, we arrive to a combinatorial analysis problem. For readers not familiarized with this topic, Appendix B covers the basic concepts and results of this theory.
In a certain lottery six numbers are chosen from 1 to 49. The probability that the numbers chosen are 1,2,3,4,5 and 6 equals:
Observe that this is the same probability that the numbers 4,23,24,35,40 and 45 have been chosen.
The probability p of 44 being one of the numbers chosen equals:
There are five couples sitting randomly at a round table. The probability p of two particular members of a couple sitting together equals:
In an electronics repair shop there are 10 TVs to be repaired, 3 of which are from brand A, 3 from brand B and 4 from brand C. The order in which the TVs are repaired is random. The probability p1 that a TV from brand A will be the first one to be repaired equals:
The probability p2 that all three TVs from the brand A will be repaired first equals:
The probability p3 that the TVs will be repaired in the order C ABC ABC ABC equals:
In a bridge game, the whole pack of 52 cards is dealt out to four players. We wish to find the probability that a player receives all 13 spades.
In this case, the total number of ways in which the pack can be dealt out is
and the total number of ways to divide the pack while giving a single player all spades equals:
Therefore, the probability p we look for is given by:
Suppose that all 365 days of the year are equally likely to be the day a person celebrates his or her birthday (we are ignoring leap years and the fact that birth rates aren’t uniform throughout the year). The probability p that, in a group of 50 people, no two of them have the same birthday is:
An urn has N balls of the same type, R of them are red color and N – R are white color. n balls are randomly drawn from the urn. We wish to find the probability that exactly k ≤ n of the balls drawn are red in color.
To simplify the argument, it will be assumed that the balls are numbered from 1 to N in such a way that the red balls are all numbered from 1 to R. We distinguish between two important cases: draw without replacement and draw with replacement. In the first case we must also consider two more alternatives: the balls are drawn one by one and the balls are drawn at the same time.
1. Draw without replacement (one by one): The n balls are extracted one by one from the urn and left outside of it. In this case the sample space is given by:
Let:
Ak := “exactly k ≤ n of the balls drawn are red”.
Clearly Ak is made of all the n-tuples from Ω with exactly k components less than or equal to R. Therefore
|Ω| = N × (N − 1) × · · · × (N − (n − 1)) =: (N)n
Then:
2. Draw without replacement (at the same time): In this case the sample space is:
Ω = {T : T {1,2, · · · , N} with |T| = n}.
Here Ak consists of all the elements of Ω having exactly k elements less than or equal to R. Therefore:
Thus:
As it can be seen, when the balls are drawn without replacement, it is irrelevant for the calculus of the probability whether the balls were extracted one by one or all at the same time.
3. Draw with replacement: In this case, each extracted ball is returned to the urn, and after mixing the balls, a new one is randomly drawn. The sample space is then given by:
Ω = {(a1, a2,· · ·, an): aj {1, 2, · · ·, N}, j = 1,2, · · ·, N}.
The event Ak consists of all n-tuples from Ω with k components less than or equal to R. Then,
and accordingly:
A rectangular box contains 4 Toblerones, 8 Cadburys and 5 Perks chocolates. A sample of size 6 is selected at random without replacement. Find the probability that the sample contains 2 Toblerones, 3 Cadbury and 1 Perk chocolates.
Solution: 
where Ω is the set of possible outcomes. 
where E is the event of interest:
If in the above problem the sample is to be drawn with replacement, then the required probability is:
(Hoel et al., 1971) Suppose that n balls are distributed in n urns in such a way that all the nn possible arrangements are equally likely. Find the probability that only the first urn is empty.
Solution: Let A be the event of having only the first urn empty. This event happens only if the n balls are distributed in the n − 1 remaining urns in such a way that none of them are empty. That means one of those n − 1 urns must contain exactly two balls while the other n − 2 must have one ball each. For j = 2, · · ·, n, let Bj be the event of having two balls in the urn j and exactly one ball in each of the other n − 2 urns. Clearly the events Bj are mutually exclusive and their union yields the event A. To calculate P(Bj), we observe that the two balls placed in the urn j can be chosen in 
ways and the remaining n − 2 balls can be distributed in the remaining urns in (n − 2)! ways. Then,
and therefore:
A wooden cube with painted faces is sawed up into 1000 little cubes all of the same size. The little cubes are then mixed up, and one is chosen at random. Find the probability that the selected cube has only two painted faces.
Solution: The probability that the selected cube has only two painted faces is:
1.3 CONDITIONAL PROBABILITY AND EVENT INDEPENDENCE
Many times, partial information about a random experiment can be obtained before its actual result is known. Resting upon this information, it is common to change the random experiment result’s probabilistic structure. For example, a poker player can at some point peek at a rival’s cards. Suppose he only managed to see that all cards had a red suit, that is, hearts or diamonds. Then our player knows his partner can’t have all four kings, an event that previously had a positive probability. On the other hand, he suspects that the event “having all cards of the same suit” is more likely than before getting the extra information.
Following, we are going to analyze the situation from the relative frequencies perspective. Let B be an event whose chance of happening must be measured under the assumption that another event A has been observed. If the experiment is then repeated n times under the same circumstances, then the relative frequency of B under the condition A is defined as
where n(A ⋂ B) indicates the number of favorable cases to A ⋂ B.
It is clear that r f(B | A) depends on n. However, when the experiment is performed for a large enough number of times, the relative frequencies tend to stabilize around a specific value between 0 and 1, known as the conditional probability of the event B under the condition A.
We observe that:
For large enough n, the numerator from the former expression tends to P(A ⋂ B) while the denominator tends to P(A). This motivates the following definition:
Definition 1.11 (Conditional Probability) Let (Ω, , P) be a probability space. If A, B with P(A) > 0, then the probability of the event B under the condition A is defined as follows:
Two fair dice are rolled once. The probability that at least one of the results is 6 given that the results obtained are different equals 
, as the following reasoning shows: Let A be the event “the results are different” and B the event “At least one of the results is 6”. It is clear that:
Then:
An urn contains 12 balls, 8 of which are white color. A sample of size 4 is taken without replacement. Then, the probability that the first and third balls extracted are white given that our sample contains three white balls equals . To this effect, let’s assume the balls are numbered from 1 to 12; then:
Ω = {(a1, a2 a3, a4) : ai {1,2,..., 12}, ai ≠ aj for all i ≠ j}.
Let:
A := “Exactly three of the balls extracted are white”.
B := “The first and the third balls removed are white”.
It is straightforward that:
Let (Ω, , P) be a probability space with
Ω = {a, b, c, d, e, f}, = (Ω)
and
Let A = {a, c, e}, B = {c, d, e, f} and C = {b, c, f}. Then:
Consider the flights starting from Bogotá to Medellín. In these flights, 90% leave on time and arrive on time, 6% leave on time and arrive late, 1% leave late and arrive on time and 3% leave late and arrive late. What is the probability that, given a flight leaves late, it will arrive on time?
solution: Given:
P(Flight leaves on time and arrives on time) = 0.9
P(Flight leaves on time and arrives late) = 0.06
P(Flight leaves late and arrives on time) = 0.01
P(Flight leaves late and arrives late) = 0.03.
Now:
The next theorem provides us with the main properties of conditional probability:
Theorem 1.3 (Conditional Probability Measure) Let (Ω, , P) be a probability space, and let A with P(A) > 0. Then:
1. P( · | A) is a probability measure over Ω centered on A, that is, P(A | A) = 1.
2. If A ⋂ B = , then P(B | A) = 0.
3. P(B ⋂ C | A) = P (B | A ⋂ C) P(C | A) if P(A ⋂ C) > 0.
4. If A1, A2,· · ·, An with P(A1 ⋂ A2 ⋂ · · · ⋂ An−1) > 0, then
Proof
1. The three properties of a probability measure must be verified:
(i) Clearly P(B | A) ≥ 0 for all B .
(ii) 
Therefore, we also have that P(A | A) = 1.
(iii) Let A1, A2, · · · be a sequence of disjoint elements from . Then:
2. Left as an exercise for the reader.
4. Left as an exercise for the reader.
An urn contains 12 balls, 4 of which are black while the remaining 8 are white. The following game is played: the first ball is randomly extracted and, after taking note of its color, it is then returned to the urn along with a new pair of balls of the same color. Find the probability that in the first three rounds of the game all the balls drawn are black. Solution: For i = 1,2,3 we define:
Ai := “a black ball was extracted on the ith round of the game”.
Clearly:
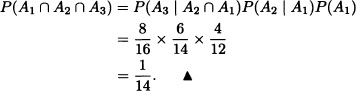
Three teenagers want to get into an R-rated movie. At the box office, they are asked to produce their IDs; after the clerk checks them and denies them the entrance, he returns the IDs randomly. Find the probability that none of the teenagers get their own ID.
Solution: Let:
A := “None of the teenagers get their own ID”.
Bi := “The ith teenager gets his own ID”.
Clearly, the probability we look for is:
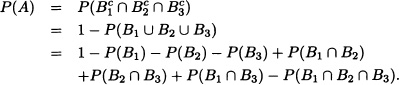
Since there are three possible cases and only one is favorable:
On the other hand, for any i ≠ j,
seeing that, after giving the ith teenager the right ID, for the jth teenager there is only one favorable option from two possible ones. In a similar fashion:
Therefore:
The reliability of a device or its separate units is understood as the probability of their trouble-free operation without failure.
Let us consider a system composed of n units. It is assumed that unit fails independently of another unit. A series system is one in which all units must operate successfully. On the other had, a parallel system is one that will fail only if all its units fail. Let reliability of each unit be p.
Then, the reliability of series system R1 is given by:
R1 = pn.
Similarly, the reliability of parallel system R2 is given by:
R2 = 1 − (1 − p)n.
In the following example, we illustrate the reliability of a non-series/parallel system.
Figure 1.1 A communication network system
Consider a communication network system in India with five network switches placed as shown in Figure 1.1. Suppose that the probability that each network switch will perform a required function without failure, i.e., reliability of each network switch, is R1 = 0.98, R2 = 0.99, R3 = 0.99, R4 = 0.96 and R5 = 0.95. Assume that each network switch is functioning independently. Find the reliability of the communication network system.
Solution: For i = 1, 2, · · ·, 5 let:
Ai := “The ith network switch functioning”.
We define:
Ri = P(Ai) for i = l, 2,· · ·, 5.
The reliability of the communication network system is:
The following results are vital for applications:
Theorem 1.4 (Total Probability Theorem) Let A1, A2,· · ·, be a finite or countable partition of Ω, that is, Ai ⋂ Aj = for all i ≠ j and 
such that P(Ai) > 0 for all Ai . Then, for any B :
and hence,
which proves the theorem.
As a corollary to the previous theorem we obtain a result known as Bayes’ rule, which constitutes the base for an important statistical theory called Bayesian theory.
Corollary 1.1 (Bayes’ Rule) Let A1, A2,· · · be a finite or countable partition of Ω with P(Ai) > 0 for all i; then, for any B 
with P(B) > 0:
Proof:
To give an interpretation of Bayes’ rule, suppose that the events A1, A2,· · · are all possible causes, mutually exclusive, of a certain event B. Under the assumption that we have indeed observed the event B, Bayes’ formula allows us to know which of these causes is most likely to have produced the event B.
Mr. Rodríguez knows that there is a chance of 40% that the company he works with will open a branch office in Montevideo (Uruguay). If that happens, the probability that he will be appointed as the manager in that branch office is 80%. If not, the probability that Mr. Rodríguez will be promoted as a manager to another office is only 10%. Find the probability that Mr. Rodríguez will be appointed as the manager of a branch office from his company.
Solution: Let:
M := “Mr. Rodríguez is appointed as a manager”.
N := “The company opens a new branch office in Montevideo”.
Then:
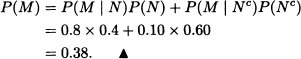
In the previous example, if we know that Mr. Rodríguez was indeed appointed manager of an office from the company he works for, what is the probability that the company opened a new office in Montevideo?
Solution: From Bayes’ rule, is clear that:
A signal can be green or red with probability 
or 
, respectively. The probability that it is received correctly by a station is 
Of the two stations A and B, the signal is first received by A and then station A passes the signal to station B. If the signal received at station B is green, then find the probability that the original signal was green?
Solution: Let:
BG(BR) := “Signal received at station B is Green (Red)”,
AG(AR) := “Signal received at station A is Green (Red)”,
Then from Bayes’ rule, it is clear that:
Now:
Hence:
It is known that each of four people A, B, C, D tells the truth in a given instance with probability 
. Suppose A makes a statement, and D says that C says that B says that A was telling the truth. What is the probability that A was actually telling the truth?
Solution: Let:
T := “A speaks the truth”.
E := “D says the statement”.
Then:
The required probability is P(TE). Now:
Hence:
A quarter of a population is vaccinated against a certain contagious disease. During the course of an epidemic due to such disease, it is observed that from every 5 sick persons only 1 was vaccinated. It is also known that from every 12 vaccinated people, only 1 is sick. We wish to find the probability that a nonvaccinated person is sick.
Solution: Let:
V := “The person is vaccinated”.
S := “The person is sick”.
From the information, we have:
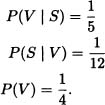
Thus
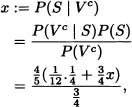
and therefore
It is known that the population of a certain city consists of 45% females and 55% males. Suppose that 70% of the males and 10% of the females smoke. Find the probability that a smoker is male.
Solution: Let S be the event that a person is a smoker, M be the event that a person is male and F be the event that a person is female:
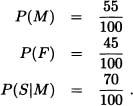
The required probability is:
Dunlop tire Company produces tires which pass through an automatic testing machine. It is observed that 5% of the tires entering the testing machine are defective. However, the automatic testing machine is not entirely reliable. If a tire is defective, there is 0.04 probability that it is not to be rejected. If a tire is not defective there is 0.06 probability that it will be rejected. What is the probability that the tires rejected are actually not defective. Also, what fraction of those not rejected are defective?
Solution: Let D be the event that the tire is defective and R be the event that the tire is rejected:
It is given that:
Similarly
Definition 1.12 (A Priori and A Posteriori Distributions) Let A1, A2, … be a finite or countable partition of Ω with P(Ai) > 0 for all i. If B is an element from 
with P(B) > 0, then (P(An))n is called the “a priori”distribution, that is, before B happens, and (P(An | B))n is called the “a posteriori”distribution, that is, after B has happened.
In a city, tests are taken to detect a certain disease. Suppose that 1% of the healthy people are registered as sick, 0.1% of the population is actually ill and 90% of the sick are reported as such. We wish to calculate the probability that a randomly chosen person reported as ill is indeed sick.
If we define the events
S := “the person is indeed sick”
R := “the person is reported as sick”
from the information stated above, we know that:
In this case:
A priori distribution = (P(S), P(Sc)) = (0.001,0.999)
A posteriori distribution = (P(S | R), P(Sc | R)) = (0.083,0.917).
Sometimes the occurrence of an event B does not affect the probability of an event A, that is:
In this case, we say the event A is ”independent” from event B. The “definition” (1.1) requires the condition that P(B) > 0. To avoid this condition, we define independence as follows:
Definition 1.13 (Independent Events) Two events A and B are said to be independent if and only if:
On the contrary, if the previous condition is not met, the events are said to be dependent.
Suppose a fair die is rolled two times. Let:
A := “The sum of the results obtained is an even number”.
B := “The result from the second roll is even”.
In this case:
Furthermore, 
Accordingly, the events are independent.
A die is biased in such a way that the probability of obtaining an even number equals 
. Let A and B be defined as in the preceding example. Under these conditions we have:
Thus, A and B are not independent.
Note 1.5 A mistake that is commonly made is to assume that two events are independent if they are mutually exclusive. Note that this is not the case. For example, if a fair coin is flipped once and we consider the events
A := “the result obtained is head”
B := “the result obtained is tail”
then, clearly, A and B are mutually exclusive. They are however not independent, since:
Theorem 1.5 Let A and B be independent events. Then:
1. A and Bc are two independent events (and hence by symmetry Ac and B are two independent events).
2. Ac and Bc are two independent events.
Proof:
1.
Therefore:
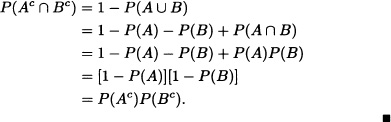
In many cases it is necessary to analyze the independence of two or more events. In this context a broader definition of independence must be given.
Definition 1.14 (Independent Family) A family of events 
is said to be independent if
for every finite subset ≠ J of I. These events are mutually independent events.
Definition 1.15 (Pairwise Independent Events) A family of events is said to be pairwise (2 × 2) independent if:
Pairwise independence does not imply the independence of the family or mutually independent events, as the following example shows:
A fair die is rolled two consecutive times. Let A, B and C be the events defined as follows:
A := “A 2 was obtained in the first toss”.
B := “A 5 was obtained in the second toss”.
C := “The sum of the results is 7”.
Clearly:
Figure 1.2 Sample and event space
The events are therefore pairwise independent, but they are however not mutually independent because:
1.4 GEOMETRIC PROBABILITY
Let 
be a measurable space, and assume that a geometric measure m, such as length, area or volume, is defined over . We define the geometric probability of an event A as follows:
Next, we give some examples showing geometric probability calculus.
Find the probability that a point chosen at random lies on a line segment 
of a line 
(see Figure 1.2).
Solution:
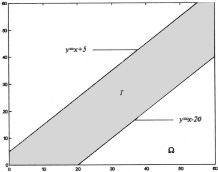
María Victoria and Carlos agreed to meet downtown between 12 noon and 1 PM. They both get there at any moment in that time interval. Assuming their arrival times to be independent, find:
(i) The probability that Carlos and María Victoria will meet if both of them waits for the other 10 minutes at most.
Figure 1.3 Event space for case (i)
(ii) The probability that Carlos and María Victoria will meet if María Victoria waits 5 minutes but Carlos waits 20.
Solution: (i) Let X and Y be events defined as follows:
X := “María Victoria’s arrival time”
Y := “Carlos’ arrival time”.
The sample space in this case is given by:
Ω := {(x, y) 
2 : 0 ≤ x ≤ 60, 0 ≤ y ≤ 60}.
We wish to measure the probability of the event:
T = {(x, y) Ω : |x − y| ≤ 10}.
Therefore (see Figure 1.3):
(ii) The set of points T representing the arrival times of Carlos and María Victoria that allow them to meet is represented in Figure 1.4. Thus, the probability we wish to find equals:
Figure 1.4 Event space for case (ii)
EXERCISES
1.1 A fair coin is flipped three times in a row. Let:
A := “The result of the first toss is head”.
B := “The result of the third toss is tail”.
Describe in words the events A ∩ B, A ∪ B, Ac, Ac ∩ Bc, A ∩ Bc and find its elements.
1.2 Let A, B and C be three arbitrary events. Give in terms of set operations of the following events:
a) A and B but not C.
b) All three of them.
c) Only A.
e) At most one of them.
f) At most two of them.
1.3 A fair die is rolled twice in a row. Let A, B and C be the events given by:
A := “The first result obtained is an even number”.
B := “The sum of the results is less than 7”.
C := “The second result obtained is a prime number”.
List the elements belonging to the following events:
a) A ∩ B ∩ C.
b) B ∪ (A ∩ Cc).
c) (A ∩ C) ∩ [(A ∪ B)c].
1.4 A random experiment consists in extracting three light bulbs and classifying them as defective “D” or nondefective “N”. Consider the events:
Ai := “The ith light bulb removed is defective”, i = 1, 2, 3.
a) Describe the sample space for this experiment.
b) List all the results in A1, A2, A1 ∪ A3, 
∩ 
∩ A3 and (A1 ∪ ) ∩ A3.
1.5 A worker makes n articles. The event “The ith article is defective” will be notated as Ai with i = 1,2,···, n. Describe the following events using the sets Ai and the usual operations between events:
a) B := “At least an article is defective”.
b) C := “None of the n articles is defective”.
c) D := “Exactly one article is defective”.
d) E := “At most one article is defective”.
1.6 Let A, B and C be arbitrary events. Depict the following events in terms of A, B and C:
a) E1 := “At least one of the events A, B, C happens”.
b) E2 := “Exactly two of the events A, B, C happen”.
c) E3 := “At least two of the events A, B, C happen”.
d) E4 := “At most one of the events A, B, C happens”.
1.7 Suppose that 35% of the students of a university are taking English, 7% are taking German and 2% are taking both English and German. What percentage of the student population is taking English but not German? What percentage of the students are taking neither English nor German?
1.8 Let Ω ≠ and let 
be a σ-algebra over Ω. Prove:
a) If A1, A2 ··· , then 
.
b) If A, B , then A ∪ B, A ∩ B, A B and A Δ B all belong to .
1.9 Let Ω = {1,2,3,4}. Find four different σ-algebras 
for n = 1,2,3,4 such that 
.
1.10 Let Ω and 
be nonempty sets and 
a σ-algebra over 
. If T : Ω → is a function, then prove that the collection T−1 () = {T−1(A) : A } is a σ-algebra over Ω.
1.11 Let Ω ≠ and 
be a nonempty subset of Ω. If is a σ-algebra over Ω, then prove that = {A ∩ : A } is a σ-algebra over called the trace of on .
1.12 Let A1, A2,···, An be events in the probability space (Ω, , P). Prove that:
1.13
a) Find the σ-algebra over Ω = {1,2,3} generated by {{2}, {3}}.
b) Let 
and 
be two families of subsets from a nonempty set Ω with ⊆ . Is σ() ⊆ σ()? Explain.
c) Let Ω = {1,2}, = {, Ω, {1}, {2}} and μ defined over by:
Is (Ω, , μ) a probability space? Explain.
1.14 Let Ω = {a, b, c, d}, = {, Ω, {a}, {b, c}, {d}, {a, b, c}, {b, c, d}, {a, d}} and P a map of on [0, 1] with P({a}) = 
, P({b, c}) = 
and P({d}) = α.
a) Determine the value that α should take in order for P to be a probability measure over (Ω, ).
b) Find P({a, b, c}), P({a, c, d}) and P({a, d}).
1.15 Let 
be a sequence of probability measures over a measurable space 
a sequence of nonnegative real numbers such that 
and 
defined by:
Prove that P is a probability measure over (Ω, ).
1.16 Indicate whether the following statements are true or false. Give a brief account of your choice:
a) If P(A) = 0, that A = .
b) If P(A) = P(B) = 0, then P(A ∪ B) = 0.
c) If P(A) = 
and P(B) = 
, then ≤ P(A ∪ B) ≤ 
.
d) If P(A) = P(B) = p, then P(A ∩ B) ≤ p2.
e) P(A Δ B) = P(A) + P(B) − 2P(A ∩ B).
f) If P(A) = 0.5, P(B) = 0.4 and P(A ∪ B) = 0.8, then P(Ac ∩ B) = 0.1
g)If A and B are independent events and A ⊂ B, then P(A) = 0 or P(B) = 1.
1.17 Prove that P(A ∪ B ∪ C) = P(A) + P(Ac ∩ B) + P(Ac ∩ Bc ∩ C).
1.18 Let A and B be two events with P(A) = and P(Bc) = 
Can A and B be mutually exclusive events? Justify.
1.19 A die is biased in such a way that the probability of getting an even number is twice that of an odd number. What is the probability of obtaining an even number? A prime number? An odd prime number?
1.20 From the 100 students majoring in philology and classic languages in the linguistics department of a certain University 28 take Latin classes, 26 take Greek, 16 Hebrew, 12 both Latin and Greek, 4 Latin and Hebrew and 6 Greek and Hebrew. Furthermore, 2 are taking all the aforementioned subjects.
a) If a philology and classic languages student is randomly chosen, what is the probability that he or she is taking only Hebrew?
b) If a philology and classic languages student is randomly chosen, what is the probability that he or she is taking Greek and Hebrew but not Latin?
c) If two philology and classic languages students are randomly chosen, what is the probability that at least one of them is attending one of the classes?
1.21 A company was hired to poll the 1000 subscribers of a magazine. The data presented on their report indicate that 550 subscribers axe professional, 630 are married, 650 are over 35 years of age, 127 are professional and over 35, 218 are married and over 35, 152 are professional and married and 100 are married, professional and over 35. Is the data presented in the report right? Explain.
1.22 A fair coin is flipped n times. Let
Ak := “The first head was obtained in the kth toss”
where k = 1,2,…, n. What is P(Ak) equal to?
1.23 Ten distinguishable balls are randomly distributed on 7 distinguishable urns. What is the probability that all urns have at least one ball? What is the probability that exactly two urns are left empty?
1.24 A group of 40 students is made from 20 men and 20 women. If this group is then divided in two equal groups, what is the probability that each group has the same number of men and women?
1.25 Let w be a complex cube root of unity with w ≠ 1. A fair die is thrown three times. If x, y and z are the numbers obtained on the die. Find the probability that wx + wy + wz = 0.
1.26 The coefficients a, b and c of the quadratic equation ax2+bx+c = 0 are determined by rolling a fair die three times in a row. What is the probability that both roots of the equation are real? What is the probability that both roots of the equation are complex?
1.27 What is the chance that a leap year selected at random has 53 Sundays?
1.28 There are two urns A and B. Urn A contains 3 red and 4 black balls while urn B contains 5 red and 7 black balls. If a ball is randomly drawn from each urn, what is the probability that the balls have the same color?
1.29 An urn contains 3 red and 7 black balls. Players A and B consecutively extract a ball each until a red one is drawn. What is the probability that player A will remove the red ball from the urn? Assume the extraction is carried without replacement and player A starts the game.
1.30 There are 200 ornamental fishes in a lake; 50 of them are captured and tagged and then returned to the lake. A few days later 40 fishes are captured. What is the probability that 20 out of the 40 are tagged already?
1.31 Five men and 5 women are ordered according to their grades in a test. Suppose that no two grades are the same and that all 10! arrangements are equally likely. What is the probability that the best position achieved by a man is the fourth one?
1.32 In Bogotá, the father of a certain family decides to plan weekend activities with his children according to the result of the roll of a fair die. If the result is equal to or less than 3, he will take his children to their grandmother’s house; if the result is 4 he will take them to the beach in the city of Cartagena; and if the result is 5 or 6, he will stay at home to watch movies with his children.
In order to have an idea of how his weekend activities are shaping up to be, the father decides to divide the year in 13 periods of 4 weeks each and is interested in the probability of the following events:
a) Go at least one trip to Cartagena.
b) Stay twice at home.
c) Go at least three times to grandmother’s house.
d) Do each activity at least once.
Calculate the probability of these events?
1.33 In order to illuminate a stairway 7 lamps have been placed and labeled with letters from A to G. To guarantee a proper lighting, lamps A or B must work along with lamps F or G, or any of the lamps C, D or E must be working. The probability that any given lamp will be working is 
.
a) What is the probability that the stairway will be well lit?
b) How does the probability from part i) change if the lamp D is never used?
1.34 What is the probability that among a group of 25 people at least 2 have the same birthday? Assume that the year has 365 days and that all of them are equally likely to be somebody’s birthday.
1.35 There are n people at a Christmas party, each carrying a gift. All the presents are put in a bag and mixed, then each person randomly takes one. What is the probability that no one gets their own present?
1.36 In a bridge game, the whole pack of 52 cards is dealt between 4 players.
a) What is the probability that each player gets an ace?
b) What is the probability that one player gets 5 spades while another one receives the remaining 8?
1.37 An urn contains 15 balls, 9 of which are red and the other 6 are white. The following game is played: a ball is randomly extracted and, after taking note of its color, it is returned to the urn along with a new pair of balls of the same color. Find the probability that in the first three rounds of the game all the balls drawn are white.
1.38 Find the probability that in a group of 13 cards, from a pack of 52, there are exactly two kings and an ace. What is the probability that in such a group there is exactly one ace given that the group contains exactly two kings?
1.39 Let A and B be events such that P(A) = 0.5, P(B) = 0.3 and P(A ∩ B) = 0.1. Find P(A | B), P(A | Bc), P(A | A ∩ B), P(Ac | A ∪ B) and P(A ∩ B | A ∪ B).
1.40 A math student must take on the same day a probability and an algebra exam. Let:
A := “The student fails the probability exam”.
B := “The student fails the algebra exam”.
Let P(A) = 0.4, P(B) = 0.3 and P(A ∩ B) = 0.2. What is the probability that the student passes the algebra exam given that he passed the probability one? What is the probability that the student passes the probability exam given that he failed the algebra one?
1.41 A survey was taken in a certain city producing the following results:
| 90% | of the families owns both a radio and a TV. |
| 8% | of the families owns a radio but not a TV. |
| 2% | of the families owns a TV but not a radio. |
| 95% | of the families that owns a radio and a TV knows who the city mayor is. |
| 80% | of the families that owns a radio but not a TV knows who the city mayor is. |
| 1% | of the families that owns a TV but not a radio does not know who the city mayor is. |
A family is randomly chosen in this city. Consider the events:
T := “The family owns a TV”
R := “The family owns a radio”
B := “The family knows who is the city mayor”.
Find the following probabilities:
a) P(T ∪ R).
b) P(B ∩ T).
c) P(T | B).
1.42 Consider a population that develops according to the following rules: an initial individual constitutes the 0th generation and it can have 0, 1 or 2 descendants with probabilities of 
, 
and , respectively. After giving its offspring, the individual dies. Each descendant reproduces independently from one another and the family history, following the same rule as the original individual. The first generation will be made from the children of the first individual, the second generation will be made from its grandchildren, and so on. Given that there is only one individual in the second generation, what is the probability that the first generation had two individuals? What is the probability that there is at least one individual in the second generation?
1.43 Consider two urns A and B. Urn A contains 7 red balls and 5 white ones while urn B contains 2 red balls and 4 white ones. A fair die is rolled, if we obtain a 3 or a 6 a ball is taken from B and put into A and, after this, a ball is extracted from A. If the result is any other number, a ball is taken from A and put into B and then a ball is extracted from B. What is the probability that both balls extracted are red?
1.44 Suppose that you ask a classmate to sign you up for the class “Mathematics with no effort” that is being offered for the next term. If your classmate forgets to make the registration by the deadline set by the Mathematics Department, the probability that the class won’t have its quota filled and you can therefore register is 2%; on the other hand, if your classmate registers you on time, the probability that the class won’t have its quota filled is 80%. You are 95% sure that your classmate will register you on time. What is the probability that your classmate forgot to sign you up for the class if you could not register?
1.45 The probability that in a twin’s birth both babies are males is 0.24, while the probability that they are both females is 0.36. What is the probability that in a twin’s delivery the second baby born is a boy given that the first one was a boy? Suppose that it is equally likely for the first baby to be either male or female.
1.46 A particle starts at the origin and moves to and from on a straight line. At any move it jumps either 1 unit to the right or 1 unit to the left each with probability . All successive moves are independent. Given that the particle is at the origin at the completion of the 6th move, find the probability that it never occupied a position to the left of the origin during previous moves.
1.47 An investor is considering buying a large number of shares of a company. The stock quote of the company in the past 6 months is of great interest to him. Based on this information, he observes that the share price is closely related to the gross national product (GNP): if the GNP goes up, the probability that the share price will rise as well is 0.7; if the GNP remains stable, the probability that the share price will increase is just 0.2; if the GNP falls, however, the probability that the price share will go up is only 0.1. If the probabilities that the GNP increases, remains the same or decreases are 0.5, 0.3 and 0.2, respectively, what is the probability that the shares will go up? If the shares rose their stock quote, what is the probability that the GNP had increased as well?
1.48 A person wrote n letters, sealed them in n envelopes and wrote the n different addresses randomly one on each of them. Find the probability that at least one of the letters reaches its correct destination.
1.49 Suppose that 15 power plants are distributed at random among 4 cities. What is the probability that exactly 2 cities will receive none.
1.50 Suppose that in answering a question on a multiple-choice test an examinee either knows the answer or he guesses. Let p be the probability that he will know the answer, and let 1 − p be the probability that he will guess. Assume that the probability of answering a question correctly is unity for an examinee who knows the answer and 
for an examinee who guesses, where m is the number of multiple-choice alternatives. Find the conditional probability that an examinee knew the answer to a question given that he has correctly answered it.
1.51 There are eight coins in an urn. Two of them have two tails, three are fair coins and three are biased in such a way that the probability of getting a tail equals 
. A coin is randomly drawn from the urn. If flipping the coin produced a head, what is the probability that the coin drawn was a common one?
1.52 Let Ω = {a, b, c}, = (Ω) and P(w) = for all ω ∈ Ω. Let A = {b, c}. Find all the elements B such that A and B are independent.
1.53 Let Ω = {1, 2, 3, 4, 5, 6}, = (Ω) and P(w) = for all ω ∈ Ω. Prove that if A and B are independent elements in and A has 3 elements, then B must have an even number of elements.
1.54 Let Ω = {1, 2, 3, 4, 5, 6}, = (Ω) and P be a probability measure with P({1}) = P({2}) = 
, P({3}) = P({4}) = . Find P({5}) and P({6}) if the events {1, 3, 4} and {1, 2, 3, 5} are independent.
1.55 Cards are taken out of a standard deck of 52 cards. Let event A be a card with a spade and event B a king. Are A and B independent events?
1.56 Prove that if A = B and A and B are mutually independent (that is, A is independent of itself), then P(A) = 0 or P(A) = 1.
1.57 Let A be an event. Prove that the following conditions are equivalent:
a) A and B are independent for any event B.
b) P(A) = 0 or P(A) = 1.
1.58 Let A, B and C be independent events. Prove that A and B ∪ C; A and B ∩ C; A and (B C) are independent.
1.59 Suppose that each of three men at a party throws his hat into the center of the room. The hats are first mixed up and then each man randomly selects a hat. What is the probability that none of the men selects his own hat?
1.60 Prove that events A1, A2, …, An are independent if and only if
P(B1 ∩ B2 ∩ … ∩Bn) = P(B1)P(B2) … P(Bn)
for all possible choices of B1, B2, …, Bn with Bi = Ai or 
for all i = 1,2, ···, n.
1.61 A fair coin is flipped three times in a row. Consider the following events:
A := “The results of flips 1 and 2 are different”.
B := “The results of flips 2 and 3 are different”.
C := “The results of flips 1 and 3 are different”.
a) Verify that P(A) = P(A | B) = P(A | C) and that P(A) ≠ P(A | B ∩ C).
b) Are A, B and C 2 × 2 independent? Are A, B and C independent? Explain your answers.
1.62 Let us pick one of the four points (1, 0, 0), (0, 1, 0), (0, 0, 1) and (1, 1, 1) at random with probability each. Define, for k = 1,2,3:
Ak = {the kth coordinate equals 1}.
Show that the events A1, A2 and A3 are pairwise independent but not independent.
1.63 Let A, B and C be independent events with P(A) = P(B) = P(C) = . Find the probability that:
a) At least one event happens.
b) At least two events happen.
c) Exactly two of the events happen.
1.64 Find the probability that among seven people:
a) No two of them were born the same day of the week (Sunday, Monday, Tuesday, etc.).
b) At least two of them were born the same day.
c) Two were born on Sunday and two on Tuesday.
1.65 In a town of n + 1 inhabitants, a person tells a rumor to a second person, who in turn repeats it to a third person, etc. At each step, the recipient of the rumor is chosen at random from the n people available. Find the probability that the rumor will be told r times without returning to the originator.
1.66 Suppose that an urn contains N balls numbered from 1 to N. A random sample of size n is taken without replacement, and the numbers obtained are taken down. After returning the balls to the urn, a second sample of size m(≥ 1) is extracted without replacement. Find the probability that both samples have k balls in common.
1.67 An urn contains balls numbered from 1 to N. A ball is randomly drawn.
a) What is the probability that the number on the ball is divisible by 3 or 4?
b) What happens to the probability from the previous question when n → ∞?
1.68 Pick a number x at random out of the integers 1 through 30. Let A be the event that x is even, B that x is divisible by 3 and C that x is divisible by 5. Are the events A, B and C independent?
1.69 Let Q = (x, y) be a point chosen at random in a unit disc centered in (0,0) and with radius 1. Calculate the probabilities that Q is within 0.5 of the center; that y > 
; that both || x − y || < 1 and || x + y || < 1.
1.70 Suppose that a straight line is randomly subdivided into three parts. What is the probability that these parts can be assembled into a triangle?
1.71 An omnibus company always requires its drivers to wait for 10 minutes at a particular bus stop. The bus you hope to get arrives at this stop anywhere between noon and 1 PM. Assume that you arrive at the stop randomly between 12:30 PM and 1:30 PM and plan to spend at most 10 minutes waiting for the bus. What is the probability that you catch your bus on any day?
Figure 1.5 A system with five components
Figure 1.6 Sample space
1.72 Consider a system consisting of five independently functioning components as shown in Figure 1.5. Suppose that the reliability of the components is Ri = 0.95, i = 1, 2, …, 5. Find the reliability of the system.
1.73 A point is randomly chosen from a disk of radius R. Calculate the probability that the point is closer to the circle than to the center.
1.74 Along a line segment 
two points l and m are randomly marked. Find the probability that l is closer to a than m.
1.75 There is a circular dartboard (see Figure 1.6). It costs $5000 to throw a dart. You win $10,000 if you hit the square outside of the circle. The radius of the circle is 20 cm. How long should the side of the square be made to make this game fair?
1.76 A point Q is selected at random in the square ABCD and it is constructed a rectangle AMPN (see Figure 1.7). Calculate the probability that the perimeter of the rectangle is less than the length of the square’s side.
1.77 A communication system consists of n components, each of which will independently function with probability p. The total system will be able to operate effectively if at least half of its components function. For what values of p is a five-component system more likely to operate effectively than a three-component system?
Figure 1.7 Sample space
1.78 Suppose a long-haul airplane has four engines and needs three or more engines to work in order to fly. Another airplane has two engines and needs one engine to fly. Assume that the engines are independent and suppose each has a constant probability p of staying functional during a flight. Find the reliability of both flights and conclude which one is safer.
1.79 A technological system consists of n units, the reliability of each unit being p. The failure of at least one unit results in the failure of the entire system. To increase the reliability of the system, it is duplicated by n similar units. Which way of duplication provides higher reliability: (a) the duplication of every unit (i.e., series of n units, each with duplication); (b) the duplication of the whole system (i.e., parallel system with n units in series).