Appendix E

Partial Fraction Expansion

The technique of partial fraction expansion is very useful in the study of signals and systems, particularly in finding the time-domain signals that correspond to inverse Laplace transforms and inverse z-transforms of rational functions, that is, a ratio of two polynomials. It is based on the idea of writing a rational function, say of s or z, as a linear combination of simpler rational functions the inverse transforms of which can be easily determined. Since both the Laplace transform and the z-transform are linear transforms, writing the rational function X (z) or X (z) as a linear combination of simpler functions and finding the inverse transform of each of those simpler functions allows us to construct the inverse transform of the original function in a straightforward manner. The main problem is in determining which simpler functions should be used in the expansion, and how much weight each should have.

In this appendix we will present the details of the partial fraction expansion technique first from the perspective of the Laplace transform for continuous-time signals, and then from the perspective of the z-transform for discrete-time signals.

E.1 Partial Fraction Expansion for Continuous-Time Signals and Systems

As an example, consider a rational function X (s) with two poles, expressed in the form

$$\begin{array}{ccc}X\left(s\right)=\frac{B\left(s\right)}{\left(s-a\right)\left(s-b\right)}=\frac{k_1}{s-a}+\frac{K_2}{s-b}& & \left(\text{E}\text{.1}\right)\end{array}$$

The rational function X (s) is expressed as a weighted sum of partial fractions

$$\frac{1}{s-a}$$

and

$$\frac{1}{s-b}$$

with weights k1 and k2 respectively. The weights k1 and k2 are called the residues of the partial fraction expansion. Before we address the issue of determining the values of the residues, a question that comes to mind is: What limitations, if any, should be placed on the numerator polynomial B (s) for the expansion in Eqn. (E.1) to be valid? In order to find the answer to this question we will combine the two partial fractions under a common denominator to obtain

$$\begin{array}{ccc}\frac{k_1}{s-a}+\frac{k_2}{s-b}=\frac{\left(k_1+k_2\right)s-\left(k_{1}b+k_{2}a\right)}{\left(s-a\right)\left(s-b\right)}& & \left(\text{E}\text{.2}\right)\end{array}$$

It is obvious from Eqn. (E.2) that the numerator polynomial B (s) may not be higher than first-order since no s2 term or higher-order terms can be obtained in the process of combining the two partial fractions under a common denominator. Consider a more general case of a rational function with P poles in the form

$$\begin{array}{ccc}\begin{array}{lll}X\left(s\right)\hfill & =\hfill & \frac{B\left(s\right)}{\left(s-s_1\right)\left(s-s_2\right)\cdots \left(s-s_P\right)}\hfill \\ \hfill & =\hfill & \frac{k_1}{s-s_1}+\frac{k_2}{s-s_2}+...+\frac{k_P}{s-s_P}\hfill \end{array}& & \left(\text{E}\text{.3}\right)\end{array}$$

If the P terms in the partial fraction expansion of Eqn. (E.3) are combined under a common denominator, the highest-order numerator term that could be obtained is sP− 1.

If this is not the case, some additional steps need to be taken before partial fraction expansion can be used. Suppose X (s) is a rational function in which the numerator order is greater than or equal to the denominator order. Let

$$\begin{array}{ccc}X\left(s\right)=\frac{b_Q{s}^Q+b_{Q-1}{s}^{Q-1}+...+b_{1}s+b_0}{a_P{s}^P+a_{P-1}{s}^{P-1}+...+a_{1}s+a_0}& & \left(\text{E}\text{.4}\right)\end{array}$$

with Q ≥ P. We can use long division on numerator and denominator polynomials to write X (s) in the modified form

$$\begin{array}{ccc}X\left(s\right)=C\left(s\right)+\frac{{\overline{b}}_{P-1}{s}^{P-1}+{\overline{b}}_{P-2}{s}^{P-2}+...+{\overline{b}}_{1}s+{\overline{b}}_{1}s+{\overline{b}}_0}{a_P{s}^P+a_{P-1}{s}^{P-1}+...+a_{1}s+a_0}& & \left(\text{E}\text{.5}\right)\end{array}$$

where C (s) is a polynomial of s. Now the new function

$$\begin{array}{ccc}\overline{X}\left(s\right)=X\left(s\right)-C\left(s\right)=\frac{{\overline{b}}_{P-1}{s}^{P-1}+{\overline{b}}_{P-2}{s}^{P-2}+...+{\overline{b}}_{1}s+{\overline{b}}_0}{a_P{s}^P+a_{P-1}{s}^{P-1}+...+a_{1}s+a_0}& & \left(\text{E}\text{.6}\right)\end{array}$$

has a numerator that is of lower order than its denominator, and can therefore be expanded into partial fractions. Example E.1 will illustrate this.

Example E.1:

Consider the function

$$X\left(s\right)=\frac{\left(s+1\right)\left(s+2\right)}{\left(s+5\right)\left(s+6\right)}$$

Since both the numerator and the denominator are of second order, the function cannot be

expanded into partial fractions directly. In other words, an attempt to express X (s) as

$$X\left(s\right)\stackrel{?}{=}\frac{k_1}{s+5}+\frac{K_2}{s+6}$$

would fail since the s2 term in the numerator cannot be matched by combining the two partial fractions under a common denominator. Instead, we will use long division to extract a polynomial C (s) from X (s) so that the difference X (s) − C(s) can be expanded into partial fractions. Let us first multiply out the factors in X (s) to write it as

$$X\left(s\right)=\frac{s^2+3s+2}{s^2+11s+30}$$

Now we can divide the numerator polynomial by the denominator polynomial using long division to obtain

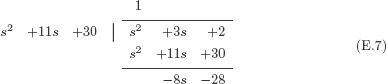
Thus, the function X (s) can be written in the equivalent form

$$\begin{array}{ccc}X\left(s\right)=1+\frac{-8s-28}{s^2+11s+30}& & \left(\text{E}\text{.8}\right)\end{array}$$

Let

$$\begin{array}{ccc}\overline{X}\left(s\right)=X\left(s\right)-1=\frac{-8s-28}{s^2+11s+30}& & \left(\text{E}\text{.9}\right)\end{array}$$

We can now expand the function $\overline{X}\left(s\right)$ into partial fractions as

$$\begin{array}{ccc}\overline{X}\left(s\right)=\frac{k_1}{s+5}+\frac{k_2}{s+6}& & \left(\text{E}\text{.10}\right)\end{array}$$

and write X (s) as

$$\begin{array}{ccc}X\left(s\right)=1+\overline{X}\left(s\right)=1+\frac{k_1}{s+5}+\frac{k_2}{s+6}& & \left(\text{E}\text{.11}\right)\end{array}$$

Example E.2:

Consider the function

$$X\left(s\right)=\frac{\left(s+1\right)\left(s+2\right)\left(s+3\right)}{\left(s+5\right)\left(s+6\right)}$$

the factors of which can be multiplied to yield

$$X\left(s\right)=\frac{s^3+6s^2+11s+6}{s^2+11s+30}$$

Using long division on X (s) we obtain

Thus, the function X (s) can be written in the equivalent form

$$\begin{array}{ccc}X\left(s\right)=s-5+X\left(s\right)=s-5+\frac{36s+156}{s^2+11s+30}& & \left(\text{E}\text{.13}\right)\end{array}$$

and can be expressed using partial fractions as

$$\begin{array}{ccc}X\left(s\right)=s-5+\frac{k_1}{x+5}+\frac{k_2}{s+6}& & \left(\text{E}\text{.14}\right)\end{array}$$

Now that we know how to deal with a function that has a numerator of equal or greater order than its denominator, we will focus our attention on determining the residues. For the purpose of determining the residues, we will assume that the order of the numerator polynomial is less than that of the denominator polynomial. In addition, we will initially consider a denominator polynomial with only simple roots. Thus, the function X (s) is in the form

$$\begin{array}{ccc}X\left(s\right)=\frac{B\left(s\right)}{\left(s-s_1\right)\left(s-s_2\right)...\left(s-s_P\right)}& & \left(\text{E}\text{.15}\right)\end{array}$$

to be expanded into partial fractions in the form

$$\begin{array}{ccc}X\left(s\right)=\frac{k_1}{s-s_1}+\frac{k_2}{s-s_2}+...+\frac{k_P}{s-s_P}& & \left(\text{E}\text{.16}\right)\end{array}$$

Let us multiply both sides of Eqn. (E.16) by (s − s1) to obtain

$$\begin{array}{ccc}\left(s-s_1\right)X\left(s\right)=k_1+\frac{k_2\left(s-s_1\right)}{s-s_2}+...+\frac{k_P\left(s-s_1\right)}{s-s_P}& & \left(\text{E}\text{.17}\right)\end{array}$$

If we now set s = s1 on both sides of Eqn. (E.17) we get

$$\begin{array}{ccc}\begin{array}{lll}\left(s-s_1\right)X\left(s\right){|}_{s=s_1}\hfill & =\hfill & k_1{|}_{s=s_1}+\frac{k_2\left(s-s_1\right)}{s-s_2}{|}_{s=s_1}+...+\frac{k_P\left(s-s_1\right)}{s-s_P}{|}_{s=s_1}\hfill \\ \hfill & =\hfill & k_1\hfill \end{array}& & \left(\text{E}\text{.18}\right)\end{array}$$

Thus, the residue of the pole at s = s1 can be found by multiplying X (s) with the factor (s − s>1) and then setting s = s1. Using the form of X (s) in Eqn. (E.15) the residue k1 is found as

$$\begin{array}{ccc}\left(s-s_1\right)X\left(s\right){|}_{s=s_1}=\frac{B\left(s_1\right)}{\left(s_1-s_2\right)...\left(s_1-s_P\right)}& & \left(\text{E}\text{.19}\right)\end{array}$$

which amounts to canceling the (s − s1) term in the denominator, and evaluating what is left for s = s1. Generalizing this result, the residue of the n-th pole is found as

$$\begin{array}{cccc}{k}_n=\left(s-s_n\right)X\left(s\right){|}_{s=s_n}& n=1,...,P& & \left(\text{E}.20\right)\end{array}$$

Example E.3:

Find a partial fraction expansion for the rational function

$$X\left(s\right)=\frac{\left(s+1\right)\left(s+2\right)}{\left(s+3\right)\left(s+4\right)\left(s+5\right)}$$

Solution: The partial fraction expansion we are looking for is in the form

$$\begin{array}{ccc}X\left(s\right)=\frac{k_1}{s+3}+\frac{k_2}{x+4}+\frac{k_3}{s+5}& & \left(\text{E}\text{.21}\right)\end{array}$$

We will use Eqn. (E.20) to determine the residues. The first residue k1 is obtained as

$$\begin{array}{lll}{k}_1\hfill & =\hfill & \left(s+3\right)X\left(s\right){|}_{s=-3}\hfill \\ \hfill & =\hfill & \frac{\left(s+1\right)\left(s+2\right)}{\left(s+4\right)\left(s+5\right)}{|}_{s=-3}\hfill \\ \hfill & =\hfill & \frac{\left(-3+1\right)\left(-3+2\right)}{\left(-3+4\right)\left(-3+5\right)}=1\hfill \end{array}$$

The remaining two residues k2 and k3 are obtained similarly:

$$\begin{array}{lll}{k}_2\hfill & =\hfill & \left(s+4\right)X\left(s\right){|}_{s=-4}\hfill \\ \hfill & =\hfill & \frac{\left(s+1\right)\left(s+2\right)}{\left(s+3\right)\left(s+5\right)}{|}_{s=-4}\hfill \\ \hfill & =\hfill & \frac{\left(-4+1\right)\left(-4+2\right)}{\left(-4+3\right)\left(-4+5\right)}=-6\hfill \end{array}$$

$$\begin{array}{lll}{k}_3\hfill & =\hfill & \left(s+5\right)X\left(s\right){|}_{s=-5}\hfill \\ \hfill & =\hfill & \frac{\left(s+1\right)\left(s+2\right)}{\left(s+3\right)\left(s+4\right)}{|}_{s=-5}\hfill \\ \hfill & =\hfill & \frac{\left(-5+1\right)\left(-5+2\right)}{\left(-5+3\right)\left(-5+4\right)}=6\hfill \end{array}$$

Thus, the partial fraction expansion for X (z) is

$$X\left(s\right)=\frac{1}{s+3}-\frac{6}{s+4}+\frac{6}{s+5}$$

Next we will consider a rational function the denominator of which has repeated roots. Let X (s) be a rational function with a pole of order r at s = s1.

$$\begin{array}{ccc}X\left(s\right)=\frac{B\left(s\right)}{{\left(s-s_1\right)}^r\left(s-s_2\right)}& & \left(\text{E}\text{.22}\right)\end{array}$$

The partial fraction expansion for X (s) needs to be in the form

$$\begin{array}{ccc}X\left(s\right)=\frac{k_{1,1}}{s-s_1}+\frac{k_{1,2}}{{\left(s-s_1\right)}^2}+...+\frac{k_{1,r}}{{\left(s-s_1\right)}^r}+\frac{k_2}{s-s_2}& & \left(\text{E}\text{.23}\right)\end{array}$$

For the multiple pole at s = s1 as many terms as the multiplicity of the pole are needed so that combining the terms on the right side of Eqn. (E.23) can yield a result that matches the function X (s) given by Eqn. (E.22).

The residue k2 of the single pole at s = s2 can easily be determined as discussed above. We will focus our attention on determining the residues of the r-th order pole at s = s1. Let us begin by multiplying both sides of Eqn. (E.23) by (s − s1)r to obtain

$$\begin{array}{ccc}{\left(s-s_1\right)}^{r}X\left(s\right)=k_{1,1}{\left(s-s_1\right)}^{r-1}+k_{1,2}{\left(s-s_1\right)}^{r-2}+...+k_{1,r}+\frac{k_2{\left(s-s_1\right)}^r}{s-s_2}& & \left(\text{E}\text{.24}\right)\end{array}$$

If we now set s = s1 on both sides of E.24) we would get

$$\begin{array}{ccc}\begin{array}{lll}{\left(s-s_1\right)}^{r}X\left(s\right){|}_{s=s_1}\hfill & =\hfill & k_{1,1}{\left(s-s_1\right)}^{r-1}{|}_{s=s_1}+k_{1,2}{\left(s-s_1\right)}^{r-2}{|}_{s=s_1}\hfill \\ \hfill & \hfill & +...+k_{1,r}{|}_{s=s_1}+\frac{k_2{\left(s-s_1\right)}^r}{s-s_2}{|}_{s=s_1}\hfill \\ \hfill & =\hfill & k_{1,r}\hfill \end{array}& & \left(\text{E}\text{.25}\right)\end{array}$$

It can be shown that the other residues for the pole at s = s1 can be found as follows:

$$\begin{array}{lll}{k}_{1,r-1}\hfill & =\hfill & \frac{d}{ds}\left[{\left(s-s_1\right)}^{r}X\left(s\right)\right]{|}_{s=s_1}\hfill \\ k_{1,r-2}\hfill & =\hfill & \frac{1}{2}\frac{d^2}{d{s}^2}\left[{\left(s-s_1\right)}^{r}X\left(s\right)\right]{|}_{s=s_1}\hfill \\ \hfill & ⋮\hfill & \hfill \\ k_{1,2}\hfill & =\hfill & \frac{1}{\left(r-2\right)!}\frac{d^{r-2}}{d{s}^{r-2}}\left[{\left(s-s_1\right)}^{r}X\left(s\right)\right]{|}_{s=s_1}\hfill \\ k_{1,1}\hfill & =\hfill & \frac{1}{\left(r-1\right)!}\frac{d^{r-1}}{d{s}^{r-1}}\left[{\left(s-s_1\right)}^{r}X\left(s\right)\right]{|}_{s=s_1}\hfill \end{array}$$

Generalizing these results, the residues of a pole of multiplicity r are calculated using

$$\begin{array}{ccc}{k}_{1,n}=\frac{1}{\left(r-n\right)!}\frac{d^{r-n}}{d{s}^{r-n}}\left[{\left(s-s_1\right)}^{r}X\left(s\right)\right]{|}_{s=s_1}& n=1,...,r& \begin{array}{cc}& \left(\text{E}\text{.26}\right)\end{array}\end{array}$$

In using the general formula in Eqn. (E.26) for n = r we need to remember that 0! = 1 and

$$\begin{array}{ccc}\frac{d^0}{d{s}^0}\left[{\left(s-s_1\right)}^{r}X\left(s\right)\right]={\left(s-s_1\right)}^{r}X\left(s\right)& & \left(\text{E}\text{.27}\right)\end{array}$$

Example E.4:

Find a partial fraction expansion for the rational function

$$X\left(s\right)=\frac{s}{{\left(s+1\right)}^3\left(s+2\right)}$$

Solution: The partial fraction expansion for X (s) is in the form

$$\begin{array}{ccc}X\left(s\right)=\frac{k_{1,1}}{s+1}+\frac{k_{1,2}}{{\left(s+1\right)}^2}+\frac{k_{1,3}}{{\left(s+1\right)}^3}+\frac{k_2}{s+2}& & \left(\text{E}\text{.28}\right)\end{array}$$

The residue of the single pole at s = −2 is easily found using the technique developed earlier:

$$k_2=\left(s+2\right)X\left(s\right){|}_{s=-2}=\frac{s}{{\left(s+1\right)}^3}{|}_{s=-2}=\frac{-2}{{\left(-2+1\right)}^3}=2$$

We will use Eqn. (E.26) to find the residues of the third-order pole at s = − 1.

$$\begin{array}{lll}{k}_{1,3}={\left(s+1\right)}^{3}X\left(s\right){|}_{s=-1}\hfill & =\hfill & \frac{-1}{\left(-1+2\right)}=-1\hfill \\ k_{1,2}=\frac{d}{ds}\left[{\left(s+1\right)}^{3}X\left(s\right)\right]{|}_{s=-1}\hfill & =\hfill & \frac{d}{ds}\left[\frac{s}{s+2}\right]{|}_{s=-1}=\frac{2}{{\left(s+2\right)}^2}{|}_{s=-1}=2\hfill \\ k_{1,1}=\frac{1}{2!}\frac{d^2}{d{s}^2}\left[{\left(s+1\right)}^{3}X\left(s\right)\right]{|}_{s=-1}\hfill & =\hfill & \frac{1}{2!}\frac{d^2}{d{s}^2}\left[\frac{s}{s+2}\right]{|}_{s=-1}=\frac{-2}{{\left(s+2\right)}^3}{|}_{s=-1}=-2\hfill \end{array}$$

Thus, the partial fraction expansion for X (z) is

$$X\left(s\right)=\frac{2}{s+1}+\frac{2}{{\left(s+1\right)}^2}-\frac{1}{{\left(s+1\right)}^3}+\frac{2}{s+2}$$

E.2 Partial Fraction Expansion for Discrete-Time Signals and Systems

The residues of the partial fraction expansion for rational z-transforms are obtained using the same techniques employed in the previous section. One subtle difference is that, when working with the inverse z-transform, we often need the partial fraction expansion in the form

$$\begin{array}{ccc}\begin{array}{lll}X\left(s\right)\hfill & =\hfill & \frac{B\left(z\right)}{\left(z-z_1\right)\left(z-z_2\right)...\left(z-z_P\right)}\hfill \\ \hfill & =\hfill & \frac{k_{1}z}{z-z_1}+\frac{k_{2}z}{z-z_2}+...+\frac{k_{P}z}{z-z_P}\hfill \end{array}& & \left(\text{E}\text{.29}\right)\end{array}$$

In order to use the residue formulas established in the previous section and still obtain the expansion in the form of Eqn. (E.29) with a z factor in each term, we simply expand X (z)/z into partial fractions:

$$\begin{array}{ccc}\begin{array}{lll}\frac{X\left(z\right)}{z}\hfill & =\hfill & \frac{B\left(z\right)}{\left(z-z_1\right)\left(z-z_2\right)...\left(z-z_P\right)z}\hfill \\ \hfill & =\hfill & \frac{k_1}{z-z_1}+\cdots +\frac{k_P}{z-z_P}+\frac{k_{P+1}}{z}\hfill \end{array}& & \left(\text{E}\text{.30}\right)\end{array}$$

The last term in Eqn. (E.30) may or may not be needed depending on whether the numerator polynomial B(z) has a root at z = 0 or not. Once the residues of the expansion in Eqn. (E.30) are found, we can revert to the form in Eqn. (E.29) by multiplying both sides with z.