Part II
Inheritance
Several of the entries appearing in this part of the dictionary consist essentially of expansions of, or elaborations on, entries marked “Without inheritance” in Part I. Such entries are marked “With inheritance” accordingly.
Examples in what follows are based for the most part on either the simple type hierarchy shown in Fig. 2 or the slightly more general type graph shown in Fig. 3. Note that Fig. 2 involves single inheritance only and Fig. 3 involves multiple inheritance.
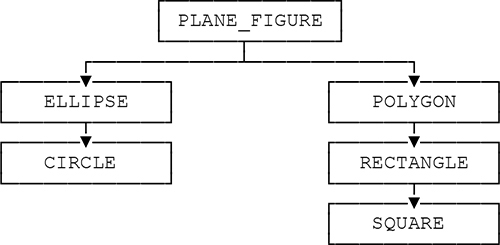
Fig. 2: Sample type hierarchy (single inheritance, q.v.)

Fig. 3: Sample type graph (multiple inheritance, q.v.)
The Type Hierarchy of Fig. 2
Fig. 2 is based on a collection of more or less self-explanatory geometric types—ELLIPSE, POLYGON, SQUARE, and so on.1 What it shows is that, e.g., type CIRCLE is a subtype of supertype ELLIPSE, which means that all circles are ellipses but the converse is false (some ellipses aren’t circles). As a consequence, all properties that apply to ellipses in general apply to—i.e., are inherited by—circles in particular, but the converse is false (circles have properties of their own that don’t apply to ellipses in general). Note: “Properties” here means, primarily, read-only operators and type constraints; in other words, read-only operators and type constraints that apply to ellipses in general apply to circles in particular (because circles are ellipses), but read-only operators and type constraints that are specific to circles don’t apply to mere ellipses (meaning ellipses that don’t happen to be circles).
Here now in outline are the type definitions for types ELLIPSE and CIRCLE (other types omitted for space reasons):
TYPE ELLIPSE
IS { PLANE_FIGURE
POSSREP { A LENGTH , B LENGTH , CTR POINT
CONSTRAINT A ≥ B } } ;
TYPE CIRCLE
IS { ELLIPSE
CONSTRAINT THE_A ( ELLIPSE ) = THE_B ( ELLIPSE )
POSSREP { R = THE_A ( ELLIPSE ) ,
CTR = THE_CTR ( ELLIPSE ) } } ;
Explanation:
The definition for type ELLIPSE contains an IS specification indicating that every ellipse is a plane figure (in other words, type ELLIPSE is a subtype of type PLANE_FIGURE; hence, properties that apply to plane figures in general apply to ellipses in particular, because ellipses are plane figures). That IS specification also contains a POSSREP specification indicating that ellipses can possibly be represented by two lengths A and B and a point CTR (where, for a given ellipse e, A and B denote the lengths of e’s major and minor semiaxis, respectively, and CTR denotes the point that’s e’s center).2 Note: As in Part I of this dictionary, (a) I’m assuming the user defined types LENGTH and POINT have already been defined, and (b) to keep the example simple, I’ve omitted the constraint B > 0 that ought by rights to be specified as well.
Likewise, the IS specification for type CIRCLE indicates that every circle “is a” ellipse (i.e., type CIRCLE is a subtype of type ELLIPSE). However, it also constrains the ellipse in question to have semiaxes of equal length. That CONSTRAINT specification is then followed by a POSSREP specification indicating (a) that circles can possibly be represented by a length R and a point CTR (where, for a given circle c, R denotes the length of c’s radius and CTR denotes the point that’s c’s center), and indicating also (b) how that CIRCLE possrep is derived from the ELLIPSE possrep. Note the use of the supertype name ELLIPSE, within both the constraint and the derived possrep definition, to denote a specific ellipse—namely, the specific ellipse that the circle under consideration happens to be.
Any possrep for ellipses is necessarily, albeit implicitly, a possrep for circles as well, because circles are ellipses. (Of course, the converse is false—a possrep for circles isn’t necessarily a possrep for ellipses.) Thus, possreps in particular might be regarded as further “properties” that are inherited by subtypes from supertypes. For technical reasons, however (see possrep inheritance), such an inherited possrep isn’t considered to be a declared one in the sense in which this latter term is defined in Part I of this dictionary.
The Type Graph of Fig. 3
Turning now to the subtype / supertype relationships illustrated in Fig. 3, the following observations should suffice to show that those relationships make good intuitive sense:
Every parallelogram has a “long” diagonal of length ld and a “short” one of length sd, where ld ≥ sd.
Every parallelogram also has two “long” sides of length ls and two “short” ones of length ss, where ls ≥ ss.
A rectangle is a parallelogram for which ld = sd. Unlike parallelograms in general, every rectangle has a unique circumscribed circle (i.e., a circle that passes through each of that rectangle’s four vertices); hence, every rectangle has a property that’s unique to those parallelograms that happen to be rectangles—viz., that circumscribed circle.
A rhombus is a parallelogram for which ls = ss. Unlike parallelograms in general, every rhombus has a unique inscribed circle (i.e., a circle that touches each of that rhombus’s four sides); hence, every rhombus has a property that’s unique to those parallelograms that happen to be rhombi—viz., that inscribed circle.
A square is a parallelogram that is both a rectangle and a rhombus. Unlike rectangles and rhombi in general, every square has a unique associated annulus that’s defined by the difference between the corresponding circumscribed and inscribed circles; hence, every square has a property that’s unique to those parallelograms that happen to be both rectangles and rhombi—viz., that annulus. Moreover, every square has both (a) a unique side length, which rectangles in general don’t have, and (b) a unique diagonal length, which rhombi in general don’t have.
Here now are some possible type definitions. First, type PARALLELOGRAM:
TYPE PARALLELOGRAM
POSSREP { A POINT , B POINT , C POINT , D POINT
CONSTRAINT DISTINCT ( A , B , C , D )
AND NOT ( COLLINEAR ( A , B , C ) )
AND NOT ( COLLINEAR ( B , C , D ) )
AND NOT ( COLLINEAR ( C , D , A ) )
AND NOT ( COLLINEAR ( D , A , B ) )
AND DIST ( A , B ) = DIST ( C , D )
AND DIST ( B , C ) = DIST ( D , A ) } ;Explanation:
Many different possreps could have been specified here; for simplicity, I show just one, consisting of the four vertices A, B, C, D. What’s more, I’ll use that same possrep for each of the other three types, again for simplicity.
DISTINCT returns TRUE if and only if its POINT arguments are all distinct. COLLINEAR returns TRUE if and only if its three POINT arguments lie on a straight line. DIST returns the distance between its two POINT arguments as a value of type LENGTH.
Next, types RECTANGLE and RHOMBUS (operators LD, SD, LS, and SS return the length of the long diagonal, short diagonal, long side, and short side, respectively, of a given parallelogram):
TYPE RECTANGLE
IS { PARALLELOGRAM
CONSTRAINT LD ( PARALLELOGRAM ) = SD ( PARALLELOGRAM )
POSSREP { A = THE_A ( PARALLELOGRAM ) ,
B = THE_B ( PARALLELOGRAM ) ,
C = THE_C ( PARALLELOGRAM ) ,
D = THE_D ( PARALLELOGRAM ) } } ;
TYPE RHOMBUS
IS { PARALLELOGRAM
CONSTRAINT LS ( PARALLELOGRAM ) = SS ( PARALLELOGRAM )
POSSREP { A = THE_A ( PARALLELOGRAM ) ,
B = THE_B ( PARALLELOGRAM ) ,
C = THE_C ( PARALLELOGRAM ) ,
D = THE_D ( PARALLELOGRAM ) } } ;
Finally, type SQUARE:
TYPE SQUARE
IS { RECTANGLE , RHOMBUS
POSSREP { A = THE_A ( RECTANGLE ) ,
B = THE_B ( RECTANGLE ) ,
C = THE_C ( RECTANGLE ) ,
D = THE_D ( RECTANGLE ) } } ;
Explanation:
The IS specification here states that a given value is of type SQUARE if and only if it’s both of type RECTANGLE and of type RHOMBUS. No additional CONSTRAINT specification is needed, or indeed permitted.
The POSSREP specification defines a possrep for type SQUARE in terms of the possrep for type RECTANGLE. However, it could equally well have defined that possrep in terms of the possrep for type RHOMBUS instead—it would have made no difference.
An Extended Example
Certain of the entries in this part of the dictionary make use of the extended example shown in Fig. 4.

Explanation:
A trapezoid is a quadrilateral with at least one pair of opposite sides parallel. Caveat: Be aware that a quadrilateral with at least one pair of opposite sides parallel is called a trapezoid in the U.S. and a trapezium in the U.K., while a quadrilateral with possibly no parallel sides at all is called a trapezium in the U.S. and a trapezoid in the U.K.
A kite is a quadrilateral with mirror symmetry about a diagonal, such that no interior angle is greater than 180°. (If this latter condition isn’t satisfied, the figure isn’t a kite, it’s a dart.) If ABCD is a kite (or a dart) that’s symmetric about diagonal AC, then AB = AD and CB = CD.
A cyclic quadrilateral is a quadrilateral whose vertices lie on a circle. A quadrilateral is cyclic if and only if its opposite angles add up to 180°.
An isosceles trapezoid is a trapezoid with mirror symmetry about the line that connects the midpoints of its parallel sides. If ABCD is an isosceles trapezoid with AB parallel to CD, then (a) BC = AD and (b) the interior angles at A and B are equal, as are the interior angles at C and D.
A right kite is a kite in which the angles subtended by the diagonal of symmetry are right angles. If ABCD is a kite that is symmetric about diagonal AC, then the angles at B and D are right angles.
Tuple and Relation Inheritance
Consider the following set of tuple types:
TUPLE { E ELLIPSE , R RECTANGLE } /* "tuple type ER" */
TUPLE { E CIRCLE , R RECTANGLE } /* "tuple type CR" */
TUPLE { E ELLIPSE , R SQUARE } /* "tuple type ES" */
TUPLE { E CIRCLE , R SQUARE } /* "tuple type CS" */
Note the informal names for these types (“tuple type ER,” etc.), as indicated in the comments. Now, observing with reference to Fig. 2 that CIRCLE is a subtype of ELLIPSE and SQUARE is a subtype of RECTANGLE, it should be clear that every tuple of type CS is also a tuple of type CR and a tuple of type ES, and further that every tuple of either type CR or type ES is also a tuple of type ER. Thus, it should be clear that type CS is a subtype of both type CR and type ES, and further that types CR and ES are both subtypes of type ER. In other words, tuple subtype / supertype relationships hold as indicated in the type graph of Fig. 5.

Fig. 5: Sample type graph (tuple or relation types)
The foregoing remarks apply to relation types also, mutatis mutandis. That is, given relation types as follows—
RELATION { E ELLIPSE , R RECTANGLE } /* "relation type ER" */
RELATION { E CIRCLE , R RECTANGLE } /* "relation type CR" */
RELATION { E ELLIPSE , R SQUARE } /* "relation type ES" */
RELATION { E CIRCLE , R SQUARE } /* "relation type CS" */
—it should be clear that relation type CS is a subtype of both relation types CR and ES, and further that relation types CR and ES are both subtypes of relation type ER. Thus, Fig. 5 can serve to depict these relation subtype / supertype relationships as well.
Possreps Revisited
With reference to Fig. 3 again, I said I’d give just one possrep for type PARALLELOGRAM, consisting of the four vertices A, B, C, D. Actually that possrep as specified is probably incomplete in at least one respect. To be specific, the very same parallelogram can clearly be specified by giving its vertices in any of several different orders; in some circumstances this state of affairs might not matter, but in general it will. In general, therefore, we’d need a way of pinning down the precise order in which the vertices are to be specified. For example, we might want to say they’re specified in terms of increasing distance from the origin (but even then we’d still need a way of breaking ties). Further details are beyond the scope of this dictionary.
A Note on Tutorial D
The current version of Tutorial D (as defined in the book Database Explorations: Essays on The Third Manifesto and Related Topics, by C. J. Date and Hugh Darwen, Trafford, 2010) has no support for inheritance. However, Chapter 21 of that same book contains some proposals for extending the language to incorporate such support, and the name “Tutorial D” in this part of the dictionary should be understood as referring to a version of the language that has been extended in accordance with the proposals of that chapter.
abstract type (With inheritance) Term sometimes used to refer to a union type, q.v. (and a type that’s not a union type is then sometimes called a concrete type accordingly). But the term union type better captures the essence of what such a type involves, and has a longer pedigree to boot; the term abstract type is thus not really appropriate for the concept at hand—especially since, as noted in Part I of this dictionary, it’s also used with other meanings anyway—and its use in this context is therefore deprecated.
alpha The maximal scalar type. Type alpha (a) contains all scalar values, (b) has no immediate supertype, and (c) is an immediate supertype for every scalar root type (with respect to the set of available types, q.v., in the case of (a) and (c)). Note that, by definition, type alpha is system defined; unique; primarily conceptual in nature; a dummy type, q.v. (and in fact a union type, q.v., except as noted below); and not a root type, q.v. Note further that the type constraint for alpha is simply TRUE; the expression IS_alpha (exp), where exp is any scalar expression, always evaluates to TRUE; and the expression TREAT_AS_alpha (exp), where exp is any scalar expression, always succeeds. See also T_alpha.
Note: Consider the extreme, and pathological, case in which the set of available types contains just one regular type (necessarily type BOOLEAN). Then that type would itself be both the sole root type (q.v.) and the sole leaf type (q.v.), and it would satisfy property (a), though not property (b) or property (c). Moreover, in this case type alpha would be indistinguishable from type BOOLEAN and would thereby violate various other prescriptions of the Manifesto model, albeit only in minor ways. Apart from this pathological exception, however, no scalar type other than type alpha possesses or can possess any of properties (a), (b), and (c).
ancestor type Term occasionally used to mean a proper supertype.
argument (With inheritance) An actual operand that replaces—i.e., is substituted for—some parameter of some operator when the operator in question is invoked. Let Op be the operator in question, let P be a parameter to Op, let T be the declared type of P, and let A be the argument that replaces P in some invocation of Op. Also, for simplicity let Op not be a generic operator (see Part I of this dictionary). Then:
If P isn’t subject to update, then A is a value, not a variable (though of course it might be denoted by some variable reference), and its most specific type can be any nonempty subtype of T. See Principle of Value Substitutability; Principle of Read-Only Operator Inheritance; signature.
By contrast, if P is subject to update, then A is a variable, not a value, and its most specific type can be either T or possibly (depending on circumstances) some proper but nonempty subtype of T. See Principle of Variable Substitutability; Principle of Update Operator Inheritance; signature.
Examples: Here’s the definition of an operator called MOVE that, loosely speaking, moves a specified ellipse such that it becomes centered on the center of a specified rectangle (CTR here is a read-only operator that returns the center of its rectangle argument):
OPERATOR MOVE ( E ELLIPSE , R RECTANGLE ) RETURNS ELLIPSE ;
RETURN ELLIPSE ( THE_A ( E ) , THE_B ( E ) , CTR ( R ) ) ;
END OPERATOR ;
This operator is read-only (neither of its parameters is subject to update). In an invocation, therefore, the argument that’s substituted for the first parameter can be a value of any nonempty subtype of type ELLIPSE, and the argument that’s substituted for the second parameter can be a value of any nonempty subtype of type RECTANGLE.
Here now by contrast is MOVE as an update operator:
OPERATOR MOVE ( E ELLIPSE , R RECTANGLE ) UPDATES { E } ;
THE_CTR ( E ) := CTR ( R ) ;
END OPERATOR ;
With this revised definition, the argument that’s substituted for the second parameter in an invocation can still be a value of any nonempty subtype of type RECTANGLE. However, the first parameter is now subject to update, so the argument that’s substituted for that parameter must be a variable specifically, and that variable will be updated as a result of the invocation in question. Hence, the declared type of that variable must be such that assignment to THE_CTR of that variable makes sense. So that declared type can be ELLIPSE (of course), and it can also be CIRCLE. But suppose type CIRCLE has a proper subtype O_CIRCLE (where an “O-circle” is a circle with center the origin):
TYPE O_CIRCLE
IS { CIRCLE
CONSTRAINT THE_CTR ( CIRCLE ) = POINT ( 0.0 , 0.0 )
POSSREP { R = THE_R ( CIRCLE ) } } ;
Then the argument that’s substituted for the first MOVE parameter can’t be of type O_CIRCLE, because the center of an O-circle is always the origin and can’t be changed (see the CONSTRAINT specification in the foregoing definition). As far as the first parameter is concerned (i.e., the one that’s subject to update), therefore, the update form of MOVE is defined for type ELLIPSE, is inherited by type CIRCLE, but isn’t inherited by type O_CIRCLE. (It can’t be inherited by any proper subtype of type O_CIRCLE, either, a fortiori. See Principle of Update Operator Inheritance.)
argument contravariance A deprecated concept much discussed in the OO literature. The concept is hard to explain—see Principle of Incoherence in Part I of this dictionary—because it seems to be based on (a) a confusion between model and implementation, (b) a confusion between arguments and parameters, and quite possibly (c) a flawed definition of the subtype concept as well. (Regarding points (b) and (c) here, see the further remarks near the end of the present entry.) Be that as it may, consider The Principle of Value Substitutability, q.v. That principle requires that if (a) Op is an operator, (b) P is a parameter to Op, (c) P isn’t subject to update, and (d) T is the declared type of P, then (e) the declared type T′ of the argument expression—and therefore the most specific type of the argument as such—corresponding to P in any given invocation of Op must be some nonempty subtype of T (not necessarily a proper subtype, of course). Unfortunately, some systems not only fail to abide by this requirement but, in effect, claim their failure as a feature! Here’s an example. Consider a read-only operator called MOVE—a variant on the operator with that same name discussed elsewhere in this part of the dictionary, as well as in Part I—which returns a result just like its first argument (an ellipse) except that it’s centered on the center of its second (a square). Thus, the specification signature (q.v.) for this operator looks like this:
MOVE ( ELLIPSE , SQUARE ) RETURNS ELLIPSE
(The type names ELLIPSE and SQUARE within the parentheses here specify the declared type of the first and second parameter, respectively; the type name ELLIPSE following the keyword RETURNS specifies the declared type of the result.)
Now suppose distinct implementation versions (q.v.) of this operator—call them CMOVE and EMOVE—are provided for the case where the first argument is a circle and the case where it’s “just an ellipse” (i.e., an ellipse that’s not a circle), respectively, and consider what happens if MOVE is invoked with first argument a circle. At run time, then, thanks to the binding process (q.v.), the system will invoke CMOVE, not EMOVE. Since the second argument to that invocation is of type SQUARE (necessarily so), it follows that the declared type of the second parameter to CMOVE could have been some proper supertype of SQUARE, say RECTANGLE, and the type checking, at both compile time and run time, would still work. And this property—the property, that is, that if (a) Op is an operator with a parameter that (according to the pertinent specification signature) is of declared type T, and (b) Op is invoked with an argument corresponding to that parameter that’s of some proper subtype of T, then (c) the declared type of some other parameter to the pertinent implementation version might be allowed to be some proper supertype of the type specified in the pertinent specification signature—is the “argument contravariance” property.
However, the notion of (in effect) allowing an operator to be invoked with an argument of type some proper supertype of the corresponding parameter declared type, as given by the pertinent specification signature, is surely more than a little suspect. In the case at hand, surely it would be better to define MOVE as having a specification signature that looks like this (note the revised declared type of the second parameter):
MOVE ( ELLIPSE , RECTANGLE ) RETURNS ELLIPSE
Now the user knows, because of value substitutability, q.v., that the arguments to any given MOVE invocation can be of any nonempty subtypes of ELLIPSE and RECTANGLE, respectively. In particular, of course, they can be of most specific types ELLIPSE and RECTANGLE as such, because every type is a subtype of itself. By contrast, the “argument covariance” property seems to be saying—in the example at hand, and now going back to the original specification signature—that MOVE can be invoked (a) with arguments of most specific types ELLIPSE and SQUARE, respectively, and (b) with arguments of most specific types CIRCLE and RECTANGLE, respectively (and therefore (c) with arguments of most specific types CIRCLE and SQUARE, respectively), but not (d) with arguments of most specific types ELLIPSE and RECTANGLE, respectively! As already noted, this state of affairs violates value substitutability—it could be argued that it violates orthogonality too—and is therefore strongly deprecated. In fact, there would be no need to introduce the argument contravariance concept at all if only value substitutability were taken seriously. (“Taking value substitutability seriously” here boils down merely to saying that every argument value should be allowed to have most specific type the same as the declared type of the corresponding parameter, as given by the pertinent specification signature. Indeed, not to allow such a state of affairs is surely perverse in the extreme.)
Note: In strong contradistinction to the foregoing, the property of result covariance, q.v., which is often spoken of in the same breath with argument contravariance, is both desirable and logically necessary.
A few further observations:
The term argument contravariance is presumably meant to reflect the fact that the type of one argument “contravaries” with that of another. But in a sense it’s parameters that “contravary,” not arguments, so at the very least the term ought really to be parameter contravariance (?).
There seems to be a tacit assumption underlying the terminology to the effect that there are exactly two parameters. In the case of MOVE (original version), there are indeed two parameters, which do seem to “contravary” (or so it might be argued, at least); but what if there had been three?
The “flawed definition” of the subtype concept mentioned earlier in this entry (at least, the relevant part of that definition) looks like this:
A type T′ is a subtype of a type T if ... for each method M of T there is a corresponding method M′ of T′ such that ... the ith argument type of M is a subtype of the ith argument type of M′ (rule of contravariance in arguments).
This definition—which is paraphrased just slightly from Elisa Bertino and Lorenzo Martino, Object-Oriented Database Systems: Concepts and Architectures (Addison-Wesley, 1993)—is flawed because it’s circular: It defines the concept of some type being a subtype of another in terms of the concept of some type being a subtype of another. Note too the apparent confusion over arguments and parameters.
Here for interest is another definition from the OO literature (it’s from Stanley B. Zdonik and David Maier, “Introduction to Object-Oriented Fundamentals,” in Readings in Object-Oriented Database Systems (Zdonik and Maier, eds.; Morgan Kaufmann, 1990):
[The] important contravariance rule ... If function signatures are viewed as types for functions, then a function type G can be viewed as a subtype of a function type F if and only if the inputs to F are subtypes of the inputs to G and the result type of G is a subtype of the result type of F.
(Incidentally, note the sloppy phrasing here; to be specific, inputs aren’t types, they have types.) Whether this definition is consistent with the explanations given previously is left as an exercise for the reader.
assignment (With inheritance) Let X and x be a variable and a value, respectively, such that the most specific type MST(x) of x is some subtype of the declared type DT(X) of X. Then (and only then) x can be assigned to X; the assignment has the effect of setting v(X) equal to x and MST(X) equal to MST(x). Note: In order for the assignment to be syntactically valid, the declared type DT(exp) of the expression exp used to denote the value x must be some subtype of the declared type DT(X) of the variable X (this condition is implied by the fact that MST(x) is required to be some subtype of DT(X), and is a compile time check).
Examples: With reference to Fig. 2, let variables E and C be of declared types ELLIPSE and CIRCLE, respectively, and consider the following assignment:
E := C ;
In this example, compile time type checking succeeds (DT(C) is a subtype of DT(E)), and at run time v(E) and MST(E) are set equal to v(C) and MST(C), respectively.
Now consider this assignment:
C := E ;
This example raises a compile time type error, because DT(E) isn’t a subtype of DT(C). By contrast, if the expression E in this example were replaced by the expression TREAT_AS_CIRCLE (E), thus—
C := TREAT_AS_CIRCLE ( E ) ;
—then compile time type checking would succeed; however, this TREAT expression will raise a run time type error if MST(E) isn’t some subtype of CIRCLE at run time. See TREAT; see also relation assignment; tuple assignment.
automatic definition (With inheritance) Defining a scalar type T automatically causes the following associated operators to be defined as well: (a) assignment (“:=”); (b) equality (“=”); (c) IS_T, q.v.; (d) TREAT_AS_T, q.v.; and—so long as T is a regular type, q.v.—(e) at least one selector and at least one set of THE_ operators. Note: Operators analogous to the ones that are the subject of this entry are defined automatically for tuple and relation types as well, even though such types are generated instead of being explicitly defined. With regard to parts (c) and (d) of the definition in particular, see IS_SAME_TYPE_AS; TREAT_AS_SAME_TYPE_AS.
available types In any given situation there will be some specific set—necessarily nonempty, and effectively unbounded, though obviously finite—of types available for use. That set provides the context for certain of the concepts defined elsewhere in this dictionary. Obvious examples of such concepts are root type, q.v., and leaf type, q.v.; in other words, those concepts are relative, not absolute. For example, suppose T is a leaf type. Clearly, then, T will cease to be a leaf type if some new immediate subtype of T is introduced as an additional “available type.”
Example: Given the type hierarchy of Fig. 2, the available types are (a) PLANE_FIGURE, ELLIPSE, CIRCLE, POLYGON, RECTANGLE, and SQUARE; (b) the types in terms of which the possreps for those types are defined; (c) the types in terms of which the possreps for the types included under (b), such as LENGTH and POINT, are defined (and so on, recursively, all the way down to and including the pertinent primitive types—see Part I of this dictionary); (d) the maximal scalar type alpha, q.v., and the minimal scalar type omega, q.v.; and (e) tuple and relation types that can be generated using any or all of these available types.
base type (With inheritance) See extends relationship.
behavioral inheritance Somewhat deprecated term, used in OO contexts in particular, to refer to the fact that if type T′ is a subtype of type T, then objects of type T′ inherit the “behavior” of objects of type T (see behavior in Part I of this dictionary)—meaning in particular that if operator Op applies to objects of type T, it also applies to objects of type T′. Contrast structural inheritance. Caveat: Whether “objects” in the foregoing definition is intended to include variables as well as values is unclear (the answer might vary from system to system, and probably does). Likewise, whether “operator Op” is allowed to be an update operator and not just a read-only operator is also unclear (again the answer might vary from system to system, and probably does).
Note: The Manifesto inheritance model might be said (very loosely) to support behavioral inheritance, so long as (a) “objects” is indeed interpreted as including both values and variables and (b) “behavior” is interpreted in turn as including type constraints as well as operators. However, the “behavioral inheritance” in question applies to values and read-only operators unconditionally but to variables and update operators only where it makes sense. See Principle of Value Substitutability; Principle of Variable Substitutability.
binding (With inheritance) The process of determining which implementation version of a given operator is to be executed in response to a given invocation of the operator in question. See the discussion under implementation version for examples and further explanation. Note that, as that discussion makes clear, binding—at least in the sense here defined—is an implementation concern, not a model concern (but see changing semantics). However, the Manifesto model does require that all arguments to the operator invocation in question participate equally in the binding process; in other words, it doesn’t support the concept of selfish methods, q.v., nor the concept of a distinguished parameter, q.v., nor the concept of “messages,” all of which it regards as both unnecessary and undesirable. See also compile time binding; run time binding.
changing most specific type (Of a variable) See assignment; generalization; specialization.
changing semantics (Of an operator) See implementation version.
child type Term occasionally used to mean an immediate subtype.
circular noncircle A contradiction in terms, typical of the logical absurdities that can and do occur if S by C, q.v., and G by C, q.v., aren’t supported, and used as a convenient shorthand to refer to such absurdities in general. To spell out the details of this particular solecism: Consider the type hierarchy of Fig. 2; however, let’s agree for simplicity to ignore all of the types in that figure apart from types ELLIPSE and CIRCLE. Then a circular noncircle is something the system thinks isn’t a circle but actually is—i.e., it’s a value whose most specific type as far as the system is concerned is ELLIPSE and yet has equal semiaxis lengths, and thus logically ought to have most specific type CIRCLE. Note: Circular noncircles and suchlike solecisms can’t occur in the Manifesto model. See also noncircular circle.
class hierarchy See type hierarchy.
classification Systems and languages (especially OO systems and languages) that use the term class to mean a type—see Part I of this dictionary—sometimes also use the term classification to refer to the process, or the result of the process, of determining the type(s) possessed by some object.
code reuse 1. (Of implementation versions) Loosely, using the type T implementation version of some operator Op to operate without change on values or variables of some proper subtype T′ of T. See implementation version. 2. (Of application programs) Using an application program that operates on values or variables of type T to operate without change on values or variables of some proper subtype T′ of T. Note that the amount of such application program reuse achievable in practice is likely to be quite limited if G by C, q.v., isn’t supported. See Principle of Update Operator Inheritance. 3. (Via delegation) See delegation.
coercion vs. substitutability It’s sometimes argued that permitting coercions (see Part I of this dictionary) can undermine the goal of value substitutability, q.v. Essentially, that argument goes something like this. Suppose for the sake of discussion that type INTEGER (integers) is defined to be a subtype of type RATIONAL (rational numbers). Then:
By definition, every integer is a rational number.
Therefore, any code that works for rational numbers should also work for integers, even if type INTEGER hadn’t been defined when the code in question was written (see code reuse). Note: Let’s agree throughout this discussion that the code in question concerns itself with rational number (or integer) values only, and not with rational number (or integer) variables. The reason is that value substitutability works unconditionally but variable substitutability works only conditionally, and it’s better not to get sidetracked into issues that are secondary to the main point of the discussion. See Principle of Value Substitutability; Principle of Variable Substitutability.
In other words, it should be possible to invoke such code and pass it an integer instead of a rational number and have it still work.
Thus, wherever a rational number is expected, it should be possible to substitute an integer.
However, value substitutability also requires that even if an integer is substituted for a rational number in this way, it remains an integer and retains an integer’s specific properties—e.g., the property of having a successor. (Note that, in mathematics at least if not in computer science, rational numbers don’t have successors; that is, if r is a rational number, there’s no such thing as “the next” rational number after r.)
But if passing an integer when a rational number is expected were to cause that integer to be coerced to type RATIONAL, then that integer would become “just a rational number” (thus ceasing to be an integer as such) and would thereby lose its specific properties.
Therefore—it’s claimed—coercions undermine value substitutability.
But the foregoing argument is incorrect. Suppose for a moment that INTEGER isn’t defined to be a subtype of RATIONAL after all. Then:
The concept of value substitutability doesn’t arise (i.e., integers can’t be substituted for rationals).
Therefore the idea of converting integers to rationals seems useful.
Therefore it seems reasonable to assume that an operator to perform such conversions will have been defined.
Therefore no harm is done to value substitutability by invoking that conversion operator implicitly in, e.g., an INTEGER-to-RATIONAL comparison or an INTEGER-to-RATIONAL assignment. To be more specific, value substitutability isn’t undermined because, as already noted, the concept simply doesn’t apply.
Alternatively, suppose INTEGER is defined to be a subtype of RATIONAL. Then:
Integers can be substituted for rationals (i.e., value substitutability does apply).
Therefore there’s no point in defining an operator to convert integers to rationals, because integers are rationals.
Therefore no such operator will be defined.
Therefore the question of invoking such an operator implicitly simply doesn’t arise, and so (again) value substitutability isn’t undermined.
In other words, coercions are likely to be useful precisely in those situations where substitutability doesn’t apply. Of course, it’s true that (as noted in Part I of this dictionary) prohibiting coercions in general is a good idea anyway, for a variety of reasons; however, undermining value substitutability isn’t one of them.
One final point: Actually, the idea of defining type INTEGER to be a subtype of type RATIONAL is more than a little suspect, as is shown in Chapter 22 (“Numeric Data Types”) of Database Explorations: Essays on The Third Manifesto and Related Topics, by C. J. Date and Hugh Darwen (Trafford, 2010). However, this state of affairs doesn’t undermine the foregoing argument in any essential respect.
colored circle A typical example of the kind of construct often but misleadingly used to illustrate inheritance ideas—“misleadingly,” because the idea that type COLORED_CIRCLE (“colored circles”) is a plausible example of a proper subtype of type CIRCLE (“just plain circles”) might sound reasonable but isn’t. Here are some reasons why not. Let type T′ be a proper subtype of type T. Then:
There can’t be more values of type T′ than there are of type T (see subtype). But—on the assumption that two circles that differ in color but are otherwise identical are the same circle but different colored circles—there are clearly more colored circles than there are just plain circles.
If S is a selector for type T, then every value of type T—including values of type T′ in particular—must be producible by means of some invocation of S. But no invocation of any selector for type CIRCLE can possibly produce a value of type COLORED_CIRCLE, because no such selector has a color parameter.
Every possrep for type T is a possrep for type T′ also, at least implicitly. But no CIRCLE possrep is a possrep for type COLORED_CIRCLE, because no such possrep has a color component.
There’s no way to obtain a colored circle from a circle via S by C, q.v.—i.e., there’s no constraint that can be specified for type COLORED_CIRCLE that, if satisfied by some value of type CIRCLE, means the circle in question is really a colored circle (because, to say it again, no CIRCLE possrep has a color component, and any such constraint would necessarily have to be expressed in terms of some such possrep).
It follows that colored circles in particular aren’t a special case of circles in general; rather, they’re images (on a display screen, perhaps), whereas circles as such aren’t images but abstract geometric figures. Thus, it seems reasonable to regard COLORED_CIRCLE not as a subtype of CIRCLE but rather as a completely separate type. Now, that separate type will almost certainly have a possrep in which one component is of type CIRCLE, perhaps as follows (irrelevant details omitted):
TYPE COLORED_CIRCLE POSSREP { CIR CIRCLE , COL COLOR } ;
To repeat, however, this type isn’t a subtype of type CIRCLE; in fact, it’s no more a subtype of type CIRCLE than it is a subtype of type COLOR. Another, albeit informal, way of saying the same thing is to say that every colored circle has a circle property but isn’t a circle (just as it has a color property but isn’t a color). In other words, the relationship between colored circles (i.e., images) and circles as such (i.e., abstract figures) is the HAS A relationship, q.v., not the IS A relationship, q.v., that characterizes subtyping as such. See also extends relationship.
Note: If (as in the example above) type COLORED_CIRCLE does indeed have a possrep PR in which one component is of type CIRCLE, then (e.g.) the operator—call it CTR—that returns the center of a given colored circle is basically just the THE_CTR operator that applies to the CIRCLE component CIR of PR. In other words, the example illustrates the notion of delegation, q.v.: The responsibility for implementing CTR for type COLORED_CIRCLE is delegated to the type, CIRCLE, of a certain component of a certain possrep for that type (where “that type” is type COLORED_CIRCLE, in the example under consideration). Indeed, it seems plausible to suggest in general that the IS A relationship—i.e., subtyping as such—leads to inclusion polymorphism, q.v., while the HAS A relationship leads to delegation, q.v.
common subtype Let T1, T2, ..., Tm (m ≥ 0) be types from the same type lattice, q.v. Then type T′ is a common subtype for types T1, T2, ..., Tm if and only if, whenever a given value is of type T′, it’s also of each of types T1, T2, ..., Tm. (More formally, T′ is a common subtype for T1, T2, ..., Tm if and only if the following predicate—
FORALL v ( IF v ∊ T′ THEN v ∊ INTERSECT { T1 , T2 , ..., Tm } )
—is satisfied by T′.) Note that T′ must necessarily be from the same type lattice as T1, T2, ..., Tm. Note too that every such set of types T1, T2, ..., Tm does have at least one common subtype, though it might be one of those specified types T1, T2, ..., Tm, or even the pertinent minimal type. Note finally that (a) if m = 1, then the set of types T1, T2, ..., Tm reduces to just T1, and T1 itself is a common subtype for that set; (b) if m = 0, then the set of types T1, T2, ..., Tm is empty, and every type in the pertinent type lattice, including both the pertinent maximal type and the pertinent minimal type in particular, is a common subtype for that set. See also least specific common subtype; most specific common subtype. Contrast common supertype.
Examples: With reference to Fig. 4, (a) SQUARE is a common subtype for RECTANGLE, RIGHT KITE, and RHOMBUS; (b) SQUARE is also a common subtype for TRAPEZOID and CYCLIC QUADRILATERAL; (c) KITE is a common subtype for KITE and QUADRILATERAL; (d) omega is a common subtype for every subset of the set of types in the figure; and so on. Note: For examples involving tuple and relation types, see common subtype (tuple types) and common subtype (relation types), respectively.
common subtype (relation types) Let T1, T2, ..., Tm (m ≥ 0) be relation types from the same type lattice, q.v.; by definition, then, those types all have the same attribute names, say A1, A2, ..., An (n ≥ 0). Let the type of attribute Aj (j = 1, 2, ..., n) within type Ti (i = 1, 2, ..., m) be Tij. Then type T′ = RELATION {<A1,T01′>,<A2,T02′>,...,<An,T0n′>} is a common subtype for types T1, T2, ..., Tm if and only if, for all j (j = 1, 2, ..., n), type T0j′ is a common subtype for types T1j, T2j, ..., Tmj. See also common subtype; contrast common supertype (relation types).
Examples: With reference to Fig. 5, (a) relation type CS is a common subtype for relation types CR and ES; (b) relation type CS is also a common subtype for relation types ES and ER; (c) relation type ES is also a common subtype for relation types ES and ER; (d) type RELATION {E omega, R omega}—which contains just one value, viz., an empty relation—is a common subtype for every subset of the set of relation types in the figure; and so on.
common subtype (tuple types) Let T1, T2, ..., Tm (m ≥ 0) be tuple types from the same type lattice, q.v.; by definition, then, those types all have the same attribute names, say A1, A2, ..., An (n ≥ 0). Let the type of attribute Aj (j = 1, 2, ..., n) within type Ti (i = 1, 2, ..., m) be Tij. Then type T′ = TUPLE {<A1,T01′>,<A2,T02′>,...,<An,T0n′>} is a common subtype for types T1, T2, ..., Tm if and only if, for all j (j = 1, 2, ..., n), type T0j′ is a common subtype for types T1j, T2j, ..., Tmj. See also common subtype; contrast common supertype (tuple types).
Examples: With reference to Fig. 5, (a) tuple type CS is a common subtype for tuple types CR and ES; (b) tuple type CS is also a common subtype for tuple types ER and ES; (c) tuple type ES is also a common subtype for tuple types ES and ER; (d) type TUPLE {E omega, R omega}—which is an empty type—is a common subtype for every subset of the set of tuple types in the figure; and so on.
common supertype Let T1, T2, ..., Tm (m ≥ 0) be types from the same type lattice, q.v. Then type T is a common supertype for types T1, T2, ..., Tm if and only if, whenever a given value is of any of types T1, T2, ..., Tm, it’s also of type T. (More formally, T is a common supertype for T1, T2, ..., Tm if and only if the following predicate—
FORALL v ( IF v ∊ UNION { T1 , T2 , ..., Tm } THEN v ∊ T )
—is satisfied by T.) Note that T must necessarily be from the same type lattice as T1, T2, ..., Tm. Note too that every such set of types T1, T2, ..., Tm does have at least one common supertype, though it might be one of those specified types T1, T2, ..., Tm, or even the pertinent maximal type. Note finally that (a) if m = 1, then the set of types T1, T2, ..., Tm reduces to just T1, and T1 itself is a common supertype for that set; (b) if m = 0, then the set of types T1, T2, ..., Tm is empty, and every type in the pertinent type lattice, including the pertinent maximal type and the pertinent minimal type in particular, is a common supertype for that set. See also least specific common supertype; most specific common supertype. Contrast common subtype.
Examples: With reference to Fig. 4, (a) QUADRILATERAL is a common supertype for RECTANGLE, RIGHT KITE, and RHOMBUS; (b) KITE is a common supertype for RIGHT KITE and RHOMBUS; (c) KITE is a common supertype for KITE and RHOMBUS; (d) alpha is a common supertype for every subset of the set of types in the figure; and so on. Note: For examples involving tuple and relation types, see common supertype (tuple types) and common supertype (relation types), respectively.
common supertype (relation types) Let T1, T2, ..., Tm (m ≥ 0) be relation types from the same type lattice, q.v.; by definition, then, those types all have the same attribute names, say A1, A2, ..., An (n ≥ 0). Let the type of attribute Aj (j = 1, 2, ..., n) within type Ti (i = 1, 2, ..., m) be Tij. Then type T = RELATION {<A1,T01>,<A2,T02>,...,<An,T0n>} is a common supertype for types T1, T2, ..., Tm if and only if, for all j (j = 1, 2, ..., n), type T0j is a common supertype for types T1j, T2j, ..., Tmj. See also common supertype; contrast common subtype (relation types).
Examples: With reference to Fig. 5, (a) relation type ER is a common supertype for relation types CR and ES; (b) relation type ER is also a common supertype for relation types ER and ES; (c) relation type CR is a common supertype for relation types CR and CS; (d) type RELATION {E alpha, R alpha} is a common supertype for every subset of the set of relation types in the figure; and so on.
common supertype (tuple types) Let T1, T2, ..., Tm (m ≥ 0) be tuple types from the same type lattice, q.v.; by definition, then, those types all have the same attribute names, say A1, A2, ..., An (n ≥ 0). Let the type of attribute Aj (j = 1, 2, ..., n) within type Ti (i = 1, 2, ..., m) be Tij. Then type T = TUPLE {<A1,T01>,<A2,T02>,...,<An,T0n>} is a common supertype for types T1, T2, ..., Tm if and only if, for all j (j = 1, 2, ..., n), type T0j is a common supertype for types T1j, T2j, ..., Tmj. See also common supertype; contrast common subtype (tuple types).
Examples: With reference to Fig. 5, (a) tuple type ER is a common supertype for tuple types CR and ES; (b) tuple type ER is also a common supertype for tuple types ER and ES; (c) tuple type CR is a common supertype for tuple types CR and CS; (d) type TUPLE {E alpha, R alpha} is a common supertype for every subset of the set of tuple types in the figure; and so on.
compile time binding As noted under binding, q.v., the term binding is used in the inheritance context to refer to the process of determining which implementation version of a given operator is to be executed in response to a given invocation of the operator in question. Such binding can be done at compile time or run time or both. Compile time binding in particular (at least as that term is understood in the Manifesto model) can be defined thus: Given an expression exp denoting an invocation of some operator Op, it’s the process of finding, at compile time, the unique invocation signature for Op—see signature—for which the declared types of the parameters exactly match the declared types of the corresponding argument expressions in exp, thereby causing the unique corresponding implementation version, q.v., of Op to be invoked at run time (unless the compiler’s decision is overridden at run time by run time binding, q.v.). Note: In principle, binding can always be done at compile time—run time binding is logically unnecessary (though it might lead to better performance). See implementation version for further discussion; see also run time binding.
compile time type checking Checking at compile time that the types of the arguments to an invocation of some operator conform to that operator’s parameter type requirements, as specified by that operator’s specification signature. In other words, given an expression exp that denotes an invocation of some operator Op, compile time type checking is the process of ensuring at compile time that there exists a unique invocation signature for Op—see signature—for which the declared types of the parameters exactly match the declared types of the corresponding argument expressions in exp. Contrast run time type checking.
compile time type error The error that occurs if compile time type checking (q.v.) fails.
concrete type Term sometimes used, especially in systems that use the term abstract type to mean a union type, to mean a type that’s not a union type. In other words, a concrete type is a type with the property that there exists at least one value having the type in question as its most specific type. But since (as noted under abstract type) the foregoing use of the term abstract type is deprecated, the term concrete type is deprecated also, somewhat.
CONSTRAINT (With inheritance) A Tutorial D construct, used in connection with the definition of type constraints for regular—and hence necessarily scalar—types. (It’s also used in connection with database constraints. See Part I of this dictionary.) There are two basic cases to consider. First, if T is a regular root type, then the explanation from Part I of this dictionary applies unchanged, because all scalar types are regular root types in the absence of support for inheritance. So consider the second case, where T is a regular proper subtype. Let T have precisely one immediate supertype. (What happens if T has two or more immediate supertypes is described under IS, q.v.) This case in turn divides into two subsidiary cases: one where the immediate supertype is a dummy type, and one where it’s a regular type. For an example of the first of these possibilities, let PLANE_FIGURE be a dummy type and let ELLIPSE be an immediate subtype of that dummy type (see Fig. 2). Then the ELLIPSE type definition might look like this (irrelevant details omitted):
TYPE ELLIPSE
IS { PLANE_FIGURE
POSSREP { A LENGTH , B LENGTH , CTR POINT
CONSTRAINT A ≥ B } } ;
This case is very similar to the first (where T is a regular root type), except that the POSSREP specification and implicit or explicit CONSTRAINT specification—which is actually part of that POSSREP specification—are now part of the IS specification (see IS). The type constraint for type ELLIPSE here is exactly the same as it would have been if that type had been a regular root type.
Turning now to the case where the immediate supertype is a regular type instead of a dummy type, consider type CIRCLE, which has just one immediate supertype (ELLIPSE), which is indeed a regular type (again, see Fig. 2). The CIRCLE type definition might look like this (irrelevant details omitted):
TYPE CIRCLE
IS { ELLIPSE
CONSTRAINT THE_A ( ELLIPSE ) = THE_B ( ELLIPSE )
POSSREP { R = THE_A ( ELLIPSE ) ,
CTR = THE_CTR ( ELLIPSE ) } } ;
Now the CONSTRAINT specification—which in cases like the one under discussion must be stated explicitly—is part of the IS specification, not the POSSREP specification (which is likewise part of the IS specification and now defines a derived possrep, q.v.). Let c be a scalar value. Then c is a value of type CIRCLE if and only if the following constraint—call it CTC—is satisfied: The value c is of type ELLIPSE, and so has a major semiaxis of length a and a minor semiaxis of length b, and a = b. CTC here is the type constraint for type ELLIPSE. Note, therefore, that (as in fact was pointed out under CONSTRAINT in Part I of this dictionary) the CONSTRAINT specification as such doesn’t define the type constraint in its entirety, though it’s often referred to informally as if it did.
constraint inheritance Inheritance of type constraints. See type inheritance.
containment hierarchy A term used in OO systems to refer (somewhat loosely) to an object that contains other objects or an object type that’s defined to contain other object types. For example, a department object might contain a set of employee objects, and the relationship from departments to employees is thus indeed one of containment. Moreover, that relationship is hierarchic, in that the containing object can be regarded as superior, in a sense, to the contained objects (likewise, of course, the contained objects can be regarded as inferior, in a sense, to the containing object).
Note: Actually there’s some confusion, or even sleight of hand, here. Typically, the “containing” object doesn’t really contain the “contained” objects; instead, it contains object IDs of—i.e., pointers to—those “contained” objects, and these latter objects might thus be “contained” in several distinct “containing” objects simultaneously. If such is indeed the case, the semantics are, of course, quite different. For example, does deleting the containing object cascade to delete the contained objects? The answer is probably yes if those contained objects truly are contained, no if not (because in the latter case it’s likely that it’ll just be the pointers that are deleted, not the “contained objects” as such).
contravariance See argument contravariance.
covariance See result covariance.
current most specific type Same as most specific type (of a variable in particular).
current type Abbreviation for current most specific type, q.v.
declared type (With inheritance) 1. (Of a constant, variable, attribute, or parameter) The type specified when the constant, variable, attribute, or parameter in question is declared. 2. (Of a read-only operator) The type of the result, specified when the operator in question is declared. Note, however, that the concept of operator declared type, as such, isn’t all that important in the inheritance context; what’s more important is the related concept of the declared type of an invocation of the operator in question, which largely subsumes the former notion (see signature for further explanation). 3. (Of an expression) Let exp be a read-only operator invocation (note that constant, variable, attribute, and parameter references can all be regarded as read-only operator invocations, as can literals also). Then the declared type of exp is the declared type of the pertinent invocation signature (again, see signature for further explanation). Note: If exp is in fact a constant, variable, attribute, or parameter reference or a literal, the declared type of the pertinent invocation signature is of course just the declared type of the constant, variable, attribute, parameter, or literal in question. See also most specific type (relation types).
Note: Elsewhere in this part of the dictionary, the declared type of some construct X is denoted DT(X). Note that DT(X) can be empty only if X is an attribute of some tuple or relation type. (This latter point applies to attributes of minimal tuple and relation types, q.v., in particular. However, a tuple or relation type doesn’t have to be a minimal type in order to have such an attribute.)
delegation A mechanism according to which the implementation of some operator Op is delegated to—i.e., defined in terms of—the analog of Op on some component(s) of some possrep(s) for the parameter(s) to Op. For example, suppose type LENGTH has a possrep consisting of a single component, say M, of type RATIONAL. Then the operator for adding two lengths can be implemented in terms of regular rational addition on the pertinent M values; in other words, the responsibility for implementing addition for type LENGTH can be delegated to the type, RATIONAL, of a certain component of one of its possreps, and some code reuse can thus be obtained. However, delegation has nothing to do with type inheritance as such, even though code reuse is indeed one of the objectives of type inheritance. See colored circle; HAS A. Note: The operator being implemented and the operator providing the implementation will very likely have the same name—for example, the name “+” might be used both for addition of rational numbers and for addition of lengths—in which case that name will be overloaded. See overloading polymorphism in Part I of this dictionary.
DELETE ONLY Let T′ be a subtable of supertable T (see subtables and supertables). Then DELETE ONLY is an operator—not supported by SQL, incidentally, even though SQL does support subtables and supertables as such—that deletes a row from T′ without simultaneously deleting the corresponding row from T.
Example: With reference to the example under subtables and supertables, it should be possible to use DELETE ONLY to delete a row from table PGMR without at the same time deleting the corresponding row from table EMP, to reflect the fact that some existing employee has ceased to be a programmer.
derived possrep Let T′ be a regular type with at least one regular immediate supertype. Then each possrep specified for type T′ is a derived possrep, explicitly derived in some way from—in fact, explicitly defined in terms of—some possrep for some regular immediate supertype of type T′. Note that there’s a logical difference between a derived possrep and an inherited one (see possrep inheritance), as follows. First, to repeat, a derived possrep for type T′ is explicitly declared for that type T′, and it’s defined in terms of some possrep for some regular immediate supertype of that type T′. By contrast, an inherited possrep for type T′ isn’t explicitly declared for that type T′; rather, it’s simply any possrep—derived, inherited, or otherwise—that applies to some regular immediate supertype of type T′, and hence applies to type T′ as well a fortiori.
Example: With reference to Fig. 2, the sole possrep for type CIRCLE—a derived possrep, by definition—is defined as follows:
POSSREP { R = THE_A ( ELLIPSE ) ,
CTR = THE_CTR ( ELLIPSE ) } } ;
In other words, circles can possibly be represented by a length r and a point ctr. The length r is identical to the a component of a certain possrep that applies to type ELLIPSE; likewise, the point ctr is identical to the ctr component of that same ELLIPSE possrep. Thus, the explicitly specified possrep shown for type CIRCLE is derived from, or defined in terms of, a certain possrep—actually the only one explicitly declared—for type ELLIPSE.
Incidentally, note that it’s perfectly possible for some type T′ to have a possrep PR′ that differs markedly from any of the possreps declared for the pertinent immediate supertype T, even though as just explained PR′ is necessarily derived from one of those possreps for T. For example, let T and T′ be POLYGON and RECTANGLE, respectively. Then T might have a possrep PR consisting of a sequence of n points, representing the n vertices of the polygon in some specific order, while T′ has a possrep PR′ consisting of a pair of points, representing the center and the bottom left vertex of the rectangle. (The assumption here is that rectangles always have their long side horizontal and their short side vertical, so that the center and the bottom left vertex can indeed validly serve as a possrep.) Nevertheless, it’s still the case—in fact, it must be the case—that if PR is a possrep for T, then every explicitly declared possrep PR′ for T′ is expressible in terms of, and thus derivable from, PR.
derived type See extends relationship.
derived type graph Not a graph of derived types (q.v.), but a type graph that’s derived from another type graph. Let TG be a type graph, q.v.; then TG can be divided into a set of disjoint partitions—a nonempty set, unless TG itself is empty—such that (a) each partition in the set has exactly one root node and one or more leaf nodes, and (b) no type in any partition in the set overlaps any type in any other partition in the set. Then:
Let G be a graph obtained from TG by removing zero or more partitions. Then G is a derived type graph—specifically, a type graph derived from TG. Note: It follows that TG itself and the empty graph can both be regarded as type graphs derived from TG.
Let G be a type graph derived from TG; let P be a partition within G; and let P be in fact a type hierarchy, q.v. Then any graph obtained from G by replacing P by some type hierarchy derived from P (see derived type hierarchy) is a derived type graph—again, a type graph derived from TG.
derived type hierarchy Not a hierarchy of derived types (q.v.), but a type hierarchy that’s derived from another type hierarchy. Let TH be a type hierarchy, q.v. Then:
TH itself is considered to be a type hierarchy derived from TH.
Let DH be a graph obtained from TH by choosing the node corresponding to some type T and removing (a) all nodes not corresponding to some subtype T′ of T and (b) all arcs emanating from those nodes. Then DH is a derived type hierarchy, with T as its root—specifically, a type hierarchy derived from TH.
Let DH be a type hierarchy derived from TH. Then any graph obtained from DH by removing the node corresponding to some type T is a derived type hierarchy, with the root of DH as its root (unless the node corresponding to the root of DH was the one deleted)—specifically, a type hierarchy derived from TH—provided that removal of a node is always accompanied by removal of (a) the arc, if any, entering into that node and (b) all corresponding immediate subtype nodes. Note: It follows that the empty graph can be regarded as a type hierarchy derived from TH.
By contrast, if (a) TH is a type hierarchy with root T, and if (b) type T is an immediate supertype of type T′ and type T′ is an immediate supertype of type T′′ (and if—let’s assume for simplicity—type T′ is an immediate supertype of no type other than type T′′), and if (c) XH is the graph derived from TH by removing node T′ and coalescing the arc connecting nodes T and T′ and the arc connecting nodes T′ and T′′ into a single arc connecting nodes T and T′′, then (d) XH is not a derived type hierarchy (at least, not one that can be derived from TH), because it causes T′′ to lose some of its inheritance, as it were.
Examples: The following are all type hierarchies that can be derived from the type hierarchy of Fig. 2 (assuming in all cases that pertinent connecting arcs are retained):
The graph that’s obtained by removing all nodes except POLYGON, RECTANGLE, and SQUARE
The graph that’s obtained by removing all nodes except POLYGON and RECTANGLE
The graph that’s obtained by removing just the CIRCLE and SQUARE nodes
The graph that’s obtained by removing all nodes
(and so on). By contrast, the graph that’s obtained by removing all nodes except POLYGON and SQUARE isn’t a derived type hierarchy—at least, not one that can be derived from the type hierarchy of Fig. 2. Note: As a matter of interest, there are exactly 22 distinct type hierarchies that can be derived from the type hierarchy of Fig. 2.
descendant type Term occasionally used to mean a proper subtype.
difference (With inheritance) See dyadic relational operators.
direct subtype SQL term for an immediate subtype.
direct supertype SQL term for an immediate supertype.
disjoint types Types T1 and T2 are disjoint if and only if no value is a value of both. Note that:
If T1 and T2 are distinct scalar leaf types, they’re certainly disjoint.
If T1 and T2 are distinct scalar types, they’re certainly disjoint if one is type omega.
If T1 and T2 are distinct root types (scalar or otherwise), they’re certainly disjoint.
If T1 and T2 are from distinct type lattices, they’re certainly disjoint.
If T1 and T2 are distinct leaf types from the same tuple type lattice, they’re certainly disjoint.
If T1 and T2 are distinct types from the same relation type lattice, they’re not disjoint, even if they’re leaf types or if one is the pertinent minimal type.
Contrast overlapping types.
Examples: 1. With reference to Fig. 2, scalar types ELLIPSE and RECTANGLE are disjoint; by contrast, with reference to Fig. 3, scalar types RECTANGLE and RHOMBUS overlap. 2. With reference to Fig. 5, tuple types CR and ES overlap, as do tuple types ER and CS (in this latter case, of course, one is a proper subtype of the other). 3. Let scalar type PARALLELOGRAM be a union type, with immediate subtypes RECTANGLE and NONRECTANGLE (with the intuitively obvious semantics), and consider relation types RELATION {P RECTANGLE} and RELATION {P NONRECTANGLE}. Then these relation types might be thought to be disjoint, but they’re not. The reason is that the empty relation of type RELATION {P PARALLELOGRAM} is a value of both of them. In fact, that empty relation—whose most specific type is RELATION {P omega}, incidentally—is a value of every type in the pertinent type lattice, including even the corresponding minimal type RELATION {P omega}.
disjointness assumption A simplifying assumption, valid with single but not multiple inheritance, to the effect that types T1 and T2 are disjoint if and only if neither is a subtype of the other. Note, however, that single inheritance is possible in general only with scalar types (and even then only if type omega is ignored—but the fact that type omega is a subtype of every scalar type does not in and of itself violate the disjointness assumption).
Examples: With reference to Fig. 2, let T1 and T2 be any nonempty subtype of ELLIPSE and any nonempty subtype of POLYGON, respectively; then neither of types T1 and T2 is a subtype of the other, and they’re disjoint.
Note: It follows directly from the disjointness assumption that (a) distinct root types are disjoint; (b) distinct leaf types are disjoint; and (c) every value has a unique most specific type. (In fact, if v is a value of most specific type T, then the set of types possessed by v is, precisely, the set of all supertypes of T.) Now, it should be obvious that these properties hold with single inheritance; as a matter of fact, however, they hold with multiple inheritance as well, even though the disjointness assumption doesn’t. In particular, therefore, they hold for tuple and relation types as well as for scalar types, even though (to say it again) the disjointness assumption doesn’t.
dispatching / despatching Terms sometimes used, especially in OO contexts, as synonyms for binding, q.v. (especially run time binding, q.v.). Here’s a (very loose!) definition from the OO literature: “[Dispatching is the] execution of methods based on polymorphism” (from Douglas K. Barry, The Object Database Handbook: How to Select, Implement, and Use Object-Oriented Databases, Wiley Publishing, 1996).
distinguished parameter See selfish method.
DT (...) Declared type of. See model of a variable; model of an expression.
dummy type A given type T is a dummy type if and only if (a) it’s either alpha or omega, q.v., or (b) all three of the following are true:
T is a union type, q.v. (and hence a scalar type, necessarily).
T has no declared possrep (and hence no selector and no “automatic” THE_ operators).
T has no regular supertype.
(In fact type alpha satisfies the second and third of these conditions anyway, and usually the first as well; type omega satisfies the first of them—albeit vacuously—and the second, but not the third.) Note that, by definition, (a) dummy types are always scalar (but see the further remarks below regarding tuple and relation types); (b) a dummy type has no values that aren’t values of some regular proper subtype of the dummy type in question (see regular type); and (c) if T is a dummy type other than type omega, all of T’s proper supertypes are dummy types also. Note too, however, that—to spell the point out explicitly—defining a variable to be of type T is perfectly legitimate even if T is a dummy type, though of course such a variable can never have a value whose most specific type is T.
Examples: Consider the following outline type definitions (based on a revised version of the type hierarchy of Fig. 2):
TYPE ELLIPSE UNION
IS { PLANE_FIGURE } ;
TYPE CIRCLE
IS { ELLIPSE
POSSREP { R LENGTH , CTR POINT } } ;
TYPE NONCIRCLE
IS { ELLIPSE
POSSREP { A LENGTH , B LENGTH , CTR POINT
CONSTRAINT A > B } } ;
Explanation:
Type ELLIPSE as defined here is a dummy type: It has no possrep, and therefore no possrep constraint, no selector, and no “automatic” THE_ operators. (It might have some explicit THE_ operators, though. See further discussion below.)
No variable can ever have a value of most specific type ELLIPSE, even if its declared type is ELLIPSE.
Type CIRCLE has a selector and THE_ operators THE_R and THE_CTR; type NONCIRCLE has a selector and THE_ operators THE_A, THE_B, and THE_CTR. Note in particular that the operators THE_A and THE_B don’t apply to type CIRCLE.
Specialization by constraint (q.v.) doesn’t apply to types CIRCLE and NONCIRCLE—i.e., there’s no formal way, given these definitions, that a circle or a noncircle can be derived from an ellipse—because type ELLIPSE has no possrep in terms of which the pertinent specialization constraints (q.v.) can be formulated.
Let AREA_OF (“return the area of”) be an operator that applies to both circles and noncircles. No implementation code can be provided for that operator at the ELLIPSE level, because type ELLIPSE has no possrep—and (let’s assume for the sake of the example, at least) no physical representation either—in terms of which that code can be formulated. However, an appropriate specification signature, at least, can be defined at that level (see signature). In Tutorial D, that signature might look like this (note the declared type AREA of the result):
AREA_OF ( ELLIPSE ) RETURNS AREA
Two implementation versions will now have to be provided, one for circles and one for noncircles, perhaps as follows (note the explicit VERSION specifications):
OPERATOR AREA_OF VERSION C_AREA ( C CIRCLE ) RETURNS AREA ;
RETURN 3.14159 * ( THE_R ( C ) ↑ 2 ) ;
END OPERATOR ;
OPERATOR AREA_OF VERSION NC_AREA ( NC NONCIRCLE ) RETURNS AREA ;
RETURN 3.14159 * ( THE_A ( NC ) * THE_B ( NC ) ) ;
END OPERATOR ;The foregoing discussion of operator AREA_OF gives some idea of the purpose of dummy types: Union types in general (q.v.) provide a way of specifying operators that apply to values or variables of several different types, all of them proper subtypes of the union type in question—and the same is true of dummy types in particular; the difference is simply that for some union types, there might not exist a reasonable possrep, in which case the union type in question thus becomes a dummy type (see further discussion below).
Now, the foregoing example isn’t very realistic, because we could easily make ELLIPSE a regular union type (i.e., one with a possrep) instead of a dummy type, and then we could define an implementation version of AREA_OF at the ELLIPSE level that would work for both circles and noncircles (see the first example under implementation version). But consider type PLANE_FIGURE. That type would almost certainly be a dummy type—it’s hard to think of a sensible possrep that could work for an arbitrary plane figure!—and so it might well make sense to define just a specification signature for AREA_OF at the PLANE_FIGURE level and implementation versions at (say) the ELLIPSE and POLYGON levels. Note: Actually the foregoing remarks are slightly oversimplified. See signature for further discussion.
Despite the foregoing, let’s stay with the example of ELLIPSE as a dummy type, for simplicity. Observe now that the operator THE_CTR applies to both values of type CIRCLE and values of type NONCIRCLE—i.e., values of every proper subtype of type ELLIPSE—and yet not to values of type ELLIPSE itself. But such a state of affairs is clearly absurd; to say that every ellipse is either a circle or a noncircle, and circles and noncircles both have a center but ellipses don’t, is an affront to common sense. The anomaly is easily fixed, however—we define THE_CTR explicitly to be an operator that applies at the ELLIPSE level, as follows (note that implementation versions of that operator are certainly available for both circles and noncircles):
OPERATOR THE_CTR VERSION E_CTR ( E ELLIPSE ) RETURNS POINT ;
RETURN ( CASE
WHEN IS_CIRCLE ( E ) THEN
THE_CTR ( TREAT_AS_CIRCLE ( E ) )
WHEN IS_NONCIRCLE ( E ) THEN
THE_CTR ( TREAT_AS_NONCIRCLE ( E ) )
END CASE ) ;
END OPERATOR ;
Note: Actually there’s no need to define the implementation code for this operator as shown—it would be sufficient to define just the appropriate specification signature at the ELLIPSE level:
THE_CTR ( ELLIPSE ) RETURNS POINT
Here’s another moderately realistic example of an operator for which implementation code can be—and this time definitely should be—defined at a dummy type level:
OPERATOR DOUBLE_AREA_OF
VERSION PF_DOUBLE_AREA ( PF PLANE_FIGURE ) RETURNS AREA ;
RETURN 2 * AREA_OF ( PF ) ;
END OPERATOR ;
What about tuple and relation dummy types? For definiteness, let’s focus on tuple types specifically. Now, tuple types, like dummy types, have no declared possreps; unlike dummy types, however, they do have selectors (except in the very special case where the tuple type in question is empty, which can happen if and only if one of the attributes of the tuple type in question is an empty type in turn). Partly for such reasons, the concept of a “dummy tuple type” doesn’t really make much sense (and the same goes for the concept of a “union tuple type,” come to that). However, we might informally regard a tuple type that has at least one attribute of a dummy type as a dummy tuple type, if we wanted to. For example, suppose once again that scalar type ELLIPSE is a dummy type, with immediate regular subtypes CIRCLE and NONCIRCLE, and consider the following tuple types:
TUPLE { E ELLIPSE }
There aren’t any values of this type that aren’t values of some proper subtype of the type; thus, the type might implicitly be considered a union tuple type, and in fact a dummy tuple type to boot. Such notions seem to serve little practical purpose, however, which is why they’re not formally defined in this dictionary.
TUPLE { E CIRCLE , X alpha }
This one too might be considered a tuple dummy type, if it were thought useful to do so.
TUPLE { E omega }
This is an example of an empty tuple type. It too might be regarded as a dummy tuple type.
Remarks analogous to the foregoing apply to relation types also, except that relation types are never empty (not even if they have an attribute of some empty type).
Now getting back to scalar types specifically: We’ve seen that if T is a dummy type, it has no possrep—but the converse isn’t true. To be specific, certain system defined types (e.g., type INTEGER, perhaps) are allowed not to have a possrep; however, such types certainly aren’t dummy types, because (a) values do exist whose most specific type is the type in question and (b) the system is required to provide at least one corresponding selector operator for each such type (see selector in Part I of this dictionary).
One final point: Some systems use dummy types to provide a kind of type generator facility. For example, RELATION might be defined as a dummy type in such a system, and then every specific relation type would be a proper subtype of that RELATION type. The Manifesto model rejects such a scheme, however, for the following reasons (and possibly others):
First, we don’t want type generator support to be conditional on support for type inheritance.
Second, we certainly don’t want to have to define specific implementation versions of the usual relational operators—restrict, project, join, and so on—for every specific relation type.
Third, we don’t believe in the kind of “relation type inheritance” such a scheme would provide (it doesn’t give us the kind of substitutability we want).
dyadic relational operators Let relational expressions R1 and R2 denote relations r1 and r2, respectively, and let Ai and Aj be attributes of r1 and r2, respectively. Note that Ai can be regarded as an attribute of R1 per se and Aj can be regarded as an attribute of R2 per se. Let the declared types of Ai and Aj within R1 and R2 be DT1 and DT2, respectively. Finally, let attributes <A1,DT1> and <A2,DT2> be said to correspond if and only if their names Ai and Aj are the same, A say, and their declared types DTi and DTj have a common supertype (i.e., DTi and DTj belong to the same type lattice, q.v.). Then the expressions R1 UNION R2, R1 INTERSECT R2, and R1 MINUS R2 are each defined if and only if each attribute of R1 corresponds in the foregoing sense to some attribute of R2 and vice versa. Moreover, for each pair of corresponding attributes <A,DT1> in R1 and <A,DT2> in R2—here we change our notation slightly—the declared type DT(A) of attribute A within each of these expressions is as follows:
(Union) The most specific common supertype DT of DT1 and DT2. Note: In practice, the implementation might want to outlaw, or at least flag, any attempt to form such a union if DT is the pertinent maximal type (because such a situation probably constitutes an error on the user’s part).
(Intersection) The least specific common subtype DT′—the intersection type, in fact—of DT1 and DT2. Note: In practice, the implementation might want to outlaw, or at least flag, any attempt to form such an intersection if DT′ is the pertinent minimal type (again because such a situation probably constitutes an error on the user’s part).
(Difference) DT1. Note: In practice, the implementation might want to outlaw, or at least flag, any attempt to form such a difference if the most specific common supertype DT of DT1 and DT2 is the pertinent maximal type and/or if their least specific common subtype DT′ is the pertinent minimal type (once again because either of these situations probably constitutes an error on the user’s part).
Note: The concept of corresponding attributes is introduced purely for the purposes of the the foregoing definitions, in order to allow the rules regarding declared types to be stated precisely. In fact, however, those rules can be stated without using the notion of corresponding attributes at all, as follows. First, DT(R1) and DT(R2) must have a common supertype in all three cases. Then the declared type of each of the three expressions is as follows:
(Union) The most specific common supertype of DT(R1) and DT(R2).
(Intersection) The least specific common subtype—the intersection type, in fact—of DT(R1) and DT(R2).
(Difference) DT(R1).
As for join, the expression R1 JOIN R2 is defined if and only if r1 and r2 are joinable, q.v. If they are, then for each pair of corresponding attributes <A,DT1> in R1 and <A,DT2> in R2, the declared type of the corresponding attribute within that expression is the least specific common subtype—the intersection type, in fact—of DT1 and DT2. (As for attributes in r1 that have no corresponding attribute in r2 or vice versa, such attributes simply become attributes of the result in the usual way.) Note: Of course, join is basically a generalization of intersection, and the declared type of the result overall is thus just the least specific common subtype—the intersection type, in fact—of DT(R1) and DT(R2).
Examples: With reference to Fig. 3, let relations r1 and r2 be as follows:
r1 r2
┌────────────────┐ ┌──────────────┐
│ P : RECTANGLE │ │ P : RHOMBUS │
├════════════════┤ ├══════════════┤
│ px : rectangle │ │ py : square │
│ py : square │ │ pz : rhombus │
└────────────────┘ └──────────────┘
(Most specific types are shown in lowercase italics.) Then r1 UNION r2, r1 INTERSECT r2, and r1 MINUS r2 are as shown below (r1 JOIN r2 is identical to r1 INTERSECT r2 in this example). Note the result attribute declared types in particular.
r1 UNION r2 r1 INTERSECT r2 r1 MINUS r2
┌────────────────────┐ ┌─────────────┐ ┌────────────────┐
│ P : PARALLELOGRAM │ │ P : SQUARE │ │ P : RECTANGLE │
├════════════════════┤ ├═════════════┤ ├════════════════┤
│ px : rectangle │ │ py : square │ │ px : rectangle │
│ py : square │ └─────────────┘ └────────────────┘
│ pz : rhombus │
└────────────────────┘
Finally, the rules for other dyadic relational operators—D_UNION, I_MINUS, XUNION, MATCHING, NOT MATCHING, and COMPOSE—can be derived straightforwardly from the rules presented above for union, intersection, difference, and join.
dynamic binding Term sometimes used as a synonym for run time binding, q.v.
dynamic classification Systems and languages (especially OO systems and languages) that use the term class to mean a type—see Part I of this dictionary—sometimes also use the term dynamic classification to refer to the process, or the result of the process, of determining at run time the type(s) possessed by some object.
dynamic dispatching / dynamic despatching Term sometimes used (especially in OO systems and languages) as a synonym for run time binding, q.v.
dynamic type checking Term sometimes used as a synonym for run time type checking, q.v.
early binding Compile time binding, q.v.
empty set of types The least specific common subtype and least specific common supertype for an empty set of types are both T_alpha (q.v.), the pertinent maximal type; likewise, the most specific common subtype and most specific common supertype for an empty set of types are both T_omega (q.v.), the pertinent minimal type. Note: To see that these definitions are reasonable, consider the following. Let TL be a type lattice, q.v., with maximal and minimal types GT and LT, respectively, and let S = {T1,T2,. .,Tm} (m ≥ 0) be a subset of the types in TL. If m = 0—i.e., if S is empty—then (a) by definition, every type in TL is a common subtype for T1, T2, ..., Tm, and so the corresponding least specific and most specific common subtype are GT and LT, respectively; likewise (b) again by definition, every type in TL is also a common supertype for T1, T2, ..., Tm, and so the corresponding least specific and most specific common supertype are also GT and LT, respectively.
empty type (With inheritance) A scalar type is empty if and only if it’s type omega, q.v. A tuple type is empty if and only if it has an attribute of some empty type. A relation type is never empty, even if it has an attribute of some empty type (because if T is a relation type, there always exists at least one relation of type T—viz., the empty relation of that type).
Examples: Here are some examples of empty tuple types:
TUPLE { E omega }
TUPLE { E omega , R omega }
TUPLE { X CIRCLE , Y TUPLE { Z omega } }
By contrast, the following tuple type isn’t empty (instead, it contains exactly one value—viz., the 0-tuple):
TUPLE { }
(Incidentally, this type has just one valid corresponding selector invocation, which looks like this in Tutorial D: TUPLE { }.)
The following relation type is also nonempty (as are all relation types), even though it has at least one attribute of an empty type:
RELATION { E omega , R RECTANGLE }
Another interesting (necessarily nonempty) relation type is the one with an empty heading:
RELATION { }
This type contains exactly two values—namely, TABLE_DUM and TABLE_DEE, the only relations of degree zero.
Note: An empty type is permitted to appear (a) as the declared type of some attribute of some tuple or relation type and (b) nowhere else. To be more specific:
Scalar and tuple variables: An attempt to define a scalar or tuple variable with an empty declared type will fail at run time (if not at compile time), because there’s no initial value that can be assigned to that variable.
Relation variables: A relvar can’t be defined with an empty declared type because there aren’t any empty relation types.
Possrep components: An attempt to define a scalar type T with a possrep component of some empty declared type will fail at run time (if not at compile time) because there’s no example value—see Part I of this dictionary—that can be specified for T.
Read-only operators: An attempt to define a read-only operator Op—or, more precisely, an attempt to define an invocation signature, q.v., for such an operator—with a result of some empty declared type is illegal. If the violation isn’t caught at compile time, an invocation coresponding to that signature will certainly fail at run time.
Expressions: By definition, every expression denotes a value. It follows that no expression can be of an empty declared type.
Parameters: An attempt to define an operator Op with a parameter of some empty declared type is illegal. If the violation isn’t caught at compile time, an invocation of Op will certainly fail at run time.
Attributes: Attributes of tuple and relation types are allowed to be of an empty declared type. However, if T is a tuple type with an attribute of declared type some empty type, then T can’t be used as the declared type of anything other than some attribute of some other tuple or relation type. Note that no analogous remark applies to relation types.
equality (With inheritance) Let x and y be values such that the most specific types MST(x) and MST(y) overlap. Then (and only then) x and y can be compared for equality; the comparison returns TRUE if and only if x is equal to y (in which case MST(x) is equal to MST(y) also). Note: In order for the comparison to be syntactically valid, the declared types DT(expx) and DT(expy) of the expressions expx and expy used to denote the values x and y, respectively, must overlap (this condition is implied by the fact that MST(x) and MST(y) are required to overlap, and is a compile time check).
Examples: With reference to Fig. 2, let variables EX, EY, C, and R be of declared types ELLIPSE, ELLIPSE, CIRCLE, and RECTANGLE, respectively. Of the following comparisons, then, the first two are syntactically valid and the third isn’t:
EX = EY
EX = C
EX = R
The first two of these comparisons will certainly give FALSE if the most specific types of the comparands are different; they’ll also give FALSE if the most specific types are the same but the current values are different; otherwise they’ll give TRUE.
Now consider Fig. 3. Let variables S, RE, RH, and P be of declared types SQUARE, RECTANGLE, RHOMBUS, and PARALLELOGRAM, respectively. Then all of the following comparisons are syntactically valid:
P = RH
RH = RE
RE = S
S = P
In all cases, the comparison will give TRUE if and only if the current values of the comparands are the same (in which case the most specific types will be the same as well, necessarily).
example value 1. A value of scalar type T that’s specified when T is defined, thereby ensuring that T is nonempty. 2. (With inheritance) A value of scalar type T and not T′ (where T′ is an immediate subtype of T) that’s specified as part of the definition of T′, thereby ensuring that the set of values constituting T′ is a proper subset of the set of values constituting T. Note that T′ here can’t be a root type (i.e., T is not type alpha).
Examples (second definition): 1. With reference to the type hierarchy of Fig. 2, the complete definition for type CIRCLE might look as follows:
TYPE CIRCLE
IS { ELLIPSE
CONSTRAINT THE_A ( ELLIPSE ) = THE_B ( ELLIPSE )
POSSREP { R = THE_A ( ELLIPSE ) ,
CTR = THE_CTR ( ELLIPSE ) }
NOT { ELLIPSE ( LENGTH ( 2.0 ) ,
LENGTH ( 1.0 ) ,
POINT ( 0.0 , 0.0 ) ) } } ;
The intent of the NOT specification here is to say that the specified ELLIPSE value is a value of type ELLIPSE that’s not a value of type CIRCLE. (It might be nice to find a better keyword than NOT for this purpose.) 2. With reference to the type graph of Fig. 3, the complete definition for type SQUARE might look as follows:
TYPE SQUARE
IS { RECTANGLE , RHOMBUS
POSSREP { A = THE_A ( RECTANGLE ) ,
B = THE_B ( RECTANGLE ) ,
C = THE_C ( RECTANGLE ) ,
D = THE_D ( RECTANGLE ) }
NOT { RECTANGLE ( POINT ( 0.0 , 0.0 ) ,
POINT ( 0.0 , 1.0 ) ,
POINT ( 2.0 , 1.0 ) ,
POINT ( 2.0 , 0.0 ) ) ,
RHOMBUS ( POINT ( 0.0 , 0.0 ) ,
POINT ( √3.0 , 1.0 ) ,
POINT ( √3.0 + 2 , 1.0 ) ,
POINT ( 2.0 , 0.0 ) ) } } ;
Note: In type definitions elsewhere in this dictionary, such NOT specifications would just be a distraction and are therefore omitted. In any case, they aren’t currently supported in Tutorial D.
extends relationship Let type T′ inherit public instance variables (see Part I of this dictionary) from type T—i.e., let structural inheritance, q.v., apply to types T and T′—and let type T′ have additional public instance variables of its own. Then type T′ is said to extend type T (and types T and T′ are said to be the base type and the derived type, respectively, for the “extends relationship” in question). To quote The Object Data Standard: ODMG 3.0 (R. G. G. Cattell and Douglas K. Barry, eds., Morgan Kaufmann, 2000):
The EXTENDS relationship is a single inheritance relationship between two classes whereby the subordinate class inherits all of the properties ... of the class that it extends.
(And elsewhere that same reference defines properties as “attributes of the object itself or relationships between the object and one or more other objects”—although elsewhere again it defines them as “state variables,” and, as noted in Part I of this dictionary, state variables are usually understood to be merely instance variables by another name (?).) See also HAS A; structural inheritance; subtables and supertables.
Example: In an OO system, circles might have a CTR (“center”) public instance variable, because all ellipses have such an instance variable; however, they might also have an R (“radius”) public instance variable, which ellipses in general don’t have. In this example, therefore, type CIRCLE might be said to extend type ELLIPSE.
Note: The foregoing example is actually not very realistic, because circles will presumably have A and B public instance variables as well—inherited from type ELLIPSE and corresponding to the major and minor semiaxis length, respectively—and for a given circle the values of A, B, and R will all be the same. A more realistic example in the OO context might involve “colored circles,” which extend circles by adding a COLOR public instance variable (see colored circle.) Moreover, the “colored circles” example—in which CIRCLE is the base type and COLORED_CIRCLE the derived type—makes it very clear that the derivation process (i.e., the process by which a derived type, in an “extends relationship” context, is derived from the corresponding base type) is most certainly not specialization by constraint, q.v. More specifically, that derivation process doesn’t occur automatically but is, rather, a matter of explicit definition—by fiat, as it were.
Since the type theory espoused by The Third Manifesto has no support for public instance variables, it has no support for the extends relationship a fortiori.
four out of five rule The three out of four “rule” (q.v.) asserts that at most three of the following four allegedly desirable features can be supported at the same time: (a) substitutability; (b) compile time type checking; (c) mutability; and (d) “specialization via constraints,” q.v. By contrast, the four out of five rule asserts that all four of those features can be supported at the same time after all (at least insofar as is logically possible), just so long as objects in the OO sense—meaning object IDs in particular—aren’t supported! In other words, the feature that can and should be dropped is objects as such, not one of the four features here alleged to be desirable. Detailed arguments in support of this position (which is the position adopted in the Manifesto model) can be found in the Manifesto book.
function resolution Term sometimes used as a synonym for binding, q.v. (especially run time binding, q.v.).
G by C Generalization by constraint.
generalization Let types T′′, T′, and T be such that T′′ is a subtype of T′ and T′ is a subtype of T, and let v′ be a value of most specific type T′. Also, let V be a variable of declared type T, and let the current most specific type MST(V) of V be T′′. Finally, let the value v′ be assigned to V. Then the current most specific type of V is now T′; in other words, MST(V) has been generalized from T′′ to T′. (Of course, T′′ and T′ might be one and the same, and so might T′ and T, but in general they won’t be.) Contrast generalization by constraint; specialization.
Note: The foregoing definition explains how the Manifesto model works. In most systems, however, such generalization doesn’t happen at all. For example, with reference to Fig. 2, let variable E be of declared type ELLIPSE, and consider the following sequence of events. First, a value of most specific type CIRCLE is assigned to E; the most specific type of E thus becomes CIRCLE (see assignment). Next, a value of most specific type ELLIPSE is assigned to E. In the Manifesto model, then, the most specific type of E now becomes ELLIPSE again (again, see assignment); in those other systems, by contrast, the most specific type of E remains unchanged—i.e., it’s still CIRCLE—and so E now contains a “noncircular circle,” q.v.
generalization by constraint Let types T′′, T′, and T be such that T′′ is a subtype of T′ and T′ is a subtype of T, and let v′ be a value that satisfies the type constraint for type T′ (and not for any proper subtype of T′). Also, let V be a variable of declared type T, and let the current most specific type MST(V) of V be T′′. Finally, let the value v′ be assigned to V. Then the current most specific type of V is now T′; in other words, MST(V) has been generalized from T′′ to T′. (Of course, T′′ and T′ might in fact be one and the same, and so might T′ and T, but in general they won’t be.) Moreover, that generalization is said to be “by constraint” (“G by C”), because it occurs as a consequence of the fact that v′ satisfies the type constraint for T′ (and not for any proper subtype of T′). Contrast generalization; specialization by constraint.
Example: See the examples under generalization and specialization by constraint. Note: All generalization in the Manifesto model is by constraint, because a value in that model is of a given type if and only if it satisfies the type constraint for that type. But in a system that permits such absurdities as circular noncircles (q.v.) and noncircular circles (q.v.), generalization—if it even happens at all—will almost certainly not be by constraint. See specialization by constraint for further discussion.
GLB Greatest lower bound.
greatest lower bound Let s be a set; let a partial ordering be defined on s; and let s′ be a subset of s. Then x is a lower bound for s′ if and only if x ∊ s and x is less than or equal to every element of s′ with respect to the specified ordering. Moreover, if there do exist any such x’s, it’s easy to show there must be a largest one, and that largest x is the greatest lower bound (GLB) for s′ with respect to the specified ordering. (Note that the GLB for s′ might or might not itself be contained within s′.) See also lattice.
Examples: See the examples under type lattice.
HAS A Let types T1 and T2 be such that all of the properties (i.e., type constraints and read-only operators) that apply to type T1 apply to type T2 also. However, let some additional property P apply to T2, where P is such that it can’t be derived in any way from the properties that apply to T1. Then (a) the IS A relationship, q.v., doesn’t apply (i.e., T2 isn’t a subtype of T1—at least, not according to the Manifesto model); (b) by contrast, the HAS A relationship does apply (a value of type T2 does “have a” property P). Note that IS A always implies inclusion polymorphism, q.v., whereas HAS A typically seems to imply delegation, q.v. See also extends relationship; subtables and supertables.
Example: See the discussion under colored circle. Caveat: Unfortunately, the informal terms “IS A” and “HAS A” can be seriously misleading (not to say confusing). For example, consider employees and programmers. In natural language, we might very reasonably say that every programmer “is a” employee, suggesting rather strongly that what we have here is an example of “the IS A relationship.” But it isn’t; rather, programmers “have a” property, say language skill, that employees in general don’t have—a property, what’s more, that can’t be derived in any way from the properties that employees in general do have. So the crucial issue here isn’t the IS A relationship but, rather, the HAS A relationship; that is, it’s not the case that a programmer “is a” employee—rather, it’s the case that a programmer “has a” language skill. Contrast the situation with, e.g., ellipses and circles: Although we might say, informally, that a circle “has a” property (the radius length) that ellipses in general don’t have, that property is really just a degenerate form of a property (a semiaxis length) that ellipses in general do have. By contrast, to say it again, a programmer’s language skill doesn’t correspond to any property of employees in general. Note in particular, therefore, that—as a direct consequence of the foregoing point—S by C doesn’t apply: There’s no constraint, expressible purely in terms of employee properties as such, that an employee can and must satisfy in order to be a programmer.
immediate subtype Type T′′ is an immediate subtype of type T if and only if (a) it’s a proper subtype of T and (b) there’s no type T′ that’s both a proper supertype of T′′ and a proper subtype of T. See also immediate supertype.
Examples: 1. With reference to Fig. 2, CIRCLE is an immediate subtype of ELLIPSE, and ELLIPSE is an immediate subtype of PLANE_FIGURE (CIRCLE is a subtype of PLANE_FIGURE too, but not an immediate one). 2. With reference to Fig. 3, SQUARE is an immediate subtype of RECTANGLE and RHOMBUS, each of which is an immediate subtype of PARALLELOGRAM. 3. With reference to Fig. 5, relation type CS is an immediate subtype of relation types CR and ES, each of which is an immediate subtype of relation type ER.
immediate supertype Type T is an immediate supertype of type T′′ if and only if (a) it’s a proper supertype of T′′ and (b) there’s no type T′ that’s both a proper subtype of T and a proper supertype of T′′. See also immediate subtype.
Examples: 1. With reference to Fig. 2, PLANE_FIGURE is an immediate supertype of ELLIPSE, and ELLIPSE is an immediate supertype of CIRCLE (PLANE_FIGURE is a supertype of CIRCLE too, but not an immediate one). 2. With reference to Fig. 3, PARALLELOGRAM is an immediate supertype of RECTANGLE and RHOMBUS, each of which is an immediate supertype of SQUARE. 3. With reference to Fig. 5, relation type ER is an immediate supertype of relation types CR and ES, each of which is an immediate supertype of relation type CS.
implementation version Let scalar type T be a proper supertype of scalar type T′, and let PR and PR′ be possreps for T and T′, respectively, such that PR ≠ PR′. Further, let Op be a read-only operator that applies to values of type T and hence, by definition, to values of type T′ also (read-only just to be definite; the discussion that follows pertains to update operators too, mutatis mutandis). Then it’s at least possible for Op to have two distinct implementation versions, one implemented in terms of PR, which works for values of type T (and therefore, necessarily, for values of type T′ also—see possrep inheritance), and the other in terms of PR′, which works for values of type T′ only. To illustrate:
Let types T and T′ be ELLIPSE and CIRCLE, respectively, and let AREA_OF be an operator that takes an ellipse as input and returns the corresponding area as output. For type ELLIPSE, the sole declared possrep consists of a, b, and the center (where a and b are the lengths of the semiaxes); for type CIRCLE, the sole declared possrep consists of r and the center (where r is the length of the radius). The area of an ellipse is πab. But if the ellipse happens to be a circle, the semiaxes degenerate to the radius, the formula degenerates to πr², and so the code that implements AREA_OF for ellipses in general will still work if the ellipse is in fact a circle.
For a counterexample, let types T and T′ be POLYGON and RECTANGLE, respectively, and assume now that the operator AREA_OF is defined for polygons. The algorithm (based on integral calculus) that computes the area of a general polygon will certainly work for a rectangle; for rectangles, however, a much more efficient algorithm—viz., multiply the height by the width—is available. At least for performance reasons, therefore, it might be desirable to have two implementation versions of the operator, thus (in outline only, but note the VERSION specifications in particular):
OPERATOR AREA_OF VERSION P_AREA ( P POLYGON ) RETURNS AREA ;
RETURN ... ;
END OPERATOR ;
OPERATOR AREA_OF VERSION R_AREA ( R RECTANGLE ) RETURNS AREA ;
RETURN ... ;
END OPERATOR ;
The net of the foregoing discussion is that what appears to be a single operator above the covers can have any number n (n > 0) of implementation versions—versions for short—under the covers. (We note in passing that each such version might be regarded as having its own version signature, but version signatures are purely an implementation concern, not part of the model as such.) Of course, it makes no difference to the user how many implementation versions exist; in the case of AREA_OF, for example, the user knows the operator works for, say, ellipses, and therefore it works for circles too, by definition, because circles are ellipses (see inclusion polymorphism).
So what are the consequences? Consider the following example. Suppose with reference to Fig. 2 that some program needs to display some diagram, made up of squares, circles, ellipses, etc. Without support for implementation versions, the code for this task will look something like this:
FOR EACH x ∊ DIAGRAM
CASE ;
WHEN IS_SQUARE ( x ) THEN DISPLAY_SQUARE ... ;
WHEN IS_CIRCLE ( x ) THEN DISPLAY_CIRCLE ... ;
WHEN ............................................ ;
END CASE ;
With such support, by contrast, the code is much simpler:
FOR EACH x ∊ DIAGRAM DISPLAY ( x ) ;
Note: The argument expressions to the various DISPLAY operator invocations in the first version of this code are omitted in order to avoid distracting irrelevancies. For the record, however, in the case of DISPLAY_SQUARE that argument expression will probably take the form TREAT_AS_SQUARE (x) (see TREAT), and of course the other cases are analogous.
Explanation: DISPLAY in the second version of the code is a polymorphic operator, defined—let’s assume for the sake of the example—for type PLANE_FIGURE (i.e., the sole parameter to that operator is of declared type PLANE_FIGURE). SQUARE, CIRCLE, etc., are all subtypes of that type, of course. Now, if it turns out to be desirable, for some given subtype, to define a specific version of that operator for values of the subtype in question, then that version will typically be defined when that subtype is defined. Then, at run time, when the system encounters the DISPLAY invocation with argument x, it will determine the implementation version that’s appropriate to the type of x—i.e., MST(x)—and will invoke that version. (See run time binding. Note, however, that it’s at least theoretically possible to do the binding at compile time. See further discussion of this possibility below.) Thus, inclusion polymorphism effectively leads to certain CASE expressions and CASE statements that would otherwise have had to appear in the user’s source code being moved under the covers: in effect, being performed by the system on the user’s behalf.
Observe now the implications of the foregoing for program maintenance. Suppose a new type TRIANGLE is defined (another subtype of PLANE_FIGURE, and in fact an immediate subtype of POLYGON) and a corresponding new implementation version of DISPLAY is defined as well. Without support for implementation versions, it would be necessary to examine every source program to see whether any CASE expression or statement needed to be modified to include the following:
WHEN IS_TRIANGLE ( x ) THEN DISPLAY_TRIANGLE ... ;
With such support, however, no such modifications will be needed.
Because of examples like the foregoing, inclusion polymorphism is sometimes characterized, a little colorfully, as meaning that “old code can invoke new code”; that is, a program P can effectively invoke some version of an operator Op that didn’t exist—the version, that is—when P was written. Thus, we have, at least potentially, what’s called code reuse, q.v.: The very same program P might be usable on data of a type that wasn’t defined when P was written. (Certainly the code of program P is being reused here. The code that implements operator Op under the covers might or might not be; for example, the code that implements the AREA_OF operator for polygons might or might not be reused for rectangles, as previously discussed.)
Unfortunately, there’s a fly in the ointment. To be specific, there can be no guarantee that the various implementation versions of a given operator all implement the same semantics. If they don’t, then we don’t have true inclusion polymorphism any more, we have overloading polymorphism instead; such a state of affairs constitutes a violation of the model (the Manifesto model, that is), and the consequences are unpredictable. Regrettably, however, the requirement that all versions of a given operator do implement the same semantics is unenforceable. What’s more, some writers even claim, in effect, that the ability to change semantics is desirable! To quote The Object Data Standard: ODMG 3.0 (R. G. G. Cattell and Douglas K. Barry, eds.; Morgan Kaufmann, 2000):
For example, the Employee type might have an operation for calculate_paycheck. The Salaried_Employee and Hourly_Employee class implementations might each refine that behavior to reflect their specialized needs.
(Refine that behavior here means, precisely, changing the semantics. Note, however, that there does seem to be a tacit assumption in the example that the “subtypes” in question aren’t true subtypes as such but rather are “derived types.” See extends relationship for further explanation.)
To return to ellipses and circles for a moment, observe now that the ellipse AREA_OF code will definitely not work for circles if it’s written in terms of a physical representation instead of a possible one, and the physical representations for types ELLIPSE and CIRCLE differ. The practice of implementing operators in terms of physical representations is thus clearly contraindicated. As a general rule, in fact, the only code that accesses physical representations at all should be the code that implements (a) selectors, (b) THE_ operators, and (c) IS_T operators (see privileged operator in Part I of this dictionary). Note that most if not all of this implementation code will probably be provided by the system anyway.
Finally (and just to spell the point out), again let scalar type T be a proper supertype of scalar type T′, and let PR and PR′ be possreps for T and T′, respectively (PR ≠ PR′). Let Op be a read-only operator that applies to values of type T and hence, by definition, to values of type T′ also. Finally, let OpV and OpV′ be versions of Op that apply to values of type T and values of type T′, respectively, where OpV is implemented in terms of PR and OpV′ is implemented in terms of PR′. By definition, then, PR is an “inherited possrep” (see possrep inheritance) for type T′. As previously indicated, then, OpV will always at least work—perhaps not as efficiently as OpV′ does—for values of type T′; hence, compile time binding should always work too, and run time binding is logically unnecessary, though it might be desirable for performance reasons. Of course, this argument does assume (a) that implementation versions are written in terms of possreps, not physical representations, and (b) that distinct versions of the same operator do implement the same semantics.
inclusion polymorphism By definition (see type inheritance), any read-only operator that applies to values of a given type T necessarily applies to values of every proper subtype T′ of T. Such an operator is thus polymorphic, and the kind of polymorphism it exhibits is called inclusion polymorphism, on the grounds that the relationship between T and T′ is that of set inclusion (because the set of values constituting type T is a superset—in general a proper superset—of the set of values constituting type T′). Note that this kind of polymorphism is a logical consequence of the very notion of type inheritance. Contrast overloading. Note: An update operator that applies to variables of type T might or might not apply to variables of some proper subtype T′ of T (see Principle of Variable Substitutability). If it does, then it too is said to exhibit inclusion polymorphism.
Example: With reference to Fig. 2, let AREA_OF (“return the area of”) be an operator that applies to values of type RECTANGLE. Then AREA_OF also applies to values of type SQUARE, necessarily, because squares are rectangles. See also the examples under argument.
inherited possrep See possrep inheritance.
INSERT ONLY Let T′ be a subtable of supertable T (see subtables and supertables). Then INSERT ONLY is an operator—not supported by SQL, incidentally, even though SQL does support subtables and supertables as such—that inserts a row into T′ without simultaneously inserting a corresponding row into T.
Example: With reference to the example under subtables and supertables, it should be possible to use INSERT ONLY to insert a row into table PGMR without at the same time inserting a corresponding row into table EMP, to reflect the fact that some existing employee has become a programmer.
instantiable type Term sometimes used in OO contexts to mean a type that’s not a union type. The name presumably derives from the fact that such a type has “instances,” where the term “instances” presumably means—at least in this context—values whose most specific type is the type in question; it has nothing to do with instance variables, q.v., nor with instantiation in the sense of logic (see Part I of this dictionary). Note, however, that elsewhere in those same OO contexts that same term instance is certainly taken to include variables, etc., as well as values as such; in fact, it’s often used a synonym for object. Contrast noninstantiable type.
interface (With inheritance) Term used in some OO systems to mean a union type (possibly a dummy type). Note: Such systems typically refer to nonunion types simply as types, implying, tacitly, that union types (“interfaces”) aren’t considered to be types at all. This somewhat idiosyncratic use of both terms (i.e., type and interface) is deprecated accordingly.
intersection (With inheritance) See dyadic relational operators.
intersection subtype Same as intersection type.
intersection type Same as least specific common subtype. The term intersection type is perhaps to be preferred, at least in informal contexts, because it’s intuitively easier to understand. (On the other hand, it does carry with it an implicit suggestion that union type might be just another term for most specific common supertype, which is incorrect. Why? Because if T is the most specific common supertype of types T1, T2, ..., Tm, then it might legitimately contain a value that’s not a value of any of types T1, T2, ..., Tm—in which case it isn’t the union, as such, of those types T1, T2, ..., Tm, but is, rather, a proper superset of that union. See most specific common supertype.)
invocation signature (With inheritance) See signature.
IS The Tutorial D construct that defines some (scalar) subtype / supertype relationship; more specifically, the construct that defines some scalar type T′ to be an immediate subtype of another scalar type T (single inheritance) or an immediate subtype of two or more other scalar types T1, T2, ..., Tm (multiple inheritance). There are thus two basic cases to consider. The first case (single inheritance) subdivides into two further cases, one in which the immediate supertype is a dummy type and one in which it’s a regular type. For example, with reference to Fig. 2, let PLANE_FIGURE be a dummy type; then the definitions for types ELLIPSE and CIRCLE illustrate both of these two “further cases.” First, type ELLIPSE:
TYPE ELLIPSE
IS { PLANE_FIGURE
POSSREP { A LENGTH , B LENGTH , CTR POINT
CONSTRAINT A ≥ B } } ;
The IS specification here defines a value e to be of type ELLIPSE if and only if it conforms to the indicated POSSREP specification (including the constraint a ≥ b). It also defines—by fiat, as it were—such values to be of type PLANE_FIGURE as well as type ELLIPSE (i.e., if e does conform to the indicated POSSREP specification, then IS_PLANE_FIGURE(e) evaluates to TRUE).
Now here’s the definition for type CIRCLE (in outline):
TYPE CIRCLE
IS { ELLIPSE
CONSTRAINT THE_A ( ELLIPSE ) = THE_B ( ELLIPSE )
POSSREP { ... } } ;
Here the IS specification defines both (a) a specialization constraint, q.v., which in turn defines a value c to be of type CIRCLE if and only if IS_ELLIPSE(c) and THE_A(c) = THE_B(c) both evaluate to TRUE, and (b) a derived possrep, q.v.—details omitted here for simplicity—for type CIRCLE in terms of (some possrep for) its sole immediate supertype ELLIPSE.
The other case (multiple inheritance), in which type T′ has m immediate supertypes T1, T2, ..., Tm (m > 1), is straightforward: The IS specification simply names those supertypes and—if and only if T′ is a regular type—defines at least one derived possrep, q.v., for that type T′. With reference to Fig. 3, for example, the definition for type SQUARE might look like this (in outline):
TYPE SQUARE
IS { RECTANGLE , RHOMBUS
POSSREP { ... } } ;
The specialization constraint here (q.v.) defines a value s to be of type SQUARE if and only if IS_RECTANGLE(s) and IS_RHOMBUS(s) both evaluate to TRUE. No additional CONSTRAINT specification is stated, or indeed permitted (because a rectangle is a square if and only if it’s a rhombus, and a rhombus is a square if and only if it’s a rectangle). The POSSREP specification—details again omitted for simplicity—defines a derived possrep for type SQUARE in terms of some possrep for one of its immediate supertypes (viz., either RECTANGLE or RHOMBUS, in the case at hand).
IS A The subtype / supertype relationship; i.e., the relationship between a subtype T′ and any (usually proper) supertype T of T′. For example, every circle “is a” ellipse, and “is a” plane figure as well. As noted elsewhere in this dictionary, the IS A relationship leads directly to inclusion polymorphism, q.v., and value substitutability, q.v. Contrast HAS A.
IS_SAME_TYPE_AS See IS_T.
IS_T Let exp be a scalar expression, let T be a scalar type, and let DT(exp) and T overlap (this is a compile time check). Then the “type testing” expression IS_T (exp)—or some logical equivalent to that expression—returns TRUE if and only if v(exp) is of type T (equivalently, if and only if MST(exp) is some subtype of T).
Tutorial D additionally supports a generalized version of this operator, of the form IS_SAME_TYPE_AS (exp1,exp2), where the expressions exp1 and exp2 aren’t limited to being scalar. This generalized version is effectively equivalent to the expression IS_T1 (exp2), where T1 is DT(exp1)—assuming for definitional purposes here that the expression IS_T1 (exp2) is syntactically valid—and thus returns TRUE if and only if MST(exp2) is some subtype of DT(exp1).
Note: It might be desirable to support negated forms of these operators, too—IS_NOT_T (exp) and IS_NOT_SAME_TYPE_AS (exp1,exp2)—with the obvious semantics.
Examples: 1. With reference to Fig. 2, let E be a variable of declared type and current most specific type both ELLIPSE; then IS_PLANE_FIGURE (E) and IS_ELLIPSE (E) both return TRUE and IS_CIRCLE (E) returns FALSE. 2. With reference to Fig. 3, let RE be a variable of declared type RECTANGLE and current most specific type SQUARE; then IS_SQUARE (RE), IS_RECTANGLE (RE), IS_RHOMBUS (RE), and IS_PARALLELOGRAM (RE) all return TRUE. 3. With reference to Fig. 5, let ERV be a relvar of declared type ER and current most specific type CS, and let ESV be a relvar of declared type and most specific type both ES; then IS_SAME_TYPE_AS (ERV,ESV) returns TRUE.
join (With inheritance) See dyadic relational operators.
joinable (With inheritance) 1. (Dyadic case) Relations r1 and r2 are joinable if and only if attributes with the same name are such that their types have a common supertype (i.e., those types belong to the same type lattice, q.v.). 2. (N-adic case) Relations r1, r2, ..., rn (n ≥ 0) are joinable—sometimes n-way joinable, for emphasis—if and only if for all i and j, relations ri and rj are joinable (1 ≤ i ≤ n, 1 ≤ j ≤ n).
late binding Run time binding, q.v.
lattice Let s be a set, and let a partial ordering be defined on s. Then the combination of s and that partial ordering is a lattice if and only if every two elements of the set have both a least upper bound, q.v., and a greatest lower bound, q.v., with respect to that ordering. Note: It follows from this definition that a set of cardinality either one or zero can always be regarded as a lattice.
Examples: See the examples under type lattice.
leaf Abbreviation for leaf type.
leaf type A type with no immediate subtype other than the pertinent minimal type, q.v.
Examples: 1. In Fig. 2, CIRCLE and SQUARE are leaf types. What’s more, they’re disjoint (see further discussion below). 2. In Figs. 3 and 4, SQUARE is the only leaf type. 3. In Fig. 5, type CS is the only leaf type.
Note: Let T1 and T2 be distinct leaf types from the same type lattice, q.v. If those types are scalar or tuple types, they’re certainly disjoint; by contrast, if they’re relation types, they’re not disjoint. With reference to Fig. 2, for instance, let T1 and T2 be the relation types RELATION {PF CIRCLE} and RELATION {PF SQUARE}, respectively. Then T1 and T2 overlap because they both contain the (empty) relation RELATION {PF omega} { }. In fact, every type in that same type lattice—even the minimal type RELATION {PF omega}—contains that same empty relation as a value.
least specific common subtype Let T1, T2, ..., Tm (m ≥ 0) be types from the same type lattice, q.v. Then type T′ is the least specific common subtype for types T1, T2, ..., Tm if and only if it’s a common subtype (q.v.) for those types and no proper supertype of T′ is also a common subtype for those types. Note: It can be shown—see the Manifesto book—that, given types T1, T2, ..., Tm, the corresponding least specific common subtype T′ always exists and is unique (though it might be one of those specified types T1, T2, ..., Tm, or even the pertinent minimal type, q.v.); in fact, it’s the greatest lower bound, q.v., of types T1, T2, ..., Tm. It can also be shown—again, see the Manifesto book—that whenever a value is of each of types T1, T2, ..., Tm, it’s also of type T′ (hence the alternative, and sometimes preferred, names intersection type and intersection subtype). Note too that (a) if m = 1, then the set of types T1, T2, ..., Tm reduces to just T1, and T1 itself is the least specific common subtype for that set; (b) if m = 0, then the set of types T1, T2, ..., Tm is empty, and the least specific common subtype is the pertinent maximal type. Contrast least specific common supertype; most specific common subtype; most specific common supertype.
Examples: 1. With reference to Fig. 2, the least specific common subtype for types PLANE_FIGURE, POLYGON, and RECTANGLE is RECTANGLE, and the least specific common subtype for ELLIPSE and SQUARE is omega. 2. With reference to Fig. 3, the least specific common subtype for types RECTANGLE and RHOMBUS is SQUARE. 3. With reference to Fig. 4, the least specific common subtype for types KITE and CYCLIC QUADRILATERAL is RIGHT KITE. Note that SQUARE is also a common subtype in this example, but it’s not the least specific one (i.e., it’s not the intersection type as such).
Note: Of course, it’s always possible that the type designer could make a mistake and omit the definition of some intersection type that’s logically required. For example, with reference to Fig. 3, the designer might specify types RECTANGLE and RHOMBUS as immediate subtypes of type PARALLELOGRAM and forget that some parallelograms are both a rectangle and a rhombus. The consequences of such violations (violations of the prescriptions of the model, that is) will be unpredictable, in general. Although this fact is of no concern from the point of view of the model—a violation is simply a violation, and there’s no need as far as the model is concerned to spell out what the consequences might be—in practice it’s to be hoped that some kind of mechanical aid would be available to help avoid such errors.
least specific common subtype (relation types) Let T1, T2, ..., Tm (m ≥ 0) be relation types from the same type lattice, q.v.; by definition, then, those types all have the same attribute names, say A1, A2, ..., An (n ≥ 0). Let the type of attribute Aj (j = 1, 2, ..., n) within type Ti (i = 1, 2, ..., m) be Tij. Then type T′ = RELATION {<A1,T01′>,<A2,T02′>,...,<An,T0n′>} is the least specific common subtype for types T1, T2, ..., Tm if and only if, for all j (j = 1, 2, ..., n), type T0j′ is the least specific common subtype for types T1j, T2j, ..., Tmj. See also least specific common subtype; contrast least specific common supertype (relation types); most specific common subtype (relation types); most specific common supertype (relation types).
Example: With reference to Fig. 5, the least specific common subtype for relation types CR and ES is relation type CS.
least specific common subtype (tuple types) Let T1, T2, ..., Tm (m ≥ 0) be tuple types from the same type lattice, q.v.; by definition, then, those types all have the same attribute names, say A1, A2, ..., An (n ≥ 0). Let the type of attribute Aj (j = 1, 2, ..., n) within type Ti (i = 1, 2, ..., m) be Tij. Then type T′ = TUPLE {<A1,T01′>,<A2,T02′>,...,<An,T0n′>} is the least specific common subtype for types T1, T2, ..., Tm if and only if, for all j (j = 1, 2, ..., n), type T0j′ is the least specific common subtype for types T1j, T2j, ..., Tmj. See also least specific common subtype; contrast least specific common supertype (tuple types); most specific common subtype (tuple types); most specific common supertype (tuple types).
Example: With reference to Fig. 5, the least specific common subtype for tuple types ER and ES is tuple type ES.
least specific common supertype Let T1, T2, ..., Tm (m ≥ 0) be types from the same type lattice, q.v. Then type T is the least specific common supertype for types T1, T2, ..., Tm if and only if it’s the maximal type with respect to the type lattice in question. Note: Informally, least specific common supertypes are sometimes defined to exclude the pertinent maximal type, in which case the term is taken to apply to the pertinent root type. With reference to Fig. 4, for example, the least specific common supertype for types RECTANGLE and RHOMBUS is either type alpha, q.v., or (if maximal types are excluded) type QUADRILATERAL. Contrast least specific common subtype; most specific common subtype; most specific common supertype.
least specific common supertype (relation types) See least specific common supertype.
least specific common supertype (tuple types) See least specific common supertype.
least specific type Let value x be of type T and not of any proper supertype of T; then T is the least specific type of x. Note that T is necessarily a maximal type (and is thus unique). Further, let exp be an expression. Then exp has the same least specific type as the value it denotes. Note: Informally, least specific types are sometimes defined to exclude the pertinent maximal type, thus: Let x be of type T and not of any proper supertype of T (apart from the pertinent maximal type, q.v.); then T—which is necessarily a root type and is thus unique—is the least specific type of x. Contrast most specific type.
Examples: 1. Let x be a value of any of the types shown in Fig. 2. Then the least specific type of x is either alpha or (if maximal types are excluded) PLANE_FIGURE. 2. Let x be a relation of any of the types shown in Fig. 5. Then the least specific type of x is RELATION {E alpha, R alpha} or (if maximal types are excluded) type ER = RELATION {E ELLIPSE, R RECTANGLE}. 3. The least specific type of the sole tuple of type TUPLE { }—viz., the 0-tuple—is TUPLE { } itself. 4. The least specific type of any relation—necessarily either TABLE_DUM or TABLE_DEE—of type RELATION { } is RELATION { } itself.
least specific type (relation types) See least specific type.
