
4.2. INFORMATION FROM THE DERIVATIVE 147
where n is a positive whole number including the way the function approaches the asymptotes.
Hint: there are two outcomes.
Problem 4.21 If f .x/ and g.x/ are both polynomials, what is the largest number of horizontal
asymptotes that
h.x/ D
f .x/
g.x/
can have? Explain your answer carefully.
Problem 4.22 Find the number of horizontal asymptotes of
f .x/ D
ˇ
ˇ
x
3
ˇ
ˇ
x
3
C 1
4.2 INFORMATION FROM THE DERIVATIVE
ere are two sorts of useful information for sketching a curve that we can pull out of the
derivatives of a function. We can compute where it is increasing and decreasing, and we can
compute where it is curved up (concave up) or curved down (concave down).
4.2.1 INCREASING AND DECREASING RANGES
Remember that a derivative is a rate of change. is means that when f
0
.x/ > 0 in a range,
the function is increasing in that range, and when f
0
.x/ < 0 the function is decreasing in that
range. Let’s nail down exactly what it means to be increasing or decreasing on a range.
Definition 4.5 A function is increasing on an interval if, for each u < v in the interval f .u/ <
f .v/.
Definition 4.6 A function is decreasing on an interval if, for each u < v in the interval f .u/ >
f .v/.
Now we are ready for the derivative-based rules on when a function is increasing or decreasing.
148 4. CURVE SKETCHING
Knowledge Box 4.6
Derivative-based function rules
• A function f .x/ is increasing where f
0
.x/ > 0
• A function f .x/ is decreasing where f
0
.x/ < 0
• ose x D c where f
0
.c/ D 0 are called critical values
• e points .c; f .c// where f
0
.c/ D 0 are called critical points
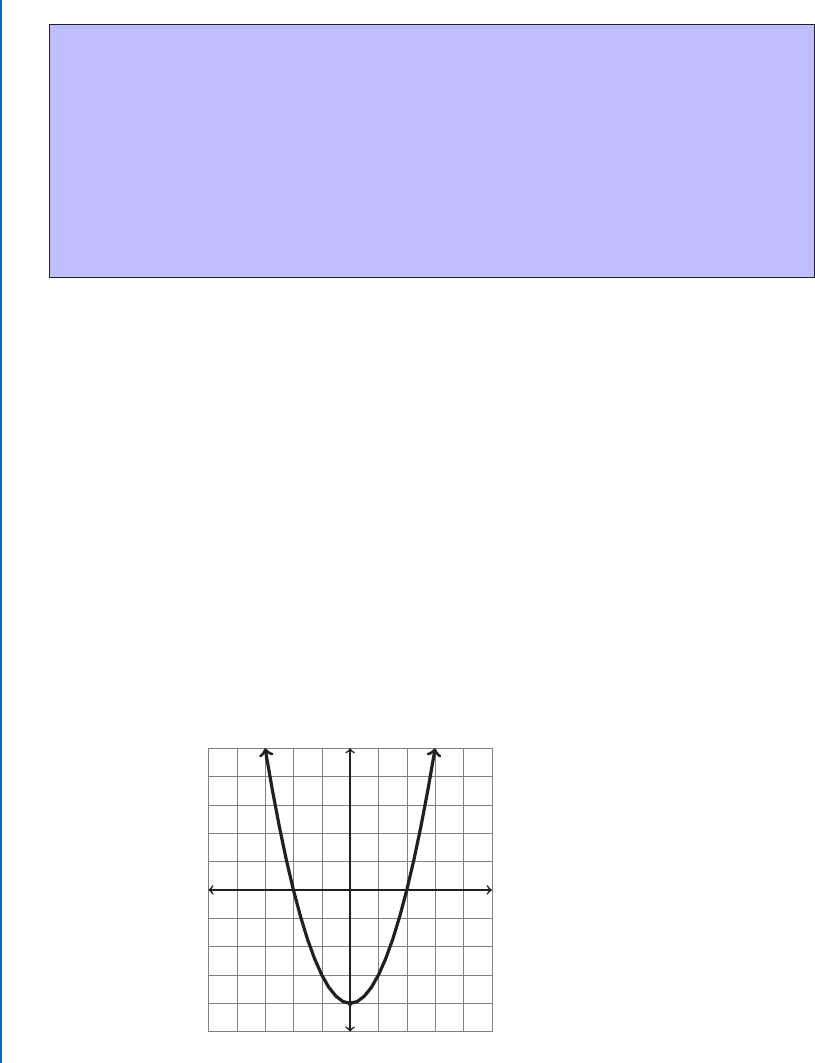
Example 4.23 Find the critical point(s) and increasing and decreasing ranges for
f .x/ D x
2
4:
Solution:
We see f
0
.x/ D 2x. Solving 2x D 0 we get that x D 0 is the only critical value. So the critical
point is .0; 4/.
Solving 2x < 0 we see f
0
.x/ < 0 on .1; 0/; similarly f
0
.x/ > 0 on .0; 1/.
e following graph permits us to check all this against the actual behavior of the func-
tion.
f
0
.x/
- - - - -
0
+ + + + +
f .x/ D x
2
4
Critical point: (0,-4)
Decreasing: .1; 0/
Increasing: .0; 1/
5
-5
-5 5

4.2. INFORMATION FROM THE DERIVATIVE 149
Notice that we have a row of +, -, 0 symbols across the top of the graph: these show the sign of
f
0
.x/ and are handy for analysis of increasing and decreasing ranges, as we will see in a minute.
˙
Example 4.24 Find the critical point(s) and increasing and decreasing ranges for
f .x/ D x
3
4x:
Solution:
Finding the increasing and decreasing ranges requires that we first find the critical values, where
f
0
.c/ D 0.
f
0
.x/ D 3x
2
4
3x
2
4 D 0
3x
2
D 4
x
2
D
4
3
x D ˙
2
p
3
e derivative can only change between positive and negative at c D ˙
2
p
3
, so we plug in values
in each of the resulting ranges. e value c D
2
p
3
is a little larger than one, so let’s look at 2
and 2. We can make a table of values.
x f
0
.x/ ˙
1 na na
2 8 > 0 +
2
p
3
0 0
0 4 < 0 -
2
p
3
0 0
2 8 > 0 +
1 na na
So, the function is:
Increasing on: .1;
2
p
3
/ [ .
2
p
3
; 1/
Decreasing on: .
2
p
3
;
2
p
3
/
with critical points at
˙
2
p
3
;
16
3
p
3

150 4. CURVE SKETCHING
Notice that the use of means that the sign of the second coordinate of the critical points is
the opposite of the sign of the first. We also usually use a much more compact form for the table
of signs given above:
f
0
.x/ W .1/ C C C
2
p
3
2
p
3
C C C .1/
Numbers inserted into the chain of “+” and “” symbols represent critical points. is device is
called a sign chart for increasing and decreasing ranges. Below is a picture of the function with
the features we just located shown. e critical points are plotted.
f .x/ D x
3
4x
Critical point: (
˙2
p
3
,
16
3
p
3
)
Increasing: .1;
2
p
3
/ [ .
2
p
3
; 1/
Decreasing: .
2
p
3
;
2
p
3
/
5
-5
-3 3
˙
An alert reader will have noticed that we carefully avoided, so far in this section, examples involv-
ing asymptotes. e reason for this is that they can influence the increasing/decreasing ranges
as well.
Knowledge Box 4.7
A continuous, differentiable function can only change between increasing and de-
creasing at a critical value or at a vertical asymptote.

4.2. INFORMATION FROM THE DERIVATIVE 151
is means that we include the position of vertical asymptotes along with critical values on the
sign chart for finding increasing and decreasing ranges for a function.
Example 4.25 Find the critical points, vertical asymptotes, and increasing and decreasing
ranges for
f .x/ D
x
2
1
x
2
4
Solution:
e vertical asymptotes are easy: x
2
4 D 0 at x D ˙2. e critical points require us to solve
f
0
.x/ D 0, which gives us:
.x
2
1/.2x/ .x
2
4/.2x/
.
x
2
4
/
2
D 0
.x
2
1/.2x/ .x
2
4/.2x/ D 0
2x
3
2x 2x
3
C 8x D 0
6x D 0
x D 0
So there is a critical value at x D 0 and a critical point at .0;
1
4
/. Remember that a fraction is zero
only where its numerator is zero. Let’s make the sign chart with the critical values and vertical
asymptotes. We can plug in any value in an interval to get the ˙ value for f
0
.x/:
.1/ C C C .2/ C C C .0/ .2/ .1/
f .x/ D
x
2
1
x
2
4
Critical point: (0, 1/4)
Increasing: .1; 2/ [ .2; 0/
Decreasing: .0; 2/ [ .2; 1/
5
-5
-5 5
x D 2x D 2
x D 1
x D 1
..................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.
