The police break down your door and hustle you downtown for interrogation. Seems you’ve been using illicit cryptography to exchange information about—well, they’re not exactly sure, because you used cryptography, but they know it must be sinister because you used cryptography. And they know who you were talking to; their packet sniffers (and subpoenaed router logs) revealed that you were communicating with your friend a few miles away. They’ve arrested him too.
You’re going to jail. The question is, for how long?
The police don’t have enough evidence to convict you of the new crime, Encoding In The First Degree, carrying a penalty of five years in jail. But they can convict you of Second Degree Encoding, and that’s two long years in the overcrowded Minimum Security Federal Penitentiary for Computer Abusers.
They offer you a deal: if you agree to confess, and testify against your friend, they’ll let you go free. They offer your friend the same deal. But if you both decide to testify against one another, you each get four years in jail. You must both decide what to do in solitude, without communicating. (That’s why they split you up.)
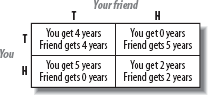
You can either Testify (T) or Hold Out (H), and your friend can do the same. The outcomes are shown in the payoff matrix depicted in Figure 28-1.
What should you do? You might think to yourself:
If I testify, I’ll get either four years or zero years. And if I hold out, I’ll get either five years or two years. I have no idea what my friend will do, and I can’t talk to him. Maybe I should assume that he’ll choose at random, in which case I’m better off testifying.
If your friend thinks the same way, you’ll both testify and get four years each. That’s unfortunate, since the outcome with the fewest number of man-years in jail occurs when you both hold out.
This problem is called the Prisoner’s Dilemma, and it’s the foundation for the mathematical discipline of game theory. It’s been used to represent scenarios in gambling, genetics, business, and thermonuclear war, by using different payoffs: money, offspring, more money, and death.
There’s not a whole lot to say about the one-shot Prisoner’s Dilemma: either you should testify or you shouldn’t, and you can construct compelling arguments for both decisions.
Here’s when things get interesting: forget about the prison terms and think of the payoff matrix as abstract “points.” Now pit you and your friend against one another in a series of matches, say 100. Your goal is to minimize the number of points you accrue during the 100 matches. This is the Iterated Prisoner’s Dilemma.
Now there’s a little bit of communication between you and your friend: for any given match, you can consider all of the previous matches before making your decision. If your friend held out on all the previous matches, you might think that he’ll remain consistent, and hold out again. But maybe that’s just what he wants you to think, so that he can testify, adding five points to your score and none to his. (Remember, he’s a criminal too!)
Here’s a simple always-hold-out strategy:
sub nice_guy {
return "H";
}Here’s a strategy that chooses at random:
sub random {
return "H" if rand() < 0.5;
return "T";
}Here’s parting_shot, which
holds out on the first 99 matches, and testifies on the last (100th)
match. The history of your choices is stored in the array reference
$my_choices_ref (which becomes the
array @my_choices). parting_shot uses that array only to
determine when the 100th match has been reached.
sub parting_shot {
my ($my_ref, $friend_ref) = @_;
my (@my_choices) = @$my_ref;
if (@my_choices == 99) {
return "T"
} else { return "H" }
}Here’s a strategy called tit-for-tat, which holds out on the first
match, and then chooses whatever the friend chose on the previous
match:
sub tit_for_tat {
my ($my_ref, $friend_ref) = @_;
my (@friend_choices) = @$friend_ref;
return "H" unless @friend_choices;
return $friend_choices[$#friend_choices];
}Tit-for-tat variants usually perform well in Prisoner’s Dilemma contests. Random strategies aren’t so bad either. Of course, that all depends on which other strategies participate. There’s no single best strategy—just the best strategy for a given match.
Let’s add another level of complexity: a three-person Prisoner’s Dilemma, in which three strategies compete simultaneously. The payoff matrix (actually a payoff cube) is shown in Figure 28-2.
When one person testifies and the other two hold out, the fink gets off scot-free, and the holdouts get five years each. When two people testify, they get one year each, and the holdout gets seven.
As before, the only communication between the prisoners is through their actions on previous matches. Here’s a sample strategy for a three-way contest:
# Testify only if both friends testified
# during the last match.
sub fool_me_twice {
my ($my_ref, $friend1_ref, $friend2_ref) = @_;
my (@friend1_choices) = @$friend1_ref;
my (@friend2_choices) = @$friend2_ref;
if ($friend1_choices[$#friend1_choices] eq "T" &&
$friend2_choices[$#friend2_choices] eq "T") {
return "T";
} else { return "H" }
}We invite you to design your own three-way strategy, to be pitted against the rest of the Perl community.
Every strategy should be a single subroutine. During a match,
the subroutine will be passed three array references (as with fool_me_twice above): the first will contain
an array of your past decisions, and the second and third will contain
the decision arrays for friend1 and
friend2 respectively. Here are the
rules:
Your subroutine must always return either
HorT.Your subroutine will play every other subroutine at least once, in a series of exactly 100 matches.
The winning strategy will be the one with the lowest cumulative score over all matches.
Your entry must have comments before the subroutine with your name, email address, and a truthful explanation of the strategy.
The random number generator will be initialized before every series of 100 matches, should you care to use it.
One entry per person.
Good luck!
Each strategy, encoded as a single Perl subroutine, was pitted against every other pair of strategies in a “duel” of exactly 100 matches. The distinction between a duel and a match is important, since in a series of matches each strategy can observe the others and decide how to act based on their past behavior.
A total of 31 strategies were submitted, yielding:
duels, or about 450,000 matches, in which each strategy returned
a single letter: either an H to
Hold out (or cooperate, in game theory parlance) or a T to Testify (or defect).
This particular contest was inspired by Profs. Mitch Resnick and Mike Eisenberg, who in 1987 conducted a three-way Prisoner’s Dilemma contest at MIT. I entered that contest (in which the strategies were Scheme functions instead of Perl subroutines), noticed that the four contest rules didn’t prohibit functions that modified their inputs, and wrote a revisionist function that changed its opponents’ histories, yielding the highest possible score by tampering with the past. I was disqualified, and a fifth rule excluding such strategies was added the next year.
I’ve been seething over this for a decade, and wanted some moral validation for what I thought was a clever insight. That’s why I left the door wide open for similar strategies in this contest: there was nothing prohibiting subroutines from poking around the filesystem or the symbol table to locate, dissect, or modify other strategies, or even the judging program itself.
A few hackers, notably Felix Gallo and Randal Schwartz, spotted these possibilities, but no one actually submitted such an entry. (I don’t know whether this was because of a lack of time or a surplus of scruples.) Felix also pointed out another devious tactic: collude with other contestants so that their strategies could recognize one another by their behavior. Then a previously-elected “master” could defect while the other “slaves” all cooperated, sacrificing themselves for the good of the master.
That’s exactly what Ken Albanowski, Earle Ake, and Dan Wisehart did: their three gestalt entries identify whenever Ken’s
strategy is playing one of the other two. If so, the slave holds out
while the master testifies, resulting in a bad score for Earle or Dan
but a good score for Ken. It worked: Ken’s strategy finished first,
and martyrs Earle and Dan finished 27th and 28th.
The top ten, along with the number of years their strategy spent in jail, are shown in Table 28-1.
Table 28-1. Top ten finalists in the Prisoner’s Dilemma
Years spent in jail | |
|---|---|
Kenneth Albanowski (with sacrifices by Earle Ake and Dan Wisehart) | 135,164 |
Peter Frodin | 147,341 |
Eric Le Saux | 147,624 |
Francisco Azevedo | 147,678 |
Dave Pavlick and Beirne Konarski | 148,527 |
Bill England | 149,053 |
Peter Seibel | 149,317 |
Steve Frost | 149,328 |
Ravi Kolagotla | 149,396 |
Giovanni Marzot | 149,412 |
Peter Frodin’s second-place strategy is a less tolerant
version of the fool_me_twice
strategy explained earlier in this chapter: his fool_me_once testifies if either of the
opponents testified during the previous match. (An honorable mention
goes to Brian Gough, whose subroutine is identical to Peter’s, but
didn’t score in the top ten because of other strategies that behaved
nondeterministically.) Eric Le Saux’s elephant placed third by noticing whether
opposing strategies retaliate against testifying. Francisco Azevedo’s strategy was nice but unforgiving: it holds
out until someone testifies, and then testifies forever after. Dave
Pavlich and Beirne Konarski collaborated on the most complex strategy
submitted: their subroutine contains five additional subroutines,
implementing a temporary “probation” state for opponents. It testifies
if both opponents are on probation and either one violated his
probation by testifying last round.
Then the backstabbing began: the bottom half of the top ten, and
ten out of the 31 strategies overall, simply testified each and every
time. (The differences in score were due to the random behavior
exhibited by other strategies.) Peter Seibel used genetic programming to breed winning
strategies, and found nothing that performed better than a pure
testifier. Georg Rehfeld’s be_a_good_boy_all_the_time was the exact
opposite: it cooperated regardless of the other strategies’ actions.
In his description, Georg said:
I think this is the only strategy to save the world: don’t do any harm to anybody, be helpful and cooperative all the time. This holds true in real life, I believe…