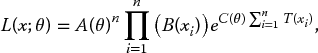2
Foundations of Bayesian Analysis
2.1 Education and Wages
Common wisdom states that one’s salary or wages should have something to do with one’s education level. Otherwise, why is higher education so expensive and time consuming? Is it not reasonable that more educated people should be paid more?
Let us define two variables, representing (a) education level of a random person (denote it by E) defined as the number of years of formal education and (b) hourly wage level of the same person (denote it by W) in USD per hour. These variables can be measured for the population of US wage earners. As usual, we will reserve the capital letters E and W for the random variables, while by lowercase e and w we denote particular data: numeric values of these variables. We collect such data for 534 respondents, which constitutes a sample from 1985 census according to Berndt [5].
As we have suggested in the beginning, these two variables must be somewhat related. And if they are, we can use one of these variables measured for a new subject (outside of our sample) to predict the other. For instance, it is logical to believe that if the education level of a person is known, we can make certain predictions regarding their wage. On the other hand, if a person’s wage is known, we can make some suggestions regarding their education level. Let us make the latter our primary objective. We will make statistical inference on an unknown parameter (education level) based on available data (wages).
The relationship between these two variables is anything but deterministic. This may be due to many factors which we will not consider for a simple reason: our data contains no information on these factors. There exists a taunt often used by less educated people toward the more educated: If you are so smart, why are you so poor? No doubt, there is a grain of sad truth in this taunt. The authors of the book, both professors of statistics, have to agree.
However, even if this relationship is not deterministic, it still deserves a rigorous probabilistic or statistical treatment. For that, we will consider a function of these two variables: E and W. With both variables being nonnegative, analysis of our data for 534 respondents suggests the following functional representation
Model function (2.1) is graphically represented in three dimensions in Figure 2.1. This representation can go two ways: first, we will take the probabilistic approach and consider the value of education level E = e known and fixed. Then we look at the distribution of hourly wages W given E = e. This is the direct view (logically and chronologically), since education comes first, and wages are paid later on, as a consequence. This way E appears to be the parameter of the distribution of random variable W, which can be represented for our data by the probability density function

Figure 2.1 Model function of E and W.
which for any given value of parameter E could be recognized as a member of gamma distribution family (1.18). Figure 2.2 shows the graphs of such density functions for the parameter values: 7, 12, and 18 years. We see that for larger values of the parameter the distribution mode shifts to the right and the shape of the graph becomes less steep.

Figure 2.2 Graphs of p.d.f.’s.
This is a familiar view of several density functions from one family differing only by their parametric values. However, let us take the second view, which can be characterized as statistical. We will consider the hourly wages W (our data) fixed and known. The function of unknown parameter E
is known as the likelihood function. Figure 2.3 demonstrates the graphs of this function for different data values of W equal to 8, 10, and 15 USD per hour.

Figure 2.3 Graphs of likelihood functions.
Formally speaking, these are not the graphs of probability density functions. The area under each graph does not have to equal to one. Notice that the modes shift right with the increase of W, and for our chosen wage levels the most likely education levels are approximately 12 (high school), 14 (two-year college), and 17 (four-year college plus).
This is an example of statistical inference based on likelihood. Starting with the matched sample of 534 pairs (education, wages), we develop model (2.1). This model is used to construct the three-dimensional graph in Figure 2.1, and also its cross-sections: likelihood curves in Figure 2.3. Then, we pick the likelihood curve corresponding to a new data point W (from the sample or outside of the sample). Finally, we determine the most likely value of the parameter E corresponding to this W. The objective of the inference is met. This example illustrates a typical application of statistical inference based on the likelihood function. We will need another example to demonstrate some problems related to this approach.
2.2 Two Envelopes
This problem has been discussed extensively in a number of papers and online communications, see a comprehensive review by Bliss [6] or Tsikogiannopoulos [24]. We will consider a specific version of the problem which will help us to illustrate a very important point for further discussion. Suppose you are looking for a job. You are at the end of a tedious interview process, but finally you are hired by a company, and you are ready to take the offer. The only issue remaining to be discussed is your salary. The boss, who is genuinely nice but rather eccentric, suggests that you play a game. He puts two envelopes on the table and informs you that each envelope contains your contract with the exact salary figure, but one number is two times greater than the other. You are allowed to choose one of the envelopes, open it and read the number. Then you have to make the decision: will you take the open envelope, or opt for the closed one (without being able to read the number it contains). What shall you do? Let us take a formal standpoint. The open envelope contains a number, say W1. The closed one contains an unknown number W2, which is either 2W1 or ![]() . Your choice of an envelope was random and you were equally likely to pick a smaller or a larger number. So we have to deduce that
. Your choice of an envelope was random and you were equally likely to pick a smaller or a larger number. So we have to deduce that
Then, we have to opt for the closed envelope! As we can see from the definition of expected value for discrete variables,
If we think a little harder, we will have to agree that this solution is absurd. Why so? Let us suppose this line of thought is correct and whatever is the number in the open envelope, you should take the other one. Then, why do you have to read this number? You can just open one envelope and (without reading the salary figure) choose the one in the closed envelope. Do you not see the problem yet? Taking it a step further, why do you need to open an envelope at all? You just barely touch it, and immediately opt for the other. But then: what do you do with the other? Open? As soon as you open it, you would be better with a different choice! So you have to walk around a vicious circle: You can never open any envelope.
Why is this solution wrong? It can be explained on two levels; intuitive and mathematical. The intuitive point is that in the real world any solution ignoring the salary figure in the open envelope is very suspicious. You must have an idea of what you are worth on the labor market, coming from you prior experience, which we would call prior information. If you see 100K ($100,000) in the first envelope, would you expect 200K or 50K in the second one? If you see 30K in the first, what is more likely to be in the second: 60K or 15K? It is interesting that the prior information is highly subjective: it depends both on your actual worth and its perception. Two people might never agree on it, but two different people should indeed have different solutions to this problem.
At the mathematical level, we have made a wild assumption to obtain (2.4). In reality,
at least for some numeric values w between 0 and infinity. It is not difficult to check that the correct expression for conditional expected value of the number in the second envelope is given not by (2.5), but by
Mathematically, the most convenient way to quantify prior information would be to define a continuous distribution by a distribution density function π(w) defined for all w from 0 to infinity. We can call it prior distribution. In terms of prior distribution, we can rewrite (2.6) as
and
These two probabilities, taking into account both prior information and the data of the experiment (the number in the first envelope), will be called posterior probabilities. They correspond to the only possible outcomes, describing entire probability distribution of the number in the second envelope W2 conditional on the value in the first one, w (we will also call it posterior distribution).
We can also rewrite (2.7) as conditional expected value
which, as we can easily see, could be either greater or less than w, depending on the prior distribution. In fact, the only case when (2.6) gives the same answer as (2.4) corresponds to π(w) ≡ c for all w from 0 to infinity (uniform on the positive semiaxis), which is not a proper probability density function.
Let us consider a numeric example. Suppose, random variable W (our worth) can be described by the uniform distribution from 25K to 100K. It corresponds to

Therefore,

Using (2.7), you can easily finish the problem.
We have to conclude that for this simple example the approach allowing for the incorporation of prior information brings about a pretty elegant solution. This sequence of steps:
- elicitation of prior distribution,
- formal development of posterior distribution (based both on prior and data),
- making conclusions based exclusively on the posterior,
informally constitutes the Bayesian inference.
Notice that if we wanted now to get back to the first example (education and wages), we could also think about incorporating some prior information. If you know somebody in person, have a chance to talk and get a personal impression, and then you are informed of her exact wages, will the wage be the only source for your conclusions regarding her education level? It would be a little harder to quantify your visual and verbal impressions of a person as a neat prior distribution for her education level (unless you ask directly and trust the answer completely), but in principle it could be done. This process is known as prior elicitation, and we will discuss it more than once in the sequel.
At this time we conclude the informal introduction. The following two sections discuss the main formal concepts of Bayesian inference related to hypothesis testing and parametric estimation. Classical procedures will be reviewed first, and then Bayesian modifications will be suggested allowing us to properly incorporate the prior information.
2.3 Hypothesis Testing
2.3.1 The Likelihood Principle
Let us consider an i.i.d. sample x = (x1, …, xn) from an infinite population, characterized by a distribution density function f(x, θ), where x is the vector of data and θ is a (maybe, vector) parameter. Recall from basic statistics course that the likelihood function is defined as
In the context of incomplete data, which is typical for many risk management and reliability applications, including some of those which will be used in the following chapters, we may observe exact values x = (x1, …, xm), m < n and just know the lower limits for the other cases: xj > cj, j = m + 1, …, n. This corresponds to the so-called right censoring of the dataset. In this case we can modify the likelihood formula:

where S(c, θ) = P(X > c ; θ) is the survival function corresponding to the distribution with density f(x, θ).
The likelihood principle is a practically undisputed basic principle of mathematical statistics. According to the likelihood principle, all information regarding the unknown parameter, which could be found in data, is contained in the likelihood function.
2.3.2 Review of Classical Procedures
Let us review the main definitions and procedures of hypothesis testing for the simplest case of two parametric hypotheses. We believe that there exist two exhaustive and mutually exclusive possibilities regarding the parameter θ of the distribution f(x, θ). One is designated as the null hypothesis and is denoted by H0: θ = θ0. The other is described as the alternative H1: θ = θ1. A test statistic (a function of the sample) T(x) and critical region RT⊂Range(T) are used to define a test, which is a basic binary decision rule:
“Reject H0” if T(x) ∈ RT or “Do not reject H0” if T(x)∉RT.
Notice that although in the formal context of two simple hypotheses “Do not reject H0” seems to be equivalent to “Accept H0” or “Reject H1,” in common applications we find the first of the three statements the most appropriate. Null hypothesis is also known as status-quo or zero-effect hypothesis requiring no immediate action if not rejected. Typical examples of a null hypothesis would be: “new drug is no good,” “surgery is not required,” “new technology is exactly as effective as the old one.” Rejecting null is something which requires an action: “approve a new drug,” “proceed with the surgery,” “implement the new technology” and is associated with additional cost or risk. The burden of proof is higher for rejecting the null. Not rejecting the null might call for more testing to be performed and more proofs to be provided before we take the action. It does not necessarily mean accepting the null or rejecting the alternative. In the context of classical hypotheses testing, one usually speaks of statistical significance of the results, if the null hypothesis can be rejected.
We can judge the quality of the tests using definitions of two errors which we want to be as small as possible:
- Type I error (reject true null) with probability α = P(T(x) ∈ RT∣H0)
- Type II error (do not reject false null) with probability β = P(T(x)∉RT∣H1)
Quantity 1 − β is also known as the power of the test.
In general, type I error is the one which is more important in the context of the study. Therefore, a common approach is to choose the largest admissible probability of type I error, which is called significance level, and then find tests which will make type II error as small as possible. Neyman–Pearson theory of hypothesis testing suggests that in a very general setting the most powerful tests (those minimizing type II error for type I error not exceeding the significance level) should be based on the likelihood ratio:
If we use the likelihood ratio as the test statistic, the only thing we need to specify the test procedure is the critical region, which will take the form RΛ = {x: Λ(x) > cα}. Here cα is the critical value of the test, which can be determined by α, if the distribution of the likelihood ratio under the condition of null hypothesis is known. In practical applications, we usually look for a simpler test statistic T(x) equivalent to the likelihood ratio in the sense that RT = {x: T(x) > kα} = RΛ = {x: Λ(x) > cα}.
Ten Coin Tosses
A random variable X has Bernoulli distribution (see Section 1.2) if it may assume two values only: 0 or 1, and is described by a discrete probability function f(x, θ) = θx(1 − θ)1 − x, where the value of the parameter θ = P(X = 1) is unknown. Consider a random i.i.d. sample x = (x1, …, xn) from this distribution. Write down the likelihood function
Let us perform a series of ten trials: tosses of the same coin. Suppose we record “heads” seven times. This series is treated as an i.i.d. sample x = (x1, …, xn), n = 10, where the underlying variable X has Bernoulli distribution and θ is unknown probability of “heads” (success). We will consider null hypothesis H0: θ = θ0 = 0.5 (fair coin) versus a simple alternative H1: θ = θ1 = 0.7 (coin biased in a special way). How can we construct the likelihood ratio test?
In our case,
so
The exact formula with logarithms on the right-hand side of the last expression is irrelevant as soon as we can see that ![]() for some kα, and the equivalent form of the likelihood ratio test is:
for some kα, and the equivalent form of the likelihood ratio test is:
“Reject H0” if ![]() or “Do not reject H0” if
or “Do not reject H0” if ![]() .
.
Picking up an “industry standard” α = 0.05, from the table of binomial distribution we can see that, P(∑Xi > 7∣H0) = 0.055, P(∑Xi > 8∣H0) = 0.011, and the rejection region consists of ![]() so in our example with seven heads we do not reject the null hypothesis that the coin is fair. Notice also that our final verdict does not depend on the alternative if instead of θ1 = 0.7 we choose another value larger than 0.5. The test might have less power, but its significance level stays the same.
so in our example with seven heads we do not reject the null hypothesis that the coin is fair. Notice also that our final verdict does not depend on the alternative if instead of θ1 = 0.7 we choose another value larger than 0.5. The test might have less power, but its significance level stays the same.
2.3.3 Bayesian Hypotheses Testing
Consider the same general setting of two simple hypotheses. Incorporating prior information in this case means assigning prior probabilities to the null hypothesis P(H0) and the alternative P(H1) = 1 − P(H0).
Let us also consider the observed data x and the likelihoods L(x, θ0) and L(x, θ1). Since the two hypotheses are mutually exclusive and exhaustive, the Law of Total Probability suggests to “integrate out” the parameter and obtain a parameter-free weighted likelihood, where the prior probabilities of the hypotheses play the role of weights:
As a function of data, m(x) is usually called the marginal distribution. For given data it is a constant, and as we will see very soon, it plays very little role in the following analysis. However, we will need it during the derivation of the Bayesian test. According to the definition of conditional probability or a simplified version of the Bayes theorem,
and the ratio of these two expressions, after m(x) cancels out, is
The ratio on the left-hand side is known as posterior odds. The first ratio on the right-hand side is the likelihood ratio, which we have encountered while developing classical testing procedures. The second is the ratio of prior probabilities or prior odds. When the prior odds equal one, the posterior odds has the Bayesian name of the Bayes factor, see [15]. In this case of two simple hypotheses, the Bayes factor coincides with the likelihood ratio. In general, both the Bayes factor and the prior odds will be needed to evaluate the posterior odds.
Finally, in order to decide whether to reject the null hypothesis or not, without any prior information (that means, setting prior odds to one, or in other words, assuming P(H0) = P(H1) = 0.5), we have to establish a reasonable benchmark for the posterior odds. We can consider the posterior odds 3:1 to provide “substantial” evidence against the null and 10:1 to provide “strong” evidence. Jeffreys [14] used these benchmarks for the Bayes factors, see also [15]. So for substantial evidence against the null, the Bayesian test takes the form:
“Reject H0” if ![]() or “Do not reject H0” if
or “Do not reject H0” if ![]()
For strong evidence,
“Reject H0” if ![]() or “Do not reject H0” if
or “Do not reject H0” if ![]()
Ten Coin Tosses
Returning to the ten coin toss experiment in Bayesian setting, we need to specify the priors. Let us say that our prior belief in fairness of the coin can be expressed by P(H0) = 0.5 or in the prior odds of 1:1. From (2.17) we may calculate the Bayes factor as
bringing about the posterior odds of 2.28:1 which gives less than substantial (and much less than strong) evidence against the null hypothesis. Notice that the classical procedure introduced in Subsection 2.3.2 did not require the computation of the likelihood ratio, but it called for the computation of binomial probabilities.
To extend the analogy with the classical procedure, assume that for the same null and alternative and choice of priors we observe a different result: instead of seven, we have nine “heads” in a series of ten coin tosses. Then the Bayes factor is
which provides a strong evidence against the null. Noticing that ![]() lies in the critical region for α = 0.05, we may conclude that in this case both classical and Bayesian approaches to hypotheses testing lead us to similar results.
lies in the critical region for α = 0.05, we may conclude that in this case both classical and Bayesian approaches to hypotheses testing lead us to similar results.
2.4 Parametric Estimation
2.4.1 Review of Classical Procedures
Let us recall some concepts of classical theory of statistical estimation. Consider a random sample x = (x1, …, xn) from a certain population with p.d.f. f(x, θ). A statistic is defined as any function of the random sample. A statistic used as an approximate value of unknown parameter of the distribution (population) can be considered an estimator of the parameter. All estimators are random variables. We have to distinguish an estimate as a specific numeric value used to approximate the unknown parameter from an estimator which is a rule leading to different numerical estimates for different samples from the same distribution (population). We will try not to mix up these two terms, though it might be confusing at times.
From the classical standpoint, desirable properties of estimators are: consistency, unbiasedness, and efficiency. An estimator is consistent if it converges in a certain sense to the true parameter value when the sample size grows to infinity. An estimator is unbiased if its expected value (mean) coincides with the true value of the estimated parameter. An estimator is called the most efficient within a certain class if for the given class its mean square error is the smallest.
2.4.2 Maximum Likelihood Estimation
There exist several popular methods to obtain parametric estimators in a general setting: the method of moments, the method of least squares, etc. However the method of maximum likelihood is probably the most important for classical statistics. A maximum likelihood estimator (MLE) ![]() for unknown k-dimensional vector parameter θ is a statistic, which maximizes the likelihood function defined in (2.13). When the sample sizes are large, or ideally, are allowed to grow to infinity, MLEs have all nice properties: they are consistent, asymptotically unbiased, asymptotically efficient, and even asymptotically normal (their distribution is close to normal). However for small sample sizes MLEs do not always behave that well, and may be substantially inferior to the estimators obtained by other methods.
for unknown k-dimensional vector parameter θ is a statistic, which maximizes the likelihood function defined in (2.13). When the sample sizes are large, or ideally, are allowed to grow to infinity, MLEs have all nice properties: they are consistent, asymptotically unbiased, asymptotically efficient, and even asymptotically normal (their distribution is close to normal). However for small sample sizes MLEs do not always behave that well, and may be substantially inferior to the estimators obtained by other methods.
Let us recall the algorithm used to obtain MLE in regular cases.
- Write down the likelihood function (2.13).
- Calculate logarithmic likelihood or log-likelihood l(x1, …, xn, θ) = ln L (a technical step simplifying further derivation).
- Calculate partial derivatives of the log-likelihood with respect to parameters.
- Find the critical points of the logarithmic likelihood, that is, the solutions of the system of equations
- Check if the critical point found is indeed the absolute maximum point (not a local maximum, nor a minimum or a saddle point). The value of absolute maximum obtained herewith
 is the MLE.
is the MLE.
This algorithm cannot be used in nonregular cases (e.g., if the partial derivatives are not defined). Sometimes it does not lead to a unique solution. Notice also that the exact solution of system (2.20) is available only in some simple textbook cases. In more complex situations one has to use numerical methods of optimization to find an approximate solution. Let us recall two simple examples illustrating both analytical and numerical methods.
Ten Coin Tosses
Returning to the ten coin toss experiment, we will once again use the likelihood function defined in (2.16). Then we will calculate its logarithm, the log-likelihood
It is easy to find the derivative w.r.t θ and solve the following equation
The solution is not unexpected: ![]() . To check if this critical point is a maximum, find the second derivative
. To check if this critical point is a maximum, find the second derivative
Since for Bernoulli distributed samples ![]() , this second derivative is never positive. Therefore, the critical point we have found is a local maximum point. As soon as it is the only critical point, it is also the absolute maximum. Thus
, this second derivative is never positive. Therefore, the critical point we have found is a local maximum point. As soon as it is the only critical point, it is also the absolute maximum. Thus ![]() is the MLE for the parameter of Bernoulli distribution.
is the MLE for the parameter of Bernoulli distribution.
We perform a series of 10 trials (coin tosses): n = 10. Suppose we record “heads” seven times (x = 7). So ![]() .
.
Life Length
Many random variables in insurance or reliability applications representing “life length” or “time to failure” can be conveniently described by gamma distribution with density function
where the values of two parameters α (shape) and λ (rate or reciprocal scale) are unknown, see also Section 1.4. Gamma class of distribution was introduced in Chapter 1. The variety of forms of gamma densities for different combinations of parameter values (see Figure 1.17) makes this class very attractive in modeling survival.
Suppose we obtain an i.i.d. sample from gamma distribution (x1, …, xn). Let us write down the log-likelihood function
As we can see, the approach of the previous example will not work that easily: differentiation in both α and λ is way too difficult to allow for a simple analytical solution. However, numerical optimization procedures might help (see Exercises at the end of the chapter).
An alternative to MLE is known as the method of moments, which is a particular case of a more general plug-in principle. It uses the fact that if there exists a convenient formula expressing the unknown parameters of a distribution through its moments (say, the mean and the variance), then plugging sample moments in instead of theoretical moments often brings about consistent (not necessarily unbiased or efficient) estimators.
From (1.19) we know that E(X) = α/λ and Var(X) = α/λ2, therefore
after plug-in leading to the method of moment estimators:
Method of moments estimators sometimes are attractively simple, but are lacking certain large sample optimality properties of MLE. Returning to 10 coins example, we can easily see that due to E(X) = θ, the method of moments estimator of θ coincides with the MLE.
2.4.3 Bayesian Approach to Parametric Estimation
Let us assume that all relevant prior information regarding parameter θ is summarized in π(θ), which is the p.d.f. of the prior distribution. In order to obtain the posterior distribution, we can use continuous version of the Bayes Theorem, the most important formula in this chapter!
The left-hand term of (2.26) is the p.d.f. of the posterior distribution. The right-hand term is just a product of prior and likelihood. Symbol ∝ denotes proportionality of its left and right hand sides or equivalence of those to within a constant multiple. The constant multiple in question is the integral in the denominator of the central term of (2.26). This integral depends on x only and does not depend on the parameter which is integrated out. It represents the marginal distribution of the data, and is an absolute constant when data are provided. The bad news is: In most applications this constant is hard to determine. The good news is: In most cases it is not necessary. There exist some ways around.
For now let us suppose that this integral is not a problem, the posterior distribution is defined completely, and it has a nice analytical form. This is possible in a limited number of simple examples. The posterior distribution is what we need to provide Bayesian inference. What information can we get out of the posterior distribution?
Point Estimation
The mean, median, or mode of the posterior distribution (in the sequel: the posterior mean, the posterior median, and the posterior mode) can play the role of point estimators of the parameter:
The first one (by far, the most popular choice) minimizes posterior Bayes risk which is defined as the mean square deviation of the estimator from the parameter averaged over all parameter values, while the second minimizes the absolute deviation of the estimator. Sometimes, the posterior mode is the easiest to use.
Interval Estimation
Having chosen the level 1 − α in advance, we are looking for an interval (θl, θu) such that

Such an interval is called a credible interval. Unlike classical confidence intervals, Bayesian credible intervals allow for a simple probabilistic interpretation as intervals of given posterior probability. We can always choose a symmetric interval, though it is not the only possible choice:

2.5 Bayesian and Classical Approaches to Statistics
As we have noticed already, the likelihood principle is universally accepted in modern statistics. Neither classical nor Bayesian approaches are disputing it. The main difference between the two approaches is in the interpretation of parameters. In classical statistics parameters are unknown but fixed. There exists the “true” value of the parameter, which Nature stores for us somewhere, though we might never hope to find it. According to Bayesian interpretation, parameters are random variables, which can be described by distribution laws. There is no such thing as the “true” value of the parameter.
This principal difference between two approaches has many dimensions: from simple procedural considerations to the fundamental worldview issues.
On the most general philosophical level, classical statistics is deterministic: It considers populations and processes along with their characteristics such as population mean and variance (true values of parameters) to belong to the objective reality. It also suggests at least a distant possibility to learn or guess the true values of parameters. Moreover, if our methods are good and consistent, we believe that we can approximate these true values very well. All events around us are actually pre-determined. We perceive them as random due to the limitations of human knowledge.
The Bayesian approach, however, considers characteristics of populations and processes being random in principle. All our knowledge regarding random events contains some level of uncertainty and is subjective. Any statement regarding the population parameters expresses just the degree of rational belief in the characteristics of the population.
Such philosophical differences arise in many fields of knowledge: for instance, in physics they are epitomized by an elegant question: “Does God play dice?” As the history of philosophy testifies, this question cannot be successfully answered, this way or another. As the history of science testifies, both approaches have proven to be fruitful. In particular, representatives of both points of view made substantial contributions in the development of Statistics as a discipline [3].
Going down to a more practical standpoint, we can notice two important differences between Bayesian and classical approaches. The first difference is in the interpretation of data. Classical approach assumes a probability model in which data are allowed to vary for a given parameter value. In education/wages example (education level being the parameter, wages being the data) the reference group for our inference is formed by all respondents with the same education level. A good statistical procedure in the classical sense is a procedure which is good enough for any member of the reference group.
The data we obtain is just one random sample from a potentially huge reference group, a variety including other random samples, which we will possibly never see. We can always consider a possibility (at least, theoretically) of repeating our experiments and increasing the amount of available data. We judge the statistical procedures by their behavior in this unlimited data world, therefore we often tend to integrate over data samples, including those obtained and those only theoretically possible, while keeping our parameters fixed. Probability of an event is the limit of relative frequency of its occurrence in an infinitely long series of identical experiments. That is why classical statistics is also frequently dubbed (especially among the Bayesians) “frequentist.”
The Bayesian approach does not assume a possibility of obtaining unlimited data. All inference has to be based solely on the data obtained in the experiment and possibly on some prior information. We do not assume a possibility of our data being different and do not integrate over the reference group. We have just one person whose wages are reported, and we have to make inferences regarding this person’s education level. Our reference group is the set of possible parameter values. Parameters of the distribution of data are considered random, and we judge our procedures integrating over possible values of parameters, and keeping the data fixed. Probability rules are used directly to obtain the rules of statistical inference [1, 4, 17].
The choice between these two approaches in applied statistics is often determined by specifics of the application. In some classes of problems we can easily afford repetitive experiments and increasing the sample size is just a technical difficulty. In other classes we are “doomed” to work with small samples, seeing no principal possibility of getting additional data.
The other practical difference between two approaches related to the first one is the use of prior information at our disposal before the statistical data are obtained. Such prior information is very likely to be nontrivial in many problem settings. Let us once again recall the education/wage example, or even better, the problem of two envelopes. The amount and role of prior information widely varies for different applications. However, the classical approach allows the use of prior information in a very narrow sense: at the stage of formalizing the model setting the likelihood. After the likelihood is written down, there is no conceivable way to incorporate any additional information. Bayesian approach allows for the use of prior information in the form of a prior distribution.
2.5.1 Classical (Frequentist) Approach
Classical approach, in our view, found its most logical representation in the ideas and works of a prominent British statistician Sir Ronald Aylmer Fisher (1890–1962) (Figure 2.4). As the portrait reveals, Fisher was an avid smoker and did some research on the effect of smoking tobacco on human health. What is more important, he made a great contribution to the development of Statistics in the twentieth century. He worked in multiple applications and obtained many deep theoretical results. He also contributed to the formulation of basic principles of what we call here the classical approach. He also happened to be very anti-Bayesian.

Figure 2.4 Sir Ronald Aylmer Fisher (1890–1962). Reproduced with permission of R. A. Fisher Digital Archive, The Barr Smith Library, The University of Adelaide.
Let us recall the main principles of classical statistical analysis:
- Parameters (numerical characteristics of populations and processes) are fixed unknown constants.
- Probabilities are always interpreted as the limits of relative frequencies in unlimited series of repetitive experiments.
- Statistical methods are judged by their large sample behavior.
A typical method of statistical estimation is the maximum likelihood method. Hypotheses testing is based on the likelihood ratio. The likelihood function is treated as a function of data and is not considered to describe the distribution of the parameter.
However, in order to cast some doubt in practical infallibility of this approach, we may use a classical experiment performed by Fisher and discussed in his book [10] to illustrate Fisher’s exact test. In our description of this experiment we will follow [20], though this story being told by many statisticians has many different versions.
2.5.2 Lady Tasting Tea
At a summer tea party in Cambridge, England, a lady (some sources identify her as Dr. Muriel Bristol) states that tea poured into milk tastes differently than that of milk poured into tea. The lady claims to be able to tell whether the tea or the milk was added first to a cup. Her notion is taken sceptically by the scientific minds of the group. But one guest, happening to be Ronald Aylmer Fisher, proposes to scientifically test the lady’s hypothesis. Fisher proposes to give her eight cups, four of each variety, in random order. One could then ask what the probability was for her getting the number she got correct, but just by chance (the null hypothesis). The experiment provides the lady with eight randomly ordered cups of tea, four prepared by first adding milk, four prepared by first adding the tea. She is to select the four cups prepared by one method. She was reported [22] to prove correct all eight times. Using permutation formula, one can suggest that under the null hypothesis her chances to guess correctly, or randomly select one out of 8!/(4!(8 − 4)!) = 70 possible permutations of eight cups are about 0.014, which is the p-value of Fisher’s exact test.
Putting aside interesting connotations of this problem for experimental design and randomization (the latter to be discussed in the next chapter), we can consider a slightly different setup, where each of the eight cups is randomly and independently prepared in one of the two possible fashions (the milk first or the tea first) according to the results of a fair coin toss. Then the chances of the lady to guess correctly all eight times become 1/28 = 1/256, which is approximately 0.004. If we increase the number of cups from 8 to 10, then in the case of all 10 correct guesses the p-value or the significance level of the test goes down to 0.001. However, what exactly does this p-value mean?
Let us cite a letter from an outstanding American Bayesian statistician L. J. Savage (Figure 2.5) to a well-known colleague, biostatistician J. Cornfield, where this experiment (discussing a version with 10 cups) is used to cast some doubt on the practicality of using classical procedures based solely on likelihood and suggesting some role of the context of the experiment and thus the prior information.

Figure 2.5 Leonard Jimmie Savage (1917–1971). Courtesy of Gonalo L. Fonseca.
“There is a sense in which a given likelihood ratio does have the same sense from one problem to another, at least from the Bayesian point of view. It is always the factor by which the posterior odds differ from the prior odds. However, all schools of thought are properly agreed that the critical likelihood ratio will vary from one application to another. The Neyman-Pearson school expresses this by saying that the choice of the likelihood ratio is subjective and should be made by the user of the data for his particular purpose. As a Bayesian, I would say that a critical likelihood ratio for a dichotomous decision about a simple dichotomy depends (in an evident way) on the loss associated with the decision and on the prior probabilities associated with the dichotomy.
The fact that the reaction to an experiment depends on the content of the experiment as well as on its mathematical structure and whatever economic issues might be involved seems to me to be brought out by the following triplet of examples that occurred to me the first time I taught statistics, when I still had a completely orthodox orientation. Imagine the following three experiments: 1. Fisher’s lady has correctly dealt with ten pairs of cups of tea. Many readers will recognize this example to be from R. A. Fisher’s famous lady tasting tea experiment. 2. The professor of 18-th century musicology at the University of Vienna has correctly decided for each of 10 pairs of pages of music which was written by Mozart and which by Haydn. 3. A drunk in a parlor has succeeded 10 times in correctly calling a coin secretly tossed by you. These three experiments all have the same mathematical structure and the same high significance level. Can there, however, be any question that your reaction to them is justifiably different? My own would be: 1. I am still skeptical of the lady’s claim, but her success in her experiment has definitely opened my mind. 2. I would originally have expected the musicologist to make this discrimination; I would even expect some success in making it myself; he, an expert in the matter, felt sure that he could make it. His success in 10 correct trials confirms my original judgment and leaves no practical doubt that he would be correct in substantially more than half of future trials, though I would not be surprised if he made occasional errors. 3. My original belief in clairvoyance was academic, if not utterly nonexistent. I do not even believe that the trial was conducted in such a way that trickery is a plausible hypothesis, and feel sure that the drunk simply had an unusual run of luck. Of course, these tests are not simple dichotomies, but I think you will find them germane to your question” [21].
2.5.3 Bayes Theorem
History of the Bayesian approach in statistics traditionally goes back to the times of Reverend Thomas Bayes (Figure 2.6). One can argue though that Laplace and other prominent contemporaries did a lot of what we now call Bayesian reasoning. Not much is known for sure about Bayes including his date of birth. Even his portrait included in this book, according to modern studies, is no longer believed to be his.

Figure 2.6 Rev. Thomas Bayes (circa 1702–1761). https://commons.wikimedia.org/wiki/ File:Thomas_Bayes.gif. CC0-1.0 public domain https://en.wikipedia.org/wiki/Public_domain
Thomas Bayes in his posthumous treatise formulated the statement known now as the Bayes Theorem. This theorem indicates how one should calculate inverse conditional probabilities of hypotheses after the experiment related to these hypotheses. This theorem can be rigorously formulated for the discrete case

Here Bi are hypotheses, and A is some event, which is influenced by the hypotheses, thus the post-event probabilities of the hypotheses are also influenced by the event. This formula in a simple form was used in the Bayesian treatment of two simple hypotheses in Section 2.3. In estimation problems we are more likely to use the continuous version of the theorem which was introduced in (2.26).
Bayes’ work and ideas were never completely forgotten, but they also were out of the mainstream for a very long time. The revival of Bayesian approach is probably due to two factors. The first factor is the recent expansion of new applications of statistics (insurance, biology, medicine) characterized by relatively small sample sizes (limited data) and ample prior information. The second is the development of computational techniques which substantially extends the practical applicability of Bayesian methods.
It would probably be most accurate to name another outstanding British scientist Sir Harold Jeffreys (1891–1989) (Figure 2.7) as the founder of the modern Bayesian statistics. One of his main contributions was his seminal book [14] containing the foundations of Bayesian statistics. However many other great statisticians, including Bruno De Finetti, the famous proponent of subjective probability; David Lindley; already cited Jimmie Savage; and Arnold Zellner (Figure 2.8) should be honorably mentioned among those who brought attention back to this eighteenth century approach.

Figure 2.7 Sir Harold Jeffreys (1891–1989). Reproduced with permission of the Master and Fellows of St. John’s College, Cambridge.

Figure 2.8 Arnold Zellner (1927–2010), the first president of ISBA. Reproduced with permission of International Society for Bayesian Analysis.
2.5.4 Main Principles of the Bayesian Approach
Let us summarize the main principles of Bayesian statistical analysis keeping close to the treatment of Bolstad [7].
- True values of parameters are unknown, are not likely to become known, and therefore will be considered random.
- Prior information regarding the parameters before the experiment is allowed and is mathematically expressed in the form of the prior distribution of the random parameter.
- All probabilistic statements expressed by the researcher regarding the parameters express the “degree of rational belief” and are subjective.
- Likelihood function is the only source of information regarding the parameter which is contained in data (weak likelihood principle).
- We do not consider the feasibility of obtaining new data and do not consider the data which could theoretically be obtained.
- Probability rules and laws are applied directly to the statistical inference.
- Our information regarding the parameters is updated using the data.
- Posterior distribution incorporates the prior information and the information from data in the only mathematically consistent way: using the Bayes formula.
The main advantages of Bayesian approach are well known and are discussed in different terms and at different levels in such books as [1, 4, 7, 11], and [16]. From decision theoretic standpoint, we can prove that all admissible estimation procedures can be obtained using Bayesian approach. Sometimes, Bayesian procedures outperform classical procedures even using classical criteria of performance. Bayesian estimation can be substantially more reliable for small samples, while it will lead to the same results as MLE when the sample size grows to infinity. Bayesian procedures behave better than classical ones when there exists substantial amount of prior information which should not be neglected. However, even with very weak prior information, Bayesian approach sometimes performs better than the classical approach. One explanation to this phenomenon is a possible difference in numerical stability between mathematical procedures of optimization (MLE) and integration (Bayesian estimators).
The development of Bayesian procedures in the past faced a very important obstacle. The problem may sound technical, but it was grave. The continuous version of the Bayes theorem (2.26) allows one to determine the posterior density to within a multiplicative constant. Combining (2.26) and (2.27) we can write down the following formula for the most popular Bayes estimator: the posterior mean.
Unfortunately, exact analytical solution for these integrals is rarely available, although we will consider some nice exclusions in Section 2.7. Numerical integration is possible but is far from trivial especially for higher dimensions of parametric space (multiple parameters). That is why Bayesian statistics was stuck in a rut for a long time, being restricted to handling very special cases and not being able to spread the wings.
A “Bayesian revolution” took place in the middle of the twentieth century. What Bayes could not dream of, and what Jeffreys could not carry out, was made possible by the development of the toolkit widely known as MCMC—Markov chain Monte Carlo methods. International Society for Bayesian Analysis (ISBA) was founded in 1992 as the result of increased interest to Bayesian approach, and since then Bayes methods have been growing in popularity even more. Modern Bayesian statistics provides ample tools for such integration developed since the 1950s and still under active development. Chapter 4 of the book is dedicated to some of these methods.
However, the first question we have to ask before we face the problems with evaluating the posterior in (2.33) is: How do we specify the prior?
2.6 The Choice of the Prior
Contemporary Bayesian statisticians do not form a homogeneous group. There are serious differences in the ways people understand and apply the Bayesian principles. One of the most discussed issues is the prior elicitation a.k.a. the choice of the prior in particular problems [15]. In the following three subsections we will illustrate three popular approaches using one simple example of ten coin tosses.
2.6.1 Subjective Priors
Consider a particular problem with a substantial amount of available prior information: Before the experiment we already know something important about the parameter of interest. This knowledge can be expressed in terms of the parameter’s probability distribution. If probabilities are understood as the degrees of rational belief, no wonder that different people may have different subjective beliefs which will lead to different subjective distributions. Two medical doctors read a patient’s chart and make different observations. Two investors interpret long-term market information in two different ways. They will have different priors.
Assume that both doctors perform the same necessary tests and both investors observe the same results of the recent trades, meaning both parties get the same data and agree on the likelihood. Their final conclusions may still differ because of their priors being different.
This difference in the final decisions due to the difference of priors is both the curse and the blessing of Bayesian statistics. If the use of prior information is allowed, subjectivity is inevitably incorporated in the final decision. Therefore the best thing to do is to develop the rules which will translate subjective prior beliefs into a properly specified prior distribution.
Imagine you are a statistician hired to help with an applied problem: You have to determine how likely a given coin is to fall heads up. One should understand that when we are talking “coin tosses” and “heads,” we do not necessarily have actual coins in mind. We might model binary random events with probability of success being represented by a “head,” and probability of failure represented by a “tail” in a clinical trial setting, as well as while recommending medical treatment or investment decisions.
Statisticians rarely work on applied problems on their own; they become team members along with experts in the object field. An expert on coins joins you on the team and you two have to state the problem statistically and develop an experiment together. Both of you have agreed that available time and resources allow you to perform 10 independent identical tosses of the coin. The parameter of interest is probability of heads θ and the experimental data X = (X1, …, Xn) are results of tosses, n = 10, P(Xi = 1) = θ, P(Xi = 0) = 1 − θ, Xi being the random number of heads on each toss. This problem was considered above as an illustration of maximum likelihood estimation.
However, now you are allowed to observe the coin prior to the experiment and summarize the prior information. The coin expert can provide the knowledge and you will assist with putting this knowledge into the form of prior distribution on θ. The expert agrees that chances of the coin landing on its edge or disappearing in thin air during any toss are negligible, so that any outcomes other than heads or tails should not be taken into account. He also observes the coin and it looks symmetric. It is likely that the coin is fair, but the past experience tells the expert that some coins are biased either toward the heads or toward the tails. You ask him to quantify these considerations in terms of average expectations. Suppose that the expert concludes: on the average, θ is about 0.5, but this guess is expected to be off on the average by 0.1. You interpret this expert opinion in terms of two numbers: mean value E(θ) = 0.5 and variance Var(θ) = [st.dev.(θ)]2 = 0.01.
Now it is your time to specify the prior. The choice of beta family of distributions introduced in Section 1.5 for random θ is logical. It is a wide class including both symmetric and skewed, flat and peaked distributions: θ ∼ Beta(α, β), if its p.d.f. according to (1.25) is
for 0 < θ < 1, α ≥ 0, β ≥ 0. The cluster of gamma functions on the right-hand side does not depend on θ thus it is irrelevant for further analysis so we can write
Several Beta p.d.f.s for various parameter values are depicted in Figure 2.9, see also Figure 1.11.

Figure 2.9 Graphs of beta p.d.f.’s.
One of the representatives of the beta family will fit the requirements of E(θ) = 0.5 and Var(θ) = 0.01. Using formulas from Chapter 1 (1.26)
we can solve for α and β:
and
Then the expert’s opinion can be paraphrased as θ ∼ Beta(12, 12). This is our subjective prior. We will use this example in future because it works so well numerically.
Ten Coin Tosses
To complete our analysis and obtain the Bayes estimate for θ, consider an experiment with 7 heads in 10 tosses, ![]() . Using (2.16), we obtain the likelihood
. Using (2.16), we obtain the likelihood
and using (2.26), the posterior
The posterior is also a beta distribution shown along with the prior in Figure 2.10, so using the first part of formula (2.35) with new values α = 19 and β = 15, we obtain the numerical value of the Bayes estimate for θ
while the second part of (1.26) provides an error estimate

Figure 2.10 Graphs of prior (dotted) and posterior (solid) for subjective prior.
2.6.2 Objective Priors
The main benefit of the Bayesian approach to statistics is the ability to incorporate prior information. Suppose no prior information is available, and even object field experts cannot help. What could be the rationale for applying Bayesian approach instead of classical in such cases anyway? Why should we do it at all? One of possible motivations is the desire to stay within the Bayesian framework, which allows us to use integration instead of optimization (a purely technical reason) or assume randomness of parameters (a philosophical reason). This motivation is especially important in complex multiparameter studies, when prior information can be elicited for some of the parameters, but not for the others. If we could express the idea of no prior information as a special noninformative prior distribution, it would allow us to maintain Bayesian setting and derive joint posteriors for our multivariate parameters. For instance, we will be able to use nifty Bayesian software without the necessity to laboriously develop the prior distribution and to justify our subjective point. Just fill the blanks with objective noninformative priors and let computer do the work.
Objective priors are the priors that every expert should agree to use. They are usually weak, nonintrusive, nonviolent priors, which express as little reliance on the prior information as possible and put the emphasis on the data instead. There exist many approaches to the construction of noninformative priors based on certain mathematical principles: Jeffreys prior defined through Fisher information is justified by the idea of invariance to reparameterization [13]; reference priors introduced by Berger and Bernardo maximize the impact of the data on the posterior [2, 4]; maximum entropy priors introduced by Jaynes [12] and Zellner are derived from information-theoretical considerations; and probability matching priors use the idea that Bayesian credible intervals in the absence of prior information should be closely related to the classical confidence intervals.
Bayesian procedures with objective noninformative priors derived by all of these methods bring about results in most cases consistent with the procedures of classical (frequentist) statistics. However the choice of objective prior is not always obvious and sometimes no agreement is achieved between different constructions. Let us use the illustration from the previous subsection.
Ten Coin Tosses
Let us say the coin expert has no past experience with similar coins, and therefore has no opinion at all regarding the probability of heads θ prior to the experiment. Then the envelope is pushed to the statistician (that is you) to decide what prior to put in. An alternative would be to forget about Bayesian approach and resort to MLE, which for 7 observed heads out of 10 tosses provided us in Section 2.4 with the intuitively plausible estimate ![]() . However, if we still want to follow the Bayesian approach and take the posterior mean as the estimate of θ, we need to specify the prior, which in our case should be noninformative. An intuitively attractive uniform prior Beta(1, 1) happens to be off. Jeffreys’ prior, reference prior approach, and probability matching prior all point at a different choice of Beta(0.5, 0.5) with a horseshoe-shaped p.d.f
. However, if we still want to follow the Bayesian approach and take the posterior mean as the estimate of θ, we need to specify the prior, which in our case should be noninformative. An intuitively attractive uniform prior Beta(1, 1) happens to be off. Jeffreys’ prior, reference prior approach, and probability matching prior all point at a different choice of Beta(0.5, 0.5) with a horseshoe-shaped p.d.f
This choice of the horseshoe distribution, though a bit strange at first sight, is justifiable not just mathematically (three different approaches lead to the same decision!) but also intuitively. Just think outside of the coin framework. In general, we are talking about some random event of which we know nothing in advance. What can we say about the probability of this event? Should it be uniformly spread on the interval from 0 to 1? Is it equally likely to be almost impossible (probability close to 0), 50-50 like a fair coin toss (close to the middle of the interval), or almost inevitable (probability close to 1?) Where do the majority of random events in our lives belong?
One can argue that most of the random events in our everyday lives are either almost impossible or almost inevitable. The authors of this book, as most of the other people, have daily routines they tend to follow. Coffee in the morning? Almost inevitable for one of us and almost impossible for the other. Walking to work and back? Almost impossible for one of us and almost inevitable for the other. Both of us show up for classes according to our schedules. There are always slight chances for the opposite to happen, but most of the daily routines are set up firmly. Sun rises, traffic flows, birds fly south in the Fall. You do not often toss a coin to determine whether to eat a lunch or whether to teach a class. If we look closely, there are many random events in our everyday lives, but very few of them have 50-50 chances to happen. Visualize a horseshoe-shaped p.d.f. with the minimum in the middle and most of the probability mass concentrated at both ends.
If you are satisfied with the justification above, let us adopt Beta(0.5, 0.5) prior and evaluate the posterior as we did for subjective prior:
The numerical value of the objective Bayes estimate is
If you still insist on the uniform (you could), this is still a possibility, even if it lacks a good mathematical justification. If taken as a prior, it will not lead us to a grave mistake. We obtain the posterior
and
You can see both priors (uniform and horseshoe) and both corresponding posteriors in Figure 2.11. You can see that the posteriors are relatively close. It can be easily seen that for larger dataset sizes the role of prior becomes less and less visible, and all posteriors look alike. By the way, it is also true for subjective priors.

Figure 2.11 Graphs of priors and posteriors for objective priors.
As we see from Figure 2.11, both Beta(0.5, 0.5) and uniform Beta(1, 1) are not completely uninformative: objective Bayes estimates are still numerically different from MLE. In order to assign a prior for which posterior mean is exactly equal to MLE, we will have to consider an even more radical option Beta(0, 0), also known as Haldane’s prior. This prior is improper. It means that it is not a proper probability distribution in the sense that the area under its density does not integrate to 1 and it even admits events of infinite probability. Though it seems a horrible thing to happen, improper priors play their role in Bayesian analysis, and their use does not bring about any big problems unless they lead to improper posteriors, which is a real disaster preventing any meaningful Bayesian inference. Haldane’s prior with nonempty dataset n ≥ 1 leads to proper posteriors, thus it is usable. We will not emphasize the use of improper priors though sometimes they provide valid noninformative choices.
2.6.3 Empirical Bayes
The empirical Bayes approach to the development of priors is all about using empirical information. In general, we should not use the information from our data to choose the prior. That would constitute a clear case of double dipping: One should not use the same data twice—to choose a prior first, and then to develop the posterior. However, if additional information regarding the distribution of parameter is available, it can be used even if it is not directly relevant to our experiment [9, 19].
Ten Coin Tosses
Suppose we have never tossed our coin yet, so the experiment was not yet performed. It is possible though to have a record of five similar experiments with five other coins which have been tossed before. For the sake of simplicity, assume that each of these five coins was tossed 10 times leading to different numbers of heads: 5, 3, 6, 7, 5. These coins are different from ours, so these results are not directly relevant to the value of θ we want to estimate. However, if we believe the five coins in prior experiments to be somewhat similar to ours, they give us an idea of the distribution of θ over the population of all coins.
If we still decide to go for a beta prior, we will use neither expert estimates nor objective priors, but will estimate prior parameters α and β directly from the empirical data of five prior experiments. We can obtain method of moments estimates
and then using (1.26) solve for ![]() and
and ![]() :
:
Then the empirical Bayes prior is θ ∼ Beta(5.38, 4.97) in Figure 2.12.

Figure 2.12 Graphs of prior (dotted) and posterior (solid) for empirical prior.
To obtain the Bayes estimate for θ for the experiment with 7 heads in 10 tosses, ![]() , calculate the posterior
, calculate the posterior
and the estimate for θ is given by
The empirical Bayes approach is more powerful than this example may suggest. First of all, in the presence of empirical information it is not always necessary even to define the prior distribution as belonging to a certain parametric family. Instead, one can use nonparametric Bayes approach.
Nonparametric Bayes modeling is a very hot topic in modern statistics. A Bayesian nonparametric model is by definition a Bayesian model on an infinite-dimensional parametric space, which represents the set of all possible solutions for a given problem (such as the set of all densities in nonparametric density estimation). Bayesian nonparametric models have recently been applied to a variety of machine learning problems including regression, classification, and sequential modeling. However this is out of the focus of the book. We will illustrate nonparametric empirical Bayes on the classical compound Poisson example by Robbins [18], see also Carlin and Louis [8].
Compound Poisson Sample
Let us consider an integer-valued sample x = (x1, …, xn) from compound Poisson distribution, where each element has Poisson distribution with its own individual parameter value θi corresponding to the distribution mean. This sample can represent a heterogeneous population of insurance customers with Poisson claims rates that vary across the population. Our goal is to estimate the entire vector of parameters θ = (θ1, …, θn). Bayesian approach suggests calculating posterior means
and we will try to do it without explicitly specifying the prior π(θ). Recall that the integral in the denominator of (2.41) is known as the marginal distribution of the data point xi:
and manipulating the formula of Poisson likelihood

we can also rewrite the numerator in (2.41) as
Combining expressions for the numerator and the denominator, obtain
The only way the prior is included in this formula is inside the marginals. But the marginals can be estimated directly from the data. Suppose that the initial sample contains only k ≤ n distinct values yj, so that x = (y1, …, yk), ![]() is the number of xi: xi = yj, and n = ∑kj = 1N(yj). Then it is reasonable to use
is the number of xi: xi = yj, and n = ∑kj = 1N(yj). Then it is reasonable to use

to estimate the Poisson rates of individual observations.
Nonparametric Bayes approach is becoming increasingly popular in the recent years, especially in the context of discrete distributions for relatively small samples with a large number of parameters.
2.7 Conjugate Distributions
The continuous version of the Bayes theorem completely solves the problem of representing the posterior through the prior and the likelihood. However the analytical derivation of the posterior is rarely feasible. In particular, such solution is possible if the data distribution obtains a so-called conjugate prior.
Definition A family of parameter distributions is called conjugate with respect to given data distribution (likelihood), if application of the Bayes Theorem to the data with a prior from this family brings about a posterior from the same family.
If we start with a prior, it is not hard to determine whether, after multiplication by the likelihood, the posterior belongs to the same family as the prior. We have done exactly that in the previous section with the ten coin example, where a prior distribution from Beta family seems logical. However, not all likelihoods will have a conjugate family. In some (but not all) interesting examples a sufficient condition for a likelihood to obtain a conjugate prior can be formulated.
2.7.1 Exponential Family
The condition of existence of a conjugate prior (2.42) is satisfied for the exponential family, see [7]. Distribution density function for the exponential family can be represented as
Many well-known distributions belong to the exponential family (do not confuse with the exponential distribution defined in Section 1.4: the latter is just a particular case of the exponential family).
The likelihood has a similar form
but the data are fixed and the parameter is treated as a random variable. Thus the factor ∏ni = 1B(xi) is a constant with no further effect. The conjugate prior has the same form as the likelihood:
Here k and l are some constants determining the shape of the distribution. Since posterior is proportional to the product of the prior and likelihood, we obtain
Therefore, the posterior belongs to the same conjugate family as the prior with constants k* = k + n; l* = l + ∑ni = 1T(xi) depending on the likelihood. Let us provide one example of a conjugate family.
2.7.2 Poisson Likelihood
Poisson distribution introduced in Section 1.2 characterizes random number X of events in a stationary flow occurring during a unit of time. Let us denote the intensity parameter (average number of events during the unit of time) by θ. Distribution of this random variable can be presented as
Poisson distribution belongs to the exponential family with
From this expression, the conjugate prior distribution is
which corresponds to Gamma(α, λ) family with k = λ, l = α − 1.
Let us arrange a sample of n independent copies of the variable X and denote it by (x1, …, xn). Likelihood function then can be expressed as
Therefore the posterior can be represented as
which is also a gamma distribution with parameters α + ∑xi and λ + n. Using formulas for the moments of gamma distribution (1.19), we also obtain the general form of Bayes estimator as the posterior mean:
The smooth transition from prior to posterior in the problem of ten coin tosses discussed in Sections 2.3, 2.4, and 2.6 is explained by conjugate beta prior for binomial likelihood.
2.7.3 Table of Conjugate Distributions
Let us list the basic conjugate families of distributions.
| Distribution of data (likelihood) | Conjugate prior/posterior |
| Normal (known variance) | Normal |
| Exponential | Gamma |
| Uniform | Pareto |
| Poisson | Gamma |
| Binomial | Beta |
| Pareto | Gamma |
| Negative binomial | Beta |
| Geometric | Beta |
| Gamma | Gamma |
References
- Berger, J. O. (1993). Statistical Decision Theory and Bayesian Analysis. Springer Verlag.
- Berger, J. O., Bernardo, J. M., and Sun, D. (2009). The formal definition of reference priors. Annals of Statistics, 37(2), 905.
- Berger, J. O., and Berry, D.A. (1988). Statistical analysis and the illusion of objectivity. American Scientist, 76(2), 159–165.
- Bernardo, J., and Smith, A. F. M. (1994). Bayesian Theory. New York: John Wiley & Sons, Inc.
- Berndt, E. R. (1991). The Practice of Econometrics: Classic and Contemporary. Addison-Wesley.
- Bliss, E. (2012). A concise resolution to two envelope paradox, arXiv:102.4669v3.
- Bolstad, W.M. (2007). Introduction to Bayesian Statistics, 2nd ed. John Wiley and Sons, Ltd.
- Carlin, B. P., and Louis, T. A. (2008). Bayesian Methods for Data Analysis, 3rd ed. Oxford: Chapman & Hall.
- Casella, G. (1985). An introduction to empirical Bayes data analysis. American Statistician, 39(2), 83.
- Fisher, R. A. (1935). The Design of Experiments, Macmillan.
- Gelman, A.,Carlin, J., Stern, H., and Rubin, D. (1995). Bayesian Data Analysis. London: Chapman & Hall.
- Jaynes, E. T. (2003). Probability Theory: The Logic of Science, Cambridge University Press.
- Jeffreys, H. (1961). Theory of Probability, 3rd ed. Classic Texts in the Physical Sciences. Oxford: Oxford University Press.
- Kass, R. E., and Raftery, A. E. (1995). Bayes factors. Journal of the American Statistical Association, 90(430), 773–795.
- Kass, R. E, and Wasserman, L. A. (1996). The selection of prior distributions by formal rules. Journal of the American Statistical Association, 91(435), 1343–1370.
- Kruschke, J. (2014). Doing Bayesian Data Analysis. A Tutorial with R, JAGS and Stan, 2nd ed. Elsevier, Academic Press.
- Lee, P. M. (1989). Bayesian Statistics. London: Arnold.
- Robbins, H. (1956). An empirical Bayes approach to statistics. In: Proceedings of the Third Berkeley Symposium on Mathematical Statistics and Probability, Volume 1: Contributions to the Theory of Statistics, 157–163.
- Rossi, P. E., Allenby, G. M., and McCulloch, R. (2006). Bayesian Statistics and Marketing, John Wiley & Sons, Ltd.
- Salsburg, D. (2002). The Lady Tasting Tea: How Statistics Revolutionized Science in the Twentieth Century, W. H. Freeman/Owl Book.
- Savage, L. J. (1962). Letter to J. Cornfield, 22 February 1962, Leonard Savage Papers (MS 695), New Haven, CT: Yale University Library, 6, 161.
- Tsikogiannopoulos, P. (2014). Variations on the two envelopes problem. Hellenic Mathematical Society Journal, 3, 77.
Exercises
-
Suppose that the hourly wage W has a gamma distribution. Suppose that the mean value E(W) of this variable is 20 USD per hour and the standard deviation σ(W) is 5 USD.
Recall from (1.19) that gamma distribution Gamma(α, λ) has moments E(W) = α/λ and Var(W) = α/λ2.
Suppose that in the setting of the two envelope problem the job offer is applied not to annual salaries, but to hourly wages. The open envelope has an offer of 18 USD per hour. Calculate the values of the distribution density f(w) for w = 9 and w = 36 (using < ?TeXR? > or other software). What is the more likely value? Which of the envelopes should be chosen?
-
Suppose that the sample of human life lengths in years provided on the companion website in the file survival.xlsx comes from a Gamma(α, λ) distribution. Estimate it using MLE (numerical optimization in Excel or R using formula (1.19), see MLE.xlsx) and the method of moments. Compare the results.
-
Supose that the sample of human life lengths in years provided in the file survival.xlsx comes from a Weibull(λ, τ) distribution. Estimate its parameters using MLE (write down the likelihood function and use numerical optimization in Excel or R).
-
For the following problem of deciding between two simple hypotheses (normal with unknown mean and known variance) by a sample of size 1 (single observation), H0: N(0, 1) versus simple alternative H1: N(2, 1) use the test statistic
 and determine its critical region for
and determine its critical region for- Classical test with significance level 0.05 (also, what is the power of this test?)
- Bayesian test with prior probability P(H0) = 3/4 using posterior odds 1:1.
-
Suppose that a single observation is to be drawn from the following p.d.f.: f(x|θ) = (θ + 1)x− (θ + 2), 1 ≤ x < ∞, where the value of θ is unknown. Suppose that the following hypotheses are to be tested: null hypothesis H0: θ = 0 versus simple alternative H1: θ = 1
-
Determine (in terms of the rejection region) the Bayesian test procedure, corresponding to prior probability P(H0) = 1/2 and posterior odds (the Bayes factor) 1: 1; 3: 1 (substantial evidence) and 10: 1 (strong evidence).
-
Determine (in terms of the rejection region) the Bayesian test procedure, corresponding to prior probability P(H0) = 1/3 and posterior odds 1: 1.
-
Determine (in terms of the rejection region) the Bayesian test procedure, corresponding to prior probability P(H0) = 2/3 and posterior odds 1: 1.
-
-
Estimate posterior mean θ with Poisson likelihood for the exponential prior with the prior mean E(θ) = 2 and the data vector x = (3, 1, 4, 3, 2).
-
Random variable X corresponds to the daily number of accidents in a small town during the first week of January. From the previous experience (prior information), local police Chief Smith tends to believe that the mean daily number of accidents is 2 and the variance is also 2. We also observe for the current year the sample number of accidents for 5 days in a row: 5 , 2 , 1 , 3 , 3. Let us assume that X has Poisson distribution with parameter θ. Using the gamma prior (Hint: suggest values for the parameters of prior distribution using Chief Smith’s previous experience and formulas for the moments of gamma distribution), determine:
-
the posterior distribution of the parameter θ given the observed sample;
-
according to Chief Smith, the Bayesian estimate of the parameter θ (posterior mean);
-
ignoring the prior information, the maximum likelihood estimate of the parameter θ.
-
-
Prove that using posterior mean as an estimator of θ for normal data with unknown mean and known variance Xi ∼ N(θ, σ2), i = 1, …, n with normal prior π(θ) ∼ N(μ, τ2) brings about

(Hint: Use the definition of normal density, basic algebra, and complete the square in the exponential term of the formula for posterior density). Use this formula to obtain Bayesian estimate for the case n = 10,
 , σ2 = 3, μ = 0, τ2 = 2.
, σ2 = 3, μ = 0, τ2 = 2. -
Prove that binomial distribution Bin(n, θ) for fixed n with unknown probability of success θ belongs to the exponential family. Provide a factorization similar to (2.42).
-
Using the result of the previous problem, prove that beta family provides conjugate priors for binomial distribution.