Appendix A Complex Numbers
A.1 Arithmetic Operations and Properties
Introduction No one person “invented” complex numbers, but controversies surrounding the use of these numbers existed in the sixteenth century. In their quest to solve polynomial equations by formulas involving radicals early dabblers in mathematics were forced to admit that there were other kinds of numbers besides positive integers. Equations such as x2 − 2x + 2 = 0 and x3 + 6x2 + 11x = 0 that yielded “solutions” 1 + ![]() and − 3 −
and − 3 − ![]() caused particular consternation within the community of fledgling mathematical scholars because everyone knew that there are no numbers such as
caused particular consternation within the community of fledgling mathematical scholars because everyone knew that there are no numbers such as ![]() and
and ![]() , numbers whose square is negative. Such “numbers” exist only in one’s imagination, or as one philosopher opined “the imaginary, the bosom child of complex mysticism.” Over time these “imaginary numbers” did not go away, mainly because mathematicians as a group are tenacious and some are even practical. A famous mathematician held that even though “they exist in our imagination … nothing prevents us from … employing them in calculations.” Mathematicians also hate to throw anything away. After all, a collective memory still lingered that negative numbers at first were branded “fictitious.” The concept of number evolved over centuries; gradually the set of numbers grew from just positive integers to include rational numbers, negative numbers, and irrational numbers. But in the eighteenth century the number concept took a gigantic evolutionary step forward when the German mathematician Carl Friedrich Gauss put the so-called imaginary numbers, or as they were now beginning to be called complex numbers, on a logical and consistent footing by treating them as an extension of the real number system.
, numbers whose square is negative. Such “numbers” exist only in one’s imagination, or as one philosopher opined “the imaginary, the bosom child of complex mysticism.” Over time these “imaginary numbers” did not go away, mainly because mathematicians as a group are tenacious and some are even practical. A famous mathematician held that even though “they exist in our imagination … nothing prevents us from … employing them in calculations.” Mathematicians also hate to throw anything away. After all, a collective memory still lingered that negative numbers at first were branded “fictitious.” The concept of number evolved over centuries; gradually the set of numbers grew from just positive integers to include rational numbers, negative numbers, and irrational numbers. But in the eighteenth century the number concept took a gigantic evolutionary step forward when the German mathematician Carl Friedrich Gauss put the so-called imaginary numbers, or as they were now beginning to be called complex numbers, on a logical and consistent footing by treating them as an extension of the real number system.
Our goal in this first appendix section is to examine some basic definitions and the arithmetic of complex numbers.
![]() The Imaginary Unit Even after gaining wide respectability, through the seminal works of Carl Friedrich Gauss and the French mathematician Augustin Louis Cauchy (1789–1857), the unfortunate name “imaginary” has survived down the centuries. The symbol i was originally used as a disguise for the embarrassing symbol
The Imaginary Unit Even after gaining wide respectability, through the seminal works of Carl Friedrich Gauss and the French mathematician Augustin Louis Cauchy (1789–1857), the unfortunate name “imaginary” has survived down the centuries. The symbol i was originally used as a disguise for the embarrassing symbol ![]() . We now say that i is the imaginary unit and define it by the property i2 = −1. Nevertheless, it is still common practice to write i =
. We now say that i is the imaginary unit and define it by the property i2 = −1. Nevertheless, it is still common practice to write i = ![]() . Indeed, using the last symbol we are able to define the principal square of a negative number as follows.
. Indeed, using the last symbol we are able to define the principal square of a negative number as follows.
DEFINITION A.1.1 Principal Square Root
If c is a positive real number, then the principal square root of −c is defined by
![]()
EXAMPLE 1 Principal Square Roots
Find the principal square root of (a) ![]() and (b)
and (b) ![]() .
.
Solution From (1) of Definition A.1.1,
![]()
![]() Terminology The complex number system contains the imaginary unit i, all real numbers, products such as bi, b real, and sums such as a + bi, where a and b are real numbers. In particular, a complex number is defined to be any expression of the form
Terminology The complex number system contains the imaginary unit i, all real numbers, products such as bi, b real, and sums such as a + bi, where a and b are real numbers. In particular, a complex number is defined to be any expression of the form
![]()
Be careful here, the imaginary part of a + bi, is not bi; it is the real number b. ![]()
where a and b are real numbers and i2 = −1. The form given in (2) is called the standard form of a complex number. The numbers a and b are called the real and imaginary parts of z, respectively. A complex number of the form 0 + bi is said to be a pure imaginary number. Note that by choosing b = 0 in (2), we obtain a real number. Thus the set R of real numbers is a subset of the set C of complex numbers.
EXAMPLE 2 Real and Imaginary Parts
(a) The complex number z = 4 + (−5)i is written as z = 4 − 5i. The real part of z is 4 and its imaginary part is −5.
(b) z = 10i is a pure imaginary number.
(c) z = 6 + 0i = 6 is a real number.
EXAMPLE 3 Writing in the Standard Form a + bi
Express each of the following in the standard form a + bi.
![]()
Solution Using (1) of Definition A.1.1, we can write
![]()
In order to solve certain equations involving complex numbers, it is necessary to specify when two complex numbers are equal.
DEFINITION A.1.2 Equality of Complex Numbers
Two complex numbers are equal if and only if their real parts are equal and imaginary parts are equal. That is, if z1 = a + bi and z2 = c + di,
z1 = z2 if and only if a = c and b = d.
EXAMPLE 4 A Simple Equation
Solve for x and y:
(2x + 1) + (−2y + 3)i = 2 − 4i.
Solution By Definition A.1.2 we must have
2x + 1 = 2 and −2y + 3 = −4.
Solving each equation yields ![]() and
and ![]() .
.
Addition and multiplication for complex numbers are defined as follows.
DEFINITION A.1.3 Sum, Difference, and Product
If z1 + a + bi and z2 = c + di, then
| (i) their sum is given by | z1 + z2 = (a + c) + (b + d)i |
| (ii) their difference is given by | z1 − z2 = (a − c) + (b − d)i |
| (iii) and their product is given by | z1z2 = (ac − bd) + (bc + ad)i |
![]() Properties of Complex Numbers Using the definition of addition and multiplication of complex numbers, it can be shown that many of the basic properties of the real number system also apply to the complex number system. In particular, the associative, commutative, and distributive laws hold for complex numbers. We further observe that in Definition A.1.3(i):
Properties of Complex Numbers Using the definition of addition and multiplication of complex numbers, it can be shown that many of the basic properties of the real number system also apply to the complex number system. In particular, the associative, commutative, and distributive laws hold for complex numbers. We further observe that in Definition A.1.3(i):
• The sum of two complex numbers is obtained by adding their corresponding real and imaginary parts.
Similarly, Definition A.1.3(ii) shows that
• The difference of two complex numbers is obtained by subtracting their corresponding real and imaginary parts.
Also, rather than memorizing (iii) of Definition A.1.3:
• The product of two complex numbers can be obtained by using the associative, commutative, and distributive laws and the fact that i2 = −1.
Applying this approach, we find that

This is the same result as the product given by Definition A.1.3(iii). These techniques are illustrated in the following example.
EXAMPLE 5 Sum, Difference, and Product
If z1 = 5 − 6i and z2 = 2 + 4i, find (a) z1 + z2, (b) z1 − z2, and (c) z1z2.
Solution (a) The colors in the diagram below show how to add z1 and z2:

(b) Analogous to part (a) we now subtract the real and imaginary parts:
z1 − z2 = (5 − 6i) − (2 + 4i) = (5 - 2) + (−6 −4)i = 3 −10i.
(c) Using the distributive law, we write the product (5 − 6i)(2 + 4i) as

Note of Caution ![]()
Not all the properties of the real number system hold for complex numbers. In particular, the property of radicals ![]() is not true when both a and b are negative. To see this, consider that
is not true when both a and b are negative. To see this, consider that
![]()
Thus, ![]() . However, if only one of a or b is negative, then we do have
. However, if only one of a or b is negative, then we do have ![]() .
.
In the set C of complex numbers, the additive identity is the number 0 = 0 + 0i, and the multiplicative identity is the number 1 = 1 + 0i. The number −z = −a − bi is called the additive inverse of z = a + bi because
z + (− z) = z − z = (a − a) + (b − b)i = 0 + 0i = 0.
In order to obtain the multiplicative inverse of a nonzero complex number z = a + bi, we introduce the concept of the conjugate of a complex number.
DEFINITION A.1.4 Conjugate
If z = a + bi is a complex number, then the number ![]() = a − bi is called the conjugate of z.
= a − bi is called the conjugate of z.
In other words, the conjugate of a complex number z = a + bi is the complex number obtained by changing the sign of its imaginary part. For example, the conjugate of 8 + 13i is 8 − 3i, and the conjugate of −5 − 2i is −5 + 2i.
The following computations show that both the sum and the product of a complex number z and its conjugate ![]() are real numbers:
are real numbers:
![]()
The latter property makes conjugates very useful in finding the multiplicative inverse 1/z, z ≠ 0, and in dividing two complex numbers.
We summarize the procedure.
• To divide a complex number z1 by a complex number z2, multiply the numerator and denominator of z1/z2 by the conjugate of the denominator z2. That is,
![]()
and then use the fact that the product ![]() is the sum of the squares of the real and imaginary parts of z2.
is the sum of the squares of the real and imaginary parts of z2.
EXAMPLE 6 Division
For z1 = 3 − 2i and z2 = 4 + 5i, express the given complex number in the form a + bi.
![]()
Solution In each case, we multiply both the numerator and the denominator by the conjugate of the denominator and simplify.

From the definition of addition and subtraction of two complex numbers, it is readily shown that the conjugate of a sum and difference of two complex numbers is the sum and difference of the conjugates. This property, along with three other properties of the conjugate are summarized as a theorem.
THEOREM A.1.1 Properties of the Conjugate
Let z1 and z2 be any two complex numbers. Then

Of course, the conjugate of any finite sum (product) of complex numbers is the sum (product) of the conjugates.
![]() Quadratic Equations Complex numbers make it possible to solve quadratic equations ax2 + bx + c = 0 when the discriminant b2 − 4ac is negative. We now see that the solutions from the quadratic formula
Quadratic Equations Complex numbers make it possible to solve quadratic equations ax2 + bx + c = 0 when the discriminant b2 − 4ac is negative. We now see that the solutions from the quadratic formula
![]()
represent complex numbers. Note that in fact the solutions are conjugates of each other. As the next example shows these solutions can be written in standard form.
EXAMPLE 7 Complex Solutions
Solve x2 − 8x + 25 = 0.
Solution From the quadratic formula, we obtain
![]()
Using ![]() we obtain
we obtain
![]()
Thus, the solution set of the equation is ![]() .
.
![]() Conjugate Solutions As we already know from Theorem 3.3.4 on page 151, if a polynomial function f(x) has real coefficients, then complex roots of the polynomial equation f(x) = 0 appear in conjugate pairs. Observe in Example 7 that if x1 = 4 − 3i and x2 = 4 + 3i, then
Conjugate Solutions As we already know from Theorem 3.3.4 on page 151, if a polynomial function f(x) has real coefficients, then complex roots of the polynomial equation f(x) = 0 appear in conjugate pairs. Observe in Example 7 that if x1 = 4 − 3i and x2 = 4 + 3i, then ![]() = x1. Moreover, it is easily seen that
= x1. Moreover, it is easily seen that ![]() = x2.
= x2.
A.1 Exercises Answers to selected odd-numbered problems begin on page ANS-31.
In Problems 1–10, find the indicated power of i.
1. i3
2. i4
3. i5
4. i6
5. i7
6. i8
7. i−1
8. i−2
9. i−3
10. i−6
In Problems 11–56, perform the indicated operation. Write the answer in standard form a + bi.
11. ![]()
12. ![]()
13. ![]()
14. ![]()
15. (3 + i) − (4 − 3i)
16. (5 + 6i) + (−7 + 2i)
17. 2(4 − 5i) + 3(−2 −i)
18. −2(6 + 4i) + 5(4 − 8i)
19. i(−10 + 9i) − 5i
20. i(4 + 13i) − i(1 − 9i)
21. 3i(1 + i) − 4(2 − i)
22. i + i(1 − 2i) + (i4 + 3i)
23. (3 − 2i)(1 − i)
24. (4 + 6i)(−3 + 4i)
25. (7 + 14i)(2 + i)
26. ![]()
27. (4 + 5i) − (2 − i)(1 + i)
28. (− 3 + 6i) + (2 + 4i)(−3 + 2i)
29. i(1 − 2i)(2 + 5i)
30. ![]()
31. (1 + i)(1 + 2i)(1 + 3i)
32. (2 + i)(2 − i)(4 − 2i)
33. (1 − i)[2(2 − i) − 5(1 + 3i)]
34. (4 + i)[i(1 + 3i) − 2(−5 + 3i)]
35. (4 + i)2
36. (3 − 5i)2
37. (1 − i)2(1 + i)2
38. (2 + i)2(3 + 2i)2
39. ![]()
40. ![]()
41. ![]()
42. ![]()
43. ![]()
44. ![]()
45. ![]()
46. ![]()
47. ![]()
48. ![]()
49. ![]()
50. ![]()
51. ![]()
52. ![]()
53. ![]()
54. ![]()
55. ![]()
56. ![]()
In Problems 57–64, use Definition A.1.2 to solve for x and y.
57. 2(x + yi) = i(3 − 4i)
58. (x + yi) + 4(1 − i) = 5 − 7i
59. i(x + yi) = (1 − 6i)(2 + 3i)
60. 10 + 6yi = 5x + 24i
61. (1 + i)(x − yi = i(14 + 7i) − (2 + 13i)
62. i2(1 − i)(1 + i) = 3x + yi + i(y + xi)
63. ![]()
64. 25 − 49i = x2 − y2i
In Problems 65–76, solve the given equation.
65. x2 + 9 = 0
66. x2 + 8 = 0
67. 2x2 = −5
68. 3x2 = −1
69. 2x2 − x + 1 = 0
70. x2 − 2x + 10 = 0
71. x2 + 8x + 52 = 0
72. 3x2 + 2x + 5 = 0
73. 4x2 − x + 2 = 0
74. x2 + x + 2 = 0
75. x4 + 3x2 + 2 = 0
76. 2x4 + 9x2 + 4 = 0
77. The two square roots of the complex number i are the two numbers z1 and z2 that are solutions of the equation z2 = i. Let z = x + iy and find z2. Then use Definition A.1.2 to find z1 and z2.
78. Proceed as in Problem 77 to find two numbers z1 and z2 that satisfy the equation z2 = −3 + 4i.
For Discussion
In Problems 79–82, prove the given properties involving the conjugates of z1 = a + bi and z2 = c + di.
79. ![]() if and only if z1 is a real number.
if and only if z1 is a real number.
80. ![]()
81. ![]()
82. ![]()
A.2 Trigonometric Form of Complex Numbers
Introduction A complex number z = a + bi is uniquely determined by an ordered pair of real numbers (a,b). The first and second entries of the ordered pairs correspond, in turn, with the real and imaginary parts of the complex number. For example, the ordered pair (2, −3) corresponds to the complex number z = 2 − 3i. Conversely, the complex number z = 2 − 3i determines the ordered pair (2, −3). The numbers 10, i, and −5i are equivalent to (10, 0), (0, 1), and (0, −5), respectively. In this manner we are able to associate a complex number z = a + bi with a point (a,b) in a rectangular coordinate system.
![]() Complex Plane Because of the correspondence between a complex number z = a + bi and one and only one point P(a, b) in a coordinate plane we shall use the terms complex number and point interchangeably. The coordinate plane illustrated in FIGURE A.2.1 is called the complex plane or simply the z-plane. The horizontal or x-axis is called the real axis because each point on that axis represents a real number. The vertical or y-axis is called the imaginary axis because a point on that axis represents a pure imaginary number.
Complex Plane Because of the correspondence between a complex number z = a + bi and one and only one point P(a, b) in a coordinate plane we shall use the terms complex number and point interchangeably. The coordinate plane illustrated in FIGURE A.2.1 is called the complex plane or simply the z-plane. The horizontal or x-axis is called the real axis because each point on that axis represents a real number. The vertical or y-axis is called the imaginary axis because a point on that axis represents a pure imaginary number.
FIGURE A.2.1 Complex plane
FIGURE A.2.2 The complex numbers in Example + interpreted as points
EXAMPLE 1 Graphing Complex Numbers
Graph the complex numbers
z1 = 5 + 4i, z2 = −2i, z3 = −2 − 3i and z4 = −4 + 2i
Solution We identify the complex numbers z1, z2,z3,z4 with the points (5, 4), (0, −2), (−2, −3), (−4, 2), respectively. These points are, in turn, the red, blue, green, and orange dots in FIGURE A.2.2.
FIGURE A.2.3 Modulus and argument of a complex number z
![]() Trigonometric Form If z = a + bi is a nonzero complex number and P(a, b) is its geometric representation, as shown in FIGURE A.2.3, then the distance from P to the origin is given by
Trigonometric Form If z = a + bi is a nonzero complex number and P(a, b) is its geometric representation, as shown in FIGURE A.2.3, then the distance from P to the origin is given by ![]() . This distance is called the modulus, magnitude, or absolute value of z and is denoted by |z|,
. This distance is called the modulus, magnitude, or absolute value of z and is denoted by |z|,
![]()
For example, if z = i, then |i| = ![]() ; if z = 3 − 4i, then |3 − 4i| =
; if z = 3 − 4i, then |3 − 4i| = ![]() . From (4) of Section A.1, we know that if
. From (4) of Section A.1, we know that if ![]() = a − bi is the conjugate of z = a + bi, then
= a − bi is the conjugate of z = a + bi, then ![]() . Hence (1) can also be written as
. Hence (1) can also be written as
![]()
If we let θ be the angle in standard position whose terminal side passes through P(a, b) and r = |z|, then cos θ = a/r and sin θ = b/r, from which we obtain a = r cos θ and b = r sin θ. Substituting these expressions for a and b in z = a + bi, we obtain z = a + bi = (r cosθ) + (r sin θ)i or
![]()
We say that (2) is the trigonometric form, or polar form, of the complex number z. The angle θ is called the argument of z and satisfies tan θ = b/a. However, θ is not necessarily arctan(b/a) since θ is not restricted to the interval (−π/2, π/2). See Examples 2 and 3 that follow. Also, the argument θ is not uniquely determined, since cos θ = cos(θ + 2kπ;) and sin θ = sin(θ + 2kπ) for any integer k. If z = a + bi = 0, then a = b = 0. In this case, r = 0 and we can take any angle θ as the argument.
FIGURE A.2.4 Complex number in part (a) of Example 2
FIGURE A.2.5 Complex number in part (b) of Example 2
EXAMPLE 2 Trigonometric Form
Write the complex numbers in trigonometric form: (a) 1 + i (b) 1 − ![]() .
.
Solution (a) If we identify a = 1 and b = 1, then the modulus of 1 + i is
![]()
Because tan θ = b/a = 1 and the point (1, 1) lies in the first quadrant, we can take the argument of the complex number to be θ = π/4, as shown in FIGURE A.2.4. Thus,
![]()
(b) In this case,
![]()
From tan θ = ![]() and the fact that
and the fact that ![]() lies in the fourth quadrant, tan−1
lies in the fourth quadrant, tan−1![]() , as shown in FIGURE A.2.5. Thus, we take
, as shown in FIGURE A.2.5. Thus, we take
![]()
Following convention, in the remainder of the discussion as well as in Exercises A.2 we will take the argument θ of a complex number z either as an angle in measured radians in the interval [0, 2π) or an angle measured in degrees that satisfies 0 ≤ θ <, 360°. For example, the answer in part (b) of Example 2 can be written in the alternative form
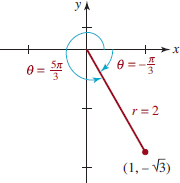
Note ![]()
![]()
The argument of 1 − ![]() that lies in the interval [0, 2π) is θ = 5π/3, as is shown in Figure A.2.5.
that lies in the interval [0, 2π) is θ = 5π/3, as is shown in Figure A.2.5.
EXAMPLE 3 Trigonometric Form
Express the complex number
![]()
in the standard form z = a + bi.
Solution By using the reference angle concept discussed in Section 4.2, we find cos(7π/4) = ![]() and sin(7π/4) =
and sin(7π/4) = ![]() . Therefore,
. Therefore,
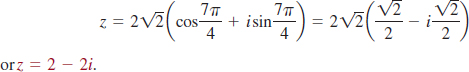
EXAMPLE 4 Trigonometric Form
Find the trigonometric form of z = −4 + 5i.
Solution The modulus of z = −4 + 5i is
![]()
Because the point (−4, 5) lies in the second quadrant, we must take care to adjust the value of the angle obtained from tanθ = ![]() and a calculator so that our final answer is a quadrant II angle. See FIGURE A.2.6. One approach is to use a calculator set in radian mode to obtain the reference angle θ′ = tan
and a calculator so that our final answer is a quadrant II angle. See FIGURE A.2.6. One approach is to use a calculator set in radian mode to obtain the reference angle θ′ = tan![]() radian. The desired second-quadrant angle is then θ = π − θ′ ≈ = 2.2455. Thus,
radian. The desired second-quadrant angle is then θ = π − θ′ ≈ = 2.2455. Thus,
![]()
Alternatively the foregoing trigonometric form can be written using a degree-measured angle. With the calculator set in degree mode, we would obtain θ′ ≈ 51.34° and θ = 180° − θ′ ≈ 128.66°, from which it follows that
![]()
FIGURE A.2.6 Complex number in Example 4
EXAMPLE 5 Modulus and Argument of a Product
Find the modulus and the argument of z1z2, where z1 = 2i and z2 = 1 + i.
Solution The product is
z1z2 = 2i(1 + i) = −2 + 2i,
and hence the modulus is
![]()
By identifying a = −2 and b = 2, we have tan θ = −1. Since θ is a second quadrant angle, we conclude that the argument of z1z2 is θ = 3π/4. See FIGURE A.2.7.
FIGURE A.2.7 The product in Example 5
![]() Multiplication and Division In Example = notice that the modulus r = 2
Multiplication and Division In Example = notice that the modulus r = 2![]() of the product z1z2 is the product of the modulus r1 = 2 of z1 and the modulus r2 =
of the product z1z2 is the product of the modulus r1 = 2 of z1 and the modulus r2 = ![]() of z2. Also, the argument θ = 3π/4 of z1z2 is the sum of the arguments θ1 = π/2 and θ2 = π/4 of z1 and z2, respectively. We have illustrated a particular case of the following theorem, which describes how to multiply and divide complex numbers when they are written in trigonometric form.
of z2. Also, the argument θ = 3π/4 of z1z2 is the sum of the arguments θ1 = π/2 and θ2 = π/4 of z1 and z2, respectively. We have illustrated a particular case of the following theorem, which describes how to multiply and divide complex numbers when they are written in trigonometric form.
THEOREM A.2.1 Product and Quotient
If z1 = r1(cosθ1 + isinθ1) and z2 = r2(cos θ2 + isin θ2), then

PROOF: We will prove only (4) of Theorem A.2.1; the proof of (3) is very similar. If we multiply the numerator and the denominator of
![]()
by cos θ2 − isin θ2, we obtain
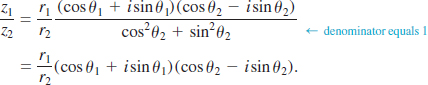
Performing the multiplication and then using the difference formulas from Section 4.6, we have

EXAMPLE 6 Product and Quotient
If z1 = 4(cos75° + isin 75°) and ![]() , find (a) z1z2 (b) z1/z2. Express each answer in the standard form a + bi.
, find (a) z1z2 (b) z1/z2. Express each answer in the standard form a + bi.
Solution (a) From (3) of Theorem A.2.1 we can write the product as

and so ![]()
(b) Now from (4) of Theorem A.2.1 the quotient is

A.2 Exercises Answers to selected odd-numbered problems
In Problems 1–10, graph the given complex number(s) and evaluate and graph the indicated complex number.
1. ![]()
2. ![]()
3. z = 1 + i, z2 = 2 − 2i; z1 + z2
4. z1 = 4i, z2 = −4 + i; z1 − z2
5. ![]()
6. ![]()
7. z1 = −2i, z2 = −i; z1z2
8. z1 = + 1 i, z2 = 1 −i; z1z2
9. ![]()
10. ![]()
In Problems 11–22, find the modulus and an argument of the given complex number.
11. ![]()
12. z = 4 + 3i
13. ![]()
14. z = −5 + 2i
15. ![]()
16. z = −8 −2i
17. z = 3 + 3i
18. z = −1 −i
19. ![]()
20. ![]()
21. z = 2 −i
22. z = 4 + 8i
In Problems 23–32, write the given complex number in trigonometric form.
23. z = −4i
24. z = 15i
25. ![]()
26. z = 3 + i
27. z = −2 + 5i
28. ![]()
29. z = 3 − 5i
30. z = −10 + 6i
31. z = −2 − 2i
32. z = 1 − i
In Problems 33–42, write the given complex number in the standard form z = a + bi. Do not use a calculator.
33. 
34. ![]()
35. ![]()
36. ![]()
37. ![]()
38. ![]()
39. 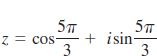
40. ![]()
41. ![]()
42. ![]()
In Problems 43–48, find z1z2 and z1/z2 in trigonometric form by first writing z1 and z2 in trigonometric form.
43. z1 = 3i, z2 = 6 + 6i
44. z1 = 1 + i, z2 = −1 + i
45. ![]()
46. z1 = 5i, z2 = −10i
47. ![]()
48. ![]()
In Problems 49–52, find z1z2 and z1/z2. Write the answer in the standard form z = a + bi.
49. ![]()
50. ![]()
51. ![]()
52. ![]()
A.3 Powers and Roots of Complex Numbers
Introduction The trigonometric form of a product z 1 z2 given in (3) of Theorem A.2.1 of the last section also gives a means of computing powers of a complex number, that is, zn, where n is a positive integer. In this section we also show how to find the n distinct nth roots of a complex number z.
We begin the discussion with an example.
![]() Powers of a Complex Number Suppose z = 1 + i and we wish to compute z3. Of course, there are several ways of proceeding. We can carry out the multiplications zz and (zz)z using the standard forms of the numbers or we can treat the number z = 1 + i as a binomial and use the binomial expansion
Powers of a Complex Number Suppose z = 1 + i and we wish to compute z3. Of course, there are several ways of proceeding. We can carry out the multiplications zz and (zz)z using the standard forms of the numbers or we can treat the number z = 1 + i as a binomial and use the binomial expansion
(a + b)3 = a3 + 3a2b + 3ab2 + b3
See (iii ) of Definition A.1.3 on page APP-3. ![]()
with a = 1 and b = i.Alternatively, we can use the trigonometric form
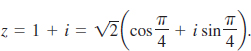
With z = z1 = z2 in (3) of Theorem A.2.1, we obtain the square of z:

Then (3) of Theorem A.2.1 also gives

After simplifying the last expression we get z3 = −2 + 2i.
The result in (1),

illustrates a particular case of the following theorem named after the French mathematician Abraham DeMoivre (1667–1754). The formal proof of this theorem requires mathematical induction, which is discussed in Section 10.3.
THEOREM A.3.1 DeMoivre’s Theorem
If z = r (cos θ + i sin θ) and n is a positive integer, then
![]()
Inspection of (2) shows that the result is DeMoivre’s theorem with z = 1 + i, r = ![]() , θ = π/4 in blue, and n = 3 in red.
, θ = π/4 in blue, and n = 3 in red.
EXAMPLE 1 Power of a Complex Number
Evaluate ![]() .
.
Solution First, the modulus of ![]() + i is
+ i is ![]() . Then from tan θ = 1/
. Then from tan θ = 1/![]() , an argument of the number is θ = π/6 since (
, an argument of the number is θ = π/6 since (![]() , 1) lies in quadrant I. Hence from DeMoivre’s theorem,
, 1) lies in quadrant I. Hence from DeMoivre’s theorem,
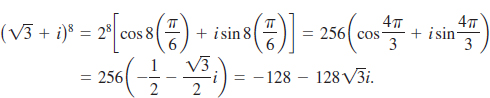
![]() Roots of a Complex Number Recall from algebra that −2 and 2 are said to be square roots of the number 4 because (−2)2 = 4 and 22 = 4. In other words, the two square roots of 4 are distinct solutions of the equation w2 = 4. In like manner we say w = 3 is a cube root of −7 since w3 = 33 = 27. In general, we say that a number w = a + bi is a complex nth root of a nonzero complex number z if wn = (a + bi)n = z, where n is a positive integer. For example, you are urged to verify that
Roots of a Complex Number Recall from algebra that −2 and 2 are said to be square roots of the number 4 because (−2)2 = 4 and 22 = 4. In other words, the two square roots of 4 are distinct solutions of the equation w2 = 4. In like manner we say w = 3 is a cube root of −7 since w3 = 33 = 27. In general, we say that a number w = a + bi is a complex nth root of a nonzero complex number z if wn = (a + bi)n = z, where n is a positive integer. For example, you are urged to verify that ![]() and
and ![]() are the two square roots of the complex number z = i because
are the two square roots of the complex number z = i because ![]() and
and ![]() . See also Problem 77 in Exercises A.1.
. See also Problem 77 in Exercises A.1.
We will now demonstrate that there are exactly n solutions of the equation wn = z.
Let the modulus and the argument of w be ρ and Φ;, respectively, so that w = ρ (cos Φ; + isin Φ;). If w is an nth root of the complex number z = r (cos θ + i sin θ), then wn = z. DeMoivre’s theorem enables us to write the last equation as
ρn(cosnΦ; + isinnΦ;) = r(cos θ + isin θ).
When two complex numbers are equal, their moduli are necessarily equal. Thus we have
ρn = r or ρ = r1/n
and cosnΦ; + isinnΦ; = cos θ + isinθ.
Equating the real and imaginary parts in this equation gives
cos nΦ; = cosθ, sin nΦ; = sin θ,
from which it follows that nΦ; = θ + 2kπ, or
![]()
where k is any integer. As k takes on the successive integer values 0, 1, 2, …, n − 1, we obtain n distinct roots of z. For k ≥ n, the values of sinΦ; and cosΦ; repeat the values obtained by letting k = 0, 1, 2, …, n − 1. To see this, suppose that k = n + m, where m = 0, 1, 2, …. Then
![]()
Since the sine and cosine each have period 2π, we have
![]()
and so no new roots are obtained for k ≥ n. Summarizing these results gives the following theorem.
THEOREM A.3.2 Complex Roots
If z = r (cos θ + i sin θ) and n is a positive integer, then n distinct complex nth roots of z are given by

where k = 0, 1, 2, …, n − 1.
We will denote the n roots by w0, w1, …, wn−1 corresponding to k = 0, 1,…, n − 1, respectively, in (4).
EXAMPLE 2 Three Cube Roots
Find the three cube roots of i.
Solution In the trigonometric form for i, r = 1 and θ = π/2, so that
![]()
With n = 3 we find from (4) of Theorem A.3.2 that
![]()
Now for
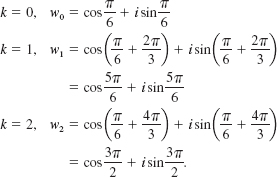
Therefore, in standard form the three cube roots of i are ![]() . and w2 = −i.
. and w2 = −i.
FIGURE A.3.1 Three cube roots of i in Example 2
The three cube roots of i found in Example 2 are plotted in FIGURE A.3.1. We note that they are equally spaced around a circle of radius 1 centered at the origin. In general, the n distinct nth roots of a nonzero complex number z are equally spaced on the circumference of the circle of radius |z|1/n with center at the origin.
As the next example shows, the roots of a complex number do not have to be “nice” numbers as in Example 2.
EXAMPLE 3 Solving an Equation
Solve the equation z4 = 1 + i.
Solution Solving this equation is equivalent to finding the four complex fourth roots of the number 1 + i. In this case, the modulus and an argument of 1 + i are r = ![]() and θ = π/4, respectively. From (4) with n = 4 and the symbol zk playing the part of wk we obtain
and θ = π/4, respectively. From (4) with n = 4 and the symbol zk playing the part of wk we obtain

FIGURE A.3.2 Four fourth roots of 1 + i in Example 3
With the aid of a calculator we find the approximate standard forms,
z0 ≈ 1.0696 + 0.2127i
z1 ≈ −0.2127 + 1.0696i
z2 ≈ −1.0696 − 0.2127i
z3 ≈ 0.2127 − 1.0696i.
As shown in FIGURE A.3.2 the four roots lie on a circle centered at the origin of radius ![]() and are spaced at equal angular intervals of 2π/4 = π/2 radians beginning with the root whose argument is π/16.
and are spaced at equal angular intervals of 2π/4 = π/2 radians beginning with the root whose argument is π/16.
A.3 Exercises Answers to selected odd-numbered problems begin on page ANS-31.
In Problems 1–10, use DeMoivre’s theorem to calculate the given power. Write your answer in the standard form z = a + bi. If necessary, use a calculator.
1. ![]()
2. ![]()
3. ![]()
4. ![]()
5. ![]()
6. ![]()
7. ![]()
8. ![]()
9. ![]()
10. ![]()
In Problems 11 and 12, use (3) of this section and (4) of Section A.2 to simplify the given complex number. Write your answer in the standard form z = a + bi.
11. 
12. 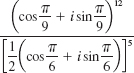
In Problems 13–24, use the trigonometric form of a complex number along with DeMoivre’s theorem to calculate the given power. Write your answer in the standard form z = a + bi.
13. i30
14. i15
15. (1 + i)6
16. (1 − i)9
17. (−2 + 2i)4
18. (−4 − 4i)3
19. ![]()
20. ![]()
21. ![]()
22. ![]()
23. ![]()
24. ![]()
In Problems 25–34, find the indicated roots. Write your answer in the standard form z = a + bi.
25. The three cube roots of −8
26. The three cube roots of 1
27. The four fourth roots of i
28. The two square roots of i
29. The four fourth roots of − 1 − ![]() i
i
30. The two square roots of − 1 + ![]() i
i
31. The two square roots of 1 + i
32. The three cube roots of ![]()
33. The six sixth roots of 64(cos 54° + isin54°)
34. The two square roots of 81 ![]()
In Problems 35 and 36, find the indicated roots. Proceed as in Example 3 and plot these roots on an appropriate circle.
35. The six sixth roots of 1
36. The eight eighth roots of 1
37. For what positive integers n will ![]() be equal to 1? Equal to i? Equal to −
be equal to 1? Equal to i? Equal to −![]() /2 —
/2 — ![]() i/2? Equal to
i/2? Equal to ![]() /2 +
/2 + ![]() i/2?
i/2?
38. (a) Verify that (4 + 3i)2 = 7 + 24i.
(b) Use part (a) to find the two values of (7 + 24i)1/2.
In Problems 39–42, solve the given equation. Write your answer in the standard form z = a + bi.
39. z4 + 1 = 0
40. z3 − 125i = 0
41. ![]()
42. z2 − 8z + 18 = 8i
For Discussion
43. DeMoivre’s theorem implies
(cos θ + isinθ)2 = cos 2θ + isin2θ.
Use this information to derive trigonometric identities for cos 2θ and sin 2θ by multiplying out the left-hand side of the equation and then equating real and imaginary parts.
44. Use a procedure analogous to that outlined in Problem 43 to find trigonometric identities of cos 3θ and sin 3θ.