5. Data Mining Algorithms
Data mining methods, especially the ones used to build predictive models, are derived from either traditional statistical techniques/algorithms or from contemporary machine learning techniques/systems. While statistical techniques are well established and theoretically sound, machine learning techniques are more practical and accurate (according to a wealth of comparative studies published in the literature). The statistical techniques that made the biggest impact in the evolution of data mining include discriminant analysis, linear regression, and logistic regression. The most popular machine learning techniques used in numerous successful data mining projects include nearest neighbor, artificial neural networks, and support vector machines. All three of these machine learning techniques can handle both classification- as well as regression-type prediction problems. Often, they are applied to complex prediction problems where other techniques are not capable of producing satisfactory results.
Because of the popularity of machine learning techniques in the data mining literature, in this chapter we explain these techniques in detail but without getting too technical in their algorithmic background. We also briefly explain the previously mentioned statistical techniques to provide balanced coverage of the technical spectrum of data mining.
Nearest Neighbor
Data mining algorithms tend to be highly mathematical and computationally intensive. Two popular ones—artificial neural networks and support vector machines—are involved in time-demanding, computationally intensive iterative mathematical derivations. In contrast, the k-nearest neighbor algorithm (k-NN) seems overly simplistic for a competitive prediction method. It is easy to understand (and explain to others) what it does and how it does it. k-NN is a prediction method for classification as well as regression-type prediction problems. k-NN is a type of instance-based learning (or lazy learning) where the function is only approximated locally, and all computations are deferred until the actual prediction.
The k-NN algorithm is among the simplest of all machine learning algorithms. For instance, in classification-type prediction, a case is classified by a majority vote of its neighbors, with the object being assigned to the class most common among its k nearest neighbors (where k is a positive integer). If k = 1, then the case is simply assigned to the class of its nearest neighbor. To illustrate the concept with an example, Figure 5.1 shows a simple two-dimensional space representing the values for the two variables x and y; the star represents a new case (or object), and circles and squares represent known cases (or examples). The task is to assign the new case either to circles or squares, based on its closeness (similarity) to one or the other. If you set the value of k to 1 (k = 1), the assignment should be made to square because the closest example to a star is a square. If you set the value of k to 3 (k = 3), then the assignment should be made to a circle because there are two circles and one square, and hence by simple majority vote rule, the circle gets the assignment of the new case. Similarly, if you set the value of k to 5 (k = 5), then the assignment should be made to the square class. This overly simplified example is meant to illustrate the importance of the value assigned to k.
The same method can also be used for regression-type prediction tasks, by simply averaging the values of the k nearest neighbors and assigning that result to the case being predicted. It can be useful to weight the contributions of the neighbors so that the nearer neighbors contribute more to the average than do the more distant ones. A common weighting scheme is to give each neighbor a weight of 1/d, where d is the distance to the neighbor. This scheme is essentially a generalization of linear interpolation.
The neighbors are taken from a set of cases for which the correct classification (or, in the case of regression, the numeric value of the output value) is known. This can be thought of as the training set for the algorithm, even though no explicit training step is required. The k-nearest neighbor algorithm is sensitive to the local structure of the data.
Similarity Measure: The Distance Metric
One of the two critical decisions that an analyst has to make while using k-NN is to determine the similarity measure; the other is to determine the value of k, which is explained below. In the k-NN algorithm, the similarity measure is a mathematically calculable distance metric. Given a new case, k-NN makes predictions based on the outcome of the k neighbors closest in distance to that point. Therefore, to make predictions with k-NN, an analyst needs to define a metric for measuring the distance between the new case and the cases from the examples. One of the most popular choices for measuring this distance is known as Euclidean (Equation 3), which is simply the linear distance between two points in a dimensional space; the other popular one is the rectilinear (a.k.a. city-block or Manhattan distance) (Equation 2). Both of these distance measures are special cases of Minkowski distance (Equation 1).
Here is the equation for finding the Minkowski distance:
where i = (xi1, xi2, ..., xip) and j = (xj1, xj2, ..., xjp) are two p-dimensional data objects (e.g., a new case and an example in the data set), and q is a positive integer.
If q = 1, then d is called Manhattan distance and is found using this equation:
If q = 2, then d is called Euclidean distance and is found using this equation:
Obviously, these measures apply only to numerically represented data. What happens with nominal data? There are ways to measure distance for nonnumeric data as well. In the simplest case, for a multivalue nominal variable, if the value of that variable for the new case and the example case is the same, the distance would be zero; otherwise, it would be one. In cases such as text classification, more sophisticated metrics exist, such as the overlap metric (or Hamming distance). Often, the classification accuracy of k-NN can be improved significantly if the distance metric is determined through an experimental design where different metrics are tried and tested to identify the best one for the given problem.
Parameter Selection
The best choice for k depends on the data; generally, larger values of k reduce the effect of noise on the classification (or regression) but also make boundaries between classes less distinct. An “optimal” value of k can be found by using some heuristic techniques, such as cross-validation. The special case where the class is predicted to be the class of the closest training sample (i.e., when k = 1) is called the nearest-neighbor algorithm.
Cross-Validation
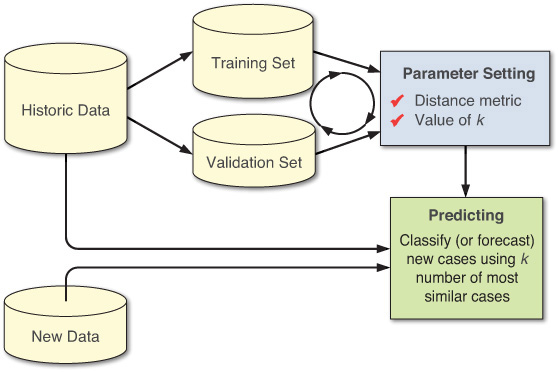
Cross-validation is a well-established experimentation technique that can be used to determine optimal values for a set of unknown model parameters. It applies to most, if not all, of the machine learning techniques, where there are a number of model parameters to be determined. The general idea of this experimentation method is to divide the data sample into a number of randomly drawn, disjointed subsamples (i.e., v number of folds). For each potential value of k, the k-NN model is used to make predictions on the vth fold while using the v – 1 folds as the examples, and evaluate the error. The common choice for this error is the root-mean-squared-error (RMSE) for regression-type predictions and percentage of correctly classified instances (i.e., hit rate) for classification-type predictions. This process of testing each fold against the remaining of examples repeats v times. At the end of the v number of cycles, the computed errors are accumulated to yield a goodness measure of the model (i.e., how well the model predicts with the current value of the k). At the end, the k value that produces the smallest overall error is chosen as the optimal value for that problem. Figure 5.2 shows a simple process where training data is used to determine optimal values for k and distance metric, which are then used to predict new incoming cases.
As in the simple example given above, the accuracy of the k-NN algorithm can be significantly different with different values of k. Furthermore, the predictive power of the k-NN algorithm degrades in the presence of noisy, inaccurate, or irrelevant features. Much research effort has been put into feature selection and normalization/scaling to ensure reliable prediction results. A particularly popular approach is the use of evolutionary algorithms (e.g., genetic algorithms) to optimize the set of features included in the k-NN prediction system. In binary (two-class) classification problems, it is helpful to choose an odd number for k to avoid tied votes.
A drawback to the basic majority voting classification in k-NN is that the classes with the more frequent examples tend to dominate the prediction of the new vector, as they tend to come up in the k nearest neighbors when the neighbors are computed due to their large number. One way to overcome this problem is to weigh the classification, taking into account the distance from the test point to each of its k nearest neighbors. Another way to overcome this drawback is to use one level of abstraction in data representation.
The naïve version of the algorithm is easy to implement by computing the distances from the test sample to all stored vectors, but it is computationally intensive, especially when the size of the training set grows. Many nearest-neighbor search algorithms have been proposed over the years; they generally seek to reduce the number of distance evaluations actually performed. Using an appropriate nearest-neighbor search algorithm makes k-NN computationally tractable even for large data sets.
Artificial Neural Networks
Neural networks use a brain metaphor for information processing. These models are biologically inspired rather than an exact replica of how the brain actually functions. Neural networks have been shown to be very promising systems in many forecasting and business classification applications due to their ability to “learn” from the data, their nonparametric nature (i.e., no rigid assumptions), and their ability to generalize. Neural computing refers to a pattern-recognition methodology for machine learning. The resulting model from neural computing is often called an artificial neural network (ANN) or a neural network. Neural networks have been used in many business applications for pattern recognition, forecasting, prediction, and classification. Neural network computing is a key component of any data mining toolkit. Applications of neural networks abound in finance, marketing, manufacturing, operations, information systems, and so on. Therefore, we devote this chapter to developing a better understanding of neural network models, methods, and applications.
The human brain possesses astonishing capabilities for information processing and problem solving that even the most advanced computers of this era cannot compete with in many aspects. It has been claimed that a model or a system that is enlightened and supported by the results from brain research, with a structure similar to that of biological neural networks, could exhibit similar intelligent functionality. Based on this bottom-up approach, ANNs (also known as connectionist models, parallel distributed processing models, neuromorphic systems, or simply neural networks) have been developed as biologically inspired and plausible models for various tasks.
Biological neural networks are composed of many massively interconnected neurons. Each neuron possesses axons and dendrites, fingerlike projections that enable the neuron to communicate with its neighboring neurons by transmitting and receiving electrical and chemical signals. More-or-less resembling the structure of their biological counterparts, ANNs are composed of interconnected, simple processing elements called artificial neurons. When processing information, the processing elements in an ANN operate concurrently and collectively, much as in biological neurons. ANNs possess some desirable traits similar to those of biological neural networks, such as the abilities to learn, self-organize, and support fault tolerance.
For more than half a century, researchers have been investigating ANNs. The formal study of ANNs began with the pioneering work of McCulloch and Pitts in 1943. Inspired by the results of biological experiments and observations, McCulloch and Pitts (1943) introduced a simple model of a binary artificial neuron that captured some of the functions of biological neurons. Using information-processing machines to model the brain, McCulloch and Pitts built their neural network model using a large number of interconnected artificial binary neurons. From these beginnings, neural network research became quite popular in the late 1950s and early 1960s. After a thorough analysis of an early neural network model (called the perceptron, which used no hidden layer) as well as a pessimistic evaluation of the research potential by Minsky and Papert in 1969, interest in neural networks diminished.
During the past two decades, there has been an exciting resurgence in ANN studies due to the introduction of new network topologies, new activation functions, and new learning algorithms, as well as progress in neuroscience and cognitive science. Advances in theory and methodology have overcome many of the obstacles that hindered neural network research a few decades ago. Evidenced by the appealing results of numerous studies, neural networks are gaining acceptance and popularity. In addition, the desirable features in neural information processing make neural networks attractive for solving complex problems. ANNs have been applied to numerous complex problems in a variety of application settings. The successful use of neural network applications has inspired renewed interest from industry and business.
Biological and Artificial Neural Networks
The human brain is composed of special cells called neurons. These cells do not die and replenish when a person is injured. (All other cells reproduce to replace themselves and then die.) This phenomenon may explain why humans retain information for an extended period of time and start to lose it when they get old—as the brain cells gradually start to die. Information storage spans sets of neurons. The brain has anywhere from 50 billion to 150 billion neurons, of which there are more than 100 different kinds. Neurons are partitioned into groups called networks. Each network contains several thousand highly interconnected neurons. Thus, the brain can be viewed as a collection of neural networks.
The ability to learn and to react to changes in our environment requires intelligence. The brain and the central nervous system control thinking and intelligent behavior. People who suffer brain damage have difficulty learning and reacting to changing environments. Even so, undamaged parts of the brain can often compensate with new learning.
A portion of a network composed of two cells is shown in Figure 5.3. The cell itself includes a nucleus (the central processing portion of the neuron). To the left of the first cell, the dendrites provide input signals to the cell. To the right, the axon sends output signals to the second cell via the axon terminals. These axon terminals merge with the dendrites of the second cell. Signals can be transmitted unchanged, or they can be altered by synapses. A synapse is able to increase or decrease the strength of the connection between neurons and cause excitation or inhibition of a subsequent neuron. This is how information is stored in the neural networks.
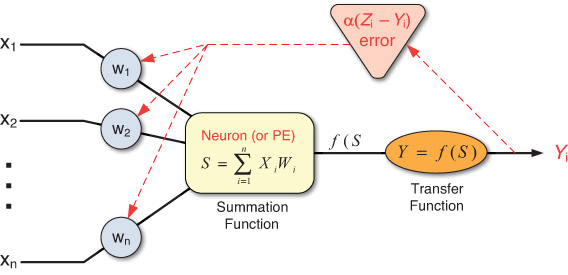
An ANN emulates a biological neural network. Neural computing actually uses a very limited set of concepts from biological neural systems. A simple terminology mapping between biological and artificial neural networks is shown in Table 5.1. It is more of an analogy to the human brain than an accurate model of it. Neural concepts usually are implemented as software simulations of the massively parallel processes involved in processing interconnected elements (also called artificial neurons, or neurodes) in a network architecture. The artificial neuron receives inputs analogous to the electrochemical impulses that dendrites of biological neurons receive from other neurons. The output of the artificial neuron corresponds to signals sent from a biological neuron over its axon. These artificial signals can be changed by weights in a manner similar to the physical changes that occur in the synapses (see Figure 5.4).
Several ANN paradigms have been proposed for applications in a variety of problem domains. Perhaps the easiest way to differentiate among the various neural models is on the basis of how they structurally emulate the human brain, the way they process information, and how they learn to perform their designated tasks.
Because they are biologically inspired, the main processing elements of a neural network are individual neurons, analogous to the brain’s neurons. These artificial neurons receive information from other neurons or external input stimuli, perform a transformation on the inputs, and then pass on the transformed information to other neurons or external outputs. This is similar to how it is presently thought that the human brain works. Passing information from neuron to neuron can be thought of as a way to activate, or trigger, a response from certain neurons based on the information or stimulus received.
How information is processed by a neural network is inherently a function of its structure. Neural networks can have one or more layers of neurons. These neurons can be highly or fully interconnected, or only certain layers can be connected. Connections between neurons have an associated weight. In essence, the “knowledge” possessed by the network is encapsulated in these interconnection weights. Each neuron calculates a weighted sum of the incoming neuron values, transforms this input, and passes on its neural value as the input to subsequent neurons. Typically, although not always, this input/output transformation process at the individual neuron level is performed in a nonlinear fashion.
Basic Components of an ANN
A neural network is composed of processing elements that are organized in different ways to form the network’s structure. The basic processing unit is the neuron. A number of neurons are organized into a network. Neurons can be organized in a number of different ways; these various network patterns are referred to as topologies. One popular approach, known as the feed-forward/back-propagation paradigm (or simply back-propagation), allows all neurons to link the output in one layer to the input of the next layer, but it does not allow any feedback linkage (Haykin, 2009). Back-propagation is the most commonly used network paradigm.
Processing Elements
The processing elements (PEs) of an ANN are artificial neurons. Each neuron receives inputs, processes them, and delivers a single output, as shown in Figure 5.4. The input can be raw input data or the output of other processing elements. The output can be the final result (e.g., 1 means yes, 0 means no), or it can be input to other neurons.
Network Structure
Each ANN is composed of a collection of neurons that are grouped into layers. A typical structure is shown in Figure 5.5. Note the three layers: input, intermediate (called the hidden layer), and output. A hidden layer is a layer of neurons that takes input from the previous layer and converts those inputs into outputs for further processing. Several hidden layers can be placed between the input and output layers, although it is common to use only one hidden layer. In that case, the hidden layer simply converts inputs into a nonlinear combination and passes the transformed inputs to the output layer. The most common interpretation of the hidden layer is as a feature-extraction mechanism; that is, the hidden layer converts the original inputs in the problem into a higher-level combination of such inputs.
There are several neural network structures (or architectures) for a variety of analytics problems. The most common ones include feed-forward (multilayer perceptron with back-propagation), associative memory, recurrent networks, Kohonen’s self-organizing feature maps, and Hopfield networks. Perhaps the most commonly used one is the feed-forward neural network with a multilayered perceptron (commonly known as MLP). The generic architecture of a feed-forward network is shown in Figure 5.5, where the information flows unidirectionally from the input layer to hidden layers and from hidden layers to the output layer.
Like a biological network, an ANN can be organized in several different ways (i.e., topologies or architectures); that is, the neurons can be interconnected in different ways. When information is processed, many of the processing elements perform their computations at the same time. This parallel processing resembles the way the brain works, and it differs from the serial processing of conventional computing.
How Does the Learning Happen?
MLP architecture in ANN uses supervised learning, where the learning process is inductive; that is, the values of parameters (i.e., the connection weights) are derived from existing cases. The usual process of learning in MLP-type ANNs involves three tasks (see Figure 5.6):
1. Compute temporary outputs.
2. Compare outputs with desired targets.
3. Adjust the weights and repeat the process.
Back-Propagation
Back-propagation (or back-error propagation) is the most widely used supervised learning algorithm in neural networks. It is relatively easy to implement and produces surprisingly accurate results. A back-propagation network includes one or more hidden layers. This type of network is considered feed-forward because there are no interconnections between the output of a processing element and the input of a node in the same layer or in a preceding layer. Externally provided correct patterns are compared with the neural network’s output during (supervised) training, and feedback is used to adjust the weights until the network has categorized all the training patterns as correctly as possible. (The error tolerance is set in advance.)
Starting with the output layer, errors between the actual and desired outputs are used to correct the weights for the connections to the previous layer (see Figure 5.7). For any output neuron, the error is calculated as the difference between the network output (Y) and the actual outputs (Z). Using some type of nonlinear function, this error is propagated back to the network weight for proper adjustment (increase or decrease).
Specifically, the learning algorithm includes the following steps:
1. Initialize weights with random values and set other parameters.
2. Read in the input vector and the desired output.
3. Compute the actual output via the calculations, working forward through the layers.
4. Compute the error.
5. Change the weights by working backward from the output layer through the hidden layers.
This procedure is repeated for the entire set of input vectors until the desired output and the actual output agree to within some predetermined tolerance. Given the calculation requirements for one iteration, a large network can take a very long time to train; therefore, in one variation, a set of cases is run forward, and an aggregated error is fed backward to speed up learning. Sometimes, depending on the initial random weights and network parameters, the network does not converge to a satisfactory performance level. When this is the case, new random weights must be generated, and the network parameters, or even its structure, may have to be modified before another attempt is made.
Sensitivity Analysis in Artificial Neural Networks
Neural networks have been used as effective tools for solving highly complex real-world problems in a wide range of application areas. Even though ANNs have been proven in many problem scenarios to be superior predictors and/or cluster identifiers (compared to their traditional counterparts), in some applications, there exists an additional need to know how the ANN does what it does. ANNs are typically thought of as black boxes, capable of solving complex problems but lacking explanations for their capabilities. This phenomenon is commonly referred to as black-box syndrome.
It is important to be able to explain a model’s “inner being”; such an explanation offers assurance that the network has been properly trained and will behave as desired once deployed in a business intelligence environment. The need to “look under the hood” might be attributable to a relatively small training set (as a result of the high cost of data acquisition) or a very high liability in the case of a system error. One example of such an application is the deployment of airbags in automobiles. Here, both the cost of data acquisition (crashing cars) and the liability concerns (danger to human lives) are rather significant. Another representative example for the importance of explanation is loan-application processing. If an applicant is refused for a loan, the applicant has a right to know why. Having a prediction system that does a good job differentiating good applications from bad ones may not be sufficient if it does not also provide justification for its decisions.
A variety of techniques have been proposed for analysis and evaluation of trained neural networks. These techniques provide a clear interpretation of how a neural network does what it does—that is, specifically how (and to what extent) the individual inputs factor into the generation of specific network output. Sensitivity analysis has been the front-runner among the techniques proposed for shedding light into the black-box characterization of trained neural networks.
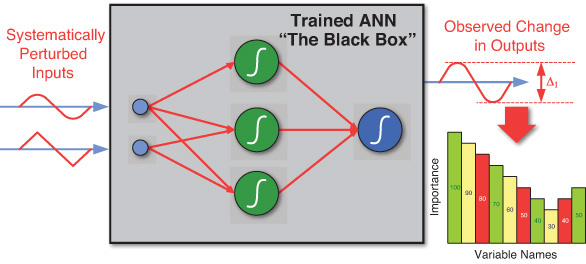
Sensitivity analysis is a method for extracting the cause-and-effect relationships among the inputs and outputs of a trained neural network model. In the process of performing sensitivity analysis, the trained neural network’s learning capability is disabled so that the network weights are not affected. The basic procedure involved in sensitivity analysis is to systematically perturb the inputs to the network within the allowable value ranges and to record the corresponding changes in the output for each and every input variable. Figure 5.8 shows a graphical illustration of this process. The first input is varied between its mean plus and minus a user-defined number of standard deviations (or, for categorical variables, all the possible values are used), while all other input variables are fixed at their respective means (or modes). The network output is computed for a user-defined number of steps above and below the mean. This process is repeated for each input. As a result, a report is generated that summarizes the variation of each output with respect to the variation in each input. The generated report often contains a column plot (where numeric importance values are presented on the y-axis and input variables are listed in the x-axis) reporting the relative sensitivity/importance values for each input variable.
Support Vector Machines
Support vector machines (SVMs) are among the most popular machine learning techniques in the recent past, largely because of their superior predictive performance and their theoretical foundation. SVMs are among the supervised learning methods that produce input/output functions from a set of labeled training data. The function between the input and output vectors can be either a classification function (used to assign cases into predefined classes) or a regression function (used to estimate the continuous numeric value of the desired output). For classification, nonlinear kernel functions are often used to transform the input data (naturally representing highly complex nonlinear relationships) to a high dimensional feature space in which the input data becomes linearly separable. Then, the maximum-margin hyperplanes are constructed to optimally separate the output classes from each other in the training data.
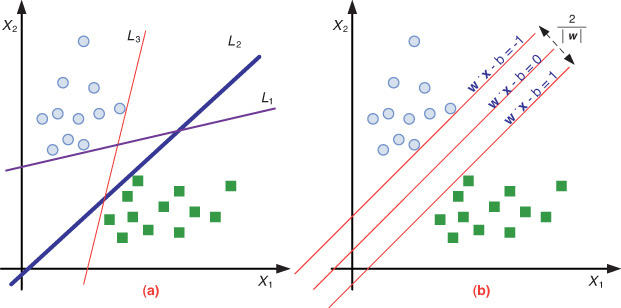
For a given classification-type prediction problem, generally speaking, many linear classifiers (hyperplanes) can separate the data into multiple subsections, each representing one of the classes (see Figure 5.9a, where the two classes are represented with circles [![]() ] and squares [
] and squares [![]() ]). However, only one hyperplane achieves the maximum separation between the classes (see Figure 5.9b, where the hyperplane and the two maximum-margin hyperplanes are separating the two classes).
]). However, only one hyperplane achieves the maximum separation between the classes (see Figure 5.9b, where the hyperplane and the two maximum-margin hyperplanes are separating the two classes).
Data used in SVMs may have more than two dimensions (i.e., two distinct classes). In that case, we would be interested in separating data using n – 1 dimensional hyperplanes, where n is the number of dimensions (i.e., class labels). This may be seen as a typical form of linear classifier, where we are interested in finding n – 1 hyperplanes so that the distance from the hyperplanes to the nearest data points are maximized. The assumption is that the larger the margin or distance between these parallel hyperplanes, the better the generalization power of the classifier (i.e., prediction power of the SVM model). If such hyperplanes exist, they can be mathematically represented using quadratic optimization modeling. These hyperplanes are known as the maximum-margin hyperplanes, and a linear classifier is known as a maximum-margin classifier.
In addition to their solid mathematical foundation in statistical learning theory, SVMs have also demonstrated highly competitive performance in numerous real-world prediction problems, such as medical diagnosis, bioinformatics, face/voice recognition, demand forecasting, image processing, and text mining, which has established SVMs as one of the most popular analytics tools for knowledge discovery and data mining. Similarly to artificial neural networks, SVMs can be used to approximate any multivariate function to any desired degree of accuracy. Therefore, they are of particular interest in modeling highly nonlinear, complex problems, systems, and processes.
The Process of Building SVM Models
Recently, using support vector machines has become a popular technique for classification-type problems because of their predictive accuracy and self-expandability. Even though people consider them easier to use than artificial neural networks, users who are not familiar with the intricacies of SVMs often get unsatisfactory results. In this section we provide a simple process-based approach to model building with and use of SVMs that is likely to produce good results. A pictorial representation of the three-step process is given in Figure 5.10.
Following are short descriptions of the steps in this process.
Step 1: Preprocess the Data
Because real-world data is anything but perfect, a data mining analyst needs to do the due diligence to scrub and transform the data for SVM. As is the case with any other data mining methods and algorithms, this step is likely to be the most time-demanding and least enjoyable, yet most essential, part of working with SVMs. Some of the tasks in this step include handling missing, incomplete, and noisy values and numerisizing, normalizing, and standardizing the data:
• Numerisizing the data. SVMs require that each data instance be represented as a vector of real numbers. Hence, if there are categorical attributes, an analyst has to first convert them into numeric data. A common recommendation is to use m pseudo binary variables to represent an m-class attribute (where m ≥ 3). In practice, only one of the m variables assumes the value of 1, and others assume the value of 0, based on the actual class of the case; this is also called 1-of-m representation. For example, a three-category attribute such as {red, green, blue} can be represented as (0,0,1), (0,1,0), and (1,0,0).
• Normalizing the data. As is the case with artificial neural networks, SVMs also require normalization and/or scaling of numeric values. The main advantage of normalization is to avoid having attributes in greater numeric ranges dominate those in smaller numeric ranges. Another advantage is that it helps perform numeric calculations during the iterative process of model building. Because kernel values usually depend on the inner products of feature vectors (e.g., the linear kernel, the polynomial kernel), large attribute values might slow the training process. The usual recommendation is to normalize each attribute to the range [-1, +1] or [0, 1]. Of course, an analyst has to use the same normalization method to scale testing data before testing.
Step 2: Develop the Model
Once the data is preprocessed, the model building step starts. Compared to the other two steps, this is the most enjoyable part of the process, where the prediction model comes alive. Because SVM has a number of parameter options, the process requires a lengthy process of determining the optimal combination of those parameters for the best possible performance. The most important of those parameters are the kernel type and consequently kernel-related subparameters.
There are four common kernels, and an analyst must decide which one to use (or whether to try them all, one at a time, using a simple experimental design approach). Once the kernel type is selected, the analyst needs to select the value of penalty parameter C and the kernel parameters. Generally speaking, RBF is a reasonable first choice for the kernel type. The RBF kernel aims to nonlinearly map data into a higher dimensional space, and this (unlike with a linear kernel) handles the cases where the relationship between input and output vectors is highly nonlinear. Besides, the linear kernel is just a special case of the RBF kernel. There are two parameters to choose for RBF kernels: C and γ. It is not known beforehand which C and γ are the best for a given prediction problem; therefore, some kind of parameter search method needs to be used. The goal for the search is to identify optimal values for C and γ so that the classifier can accurately predict unknown data (i.e., testing data). The two most commonly used search methods are cross-validation and grid search.
Step 3: Deploy the Model
Once an optimal SVM prediction model is developed, the next step is to integrate it into the decision support system. For that, there are two options: (1) converting the model into a computational object (e.g., a Web service, a Java Bean, or a COM object) that takes the input parameter values and provides output prediction or (2) extracting the model coefficients and integrating them directly into the decision support system. The SVM models are useful (i.e., accurate and actionable) only if the behavior of the underlying domain stays the same. For some reason, if the behavior changes, so does the accuracy of the model. Therefore, it’s important to continuously assess the performance of the models and decide when they are no longer accurate and, hence, need to be retrained.
Support Vector Machines Versus Artificial Neural Networks
Even though some people characterize SVMs as a special case of ANNs, most recognize these as two competing machine learning techniques with different qualities. Let’s look at a few points that help SVMs stand out against ANNs. Historically, the development of ANNs followed a heuristic path, with applications and extensive experimentation preceding theory. In contrast, the development of SVMs involved sound statistical learning theory first, followed by implementation and experiments. A significant advantage of SVMs is that while ANNs may suffer from multiple local minima, the solutions to SVMs are global and unique. Two more advantages of SVMs are that they have simple geometric interpretations and give sparse solutions. The reason that SVMs often outperform ANNs in practice is that they successfully deal with the “overfitting” problem, which is a big issue with ANNs.
Besides the above-mentioned advantages of SVMs (from a practical point of view), they also have some limitations. An important issue that is not entirely solved is the selection of the kernel type and kernel function parameters. Other, perhaps more important, limitations of SVMs are the speed and size, both in training and testing cycles. Model building with SVMs involves complex and time-demanding calculations. From a practical point of view, perhaps the most serious problems with SVMs are the high algorithmic complexity and extensive memory requirements of the required quadratic programming in large-scale tasks. Despite these limitations, because SVMs are based on a sound theoretical foundation and the solutions they produce are global and unique in nature (as opposed to getting stuck in suboptimal alternatives as local minima do), today’s SVMs are some of the most popular prediction modeling techniques in the data mining arena. Their use and popularity will only increase as the popular commercial data mining tools start to incorporate them into their modeling arsenals.
Linear Regression
Regression, especially linear regression, is perhaps the most widely used analysis technique in statistics. Historically speaking, the roots of regression date back to the 1920s and 1930s, to the early work on inherited characteristics of sweet peas by Sir Francis Galton and subsequently Karl Pearson. Since then, regression has become the statistical technique for characterization of relationships between explanatory (input) variable(s) and response (output) variable(s).
As popular as it is, regression is essentially a relatively simple statistical technique to model the dependence of a variable (response or output variable) on one (or more) explanatory (input) variables. Once identified, this relationship between the variables can be formally represented as a linear/additive function or equation. As is the case with many other modeling techniques, regression aims to capture the functional relationship between and among the characteristics of the real world and describe this relationship with a mathematical model, which may then be used to discover and understand the complexities of reality—explore and explain relationships or forecast future occurrences.
Regression can be used for two different purposes: hypothesis testing—investigating potential relationships between different variables—and prediction/forecasting—estimating values of response variables based on one or more explanatory variables. These two uses are not mutually exclusive. The explanatory power of regression is also the foundation of its prediction ability. In hypothesis testing (theory building), regression analysis can reveal the existence and strength and the directions of relationships between a number of explanatory variables (often represented with xi) and the response variable (often represented with y). In prediction, regression identifies additive mathematical relationships (in the form of an equation) between one or more explanatory variables and a response variable. Once determined, this equation can be used to forecast the values of response variable for a given set of values of the explanatory variables.
Correlation Versus Regression
Because regression analysis originated in correlation studies, and because both methods attempt to describe the association between two (or more) variables, these two terms are often confused by professionals and even by scientists. Correlation makes no a priori assumption as to whether one variable is dependent on the other(s) and is not concerned with the relationship between variables; instead, it gives an estimate about the degree of association between the variables. On the other hand, regression attempts to describe the dependence of a response variable on one or more explanatory variables, where it implicitly assumes that there is a one-way causal effect from the explanatory variables to the response variable, regardless of whether the path of effect is direct or indirect. Also, whereas correlation is interested in low-level relationships between two variables, regression is concerned with the relationships between all explanatory variables and the response variable.
Simple Versus Multiple Regression
If a regression equation is built between one response variable and one explanatory variable, then it is called simple regression. For instance, the regression equation built to predict or explain the relationship between the height of a person (explanatory variable) and the weight of a person (response variable) is a good example of simple regression. Multiple regression is an extension of simple regression in which there are multiple explanatory variables. For instance, in the previous example, if we were to include not only the height of a person but also other personal characteristics (e.g., BMI, gender, ethnicity) to predict the weight of the person, then we would be performing multiple regression analysis. In both cases, the relationships between the response variables and the explanatory variables are linear and additive in nature. If the relationships are not linear, then we might want to use one of many other nonlinear regression methods to better capture the relationships between the input and output variables.
How to Develop a Linear Regression Model
To understand the relationship between two variables, the simplest thing to do is to draw a scatter plot, where the y-axis represents the values of the response variable and the x-axis represents the values of the explanatory variable (see Figure 5.11). Such a scatter plot would show the changes in the response variable as a function of the changes in the explanatory variable. In the example shown in Figure 5.11, there seems to be a positive relationship between the two: As the explanatory variable values increase, so does the response variable.
Simple regression analysis aims to find a mathematical representation of this relationship. In reality, it tries to find the signature of a straight line passing right in between the plotted dots (representing the observation/historical data) in such a way that it minimizes the distance between the dots and the line (the predicted values on the theoretical regression line). Several methods/algorithms have been proposed to identify the regression line, and the one that is most commonly used is called the ordinary least squares (OLS) method. The OLS method aims to minimize the sum of squared residuals (i.e., squared vertical distances between the observation and the regression point) and leads to a mathematical expression for the estimated value of the regression line (known as the β parameter). For simple linear regression, the aforementioned relationship between the response variable (y) and the explanatory variable(s) (x) can be shown as a simple equation, as follows:
y = β0 + β1x
In this equation, β0 is called the intercept, and β1 is called the slope. Once OLS determines the values of these two coefficients, the simple equation can be used to forecast the values of y for given values of x. The sign and the value of β1 also reveal the direction and the strength of the relationship between the two variables.
If the model is of a multiple linear regression type, then more coefficients need to be determined—one for each additional explanatory variable. As the following formula shows, the additional explanatory variable would be multiplied with new βi coefficients and summed together to establish a linear additive representation of the response variable.
y = β0 + β1x1 + β2x2 + ... + βnxn
How to Tell if a Model Is Good Enough
For a variety of reasons, sometimes models do not do a good job representing reality. Regardless of the number of explanatory variables included, there is always a possibility of not having a good model, and therefore a linear regression model needs to be assessed for its fit (the degree to which it represents the response variable). In the simplest sense, a well-fitting regression model results in predicted values close to the observed data values. For the numeric assessment, three statistical measures are often used in evaluating the fit of a regression model. R2 (R-squared), the overall F-test, and the root mean square error (RMSE). All three of these measures are based on sums of square errors (how far the data is from the mean and how far the data is from the model’s predicted values). Different combinations of these two values provide different information about how the regression model compares to the mean model.
Of the three, R2 has the most useful and understandable meaning because of its intuitive scale. The value of R2 ranges from 0 to 1 (corresponding to the amount of variability, expressed as a percentage), with 0 indicating that the relationship and the prediction power of the proposed model is not good and 1 indicating that the proposed model is a perfect fit that produces exact predictions (which is almost never the case). Good R2 values usually come close to 1, and the closeness is a matter of the phenomenon being modeled; for example, while an R2 value of 0.3 for a linear regression model in social science may be considered good enough, an R2 value of 0.7 in engineering might not be considered a good fit. Improvement in the regression model can be achieved by adding more explanatory variables, taking some of the variables out of the model, or using different data transformation techniques, which would result in comparative increases in an R2 value.
Figure 5.12 shows the process flow involved in developing regression models. As shown in the figure, the model development task is followed by model assessment. Model assessment involves assessing the fit of the model and also, because of restrictive assumptions with which linear models have to comply, it also involves examining the validity of the model.
The Most Important Assumptions in Linear Regression
Even though they are still the top choice of many data analysis (both for explanatory as well as predictive modeling purposes), linear regression models suffer from several highly restrictive assumptions. The validity of a linear model depends on its ability to comply with these assumptions. Here are the most common assumptions:
• Linearity. This assumption states that the relationship between the response variable and the explanatory variables are linear. That is, the expected value of the response variable is a straight-line function of each explanatory variable, while holding all other explanatory variables fixed. Also, the slope of the line does not depend on the values of the other variables. This implies that the effects of different explanatory variables on the expected value of the response variable are additive in nature.
• Independence (of errors). This assumption states that the errors of the response variable are uncorrelated with each other. This independence of the errors is weaker than actual statistical independence, which is a stronger condition and is often not needed for linear regression analysis.
• Normality (of errors). This assumption states that the errors of the response variable are normally distributed. That is, they are supposed to be totally random and should not represent any nonrandom patterns.
• Constant variance (of errors). This assumption, also called homoscedasticity, states that the response variables must have the same variance in their error, regardless of the values of the explanatory variables. In practice, this assumption is invalid if the response variable varies over a wide enough range or scale.
• Multicollinearity. This assumption states that the explanatory variables are not correlated (i.e., do not replicate the same but provide a different perspective of the information needed for the model). Multicollinearity can be triggered by having two or more perfectly correlated explanatory variables present in the model (e.g., if the same explanatory variable is mistakenly included in the model twice, one with a slight transformation of the same variable). A correlation-based data assessment usually catches this error.
Statistical techniques have been developed to identify the violation of these assumptions, and several techniques have been created to mitigate them. A data modeler needs to be aware of the existence of these assumptions and put in place a way to assess models to make sure they are compliant with the assumptions they are built on.
Logistic Regression
Logistic regression is a very popular, statistically sound, probability-based classification algorithm that employs supervised learning. It was developed in the 1940s as a complement to linear regression and linear discriminant analysis methods. It has been used extensively in numerous disciplines, including the medical and social science fields. Logistic regression is similar to linear regression in that it also aims to regress to a mathematical function that explains the relationship between the response variable and the explanatory variables, using a sample of past observations (training data). It differs from linear regression on one major point: Its output (response variable) is a class as opposed to a numeric variable. That is, whereas linear regression is used to estimate a continuous numeric variable, logistic regression is used to classify a categorical variable. Even though the original form of logistic regression was developed for a binary output variable (e.g., 1/0, yes/no, pass/fail, accept/reject), the present-day modified version is capable of predicting multiple-class output variables (i.e., multinomial logistic regression). If there is only one predictor variable and one predicted variable, the method is called simple logistic regression; this is similar to using the term simple linear regression for a linear regression model with only one independent variable.
In predictive analytics, logistic regression models are used to develop probabilistic models between one or more explanatory or predictor variables (which may be a mix of both continuous and categorical variables) and a class or response variable (which may be binomial/binary or multinomial/multiple-class variables). Unlike ordinary linear regression, logistic regression is used for predicting categorical (often a binary) outcomes of the response variable—treating the response variable as the outcome of a Bernoulli trial. Therefore, logistic regression takes the natural logarithm of the odds of the response variable to create a continuous criterion as a transformed version of the response variable. Thus the logit transformation is referred to as the link function in logistic regression; even though the response variable in logistic regression is categorical or binomial, the logit is the continuous criterion on which linear regression is conducted.
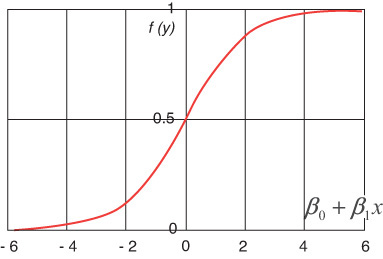
Figure 5.13 shows a logistic regression function where the odds are represented on the x-axis (i.e., a linear function of the independent variables), and the probabilistic outcome is shown on the y-axis (i.e., response variable values change between 0 and 1).
The logistic function, which is f(y) in Figure 5.13, is the core of logistic regression, which can only take values between 0 and 1. The following equation is a simple mathematical representation of this function:
The logistic regression coefficients (the βs) are usually estimated using the maximum-likelihood estimation method. Unlike with linear regression with normally distributed residuals, it is not possible to find a closed-form expression for the coefficient values that maximizes the likelihood function, so an iterative process must be used instead. This process begins with a tentative starting solution and then revises the parameters slightly to see if the solution can be improved; it repeats this iterative revision until no improvement can be achieved or the improvements are very minimal, at which point the process is said to have completed or converged.
Time-Series Forecasting
Sometimes the variable of interest (i.e., the response variable) may not have distinctly identifiable explanatory variables, or there may be too many of them in a highly complex relationship. In such cases, if the data is available in the desired format, a prediction model, called a time-series forecast, can be developed. A time series is a sequence of data points of the variable of interest, measured and represented at successive points in time and spaced at uniform time intervals. Examples of time series include monthly rain volumes in a geographic area, the daily closing value of the stock market indices, and daily sales totals for a grocery store. Often, time series are visualized using a line chart. Figure 5.14 shows an example of a time series of sales volumes for the years 2008 through 2012, on a quarterly basis.
Time-series forecasting involves using a mathematical model to predict future values of the variable of interest, based on previously observed values. Time-series plots or charts look very similar to simple linear regression scatter plots in that there are two variables: the response variable and the time variable. Beyond this similarity, there is hardly any other commonality between the two. While regression analysis is often used in testing theories to see if current values of one or more explanatory variables explain (and hence predict) the response variable, time-series models are focused on extrapolating the time-varying behavior to estimate future values.
Time-series forecasting assumes that all the explanatory variables are aggregated and consumed in the response variable’s time-variant behavior. Therefore, capturing time-variant behavior is a way to predict the future values of the response variable. To do that, the pattern is analyzed and decomposed into its main components: random variations, time trends, and seasonal cycles. The time-series example shown in Figure 5.14 illustrates all these distinct patterns.
The techniques used to develop time-series forecasts ranges from very simple (e.g., the naïve forecast which suggests that today’s forecast is the same as yesterday’s actual) to very complex (e.g., ARIMA, which combines autoregressive and moving average patterns in data). The most popular techniques are perhaps the averaging methods that include simple averages, moving averages, weighted moving averages, and exponential smoothing. Many of these techniques also have advanced versions where seasonality and trend can also be taken into account for better and more accurate forecasting. The accuracy of a method is usually assessed by computing its error (i.e., calculated deviation between actuals and forecasts for the past observations) via mean absolute error (MAE), mean squared error (MSE), or mean absolute percent error (MAPE). Even though they all use the same core error measure, these three assessment methods emphasize different aspects of the error, some panelizing larger errors more so than the others.
References
Aizerman, M., E. Braverman, & L. Rozonoer. (1964). “Theoretical Foundations of the Potential Function Method in Pattern Recognition Learning,” Automation and Remote Control, 25: 821–837.
Collins, E., S. Ghosh, & C. L. Scofield. (1988). “An Application of a Multiple Neural Network Learning System to Emulation of Mortgage Underwriting Judgments.” IEEE International Conference on Neural Networks, 2: 459–466.
Das, R., I. Turkoglu, & A. Sengur. (2009). “Effective Diagnosis of Heart Disease Through Neural Networks Ensembles,” Expert Systems with Applications, 36: 7675–7680.
Delen, D., A. Oztekin, & L. Tomak. (2012). “An analytic approach to better understanding and management of coronary surgeries,” Decision Support Systems, 52(3): 698–705.
Delen, D., R. Sharda, & M. Bessonov. (2006). “Identifying Significant Predictors of Injury Severity in Traffic Accidents Using a Series of Artificial Neural Networks,” Accident Analysis and Prevention, 38(3): 434–444.
Delen, D., & E. Sirakaya. (2006). “Determining the Efficacy of Data-Mining Methods in Predicting Gaming Ballot Outcomes,” Journal of Hospitality & Tourism Research, 30(3): 313–332.
Fadlalla, A., & C. Lin. (2001). “An Analysis of the Applications of Neural Networks in Finance,” Interfaces, 31(4).
Haykin, S. S. (2009). Neural Networks and Learning Machines, 3rd ed. Upper Saddle River, NJ: Prentice Hall.
Hill, T., T. Marquez, M. O’Connor, & M. Remus. (1994). “Neural Network Models for Forecasting and Decision Making,” International Journal of Forecasting, 10.
Hopfield, J. (1982). “Neural Networks and Physical Systems with Emergent Collective Computational Abilities,” Proceedings of the National Academy of Science, 79(8).
Liang, T. P. (1992). “A Composite Approach to Automated Knowledge Acquisition,” Management Science, 38(1).
Loeffelholz, B., E. Bednar, & K. W. Bauer. (2009). “Predicting NBA Games Using Neural Networks,” Journal of Quantitative Analysis in Sports, 5(1).
McCulloch, W. S., & W. H. Pitts. (1943). “A Logical Calculus of the Ideas Imminent in Nervous Activity,” Bulletin of Mathematical Biophysics, 5.
Minsky, M., & S. Papert. (1969). Perceptrons. Cambridge, MA: MIT Press.
Piatesky-Shapiro, G. ISR: Microsoft Success Using Neural Network for Direct Marketing, http://kdnuggets.com/news/94/n9.txt (accessed May 2009).
Principe, J. C., N. R. Euliano, & W. C. Lefebvre. (2000). Neural and Adaptive Systems: Fundamentals Through Simulations. New York: Wiley.
Sirakaya, E., D. Delen, & H-S. Choi. (2005). “Forecasting Gaming Referenda,” Annals of Tourism Research, 32(1): 127–149.
Tang, Z., C. de Almieda, & P. Fishwick. (1991). “Time-Series Forecasting Using Neural Networks vs. Box-Jenkins Methodology,” Simulation, 57(5).
Walczak, S., W. E. Pofahi, & R. J. Scorpio. (2002). “A Decision Support Tool for Allocating Hospital Bed Resources and Determining Required Acuity of Care,” Decision Support Systems, 34(4).
Wallace, M. P. (2008, July). “Neural Networks and Their Applications in Finance,” Business Intelligence Journal, 67–76.
Wen, U-P., K-M. Lan, & H-S. Shih. (2009). “A Review of Hopfield Neural Networks for Solving Mathematical Programming Problems,” European Journal of Operational Research, 198: 675–687.
Wilson, C. I., & L. Threapleton. (2003, May 17–22). “Application of Artificial Intelligence for Predicting Beer Flavours from Chemical Analysis,” Proceedings of the 29th European Brewery Congress, Dublin, Ireland. http://neurosolutions.com/resources/apps/beer.html (accessed May 2009).
Wilson, R., & R. Sharda. (1994). “Bankruptcy Prediction Using Neural Networks,” Decision Support Systems, 11.
Zahedi, F. (1993). Intelligent Systems for Business: Expert Systems with Neural Networks. Belmont, CA: Wadsworth.