Part III

Intervals

Examples in this part of the dictionary are based for the most part on a drastically revised version of the suppliers-and-parts database, involving suppliers and shipments only (“the suppliers-and-shipments database”). Sample values are shown in Fig. 6.

Fig. 6: The suppliers-and-shipments database with both since and during relvars—sample values

The relvars illustrated in Fig. 6 are all base relvars. The predicates are as follows:

• Relvar S_SINCE: Supplier SNO has been under contract ever since day SNO_SINCE (and not the day immediately before day SNO_SINCE) and will continue to be so until further notice, and has had status STATUS ever since day STATUS_SINCE (and not the day immediately before day STATUS_SINCE) and will continue to do so until further notice.

• Relvar SP_SINCE: Supplier SNO has been able to supply part PNO ever since day SINCE (and not the day immediately before day SINCE) and will continue to be so until further notice.

• Relvar S_DURING: DURING denotes a maximal interval of days throughout which supplier SNO was under contract.

• Relvar S_STATUS_DURING: DURING denotes a maximal interval of days throughout which supplier SNO had status STATUS.

• Relvar SP_DURING: DURING denotes a maximal interval of days throughout which supplier SNO was able to supply part PNO.

  Points arising:

• First of all, note the subtle change in semantics with respect to shipments in particular. In the original suppliers-and-parts database (with respect to relvar SP specifically), the term “shipments” referred to actual shipments—the specified supplier was actually supplying the specified part. By contrast, in the suppliers-and-shipments database (with respect to relvars SP_SINCE and SP_DURING specifically), the term refers to what might be called potential shipments—the specified supplier is able to supply the specified part, but might or might not actually be doing so at any given time.

• The symbols d01, d02, etc. in Fig. 6 can be read as “day 1,” “day 2,” etc., where day 1 immediately precedes day 2, day 2 immediately precedes day 3, and so on. The symbols in question can be thought of as shorthand for literals of type DATE (see DATE). Note: For simplicity, insignificant leading zeros are dropped from expressions such as “day 1.” Also, the symbol d99 (“day 99”) is special—it’s used to denote “the last day” (see end of time).

• Analogously, the symbols t01, t02, ..., t99 (not illustrated in Fig. 6) stand for specific times;¹ they can be thought of as shorthand for literals of type TIME or some TIMESTAMP type (see TIME; TIMESTAMP), depending on context. Also, t99, like d99, is special (see bitemporal table (SQL); system time).

• Symbols of the form [di:dj] in Fig. 6 stand for intervals—to be specific, the interval from day i to day j, inclusive (see interval value). They can be thought of as shorthand for certain literals of type INTERVAL_DATE (see interval selector). Analogously, symbols of the form [ti:tj] (not illustrated in Fig. 6) also stand for certain intervals; they can be thought of as shorthand for certain literals of type INTERVAL_TIME or INTERVAL_ TIMESTAMP (again, see interval selector), depending on context. Note: More generally, symbols of the form [b:e]—b for begin and e for end—are used to stand for intervals whose contained points aren’t necessarily temporal ones (they might be or they might not).

• To say that (e.g.) DURING in relvar S_DURING denotes a “maximal” interval of days throughout which supplier SNO was under contract means that if there’s a tuple in that relvar showing supplier S2 as under contract from, say, day 2 to day 4 inclusive—which indeed there is, in Fig. 6—then there isn’t a tuple in that relvar showing that supplier as under contract on either day 1 or day 5. See maximal interval.

• Use of the past tense in the predicates for relvars S_DURING, S_STATUS_DURING, and SP_DURING is merely a matter of convention. For example, the predicate for S_DURING refers to an interval throughout which the specified supplier was under contract (emphasis added). In general, however, intervals can refer to the past and/or the present and/or the future; thus, the predicate for S_DURING might more accurately be stated as follows: DURING denotes a maximal interval of days throughout which supplier SNO was, is, or will be under contract.

• That said, the relvars illustrated in Fig. 6 are in fact subject to a variety of constraints that ensure among other things that the intervals in relvar S_DURING (also in relvars S_STATUS_DURING and SP_DURING) always refer to the past specifically. Unfortunately the constraints in question are a little complicated, and detailed discussion of them is beyond the scope of this dictionary; suffice it to say that one of the effects of those constraints is to ensure that there’s no “overlap” between the since and during relvars. In other words (to spell the point out), no supplier is shown (a) as being under contract on some given day in both S_SINCE and S_DURING, or (b) as having some status on some given day in both S_SINCE and S_STATUS_DURING, or (c) as being able to supply some given part on some given day in both SP_SINCE and SP_DURING.

• The previous point notwithstanding, Fig. 7 below does at least show a definition for the suppliers-and-shipments database that includes the constraints in question. For further discussion and explanation, including in particular an explanation of the various constraint names (BR12, etc.), see the book Time and Relational Theory: Temporal Data in the Relational Model and SQL, by C. J. Date, Hugh Darwen, and Nikos A. Lorentzos (Morgan Kaufmann, 2014).

Fig. 7: Complete definition for the database of Fig. 6 (part 1 of 2)

Next, certain of the examples in what follows make use of a revised version of the suppliers-and-shipments database, with sample values as shown in Fig. 8. Exactly how the relvars of Fig. 8 are related to—in fact, are derived from—those of Fig. 6 is explained in the entry for COMBINED_IN, q.v., where the pertinent predicates can also be found.

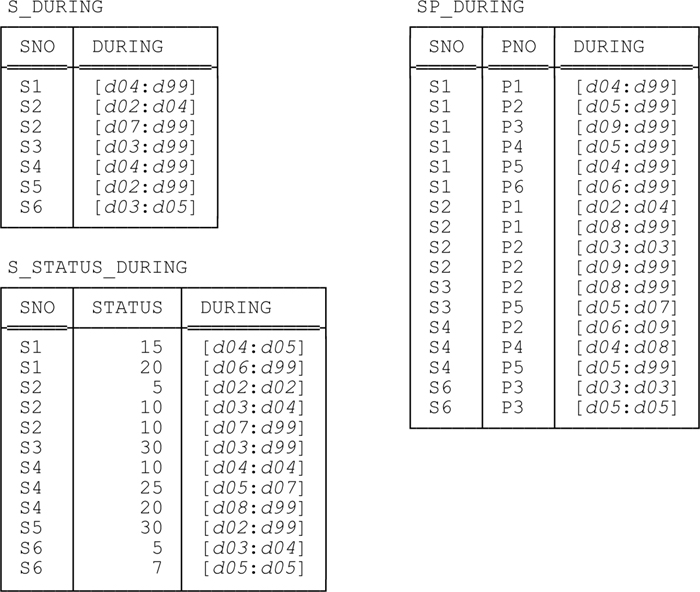
Fig. 8: Fig. 6 revised to use during relvars only

A Note on Redundancy

Take another look at Fig. 8; in particular, take a look at the tuples for supplier S6 in relvars S_DURING and S_STATUS_DURING. For convenience, we show those tuples again below (more precisely, we show the S_DURING and S_STATUS_DURING relation values from the figure, restricted in each case to just the tuples for supplier S6):

 S_DURING                           S_STATUS_DURING
┌─────┬───────────┐                ┌─────┬────────┬───────────┐
│ SNO │ DURING    │                │ SNO │ STATUS │ DURING    │
├═════┼═══════════┤                ├═════┼════════┼═══════════┤
│ S6  │ [d03:d05] │                │ S6  │      5 │ [d03:d04] │
└─────┴───────────┘                │ S6  │      7 │ [d05:d05] │
                                   └─────┴────────┴───────────┘

Observe now that the information represented explicitly in S_DURING to the effect that supplier S6 was under contract throughout the interval from day 3 to day 5, inclusive, is represented implicitly in S_STATUS_DURING as well. (More precisely, one of the tuples for supplier S6 in S_STATUS_DURING tells us that that supplier had some status on days 3 and 4, and the other tells us that that same supplier had some status on day 5 as well—from which it follows that supplier S6 must indeed have been under contract throughout those three days.) And, of course, similar remarks apply to every individual supplier; we chose supplier S6 just by way of example. In other words, relvar S_DURING is 100% redundant in the design of Fig. 8! Indeed, given that whenever the database shows a supplier as being under contract, it must also show that supplier as having some status, it should be intuitively obvious that S_DURING is indeed redundant as claimed.

As noted in Part I of this dictionary, however, redundancy in the database shouldn’t be a problem so long as it’s controlled, meaning it’s guaranteed never to lead to any formal inconsistencies. In order to ensure that the particular redundancy under discussion is controlled in this sense, what’s needed is for a certain constraint to be stated and enforced—to be precise, a certain foreign U_key constraint (q.v.) from S_DURING to S_STATUS_DURING, which will ensure that for every day on which, according to S_DURING, a given supplier is under contract, there’ll be a tuple that effectively asserts the same thing in S_STATUS_DURING.²

Of course, the obvious question is: If S_DURING is indeed redundant as described, why do we include it in our design at all? The answer is: We do so in order to avoid a certain degree of awkwardness, arbitrariness, and asymmetry that would otherwise occur. Further specifics are beyond the scope of this brief discussion; suffice it to say that S_DURING plays a role with respect to the design of Fig. 8 that’s analogous, somewhat, to the role played by E-relvars in an RM/T design (see Part I of this dictionary).

Note: Remarks analogous to the foregoing apply to the design of Fig. 6 as well, though the specifics are a little more complicated. Again, for detailed discussion see the book Time and Relational Theory: Temporal Data in the Relational Model and SQL, by C. J. Date, Hugh Darwen, and Nikos A. Lorentzos (Morgan Kaufmann, 2014).

A Note on SQL

This part of the dictionary contains rather more definitions, examples, and discussions having to do with SQL specifically than Parts I and II did. The reason is that the pertinent features of SQL were added to the standard only comparatively recently, as part of SQL:2011 (see Part I of this dictionary), and for the most part they haven’t yet found their way into commercial products. For that reason, they’re likely to be unfamiliar to most readers. Note: Those SQL examples in particular make use of the database shown in Fig. 9 (a variation on the database of Fig. 8). Tables S_FROM_TO, S_STATUS_FROM_TO, and SP_FROM_TO in that database are all base tables. Note in particular that those tables involve no intervals, as such, at all—they have periods instead, q.v., made up of column pairs (DFROM and DTO, in the figure). In the body of the dictionary, we use SQL-style expressions of the form PERIOD (f,t) to denote such periods.

Fig. 9: SQL analog of Fig. 8

As for the predicates for these SQL tables, see the entry for table predicate (SQL).

A Note on Tutorial D

The current version of Tutorial D as defined in the book Database Explorations: Essays on The Third Manifesto and Related Topics, by C. J. Date and Hugh Darwen (Trafford, 2010), has no support for intervals. However, the book mentioned a couple of times already, Time and Relational Theory: Temporal Data in the Relational Model and SQL, by Date, Darwen, and Lorentzos, contains some proposals for extending the language to incorporate such support, and the name “Tutorial D” in this part of the dictionary should be understood as referring to a version of the language that has been extended in accordance with the proposals in that book.

adding temporal support See temporal upward compatibility.

AFTER One of Allen’s operators, q.v. Let i1 = [b1:e1] and i2 = [b2:e2] be intervals of the same type. Then i1 AFTER i2 is true if and only if b1 > e2 is true.

Examples: Let i1 and i2 be [d08:d10] and [d02:d03], respectively; then i1 AFTER i2 is true. By contrast, if i1 and i2 are [d08:d10] and [d02:d08], respectively, then i1 AFTER i2 is false. Observe that i1 AFTER i2 and i2 BEFORE i1 are equivalent (i.e., i1 AFTER i2 is true if and only if i2 BEFORE i1 is true).

Note: SQL uses the keyword SUCCEEDS in place of AFTER. For example, let p1 and p2 be the SQL periods PERIOD (d08,d11) and PERIOD (d02,d04), respectively; then the SQL expression p1 SUCCEEDS p2 is true.

Allen’s operators A set of operators for comparing two intervals of the same type to see whether they’re equal, whether they overlap, and so on. The operators are referred to collectively as Allen’s operators because most of them—not all—were first proposed by James F. Allen in “Maintaining Knowledge about Temporal Intervals” (CACM 26, No. 11, November 1983). The following table lists the Allen operators defined in this dictionary and shows their direct SQL analogs, where such analogs exist (p1 and p2 denote SQL periods):

┌─────────────────────────┬───────────────────────────────┐
│ Operator                │ SQL analog                    │
├═════════════════════════┼───────────────────────────────┤
│ equality                │ p1 EQUALS p2                  │
│ includes                │ p1 CONTAINS p2                │
│ properly includes       │                               │
│ is included in          │                               │
│ is properly included in │                               │
│ AFTER                   │ p1 SUCCEEDS p2                │
│ BEFORE                  │ p1 PRECEDES p2                │
│ BEGINS                  │                               │
│ ENDS                    │                               │
│ DISJOINT                │                               │
│ OVERLAPS                │ p1 OVERLAPS p2                │
│ MEETS                   │ p1 IMMEDIATELY PRECEDES p2 OR │
│                         │ p1 IMMEDIATELY SUCCEEDS p2    │
│ MERGES                  │                               │
└─────────────────────────┴───────────────────────────────┘

Note: Despite the title of Allen’s paper, the operators don’t apply just to temporal intervals as such. Also, (a) the operators defined in this dictionary aren’t the only ones possible, but they’re probably the most useful ones in practice; (b) the names used in this dictionary to refer to those operators—and indeed the definitions too—do sometimes differ (deliberately, of course) from the ones originally proposed by Allen.

application time SQL term for stated time, q.v. An SQL base table can have at most one application time period (see period). However, such periods don’t “carry through” operational expressions; thus, no SQL table other than a base table has, or can have, any application time period at all.

Examples: Each of the tables in Fig. 9 has an application time period, represented by the (DFROM,DTO) column pair in the table in question. By contrast, the table resulting from, e.g., the SQL expression

SELECT *
FROM   S_FROM_TO

has no application time period at all, even though it’s essentially identical to the current value of table S_FROM_TO, and in particular does have a (DFROM,DTO) column pair. See period for further discussion and explanation.

application time period See application time.

BEFORE One of Allen’s operators, q.v. Let i1 = [b1:e1] and i2 = [b2:e2] be intervals of the same type. Then i1 BEFORE i2 is true if and only if e1 < b2 is true.

Examples: Let i1 and i2 be [d02:d03] and [d08:d10], respectively; then i1 BEFORE i2 is true. By contrast, if i1 and i2 are [d02:d08] and [d08:d10], respectively, then i1 BEFORE i2 is false. Observe that i1 BEFORE i2 and i2 AFTER i1 are equivalent (i.e., i1 BEFORE i2 is true if and only if i2 AFTER i1 is true).

Note: SQL uses the keyword PRECEDES in place of BEFORE. For example, let p1 and p2 be the SQL periods PERIOD (d02,d04) and PERIOD (d08,d11), respectively; then the SQL expression p1 PRECEDES p2 is true.

BEGIN See begin point.

begin point The begin point of the interval i = [b:e], denoted BEGIN (i), is the point b. Note: SQL has no support for the BEGIN operator as such. Rather, if p denotes the SQL period PERIOD (f,t), then the SQL expression f is effectively equivalent to the hypothetical SQL expression “BEGIN (p).” See period for further explanation.

beginning of time See timeline.

BEGINS One of Allen’s operators, q.v. Let i1 = [b1:e1] and i2 = [b2:e2] be intervals of the same type. Then i1 BEGINS i2 is true if and only if b1 = b2 and e1 ≤ e2 are both true.

Examples: Let i1 and i2 be [d02:d05] and [d02:d10], respectively; then i1 BEGINS i2 is true. By contrast, if i1 and i2 are [d02:d05] and [d01:d10], respectively, then i1 BEGINS i2 is false.

Note: SQL has no direct support for the BEGINS operator. However, if p1 and p2 denote the SQL periods PERIOD (f1,t1) and PERIOD (f2,t2), respectively, then the SQL expression f1 = f2 AND t1 ≤ t2 is effectively equivalent to the hypothetical SQL expression “p1 BEGINS p2.” See period for further explanation.

bitemporal An informal and somewhat deprecated term used to characterize a heading (or a tuple, or a relation, or a relvar, or an SQL row or table) having exactly two temporal components, one representing stated time, q.v., and the other logged time, q.v. Note: Actually it’s not so much the term as such, but rather the concept denoted by that term, that’s deprecated. Indeed, the term as such can be useful in referring to that otherwise deprecated concept.

Example: Consider the following tuple:

┌─────┬───────────┬────────────┐
│ SNO │ DURING    │ X_DURING   │
├─────┼───────────┼────────────┤
│ S2  │ [d02:d04] │ [t50:t75]  │
└─────┴───────────┴────────────┘

This tuple is bitemporal; the intended interpretation—deliberately stated a little loosely here—is “From time t50 to time t75, inclusive, the database said that supplier S2 was under contract from day 2 to day 4, inclusive.” In other words, attribute DURING denotes the stated time for a certain proposition (viz., “Supplier S2 was under contract,” in the case at hand), and attribute X_DURING denotes the logged time for another, different, proposition (viz., “Supplier S2 was under contract from day 2 to day 4, inclusive,” in the case at hand).

So much for the basic idea. Unfortunately, the term and the concept both have their origins in a nonrelational approach to temporal data—an approach in which time is regarded as special, and intervals like [d02:d04] and [t50:t75] are represented not by regular relational attributes as in the foregoing example, but rather in some special and ad hoc kind of way. And it’s generally assumed in such nonrelational approaches that data can never be “more than” bitemporal, meaning that a given heading (or tuple, or relation, etc.) can never involve more than one “stated time” component and/or more than one “logged time” component. What are the implications? Well, consider the following two perfectly reasonable tuples (each of which might perhaps be characterized as “unitemporal”):

┌────────┬───────────┐      ┌────────┬─────────────┐
│ PERSON │ DAYS      │      │ PERSON │ HOURS       │
├────────┼───────────┤      ├────────┼─────────────┤
│ p      │ [Sun:Thu] │      │ p      │ [1030:1830] │
└────────┴───────────┘      └────────┴─────────────┘

The intended interpretations are “Person p works on Sunday to Thursday” and “Person p works from 10:30 am to 6:30 pm.” Observe that each of these tuples has just one temporal attribute, each representing a certain “stated time.” So what happens if these two tuples are joined together? Clearly, the result is:

┌────────┬───────────┬─────────────┐
│ PERSON │ DAYS      │ HOURS       │
├────────┼───────────┼─────────────┤
│ p      │ [Sun:Thu] │ [1030:1830] │
└────────┴───────────┴─────────────┘

But this tuple has two “stated time” temporal attributes, and is thus not legal under a scheme in which tuples are limited to being at most bitemporal—meaning, to repeat, that they can have at most one stated time component and/or at most one logged time component.

By way of another example, here are two more “unitemporal” tuples:

┌────────┬─────────────┐  ┌────────┬─────────────┐
│ PERSON │ PRIMARY     │  │ PERSON │ SECONDARY   │
├────────┼─────────────┤  ├────────┼─────────────┤
│ p      │ [1946:1951] │  │ p      │ [1951:1959] │
└────────┴─────────────┘  └────────┴─────────────┘

The intended interpretations are “Person p’s primary education lasted from 1946 to 1951” and “Person p’s secondary education lasted from 1951 to 1959.” And here’s the bitemporal tuple that results if these two tuples are joined together:

┌────────┬─────────────┬─────────────┐
│ PERSON │ PRIMARY     │ SECONDARY   │
├────────┼─────────────┼─────────────┤
│ p      │ [1946:1951] │ [1951:1959] │
└────────┴─────────────┴─────────────┘

bitemporal table (SQL) Unofficial but useful term for an SQL table (necessarily a base table) having both an application time period, q.v. (necessarily unique), and a system time period, q.v. (also necessarily uniqe).

Example: Suppose we want to keep system time information as well as application time information for suppliers and their status values. Then instead of table S_STATUS_FROM_TO as illustrated in Fig. 9 (and as defined in the examples under period, q.v.), we might define a bitemporal table BS_STATUS_FROM_TO as shown here:

CREATE TABLE BS_STATUS_FROM_TO
     ( SNO    SNO     NOT NULL ,
       STATUS INTEGER NOT NULL ,
       DFROM  DATE    NOT NULL ,
       DTO    DATE    NOT NULL ,
       PERIOD FOR DPERIOD ( DFROM , DTO ) ,
       UNIQUE ( SNO , DPERIOD WITHOUT OVERLAPS ) ,
       FOREIGN KEY ( SNO , PERIOD DPERIOD )
               REFERENCES BS_FROM_TO ( SNO , PERIOD DPERIOD ) ,
       XFROM  TIMESTAMP(12) GENERATED ALWAYS AS ROW START NOT NULL ,
       XTO    TIMESTAMP(12) GENERATED ALWAYS AS ROW END   NOT NULL ,
       PERIOD FOR SYSTEM_TIME ( XFROM , XTO ) )
       WITH SYSTEM VERSIONING ;

See the examples under period and system time for further explanation, in particular regarding queries on tables like BS_STATUS_FROM_TO. (Updates are discussed below, though again further explanation can be found under system time. Here we just note that the system time columns XFROM and XTO can’t be directly updated by the user.)

Note: The FOREIGN KEY specification in the foregoing definition assumes the existence of another bitemporal table called BS_FROM_TO, with the obvious definition and semantics. For simplicity, however, we ignore foreign keys in the discussion of updates below. However, we note for the record that, while SQL does indeed call the constructs in question “foreign keys,” it would be closer to the truth, though still not entirely accurate, to refer to them as foreign U_keys, q.v. See foreign key (SQL) for further explanation.

Table BS_STATUS_FROM_TO is initially empty, of course. Suppose we now execute the following INSERT:

INSERT INTO BS_STATUS_FROM_TO ( SNO , STATUS , DFROM , DTO )
       VALUES ( SNO('S2') , 5 , d02 , d05 ) ;

Further, suppose this INSERT statement is executed at time t11 by the system clock (see system time). Then the row that’s actually inserted looks like this:

┌─────┬────────┬───────┬─────┬───────┬─────┐
│ SNO │ STATUS │ DFROM │ DTO │ XFROM │ XTO │
├─────┼────────┼───────┼─────┼───────┼─────┤
│ S2  │  5     │ d02   │ d05 │ t11   │ t99 │
└─────┴────────┴───────┴─────┴───────┴─────┘

In other words, the system automatically appends (a) an XFROM value denoting the time of the update, and (b) an XTO value of t99 denoting “the end of time,” to the row before inserting it. Thus, the row that’s actually inserted effectively says: “During the interval [t11:t99), the database said that supplier S2 had status 5 during the interval [d02:d05).” Note: In accordance with SQL conventions, these intervals are given in closed:open style, q.v.

Now suppose we execute the following UPDATE statement at time t22 by the system clock:

UPDATE BS_STATUS_FROM_TO
FOR    PORTION OF DPERIOD FROM d03 TO d04
SET    STATUS = 10
WHERE  SNO = SNO('S2') ;

After this UPDATE, the table looks like this:

┌─────┬────────┬───────┬─────┬───────┬─────┐
│ SNO │ STATUS │ DFROM │ DTO │ XFROM │ XTO │
├═════┼────────┼═══════┼─────┼═══════┼─────┤
│ S2  │      5 │ d02   │ d05 │ t11   │ t22 │
│ S2  │      5 │ d02   │ d03 │ t22   │ t99 │
│ S2  │     10 │ d03   │ d04 │ t22   │ t99 │
│ S2  │      5 │ d04   │ d05 │ t22   │ t99 │
└─────┴────────┴───────┴─────┴───────┴─────┘

In other words, the table now says “During the interval [t11:t22), the database said that supplier S2 had status 5 during the interval [d02:d05); during the interval [t22:t99), it said that supplier S2 had status 5 during the intervals [d02:d03) and [d04:d05), but status 10 during the interval [d03:d04).”

Now suppose we execute the following DELETE statement at time t33 by the system clock:

DELETE
FROM   BS_STATUS_FROM_TO
FOR    PORTION OF DPERIOD FROM d03 TO d05
WHERE  SNO = SNO('S2') ;

Now the table looks like this:

┌─────┬────────┬───────┬─────┬───────┬─────┐
│ SNO │ STATUS │ DFROM │ DTO │ XFROM │ XTO │
├═════┼────────┼═══════┼─────┼═══════┼─────┤
│ S2  │      5 │ d02   │ d05 │ t11   │ t22 │
│ S2  │      5 │ d02   │ d03 │ t22   │ t99 │
│ S2  │     10 │ d03   │ d04 │ t22   │ t33 │
│ S2  │      5 │ d04   │ d05 │ t22   │ t33 │
└─────┴────────┴───────┴─────┴───────┴─────┘

Thus, the table now says “During the interval [t11:t22), the database said that supplier S2 had status 5 during the interval [d02:d05); during the interval [t22:t33), it said that supplier S2 had status 5 during the interval [d04:d05) but status 10 during the interval [d03:d04); and during the interval [t22:t99), it said that supplier S2 had status 5 during the interval [d02:d03).”

Finally, we execute the following DELETE statement at time t44:

DELETE
FROM   BS_STATUS_FROM_TO
WHERE  SNO = SNO('S2') ;

Then the final version of the table looks like this:

┌─────┬────────┬───────┬─────┬───────┬─────┐
│ SNO │ STATUS │ DFROM │ DTO │ XFROM │ XTO │
├═════┼────────┼═══════┼─────┼═══════┼─────┤
│ S2  │      5 │ d02   │ d05 │ t11   │ t22 │
│ S2  │      5 │ d02   │ d03 │ t22   │ t44 │
│ S2  │     10 │ d03   │ d04 │ t22   │ t33 │
│ S2  │      5 │ d04   │ d05 │ t22   │ t33 │
└─────┴────────┴───────┴─────┴───────┴─────┘

The table now says “During the interval [t11:t22), the database said that supplier S2 had status 5 during the interval [d02:d05); during the interval [t22:t33), it said that supplier S2 had status 5 during the interval [d04:d05) but status 10 during the interval [d03:d04); and during the interval [t22:t44), it said that supplier S2 had status 5 during the interval [d02:d03).”

boundary column (SQL) See period.

boundary point Let i be the interval [b:e]. Then the begin point b and the end point e of i are sometimes said to be the boundary points of i. The term is fuzzy, however (and best avoided for that reason, unless the context makes the intended meaning clear), because it’s also used to refer:

• If i is expressed using closed:open style as [b:es), to the specified points b and es;

• If i is expressed using open:closed style as (pb:e], to the specified points pb and e;

• If i is expressed using open:open style as (pb:es), to the specified points pb and es.

See interval selector for further explanation.

boundary value (SQL) See period.

business time Term used in certain DBMS products as a synonym for stated time, q.v.

cardinality (Of an interval) The number of points in the interval in question. See also COUNT; duration; length.

chronon A “time quantum”; the smallest unit of time capable of representation in a given system (and hence the smallest possible time point, q.v., capable of representation in the system in question as well, a fortiori). Contrast time point.

chronon timeline See timeline.

circumlocution problem A problem that can arise in connection with relvars with interval attributes, absent suitable controls: specifically, the problem that two tuples appearing in such a relvar at the same time might together represent propositions that could better be represented by a single tuple. For example, suppose with reference to either Fig. 6 or Fig. 7 that the following tuples were both to appear in relvar S_STATUS_DURING at the same time:

┌─────┬────────┬───────────┐       ┌─────┬────────┬───────────┐
│ SNO │ STATUS │ DURING    │       │ SNO │ STATUS │ DURING    │
├─────┼────────┼───────────┤       ├─────┼────────┼───────────┤
│ S4  │     25 │ [d05:d05] │       │ S4  │     25 │ [d06:d07] │
└─────┴────────┴───────────┘       └─────┴────────┴───────────┘

Clearly, the propositions represented by these tuples could alternatively (and better) be represented by a single tuple, thus:

┌─────┬────────┬───────────┐
│ SNO │ STATUS │ DURING    │
├─────┼────────┼───────────┤
│ S4  │     25 │ [d05:d07] │
└─────┴────────┴───────────┘

Formally, the problem illustrated by this example is that the two original tuples (a) agree on their SNO and STATUS values and (b) have DURING values i1 and i2 such that i1 MEETS i2 is true (see MEETS). Note that if those original tuples were indeed both allowed to appear, then the relvar would be in violation of its own predicate, because neither [d05:d05] nor [d06:d07] would be a maximal interval, q.v., of days during which supplier S4 had status 25. (In fact, it’s not entirely clear that the relvar would even have a proper relvar predicate, if those original tuples were both allowed to appear. See table predicate (SQL) for further discussion.) Note finally that enforcing a constraint to the effect that {SNO,DURING} is a key for S_STATUS_DURING—which it is—isn’t sufficient to prevent the foregoing problem from occurring. See PACKED ON for further discussion.

closed (Of an interval) See interval selector; interval value.

closed:closed (Of an interval) See interval selector.

closed:open (Of an interval) See interval selector.

coalescing Term sometimes used as a synonym for packing, q.v. (or for an operation of the same general nature as packing). Note: SQL supports an operator it calls COALESCE, but that operator has nothing to do with coalescing as here defined. An example of the use of that SQL operator can be found under summarization in Part I of this dictionary.

COLLAPSE See collapsed form. Note: SQL has no direct support for the COLLAPSE operator.

collapsed form 1. (Sets of intervals) Let x be a set of intervals all of the same type T. Then the expression COLLAPSE (x) denotes the collapsed form of x, and it returns the unique set y of intervals (necessarily also all of that same type T) such that (a) x and y have the same expanded form, q.v., and (b) no two distinct intervals i1 and i2 in y are such that i1 MERGES i2 is true (see MERGES); equivalently, no two distinct intervals i1 and i2 in y are such that i1 UNION i2 is defined—see union (interval theory). Observe that y can be computed from x by successively replacing pairs of intervals in x by their union until no further such replacements are possible. Observe further that no two distinct intervals i1 and i2 in y are such that i1 INTERSECT i2 is defined—see intersection (interval theory). Observe finally that if the cardinality of x is either zero or one, then COLLAPSE (x) is equal to x. 2. (Unary relations) Let x be a unary relation whose sole attribute is of some interval type. Then the expression COLLAPSE (x) denotes the collapsed form of x, and it returns the unique relation y of the same type as x such that (a) x and y have the same expanded form and (b) no two distinct tuples t1 and t2 in y are such that the intervals i1 and i2 contained in t1 and t2, respectively, are such that i1 MERGES i2 is true. 3. (Nullary relations) Let x be a nullary relation (i.e., let x be either TABLE_DUM or TABLE_DEE). Then the expression COLLAPSE (x) denotes the collapsed form of x, and it returns the relation x itself (i.e., each of TABLE_DUM and TABLE_DEE is its own collapsed form). Contrast expanded form.

Example (second definition only): Let relation x look like this:

┌───────────┐
│ DURING    │
├═══════════┤
│ [d06:d09] │
│ [d04:d08] │
│ [d05:d10] │
│ [d01:d01] │
└───────────┘

Then y = COLLAPSE (x) looks like this:

┌───────────┐
│ DURING    │
├═══════════┤
│ [d01:d01] │
│ [d04:d10] │
└───────────┘

Note: The relational version of COLLAPSE is actually a special case of PACK (see packed form). To be specific, (a) if relation x has just one attribute, say A, and that attribute is interval valued, then COLLAPSE (x) and PACK x ON (A) are equivalent; moreover, (b) if relation x has no attributes at all, then COLLAPSE (x) and PACK x ON ( )—the packing here necessarily being on no attributes at all—are also equivalent.

Here for the record is a more formal version of the first (only) of the foregoing definitions. Again let x be a set of intervals all of the same type T; also, let the underlying point type for T be PT. Let p be a point of type PT, and let i = [b:e], i1 = [b1:e1], i2 = [b2:e2], and j be intervals of type T. Then y = COLLAPSE (x) can be defined thus:

y { i : FORALL p ∊ i ( EXISTS j ∊ x ( p ∊ j ) )
           AND
           EXISTS i1 ∊ x ( EXISTS i2 ∊ x
              ( b = b1 AND e = e2 AND b1 ≤ b2 AND e1 ≤ e2
                AND
                IF b2 ≠ FIRST_PT ( ) THEN
                   IF e1 < PRE ( i2 ) THEN
                      FORALL p ∊ ( e1 : b2 )
                        ( EXISTS j ∊ x ( p ∊ j ) ) END IF END IF
                AND
                FORALL p ∊ i
                   ( IF p ≠ FIRST_PT ( ) THEN
                        NOT EXISTS j ∊ x ( PRE ( i ) ∊ j ) END IF
                     AND
                     IF p ≠ LAST_PT ( ) THEN
                        NOT EXISTS j ∊ x ( POST ( i ) ∊ j ) END IF ) ) ) }

COMBINED_IN A syntactic shorthand, intended to make certain operations on a temporal database (to be specific, certain queries, constraints, and updates) easier to formulate. By way of example, consider shipments. Given the database of Fig. 6, it should be intuitively obvious that certain operations on shipments—both read-only and update operations, in general—will need to refer to two distinct relvars (viz., SP_SINCE and SP_DURING), because shipment information is split across those two relvars in that database. By contrast, it should also be intuitively obvious that analogous operations on the database of Fig. 8 will need to refer to just one relvar (viz., SP_DURING), and hence that these latter operations stand a chance of being conceptually simpler, or at least superficially easier to understand, than their counterparts on Fig. 6. So the idea is that the relvars illustrated in Fig. 8 might be defined as appropriate views of the ones illustrated in Fig. 6, thereby allowing users to operate in terms of Fig. 8 even if the underlying database looks like Fig. 6.

With the foregoing in mind by way of motivation, therefore, consider the following expression:

WITH ( t1 := EXTEND S_SINCE : { DURING :=
                INTERVAL_DATE ( [ SNO_SINCE : LAST_DATE ( ) ] ) } ,
       t2 := t1 { SNO , DURING } ) :
t2 UNION S_DURING

Given the sample values for S_SINCE and S_DURING shown in Fig. 6, this expression evaluates to the relation shown as the sample value for S_DURING in Fig. 8. (The expression INTERVAL_DATE (...) in line 2 is an interval selector invocation, and the subexpression LAST_DATE ( ) within that selector invocation denotes “the last day,” which is shown as d99 in Figs. 6 and 8.) In analogous fashion, given the sample values shown in Fig. 6 for S_SINCE, S_STATUS_DURING, SP_SINCE, and SP_DURING, (a) the expression

WITH ( t1 := EXTEND S_SINCE : { DURING :=
                INTERVAL_DATE ( [ STATUS_SINCE : LAST_DATE ( ) ] ) } ,
       t2 := t1 { SNO , STATUS , DURING } ) :
t2 UNION S_STATUS_DURING

evaluates to the relation shown as the sample value for S_STATUS_DURING in Fig. 8, and (b) the expression

WITH ( t1 := EXTEND SP_SINCE : { DURING :=
                INTERVAL_DATE ( [ SINCE : LAST_DATE ( ) ] ) } ,
       t2 := t1 { SNO , PNO , DURING } ) :
t2 UNION SP_DURING

evaluates to the relation shown as the sample value for SP_DURING in Fig. 8. It follows that the design illustrated in Fig. 8 can indeed be defined as views of the design illustrated in Fig. 6. What’s more (to spell the point out), the design of Fig. 6 consists of a mixture of since and during relvars, whereas the design of Fig. 8 consists of during relvars only.

The design of Fig. 8 is thus “simpler,” in a sense, than the design of Fig. 6. On the other hand, the design of Fig. 8 suffers, as the design of Fig. 6 does not, from the fact that we have to show a specific and arguably artificial time point (viz., “the end of time,” d99) as the end point for any interval for which the actual end point is unknown. Thus, the design of Fig. 8 effectively requires us to put information into the database that we know is false, or at best ambiguous. Observe in particular that we can’t tell the difference in that design between an appearance of d99 that means what it says—i.e., day 99 as such—and one that’s just some kind of code for until further notice (q.v.). In fact, that design constitutes a violation of The Closed World Assumption (see Part I of this dictionary), unless the relvar predicates are carefully—and rather awkwardly—reformulated in such a way as to ensure adherence to the letter, if not the spirit, of that assumption. Here are such reformulated predicates (but observe that these reformulations, complicated though they undoubtedly are, still fail to get round the ambiguity problem):

• Relvar S_DURING: If END (DURING) is “the end of time,” then supplier SNO has been under contract ever since day BEGIN (DURING) (and not the day immediately before day BEGIN (DURING)) and will continue to be so until further notice; otherwise DURING denotes a maximal interval of days throughout which supplier SNO was under contract.

• Relvar S_STATUS_DURING: If END (DURING) is “the end of time,” then supplier SNO has had status STATUS ever since day BEGIN (DURING) (and not the day immediately before day BEGIN (DURING)) and will continue to do so until further notice; otherwise DURING denotes a maximal interval of days throughout which supplier SNO had status STATUS.

• Relvar SP_DURING: If END (DURING) is “the end of time,” then supplier SNO has been able to supply part PNO ever since day BEGIN (DURING) (and not the day immediately before day BEGIN (DURING)) and will continue to be so until further notice; otherwise DURING denotes a maximal interval of days throughout which supplier SNO was able to supply part PNO.

The complexity of these predicates notwithstanding, it’s still the case that designs like that of Fig. 8 can make life easier for the user in certain ways. Hence the notion of COMBINED_IN specifications. The basic idea is that, given a design like that of Fig. 6, it should be possible to get the DBMS to produce a design like that of Fig. 8 automatically in response to such specifications. For example, specifying

COMBINED_IN ( CSP_DURING )

in connection with relvars SP_SINCE and SP_DURING as illustrated in Fig. 6 (and as defined in Fig. 7) should be sufficient for the system to define, automatically, a view called CSP_DURING that looks like relvar SP_DURING as illustrated in Fig. 8.

Now, the effect of the COMBINED_IN specification in the foregoing example, and indeed the effect of COMBINED_IN specifications in general (at least as so far discussed), can be regarded as undoing certain horizontal decompositions, q.v. In practice, however, we would want to be able to undo certain vertical decompositions, q.v., as well. Unfortunately, Figs. 6-8 are a little too simple to illustrate this point, so let’s extend our running example (just for the sake of the present discussion) as follows. First, let’s extend relvar S_SINCE to add two more attributes, CITY and CITY_SINCE. Here’s a sample value:

┌─────┬───────────┬────────┬──────────────┬────────┬────────────┐
│ SNO │ SNO_SINCE │ STATUS │ STATUS_SINCE │ CITY   │ CITY_SINCE │
├═════┼───────────┼────────┼──────────────┼────────┼────────────┤
│ S1  │ d04       │     20 │ d06          │ Athens │ d06        │
│ S2  │ d07       │     10 │ d07          │ Paris  │ d07        │
│ S3  │ d03       │     30 │ d03          │ Paris  │ d03        │
│ S4  │ d04       │     20 │ d08          │ Madrid │ d10        │
│ S5  │ d02       │     30 │ d02          │ Athens │ d02        │
└─────┴───────────┴────────┴──────────────┴────────┴────────────┘

The predicate for this revised version of S_SINCE is as follows:

Supplier SNO has been under contract ever since day SNO_SINCE (and not the day immediately before day SNO_SINCE) and will continue to be so until further notice; has had status STATUS ever since day STATUS_SINCE (and not the day immediately before day STATUS_SINCE) and will continue to do so until further notice; and has been located in city CITY ever since day CITY_SINCE (and not the day immediately before day CITY_SINCE) and will continue to be so until further notice.

Second, let’s also introduce an additional base relvar, S_CITY_DURING, with attributes SNO, CITY, and DURING, and predicate as follows:

DURING denotes a maximal interval of days throughout which supplier SNO was located in city CITY.

Here’s a sample value:

┌─────┬────────┬───────────┐
│ SNO │ CITY   │ DURING    │
├═════┼────────┼═══════════┤
│ S1  │ London │ [d04:d05] │
│ S2  │ Rome   │ [d02:d04] │
│ S4  │ Athens │ [d04:d04] │
│ S4  │ Oslo   │ [d05:d07] │
│ S4  │ London │ [d08:d09] │
│ S6  │ Madrid │ [d03:d05] │
└─────┴────────┴───────────┘

Given these additions to the database of Figs. 6-7, we can now certainly define views CS_DURING, CS_STATUS_DURING, and CS_CITY_DURING, more or less as already discussed. However, there’s still a problem—the design is still vertically decomposed, implying that information regarding individual suppliers is still split across more than one relvar. What we need to do is combine those relvars into one (another view, of course), which we can do using U_join (q.v.):

USING ( DURING ) : JOIN { CS_DURING , CS_STATUS_DURING , CS_CITY_DURING }

The predicate for the result of this U_join is as follows:

If END (DURING) is “the end of time,” then supplier SNO (a) has been under contract, (b) has had status STATUS, and (c) has been located in city CITY, ever since day BEGIN (DURING) (and not the day immediately before day BEGIN (DURING)) and will continue to be or do so until further notice; otherwise DURING denotes a maximal interval of days throughout which supplier SNO (a) was under contract, (b) had status STATUS, and (c) was located in city CITY.

Note: Given the fact that (as pointed out, in effect, in the section “A Note on Redundancy” in the introduction to this part of the dictionary) there’ll be a foreign U_key constraint from CS_DURING to CS_STATUS_DURING that guarantees that for every day on which a given supplier is under contract according to CS_DURING, there’ll be a tuple that effectively asserts the same thing in CS_STATUS_DURING, there’s actually no need to include CS_DURING in the foregoing U_join. The reason is that—assuming that this foreign U_key constraint is enforced, of course—the value of CS_DURING will be equal at all times to the U_projection (q.v.) on {SNO,DURING} of CS_STATUS_DURING at the time in question, and so nothing will be either gained or lost if CS_DURING is included. (In fact, the value of CS_DURING will be equal at all times to the U_projection, q.v., on {SNO,DURING} of CS_CITY_DURING at the time in question as well, for essentially analogous reasons.)

Incidentally, it’s precisely because the value of CS_DURING is equal at all times to the U_projection on {SNO,DURING} of CS_STATUS_DURING at the time in question that Figs. 6-8 are too simple to illustrate the point under discussion (the point, that is, that we sometimes need to be able to undo vertical as well as horizontal decomposition).

Note finally that, precisely because of the existence of that (necessary) foreign U_key constraint from CS_DURING to CS_STATUS_DURING—equivalently, from the Fig. 8 version of S_DURING to the Fig. 8 version of S_STATUS_DURING—the predicate for either CS_STATUS_DURING or the Fig. 8 version of S_STATUS_DURING might more accurately be stated thus:

If END (DURING) is “the end of time,” then supplier SNO has been under contract and has had status STATUS ever since day BEGIN (DURING) (and not the day immediately before day BEGIN (DURING)) and will continue to be or do so until further notice; otherwise DURING denotes a maximal interval of days throughout which supplier SNO was under contract and had status STATUS.

(The additional text has to do with the supplier in question being under contract.) Analogous remarks apply to CS_CITY_DURING (and to S_CITY_DURING as well, if such a relvar were to be added to the database of Fig. 8).

containment (Expanded definition) Generally, the relationship between a container and the things it contains; in particular, the relationship between an interval and its points. Let p be a point of type T and let i be an interval of type INTERVAL_T. Then the expression p ∊ i (pronounced “p belongs to i” or “p is contained in i” or, more simply, just “p [is] in i”) is true if and only if BEGIN (i) ≤ p and p ≤ END (i) are both true. Also, the expression i ∍ p (pronounced “i contains p”) is true if and only if p ∊ i is true. See interval value.

Note: SQL uses the keyword CONTAINS in place of “∍” (it doesn’t support “∊”). Since it also uses that same keyword in place of “⊇” (see interval inclusion), it follows that CONTAINS in SQL is overloaded. Of course, although SQL has no direct support for the “∊” operator as such, if p denotes the SQL period PERIOD (f,t) and x is an expression of the underlying datetime type, then the SQL expression x ≥ f AND x < t is effectively equivalent to the hypothetical SQL expression “x ∊ p.” See period for further explanation.

continuity assumption Let T be a point type, q.v. Barring explicit statements to the contrary, then, T is generally assumed to be an ordinal type, q.v., meaning among other things that an associated successor function, q.v., is assumed to exist. However, it might be possible to drop that assumption of ordinality (albeit at the cost of an increase in complexity, with little if any accompanying increase in functionality), and doing so is referred to, somewhat inappropriately, as “adopting the continuity assumption.” The book Time and Relational Theory: Temporal Data in the Relational Model and SQL, by Date, Darwen, and Lorentzos, explores this possibility in some detail. Contrast discreteness assumption.

Note: The term continuity assumption derives from the fact that a point type without a successor function behaves in some respects like the real number line (see Part I of this dictionary)—which is certainly continuous—and hence that an interval defined on such a point type behaves like a section of that line. (Note that most people would surely agree that time in particular does feel as if it were continuous in this sense.) But continuity as such isn’t the real issue here; rather, the real issue is the lack of a successor function. For example, consider the rational numbers (see Part I of this dictionary), which differ from the real numbers in that they don’t form a continuum, and yet resemble the real numbers in that they’re “everywhere dense” and so have no successor function. (To say the rational numbers are everywhere dense is to say that if p and q are rational numbers such that p < q, then there’s an infinite number of rational numbers r such that p < r < q.) Thus, the problem with using rational numbers as a point type isn’t that they’re continuous—they’re not—but rather that they have no successor function; i.e., if r is a rational number, there’s no rational number r′ that can be considered the immediate successor of r.

contradiction problem A problem that can arise in connection with relations with interval attributes, absent suitable controls: specifically, the problem that two tuples appearing in such a relvar at the same time might represent propositions that can’t both be true at the same time. For example, suppose with reference to either Fig. 6 or Fig. 7 that the following tuples were both to appear in relvar S_STATUS_DURING at the same time:

┌─────┬────────┬───────────┐        ┌─────┬────────┬───────────┐
│ SNO │ STATUS │ DURING    │        │ SNO │ STATUS │ DURING    │
├─────┼────────┼───────────┤        ├─────┼────────┼───────────┤
│ S4  │     25 │ [d05:d06] │        │ S4  │     30 │ [d06:d07] │
└─────┴────────┴───────────┘        └─────┴────────┴───────────┘

Note that if these tuples were indeed both allowed to appear, the relvar would be in violation of its own predicate (because taken together, these tuples show among other things that supplier S4 had status both 25 and 30 on day 6, an impossible state of affairs). Note too that enforcing a constraint to the effect that {SNO,DURING} is a key for S_STATUS_DURING—which it is—isn’t sufficient to prevent the foregoing problem from occurring. See WHEN / THEN for further discussion.

COUNT (Of an interval) Given an interval i, the expression COUNT (i) returns the number of points in that interval. See also cardinality; duration; length. Note: SQL has no direct support for the COUNT operator. However, if p denotes the SQL period PERIOD (f,t), then the SQL expression CAST (( t – f ) AS INTEGER) is effectively equivalent to the hypothetical SQL expression “COUNT (p).” See period for further explanation.

current relation Informal term sometimes used to refer to the value of a current relvar, q.v.

current relvar Informal term sometimes used to refer to a since relvar, q.v. However, the term is deprecated, somewhat, because such relvars aren’t limited to containing information that pertains only to the current state of affairs. Indeed, they certainly contain (in general) both implicit and explicit information about the past as well as implicit information about the future, and depending on circumstances they might even contain explicit information about the future as well.

Example: Consider the sample value shown for relvar S_SINCE in Fig. 6. If we make the reasonable assumption that all of the since attribute values in that relation denote either dates in the past or (at the most recent) the date today, then it’s clear that (a) today is at least day 8 and (b) any since attribute value that’s earlier than day 8 represents explicit information about the past. For example, supplier S1 was under contract on day 4 (explicit information about the past); also, supplier S1 was under contract throughout the interval from day 5 to day 7 inclusive (implicit information about the past). Moreover, supplier S1 will remain under contract until further notice (implicit information about the future). And if we know that (say) supplier S8 will be placed under contract on day dc, where dc is in the future, and we insert a tuple into S_SINCE to say as much, then that relvar will now contain explicit information about the future as well.

current row (SQL) See system time.

cyclic point type See point type.

DATE A point type, assumed for the purposes of this dictionary to be system defined and to have values consisting of calendar dates, accurate to the day. In other words, the scale, q.v., is one day, and the successor function is basically “next day,” meaning “add one day to the specified date” (i.e., it’s a function that, given a specified DATE value d, returns the DATE value that’s the immediate successor of d according to conventional calendar ordering).

Examples: Here’s an example of a DATE literal in Tutorial D:

DATE ( '2014/8/25' )

(“August 25th, 2014”). As noted in the introduction to this part of the dictionary, symbols such as d01, d02, etc. in examples elsewhere can be thought of as shorthand for such literals. Note: An SQL version of the literal shown above would look like this:

DATE '2014-8-25'

datetime arithmetic (SQL) SQL’s support for dates and times is quite extensive (details can be found in, e.g., the book A Guide to the SQL Standard, by C. J. Date and Hugh Darwen, 4th edition, Addison-Wesley, 1997). For the purposes of this dictionary, however, it’s sufficient to note that (a) the support in question includes support for datetime arithmetic expressions of the form dx ± ix, where dx is an expression denoting an SQL-style date and ix is an SQL expression denoting an SQL-style interval (in other words, a duration, q.v.), and also that (b) expressions of that form dx ± ix can effectively be used as successor and predecessor function invocations (see successor; predecessor). Here are some examples of such “SQL successor function invocations” (“SQL predecessor function invocations” are analogous, of course—see further discussion below):

DV + INTERVAL '1' DAY

DV + INTERVAL '30' DAY

DV + INTERVAL '1' MONTH

In these examples, DV is an SQL variable of type DATE and the three subexpressions INTERVAL '1' DAY, INTERVAL '30' DAY, and INTERVAL '1' MONTH are SQL literals, each of type INTERVAL. (More precisely, the first of these literals denotes “zero years, zero months, one day”; the second denotes “zero years, zero months, 30 days”; and the third denotes “zero years, one month, zero days.”) Suppose the current value of DV is the date July 31st, 2014. Then the first of the foregoing expressions returns August 1st, 2014; the second returns August 30th, 2014; and the third returns August 31st, 2014.

There’s a trap for the unwary here, however. Suppose in the foregoing examples that the current value of DV is the date August (not July) 31st, 2014. Then the first expression returns September 1st, 2014; the second returns September 30th, 2014; but the third fails, because September 31st, 2014 isn’t a legitimate date. In general, adding an interval to a date is performed by adding the day component first, then the months component, and then the years component; but it’s important to understand that while any of these individual additions can cause a carry forward to affect the next component, they never have any effect backward on the previous one.

Subtraction is performed analogously, except that carries to the next component are replaced by borrows from that component. Thus, for example, if again the current value of DV is the date August 31st, 2014, then the expression

DV - INTERVAL '1' MONTH

returns July 31st, 2014 (but would fail if the current value of DV were, say, the date March 31st, 2014), while the expression

DV - INTERVAL '30' DAY

returns August 1st, 2014.

denseness constraint A constraint to the effect that some specified condition must be satisfied at every point within some interval (q.v.). Such constraints typically arise if the intervals in question are temporal intervals specifically.

Example: Suppose the database shows supplier S2 as being under contract throughout the interval from day 2 to day 4. Then it must also show supplier S2 as having some status throughout the interval from day 2 to day 4, and this latter is a denseness constraint.

Note: It so happens in the foregoing example that the converse holds true as well: If the database shows supplier S2 as having some status throughout the interval from day 2 to day 4, then it must also show supplier S2 as being under contract throughout the interval from day 2 to day 4 (see U_equality dependency). By way of an example in which no such converse holds, note that if the database shows a given supplier as being able to supply some part throughout some interval, then it must certainly show that supplier as being under contract throughout that same interval, but the converse is false—if the database shows a given supplier as being under contract throughout some interval, it doesn’t necessarily have to show that supplier as being able to supply some part throughout that same interval. For example, Fig. 6 shows supplier S5 as having been under contract since day 2, but it doesn’t show supplier S5 as ever having been able to supply any parts at all. For further discussion, see foreign U_key.

difference (interval theory) Let i1 = [b1:e1] and i2 = [b2:e2] be intervals of the same type. Then:

• If (a) i1 and i2 are disjoint, or (b) i1 contains either b2 or e2 but not both, or (c) exactly one of i2 BEGINS i1 and i2 ENDS i1 is true—in other words, if either b1 < b2 and e1 ≤ e2 are both true or b1 ≥ b2 and e1 > e2 are both true—then (and only then) the expression i1 MINUS i2 denotes the difference between i1 and i2 (in that order), and it returns either [b1:MIN{PRE(i2),e1}] if b1 < b2 and e1 ≤ e2 are both true, or [MAX{POST(i2),b1}:e1] if b1 ≥ b2 and e1 > e2 are both true (see POST; PRE).

• Otherwise i1 MINUS i2 is undefined.

Observe that the foregoing definition guarantees that the result (when it’s defined) isn’t just some set of points but is, rather, an interval specifically. Note: SQL has no direct support for the interval difference operator.

Example: Let i1 and i2 be [d02:d07] and [d04:d10], respectively. Then i1 MINUS i2 is [d02:d03]. By contrast, let i1 and i2 be [d02:d14] and [d04:d10], respectively; then i1 MINUS i2 is undefined.

discreteness assumption Let T be a point type, q.v. Barring explicit statements to the contrary, then, T is generally assumed to be an ordinal type, q.v., meaning among other things that an associated successor function, q.v., is assumed to exist. That assumption (viz., that a successor function exists) is referred to, somewhat inappropriately, as “adopting the discreteness assumption.” Contrast continuity assumption.

Note: The term discreteness assumption derives from the fact that values of a point type with a successor function are certainly discrete. But discreteness as such isn’t the real issue; rather, the real issue is whether a successor function exists. For example, consider the rational numbers, which are certainly discrete and yet have no successor function (in other words, if r is a rational number, there’s no rational number r′ that can be considered the immediate successor of r). Thus, the problem with using rational numbers as a point type isn’t that they’re not discrete—they are—but rather that they have no successor function.

DISJOINT One of Allen’s operators, q.v. Let i1 and i2 be intervals of the same type. Then i1 DISJOINT i2 is true if and only if i1 OVERLAPS i2 is false.

Examples: Let i1 and i2 be [d02:d03] and [d08:d10], respectively; then i1 DISJOINT i2 is true. By contrast, if i1 and i2 are [d02:d08] and [d08:d10], respectively, then i1 DISJOINT i2 is false. Observe that DISJOINT is commutative—that is, i1 DISJOINT i2 and i2 DISJOINT i1 are equivalent (so i1 DISJOINT i2 is true if and only if i2 DISJOINT i1 is true).

Note: SQL has no direct support for the DISJOINT operator. However, if p1 and p2 denote SQL periods, then the SQL expression NOT (p1 OVERLAPS p2) is effectively equivalent to the hypothetical SQL expression “p1 DISJOINT p2” (or to the equally hypothetical SQL expression “p1 NOT OVERLAPS p2”). See period for further explanation.

disjoint U_INSERT See U_INSERT.

disjoint U_UNION See U_disjoint union.

duration A length of time expressed as an integral number of time points, not anchored at any specific time point (e.g., three days; 90 minutes; two hours); equivalently, the number of points contained in some given temporal interval. See also cardinality; COUNT; length.

during Term much used in connection with temporal data; if some specified condition c holds “during” some specified temporal interval i, it means condition c holds throughout (i.e., at every time point within) interval i. Note: The term is often used, in this dictionary in particular, in a more restrictive sense, according to which the condition in question holds throughout and not immediately before and not immediately after the interval in question—in which case the interval in question is said to be maximal. See maximal interval for further discussion.

during attribute Term used informally to refer to an attribute of some temporal interval type.

Examples: The DURING attributes in relvars S_DURING, S_STATUS_DURING, and SP_DURING in the suppliers-and-shipments database of either Fig. 6 or Fig. 8.

during relation Term used informally to refer to a relation one of whose attributes is of some temporal interval type (especially a relation that’s the current value of some during relvar, q.v.).

Examples: The current values of relvars S_DURING, S_STATUS_DURING, and SP_DURING in the suppliers-and-shipments database of either Fig. 6 or Fig. 8.

during relvar Term used informally to refer to a relvar that (a) isn’t a since relvar, q.v., and (b) has a predicate that can reasonably be formulated in such a way as to include one or more qualifications of the form “during interval i” (and thus has one or more attributes of some temporal interval type); very loosely, a relvar that contains historical information.

Examples: Relvars S_DURING, S_STATUS_DURING, and SP_DURING in the suppliers-and-shipments database of either Fig. 6 or Fig. 8.

END See end point.

end of time See timeline.

end point The end point of the interval i = [b:e], denoted END (i), is the point e. Note: SQL has no support for the END operator as such. Rather, if p denotes the SQL period PERIOD (f,t)—and if we assume for definiteness that f and t are of type DATE and the scale, q.v., is one day—then the SQL expression t – INTERVAL '1' DAY is effectively equivalent to the hypothetical SQL expression “END (p).” For further explanation and discussion, see datetime arithmetic (SQL); period.

ENDS One of Allen’s operators, q.v. Let i1 = [b1:e1] and i2 = [b2:e2] be intervals of the same type. Then i1 ENDS i2 is true if and only if b1 ≥ b2 and e1 = e2 are both true.

Examples: Let i1 and i2 be [d08:d10] and [d04:d10], respectively; then i1 ENDS i2 is true. By contrast, if i1 and i2 are [d08:d11] and [d06:d10], respectively, then i1 ENDS i2 is false.

Note: SQL has no direct support for the ENDS operator. However, if p1 and p2 denote the SQL periods PERIOD (f1,t1) and PERIOD (f2,t2), respectively, then the SQL expression f1 ≥ f2 AND t1 = t2 is effectively equivalent to the hypothetical SQL expression “p1 ENDS p2.” See period for further explanation.

equality (Of intervals) See interval equality.

EXPAND See expanded form. Note: SQL has no direct support for the EXPAND operator.

expanded form 1. (Sets of intervals) Let x be a set of intervals all of the same type T. Then the expression EXPAND (x) denotes the expanded form of x, and it returns the unique set y of unit intervals [p:p] (necessarily also all of that same type T) such that p is a point in some interval in x—see unit interval. Observe that no two distinct intervals i1 and i2 in y are such that i1 INTERSECT i2 is defined—see intersection (interval theory). Observe further that if the cardinality of x is zero, then EXPAND (x) is equal to x; if the cardinality of x is one, then EXPAND (x) is equal to x if and only if the sole interval in x is a unit interval specifically. 2. (Unary relations) Let x be a unary relation whose sole attribute is of some interval type. Then the expression EXPAND (x) denotes the expanded form of x, and it returns the unique relation y of the same type as x such that tuple t, containing interval i, appears in y if and only if i is a unit interval [p:p] and p appears in some interval in some tuple in x. 3. (Nullary relations) Let x be a nullary relation (i.e., let x be either TABLE_DUM or TABLE_DEE). Then the expression EXPAND (x) denotes the expanded form of x, and it returns the relation x itself (i.e., each of TABLE_DUM and TABLE_DEE is its own expanded form). Contrast collapsed form.

Example (second definition only): Let relation x look like this:

┌───────────┐
│ DURING    │
├═══════════┤
│ [d06:d09] │
│ [d04:d08] │
│ [d05:d10] │
│ [d01:d01] │
└───────────┘

Then y = EXPAND (x) looks like this:

┌───────────┐
│ DURING    │
├═══════════┤
│ [d01:d01] │
│ [d04:d04] │
│ [d05:d05] │
│ [d06:d06] │
│ [d07:d07] │
│ [d08:d08] │
│ [d09:d09] │
│ [d10:d10] │
└───────────┘

Note: The relational version of EXPAND is actually a special case of UNPACK (see unpacked form). To be specific, (a) if relation x has just one attribute, say A, and that attribute is interval valued, then EXPAND (x) and UNPACK x ON (A) are equivalent; moreover, (b) if relation x has no attributes at all, then EXPAND (x) and UNPACK x ON ( )—the unpacking here necessarily being on no attributes at all—are also equivalent.

Here for the record is a more formal version of the first (only) of the foregoing definitions. Again let x be a set of intervals all of the same type T, and let i and j be intervals of that same type T. Then y = EXPAND (x) can be defined thus:

y { i : b = e AND EXISTS j ∊ x  ( b ∊ j ) }

FIRST_T See beginning of time; FIRST (in Part I of this dictionary); ordinality; point type. Note: SQL has no support for the FIRST_T operator as such, but an appropriate literal can be used in its place. In the case of point type DATE, for example, SQL’s analog of the expression FIRST_DATE ( ) is the following literal:

DATE '0001-01-01'

Note, however, that SQL requires the user to know the actual value involved, which the expression FIRST_T ( ) doesn’t.

folding Term sometimes used as a synonym for packing, q.v. (or for an operation of the same general nature as packing).

FOR PORTION OF (SQL) See PORTION.

FOR SYSTEM TIME (SQL) See system time.

foreign key (Expanded definition) A foreign key in the relational sense means exactly what it always did mean (see Part I of this dictionary); however, such a foreign key can, and now should, be regarded as a degenerate special case of a foreign U_key, q.v.

foreign key (SQL) Consider the following CREATE table statements (repeated from the examples under period but simplified slightly here) for the SQL tables S_FROM_TO and SP_FROM_TO from Fig. 9:

CREATE TABLE S_FROM_TO
     ( SNO   SNO  NOT NULL ,
       DFROM DATE NOT NULL ,
       DTO   DATE NOT NULL ,
       PERIOD FOR DPERIOD ( DFROM , DTO ) ,
       UNIQUE ( SNO , DPERIOD WITHOUT OVERLAPS ) ;

CREATE TABLE SP_FROM_TO
     ( SNO   SNO  NOT NULL ,
       PNO   PNO  NOT NULL ,
       DFROM DATE NOT NULL ,
       DTO   DATE NOT NULL ,
       PERIOD FOR DPERIOD ( DFROM , DTO ) ,
       UNIQUE ( SNO , PNO , DPERIOD WITHOUT OVERLAPS ) ,
       FOREIGN KEY ( SNO , PERIOD DPERIOD )
               REFERENCES S_FROM_TO ( SNO , PERIOD DPERIOD ) ) ;

Observe in particular that, first, the combination (SNO,DPERIOD) is defined to be a “key” for table S_FROM_TO, thanks to the specification UNIQUE (SNO, DPERIOD WITHOUT OVERLAPS); second, that same combination (SNO,DPERIOD) is defined to be a “foreign key” in table SP_FROM_TO, thanks to the specification FOREIGN KEY (SNO, PERIOD DPERIOD), matching that “key” in table S_FROM_TO. Note: For present purposes, let’s agree to ignore both the WITHOUT OVERLAPS specification, q.v., in the “key” definition and the keyword—effectively just a noiseword—PERIOD in the “foreign key” definition. However, note that (as the discussion below makes clear) (a) the “key” in question isn’t a true relational key and (b) the “foreign key” in question isn’t a true relational foreign key either, which is why the terms are set in quotation marks here.

Now, it’s actually quite difficult to explain the semantics of the foregoing specifications properly in purely SQL terms, because SQL has nothing analogous to the crucial UNPACK operator. However, if we overlook that omission, we can say, loosely, that what the specifications mean is this: If we unpack each of the tables on DPERIOD, then (SNO,DPERIOD) will be a key for the unpacked form of S_FROM_TO and (SNO,DPERIOD) will be a matching foreign key in the unpacked form of SP_FROM_TO. But then, noting that the symbol DPERIOD is little more than a shorthand name for columns DFROM and DTO taken in combination, we see that the “key” in question isn’t a true relational key, because it’s reducible (either DFROM or DTO could be dropped, and what remained would still have the necessary uniqueness property). In fact, that “key” is really a proper superkey. And for essentially similar reasons, the matching “foreign key” isn’t a true relational foreign key, either.

(Actually, even before the introduction of temporal support into SQL in the 2011 version of the standard, it was the case that SQL explicitly allowed “keys” and corresponding “foreign keys” to be defined that were clearly reducible. So SQL’s departures from relational theory in this area aren’t really new; in particular, they aren’t limited to the temporal context as such.)

foreign U_key Let ACL be a commalist of attribute names such that every attribute mentioned (a) is interval valued and (b) is common to relvars R1 and R2 (R1 and R2 not necessarily distinct), and let those relvars be kept packed on ACL. Let R1′ be a relvar whose value at any given time is equal to the value of UNPACK R1 ON (ACL) at the time in question; likewise, let R2′ be a relvar whose value at any given time is equal to the value of UNPACK R2 ON (ACL) at the time in question. Let K be a key in R1′ and let FK be a matching foreign key in R2′. Then (and only then) K is a U_key (q.v.) in R1, and FK is a matching foreign U_key in R2 (where the U_key and foreign U_key in question must both be understood as being with respect to ACL). Note: If ACL is empty, the U_key K in R1 reduces to a regular key and the foreign U_key FK in R2 reduces to a regular foreign key.

Examples: With reference to Fig. 8 (but not Fig. 6), {SNO,DURING} in relvar SP_DURING is a foreign U_key matching the U_key {SNO,DURING} in relvar S_DURING (where the foreign U_key and matching U_key must both be understood as being with respect to DURING). Thus, the definitions of those two relvars might look like this:

VAR S_DURING BASE RELATION
  { SNO    SNO ,
    DURING INTERVAL_DATE }
  USING ( DURING ) : KEY { SNO , DURING } ;

VAR SP_DURING BASE RELATION
  { SNO    SNO ,
    PNO    PNO ,
    DURING INTERVAL_DATE }
  USING ( DURING ) : KEY { SNO , PNO , DURING }
  USING ( DURING ) : FOREIGN KEY { SNO , DURING } REFERENCES S_DURING ;

Note the last line here in particular: It’s what defines {SNO,DURING} to be a foreign U_key in relvar SP_DURING, matching the U_key involving those same attributes (SNO and DURING) in relvar S_DURING.

By way of another example, again with reference to Fig. 8 but not Fig. 6 (and again with respect to DURING throughout), {SNO,DURING} in relvar S_STATUS_DURING is a foreign U_key matching the U_key {SNO,DURING} in relvar S_DURING. In this case, however, the converse is true as well—{SNO,DURING} in relvar S_DURING is a foreign U_key matching the U_key {SNO,DURING} in relvar S_STATUS_DURING. In other words, S_DURING and S_STATUS_DURING are together subject to the following U_EQD (q.v.):

CONSTRAINT U_EQDX USING ( DURING ) :
                  S_DURING = S_STATUS_DURING { SNO , DURING } ;

(This point was previously mentioned in a footnote in the section “A Note on Redundancy” in the introduction to this part of the dictionary.)

Note: There’s no requirement that relvars R1 and R2 in the foregoing definition be base relvars specifically; for example, there might be a foreign U_key constraint from a base relvar to a view, or from a view to a base relvar, or from one view to another. In fact (speaking a little loosely), Tutorial D allows foreign U_key constraints to be specified between arbitrary relational expressions (see foreign U_key constraint).

foreign U_key constraint A generalized form of foreign key constraint (see Part I of this dictionary) in which the roles of the pertinent key and matching foreign key are played by a U_key (q.v.) and matching foreign U_key (q.v.), respectively. Note that (as noted under foreign U_key) Tutorial D allows foreign U_key constraints to be specified not just for relvars as such, base or otherwise, but in fact for arbitrary relational expressions.

FROM value (SQL) See period.

fully packed Let relation r have interval attributes A1, A2, ..., An (and no others). Then the somewhat informal term fully packed form of r refers to any relation obtained by packing r on attributes A1, A2, ..., An in some order. (Note that different orders will give rise to different fully packed versions, in general. Contrast fully unpacked.) An analogous definition applies to relvars also, mutatis mutandis.

fully temporal Term used informally to characterize a during relvar, q.v., in contrast to a since relvar, q.v. Contrast semitemporal.

fully unpacked Let relation r have interval attributes A1, A2, ..., An (and no others). Then the somewhat informal term fully unpacked form of r refers to the relation obtained by unpacking r on attributes A1, A2, ..., An in some order. (Note that different orders will always give rise to the same fully packed version. Contrast fully packed.) An analogous definition applies to relvars also, mutatis mutandis.

granularity Informal term sometimes used to refer to the “size,” or scale (q.v.), of a value of some given point type, or equivalently to the “size” of the gap between one such value and its successor according to the pertinent ordering. See scale for further discussion.

Example: For the time points involved in the stated times (q.v.) in the various versions of the suppliers-and-shipments database (see Figs. 6-9), the granularity is one day. In other words, we’re ignoring in this context the fact that a day is made up of hours, which are made up of minutes, etc. Such notions can be expressed only by recourse to finer levels of granularity, or in other words finer scales.

granule Informal term sometimes used as a synonym for point, q.v. See scale for further discussion; contrast chronon.

historical relation Informal term sometimes used to refer to the value of a historical relvar, q.v.

historical relvar Informal term sometimes used to refer to a during relvar, q.v. However, the term is deprecated, somewhat, because such relvars aren’t limited to containing information that pertains only to some historical state of affairs—depending on circumstances, they might contain information that pertains to past and/or current and/or even future states of affairs.

Example: Consider the relation shown as a sample value for relvar S_DURING in Fig. 8. If we make the reasonable assumption that at least some of the BEGIN (DURING) values in that relation denote dates in the past, then that relation clearly contains information concerning the current state of affairs; for example, the sole tuple for supplier S1, with DURING value [d04:d99], presumably shows that supplier as currently being under contract, since that d99 really means until further notice, q.v. (see the discussion under COMBINED_IN). Indeed, and for the same reason, that tuple also contains information about the future, at least implicitly. What’s more, if we know that (say) supplier S8 will be placed under contract on day dc, where dc is in the future, and we insert a tuple into S_DURING to say as much, then that relvar will now contain explicit information about the future as well.

historical row (SQL) See system time.

horizontal decomposition (Of temporal relvars) Informal term used to refer to the decomposition of a temporal relvar into a combination of since relvars, q.v., and during relvars, q.v.

Example: The relvars of Fig. 6 can be regarded as the result of applying horizontal decomposition to the relvars of Fig. 8. Note that Fig. 8 contains during relvars only, but those during relvars aren’t purely historical, because they contain information that pertains to the current state of affairs (as well as to the future, at least implicitly if not explicitly). By contrast, Fig. 6 contains a mixture of since and during relvars, and those during relvars, by contrast, contain historical information only—information that pertains to the current state of affairs has been moved into the since relvars. (Note, however, that those since relvars also contain implicit information regarding both the past and the future, and they might even contain explicit information regarding the future as well. See current relvar.)

included U_DELETE See U_DELETE.

included U_difference See U_included difference.

included U_MINUS See U_included difference.

inclusion (Of intervals) See interval inclusion.

inheritance (interval types) Let IT be the interval type INTERVAL_T, with underlying point type T (see interval type). In general, then, IT has no proper subtypes; that is, the concept of inheritance doesn’t really apply to interval types. For suppose, contrariwise, that interval type IT has a proper subtype IT′ (where IT′ is INTERVAL_T′ for some point type T′, T′ ≠ T). Let i′ = [b′:e′] be an interval of type IT′ such that b′ ≠ e′. Since IT′ is a subtype of IT, i′ must be an interval of type IT as well. But i′ can’t possibly be an interval of type IT—not even if T′ is a proper subtype of T, in which case b′ and e′ are certainly both values of type T—because the points in i′ are determined by the successor function for T′, which (since T and T′ are distinct) is distinct from the successor function for T, by definition. Thus, IT′ can’t be a proper subtype of IT after all.

Example: Let T and T′ be INTEGER and EVEN_INTEGER, respectively, with the obvious semantics (so the interval types IT and IT′ are INTERVAL_INTEGER and INTERVAL_EVEN_INTEGER, respectively). Note in particular that T′ here is definitely a proper subtype of T. Now consider the intervals i = [2:6] and i′ = [2:6], of types IT and IT′, respectively. Then i and i′ aren’t the same interval, even though they have the same begin and end points, because i contains the points 2, 3, 4, 5, 6 while i′ contains only the points 2, 4, 6. Thus, i′ isn’t a value of type IT, and so IT′ isn’t a proper subtype of IT.

Given the above, it follows that we can refer unambiguously to the type of any given interval (where the type in question is basically just the corresponding declared type). See interval type.

Note: The foregoing remarks are broadly true, but there are a couple of minor exceptions—pathological cases, really—that ought at least to be mentioned. First, if T′ is empty, then IT′ is a subtype of all possible interval types (in fact, it’s a proper subtype of all such types except for itself); however, IT′, like T′, is empty in this case. Second, if T′ is a singleton type whose sole value is a value of type T, then IT′ is a proper subtype of IT after all, but it contains just one interval (necessarily a unit interval).

inheritance (point types) Elsewhere in this dictionary, the definition of what it means for a type to be usable as a point type (q.v.) includes the requirement that the type in question must have a unique successor function. However, consider the point type DATE; surely there are several different successor functions that might make sense for that type—for example, “next week,” “next business day,” “next month,” and so on? Type inheritance provides a solution to this apparent dilemma. For example, we might define proper subtypes of type DATE called WDATE, BDATE, and MDATE, representing dates measured in weeks, business days, and months, respectively. Each of these types will have its own associated set of operators, including its own successor function in particular. Further details are beyond the scope of this dictionary, except to note that remarks analogous to the foregoing apply to types TIME and TIMESTAMP as well, obviously enough.

Note: To the extent that SQL addresses the foregoing requirement—i.e., the need to support several distinct successor functions for the same point type—it does so not by means of inheritance but by means of its regular datetime arithmetic facilities, q.v. For example, if DV is an SQL variable of type DATE, then

DV + INTERVAL '1' DAY

returns the next day, and

DV + INTERVAL '1' MONTH

returns the next month. (By contrast, more specialized requirements such as “next week” and “next business day” aren’t directly supported at all.) See datetime arithmetic (SQL) for further discussion.

intersection (interval theory) Let i1 = [b1:e1] and i2 = [b2:e2] be intervals of the same type. Then:

• If i1 OVERLAPS i2 is true, then (and only then) the expression i1 INTERSECT i2 denotes the intersection of i1 and i2, and it returns [MAX{b1,b2}:MIN{e1,e2}].

• Otherwise i1 INTERSECT i2 is undefined.

Observe that the foregoing definition guarantees that the result (when it’s defined) isn’t just some set of points but is, rather, an interval specifically. Note: SQL has no direct support for the interval intersection operator.

Example: Let i1 and i2 be [d02:d07] and [d04:d10], respectively. Then i1 INTERSECT i2 is [d04:d07]. By contrast, let i1 and i2 be [d02:d04] and [d07:d10], respectively; then i1 INTERSECT i2 is undefined. Incidentally, note that interval intersection, like set theory intersection—like the intersection operator of the relational algebra also, come to that—does have a corresponding identity value: viz., the universal interval of the applicable type, q.v. Note further that the operator is both commutative and associative.

interval An interval value, q.v. Be aware, however, that SQL uses the term interval to mean a duration, q.v. The SQL term for an interval as such—or, rather, for SQL’s analog of an interval as such—is period, q.v.

interval (SQL) A duration, q.v.

interval attribute An attribute of some interval type; an interval valued attribute.

interval comparison See Allen’s operators.

interval difference See difference (interval theory).

interval equality One of Allen’s operators, q.v. Let i1 = [b1:e1] and i2 = [b2:e2] be intervals of the same type. Then i1 is equal to i2 (“i1 = i2”) if and only if b1 = b2 and e1 = e2 are both true. In other words, intervals i1 and i2 (necessarily of the same type) are equal if and only if they’re the very same interval, meaning they have the same begin point and the same end point, and hence the same contained points as well.

Note: SQL uses the keyword EQUALS in place of the symbol “=”. Let p1 and p2 be the SQL periods PERIOD (f1,t1) and PERIOD (f2,t2), respectively; then the SQL expression p1 EQUALS p2 is true if and only if f1 = f2 and t1 = t2 are both true. Oddly enough, however, while the hypothetical SQL expression “PERIOD (f1,t1) = PERIOD (f2,t2)”—note the explicit “=” symbol—is illegal, the simpler and more succinct expression (f1,t1) = (f2,t2) is not only legal but means exactly the same as PERIOD (f1,t1) EQUALS PERIOD (f2,t2). See period for further explanation.

interval expression An expression denoting an interval. Interval selector invocations (and hence interval literals) are an important special case.

interval inclusion One of Allen’s operators, q.v. Let i1 = [b1:e1] and i2 = [b2:e2] be intervals of the same type. Then i1 includes i2 (“i1 ⊇ i2”) if and only if b1 ≤ b2 and e1 ≥ e2 are both true. Also, i2 is included in i1 (“i2 ⊆ i1”) if and only if i1 ⊇ i2 is true. See also proper interval inclusion.

Examples: Let i1 and i2 be [d02:d10] and [d04:d08], respectively; then i1 ⊇ i2 is true. By contrast, if i1 and i2 are [d02:d04] and [d04:d08], respectively, then i1 ⊇ i2 is false. Note that interval i1 is equal to interval i2 (“i1 = i2”) if and only if each includes the other. Note too that every interval is included in itself. Note finally that the term interval inclusion is usually taken, a trifle arbitrarily, to refer to the operator “⊆” specifically, not the operator “⊇”.

Note: SQL supports “⊇” (for which it uses the keyword CONTAINS, which is thereby overloaded—see containment) but not “⊆”. However, if p1 and p2 denote the SQL periods PERIOD (f1,t1) and PERIOD (f2,t2), respectively, then the SQL expression f1 ≥ f2 AND t1 ≤ t2 is effectively equivalent to the hypothetical SQL expression “p1 ⊆ p2.” See period for further explanation.

interval intersection See intersection (interval theory).

interval literal A literal that denotes an interval.

Examples: See the examples under interval selector.

interval selector Let INTERVAL_T be an interval type; then the (unique) corresponding selector is an operator that allows an interval of that type to be selected or specified by supplying, either directly or indirectly (see further discussion below), the begin and end points of the interval in question. More precisely, let INTERVAL_T be an interval type, with underlying point type T. Corresponding to that interval type, then, there’s exactly one corresponding selector (having the same name as the type, in Tutorial D), such that (a) the sole argument to any given invocation of that selector is a pair of values of type T, separated by a colon and enclosed in brackets or parentheses or a mixture (again, see further discussion below); (b) every interval of that interval type is producible by means of some invocation of that selector in which those values of type T are represented by literals; and (c) every successful invocation of that selector produces an interval of that interval type.

As the foregoing paragraph suggests (and as explained further under interval value), there are actually four different ways, or styles, available for representing an interval in concrete syntax (at least in general, but note the exceptions indicated below):

• The closed:closed style, or syntax, uses brackets “[” and “]”, and it represents the given interval directly in terms of its begin and end points b and e. In other words, the syntax “[b:e]” denotes the interval stretching from the begin point b to the end point e (b ≤ e), inclusive. For example, consider the interval type INTERVAL_DATE, where the underlying point type is DATE (i.e., calendar dates accurate to the day). Then the expression

  INTERVAL_DATE ( [ d04 : d10 ] )

  constitutes an invocation of the INTERVAL_DATE selector, and it denotes the interval of type INTERVAL_DATE whose contained points are precisely the dates d04, d05, d06, d07, d08, d09, and d10. Note: Expressions such as [d04:d10], much used elsewhere in this dictionary, can be thought of as informal shorthand for an interval selector invocation of the foregoing form. Note also that, other things being equal, this dictionary does tend to favor the closed:closed style.

• The closed:open style or syntax uses an opening bracket “[” and a closing parenthesis “)”, and it represents the given interval in terms of its begin point b together with the immediate successor es of its end point e. In other words, the syntax “[b:es)” denotes the interval stretching from the begin point b to the end point e (b ≤ e), inclusive, where e is the immediate predecessor of es. For example, the interval selector invocation

  INTERVAL_DATE ( [ d04 : d11 ) )

  denotes the same interval as in the closed:closed example above. Note: Expressions such as [d04:d11) can be thought of as informal shorthand for an interval selector invocation of the foregoing form. Note too, however, that an interval for which e is “the end of time” can’t be expressed using closed:open style.

• The open:closed style or syntax uses an opening parenthesis “(” and a closing bracket “]”, and it represents the given interval in terms of the immediate predecessor pb of its begin point b, together with its end point e. In other words, the syntax “(pb:e]” denotes the interval stretching from the begin point b to the end point e (b ≤ e), inclusive, where b is the immediate successor of pb. For example, the interval selector invocation

  INTERVAL_DATE ( ( d03 : d10 ] )

  again denotes the same interval as in the previous examples. Note: Expressions such as (d03:d10] can be thought of as informal shorthand for an interval selector invocation of the foregoing form. Note too, however, that an interval for which b is “the beginning of time” can’t be expressed using open:closed style.

• Finally, the open:open style or syntax uses parentheses “(” and “)”, and it represents the given interval in terms of the immediate predecessor pb of its begin point b together with the immediate successor es of its end point e. In other words, the syntax “(pb:es)” denotes the interval stretching from the begin point b to the end point e (b ≤ e), inclusive, where b is the immediate successor of pb and s is the immediate predecessor of es. For example, the interval selector invocation

  INTERVAL_DATE ( ( d03 : d11 ) )

  again denotes the same interval as in the previous examples. Note: Expressions such as (d03:d11) can be thought of as informal shorthand for an interval selector invocation of the foregoing form. Note too, however, that an interval for which b is “the beginning of time” or e is “the end of time” can’t be expressed using open:open style.

Of course, all of the foregoing examples illustrate, not incidentally, the syntax used for interval selectors in Tutorial D specifically. Other syntactic styles might be possible, but they must be logically equivalent to the Tutorial D style. Note in particular that other separators—e.g., commas, hyphens—are typically used in the literature; Tutorial D uses colons because commas can make intervals look like subscripts and hyphens can look like minus signs.

Note: Assuming d03, d04, etc., are all DATE literals, all of the selector invocations shown above are in fact themselves literals in turn (interval literals, that is). Here by contrast is an interval selector invocation that’s not a literal:

INTERVAL_DATE ( [ FIRST_DATE ( ) : LAST_DATE ( ) ] )

This expression returns the interval of type INTERVAL_DATE whose begin and end points are the beginning of time and the end of time, respectively (accurate to the day in each case). See FIRST_T; LAST_T; timeline; see also universal interval.

interval type Let T be a point type, q.v.; then (and only then) INTERVAL_T denotes an interval type—in fact, the sole interval type—whose values are, precisely, all possible intervals of the form [b:e], where b and e are values of type T and b ≤ e. Note: Tutorial D provides nothing analogous to a TYPE statement, q.v., for defining interval types. Instead, such types can be defined only by invoking the interval type generator, q.v. It follows that, in Tutorial D at any rate, interval types always have names of the form INTERVAL_T. It also follows that there’s no way to define, e.g., an interval type consisting solely of all possible unit intervals of the form [p:p] for all possible values p of type INTEGER.

Examples: 1. Type INTERVAL_INTEGER is an interval type whose underlying point type is INTEGER; thus, values of this interval type are intervals of the form [b:e], where b and e are values of type INTEGER (for which the successor function is just “add one”) such that b ≤ e. 2. Type INTERVAL_MONEY is an interval type whose underlying point type is MONEY, which is (let’s assume) a type that represents monetary amounts measured in dollars and cents; thus, values of this interval type are intervals of the form [b:e], where b and e are values of type MONEY (for which the successor function is “add one cent”) such that b ≤ e. 3. Type INTERVAL_DATE is an interval type—used several times in the suppliers-and-shipments databases of Figs. 6-8—whose underlying point type is DATE; thus, values of this interval type are intervals of the form [b:e], where b and e are values of type DATE (for which the successor function is “add one day”) such that b ≤ e.

interval type generator The operator used to generate specific interval types (q.v.), denoted INTERVAL in Tutorial D. If T is a point type (q.v.), then the corresponding interval type—i.e., the corresponding invocation of the INTERVAL type generator—is denoted INTERVAL_T in Tutorial D.

Examples: See the examples under interval type.

interval type inheritance See inheritance (interval types).

interval union See union (interval theory).

interval value Let T be a point type, q.v. Then an interval value i (or just interval i for short) of type INTERVAL_T is a value for which two monadic operators, BEGIN and END, and one dyadic operator, “∊”, are defined, such that (a) BEGIN (i) and END (i) both return a value of type T (viz., the begin point and the end point, respectively, of interval i); (b) BEGIN (i) ≤ END (i); and (c) if p is a value of type T, then p ∊ i is true if and only if BEGIN (i) ≤ p and p ≤ END (i) are both true. Observe that intervals are never empty (i.e., every interval contains at least one point).

Let interval i have begin point b and end point e, respectively. Then, thanks to the availability of the successor function, q.v., we can say that interval i consists of a sequence—not just a set—of contiguous points: viz., the sequence b, b+1, b+2, ..., e. (Here we’re using—very informally!—the notation b+1 to denote the successor of b, b+2 to denote the successor of b+1, and so on.)

Now consider the informal phrase “the interval from day 4 to day 10.” What interval exactly is intended by such a phrase? It’s clear that the interval in question contains days 5, 6, 7, 8, and 9—but what about days 4 and 10 themselves? It turns out that if some interval i is described as stretching “from x to y,” sometimes we want to consider the points x and y as part of that interval i and sometimes we don’t. If we do want to consider x as part of i, we say i is closed at its beginning, otherwise we say it’s open at its beginning. Likewise, if we want to consider y as part of i, we say i is closed at its end, otherwise we say it’s open at its end.

Conventionally, therefore (albeit informally), we denote an interval by a pair of points x and y separated by a colon, preceded by an opening bracket or parenthesis and followed by a closing bracket or parenthesis. We use a bracket where we want the closed interpretation, a parenthesis where we want the open one. Thus, there are four distinct ways to denote, e.g., the specific interval that runs from the begin point d04 to the end point d10, inclusive:

[d04:d10]
[d04:d11)
(d03:d10]
(d03:d11)

See interval selector for further discussion.

Examples: Intervals don’t necessarily have to be temporal in nature. Here are some examples of ones that aren’t:

• Tax brackets are represented by taxable income ranges—i.e., intervals whose contained points are money values.

• Machines are built to operate within certain temperature and voltage ranges—i.e., intervals whose contained points are temperatures and voltages, respectively.

• Animals vary in the range of frequencies of light and sound waves to which their eyes and ears are receptive.

• Various natural phenomena occur and can be measured in ranges in depth of soil or sea or height above sea level.

And so on.

interval valued attribute An attribute whose type is some interval type.

key (Expanded definition) A key in the relational sense means exactly what it always did mean (see Part I of this dictionary); however, such a key can, and now should, be regarded as a degenerate special case of a U_key, q.v.

key (SQL) See foreign key (SQL).

LAST_T See end of time; LAST (in Part I of this dictionary); ordinality; point type. Note: SQL has no support for the LAST_T operator as such, but an appropriate literal can be used in its place. In the case of point type DATE, for example, SQL’s analog of the expression LAST_DATE ( ) is the following literal:

DATE '9999-12-31'

Note, however, that SQL requires the user to know the actual value involved, which the expression LAST_T ( ) doesn’t.

length (Of an interval) The number of points in the interval in question. See also cardinality; COUNT; duration.

logged time (Of a proposition) The time or times, represented as a set of temporal intervals (preferably in packed form), when the database said the proposition in question was true. Note: Other terms that might be used for this concept include system time, q.v. (this is the SQL term); system stated time; system asserted time; and transaction time, q.v. (this is the term most often encountered in the literature). Note that, by definition, logged times (a) always refer strictly to the past and (b) can’t be updated. (The reason they can’t be updated is that they represent history as such, not just somebody’s beliefs about history; the latter can and typically do change from time to time, but history as such is immutable.)

Example: Let today be day 75. Then the logged time relvar (q.v.) S_DURING_LOG corresponding to relvar S_DURING (with sample value as shown in Fig. 6) might currently look like this:

┌─────┬───────────┬───────────┐
│ SNO │ DURING    │ X_DURING  │
├═════┼═══════════┼═══════════┤
│ S2  │ [d02:d04] │ [d04:d07] │
│ S2  │ [d02:d04] │ [d10:d20] │
│ S2  │ [d02:d04] │ [d50:d75] │
│ S6  │ [d02:d05] │ [d15:d25] │
│ S6  │ [d03:d05] │ [d26:d75] │
│ S1  │ [d01:d01] │ [d20:d30] │
│ S1  │ [d05:d06] │ [d40:d50] │
└─────┴───────────┴───────────┘

In other words:

• For the proposition The interval [d03:d05] is a maximal interval of days throughout which supplier S6 was under contract, the logged time is {[d26:d75]}.

• For the proposition The interval [d02:d04] is a maximal interval of days throughout which supplier S2 was under contract, the logged time is {[d04:d07], [d10:d20], [d50:d75]}.

• For the proposition Supplier S1 was under contract throughout some interval, the logged time is {[d20:d30], [d40:d50]}. Note that the proposition in question in this example was never represented as such in the database, but is, rather, a proposition derived from those that were.

• For the proposition Supplier S6 was under contract throughout some interval, the logged time is {[d15:d75]}. Note the packing involved in this example; note too that (as with the previous example) the proposition in question was never represented as such in the database but is, rather, a proposition derived from those that were.

And so on. Note: The foregoing example shows X_DURING intervals as measured in days, for reasons of simplicity. In practice, of course, they would surely be based on some much smaller unit—microseconds, perhaps, or something even smaller. In fact, they’re probably based on readings from the system clock, q.v. (at least conceptually).

logged time relvar Let rx be a relational expression (typically but not necessarily a simple relvar reference R). Then the logged time relvar for rx is a relvar—automatically maintained by the DBMS as, in effect, an appropriately fully packed view of appropriate portions of the log—that shows, for every tuple t that has ever appeared in the fully unpacked form of the result of evaluating rx, the time or times when that tuple t did in fact appear in that fully unpacked form.

maximal interval Let P be a predicate whose sole parameter is of some interval type. Then interval i is maximal with respect to P if and only if i satisfies P and no j such that j ⊃ i satisfies P. Note: The qualifier “with respect to P” can be omitted if P is understood.

Example (repeated from the introduction to this part of the dictionary, but elaborated here): Consider the predicate for relvar S_DURING (first version, as illustrated in Fig. 6):

DURING denotes a maximal interval of days throughout which supplier SNO was under contract.

This predicate is dyadic (it involves two parameters, DURING and SNO). However, we can derive a set of monadic predicates from it, one for each SNO value appearing in some currently true instantiation of the dyadic predicate—which is to say, one for S2 and one for S6, given the sample value for relvar S_DURING shown in Fig. 6:

• DURING denotes a maximal interval of days throughout which supplier S2 was under contract. Note: This predicate applies to the result of the restriction expression S_DURING WHERE SNO = SNO('S2').

• DURING denotes a maximal interval of days throughout which supplier S6 was under contract. Note: This predicate applies to the result of the restriction expression S_DURING WHERE SNO = SNO('S6').

Each of these monadic predicates is a partial instantiation (see Part I of this dictionary) of the original dyadic predicate. For definiteness, let’s concentrate on the first one. Essentially, what that first one means is that if there’s a tuple in the relvar showing supplier S2 was under contract throughout the interval [d02:d04]—which indeed there is, in Fig. 6—then there isn’t a tuple in that relvar showing that supplier S2 was under contract on either day 1 or day 5. In other words, there’s no interval j that contains either day 1 or day 5 such that “Supplier S2 was under contract throughout interval j” is true, and the interval [d02:d04] is thus maximal with respect to the predicate DURING denotes an interval of days throughout which supplier S2 was under contract.

MEETS One of Allen’s operators, q.v. Let i1 = [b1:e1] and i2 = [b2:e2] be intervals of the same type. Then i1 MEETS i2 is true if and only if b2 = POST (i1) is true or b1 = POST (i2) is true (see POST); equivalently, i1 MEETS i2 is true if and only if e1 = PRE (i2) is true or e2 = PRE (i1) is true (see PRE).

Examples: Let i1 and i2 be [d02:d03] and [d04:d10], respectively; then i1 MEETS i2 is true. By contrast, if i1 and i2 are [d02:d04] and [d04:d10], respectively, then i1 MEETS i2 is false. Observe that MEETS is commutative—that is, i1 MEETS i2 and i2 MEETS i1 are equivalent (so i1 MEETS i2 is true if and only if i2 MEETS i1 is true).

Note: SQL uses a combination of the keywords IMMEDIATELY PRECEDES and IMMEDIATELY SUCCEEDS in place of MEETS. For example, let p1 and p2 be the SQL periods PERIOD (d02,d04) and PERIOD (d04,d11), respectively; then the SQL expression

p1 IMMEDIATELY PRECEDES p2

is true, and so is

p2 IMMEDIATELY SUCCEEDS p1

Hence

p1 IMMEDIATELY PRECEDES p2 OR p1 IMMEDIATELY SUCCEEDS p2

is true too, a fortiori, and so of course is

p2 IMMEDIATELY PRECEDES p1 OR p2 IMMEDIATELY SUCCEEDS p1

(and these two latter expressions are both effectively equivalent to either of the hypothetical SQL expressions “p1 MEETS p2” and “p2 MEETS p1”).

Oddly enough, however, while the hypothetical SQL expression “PERIOD (f1,t1) MEETS PERIOD (f2,t2)” is illegal, the simpler—and much more succinct!—expression t1 = f2 OR t2 = f1 is not only legal but means exactly the same as

p1 IMMEDIATELY PRECEDES p2 OR p1 IMMEDIATELY SUCCEEDS p2

See period for further explanation.

MERGES One of Allen’s operators, q.v. Let i1 and i2 be intervals of the same type. Then i1 MERGES i2 is true if and only if i1 MEETS i2 is true or i1 OVERLAPS i2 is true (see MEETS; OVERLAPS).

Examples: Let i1 and i2 be [d02:d04] and [d05:d10], respectively; then i1 MERGES i2 is true. Likewise, if i1 and i2 are [d02:d04] and [d03:d10], respectively; then i1 MERGES i2 is true. By contrast, if i1 and i2 are [d02:d06] and [d08:d10], respectively, then i1 MERGES i2 is false. Observe that MERGES is commutative—that is, i1 MERGES i2 and i2 MERGES i1 are equivalent (so i1 MERGES i2 is true if and only if i2 MERGES i1 is true).

Note: SQL has no direct support for the MERGES operator. However, if p1 and p2 denote SQL periods, then the SQL expression

p1 OVERLAPS p2 OR
p1 IMMEDIATELY PRECEDES p2 OR
p1 IMMEDIATELY SUCCEEDS p2

is effectively equivalent to either of the hypothetical SQL expressions “p1 MERGES p2” and “p2 MERGES p1.” See period for further explanation.

moving point now Term frequently used in the temporal database literature to refer to the present time (i.e., “the time right now”). Note: Suggestions are frequently encountered in the literature to the effect that “the moving point now” should somehow be capable of explicit representation as such within a relation (see, e.g., James Clifford, Curtis Dyreson, Tomás Isakowitz, Christian S. Jensen, and Richard T. Snodgrass, “On the Semantics of ‘Now’ in Databases,” ACM TODS 22, No. 2, June 1997). But relations are values and “the moving point now” is a variable, and the idea that values might contain variables is a logical absurdity. (To see that “the moving point now” is indeed a variable, observe that the value denoted by that phrase is always changing—in fact, of course, it’s always increasing—and if some object x denotes different values at different times, then that object x is a variable by definition.) Indeed, it’s precisely because “the moving point now,” as such, can’t be represented within a relation that horizontal decomposition, q.v., is recommended as an approach to temporal database design. See also NOW; until further notice.

NEXT_T The successor function for point type T. See NEXT (in Part I of this dictionary); ordinality; point type. Note: SQL has no support for this operator as such; instead, an expression involving explicit datetime arithmetic, such as DV + INTERVAL '1' DAY, has to be used. For further explanation and discussion, see datetime arithmetic (SQL); period.

nontemporal database A database that’s not a temporal database, q.v.. Sometimes referred to as a snapshot database (but this term is deprecated on account of possible confusion with other uses of the term snapshot—see Part I of this dictionary).

NOT U_MATCHING See U_semidifference.

NOW A construct, or marker, proposed in certain nonrelational approaches to temporal data for representing the present time (see moving point now). However, the construct in question is a variable, not a value; it follows that a “type” that contains such a construct isn’t a type, a “tuple” that contains such a construct isn’t a tuple, a “relation” that contains such a construct isn’t a relation, and a “relvar” that contains such a construct isn’t a relvar. It further follows that the NOW construct as usually understood does serious violence to the relational model, and this dictionary therefore has very little more to say regarding that construct or matters related to it.

open (Of an interval) See interval selector; interval value.

open:closed See interval selector.

open:open (Of an interval) See interval selector.

ordinality That which distinguishes an ordinal type from one that’s merely ordered (see Part I of this dictionary). Let T be an ordered type, and let Ord be the pertinent ordering. Then T is said to possess the property of ordinality if and only if (a) a first and a last value of the type, denoted FIRST_T ( ) and LAST_T ( ), respectively, exist with respect to Ord, and (b) a successor function, denoted NEXT_T (p) and returning the (unique) immediate successor of p with respect to Ord, is defined for every value p of type T except for p = LAST_T ( ). Moreover, that successor function must be such that (a) if p1 ≠ p2 then NEXT_T (p1) ≠ NEXT_T (p2), and (b) there’s exactly one value of type T, viz., FIRST_T ( ), that’s not equal to NEXT_T (p) for any p. Note: Throughout definitions and examples in this part of the dictionary, intervals are assumed to be defined over an ordinal type, unless the context demands otherwise.

OVERLAPS One of Allen’s operators, q.v. Let i1 = [b1:e1] and i2 = [b2:e2] be intervals of the same type. Then i1 OVERLAPS i2 is true if and only if b1 ≤ e2 and b2 ≤ e1 are both true.

Examples: Let i1 and i2 be [d02:d05] and [d04:d10], respectively; then i1 OVERLAPS i2 is true. By contrast, if i1 and i2 are [d02:d03] and [d04:d10], respectively, then i1 OVERLAPS i2 is false. Observe that OVERLAPS is commutative—that is, i1 OVERLAPS i2 and i2 OVERLAPS i1 are equivalent (so i1 OVERLAPS i2 is true if and only if i2 OVERLAPS i1 is true).

Note: SQL supports the OVERLAPS operator directly. For example, let p1 and p2 be the SQL periods PERIOD (d02,d06) and PERIOD (d04,d11), respectively; then the SQL expressions p1 OVERLAPS p2 and p2 OVERLAPS p1 are both true.

PACK See packing. Note: SQL has no direct support for the PACK operator.

packed constraint Same as PACKED ON constraint.

Example: See the example under PACKED ON.

packed form 1. Let relation r have interval attributes A1, A2, ..., An (n ≥ 0). Then r is in packed form with respect to A1, A2, ..., An (in that order, if n > 1) if and only if r is equal to the result of evaluating the expression PACK r ON (A1,A2,...,An). 2. Let relvar R have interval attributes A1, A2, ..., An (n ≥ 0). Then R is in packed form with respect to A1, A2, ..., An (in that order, if n > 1) if and only if every relation r that can ever be assigned to R is in packed form with respect to A1, A2, ..., An (in that order, if n > 1). Note: The phrase packed form with respect to A1, A2, ..., An can be abbreviated to just packed form if the attributes A1, A2, ..., An (in that order, if n > 1) are understood. See packing for further discussion; see also PACKED ON.

Examples: 1. The relation shown as the current value of relvar S_STATUS_DURING in Fig. 6 is in packed form with respect to attribute DURING, because whenever two tuples in that relation have the same SNO and STATUS values, their DURING values i1 and i2 are such that i1 MERGES i2 is false. The same goes for the relation shown as the current value of relvar S_STATUS_DURING in Fig. 8. 2. The two versions of relvar S_STATUS_DURING itself—both the one illustrated in Fig. 6 and the one illustrated in Fig. 8—are themselves in packed form with respect to DURING, because their definitions both at least implicitly include the specification PACKED ON (DURING) (see U_key).

PACKED ON A specification used in Tutorial D as part of a relvar definition to impose a constraint to the effect that the pertinent relvar is to be kept in a certain packed form. Let ACL be a commalist of attribute names such that every attribute mentioned (a) is an attribute of the same relvar R and (b) is interval valued. Then the specification PACKED ON (ACL)—part of the definition of relvar R—ensures that any attempt to update R will fail if the result isn’t in packed form with respect to ACL, and thereby further ensures that R won’t suffer from either the circumlocution problem (as defined elsewhere in this part of the dictionary) or the redundancy problem (again as defined elsewhere in this part of the dictionary) with respect to ACL. Note: In practice, PACKED ON specifications will usually be implicit (see U_key).

Example: Consider relvar S_STATUS_DURING (either the Fig. 6 version or the Fig. 8 version, it makes no difference). Here’s a possible definition for that relvar (irrelevant details omitted):

VAR S_STATUS_DURING BASE RELATION
  { SNO SNO , STATUS INTEGER , DURING INTERVAL_DATE }
    PACKED ON ( DURING ) ... ;

The effect of the PACKED ON specification here is to ensure that any attempt to update S_STATUS_DURING in such a way as to leave that relvar less than fully packed on DURING will fail. (Similar PACKED ON constraints can and should also be specified for relvars S_DURING and SP_DURING.) Note: A variety of U_update operators, q.v., are available to help with the process of updating a relvar to which a PACKED ON constraint applies.

The specification PACKED ON (ACL) on relvar R is trivial—i.e., has no effect—if ACL is empty or if the set of attributes of R not included in ACL is a superkey for R.

packing 1. (Single-attribute PACK) Let relation r have an interval attribute A. Then (and only then) the expression PACK r ON (A) denotes the packing of r on A, and it’s equivalent to the following:

WITH ( r1 := r GROUP { A } AS X ,
       r2 := EXTEND r1 : { X := COLLAPSE ( X ) } ) :
r2 UNGROUP X