Chapter 8 Introduction to Differential Equations

This chapter is designed to provide a brief classification of common or standard forms of elementary differential equations for the purpose of introducing the subject. In general, differential equations can be classified according to a few major categories. These include linear differential equations, non-linear differential equations, and systems of both linear and non-linear equations. Linear differential equations are usually easier to solve using general methods. Non-linear differential equations are more difficult to solve and often involve approximations and numerical methods. Differential equations are also classified according to the highest order of the derivative in the equation, such as first-order or second-order for equations containing a first derivative or second derivative.

8.1 First-Order Differential Equations

• This section includes a list of first-order differential equations and their general solution forms. These include simple differential equations that depend only on x, differential equations that have a real constant coefficient, initial value problems, separable equations, exact equations, linear first-order differential equations, and non-linear equations.

• First-order differential equations are equations representing a function that involves the first derivative of the function. Applications of first-order differential equations include modeling, electric circuits, radioactive decay, compound interest, mixing, epidemics, and elementary mechanics.

• First-order differential equations are written in the following forms:

F(x,y,y’) = 0

y’ = f(x,y)

y’ + p(x)y = r(x)

where p and r are given continuous functions. The solution and unknown function is y, and with its derivative y’ satisfies this differential equation.

• First-order differential equations can have a general solution that can involve a constant c and represent a family of solutions. Similar to indefinite integrals, the general solution of a differential equation can represent a family of curves. Similar to definite integrals, a particular solution of a differential equation can represent one of the curves. A particular solution of a differential equation satisfies a specified condition, which may be an initial condition.

• Following is a list of standard differential equations and their solution forms.

(a.) Equations in the form: y’ = f(x) are simple differential equations that depend only on x. A solution to this type of equation has the form:

y = ∫ f(t)dt + c

(b.) Equations in the form: y’ + ay = 0 are differential equations that have a real constant coefficient a.

A solution to this type of equation can be found by inspection. A function y must be found whose derivative y’ is equal to (-a)(y). The solution has the form:

y = ce^-ax where c is an arbitrary constant.

This solution represents a family of infinitely many solutions to the differential equation, which forms a family of integral curves.

(c.) Equations in the form: y’ = f(x,y) and y(x₀) = y₀ or y’ = f(x,y) and y = y₀ at x = x₀ are called initial value problems.

In these equations, x₀ and y₀ represent values of the initial condition. The initial condition y(x₀) = y₀ is used to solve for what is called a particular solution of the differential equation. A particular solution is the general solution with c specified by the initial condition.

In many applications, differential equations describe or represent a physical system or represent a mathematical model of a system where a specified condition must be satisfied by the solution that is inherent in the system. If this condition is an initial condition, such as at time = 0 or position = point (x₀,y₀), this becomes a problem called an initial value problem.

Initial value problems are more specifically represented in the form:

y’ + p(x)y = r(x) and y(x₀) = y₀

where p(x) and r(x) are continuous functions on an open interval containing x = x₀. A unique function y exists that satisfies this equation and its initial condition y(x₀) = y₀.

(d.) Equations in the forms: M(x)dx = -N(y)dy, g(y)dy = f(x)dx and (dy/dx) = f(x)g(y) are called separable equations.

Separable equations can be solved by integrating each side separately. For example, a separable equation in the form: (dy/dx) = f(x)g(y) can be rearranged as:

(dy/g(y)) = f(x)dx

and solved by integrating:

∫(dy/g(y)) = ∫ f(x)dx + c

Substitutions can sometimes be used to modify differential equations into a separable form.

(e.) Equations in the form: M(x,y)dx + N(x,y)dy = 0 are called exact equations.

In these equations, M = u/x and N = u/y and therefore, u = Mx = Ny.

Integration can occur as:

u = ∫ M ∂x + f(y) and u = ∫ N ∂y + g(x)

where f(y) and g(x) represent constants of integration.

In general, an exact equation M(x,y)dx + N(x,y)dy = 0 is one where (M dx + N dy) is an exact differential such that:

du = (∂u/∂x)dx + (∂u/∂y)dy

which yields an implicit solution u(x,y) = c.

Equations that are not inherently exact can be modified to an exact form by multiplying the non-exact equation with a function called an integrating factor. An integrating factor is a function that is multiplied to a differential equation to put it into a solvable form.

(f.) Equations in the form: dy/dx + p(x)y = r(x) are called linear first-order differential equations.

A general solution for linear first-order differential equations can be developed as follows:

Integrate dy/dx + p(x)y = r(x) by transforming it using y = u(x)z(x) so that:

dy/dx = u(dz/dx) + z(du/dx)

Substitute into the differential equation:

u(dz/dx) + z(du/dx) + p(x)u(x)z(x) = r(x)

u(dz/dx) + z[(du/dx) + p(x)u(x)] = r(x)

First consider the term z[(du/dx) + p(x)u(x)] to find u:

(du/dx) + p(x)u(x) = 0

Rearrange:

du/u = -p dx

Integrate:

log u = -∫ p dx

u = exp{-∫ p dx}

Substitute back into differential equation u(dz/dx) + z[(du/dx) + p(x)u(x)] = r(x):

exp{-j p dx}(dz/dx) + z[(-pe^{∫ p dx}) + pe^{-∫ p dx}] = r(x)

exp{-∫ p dx}(dz/dx) = r(x)

Rearrange:

dz = r(x) e^{-∫ pdx} dx

z = ∫ r(x) e^{-∫ pdx} dx + c

Therefore:

y = uz = [e^{-∫ pdx}][∫ r(x) e^{-∫ pdx} dx + c]

This is the general solution of a linear first-order differential equation.

(g.) Equations in the form: y’ = f(x,y) and y(x₀) = y₀ with a non-linear term(s) are called non-linear differential equations.

A general formula does not exist to solve this type of equation. However, approximate solutions and numerical solutions can be applied. For first-order linear equations, a family of solutions can exist that depends on the specification of the arbitrary constant. Whereas for non-linear equations, even though a solution containing an arbitrary constant may exist, there may be other solutions that cannot be obtained by specifying values for the constant.

Approximating solutions for differential equations includes using direction fields, which involve drawing or sketching families of solution curves using the slope y’. Also, approximations are made using iteration methods, such as Picard’s iteration method, which is applied to initial value problems.

Non-linear differential equations can sometimes be changed into linear form by substitution of the dependent variable and solved as linear equations. The Bernoulli equation y’ + p(x)y = g(x)yⁿ is an example of such an equation.

(h.) Equations in the form: dy/dx = f(x,y) are sometimes called homogeneous when the function f does not depend on x and y separately, but only on their ratio y/x or x/y. A so-called homogeneous equation can be written in the form: dy/dx = F(y/x)

8.2 Second-Order Linear Differential Equations

• This section includes second-order linear differential equations, homogeneous second-order linear equations with general and particular solutions, homogeneous equations with constant coefficients, and non-homogeneous linear differential equations.

• Applications of second-order linear differential equations occur in mechanics and electrical engineering, including vibrations and resonance, mechanical vibrations, free vibrations, forced vibrations, and electrical networks.

• A second-order differential equation has the general form:

F(x,y,y’,y") = 0

Within this general form are equations that can be solved for y":

y" = f(x,y,y’)

More specifically, second-order equations can be written in the following forms:

G(x)(d²y/dx²) + P(x)(dy/dx) + Q(x)y = R(x)

(d²y/dx²) + p(x)(dy/dx) + q(x)y = r(x)

where G, P, Q, R, p, q, r are given functions.

• A solution to a second-order linear differential equation on an open interval a < x < b is a function y = h(x) that has derivatives y’ = h’(x) and y”= h”(x), and satisfies the differential equation for all values of x in the interval.

• A second-order linear equation written in the form:

y”+ p(x)y’ + q(x)y = 0

is called a homogeneous second-order linear equation.

This type of equation has a linear combination of solutions referred to as the superposition or linearity principle. Two linear independent solutions for this equation are:

y = y₁(x) and y = y₂(x)

And they form the solutions where:

y = c₁y₁ + c₂y₂

This linear combination (c₁y₁ + c₂y₂) with c₁ and c₂ as arbitrary constants provide the form of a general solution.

When values for c₁ and c₂ are specified as initial conditions, then a particular solution results. For example, given initial conditions y(x₀) and y’(x₀) where x₀ is a point within a defined interval, then c₁ and c₂ are specified so that:

y(x₀)= c₁y₁(x0) + c₂y₂(x0)

y^’(x0) = c₁y₁^’(x0) + c₂y₂^’(x0)

where this system has a unique solution for c₁ and c₂ if:

Therefore, when p(x) and q(x) are continuous on an open interval and x₀ is in the interval, then a general solution exists in the interval. More specifically, when an initial condition is specified, a particular or unique solution exists.

• Equations in the form: ay”+ by’ + cy = 0 are called homogeneous equations with constant coefficients.

To solve this type of equation substitute: y e^rx

a(e^rx)”+ b(e^rx)’ + c(e^rx) = 0

Differentiate:

e^rx(ar² + br + c) = 0

where r is a root of the quadratic equation:

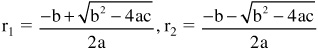
When b² — 4ac > 0, the general solution of the equation is:

y = c_xe^rlx + c2e^r2x

When b² — 4ac = 0, r₁ = r₂ = (-b/2a), the general solution of the equation is:

y = c_le^rlx+ c₂e^rlx= c_le^-bx/2a+ c₂e^-bx/2a

When the roots are complex, r₁ = λ + iω and r₂ = λ - iω, the general solution of the equation is:

y = c₁e^(λ+^iω)x + c₂e^(λ-iω)x = c₁e^λx cos ωx + c₂e^λx sin ωx

• Equations in the form: y”+ p(x)y’ + q(x)y = r(x) are called non-homogeneous linear differential equations.

In these equations, r(x) ≠ 0 and p, q, and r are continuous on a specified interval.

A general solution to this type of equation has the form:

y = y_h + y_p

where y_h is a general solution of the homogeneous equation:

y”+ p(x)y’ + q(x)y = 0

and y_p is a particular solution of the non-homogeneous equation:

y”+ p(x)y’ + q(x)y = r(x)

Therefore, the general solution of a non-homogeneous equation combines the solution of the homogeneous equation with the particular solution y_p:

y = y_h + y_p = c₁y₁ + c₂y₂ + y_p

Methods used to find y_p include the method of variation of parameters and the method of undetermined coefficients.

Numerical methods and series methods are commonly used to solve second-order differential equations that have variable coefficients.

8.3 Higher-Order Linear Differential Equations

• This section includes n_th-order linear differential equations, n_th-order homogeneous linear differential equations, n_th-order homogeneous equations with constant coefficients, n_th-order non-homogeneous linear differential equations, and n_th-order non-homogeneous differential equations with constant coefficients.

• Higher-order linear differential equations are an extension of second-order linear differential equations as far as form and solution methods.

• An n_th-order linear differential equation has the general form:

P₀(x)(d⁽ⁿ⁾/dx⁽ⁿ⁾) + P₁(x)(d⁽ⁿ-i⁾/dx⁽ⁿ-i⁾)+ ...+ P_n-1(x)(dy/dx) + Pn(x)y = r(x)

Or equivalently:

P0(x)y⁽ⁿ⁾ + P₁(x)y^(n-1) + ... + P_n-1(x)y’ + P_n(x)y = r(x)

where r and P_n are continuous in a specified interval.

If the equation is divided by P₀(x) it becomes:

y⁽ⁿ⁾ + p₁(x)y^(n-1) + ... + p_n-1(x)y’ + p_n(x)y = r(x)

• The standard form of an nth-order homogeneous differential equation is:

y⁽ⁿ⁾ + p₁(x)y^(n-1) + ... + p_n-1(x)y’ + p_n(x)y = 0

where y⁽ⁿ⁾ = dⁿy/dxⁿ is the first term.

• For n_th-order homogeneous linear differential equations in the form: y⁽ⁿ⁾ + p₁(x)y^(n-1) + ... + pn-1(x)y’ + pn(x)y = 0, linear combinations of solutions form a solution, (similar to second-order equations). This is called a basis of solutions and is comprised of n linearly independent solutions.

The general solution to n_th -order homogeneous linear differential equation is the linear combination:

y= c₁y₁ + c₂y₂ + ...+ c_ny_n

where c₁,...c_n are constants and c₁, ... , c_n satisfy:

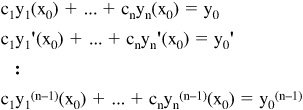
When values are specified for c₁,...c_n, a particular solution results. To obtain a unique solution, it is necessary to specify n initial conditions:

y(x₀) = y₀, y’(x₀) = y₀’, ... , y^(n-1)(x₀) = y₀^(n-1)

In general, when p₀,...p(_n-1) are continuous on an open interval and x₀ is in that interval, then a general solution can be obtained. If initial conditions are given, then a particular solution can be obtained.

• Equations in the form: a₀yⁿ + a₁y^(n-1) + ... + a_n-1y’ + a_ny = 0 are called n_th-order homogeneous equations with constant coefficients.

Solving this type of equation is similar to solving second-order homogeneous equations with constant coefficients. A solution involving y = e^rx can be found.

Substituting y = e^rx into the equation gives:

e^rx(a₀yⁿ + a₁y^(n-1) + ... + a_n-1y’ + a_ny) = 0

When roots r are real and unequal, the general solution is:

y = c₁e^r1^x + c₂e^r2^x + ... c_ne^rnx

When the roots are complex, r₁ = λ + iω and r₂ = λ — iω, the general solution is:

y = c₁e^λx cos cox + c₂e^λx sin cox + ...

• Equations in the form:

y⁽ⁿ⁾ + p₁(x)y^(n-1) + ... + p_n-1(x)y’ + p_n(x)y = r(x)

with r(x) continuous on the open interval, are called non-homogeneous n_th-order linear differential equations.

A general solution exists in the form:

y = y_h + y_p = c₁y₁ + c₂y₂ + ... + c_ny_n + y_p

where y_h is a general solution of the homogeneous equation and y_p is added as the particular solution of the non-homogeneous equation.

• Equations in the form:

y⁽ⁿ⁾ + a₁y^(n-1) + ...+ a_n-1y’ + a_ny = r(x)

are called non-homogeneous n_th-order equations with constant coefficients.

To solve this type of equation, the method of undetermined coefficients and the method of variation of parameters can be used. Methods used for constant coefficients often involve sine, cosine, and exponential functions.

• If the coefficients are not constants, solutions often involve numerical methods or series methods. In general, methods used for solving second-order differential equations can often be expanded to higher order differential equations.

8.4 Series Solutions to Differential Equations

• This section briefly describes series solutions for differential equations with variable coefficients, the power series method, and the Frobenius method.

• Series solutions can be applied to solve linear differential equations that have variable coefficients.

• Differential equations with variable coefficients can arise in modeling applications and can be in the general form:

P(x)y”+ Q(x)y’ + G(x)y = 0

or y”+ p(x)y’ + q(x)y = 0

where the coefficients P, Q, G, p, and q are polynomials.

• Series solution methods for a differential equation with variable coefficients involve solving the equation near a point x₀. Using a series solution method generally involves expressing y as an infinite series in powers of (x — x₀), where x₀ is a specified point.

• The power series method is a general method for solving linear differential equations in the form:

y”+ p(x)y’ + q(x)y = r(x)

(including higher orders) where p(x), q(x), and r(x) are variable.

The power series method provides solutions in the form of the power series:

y(x) = a₀ + a₁(x -x₀) + a₂(x - x₀)² + ...

In this method, the power series is substituted along with its derivatives into the differential equation:

y”+ p(x)y’ + q(x)y = r(x)

The coefficient a_n can therefore be determined, providing p, q, and r are analytic at x = x₀.

Note: A function f(x) is said to be analytic if it is differentiable at all points in its domain. A function f(x₀) is analytic if it is differentiable at and near point x₀. Also, a function that is real and analytic at point x = x ₀can be represented in a power series in powers of (x - x₀) with a positive radius of convergence.

• The Frobenius method allows the power series to be extended to differential equations in the form:

y”+ [b(x)/(x - x0)]y’ + [c(x)/(x - x0)²]y = 0

where the coefficients are singular (cannot be obtained from a general solution) at (x = x₀) rather than analytic, however b(x) and c(x) are analytic at (x = x₀).

These equations can have a solution in the form:

y(x) = x^r[a0 + a1(x - + a2(x - x0)² + ...]

where r is a real or complex number that is determined by substituting y(x) into the differential equation.

8.5 Systems of Differential Equations

• This section provides a brief introduction to systems of linear differential equations, including systems of first-order differential equations, systems of linear differential equations with constant coefficients a_ij, and systems of homogeneous linear differential equations with constant coefficients a_ij.

• Systems of differential equations include linear systems and non-linear systems. Systems of linear differential equations can also be homogeneous or non-homogeneous, and can be solved using methods that include vectors and matrices and phase-plane methods. Systems of higher-order differential equations can sometimes be reduced to first-order equations so that simpler methods can be applied to solve them.

• Applications of systems of differential equations include mechanical systems containing springs or masses, combined networks of circuits, and many other systems in various disciplines of engineering.

• In general, a system of first-order differential equations has the form:

y₁’ = f₁(t, y₁, y₂, y₃)

y₂’ = f₂(t, y₁, y₂, y₃)

y₃’ = f₃(t, y₁, y₂, y₃)

or in more general form:

y₁’ = f₁(t, y₁, ... , y_n)

y₂’ = f₂(t, y₁, ... , y_n) :

y_n’ = f_n(t, y₁, ... , y_n)

In such a system of differential equations, the unknown functions in the equations are solved.

• A system of differential equations in the form:

y₁’ = a₁₁y₁ + a₁₂y₂ + g₁

y₂’ = a₂₁y₁ + a₂₂y₂ + g₂

is a linear system of differential equations with constant coefficients a_ij.

This system can also be written in vector form as:

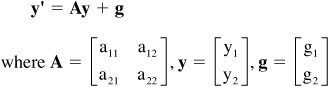
• If this system of linear differential equations with constant coefficients has g = 0, then it becomes a homogeneous linear system of differential equations with constant coefficients a_ij and can be written:

y₁’ = a₁₁y₁+ a₁₂y₂

y₂’ = a₂₁y₁ + a₂₂y₂

In vector form, these equations become:

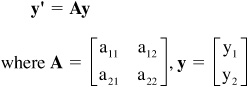
Solutions to a system of homogeneous linear equations have the form:

y = xe^λt

where λ is an eigenvalue of A and x is the eigenvector. The solution to the quadratic equations represented below is :

where eigenvector x ≠ 0, and together with its components x₁ and x₂ form:

(a₁₁-λ)x₁+ a₁₂x₂ = 0

a₁₂x₂= 0 a₁₂x₁+ (a₂₂-λ)x₂= 0

• Note that a system of differential equations can be solved using a phase-plane method where solutions to:

y’ = Ay

or equivalently, for two dimensions:

y₁’ = a₁₁y₁ + a₁₂y₂

y₂’ = a₂₁y₁ + a₂₂y₂

are found such that y₁ = y₁(t) and y₂ = y₂(t) exist as a path or curve of a solution in a y₁y₂-phase plane. A point P(y₁,y₂) is a critical point of the system and occurs where the right sides of the system equal zero. Point P can be a node, saddle point, center, or spiral point, and can be stable or unstable. (Please see a textbook on differential equations for a complete explanation of this and other solutions in this chapter.) Phase-plane methods can be applied to non-linear systems using linearization.

8.6 Laplace Transform Method

• This section provides a brief introduction to the Laplace transform method for solving differential equations.

• The Laplace transform method is used to solve differential equations and systems of differential equations and their corresponding initial and boundary value problems. The method involves transforming a complicated problem into a simple equation called a subsidiary equation, solving this equation using algebraic techniques, then transforming the solution of the subsidiary equation back to find the solution of the original problem.

• The Laplace transform of a function f(t) is written:

F(s) = (f) = ₀ ∫^∞ e^-st f(t) dt

where differentiation of f with respect to t corresponds to the multiplication of the transform F with s:

(f ’(t)) = s(f(t)) – f(0)

(f“(t)) = s²(f(t)) – sf(0) – f (0)

(fⁿ⁾(t)) = sⁿ(f(t)) – s^(n-1)f(0) – ... – sf^(n-2)(0) – f^(n-1)(0)

• To solve a given differential equation in the form:

y”+ ay’ + by = r(x)

First take the transform and set (y) = Y(s) to determine a subsidiary equation that has the form:

(s² + as + b)Y = (r) + sf(0) + f (0) + af(0)

Tables of functions and their Laplace transforms (f) can be used to obtain the transform (r).

The subsidiary equation is solved for Y(s) algebraically and the inverse transform y(t) = ^-1(Y) is determined to find the solution. This last step often involves using Laplace transform tables.

8.7 Numerical Methods for Solving Differential Equations

• This section provides a brief introduction to the use of numerical methods for solving differential equations including the Euler method, the Improved Euler method, the Runge-Kutta method, and the Adams-Moultan method.

• Numerical methods are used to solve various types of differential equations. Numerical procedures involve constructing approximate values of y₀, y₁, y₂,...y_n at points x₀, x₁, x₂,...x_n. Problems to consider when using numerical methods include convergence and error.

• To demonstrate the concept of numerical methods, consider a first-order initial value problem:

y’ = f(x,y), y(x₀) = y₀

To find the solution, begin with the Taylor series:

y(x+h) = y(x) + hy’(x) + (h²/2)y"(x) + ...

Then truncate the series after the y’ term. This results in an expression used repeatedly in the Euler method:

y_n+1 = y_n + hf(x_n,y_n) = y_n + hy_n’

where n = 0, 1, 2, ... , and h is the step size between points x₀, x₁, x₂,...x_n.

If the series is truncated to include the y”term, then the resulting expression is used in the Improved Euler method (also called the Improved Euler-Cauchy method or Heun’s method):

y_n+1 = y_n + h[f(x_n,y_n) + f(x_n+h, y_n+hf(x_n,y_n))]/2

= y_n + h[y_n’ + f(x_n+h, y_n+h y_n’)]/2

If the series is truncated to include the h⁴ term, a more accurate method results called the Runge-Kutta method of fourth-order. This method involves calculating the following:

k_n1 = f(x_n, y_n),

k_n2 = f(x_n + h/2, y_n + hk_n1/2) k

_n3 = f(x_n + h/2, y_n + hk_n2/2)

k_n4 = f(x_n + h, y_n + hk_n3

Then substituting them into the expression:

y_n+₁ = y_n + (h/6)[k_n1 + 2k_n2 + 2k_n3 + k_n4]

• Another numerical method called the Adams-Moultan method involves calculating a“predictor”given by:

y_n+1 = y_n + (h/24)[55y_n’ – 59y_n-1’ + 37y_n-2’ – 9y_n-3’]

Then calculating a“corrector”given by:

y_n+1 = y_n + (h/24)[9y_n+1’ + 19y_n’ – 5y_n-1’ + y_n-2’]

where y₁, y₂, y₃ are first calculated using the Runge-Kutta method.

• Second-order ordinary differential equations can be solved using an extension of the Runge-Kutta method called the Runge-Kutta-Nystrom method.

• Note that numerical methods are commonly used to solve partial differential equations.

8.8 Partial Differential Equations

• This section provides a brief introduction to partial differential equations.

• Partial differential equations are used to model physical and geometrical systems where there are functions that depend on two or more independent variables. Partial differential equations arise in fluid mechanics, dynamics, elasticity, heat transfer, quantum mechanics, electro-magnetic theory, and many engineering problems. In partial differential equations, the independent variables include time and space coordinates.

• Examples of second-order partial differential equations include:

One-dimensional wave equation:

∂²u/∂t² = c²(∂²u/∂x²)

Two-dimensional wave equation:

∂²u/∂t² = c²[(∂²u/∂x²) + (∂²u/∂y²)]

One-dimensional heat equation:

∂u/∂t = c²(∂²u/∂x²)

Two-dimensional Laplace equation:

∇²u = (∂²u/∂x²) + (∂²u/∂y²) = 0

Three-dimensional Laplace equation:

∇²u = (∂²u/∂x²) + (3²u/∂y²) + (∂²u/∂z²) = 0

Two-dimensional Poisson equation:

(∂²u/∂x²) + (∂²u/∂y²) = f(x,y)

• Solutions to partial differential equations are often obtained in a specified region that satisfies initial conditions or boundary conditions where values of the solution u or its derivatives on the boundary curve or surface of the region are set. For example, in wave equations initial conditions may be displacement or velocity at time t = 0. Or in heat equations an initial temperature may be specified.

• Partial differential equations can be solved using a separation of variables method or the product method in which the solutions form products of functions that each depend on one of the variables. For example, the solution form u(x,t) = F(x)G(x) can be used to solve the one-dimensional wave equation or the one-dimensional heat equation, where substituting into the partial differential equation gives an ordinary differential equation for F and G.

• Numerical methods are commonly used to solve partial differential equations. Such methods can include replacing the partial derivatives with difference quotients. The following solution forms can also be used to solve these equations:

For the Laplace equation:

u_i+1j + u_{ij + 1} + u_i-1j + u_ij-1 - 4u_ij 0

For the heat equation:

(1/k)[u_ij+₁ – u_ij] =(1/h²)[u_i+₁j – 2u_ij + u_i-1j]

For the wave equation:

(1/k²)[u_ij+₁ – 2u_ij + u_ij_-1] =(1/h²)[u_i+₁j – 2u_ij + u_i-1j]

where h and k represent the size of the sections in a grid in x- and y-directions.