Chapter 5 Vectors, Matrices, Curves, Surfaces, and Motion

5.1 Introduction to Vectors

• This section includes definitions, notation, types of vectors including displacement, velocity, zero, unit, equivalent, position, and addition and subtraction of vectors.

• Scalars are quantities that represent magnitude and can be described by one number that is positive, negative, or zero. Scalars can be compared with each other when they have the same physical dimensions or units. Examples of scalars include temperature, work, density, and mass.

• A vector represents a quantity that is described by both a numerical value for magnitude (or length) and a direction. A vector is depicted as a line segment with an initial point and a terminal point that has an arrow pointing in the direction of the terminal point. Examples of vectors include displacement, velocity, acceleration, electric field strength, force, and moment of force.

• A displacement vector represents the change or displacement between two points in a coordinate system. The length of a displacement vector is the distance between the two points and the direction of a displacement vector is the direction it is pointing.

• A velocity vector describes an object in motion and has a magnitude representing the speed of the object and a direction representing the direction of motion.

• Notation for a vector includes boldface letters A, a, B, b, etc., or one or two letters with an arrow , etc. Vectors can be written in terms of their components on a coordinate system. For example:

A = a₁i + a₂j + a₃k = [a₁, a₂, a₃]

where a₁, a₂, a₃ are the components.

Vectors can also be written in the form of column vectors and row vectors:

where a₁ and a₂ are components of A, b₁ and b₂ are components of B, v₁ and v ₂are components of v, and r₁ and r₂ are components of r. Unit vectors i, j, and k have directions pointing parallel to the axes of a coordinate system.

• The magnitude (or length) of a vector is denoted with vertical bars as used with absolute value. For example, the following represent magnitudes: |A|, |B|, . Sometimes double bars are used to represent magnitude: ||A||, ||B||.

• If vector A = and points from a to b and vector B = and points from b to a, then A = –B.

• When a vector is changed from its column format to a row format or vice versa, it is called a transposition and indicated by“^T".

Therefore, if , then v^T = [v₁ v₂]

Similarly, if v = [v₁ v ₂], then v^T =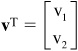

• The zero vector 0 has a length (or magnitude) of zero and no direction. Its initial and terminal points coincide.

• A unit vector u has a length (or magnitude) of one. If unit vector u is pointing in the direction of vector A and A is not a zero vector, then u A/|A|.

• Vectors that point in the same direction and have the same length are equivalent vectors even if they are not in the same location. A vector can be relocated and still be considered the same vector as long as its length and direction remain the same.

• A vector with its initial point at the origin of a coordinate system is called a position vector. A position vector is defined according to the location or coordinates of its terminal point. For example, if its terminal point is at B then vector is a position vector of point position vector represents the position of a point with respect to the origin and a displacement vector represents the change or displacement between two points in a coordinate system.

• A vector is often written in terms of its components, which are defined by its directions along the XYZ axes of a coordinate system. Generally, i, j, and k are unit vectors with magnitudes of one and directions pointing parallel to the XYZ axes respectively in a rectangular coordinate system.

• Vector A can be written using the i, j, k unit vectors as: A = a₁i a₂j + a₃k where a₁, a₂, and a₃ are scalar quantities and a₁i, a₂j, and a₃k are the components of A. The magnitude (or length) of A is given by:

• If a position vector has its starting point at the origin and its terminal point at point P = (5,6), then in two dimensions vector A is written:

A = 5i + 6j

It has length and is depicted as:

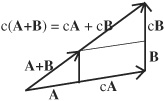
• Any vector A can be multiplied by a constant c such that:

cA = ca₁i + ca₂j + ca₃k

• The zero vector having zero length can be written in terms of i, j, k:

0 = 0i + 0j + 0k

• Unit vectors i, j, k can be represented as column vectors:

Vector A can be written in column vector format:

• Vectors can be characterized and expressed in more than three dimensions or components. For example:

A + B = (a₁, a₂, a₃, a₄) + (b₁, b₂, b₃, b₄)

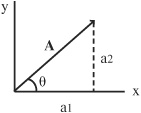
• The direction of a vector in a coordinate system is represented by the angle it makes with the positive X-axis. For example, the direction of vector A can be written in terms of the angle θ that it makes with the positive X-axis. Vector A = a₁i + a₂j makes an angle θ = tan^–1(a₂/a₁) with the X-axis and can be written as:

A = i |A| cos θ + j |A| sin θ

where a₁ = |A| cos θ and a₂ = |A| sin θ.

A unit vector u for vector A can be written as:

• A vector v divided by its length|v| results in a unit vector pointing in the direction of the vector. The direction of v is u = v/|v| and its length is |v|. Therefore, length multiplied by direction gives v as u|v| = v.

• In three dimensions the components of a unit vector U are called“direction cosines”and have angles α, β, and γ with the X-, Y-, Z-axes, respectively. In three dimensions:

U = i cos α + j cos β k cos γ

and cos²α + cos²α cos² γ = 1

Addition and Subtraction

• Two vectors can be added or subtracted if they have the same dimensions by adding or subtracting the corresponding components (or elements). For example, a two-dimensional vector can be added to another two-dimensional vector, however a two-dimensional vector cannot be added to a three-dimensional vector.

• The sum of two vectors can be depicted by positioning the vector such that the initial point of the second vector is at the terminal point of the first vector. The sum of the two vectors is a third vector with its initial point at the initial point of the first vector and its final point at the final point of the second vector. In other words, the sum of two vectors a and b is the combined displacement from applying vector a then applying vector b. Consider the figure below depicting the following two examples of adding vectors a and b:

For example, to add vectors a and b in the first illustration, place the initial point of b at the final point of a. The sum is the vector joining the initial point of a to the final point of b, or vector c.

In the second illustration, the initial point of b is already at the final point of a. The sum is the vector joining the initial point of a to the final point of b, which results in vector c.

Remember that the starting point of a vector can be moved as long as its length and direction stay the same. Also note that the sum is also the diagonal of a parallelogram that can be constructed on a and b.

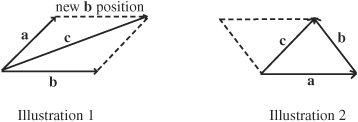
Both figures represent a + b + c.

• Subtraction of two vectors is equivalent to addition of the first vector with the negative of the second vector. The negative of a vector is a vector with the same length but pointing in the opposite direction.

• To subtract two vectors, reverse the direction of the second vector, then add the first vector with the negative of the second vector by positioning the vectors so that the initial point of the (negative) second vector is at the final point of the first vector. The sum of two vectors will be a third vector with its initial point at the initial point of the first vector and its final point at the final point of the second (negative) vector. This figure represents a − b = c:

In a second example of vector subtraction, subtract two vectors a − b = c, where a − b can be represented using the negative of b, then slide −b up to place initial point of −b at terminal point of a. The sum is the vector joining the initial point of a to the final point of −b, which results in c. This figure represents a − b = c:

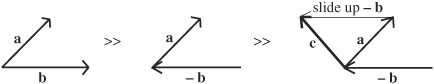
• The sum of two vectors and is written:

The sum of two vectors A and B is written:

• Two vectors can be added or subtracted and expressed using unit vectors. If vector A = a₁i + a₂j and vector B = b₁i + b₂j, then:

A + B = a₁i + a₂j + b₁i + b₂j = (a₁ + b₁)i + (a₂ + b₂)j

A − B = a₁i + a₂j − (b₁i + b₂j) = (a₁ − b₁)i + (a₂ − b₂)j

If A = 2i + 3j and B = 3i + 4j, then A + B = 5i + 7j.

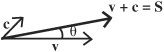
• Example: Consider a ship moving along the ocean at a velocity v = 15 km/hr relative to the water, which has a current c = 2 km/hr. An angle θ = 45° exists between the direction of the ship and the direction of the ocean current.

The true velocity of the ship with respect to land is equal to the sum of the two vectors v + c.

To calculate the actual speed of the ship relative to land, set the velocity of the ship along the X-axis so that v = (15)i and the ocean current |c| = 2. Therefore:

c = (2 cos 45°)i + (2 sin 45°)j≈ 1.4i + 1.4j

The actual velocity S of the ship relative to land is:

S = v + c = 15i + 1.4i + 1.4 j = 16.4i + 1.4j

Therefore, the speed of the ship relative to land is:

The angle the ship is deviating from v along the X-axis due to the current is: θ tan⁻¹(1.4/16.4) = 4.9° = 0.0085 radians.

5.2 Introduction to Matrices

• This section includes definitions, notation, types of matrices including square, transpose, symmetric, and skew, and addition of matrices.

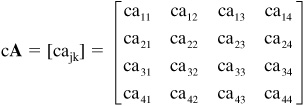
• A matrix is a rectangular array of numbers or functions. If a matrix has a single row or column, it is a vector. The components in a vector are called elements in a matrix. The array defining a matrix is enclosed in brackets and each number or function is called an element or entry.

• If a matrix has an equal number of rows and columns, it is a square matrix:

• Matrices are often used to represent and solve a set of equations. The coefficients of the equations are the elements of a coefficient matrix. For the set of equations:

2x − 3y + z = 0

3x + y + 2z = 0

x + 2y + 2z = 0

The coefficient matrix is:

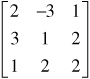
• Notation for matrices includes boldface capital letters, writing an array of numbers or functions in brackets, or using double-subscript notation as shown below. When matrices and vectors are used together, the vectors are often represented using lower-case boldface letters and the matrices in upper-case boldface letters. In a matrix the rows and columns are often denoted as m number of rows and n number of columns resulting in an m by n matrix. An m by n matrix A is can be represented as:

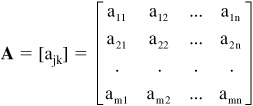
Using the a_jkdouble-subscript notation, the first subscript represents the row and the second subscript represents the column. For example, a ₃₂represents the element located in the third row and the second column. If matrix A has m n, then it is a square matrix. The elements in the main diagonal of a matrix are represented by: a₁₁, a₂₂, a₃₃,... a_mn. A submatrix of matrix A has rows and/or columns absent.

• When a matrix is transposed (indicated by "^T"), its rows and columns are changed so that the first row becomes the first column and the second row becomes the second column, and so on. The transpose of matrix A:

• For example, if A , then .

• If A^T = A, then A is called a symmetric matrix. If A^T = −A, then A is called a skew-symmetric matrix.

• Properties of transpose matrices include:

(A + B)^T = A^T + B ^T

(cA)^T = cA^T, where c is a scalar.

• Two matrices A = [a_kj] and B = [b_kj] are equal if they have the same size and the corresponding elements are equal. Therefore in equal matrices, a₁₁ = b₁₁, a₂₂ = b₂₂, a₃₃ = b₃₃, etc.

• Matrices can be added or subtracted if they are the same size by adding or subtracting the corresponding elements. For example, add C + D.

• Properties of addition of vectors and matrices where A and B are the same size include:

(A + B) + C = A + (B + C) (associative)

A + B = B + A (commutative)

A + A = 2A

A + 0 = A

A + (−A) = 0

• Note: The following properties are true for differentiating:

5.3 Multiplication of Vectors and Matrices

• This section includes multiplication of vectors and matrices with scalars, multiplication of two matrices, multiplication of a vector with a matrix, and multiplication of row and column vectors.

• The following are properties of multiplication of matrices A, B, C and scalar c:

(A + B)C = AC + BC

C(A + B) = CA + CB

(cA)B = cAB = A(cB)

A(BC) = (AB)C

(c₁ + c₂)A = c₁A + c₂A

c(A + B) = cA + c B

c₁(c₂)A = (c₁c₂)A

• Multiplying vector Awith scalar c results in a vector having a magnitude of |c||A| and a direction of A, where, |c| represents the absolute value of the scalar c and |A| represents the magnitude of vector A. When c > 0, the displacement vector cA is parallel to A and pointing in the same direction as A. When c < 0, the vector cA is parallel to A but pointing in the opposite direction as A.

• When multiplying matrices and scalars, each element in the matrix is multiplied with the scalar. If matrix A = [a_jk] is multiplied with scalar c, where _j goes from 1 to 4 and _k goes from 1 to 4, it can be written:

• To multiply two matrices, the number of columns in the first matrix must be equal to the number of rows in the second matrix. For matrix A = [a_jk], which is an m by n matrix having m rows and n columns and matrix B = [b_jk], which is a p by q matrix having p rows and q columns, the product exists if n = p.

The process for multiplying two matrices A and B, is to multiply each element in the first row with the corresponding element in the first column, then multiply each element in the second row with the corresponding element in the second column, and so on. Thereby multiplying each element in the jth row with the corresponding element in the kth column. If C is the product of matrices A and B, it can be written:

where j = 1,..., m and k = 1,..., q.

C can also be given by AB = C in matrix arrays:

The highlighted row and column depicts the order that multiplication is carried out.

• The following represents the process of multiplying two matrices:

Note that the result is a matrix of dot products (see Section 5.4 for the dot product).

For example, multiply the following two matrices:

• In general AB ≠BA, however they can be equal. Also, AB can equal zero even if neither A nor B is zero.

• When multiplying a matrix and a vector, the rule for two matrices applies, where the number of columns in the first matrix must be equal to the number of rows in the second matrix. Therefore, the number of columns in the matrix must be equal to the number of elements in the vector. For example:

Note that is undefined.

• Following are some examples of multiplying row and column vectors:

5.4 Dot or Scalar Products

• This section includes equations that define the dot product, the dot product of parallel and perpendicular vectors, and properties of the dot product.

• The dot product (also called the scalar product or inner product) of two vectors is defined as:

A • B = |A||B|cos θ

where |A| and |B| represent the magnitudes of vectors A and B and θ is the angle between vectors A and B.

• Vectors A and B are perpendicular if A • B = 0, providing A or B does not equal zero. This is true because cos 90° = cos(π/2) = 0. For example, the dot product of i = (1, 0, 0) and j = (0, 1, 0) is i • j = 0, because i and j are perpendicular to each other.

• Vectors A andB are parallel if A • B = |A||B|, providing A or B does not equal zero. This is true because cos 0 = 1. The dot product of i = (1, 0, 0) and i = (1, 0, 0) is i • i = 1.

• The dot product of a vector with itself A • A, has θ = 0 and because cos 0 = 1, then A • A = |A|² = length-squared.

• The dot product can also be used to compute cos θ:

• The dot product written in the form of |A||B| cos θ represents A • B without coordinates. The dot product can also be written in the form [a₁b₁ + a₂b₂] that does involve coordinates.

• The dot or scalar product of vector A = a₁i + a₂j and vector B = b₁i + b₂j can be written as:

Or equivalently:

A • B = (a₁i + a₂j) • (b₁i + b₂j)

= a₁b₁ i• i + a₁b₂ i• j + a₂b₁j• i + a₂b₂ j• j

= a₁b₁(1) + a₁b₂(0) + a₂b₁(0) + a₂b₂(1)

= a₁b₁ + a₂b₂

The terms with i • j and j • i equal zero and i • i and j • j equal one.

Therefore:

A • B = (a₁i + a₂j) • (b₁i + b₂j) = a₁b₁ + a₂b ₂

In three-dimensions the dot product of A and B is:

A • B = a₁b₁ + a₂b₂ + a₃b₃

• In summary, unit vectors combine as follows:

i • i = j • j = k • k = 1

i • j = i • k = j • i = j • k = k • i = k • j = 0

• One application of the dot product is to find the angle between two vectors. If vector A = 2, 3 = (2i + 3j) = and B = 3, 4 = (3i + 4j):

The angle θ between vectors A and B can be found using:

Therefore,

• Another application of the dot product is the dot product of force F and distance d, which equals work done W: F • d = W where F is acting on an object to displace it. Therefore, work done can be written:

W = F • d = |F||d| cos θ

where F is acting on an object to displace it by distance d.

The work done by F in displacement is the magnitude |F| of the force multiplied by length |d| of the displacement multiplied with cosine of the angle θ between F and d. The work is zero if F and d are perpendicular to each other.

If θ = 45° then,

If θ = 90° then,

W = F • d = |F||d|cos 90° = |F||d|(0) = 0

• Some properties of the dot product of vectors A, B, C and scalar c are:

c(A • B) = (cA) • B = A • (cB)

A • (B + C) = (A • B) + (A •C)

A • B = B • A

• The following property applies for differentiating:

5.5 Vector or Cross Product

• This section includes equations that define the cross product, the cross product of two vectors, minimum and maximum values, and applications of the cross product.

• The vector product or cross product of two vectors is defined as:

A × B = |A||B|sin θ

where |A| and |B| represent the magnitudes (or lengths) of vectors A and B and θ is the angle between vectors A and B. The product exists in three dimensions with A and B in a plane and A × B normal to the plane. The cross product of two vectors produces a third vector with a length of |A||B|sin θ and a direction perpendicular to A and B. The length of A × B depends on sin θ and is greatest when θ = 90° or sin θ = 1.

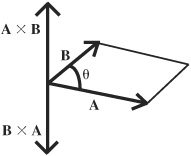
• The cross product of two vectors occurs geometrically according to what is referred to as the right-hand screw rule. This rule denotes that when taking the cross product A × B and moving from vector A to vector B through angle θ results in vector A × B, which is perpendicular to both A and B. The right-hand rule can be visualized by curling the fingers of the right hand from A to B, where A × B points in the direction of the right thumb. Conversely, for the cross product B × A, moving from vector B to vector A through angle results in a vector perpendicular to both A and B but pointing in the opposite direction of A × B. Therefore, by the right-hand rule, A × B and B × A point in opposite directions but have the same magnitude.

• The vector or cross product of two vectors written in terms of their components as vector A = a₁i + a₂j + a₃k and vector B = b₁i + b₂j + b₃k can be calculated using the same procedure as when calculating a determinant. (See Section 5.6. for a summary of determinants.)

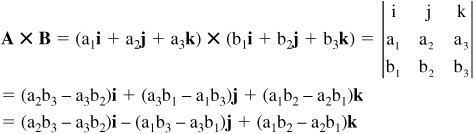
The terms with i × i, j × j, and k × k equal zero. The i, j, k unit vectors combine as follows:

i × i = j × j = k × k = 0

i × j = k, i × k = −j

j × i = −k, j × k = i

k × i = j, k × j = −i

Considering the nature of how the unit vectors combine, A × B can be written out as:

(a₁i + a₂j + a₃k) × (b₁i + b₂j + b₃k)

= a₁b₁ i × i + a₁b₂i × j + a₁b₃i × k

+ a₂b₁j × i + a₂b₂j × j + a₂b₃j × k

+ a₃b₁k × i + a₃b₂k × j + a₃b₃k × k

= 0 + a₁b₂k + a₁b₃(−j) + a₂b₁(−k) + 0 + a₂b₃i + a₃b₁j + a₃b₂(−i) + 0

= (a₂b₃ − a₃b₂)i + (a₃b₁ − a₁b₃)j + (a₁b₂ − a₂b₁)k

• The unit vectors i, j, and k are perpendicular to each other. Therefore, the angle between i and j is π/2 and by the right-hand rule the cross product of i and j is:

i × j = |i||j|sin(π/2) = k

The cross product of i with itself is:

i × i = |i||i|sin 0 = 0.

• The maximum value of the cross product of two vectors occurs when the angle θ is π/2 and sin π/2 = 1. Therefore the two vectors are perpendicular to each other. Conversely, the minimum value of the cross product of two vectors occurs when the angle θ is 0 or π and sin 0 = sin π = 0, and, therefore the two vectors are parallel.

• The cross product can represent the area of a parallelogram with sides A and B, where the value resulting from A B is both the length of vector A B and the area of the parallelogram. The length of the cross product is the area and the area of the parallelogram is. A B, which is the magnitude of the area. A parallelogram with sides A and B has area |a₁b₂ − a₂b₁|. In an XY plane A× B (a₁b₂ − a₂b₁)k.

• One important application of the cross product is torque, which is a force acting on an object to cause rotation. A force F can be applied to a lever arm or a radius vector r, which has its initial point located at the origin of rotation and causes the object to rotate. The torque is a vector having a magnitude that measures the rotation of the force and has a direction of the axis of rotation. The cross product F × r = T is the torque of the force about the origin for a force F acting at a point with position vector r.

• An application of the cross product and dot product together is the volume of a parallelepiped. A parallelepiped with sides given by vectors A, B, and C is represented by:

where |B × C| is area of base and |A| cos θ is height.

• The volume of a cube can be represented using the unit vectors i, j, k:

• Properties of the cross product involving vectors A,B, C and scalar c include:

A × B = −(B × A)

c(A × B) = (cA) × B = A × (cB)

A × (B + C) = (A × B) + (A × C)

A • B × C = A × B • C = B • C × A = C • A × B

|A • B|² + |A × B|² = |A|²|B|² cos² θ + |A|²|B|²sin² θ

= |A|²|B|²

• The following property applies to differentiating:

5.6 Summary of Determinants

• This section provides a brief review of determinants including definitions and using the method of determinants and Cramer’s rule to solve systems of equations.

• A two-by-two determinant is written as follows:

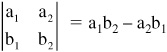
• A three-by-three determinant is written as follows:

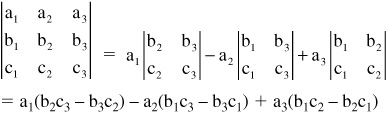
• Two equations with two unknown variables can be solved using the method of determinants and Cramer’s Rule. The two equations can be represented by:

a₁x + b₁y = c₁

a₂x + b₂y = c₂

where a, b, and c represent known coefficients or constants and x and y are unknown variables.

First create three matrices of coefficients D, D_x, and D_y and calculate the determinants:

The solutions for x and y are:

x = D_x/D and y = D_y/D, providing D ≠ 0.

• Three equations with three unknown variables can also be solved using the method of determinants and Cramer’s Rule. The three equations can be represented by:

a₁x + b₁y + c₁z = d ₁

a₂x + b₂y + c₂z = d ₂

a₃x + b₃y + c₃z = d₃

where a, b, c, and d represent known coefficients or constants and x, y, and z are unknown variables.

First create four matrices of coefficients D, D_x, D_y, and D_z and calculate the determinants:

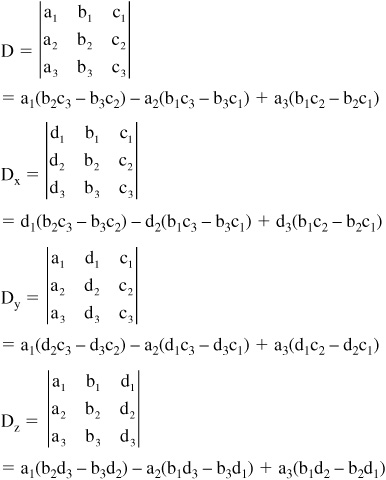
The solutions for x, y, and z are:

x = D_x/D, y = D_y/D, and z = D_z/D, providing D ≠ 0.

• Note that the values of the determinant are not affected if the determinant is transposed.

5.7 Matrices and Linear Algebra

• This section includes information about representing and solving systems of linear equations.

• Systems of linear equations can be solved using matrices. Solutions for two equations with two unknown variables exist where two lines intersect. Similarly, solutions for three equations with three unknown variables exist where three planes intersect. To solve a system of n linear equations with n unknown variables, matrices can be formed and the method of determinants as described in the previous paragraphs can be employed.

Other methods can be employed to solve systems of equations that go beyond the scope of this book. (See Master Math: Algebra Chapter 8 for a discussion of solving simple systems of two and three linear equations using various methods. Also, mathematics books dedicated to solving both linear and non-linear systems of equations should be consulted for a comprehensive discussion.)

• A system of m linear equations with n unknowns can be represented by Ax = d, where A = [a_jk] is the coefficient matrix containing given coefficients (or constants), x = x₁,...x_n is the solution set and d = d₁,...,d _nare given numbers. If d_i are all zero, the system of equations is called a homogeneous system. If at least one d_i is not zero, the system of equations is called a non-homogeneous system.

The system Ax = d can be represented as:

For two equations and two unknowns:

a₁₁x₁ + a₁₂x₂ = d₁

a₂₁x₁ + a₂₂x₂ = d₂

Ax can be written:

The solution set for Ax = d is given by x = A⁻¹d.

• To find the solution set x = A⁻¹d, the inverse of a matrix A ⁻¹ can be expressed using the determinant of A. For example for two equations:

a₁x₁ + b₁x₂ = d₁

a₂x₁ + b₂x₂ = d₂

The solution set x = A⁻¹d is:

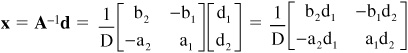
where D is the determinant of A and is given by:

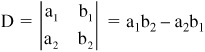
Remember, a matrix can be transposed and the determinant is unaffected.

• Note that the inverse matrix A⁻¹ multiplied by the original matrix A is the identity matrix I. The identity matrix has 1’s on the diagonal and 0’s elsewhere and behaves as the number 1. A two-by-two identity matrix is:

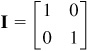
• In three-by-three matrices the inverse also uses the determinant D. The determinate of a three-by-three matrix is:

Determinant of A = a • b × c

= (a₁i + a₂j + a₃k) • (b₁i + b₂j + b₃k) × (c₁i + c₂j + c₃k)

= a₁(b₂c₃ − b₃c₂) + a₂(b₃c₁ − b₁c₃) + a₃(b₁c₂ − b₂c₁)

which represents volume of a box-shaped object.

where the column vectors a, b, c represent the edges of the box extending from the origin, the inverse of A is given by:

Note that the first row of A⁻¹ does not use the first column of A except in the calculation of 1/D.

Therefore, the solution to x A⁻¹d is:

The solutions for x, y, and z (or x₁, x₂, x₃) in three equations are ratios of determinants. Using Cramer’s Rule:

x = |d• (b × c)| / |a• (b × c)|

y = |d• (c × a)|/|a• (b × c)|

z = |d• (a × b)| / |a• (b × c)|

where D = |a • (b × c)|

• The inverse of a matrix can also be found using Gauss-Jordan elimination, which combines Gauss elimination with an identity matrix. See a text on linear algebra for a discussion of this method.

• Another standard method for solving a system of linear equations is called Gauss elimination. To use this elimination method, transform the equations into a matrix, perform operations on the matrix until an upper triangular matrix is formed, transform the triangular matrix back into equation form, and solve for the unknown variables using substitution. Operations used in forming the upper triangular matrix include multiplying a row by a non-zero constant, interchanging two rows, and adding a multiple of one row to another.

• The general procedure for Gauss elimination is:

(a.) Transform the equations into a matrix by writing the coefficients of the equations into a matrix format:

a₁x + b₁y + c₁z = d₁

a₂x + b₂y + c₂z = d ₂

a₃x + b₃y + c₃z = d₃

Then convert to a coefficient matrix:

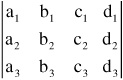
(b.) Create an upper triangular matrix by adding multiples of the coefficient rows to each other until an upper triangular matrix is formed. This involves, multiplying a row through by a non-zero constant, interchanging two rows and adding the multiple of one row to another row to yield a zero coefficient in the lower left of the upper triangular matrix. In a three-by-three upper triangular matrix, a₂, a₃, and b₃ must be converted to zeros and a₁, b₂, and c₃ must be converted to ones.

(c.) Once the upper triangular matrix is formed, transform the coefficient matrix back into the form of the equations. The known variable (from the third equation in the three-by-three matrix) can be substituted back into the reduced equation to solve for the next variable, and then both known variables can be substituted into an original equation to find the third variable.

(d.) The results can be checked by substituting the variables into the original equations.

• Example: Solve the three equations for x, y, and z:

x + y + z = −1

2x − y + z = 0 −

−x + y − z = −2

In matrix form:

Multiply row 1 by −2, then add it to row 2 to make the a₂ position zero:

row 1 × −2 is:

−2 −2 −2 2

Add this new row 1 to row 2 to get new row 2:

0 −3 −1 2

Add row 1 and row 3 to make a₃ zero resulting in new row 3:

0 2 0 −3

The new matrix is:

Switch the second and third rows:

Add row 2 and row 3 to get new row 2 and make b₂ to be 1:

0 −1 −1 −1

Multiply new row 2 by −1:

Add three times row 2 to row 3 to make b₃ to be 0:

0 0 2 5

The new matrix becomes:

Divide row 3 by 2 to make c₃ to be 1. The upper triangular matrix becomes:

The three equations take the form:

1x + 1y + 1z = −1

1y + 1z = 1

1z = 5/2

Therefore, z = 5/2.

Substitute z into equation 2:

1y + 5/2 = 1

Therefore, y = −3/2.

Substitute y and z into equation 1:

1x + (−3/2) + (5/2) = −1

1x + 1 = −1

Therefore, x = −2.

Therefore, x = −2, y = −3/2, and z = 5/2.

Check the results by substituting x, y, and z into original equations 1 and 2:

x + y + z = −1

1(−2) + (−3/2) + (5/2) = −1

−2 + 1 = −1

−1 = −1

2x − y + z = 0

2(−2) − −3/2 + 5/2 = 0

−4 + 8/2 = 0

−4 + 4 = 0

0 = 0

5.8 The Position Vector, Parametric Equations, Curves, and Surfaces

• This section provides general information about the position vector and parameterization of a line, a plane, a cylinder, a cone, a sphere, a circle, and a curve.

• A vector with its initial point at the origin of a rectangular coordinate system is called a position vector. A position vector is defined according to the location of its terminal point. A position vector can be used to locate the position of a moving object and can be written:

R(t) = x(t)i + y(t)j + z(t)k

• The position vector given by R = x i + yj + zk existing between points (x₀,y₀,z₀) and (x₁,y₁,z₁) can be written:

R = x₀i + y₀j + z₀k + t(x₁ − x₀)i + t(y₁ − y₀)j + t(z₁ − z₀)k

where t is a scalar often representing time. From this equation results the parametric equations for a line:

x = x₀ + t(x₁ − x₀)

y = y₀ + t(y₁ − y₀)

z = z₀ + t(z₁ − z₀)

These equations can also be written in the form:

• Each point along this line R = R₀ + tv where R₀ = x₀i + y₀j + z₀k can be evaluated by adding multiples of v to R₀:

• A point in a plane having coordinates (x,y) (depicted below) can be represented using the position vector R = xi + yj with its terminal point on the point (x,y) and the parametric equations x = f(t), y = g(t). After substituting for x and y the vector equation becomes:

R = F(t) = f(t)i + g(t)j

• To parameterize a plane that passes through a point R₀ = (x₀,y₀,z₀) and has two non-parallel vectors v₁ and v₂ where all points on the plane can be identified by beginning at point P₀ and moving parallel by adding multiples of v₁ and v₂ to R₀. A plane has two parameters. The parameters can be expressed as:

x = t₁, y = t₂, z = f(t₁,t₂)

where t₁ and t₂ represent the parameters.

The parametric equation can be represented by:

R(t₁,t₂) = R ₀ + t₁v ₁ + t₂v₂

The equations for the plane can be written:

x = x₀ + t₁a₁ + t₂b₁

y = x₀ + t₁a₂ + t₂b₂

z = x₀ + t₁a₃ + t₂b₃

where v₁ = a₁i + a₂j + a₃ k and v₂ = b₁i + b₂j + b₃k.

• To parameterize a surface in three dimensions such as a cylinder, first remember that a circle in two dimensions is described using x = cos t, y = sin t. If the circle is on an XY plane, then the z-dimension is zero and the equations become x = cos t, y = sin t, z = 0. If z and t are allowed to vary, then many circles along the Z-axis can exist.

Therefore, x = cos t, y = sin t, and z = z can describe many circles along z. Using position vectors:

R = (x)i + (y)j + (z)k

R = (cos t)i + (sin t)j + (z)k

• A cylinder can be described by: x² + y² = r², −1 ≤ z ≤ 1, where r is the radius and the height in the z-direction is 2 with the cylinder at origin. The cylinder can be parameterized using parameters u and v, where x = r cos u, y = r sin u, and z = v.

Parameters u and v vary in the uv plane as:

0 ≤ u ≤ 2π and −1 ≤ v ≤ 1

The parametric representation is:

R(u,v) = r cos u i + r sin u j + vk

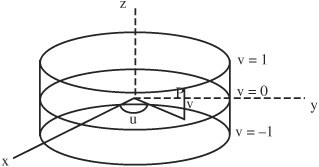
where there is a point P on the cylinder that corresponds to a (u,v) value.

• A cone given by: , 0 ≤ z ≤ h can be parameterized using parameters u and v, where:

x = u cos v, y = u sin v, and z = u.

Parameters u and v vary in the uv plane as:

0 ≤ u ≤ h and 0 ≤ v ≤ 2π

The parametric representation is:

R(u,v) = u cos v i + u sin v j + uk

• A sphere can be parameterized using spherical coordinates. In three dimensions, spherical coordinates are expressed in terms of ρ, θ, and Φ, where ρ can range from 0 to ∞, θ can range from 0 to 2 π, and Φ can range from 0 to 2π. In spherical coordinates, the ρ component is measured from the origin, the μ component measures the distance around the Z-axis, and the Φ component measures down from the Z-axis and is referred to as the polar angle. The coordinates can be defined in terms of Cartesian coordinates, x, y, and z:

The parameters of a sphere centered at origin are:

x = cos θ sin Φ

y = sin θ sin Φ

z = cos Φ

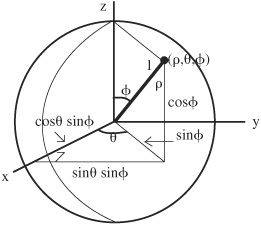
The equations can be written:

R(θ, Φ) = (cos θ sin Φ)i + (sin θ sin Φ)j + (cos Φ)k

For example, if point P is centered at (2,2,2) and the sphere has a radius of 2, then R₀ = 2i + 2j + 2k and R(θ, Φ) is multiplied by 2 to expand the radius to 2. The equation becomes:

R(θ,Φ) = 2i + 2j + 2k + (2 cosθ sinΦ)i + (2 sinθ sin Φ)j + (2 cos Φ)k = (2 + 2 cos θ sin Φ)i + (2 + 2 sin θ sin Φ)j + (2 + 2 cos Φ)k

Or

x = 2 + 2 cos θ sin Φ

y = 2 + 2 sin θ sin Φ

z = 2 + 2 cos Φ

• The circumference of a circle can be written in terms of parametric equations: x = cos t, y = sin t, 0 ≤ t ≤ 2π

The length of the curve or distance around the circle is:

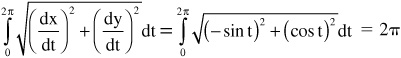
Note (−sin t)² = (sin t)²

• The length of a quarter-circle can be written in terms of parametric equations: x = cos t, y = sin t, 0 ≤ t ≤ π2

The length of the curve or distance along the arc is:

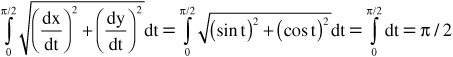
• The length of a parametric curve can also be written by a sum of incremental lines Δs, where:

(Δs)² = (Δx)² + (Δy)² and x = x(t), y = y(t)

Therefore:

In integral form:

• A unit circle can be represented implicitly, explicitly, or parametrically as follows:

implicitly: x² + y² = 1

explicitly: and

parametrically: x = cos t, y = sin t, 0 ≤ t ≤ 2π

• A curve can be represented implicitly, explicitly, or parametrically in an XY plane as: (a.) implicitly by an equation in x and y, or f(x,y); (b.) explicitly by equations for y in terms of x or x in terms of y, y = f(x) or x = g(y); or (c.) parametrically by a pair of equations for x and y in terms of a third variable or parameter, x = f(t) and y = g(t).

5.9 Motion, Velocity, and Acceleration

• This section includes motion of a particle in a line, in a plane, on a circle, along a curve, along a cycloid path, and at a constant velocity. Also included in this section is representing velocity and acceleration using the position vector and parametric form, and general expressions for velocity and acceleration.

• The motion of an object in a straight line can be described using a single variable function f(t). The motion of an object along a curve or surface in two or three dimensions can be described using all the coordinates of the curve or surface, for example x(t), y(t), and z(t). Parametric equations can be used to describe this motion.

• For uniform motion in a straight line, the speed, direction, and velocity remain constant, and the equation of the line can be written:

R(t) = R₀ + tv

where R₀ = x₀i + y₀j + z₀k, is the starting point.

The velocity is V = v₁i + v₂j + v₃k.

The speed is .

The direction of the line is the unit vector V / |V|.

Separating the x, y, and z components gives the equation of the line in terms of parameter t:

x = x₀ + t(x₁ − x₀) = x₀ + tv ₁

y = y₀ + t(y₁ − y₀) = y₀ + tv ₂

z = z₀ + t(z₁ − z₀) = z₀ + tv ₃

By rearranging:

t = (x − x₀)/v₁ = (y − y₀)/v ₂ = (z − z₀)/v ₃

which gives the equation of the line without parameter t:

• Motion of a particle in a plane can be described using two parametric equations, x = f(t) for horizontal motion along the x-coordinate and y = g(t) for vertical motion along the y-coordinate. The parameter is t for time such that at time t the particle is at point (f(t), g(t)).

• For example, the motion of a particle on a circle in a plane can be described using the parametric equations x = cos t and y = sin t, where t represents time.

A circle with radius 1 can be expressed generally as:

x² + y² = 1

which can be written using the parameters:

x = cos t and y = sin t as:

cos²t + sin²t = 1

If a particle is moving at a uniform speed, it will travel around the circle in 2 π units of time. As the particle travels around the circle, its motion can be reflected onto the X- and Y-axes such that it goes from -1 through zero to +1 in both x and y directions (for a unit circle).

If this particle is moving in a counterclockwise direction uniformly, at different t values x and y are:

at t = 0: x = 1, y = 0

at t = π/2: x = 0, y = 1

at t = π: x = −1, y = 0

at t = 3π/2: x = 0, y = −1

at t = 2π: x = 1, y = 0

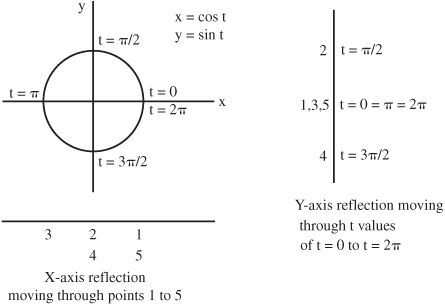
• Parametric equations can be used to describe the motion of a particle moving on a curve as well as to describe the curve itself. A curve is generally parameterized from one end to the other without retracing.

To parameterize function y = f(x), substitute the parameter t for x, x = t, y = f(t), where parameter t may or may not represent time.

• Example: The parameterization of a half-circle from 0 to π is: x = cos t, y = sin t, 0 ≤ t ≤π.

• Example: A projectile, which is defined to experience the force of gravity and no frictional forces, can be described using the x (horizontal) component, the y (vertical) component, and time t.

The initial position is x(t) = 0 and y(t) = 0, or in some cases a starting height y = h is specified. The initial velocity in the x direction is (v₀ cos Θ) and in the y direction is (v₀ sin Θ), where v₀ is the speed and Θ is the angle the projectile makes with the horizontal axis. The force (or acceleration) of gravity is in the y-direction and is given by: d²y/dt² = -g, where gravity affects the upward component of velocity so that it decreases by (-gt). The horizontal component of velocity remains constant. Therefore, the x and y components of velocity are:

v_x = dx/dt = v₀ cos θ

v_y = dy/dt = v₀ sin θ - gt

The distance along the X-axis x(t) increases with time and the height along the Y-axis y(t) increases, then decreases. The distance traveled or path of the projectile is obtained by integrating the velocity components with respect to time resulting in:

x(t) = (v₀ cos θ)t

y(t) = (v₀ sin θ)t − gt²/2

The maximum height occurs where dy/dt = 0. When

dy/dt = 0, then v₀ sin θ = gt.

Solve v₀ sin θ = gt for t:

t = (v₀ sin θ)/g

Substitute t into y(t) to obtain y_max:

y(t) at y_max = (v₀ sin θ)(v₀ sin θ)/g − g((v₀ sin θ)/g)²/2

= (v₀ sin θ)²/g − (v₀ sin θ)²/2g

= [(v₀ sin θ)²/g] (1 − 1/2) =

y_max = (v₀ sin θ)²/2g

where y_max occurs at one-half of the time the projectile is in the air.

The horizontal distance x(T) the projectile travels occurs when y = 0 and time = T, where T is the total time in the air. Therefore, at time = T:

(v₀ sin θ)T = gT²/2

The total time T is:

T = (2v₀ sin θ)/g

The total distance x(t) at t = T is:

x(T) = (v₀ cos θ)T = (v₀ cos θ)(2 v₀ sin θ)/g = (v₀² sin 2 θ)/g

Remember, 2 sin x cos x = sin 2x.

• Example: A cycloid is described by the path of a point on the perimeter of a circle as it is rolled along a line or surface. If the circle has radius r, and point P begins at the bottom at x = 0, then if it is rolled along the X-axis it makes a complete revolution at x = 2πr.

The parameter θ represents the angle through which the circle revolves. The circle rolls a distance of rθ along the X-axis and its center is at y = r and x = rθ. At θ = 0 the point is at x = 0, y = 0 and at θ = 2π, the point is at x = 2πr, y = 0. The segment between the center and the point is taken into account in measurements by subtracting (r sin θ) from x and (r cos θ) from y. Therefore:

x = rθ − r sin θ = r(θ − sin θ)

y = r − r cos θ = r(1 − cos θ)

The slope of the cycloid (dy/dx) is derived using the chain rule:

At θ = 0, the slope is infinite where the point moves straight up.

The arc length of a cycloid can be found by integrating ds from 0 to 2 π on the X-axis:

The area of a cycloid can be found by integrating y dx from 0 to 2π on the X-axis:

where y = r(1 − cos θ) and dx = r(1 − cos θ)dθ.

• A particle moving at a constant velocity can be represented using the position vector of the particle at time t, which is R(t). Then the displacement vector between positions at time t and time t + Δ t can be written generally as:

dR = R (t + Δ t) − R(t)

Therefore, V(t) ≈ Δ R/Δt.

The velocity of a moving particle in terms of the position vector R(t) at time t can be represented using:

In an XY plane the vectors R, ΔR, and V = dR/dt can be depicted as:

where ΔR is the change between two points on the curve.

• In three dimensions the velocity vector can be represented using the components of the position vector R in parametric form, where x = f(t), y = g(t), z = h(t), and:

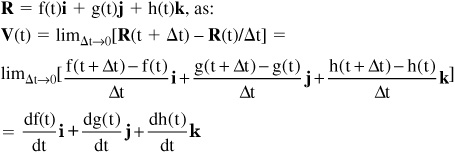
Because x = f(t), y = g(t), and z = h(t), the components of the velocity vector V in parametric form for a particle moving in three-dimensional space can be written:

• The acceleration vector A of a particle moving with a velocity V(t) at time t can be represented in general as:

For a particle moving in three-dimensional space at time t the acceleration is given by:

• If a particle is moving around a circle with radius R at a constant speed of |V|, then its acceleration vector is pointing toward the center. In this case of uniform motion the velocity vector changes in direction but not magnitude.

• Consider a position vector R at some point P on a curve in two dimensions represented with parametric equations x = f(t) and y = g(t) where t is a scalar and R is given by:

R = f(t)i + g(t)j

In three dimensions, the position vector R for point P = (x,y,z) on the curve can be written using parametric equations x = f(t), y = g(t), and z = h(t):

R = f(t)i + g(t)j + h(t)k

Because R(t) is the position vector for point P and dR/dt = V(t) is the velocity vector at point P, then the acceleration vector at P is d²R/dt² = dV/dt = A (t).

The derivative of vector R is the vector tangent to the curve in two dimensions at point P pointing in the direction of motion and represents velocity V of a moving particle at point P, providing dR/dt ≠ 0. For a moving particle, the direction of V is the direction of motion and the magnitude of V is the speed of the particle. The velocity in two dimensions is given by:

The magnitude (or length) of vector dR/dt in two dimensions is:

• Similarly, in three dimensions, the derivative of the vector R tangent to the curve at point P written is V(t):

The magnitude (or length) of vector dR/dt in three dimensions is:

The magnitude of the velocity vector also represents the speed of a particle traveling along the curve, where

Remember that velocity is a vector with magnitude and direction, while speed has only magnitude.

The unit tangent vector in three dimensions can be written:

• Note that by integrating |V|, the distance traveled of a particle along the curve and the length of the curve can be obtained:

where the curve is in a plane and a ≤ t ≤ b.

• The unit tangent vector T points in the direction of motion and depends on the shape of the curve. The curvature is sometimes referred to k as and is equal to the change in direction divided by the change in position, or the rate of turning:

k = |dT/ds| = |(dT/dt)/(ds/dt)| = |d²R/ds²|

where T and dT/dt are perpendicular to each other.

The unit normal vector N describes the direction of turning and is perpendicular to T. Therefore, the unit normal vector N coincides with dT/dt and is perpendicular to T:

The acceleration along a curve has a straight line component and a curvature component, and can be represented in several forms:

A= (d²s/dt²)T+ K(ds/dt)²N

= (d²s/dt ²)T+ K |V|²N

= (d²s/dt ²)T+ |(dT/ds)| (ds/dt)²(dT/ds)/|dT/ds|

= (d²s/dt ²)T+ (ds/dt)²(dT/ds)

= (d²s/dt ²)T+ (ds/dt)(dT/dt)

• Note, for example, that the vector 1i + 2j + 3k is constant, and the vector t²i + t²j + t²k is moving, where t is the parameter time.

• Motion in a plane in polar coordinates can be summarized using the position vector R, which points out from the origin. For circular motion such as a planet moving in a plane, the unit vector along R is:

u_r = R/r = (xi + yj)/r = cosθ i + sin θ j

where r is the radius.

The unit vector u θ is perpendicular to u_r and is around the center:

u θ = − sin θ i + cos θ j

If r varies, u_r and u θ are unaffected. However, if θ varies

u_r and u θ are:

du_r/d θ = − sin θ i + cos θj = uθ

du/d θ = − cos θ i − sin θ j = −u_r

The velocity V = dR/dt can be determined using: u_r = R/r, or R = ru_r. Using the chain rule for du_r/dt = (du_r/dθ)(dθ/dt) = (dθ/dt)uθ, then velocity becomes:

V = dR/dt = d(ru_r)/dt = u _r(dr/dt) + ruθ (dθ/dt)

where the outward speed is dr/dt and the circular speed is dθ/dt.

Using the chain rule and the equation for V, the acceleration for motion in polar coordinates is:

Using:

• In general, expressions for velocity and acceleration of a particle moving along a curve (curvilinear motion) are more complicated than for a particle moving in a straight line. The equation of the curve can be given in parametric form as x = f(t) and y = g(t), where t represents time. Velocity V is a vector tangent to the curve and has an x and a y component and is expressed in terms of magnitude (speed) and direction.

• Velocity V can be defined in terms of x and y components in two dimensions and written as follows:

The x component of velocity is v_x = dx/dt.

The y component of velocity is v_y = dy/dt.

The magnitude (speed) of V is

The direction of V is tan Ø = v_y/v_x = dy/dx.

• Acceleration is given for the x and y components in two dimensions and can be written as follows:

The x component of acceleration is a_x = dv_x/dt = d²x/dt².

The y component of acceleration is a_y = dv_y/dt = d²y/dt².

The magnitude of A is

The direction of A is tan Ø = a_y/a_x.

The acceleration vector can be expressed in a tangent component and a normal component to the curve, which are perpendicular to each other.

The tangent component of acceleration

The normal component of acceleration