Chapter 6 Partial Derivatives

6.1 Partial Derivatives: Representation and Evaluation

• This section provides the definition and notation for partial derivatives and evaluating first, second, and third partial derivatives.

• Derivatives of functions containing one variable generally represent aspects of curves, tangent lines, and rates of change. Partial derivatives involve functions of more than one variable and typically represent aspects of surfaces, tangent planes, and rates of change. In these functions each variable can change independently of the other variable(s), thus affecting change in the function as a whole.

• In a graph of y = f(x), x is the independent variable, y is the dependent variable, and points that satisfy y = f(x) fall on the curve described by y = f(x). Similarly, in a graph of z = f(x,y), x and y are the independent variables, z is the dependent variable, and points that satisfy z = f(x,y) fall on the surface described by z = f(x,y).

• Partial derivatives are represented using ∂ rather than d. Notation for single partial derivatives includes: (∂f/∂x), f_x, (∂f/∂y), f_y. Notation for second and third partial derivatives includes: (∂²f/∂x²), f_xx, (∂³f/∂x³), (∂³f/∂xxy), f_xxy.

• To differentiate or solve a partial derivative of function z = f(x,y), hold variable y constant while differentiating variable x, then hold x constant while differentiating y. The variable that is being held constant is treated as a constant during each differentiation. For each small change in variable x or variable y, the function z will change.

• For a change in x or ∆x, z changes and the definition of the partial derivative for z = f(x,y) becomes:

For a change in y or ∆y, z changes and the definition of the partial derivative for z = f(x,y) becomes:

The total partial derivative of z = f(x,y), when both x and y change, is:

• For example, if z = f(x,y) = x² + y² + x²y², then (∂f/∂x) = 2x + 2xy²and (∂f/∂y) = 2y + 2yx².

• If z = f(x,y) and x and y each depend on time t, then the total partial derivative can be written:

• If z = f(x,y) and x and y each depend on two variables u and v, such that x = x(u,v) and y = y(u,v), then the total partial derivative is written as two derivatives:

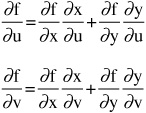
• It is possible to evaluate the partial derivatives, or slopes, (∂z/∂x) and (∂z/∂y) of function z = f(x,y) at a point. If z = x²/y², then evaluate (∂z/∂x) and (∂z/∂y) at point (3,2). To evaluate (∂z/∂x) hold y constant at 2, differentiate with respect to x, then substitute 3 into the resulting expression:

x²/y² = x²/2²

(∂z/∂x) = 2x/4

at x = 3, 6/4 = 3/2

To evaluate (∂z/∂y), hold x constant at 3, differentiate with respect to y, then substitute 2 into the resulting expression:

x²/y² = 3²/y²

(∂z/∂y) = (9)(−2y⁻²⁻¹) = −18/y³

at y = 2, −18/2³ = −18/8 = −9/4

Alternatively, (∂z/∂x) and (∂z/∂y) can be determined first, then the point (3,2) substituted into the two resulting equations:

(∂z/∂x) = 2x/y² = 6/4 = 3/2

(∂z/∂y) = −2x²/y³ = −18/8 = −9/4

• To evaluate partial derivatives with more than two variables, differentiate with respect to one variable at a time while treating the other variables as constants. For example, given a partial derivative with three variables, w = f(x,y,z) = x²y²/z, find (∂w/∂x), (∂w/∂y), and (∂w/∂z):

(∂w/∂x) = 2xy²/z

(∂w/∂y) = 2x²y/z

(∂w/∂z) = −x²y²/z²

• Second partial derivatives of a function are represented using the following notation: (∂²f/∂x²), (∂²f/∂y²), (∂²f/∂xy), (∂²f/∂yx), (∂/∂x)(∂f/∂x), (∂/∂x)(∂f/∂y), (∂/∂y)(∂f/∂y), or equivalently, f_xx, f_yy, f_xy, f_yx, (f_x)_x, (f_y)_y, (f_x)_y, where f_xx and (f_x)_x are equivalent and f_xy and f_yx are generally equivalent because the order of differentiation for most functions doesn’t matter. More specifically, if f_xy(x₁,y₁) and f_yx(x₁,y₁) are both continuous at point (x₁,y₁), then f_xy(x₁,y₁) and f_yx(x₁,y₁) are equivalent.

• For example, if z = e^x cos y, find (∂²z/∂x²), (∂²z/∂y²) and (∂²z/∂xy):

(∂²z/∂x²) = (∂/∂x) e^x cos y = e^x cos y

(∂²z/∂y²) = − (∂/∂y) e^x sin y = −e^x cos y

(∂²z/∂xy) = (∂/∂y) e^x cos y = − e^x sin y

• Notation for third derivatives includes: (∂³f/∂x³), (∂³f/∂y³), (∂³f/∂xxy), (∂³f/∂yyx), or equivalently, f_xxx, f_yyy, f_xxy, f_yyx.

6.2 The Chain Rule

• This section presents the chain rule for partial derivatives and applying it to f(g(x,y)), f(x(t),y(t)) and f(x(u,v),g(u,v)).

• The chain rule applies to partial derivatives of more complicated functions just as it does with ordinary derivatives. The chain rule provides a means to differentiate composite functions and, therefore, is used for differentiating functions of functions. In an ordinary derivative, a composite function has one function in another function such as y = f(g(x)). Similarly, in a function with more than one variable, a composite function can have more than one function substituted within a function such as, f(g(x,y)), f(x(t),y(t)), f(x(u,v),y(u,v)) and z = f(g(t),h(t)).

• Following is a summary of differentiating common forms of functions using the chain rule (it is assumed that all the derivatives are continuous):

(a.) To differentiate y = f(g(x)), calculate the ordinary derivatives, (df/dx) = (df/dg)(dg/dx).

(b.) To differentiate z = f(g(x,y)), calculate (∂f/∂x) and (∂f/∂y):

(∂f/∂x) = (df/dg)(∂g/∂x)

(∂f/∂y) = (df/dg)(∂g/∂y)

where f depends on g, and g depends on x and y.

(c.) To differentiate f(x(t),y(t)), calculate (df/dt):

df/dt = (∂f/∂x)(dx/dt) + (∂f/∂y)(dy/dt)

where a change in t influences a change in x and y and they influence a change in f.

(d.) To differentiate f(x(u,v),y(u,v)), calculate (∂f/∂u) and (∂f/∂v):

(∂f/∂u) = (∂f/∂x)(∂x/∂u) + (∂f/∂y)(∂y/∂u)

(∂f/∂v) = (∂f/∂x)(∂x/∂v) + (∂f/∂y)(∂y/∂v)

where changes in u and v influence changes in x and y and they influence a change in f.

• For example, differentiate z = (x + xy)³.

Use case (b.) above, where z = f(g(x,y)) to calculate (∂f/∂x) and (∂f/∂y), or equivalently (∂z/∂x) and (∂z/∂y):

(∂z/∂x) = (df/dg)(∂g/∂x)

(∂z/∂x) = 3(x + xy)²(∂/∂x)(x + xy) = 3(x + xy)²(1 + y)

(∂z/∂y) = (df/dg)(∂g/∂y)

(∂z/∂y) = 3(x + xy)²(∂/∂y)(x + xy) = 3x(x + xy)²

6.3 Representation on a Graph

• This section includes examples of functions having more than one variable in the form f(x,y) and their graphs and contour diagrams.

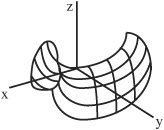
• In a graph of a one-variable function, y = f(x), (dy/dx) represents the slope of a line drawn tangent to a curve. In a graph of a two-variable function z = f(x,y), (figure below), (∂z/∂x) represents the slope of a curve sliced from the surface of f(x,y) by a plane at y = constant. Similarly, (∂z/∂y) represents the slope of a curve sliced from the surface of f(x,y) by a plane at x = constant. In the derivative (∂z/∂x), x is varied and y is held constant, and in the derivative (∂z/∂y), y is varied and x is held constant.

• For example, consider the graph of the two-variable function f(x,y) = z = x² − y²:

This graph forms a saddle-shaped surface. In this graph, there are two sets of parabolas, one set opening upward and the other set opening downward corresponding to x² values and −y² values. Each curve corresponds to f(x,y) when x is held constant and y is varied or when y is held constant and x is varied. The partial derivatives of f(x,y) are (∂z/∂x) = 2x and (∂z/∂y) = −2y. The point where the two sets of upward and downward parabolas meet is called the saddle point. The derivatives at the saddle point are zero.

A contour diagram perspective of f(x,y) = z = x² − y² can also be depicted:

• A contour diagram of curved surfaces can be depicted by connecting all of the points at the same height on the surface, such that all points satisfying f(x,y) = c at a given c lie on each contour line. The level curves form loops around the maximum point(s). As the height increases the loops get smaller. In other words, level curves, or contour lines, can be seen by slicing a surface with horizontal planes. The contour line at each height h = z is represented by f(x,y) = h. By moving in a direction parallel to an axis and crossing over the contour lines, the partial derivative equals the rate of change of the value of the function on the contour lines.

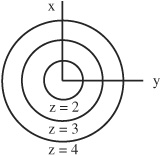
• Another example of a two-variable function is a graph of f(x,y) = z = (x² + y²)^1/2:

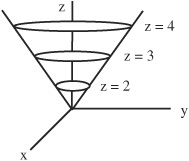
This graph has circular planes at each z value. When f(x,y) = z = (a constant), a contour map or diagram from the top-down perspective of z = (x² + y²)^1/2 can be drawn:

For example, if x and y equal 2, 3, and 4, then: f(x,y) = (x² + y²)^1/2 is equal to , and respectively. The partial derivatives of z = (x² + y²)^1/2 are obtained by varying each variable while holding the other constant:

The partial derivatives or slopes where x and y equal 2, 3, and 4 are equal to:

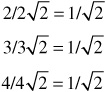
which would be expected.

6.4 Local Linearity, Linear Approximations, Quadratic Approximations, and Differentials

• This section includes linear approximations, quadratic approximations, local linearity, tangent lines and planes, the normal line equation, quadratic approximations, Taylor polynomials, and differentials.

• When calculating approximate values for complicated functions it is sometimes possible to focus in on a small region of the graph of a function, and look at that region as if it were linear. This is sometimes referred to as a point of local linearity. A tangent line can be drawn through a point in a locally linear region and the slope of the tangent line is the derivative of the function at that point. Local linearity is used in one-variable functions y = f(x) to focus in on a curve until it appears to be a straight line (which is tangent to the curve) and can be described by a linear function or linear approximation at that point.

• Similarly, in two-variable functions, local linearity can be used to focus in on a curved surface until it appears to be a flat plane (which is a tangent plane to the surface) and can be described by a linear function at that point. A function is differentiable at a point if it is locally linear and continuous at that point. The slope of a tangent plane at a point measures the change in the curve at that point. Tangents are used in representing linear approximations of functions and small changes in a function.

• When approximating values of one-variable functions, remembering the following two facts can be useful:

(a.) The slope of a line drawn tangent to a graph of a function at a point is the derivative of the function at that point. In other words, the slope of the tangent at point (a,f(a)) equals the derivative f′(a).

(b.) The equation for a tangent line passing through some point (a,f(a)) is y − f(a) = f′(a)(x − a). Equivalently, the equation for the slope of a line passing through point (x₁,y₁) is m = (y − y₁) / (x − x₁), where m is the slope of the tangent line and derivative at point (x₁,y₁).

• In the graph of function z = f(x,y), the slope of a plane drawn tangent to the curved surface through some point (a,b, f(a,b)) on the surface is the derivative of the function at point (a,b, f(a,b)). In other words, the slope of the tangent plane at point (a,b, f(a,b)) equals the partial derivative of the function in the x-direction at that point and the partial derivative of the function in the y-direction at that point. The slope of a tangent at a point measures the change in the surface at that point and is described by the equation for the plane drawn tangent to the surface.

• For a point on the surface of z = f(x,y) at x = x₁, y = y₁, z = z₁, the equation for the tangent plane (where z is the dependent variable) in that seemingly linear region is the following linear equation:

z − z₁ = (∂f/∂x)₁(x − x₁) + (∂f/∂y)₁(y − y₁)

where (∂f/∂x)₁ and (∂f/∂y)₁ represent the slopes of the tangent plane and are evaluated at point (x₁,y₁,z₁).

Similarly for F(x,y,z) = 0 with three variables, at point (x₁,y₁,z₁), the equation for the tangent plane is:

(∂F/∂x)₁(x − x₁) + (∂F/∂y)₁(y − y₁) + (∂F/∂z)₁(z − z₁) = 0

Note that a two-variable function z = f(x,y) represents a single surface and a three-variable function F(x,y,z) represents a family of level surfaces. F(x,y,z) = f(x,y) − z for one of the surfaces and z = f(x,y) is the surface at F(x,y,z) = 0.

• For example, if a surface is given by F(x,y,z) = x² + y² + z², at point (x₁,y₁,z₁) = (1,2,3) the equation for a tangent plane

(∂F/∂x)₁(x − x₁) + (∂F/∂y)₁(y − y₁) + (∂F/∂z)₁(z − z₁) = 0, is:

(2x)₁(x − x₁) + (2y)₁(y − y₁) + (2z)₁(z − z₁) = 0

At point (1,2,3) the equation becomes:

(2)(x − 1) + (4)(y − 2) + (6)(z − 3) = 0

• A useful relationship to the equation of a line is the equation for a line normal (or perpendicular) to a tangent line on the curve y = f(x) at a given point (x₁,y₁) or (a,f(a)). Because the slope is m and slopes of perpendicular lines multiply to equal −1, then the normal is −1/m. The equation for the normal line can be written:

y − y₁ = (−1/m)(x − x₁) or y − f(a) = (−1/f′(a))(x − a).

Similarly for function F(x,y,z) = 0, an equation for a line or vector normal to the tangent plane on the surface at point (x₁,y₁,z₁) is:

(∂F/∂x)₁i + (∂F/∂y)₁j + (∂F/∂z)₁k

• Quadratic approximations are similar to linear approximations but are generally more accurate. Because the equation for a tangent line passing through some point (a,f(a)), is y − f(a) = f′(a)(x − a), the linear approximation for the single variable function at that point is:

y = f(x) ≈ f(a) + f′(a)(x − a)

By using the second-order Taylor polynomial this equation form becomes a quadratic approximation for f near a:

f(x) ≈ f(a) + f′(a)(x − a) + (1/2)f′′(a)(x − a)²

• Consider a point on the surface of z = f(x,y) at x = x₁, y = y₁, z = z₁, the equation for the tangent plane is:

z − z₁ = (∂f/∂x)₁(x − x₁) + (∂f/∂y)₁(y − y₁)

where (∂f/∂x)₁ and (∂f/∂y)₁ represent the slopes of the tangent plane evaluated at point (x₁,y₁,z₁).

The linear approximation for the function at that point is:

f(x,y) ≈ f(x₁,y₁) + (∂f/∂x)₁(x − x₁) + (∂f/∂y)₁(y − y₁)

If point (x₁,y₁) is at (0,0) the approximation becomes:

f(x,y) ≈ f(0,0) + (∂f/∂x)₀(x) + (∂f/∂y)₀(y)

Using the second-order Taylor polynomial to approximate f(x,y) near (x₁,y₁) gives a quadratic approximation for f(x,y):

f(x,y) ≈ f(x₁,y₁) + (∂f/∂x)₁(x − x₁) + (∂f/∂y)₁(y − y₁)

+ (1/2)(∂²f/∂x²)₁(x − x₁)² + (∂²f/∂x∂y)₁(x − x₁)(y − y₁)

+ (1/2)(∂²f/∂y²)₁(y − y₁)²

If point (x₁,y₁) is at (0,0) the approximation becomes:

f(x,y) ≈ f(0,0) + (∂f/∂x)₀(x) + (∂f/∂y)₀(y) + (1/2)(∂²f/∂x²)₀(x)²

+ (∂²f/∂x∂y)₀(x)(y) + (1/2)(∂²f/∂y²)₀(y)²

• To solve a problem using an approximation, such as the second order Taylor series, first calculate the derivatives of the function and evaluate them at the chosen point by substituting x and y into the differentiated function, then substitute back into the series. For example, use the second-order Taylor series to evaluate the function

f(x,y) = x²y² at point (x₁,y₁) = (1,2)

f(x,y) = x²y² = (1²)(2²) = 4

The derivatives are:

(∂f/∂x) = 2xy² = 8

(∂f/∂y) = 2x²y = 4

(∂²f/∂x²) = (∂/∂x)2xy² = 2y² = 8

(∂²f/∂y²) = (d/∂y)2x²y = 2x² = 2

(∂²f/∂xy) = (d/∂y)2xy² = 4xy = 8

Substitute into the series:

f(x,y) ≈ f(x₁,y₁) + (∂f/∂x)₁(x − x₁) + (∂f/∂y)₁(y − y₁)

+ (1/2)(∂²f/∂x²)₁(x − x₁)² + (∂²f/∂x∂y)₁(x − x₁)(y − y₁)

+ (1/2)(∂²f/∂y²)₁(y − y₁)²

f(x,y) ≈ 4 + 8(x − 1) + 4(y − 2) + (1/2)8(x − 1)²

+ 8(x − 1)(y − 2) + (1/2)2(y − 2)²

= 4 + 8(x − 1) + 4(y − 2) + 4(x − 1)² + 8(x − 1)(y − 2) +(y − 2)²

• Differentials are sometimes used to assess the change in the value of a function between two points or quantities. When moving along a curve y = f(x), small movements or increments along the curve are represented by ∆x and ∆y, and small movements along a tangent line to the curve are represented by dx and dy. The respective differentials are:

∆y ≈ (dy/dx)∆x and dy = (dy/dx)dx

Similarly, moving along a curved surface z = f(x,y), where z is the dependent variable, small movements or increments along the surface are represented by ∆x, ∆y, and ∆z, and small movements along a tangent plane to the surface are represented by dx, dy, and dz. The total differential reflected on the tangent plane is given using the tangent plane equation:

z − z1 = (∂f/∂x)₁(x − x1) + (∂f/∂y)₁(y − y₁)

which becomes:

dz = (∂z/∂x)₁dx + (∂z/∂y)₁dy

• For example, the differential of z = x²y² is given by:

dz = 2xy² dx + 2x²y dy

• If the increments dx, dy, and dz are small enough and, therefore, the distances between (x − x₁), (y − y₁), and (z − z₁) are small, then the linear approximation to the function z = f(x,y) has a small error and is therefore a valid approximation at some point. For a curved surface described by z = f(x,y), the linear approximation to the surface near point (x₁,y₁) is given by:

z = f(x,y) ≈ f(x₁,y₁) + (∂f/∂x)₁(x − x₁) + (∂f/∂y)₁(y − y₁)

Therefore, ∆z ≈ (∂f/∂x)∆x + (∂f/∂y)∆y.

6.5 Directional Derivative and Gradient

• This section includes the directional derivative and the gradient and their relationship to each other, definitions and notation for the directional derivative and the gradient, magnitude of a gradient vector, and the dot product relationship between the gradient and the directional derivative.

• A surface can have slopes in all directions, not just along the axes. The directional derivative represents the slope of a tangent line to a surface at a point in any chosen direction. As discussed in the previous paragraphs, (∂z/∂x) and (∂z/∂y) represent the rate of change of surface z = f(x,y) in the directions of the X-axis and Y-axis, respectively.

• A small change ds along a surface in a specified direction can be represented using a unit vector a, that is pointed in the designated direction and has components a₁ and a₂ that are each pointed in x and y directions.

Therefore, a = a₁i + a₂j and dz/ds can be written:

dz/ds = (∂f/∂x)a₁ + (∂f/∂y)a₂

which is the directional derivative of df/ds in the direction of the unit vector a.

• Notation for the directional derivative of the unit vectors a, b, and u, include df/ds, dz/ds, D_af, f_a(x₁,y₁), D_bf, f_b(x₁,y₁), D_uf and f_u(x₁,y₁).

• For example, using the notation f_a(x₁,y₁), the directional derivative for a is written:

f_a(x₁,y₁) = f_x(x₁,y₁)a₁ + f_y(x₁,y₁)a₂

• The directional derivative can be expressed using the difference quotient in a direction of vector a at point (x₁,y₁):

This equation describes a small change represented by h in f(x,y) between points (x₁,y₁) and (x₁+ha₁, y₁+ha₂) in the direction of a. Remember from Chapter 2 that the average rate of change is represented by the quotient and the instantaneous rate of change is represented by the limit of the quotient as h approaches zero.

• The equation for the directional derivative can be thought of in terms of a linear approximation to a surface near a point. An incremental change in z = f(x,y) is:

∆z ≈ (∂f/∂x)∆x + (∂f/∂y)∆y

where ∆x is the change in the a₁ direction given by ha₁, or equivalently ∆sa₁, and ∆y is the change in the a₂ direction given by ha₂, or equivalently ∆sa₂. Therefore, the linearized curve in the direction of a can be written:

∆z ≈ (∂f/∂x)a₁∆s + (∂f/∂y)a₂∆s

Rearranging:

∆z/∆s ≈ (∂f/∂x)a₁ + (∂f/∂y)a₂

Taking the limit as ∆s approaches zero results in:

dz/ds = (∂f/∂x)a₁ + (∂f/∂y)a ₂

which is the directional derivative of dz/ds.

Note: The equation for the directional derivative is an important equation to remember.

• The gradient is a vector quantity and describes the change in a function near a point. The gradient characterizes maximum increase and indicates the direction of maximum increase of f at a selected point. The gradient of f(x,y) is written:

grad f = (∂f/∂x)i + (∂f/∂y)j

For f(x,y,z) the gradient becomes:

grad f = (∂f/∂x)i + (∂f/∂y)j + (∂f/∂z)k

Note: The equation for the gradient is an important equation to remember.

The components of the vector (grad f) are:

(∂f/∂x)i, (∂f/∂y)j, and (∂f/∂z)k

• The gradient of a scalar function f(x,y,z), is a vector function. The gradient of f(x,y,z) at point P, where f is differentiable, indicates the direction of maximum increase providing (grad f ≠ 0).

• The gradient vector of z = f(x,y) at (x₁,y₁) is pointed in the direction of where the greatest change in f(x,y) occurs, (providing f is differentiable at (x1,y1)). The gradient vector lies on the surface of f(x,y) in the x-y plane and points in the direction that the surface is rising or increasing the greatest amount. In a contour diagram, the gradient vector points perpendicular to the contour lines in the direction of greatest increase in height, which is where the contour lines are closest together.

• The magnitude or length of the gradient vector given by | grad f | is equal to the rate of change in the direction that it is pointing (providing f is differentiable). On a contour diagram the gradient vector has a magnitude corresponding to the degree (or grade) of the slope. Because the slope is greater when the contour lines are closer together, the magnitude of the gradient vector is greater for contours that are closer together. Conversely, because the slope is less when the contour lines are more separated, the magnitude of the gradient vector is smaller for contours that are farther apart.

• Notation for grad is ∇, which is also called“del”and is a vector that is an operator because its components are operations rather than numbers.

∇ = (∂/∂x)i + (∂/∂y)j + (∂/∂z)k

Therefore, grad f = ∇f = (∂f/∂x)i + (∂f/∂y)j + (∂f/∂z)k.

Notation, for the gradient of f includes:

grad f(x,y,z) = (∂f/∂x)i + (∂f/∂y)j + (∂f/∂z)k

grad f(x₁,y₁,z₁) = f_x(x₁,y₁,z₁)i + f_y(x₁,y₁,z₁)j + f_z(x₁,y₁,z₁)k

• Example: If f = 3x + 2yz − 6y², what is grad f?

grad f = ∇f = (3)i + (2z − 12y)j + (2y)k

• If the directional derivative of f(x,y) at (x₁,y₁) is zero in all directions, then the gradient vector is a zero vector.

• The gradient can be evaluated outside the context of a coordinate system by remembering that the direction of (grad f) is where the directional derivative df/ds is greatest and the length |grad f| is the greatest slope.

• The dot product of a gradient vector at point (x₁,y₁) with the unit vector a is equal to the directional derivative f_a(x₁,y₁) pointing in the direction of a at point (x₁,y₁). Therefore:

grad f(x₁,y₁) • a = f_a(x₁,y₁) = ((∂f/∂x)i + (∂f/∂y)j) • (a₁i + a₂j)

= (∂f/∂x)a₁ + (∂f/∂y)a₂

= |grad f(x₁,y₁)| cos θ = | ((∂f/∂x)i + (∂f/∂y)j) | cos θ

where a = a₁i + a₂j.

Remember the dot product of two vectors is:

A • B = | A || B | cos θ

where | A | and | B | represent the magnitudes of vectors A and B and θ is the angle between vectors A and B.

• The directional derivative f_a(x₁,y₁) will have its greatest value when its unit vector a is pointing in the same direction as the gradient of f(x₁,y₁). Therefore, the directional derivative will be greatest when the angle θ between it and the gradient is zero.

In other words, the slope of the directional derivative f_a(x₁,y₁) is greatest when a is parallel to (grad f). Therefore, writing the directional derivative in terms of the dot product gives:

f_a(x₁,y₁) = ((∂f/∂x)i + (∂f/∂y)j) • a

= | ((∂f/∂x)i + (∂f/∂y)j)||a| cos θ= |((∂f/∂x)i + (∂f/∂y)j)| cos θ

θ will be zero when f_a(x₁,y₁) has its greatest value:

f_a(x₁,y₁) = |((∂f/∂x)i + (∂f/∂y)j)| cos θ = |((∂f/∂x)i + (∂f/∂y)j)|

Therefore, f_a(x₁,y₁) = | grad f(x₁,y₁) | when they both have the same magnitude (at the maximum value) and a is pointing in the same direction as grad f(x₁,y₁).

The greatest slope is equivalent to the magnitude and occurs when (grad f) • a = |grad f|.

• The directional derivative will have a zero rate of change when the angle θ between it and the gradient is 90 degrees, where θ = π/2 and a is pointing perpendicular to (grad f). Therefore, when θ = π/2:

grad f(x₁,y₁) • a = | grad f(x₁,y₁)|cos π/2

= |((∂f/∂x)i + (∂f/∂y)j)|cos π/2 = 0

• The directional derivative will have its most negative rate when the angle θ between it and the gradient is 180 degrees, where θ = π and a is pointing in the opposite direction of (grad f). Therefore, when θ = π:

grad f(x₁,y₁) • a = | grad f(x₁,y₁) | cos π

= |((∂f/∂x)i + (∂f/∂y)j)| cos π = − | grad f(x₁,y₁)|

• When f(x,y) is a linear function, the gradient is a constant vector because the terms ∂/∂x and ∂/∂y will yield constants. Conversely, when f(x,y) is a non-linear function, the gradient is a non-constant or varying vector.

6.6 Minima, Maxima, and Optimization

• This section introduces minima and maxima problems for functions having more than one variable and is an extension of Section 2.27 for one-variable functions. This section includes the first and second derivatives for surfaces, finding minima and maxima points, and the concept of constrained optimization.

• Evaluating whether a function has minimum and maximum points is common when experiments or evaluations are conducted in science, business, engineering, etc. Data is gathered, relationships are developed, and graphs are constructed in order to assist in the understanding of the data and to predict future patterns and events. Information depicted in the graphs such as where the graph is rising or falling, convex or concave, and where the high and low points are (which correspond to the maximum and minimum values) are all crucial to the evaluation of the data.

• The graph of a function has a minimum or maximum point where the slope is zero and, therefore, the derivative is zero. In the region of a graph of a function where the graph is horizontal, the first derivative of the function is equal to zero. A point where the graph of a function is horizontal may represent a minimum or maximum point. A minimum or maximum on a graph may be the minimum or maximum of the function, global extrema, or there may be many“local”minimum or maximum points called local extrema. There are also examples where a graph will not have a minimum or maximum, such as if the graph is a straight horizontal or vertical line or plane.

• For a function with a single variable y = f(x), a minimum or maximum point occurs where df/dx = 0. For a function with more than one variable z = f(x,y), a minimum or maximum point occurs where (∂f/∂x) = 0, (∂f/∂y) = 0, the appropriate partial derivatives of the independent variables. Where the graph of a multivariable function is level, the partial derivatives are all zero.

• In a one-variable function (discussed in Section 2.27), the sign of the derivative of the function indicates the slope of the graph of the function at the point where the derivative is taken. For y = f(x), f′(x) < 0 where the graph of f is decreasing, f′(x) > 0 where the graph of f is increasing, and f′(x) = 0 where the graph of f is horizontal. The sign of f′(x) changes from positive to negative or negative to positive as the maximum or minimum is crossed. There are functions that don’t possess minimum or maximum points, such as where an inflection point exists.

• In the one-variable case, taking the second derivative of a function is used to determined whether the graph of that function is at a minimum and, therefore, concave up, or at a maximum and, therefore, concave down. For f(x) at point P, where f′(P) exists and f′(P) = 0, then if f′′(P) > 0, the graph of the function is concave up at P and has a minimum at P. Conversely, if f′(P) = 0 and if f′′(P) < 0, the graph of the function is concave down at P and has a maximum at P. See Section 2.27 for a complete discussion of minima and maxima for single variable functions.

• For a function z = f(x,y) with two independent variables, a maximum on the graph of that function exists at a point (x₁,y₁) if f(x,y) ≤ f(x₁,y₁) for all values of x and y near (x₁,y₁). Conversely, a minimum exists where f(x,y) ≥ f(x₁,y₁) for all values of x and y near (x₁,y₁). To summarize, global and local extrema occur for f(x,y) according to the following:

Global maximum exists at (x₁,y₁) if f(x,y) ≤ f(x₁,y₁) for all (x,y);

Global minimum exists at (x₁,y₁) if f(x,y) ≥ f(x₁,y₁) for all (x,y);

Local maximum exists at (x₁,y₁) if f(x,y) ≤ f(x₁,y₁) for (x,y) near (x₁,y₁); and

Local minimum exists at (x₁,y₁) if f(x,y) ≥ f(x₁,y₁) for (x,y) near (x₁,y₁).

• The following properties of f(x,y) can be compared with f(x):

(a.) The extrema points occur at (∂f/∂x) = 0 and (∂f/∂y) = 0 rather than df/dx = 0.

(b.) A tangent plane exists where derivatives are zero rather than a tangent line.

(c.) A boundary curve encompasses the region of interest rather than two endpoints.

(d.) Partial derivatives (∂²f/∂x²), (∂²f/∂xy), and (∂²f/∂y²) are used to determine whether the extrema is a minimum or maximum or a saddle point, rather than using ordinary derivatives d²f/dx², d²f/dxy, and d²f/dy².

• In a closed and bounded region, a continuous function f(x,y) will generally have a global minimum and a global maximum. A closed region contains a boundary and if a region is bounded, then it does not go to infinity in any direction. If a region is not closed and bounded or f(x,y) is not a continuous function, there may or may not be a global minimum or global maximum present.

• Local extrema generally occur at critical points where the derivative is zero or undefined. For a minimum or maximum to exist for z = f(x,y) at (x₁,y₁), it is necessary that (∂f/∂x) = 0 and (∂f/∂y) = 0 (for three variables, include (∂f/∂z) = 0). Note that this condition is not sufficient to assure that a minimum or maximum exists.

• If f(x₁,y₁) is a minimum or maximum point, then the gradient vector at that point will be zero. The slope in every direction will be zero. Therefore, (grad f(x₁,y₁)) equals zero or is undefined at a minimum or maximum point. Critical points occur where the gradient is either zero or undefined.

• To determine if maxima or minima exist for z = f(x,y) the following steps can be taken:

(a.) Calculate (∂f/∂x), (∂f/∂y), (∂²f/∂x²), (∂²f/∂y²), and (∂²f/∂xy).

(b.) Solve (∂f/∂x) = 0 and (∂f/∂y) = 0 simultaneously for the critical values of x and y that satisfy these equations. (In this case there are two equations and two unknowns.)

(c.) Determine the value given by:

D = (∂²f/∂x²)(∂²f/∂y²) − (∂²f/∂xy)² at point (x₁,y₁).

(d.) Evaluate the following criteria at point (x₁,y₁) for z = f(x,y):

Minimum if D > 0 and (∂²f/∂x²) > 0 or (∂²f/∂y²) > 0;

Maximum if D > 0 and (∂²f/∂x²) < 0 or (∂²f/∂y²) < 0;

No minimum or maximum if D < 0 (saddle point);

This test fails if D = 0.

• Example: Does a minimum or maximum exist for z = x² + y²?

Calculate:

(∂f/∂x) = 2x

(∂f/∂y) = 2y

(∂²f/∂x²) = 2

(∂²f/∂y²) = 2

(∂²f/∂xy) = 0

Solve:

2x = 0 → x = 0

2y = 0 → y = 0

Determine:

D = (∂²f/∂x²)(∂²f/∂y²) − (∂²f/∂xy)² = (2)(2) − 0 = 4

Because 4 = D > 0 and (∂²f/∂x²) = 2 > 0, then a minimum exists at (x = 0, y = 0, z = 0).

• Example: Does a minimum or maximum exist for

z = x² − y²?

Calculate:

(∂f/∂x) = 2x

(∂f/∂y) = −2y

(∂²f/∂x²) = 2

(∂²f/∂y²) = −2

(∂²f/∂xy) = 0

Solve:

2x = 0 → x = 0

2y = 0 → y = 0

Determine:

D = (∂²f/∂x²)(∂²f/∂y²) − (∂²f/∂xy)² = −4 < 0

Because −4 = D < 0, then no minimum or maximum exists and this is a saddle point that corresponds to an inflection point for a single variable function. At a saddle point there are values of x and y such that f(x₁,y₁) > f(x,y) and also f(x₁,y₁) < f(x,y).

• The graph of a quadratic function f(x,y) = ax² + bxy + cy² can be analyzed for minima, maxima, and saddle points by using a technique that involves completing the square of ax² + bxy + cy² and results in the following being true at point (0,0):

Minimum exists at (0,0) when a > 0 and (4ac − b²) > 0;

Maximum exists at (0,0) when a < 0 and (4ac − b²) > 0;

A saddle point exists at (0,0) when (4ac − b²) < 0.

Note that for a point at (x₁,y₁) rather than (0,0), the quadratic function will have the form:

f(x,y) = a(x − x₁)² + b(x − x₁)(y − y₁) + c(y − y₁)² + d

and the graph will have the same shape as it would at point (0,0) except it will be located at point (x₁,y₁) and shifted the value of d in the vertical direction.

Constrained Optimization

• The following paragraphs provide a brief introduction to constrained optimization. For a complete discussion of constrained optimization, a more advanced mathematical analysis book should be consulted.

• When a system or graph is evaluated using optimization techniques (minimization and maximization), there is often more than one function involved in describing the system or graph. When minimizing or maximizing, it can be beneficial to hold one function constant or constrained while considering the other function. Finding local minima or maxima for the two functions f(x,y) and g(x,y) involves finding the partial derivatives (∂f/∂x), (∂f/∂y), (∂g/∂x), and (∂g/∂y). When g(x,y) is constrained or held constant such that g(x,y) = C, the extrema of f(x,y) has the following properties:

(a.) f(x,y) has a global minimum at some point (x₁,y₁) when f(x,y) ≥ f(x₁,y₁) for all values of x and y.

(b.) f(x,y) has a global maximum at some point (x₁,y₁) when f(x,y) ≤ f(x₁,y₁) for all values of x and y.

(c.) f(x,y) has a local minimum at some point (x₁,y₁) when f(x,y) ≥ f(x₁,y₁) for values of x and y near (x₁,y₁).

(d.) f(x,y) has a local maximum at some point (x₁,y₁) when f(x,y) ≤ f(x₁,y₁) for values of x and y near (x₁,y₁).

• To evaluate a constrained optimization problem, the local extrema of one function f(x,y) can be found while the other function g(x,y) is constrained such that g(x,y) = C. The extrema found using such a constraint may not be the same extrema present if no constraint was present. Also, determining whether the extrema is a minimum or maximum can be observed by graphing the functions.

• Consider the graph of two functions f(x,y) and g(x,y) that are related to each other by a scalar quantity called λ (lambda), which is known as the Lagrange multiplier. When f(x,y) is at a minimum or maximum point with the constraint g(x,y) = C, the gradient of f is parallel to the gradient of g. At a minimum or maximum point, (grad f) and (grad g) are related to each other by the multiplier λ, such that for g = C, the following is true:

grad f = λ grad g

(∂f/∂x) = λ(∂g/∂x)

(∂f/∂y) = λ(∂g/∂y)

• To find extrema for f, the three equations g = C, (∂f/∂x) = λ(∂g/∂x), and (∂f/∂y) = λ(∂g/∂y) can be solved for the three unknown values, x, y, and λ.

• For a function f(x,y,z) with two constraints, g(x,y,z) = C₁ and h(x,y,z) = C₂, there are two multipliers λ₁ and λ₂. To minimize or maximize f, the following equations can be solved for x, y, z, λ₁, and λ₁:

(∂f/∂x) = λ₁(∂g/∂x) + λ₂(∂h/∂x)

(∂f/∂y) = λ₁(∂g/∂y) + λ₂(∂h/∂y)

(∂f/∂z) = λ₁(∂g/∂z) + λ₂(∂h/∂z)

g = C₁ and h = C₂

• Optimization problems are sometimes written in terms of a Lagrangian function L: L(x,y,λ) = f(x,y) − λ(g(x,y) − C).

The solution for a constrained optimization problem involving L is found using:

(∂L/∂x) = (∂f/∂x) − λ(∂g/∂x) = 0

(∂L/∂y) = (∂f/∂y) − λ(∂g/∂y) = 0

(∂L/∂λ) = C − g = 0

At a critical point (x₁,y₁,λ₁) of f(x,y) where g(x,y) = C and λ₁ is the corresponding Lagrange multiplier: grad L(x₁,y₁,λ₁) = 0.

• There are constraints involving inequalities such as g ≤ C or g ≥ C, where the multiplier λ must satisfy the same inequalities, such that λ ≤ C or λ ≥ C. For example, if the constraint is g ≤ C, then the extrema can be inside or on the constraint curve.