1.1.1. Fundamental principle of dynamics

There exists at least one reference frame g, called Galilean, and a way to measure time (called the preferred time scale), such as, at any given time and whatever the considered physical set , the dynamic torsor of the set motion through the frame g is equal to torsor representing the efforts exerted on by all in the universe, that are outside of it, which we call . So that we state:

1.1.2. Choosing a frame

The application of this principle thus suggests the existence of at least one frame considered to be preferred, serving to locate a body during its motion, and of at least one preferred time scale that allows us to follow its evolution. But there are in fact an infinity of frames and ways to measure time; it is therefore important to select a frame that is suitable to the motion in question, to be able to apply this principle.

We consider that the choice of a reference frame must depend on the motion that is studied and from where we wish to observe it. The Galilean frame is the primary one in which the fundamental principle of dynamics applies. It must respect three conditions during the study of the motion of a mechanical set . First of all, it must be in a fixed position and orientation in the space where the motion is taking place; secondly, any moving body in this space, if it doesn’t experience any exterior effect, moves uniformly on a straight line; thirdly, any body which, by its presence and the action it is likely to exert onto the motion of , also obeys the condition that its own motion may be observed and studied in the same frame (the Galilean frame is then said to be closed).

In fact, if such bodies are subject to actions from bodies outside of the frame and which are not accounted for, they could have unidentified secondary effects on the body in motion; this explains the importance of the Galilean frame being closed.

The fundamental principle of dynamics only references, concerning the motion of in g, the dynamic torsor that is defined from the acceleration of any particle of M of , considered as vector density per unit of mass. This observation leads to considerations that will not be expanded upon here, that show, when a preferred frame is identified as well as a preferred time scale to create a Galilean frame, that any other frame will be considered Galilean as well if it includes:

• – a timescale defined from the preferred scale that has already been identified and using an arbitrary transformation of the following type: t = t₀ + kτ (see section 1.1.2);
• – and a reference frame presenting a straight-line uniform motion in relation to the preferred frame previously identified, with a zero rotation rate between the two frames (see section 1.3.5).

First of all, if we are studying the observable motion of objects from our terrestrial environment, the first preferred Galilean g which naturally stands out as offering the most global view. Its origin is the center of inertia G_E of the center of the solar system with three base vectors pointed towards the stars, E₁, E₂, E₃ apparently fixed.

As the Sun represents more than 99% of the mass of the solar system, its center of inertia G_H is close to that of the solar system. We therefore introduce a direct orthonormed system where

as our preferred Galilean frame.

However, most solid motion that we study takes place within the Earth’s environment under the effect of actions that emanate from it; it therefore seems reasonable to use a frame of work that would be more accessible, joined to the Earth, with its center of inertia as origin and to which three orthogonal and normed vectors – that could either be collinear to those of the Solar system or fixed in relation to our planet (along the North-South axis and two other directions orthogonal between one another in the equatorial plane) – would be attached.

Even if we admit that the North-South axis of rotation of our planet maintains a constant direction as it travels along its ellipse around the Sun, this last frame, called the terrestrial frame T, is not in translation with the solar frame; it cannot serve as a frame for the application of the fundamental principle. And if we apply the corresponding equations to it, we are led to introduce corrective terms due to the relative motion of the frame T in relation to the solar frame. These terms are often negligible, which justifies the use of this frame when the characteristics of motion allow it.

As for considerations about the time scale, they rely on the assumed uniform nature of the Earth’s rotation around its axis and reinforce the benefits of using the terrestrial frame T as our Galilean reference frame and applying the fundamental principle of dynamics. This frame is then described as pseudo Galilean.

1.1.3. Preferred time scale

With preferred time scale t, according to the fundamental principle, we have

With a different preferred time scale τ, we would have

and the velocity and acceleration vectors would be written

With this new time scale, the reduction elements at O_S of kinetic and dynamic torsors have the following expressions:

If we examine the relation between velocities on the one hand and accelerations on the other within the two scales, we obtain

Subsequently

and lastly

The fundamental principle of dynamics is then formulated as follows with the new time scale:

When the relation between the two time scales is linear: τ = at + b, τ″ is null and τ′ = a; the fundamental principle is then written:

For this new time scale to be used as preferred, the following statement: a = 1 must be verified so that τ = t + b. We can then write

The origin of this preferred time scale is arbitrary, since in reality it is a matter of observing a motion during a corresponding time interval, and from a suitable point of origin.

1.2.1. First secondary principle of the separation of effects

In solid mechanics, the efforts exerted by over are remote actions gravitational or electromagnetic in nature, and contact actions.

Contact actions can be fluid (liquid or gas), solid (non-deformable) or elastic types.

We generally group into a first torsor written the given or calculable terms of due to gravitational or electromagnetic actions and assessable contact actions.

We group into a second torsor written the unknown link terms of .

The first secondary principle allows us to therefore state

If we now consider a partition of set such as

and an exterior partition of such as

we can express the two following secondary principles.

1.2.2. Second secondary principle of effort generators

For a considered law 'ℓ', whether it is gravitational, electromagnetic or of contact, we can state

This principle can extend to a finite number of disjoint sets that constitute a partition of .

1.2.3. Third secondary principle of effort receivers

This principle can also extend to a finite number of disjoint sets that constitute a partition of .

Considering these principles, the fundamental principle of dynamics takes on the more general following form

where subscript symbols α′ and i′ refer to the only partitions of and that are in contact.

1.3.1. Presentation of the context

We first examine the mobility of the frame λ in comparison to another frame μ on which we make no hypotheses for the time being.

The relative movement of the two frames is known, that is:

• – the situation bipoint of O_λ relative to of which the first and second derivatives according to time in this last frame are: and ;
• – the rotation rate vector λ compared to of which the first derivative according to time in the two frames is .

1.3.2. Combination of accelerations

We also know the motion of the mechanical set within frame λ and we wish to observe its motion from frame μ. The formula for combination of accelerations applied to a particle M of

introduces the Coriolis acceleration of M in the motion of λ relative to μ

and the drive acceleration of M in this same motion

where vectors and are independent of M.

1.3.3. Coriolis inertial torsor

To the material particle corresponding to point M, given its elementary mass dm(M), we attribute the vector

We therefore attach to the kinetics of the material set , in the motion of the frame λ in relation to μ, the following torsor, called the Coriolis inertial torsor and written , of which the reduction elements at a given point Q are

1.3.4. Drive inertial torsor

To the material particle corresponding to point M, given its elementary mass dm(M), we also assign the vector

We also attach to the kinetics of the material set , in the motion of the frame λ relative to μ, the torsor known as drive inertial torsor and marked , of which the reduction elements at a given point Q are

1.3.5. Relation between the dynamic torsors in the two frames

In each one of the frames λ and μ, the dynamic torsor is marked

According to combination of accelerations, the reduction elements of the dynamic torsor of the motion relative to frame μ expand as follows

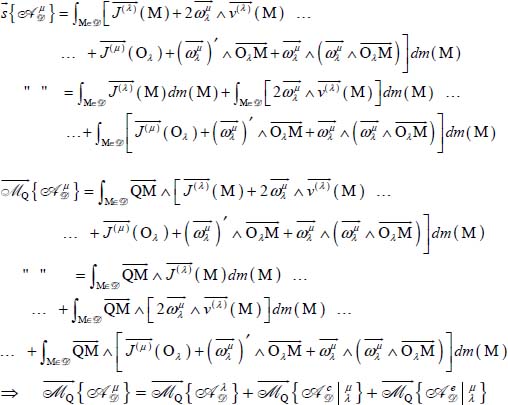
Thus the torsor equality that expresses the relation between the dynamic torsors of the motion of in both frames is

which is valid whatever the set or the frames λ and μ.

1.3.6. Applying the fundamental principle

We consider here that the frame μ is the preferred Galilean frame g. From the previous results, we can therefore state that

and that the fundamental principle of dynamics is expressed as follows

This leads to the torsor expression of the motion of the set relative to the given frame λ

Analyzing this relation shows that the relative situation of the frame λ in relation to the considered Galilean frame g is not indifferent because, in the relation above, the outside of is considered from a Galilean frame and not from λ.

In the case where the sources of the efforts acting upon , and emanating from , coincide with the ones present in λ, and that the corrections introduced by the Coriolis and drive terms are sensibly negligible compared to the efforts, the frame λ is considered as pseudo-Galilean and the fundamental principle can be applied.

We therefore see that it is possible to express the torsor equation of the motion of a mechanical set relative to a given frame λ provided the Coriolis and inertial drive torsors are incorporated to the external efforts torsor.

However, when the frame λ moves with a uniform translation on even straight line relative to g, the rate of rotation is null and the Coriolis and drive inertial torsors will be also. The frame λ is then Galilean.

1.4.1. Coriolis inertial torsor

The resultant of the Coriolis inertial torsor is then expressed as follows

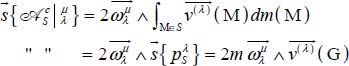
Its moment at O_s is expressed

The last integral above involves the triple vectorial product which can be expressed as follows

Subsequently

According to the definition of the inertia operator I_Os (S), we can verify that

, which is the sum of the diagonal terms of the matrix representing the operator,

hence the expression of the moment at O_s of the Coriolis inertial torsor of the non-deformable solid (S) in the motion of λ relative to μ

The moment at G of this torsor is equal to

1.4.2. Drive inertial torsor

The resultant of the drive inertial torsor is written

and its moment at Q has the following development

with

According to the easily verifiable property of the vectorial product: , the last integral above is marked

hence the moment at Q of the inertial drive torsor of the non-deformable solid (S) in the motion of λ relative to μ

and at its center of inertia G