k-Neighbors classification

In its simplest version, the k-NN algorithm only considers exactly one nearest neighbor, which is the closest training data point to the point we want to make a prediction for. The prediction is then simply the known output for this training point. Figure 2-4 illustrates this for the case of classification on the forge dataset:

In[9]:

mglearn.plots.plot_knn_classification(n_neighbors=1)

Figure 2-4. Predictions made by the one-nearest-neighbor model on the forge dataset

Here, we added three new data points, shown as stars. For each of them, we marked the closest point in the training set. The prediction of the one-nearest-neighbor algorithm is the label of that point (shown by the color of the cross).

Instead of considering only the closest neighbor, we can also consider an arbitrary number, k, of neighbors. This is where the name of the k-nearest neighbors algorithm comes from. When considering more than one neighbor, we use voting to assign a label. This means that for each test point, we count how many neighbors belong to class 0 and how many neighbors belong to class 1. We then assign the class that is more frequent: in other words, the majority class among the k-nearest neighbors. The following example (Figure 2-5) uses the three closest neighbors:

In[10]:

mglearn.plots.plot_knn_classification(n_neighbors=3)

Figure 2-5. Predictions made by the three-nearest-neighbors model on the forge dataset

Again, the prediction is shown as the color of the cross. You can see that the prediction for the new data point at the top left is not the same as the prediction when we used only one neighbor.

While this illustration is for a binary classification problem, this method can be applied to datasets with any number of classes. For more classes, we count how many neighbors belong to each class and again predict the most common class.

Now let’s look at how we can apply the k-nearest neighbors algorithm using scikit-learn. First, we split our data into a training and a test set so we can evaluate generalization performance, as discussed in Chapter 1:

In[11]:

from sklearn.model_selection import train_test_split
X, y = mglearn.datasets.make_forge()

X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)

Next, we import and instantiate the class. This is when we can set parameters, like the number of neighbors to use. Here, we set it to 3:

In[12]:

from sklearn.neighbors import KNeighborsClassifier
clf = KNeighborsClassifier(n_neighbors=3)

Now, we fit the classifier using the training set. For KNeighborsClassifier this means storing the dataset, so we can compute neighbors during prediction:

In[13]:

clf.fit(X_train, y_train)

To make predictions on the test data, we call the predict method. For each data point in the test set, this computes its nearest neighbors in the training set and finds the most common class among these:

In[14]:

print("Test set predictions:", clf.predict(X_test))

Out[14]:

Test set predictions: [1 0 1 0 1 0 0]

To evaluate how well our model generalizes, we can call the score method with the test data together with the test labels:

In[15]:

print("Test set accuracy: {:.2f}".format(clf.score(X_test, y_test)))

Out[15]:

Test set accuracy: 0.86

We see that our model is about 86% accurate, meaning the model predicted the class correctly for 86% of the samples in the test dataset.

Analyzing KNeighborsClassifier

For two-dimensional datasets, we can also illustrate the prediction for all possible test points in the xy-plane. We color the plane according to the class that would be assigned to a point in this region. This lets us view the decision boundary, which is the divide between where the algorithm assigns class 0 versus where it assigns class 1. The following code produces the visualizations of the decision boundaries for one, three, and nine neighbors shown in Figure 2-6:

In[16]:

fig, axes = plt.subplots(1, 3, figsize=(10, 3))

for n_neighbors, ax in zip([1, 3, 9], axes):
    # the fit method returns the object self, so we can instantiate
    # and fit in one line
    clf = KNeighborsClassifier(n_neighbors=n_neighbors).fit(X, y)
    mglearn.plots.plot_2d_separator(clf, X, fill=True, eps=0.5, ax=ax, alpha=.4)
    mglearn.discrete_scatter(X[:, 0], X[:, 1], y, ax=ax)
    ax.set_title("{} neighbor(s)".format(n_neighbors))
    ax.set_xlabel("feature 0")
    ax.set_ylabel("feature 1")
axes[0].legend(loc=3)

Figure 2-6. Decision boundaries created by the nearest neighbors model for different values of n_neighbors

As you can see on the left in the figure, using a single neighbor results in a decision boundary that follows the training data closely. Considering more and more neighbors leads to a smoother decision boundary. A smoother boundary corresponds to a simpler model. In other words, using few neighbors corresponds to high model complexity (as shown on the right side of Figure 2-1), and using many neighbors corresponds to low model complexity (as shown on the left side of Figure 2-1). If you consider the extreme case where the number of neighbors is the number of all data points in the training set, each test point would have exactly the same neighbors (all training points) and all predictions would be the same: the class that is most frequent in the training set.

Let’s investigate whether we can confirm the connection between model complexity and generalization that we discussed earlier. We will do this on the real-world Breast Cancer dataset. We begin by splitting the dataset into a training and a test set. Then we evaluate training and test set performance with different numbers of neighbors. The results are shown in Figure 2-7:

In[17]:

from sklearn.datasets import load_breast_cancer

cancer = load_breast_cancer()
X_train, X_test, y_train, y_test = train_test_split(
    cancer.data, cancer.target, stratify=cancer.target, random_state=66)

training_accuracy = []
test_accuracy = []
# try n_neighbors from 1 to 10
neighbors_settings = range(1, 11)

for n_neighbors in neighbors_settings:
    # build the model
    clf = KNeighborsClassifier(n_neighbors=n_neighbors)
    clf.fit(X_train, y_train)
    # record training set accuracy
    training_accuracy.append(clf.score(X_train, y_train))
    # record generalization accuracy
    test_accuracy.append(clf.score(X_test, y_test))

plt.plot(neighbors_settings, training_accuracy, label="training accuracy")
plt.plot(neighbors_settings, test_accuracy, label="test accuracy")
plt.ylabel("Accuracy")
plt.xlabel("n_neighbors")
plt.legend()

The plot shows the training and test set accuracy on the y-axis against the setting of n_neighbors on the x-axis. While real-world plots are rarely very smooth, we can still recognize some of the characteristics of overfitting and underfitting (note that because considering fewer neighbors corresponds to a more complex model, the plot is horizontally flipped relative to the illustration in Figure 2-1). Considering a single nearest neighbor, the prediction on the training set is perfect. But when more neighbors are considered, the model becomes simpler and the training accuracy drops. The test set accuracy for using a single neighbor is lower than when using more neighbors, indicating that using the single nearest neighbor leads to a model that is too complex. On the other hand, when considering 10 neighbors, the model is too simple and performance is even worse. The best performance is somewhere in the middle, using around six neighbors. Still, it is good to keep the scale of the plot in mind. The worst performance is around 88% accuracy, which might still be acceptable.

Figure 2-7. Comparison of training and test accuracy as a function of n_neighbors

k-neighbors regression

There is also a regression variant of the k-nearest neighbors algorithm. Again, let’s start by using the single nearest neighbor, this time using the wave dataset. We’ve added three test data points as green stars on the x-axis. The prediction using a single neighbor is just the target value of the nearest neighbor. These are shown as blue stars in Figure 2-8:

In[18]:

mglearn.plots.plot_knn_regression(n_neighbors=1)

Figure 2-8. Predictions made by one-nearest-neighbor regression on the wave dataset

Again, we can use more than the single closest neighbor for regression. When using multiple nearest neighbors, the prediction is the average, or mean, of the relevant neighbors (Figure 2-9):

In[19]:

mglearn.plots.plot_knn_regression(n_neighbors=3)

Figure 2-9. Predictions made by three-nearest-neighbors regression on the wave dataset

The k-nearest neighbors algorithm for regression is implemented in the KNeighborsRegressor class in scikit-learn. It’s used similarly to KNeighborsClassifier:

In[20]:

from sklearn.neighbors import KNeighborsRegressor

X, y = mglearn.datasets.make_wave(n_samples=40)

# split the wave dataset into a training and a test set
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)

# instantiate the model and set the number of neighbors to consider to 3
reg = KNeighborsRegressor(n_neighbors=3)
# fit the model using the training data and training targets
reg.fit(X_train, y_train)

Now we can make predictions on the test set:

In[21]:

print("Test set predictions:
", reg.predict(X_test))

Out[21]:

Test set predictions:
[-0.054  0.357  1.137 -1.894 -1.139 -1.631  0.357  0.912 -0.447 -1.139]

We can also evaluate the model using the score method, which for regressors returns the R² score. The R² score, also known as the coefficient of determination, is a measure of goodness of a prediction for a regression model, and yields a score that’s usually between 0 and 1. A value of 1 corresponds to a perfect prediction, and a value of 0 corresponds to a constant model that just predicts the mean of the training set responses, y_train. The formulation of R² used here can even be negative, which can indicate anticorrelated predictions.

In[22]:

print("Test set R^2: {:.2f}".format(reg.score(X_test, y_test)))

Out[22]:

Test set R^2: 0.83

Here, the score is 0.83, which indicates a relatively good model fit.

Analyzing KNeighborsRegressor

For our one-dimensional dataset, we can see what the predictions look like for all possible feature values (Figure 2-10). To do this, we create a test dataset consisting of many points on the x-axis, which corresponds to the single feature:

In[23]:

fig, axes = plt.subplots(1, 3, figsize=(15, 4))
# create 1,000 data points, evenly spaced between -3 and 3
line = np.linspace(-3, 3, 1000).reshape(-1, 1)
for n_neighbors, ax in zip([1, 3, 9], axes):
    # make predictions using 1, 3, or 9 neighbors
    reg = KNeighborsRegressor(n_neighbors=n_neighbors)
    reg.fit(X_train, y_train)
    ax.plot(line, reg.predict(line))
    ax.plot(X_train, y_train, '^', c=mglearn.cm2(0), markersize=8)
    ax.plot(X_test, y_test, 'v', c=mglearn.cm2(1), markersize=8)

    ax.set_title(
        "{} neighbor(s)
 train score: {:.2f} test score: {:.2f}".format(
            n_neighbors, reg.score(X_train, y_train),
            reg.score(X_test, y_test)))
    ax.set_xlabel("Feature")
    ax.set_ylabel("Target")
axes[0].legend(["Model predictions", "Training data/target",
                "Test data/target"], loc="best")

Figure 2-10. Comparing predictions made by nearest neighbors regression for different values of n_neighbors

As we can see from the plot, using only a single neighbor, each point in the training set has an obvious influence on the predictions, and the predicted values go through all of the data points. This leads to a very unsteady prediction. Considering more neighbors leads to smoother predictions, but these do not fit the training data as well.

Strengths, weaknesses, and parameters

In principle, there are two important parameters to the KNeighbors classifier: the number of neighbors and how you measure distance between data points. In practice, using a small number of neighbors like three or five often works well, but you should certainly adjust this parameter. Choosing the right distance measure is somewhat beyond the scope of this book. By default, Euclidean distance is used, which works well in many settings.

One of the strengths of k-NN is that the model is very easy to understand, and often gives reasonable performance without a lot of adjustments. Using this algorithm is a good baseline method to try before considering more advanced techniques. Building the nearest neighbors model is usually very fast, but when your training set is very large (either in number of features or in number of samples) prediction can be slow. When using the k-NN algorithm, it’s important to preprocess your data (see Chapter 3). This approach often does not perform well on datasets with many features (hundreds or more), and it does particularly badly with datasets where most features are 0 most of the time (so-called sparse datasets).

So, while the k-nearest neighbors algorithm is easy to understand, it is not often used in practice, due to prediction being slow and its inability to handle many features. The method we discuss next has neither of these drawbacks.

Linear models for regression

For regression, the general prediction formula for a linear model looks as follows:

• ŷ = w[0] * x[0] + w[1] * x[1] + ... + w[p] * x[p] + b

Here, x[0] to x[p] denotes the features (in this example, the number of features is p+1) of a single data point, w and b are parameters of the model that are learned, and ŷ is the prediction the model makes. For a dataset with a single feature, this is:

• ŷ = w[0] * x[0] + b

which you might remember from high school mathematics as the equation for a line. Here, w[0] is the slope and b is the y-axis offset. For more features, w contains the slopes along each feature axis. Alternatively, you can think of the predicted response as being a weighted sum of the input features, with weights (which can be negative) given by the entries of w.

Trying to learn the parameters w[0] and b on our one-dimensional wave dataset might lead to the following line (see Figure 2-11):

In[24]:

mglearn.plots.plot_linear_regression_wave()

Out[24]:

w[0]: 0.393906  b: -0.031804

Figure 2-11. Predictions of a linear model on the wave dataset

We added a coordinate cross into the plot to make it easier to understand the line. Looking at w[0] we see that the slope should be around 0.4, which we can confirm visually in the plot. The intercept is where the prediction line should cross the y-axis: this is slightly below zero, which you can also confirm in the image.

Linear models for regression can be characterized as regression models for which the prediction is a line for a single feature, a plane when using two features, or a hyperplane in higher dimensions (that is, when using more features).

If you compare the predictions made by the straight line with those made by the KNeighborsRegressor in Figure 2-10, using a straight line to make predictions seems very restrictive. It looks like all the fine details of the data are lost. In a sense, this is true. It is a strong (and somewhat unrealistic) assumption that our target y is a linear combination of the features. But looking at one-dimensional data gives a somewhat skewed perspective. For datasets with many features, linear models can be very powerful. In particular, if you have more features than training data points, any target y can be perfectly modeled (on the training set) as a linear function.⁶

There are many different linear models for regression. The difference between these models lies in how the model parameters w and b are learned from the training data, and how model complexity can be controlled. We will now take a look at the most popular linear models for regression.

Linear regression (aka ordinary least squares)

Linear regression, or ordinary least squares (OLS), is the simplest and most classic linear method for regression. Linear regression finds the parameters w and b that minimize the mean squared error between predictions and the true regression targets, y, on the training set. The mean squared error is the sum of the squared differences between the predictions and the true values, divided by the number of samples. Linear regression has no parameters, which is a benefit, but it also has no way to control model complexity.

Here is the code that produces the model you can see in Figure 2-11:

In[25]:

from sklearn.linear_model import LinearRegression
X, y = mglearn.datasets.make_wave(n_samples=60)
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=42)

lr = LinearRegression().fit(X_train, y_train)

The “slope” parameters (w), also called weights or coefficients, are stored in the coef_ attribute, while the offset or intercept (b) is stored in the intercept_ attribute:

In[26]:

print("lr.coef_:", lr.coef_)
print("lr.intercept_:", lr.intercept_)

Out[26]:

lr.coef_: [0.394]
lr.intercept_: -0.031804343026759746

The intercept_ attribute is always a single float number, while the coef_ attribute is a NumPy array with one entry per input feature. As we only have a single input feature in the wave dataset, lr.coef_ only has a single entry.

Let’s look at the training set and test set performance:

In[27]:

print("Training set score: {:.2f}".format(lr.score(X_train, y_train)))
print("Test set score: {:.2f}".format(lr.score(X_test, y_test)))

Out[27]:

Training set score: 0.67
Test set score: 0.66

An R² of around 0.66 is not very good, but we can see that the scores on the training and test sets are very close together. This means we are likely underfitting, not overfitting. For this one-dimensional dataset, there is little danger of overfitting, as the model is very simple (or restricted). However, with higher-dimensional datasets (meaning datasets with a large number of features), linear models become more powerful, and there is a higher chance of overfitting. Let’s take a look at how LinearRegression performs on a more complex dataset, like the Boston Housing dataset. Remember that this dataset has 506 samples and 104 derived features. First, we load the dataset and split it into a training and a test set. Then we build the linear regression model as before:

In[28]:

X, y = mglearn.datasets.load_extended_boston()

X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)
lr = LinearRegression().fit(X_train, y_train)

When comparing training set and test set scores, we find that we predict very accurately on the training set, but the R² on the test set is much worse:

In[29]:

print("Training set score: {:.2f}".format(lr.score(X_train, y_train)))
print("Test set score: {:.2f}".format(lr.score(X_test, y_test)))

Out[29]:

Training set score: 0.95
Test set score: 0.61

This discrepancy between performance on the training set and the test set is a clear sign of overfitting, and therefore we should try to find a model that allows us to control complexity. One of the most commonly used alternatives to standard linear regression is ridge regression, which we will look into next.

Ridge regression

Ridge regression is also a linear model for regression, so the formula it uses to make predictions is the same one used for ordinary least squares. In ridge regression, though, the coefficients (w) are chosen not only so that they predict well on the training data, but also to fit an additional constraint. We also want the magnitude of coefficients to be as small as possible; in other words, all entries of w should be close to zero. Intuitively, this means each feature should have as little effect on the outcome as possible (which translates to having a small slope), while still predicting well. This constraint is an example of what is called regularization. Regularization means explicitly restricting a model to avoid overfitting. The particular kind used by ridge regression is known as L2 regularization.⁷

Ridge regression is implemented in linear_model.Ridge. Let’s see how well it does on the extended Boston Housing dataset:

In[30]:

from sklearn.linear_model import Ridge

ridge = Ridge().fit(X_train, y_train)
print("Training set score: {:.2f}".format(ridge.score(X_train, y_train)))
print("Test set score: {:.2f}".format(ridge.score(X_test, y_test)))

Out[30]:

Training set score: 0.89
Test set score: 0.75

As you can see, the training set score of Ridge is lower than for LinearRegression, while the test set score is higher. This is consistent with our expectation. With linear regression, we were overfitting our data. Ridge is a more restricted model, so we are less likely to overfit. A less complex model means worse performance on the training set, but better generalization. As we are only interested in generalization performance, we should choose the Ridge model over the LinearRegression model.

The Ridge model makes a trade-off between the simplicity of the model (near-zero coefficients) and its performance on the training set. How much importance the model places on simplicity versus training set performance can be specified by the user, using the alpha parameter. In the previous example, we used the default parameter alpha=1.0. There is no reason why this will give us the best trade-off, though. The optimum setting of alpha depends on the particular dataset we are using. Increasing alpha forces coefficients to move more toward zero, which decreases training set performance but might help generalization. For example:

In[31]:

ridge10 = Ridge(alpha=10).fit(X_train, y_train)
print("Training set score: {:.2f}".format(ridge10.score(X_train, y_train)))
print("Test set score: {:.2f}".format(ridge10.score(X_test, y_test)))

Out[31]:

Training set score: 0.79
Test set score: 0.64

Decreasing alpha allows the coefficients to be less restricted, meaning we move right in Figure 2-1. For very small values of alpha, coefficients are barely restricted at all, and we end up with a model that resembles LinearRegression:

In[32]:

ridge01 = Ridge(alpha=0.1).fit(X_train, y_train)
print("Training set score: {:.2f}".format(ridge01.score(X_train, y_train)))
print("Test set score: {:.2f}".format(ridge01.score(X_test, y_test)))

Out[32]:

Training set score: 0.93
Test set score: 0.77

Here, alpha=0.1 seems to be working well. We could try decreasing alpha even more to improve generalization. For now, notice how the parameter alpha corresponds to the model complexity as shown in Figure 2-1. We will discuss methods to properly select parameters in Chapter 5.

We can also get a more qualitative insight into how the alpha parameter changes the model by inspecting the coef_ attribute of models with different values of alpha. A higher alpha means a more restricted model, so we expect the entries of coef_ to have smaller magnitude for a high value of alpha than for a low value of alpha. This is confirmed in the plot in Figure 2-12:

In[33]:

plt.plot(ridge.coef_, 's', label="Ridge alpha=1")
plt.plot(ridge10.coef_, '^', label="Ridge alpha=10")
plt.plot(ridge01.coef_, 'v', label="Ridge alpha=0.1")

plt.plot(lr.coef_, 'o', label="LinearRegression")
plt.xlabel("Coefficient index")
plt.ylabel("Coefficient magnitude")
plt.hlines(0, 0, len(lr.coef_))
plt.ylim(-25, 25)
plt.legend()

Figure 2-12. Comparing coefficient magnitudes for ridge regression with different values of alpha and linear regression

Here, the x-axis enumerates the entries of coef_: x=0 shows the coefficient associated with the first feature, x=1 the coefficient associated with the second feature, and so on up to x=100. The y-axis shows the numeric values of the corresponding values of the coefficients. The main takeaway here is that for alpha=10, the coefficients are mostly between around –3 and 3. The coefficients for the Ridge model with alpha=1, are somewhat larger. The dots corresponding to alpha=0.1 have larger magnitude still, and many of the dots corresponding to linear regression without any regularization (which would be alpha=0) are so large they are outside of the chart.

Another way to understand the influence of regularization is to fix a value of alpha but vary the amount of training data available. For Figure 2-13, we subsampled the Boston Housing dataset and evaluated LinearRegression and Ridge(alpha=1) on subsets of increasing size (plots that show model performance as a function of dataset size are called learning curves):

In[34]:

mglearn.plots.plot_ridge_n_samples()

Figure 2-13. Learning curves for ridge regression and linear regression on the Boston Housing dataset

As one would expect, the training score is higher than the test score for all dataset sizes, for both ridge and linear regression. Because ridge is regularized, the training score of ridge is lower than the training score for linear regression across the board. However, the test score for ridge is better, particularly for small subsets of the data. For less than 400 data points, linear regression is not able to learn anything. As more and more data becomes available to the model, both models improve, and linear regression catches up with ridge in the end. The lesson here is that with enough training data, regularization becomes less important, and given enough data, ridge and linear regression will have the same performance (the fact that this happens here when using the full dataset is just by chance). Another interesting aspect of Figure 2-13 is the decrease in training performance for linear regression. If more data is added, it becomes harder for a model to overfit, or memorize the data.

Lasso

An alternative to Ridge for regularizing linear regression is Lasso. As with ridge regression, the lasso also restricts coefficients to be close to zero, but in a slightly different way, called L1 regularization.⁸ The consequence of L1 regularization is that when using the lasso, some coefficients are exactly zero. This means some features are entirely ignored by the model. This can be seen as a form of automatic feature selection. Having some coefficients be exactly zero often makes a model easier to interpret, and can reveal the most important features of your model.

Let’s apply the lasso to the extended Boston Housing dataset:

In[35]:

from sklearn.linear_model import Lasso

lasso = Lasso().fit(X_train, y_train)
print("Training set score: {:.2f}".format(lasso.score(X_train, y_train)))
print("Test set score: {:.2f}".format(lasso.score(X_test, y_test)))
print("Number of features used:", np.sum(lasso.coef_ != 0))

Out[35]:

Training set score: 0.29
Test set score: 0.21
Number of features used: 4

As you can see, Lasso does quite badly, both on the training and the test set. This indicates that we are underfitting, and we find that it used only 4 of the 104 features. Similarly to Ridge, the Lasso also has a regularization parameter, alpha, that controls how strongly coefficients are pushed toward zero. In the previous example, we used the default of alpha=1.0. To reduce underfitting, let’s try decreasing alpha. When we do this, we also need to increase the default setting of max_iter (the maximum number of iterations to run):

In[36]:

# we increase the default setting of "max_iter",
# otherwise the model would warn us that we should increase max_iter.
lasso001 = Lasso(alpha=0.01, max_iter=100000).fit(X_train, y_train)
print("Training set score: {:.2f}".format(lasso001.score(X_train, y_train)))
print("Test set score: {:.2f}".format(lasso001.score(X_test, y_test)))
print("Number of features used:", np.sum(lasso001.coef_ != 0))

Out[36]:

Training set score: 0.90
Test set score: 0.77
Number of features used: 33

A lower alpha allowed us to fit a more complex model, which worked better on the training and test data. The performance is slightly better than using Ridge, and we are using only 33 of the 104 features. This makes this model potentially easier to understand.

If we set alpha too low, however, we again remove the effect of regularization and end up overfitting, with a result similar to LinearRegression:

In[37]:

lasso00001 = Lasso(alpha=0.0001, max_iter=100000).fit(X_train, y_train)
print("Training set score: {:.2f}".format(lasso00001.score(X_train, y_train)))
print("Test set score: {:.2f}".format(lasso00001.score(X_test, y_test)))
print("Number of features used:", np.sum(lasso00001.coef_ != 0))

Out[37]:

Training set score: 0.95
Test set score: 0.64
Number of features used: 94

Again, we can plot the coefficients of the different models, similarly to Figure 2-12. The result is shown in Figure 2-14:

In[38]:

plt.plot(lasso.coef_, 's', label="Lasso alpha=1")
plt.plot(lasso001.coef_, '^', label="Lasso alpha=0.01")
plt.plot(lasso00001.coef_, 'v', label="Lasso alpha=0.0001")

plt.plot(ridge01.coef_, 'o', label="Ridge alpha=0.1")
plt.legend(ncol=2, loc=(0, 1.05))
plt.ylim(-25, 25)
plt.xlabel("Coefficient index")
plt.ylabel("Coefficient magnitude")

Figure 2-14. Comparing coefficient magnitudes for lasso regression with different values of alpha and ridge regression

For alpha=1, we not only see that most of the coefficients are zero (which we already knew), but that the remaining coefficients are also small in magnitude. Decreasing alpha to 0.01, we obtain the solution shown as an upward pointing triangle, which causes most features to be exactly zero. Using alpha=0.0001, we get a model that is quite unregularized, with most coefficients nonzero and of large magnitude. For comparison, the best Ridge solution is shown as circles. The Ridge model with alpha=0.1 has similar predictive performance as the lasso model with alpha=0.01, but using Ridge, all coefficients are nonzero.

In practice, ridge regression is usually the first choice between these two models. However, if you have a large amount of features and expect only a few of them to be important, Lasso might be a better choice. Similarly, if you would like to have a model that is easy to interpret, Lasso will provide a model that is easier to understand, as it will select only a subset of the input features. scikit-learn also provides the ElasticNet class, which combines the penalties of Lasso and Ridge. In practice, this combination works best, though at the price of having two parameters to adjust: one for the L1 regularization, and one for the L2 regularization.

Linear models for classification

Linear models are also extensively used for classification. Let’s look at binary classification first. In this case, a prediction is made using the following formula:

• ŷ = w[0] * x[0] + w[1] * x[1] + ... + w[p] * x[p] + b > 0

The formula looks very similar to the one for linear regression, but instead of just returning the weighted sum of the features, we threshold the predicted value at zero. If the function is smaller than zero, we predict the class –1; if it is larger than zero, we predict the class +1. This prediction rule is common to all linear models for classification. Again, there are many different ways to find the coefficients (w) and the intercept (b).

For linear models for regression, the output, ŷ, is a linear function of the features: a line, plane, or hyperplane (in higher dimensions). For linear models for classification, the decision boundary is a linear function of the input. In other words, a (binary) linear classifier is a classifier that separates two classes using a line, a plane, or a hyperplane. We will see examples of that in this section.

There are many algorithms for learning linear models. These algorithms all differ in the following two ways:

• The way in which they measure how well a particular combination of coefficients and intercept fits the training data

• If and what kind of regularization they use

Different algorithms choose different ways to measure what “fitting the training set well” means. For technical mathematical reasons, it is not possible to adjust w and b to minimize the number of misclassifications the algorithms produce, as one might hope. For our purposes, and many applications, the different choices for item 1 in the preceding list (called loss functions) are of little significance.

The two most common linear classification algorithms are logistic regression, implemented in linear_model.LogisticRegression, and linear support vector machines (linear SVMs), implemented in svm.LinearSVC (SVC stands for support vector classifier). Despite its name, LogisticRegression is a classification algorithm and not a regression algorithm, and it should not be confused with LinearRegression.

We can apply the LogisticRegression and LinearSVC models to the forge dataset, and visualize the decision boundary as found by the linear models (Figure 2-15):

In[39]:

from sklearn.linear_model import LogisticRegression
from sklearn.svm import LinearSVC

X, y = mglearn.datasets.make_forge()

fig, axes = plt.subplots(1, 2, figsize=(10, 3))

for model, ax in zip([LinearSVC(), LogisticRegression()], axes):
    clf = model.fit(X, y)
    mglearn.plots.plot_2d_separator(clf, X, fill=False, eps=0.5,
                                    ax=ax, alpha=.7)
    mglearn.discrete_scatter(X[:, 0], X[:, 1], y, ax=ax)
    ax.set_title(clf.__class__.__name__)
    ax.set_xlabel("Feature 0")
    ax.set_ylabel("Feature 1")
axes[0].legend()

Figure 2-15. Decision boundaries of a linear SVM and logistic regression on the forge dataset with the default parameters

In this figure, we have the first feature of the forge dataset on the x-axis and the second feature on the y-axis, as before. We display the decision boundaries found by LinearSVC and LogisticRegression respectively as straight lines, separating the area classified as class 1 on the top from the area classified as class 0 on the bottom. In other words, any new data point that lies above the black line will be classified as class 1 by the respective classifier, while any point that lies below the black line will be classified as class 0.

The two models come up with similar decision boundaries. Note that both misclassify two of the points. By default, both models apply an L2 regularization, in the same way that Ridge does for regression.

For LogisticRegression and LinearSVC the trade-off parameter that determines the strength of the regularization is called C, and higher values of C correspond to less regularization. In other words, when you use a high value for the parameter C, LogisticRegression and LinearSVC try to fit the training set as best as possible, while with low values of the parameter C, the models put more emphasis on finding a coefficient vector (w) that is close to zero.

There is another interesting aspect of how the parameter C acts. Using low values of C will cause the algorithms to try to adjust to the “majority” of data points, while using a higher value of C stresses the importance that each individual data point be classified correctly. Here is an illustration using LinearSVC (Figure 2-16):

In[40]:

mglearn.plots.plot_linear_svc_regularization()

Figure 2-16. Decision boundaries of a linear SVM on the forge dataset for different values of C

On the lefthand side, we have a very small C corresponding to a lot of regularization. Most of the points in class 0 are at the bottom, and most of the points in class 1 are at the top. The strongly regularized model chooses a relatively horizontal line, misclassifying two points. In the center plot, C is slightly higher, and the model focuses more on the two misclassified samples, tilting the decision boundary. Finally, on the righthand side, the very high value of C in the model tilts the decision boundary a lot, now correctly classifying all points in class 0. One of the points in class 1 is still misclassified, as it is not possible to correctly classify all points in this dataset using a straight line. The model illustrated on the righthand side tries hard to correctly classify all points, but might not capture the overall layout of the classes well. In other words, this model is likely overfitting.

Similarly to the case of regression, linear models for classification might seem very restrictive in low-dimensional spaces, only allowing for decision boundaries that are straight lines or planes. Again, in high dimensions, linear models for classification become very powerful, and guarding against overfitting becomes increasingly important when considering more features.

Let’s analyze LogisticRegression in more detail on the Breast Cancer dataset:

In[41]:

from sklearn.datasets import load_breast_cancer
cancer = load_breast_cancer()
X_train, X_test, y_train, y_test = train_test_split(
    cancer.data, cancer.target, stratify=cancer.target, random_state=42)
logreg = LogisticRegression().fit(X_train, y_train)
print("Training set score: {:.3f}".format(logreg.score(X_train, y_train)))
print("Test set score: {:.3f}".format(logreg.score(X_test, y_test)))

Out[41]:

Training set score: 0.953
Test set score: 0.958

The default value of C=1 provides quite good performance, with 95% accuracy on both the training and the test set. But as training and test set performance are very close, it is likely that we are underfitting. Let’s try to increase C to fit a more flexible model:

In[42]:

logreg100 = LogisticRegression(C=100).fit(X_train, y_train)
print("Training set score: {:.3f}".format(logreg100.score(X_train, y_train)))
print("Test set score: {:.3f}".format(logreg100.score(X_test, y_test)))

Out[42]:

Training set score: 0.972
Test set score: 0.965

Using C=100 results in higher training set accuracy, and also a slightly increased test set accuracy, confirming our intuition that a more complex model should perform better.

We can also investigate what happens if we use an even more regularized model than the default of C=1, by setting C=0.01:

In[43]:

logreg001 = LogisticRegression(C=0.01).fit(X_train, y_train)
print("Training set score: {:.3f}".format(logreg001.score(X_train, y_train)))
print("Test set score: {:.3f}".format(logreg001.score(X_test, y_test)))

Out[43]:

Training set score: 0.934
Test set score: 0.930

As expected, when moving more to the left along the scale shown in Figure 2-1 from an already underfit model, both training and test set accuracy decrease relative to the default parameters.

Finally, let’s look at the coefficients learned by the models with the three different settings of the regularization parameter C (Figure 2-17):

In[44]:

plt.plot(logreg.coef_.T, 'o', label="C=1")
plt.plot(logreg100.coef_.T, '^', label="C=100")
plt.plot(logreg001.coef_.T, 'v', label="C=0.001")
plt.xticks(range(cancer.data.shape[1]), cancer.feature_names, rotation=90)
plt.hlines(0, 0, cancer.data.shape[1])
plt.ylim(-5, 5)
plt.xlabel("Feature")
plt.ylabel("Coefficient magnitude")
plt.legend()

Figure 2-17. Coefficients learned by logistic regression on the Breast Cancer dataset for different values of C

If we desire a more interpretable model, using L1 regularization might help, as it limits the model to using only a few features. Here is the coefficient plot and classification accuracies for L1 regularization (Figure 2-18):

In[45]:

for C, marker in zip([0.001, 1, 100], ['o', '^', 'v']):
    lr_l1 = LogisticRegression(C=C, penalty="l1").fit(X_train, y_train)
    print("Training accuracy of l1 logreg with C={:.3f}: {:.2f}".format(
          C, lr_l1.score(X_train, y_train)))
    print("Test accuracy of l1 logreg with C={:.3f}: {:.2f}".format(
          C, lr_l1.score(X_test, y_test)))
    plt.plot(lr_l1.coef_.T, marker, label="C={:.3f}".format(C))

plt.xticks(range(cancer.data.shape[1]), cancer.feature_names, rotation=90)
plt.hlines(0, 0, cancer.data.shape[1])
plt.xlabel("Feature")
plt.ylabel("Coefficient magnitude")

plt.ylim(-5, 5)
plt.legend(loc=3)

Out[45]:

Training accuracy of l1 logreg with C=0.001: 0.91
Test accuracy of l1 logreg with C=0.001: 0.92
Training accuracy of l1 logreg with C=1.000: 0.96
Test accuracy of l1 logreg with C=1.000: 0.96
Training accuracy of l1 logreg with C=100.000: 0.99
Test accuracy of l1 logreg with C=100.000: 0.98

As you can see, there are many parallels between linear models for binary classification and linear models for regression. As in regression, the main difference between the models is the penalty parameter, which influences the regularization and whether the model will use all available features or select only a subset.

Figure 2-18. Coefficients learned by logistic regression with L1 penalty on the Breast Cancer dataset for different values of C

Linear models for multiclass classification

Many linear classification models are for binary classification only, and don’t extend naturally to the multiclass case (with the exception of logistic regression). A common technique to extend a binary classification algorithm to a multiclass classification algorithm is the one-vs.-rest approach. In the one-vs.-rest approach, a binary model is learned for each class that tries to separate that class from all of the other classes, resulting in as many binary models as there are classes. To make a prediction, all binary classifiers are run on a test point. The classifier that has the highest score on its single class “wins,” and this class label is returned as the prediction.

Having one binary classifier per class results in having one vector of coefficients (w) and one intercept (b) for each class. The class for which the result of the classification confidence formula given here is highest is the assigned class label:

• w[0] * x[0] + w[1] * x[1] + ... + w[p] * x[p] + b

The mathematics behind multiclass logistic regression differ somewhat from the one-vs.-rest approach, but they also result in one coefficient vector and intercept per class, and the same method of making a prediction is applied.

Let’s apply the one-vs.-rest method to a simple three-class classification dataset. We use a two-dimensional dataset, where each class is given by data sampled from a Gaussian distribution (see Figure 2-19):

In[46]:

from sklearn.datasets import make_blobs

X, y = make_blobs(random_state=42)
mglearn.discrete_scatter(X[:, 0], X[:, 1], y)
plt.xlabel("Feature 0")
plt.ylabel("Feature 1")
plt.legend(["Class 0", "Class 1", "Class 2"])

Figure 2-19. Two-dimensional toy dataset containing three classes

Now, we train a LinearSVC classifier on the dataset:

In[47]:

linear_svm = LinearSVC().fit(X, y)
print("Coefficient shape: ", linear_svm.coef_.shape)
print("Intercept shape: ", linear_svm.intercept_.shape)

Out[47]:

Coefficient shape:  (3, 2)
Intercept shape:  (3,)

We see that the shape of the coef_ is (3, 2), meaning that each row of coef_ contains the coefficient vector for one of the three classes and each column holds the coefficient value for a specific feature (there are two in this dataset). The intercept_ is now a one-dimensional array, storing the intercepts for each class.

Let’s visualize the lines given by the three binary classifiers (Figure 2-20):

In[48]:

mglearn.discrete_scatter(X[:, 0], X[:, 1], y)
line = np.linspace(-15, 15)
for coef, intercept, color in zip(linear_svm.coef_, linear_svm.intercept_,
                                  mglearn.cm3.colors):
    plt.plot(line, -(line * coef[0] + intercept) / coef[1], c=color)
plt.ylim(-10, 15)
plt.xlim(-10, 8)
plt.xlabel("Feature 0")
plt.ylabel("Feature 1")
plt.legend(['Class 0', 'Class 1', 'Class 2', 'Line class 0', 'Line class 1',
            'Line class 2'], loc=(1.01, 0.3))

You can see that all the points belonging to class 0 in the training data are above the line corresponding to class 0, which means they are on the “class 0” side of this binary classifier. The points in class 0 are above the line corresponding to class 2, which means they are classified as “rest” by the binary classifier for class 2. The points belonging to class 0 are to the left of the line corresponding to class 1, which means the binary classifier for class 1 also classifies them as “rest.” Therefore, any point in this area will be classified as class 0 by the final classifier (the result of the classification confidence formula for classifier 0 is greater than zero, while it is smaller than zero for the other two classes).

But what about the triangle in the middle of the plot? All three binary classifiers classify points there as “rest.” Which class would a point there be assigned to? The answer is the one with the highest value for the classification formula: the class of the closest line.

Figure 2-20. Decision boundaries learned by the three one-vs.-rest classifiers

The following example (Figure 2-21) shows the predictions for all regions of the 2D space:

In[49]:

mglearn.plots.plot_2d_classification(linear_svm, X, fill=True, alpha=.7)
mglearn.discrete_scatter(X[:, 0], X[:, 1], y)
line = np.linspace(-15, 15)
for coef, intercept, color in zip(linear_svm.coef_, linear_svm.intercept_,
                                  mglearn.cm3.colors):
    plt.plot(line, -(line * coef[0] + intercept) / coef[1], c=color)
plt.legend(['Class 0', 'Class 1', 'Class 2', 'Line class 0', 'Line class 1',
            'Line class 2'], loc=(1.01, 0.3))
plt.xlabel("Feature 0")
plt.ylabel("Feature 1")

Figure 2-21. Multiclass decision boundaries derived from the three one-vs.-rest classifiers

Strengths, weaknesses, and parameters

The main parameter of linear models is the regularization parameter, called alpha in the regression models and C in LinearSVC and LogisticRegression. Large values for alpha or small values for C mean simple models. In particular for the regression models, tuning these parameters is quite important. Usually C and alpha are searched for on a logarithmic scale. The other decision you have to make is whether you want to use L1 regularization or L2 regularization. If you assume that only a few of your features are actually important, you should use L1. Otherwise, you should default to L2. L1 can also be useful if interpretability of the model is important. As L1 will use only a few features, it is easier to explain which features are important to the model, and what the effects of these features are.

Linear models are very fast to train, and also fast to predict. They scale to very large datasets and work well with sparse data. If your data consists of hundreds of thousands or millions of samples, you might want to investigate using the solver='sag' option in LogisticRegression and Ridge, which can be faster than the default on large datasets. Other options are the SGDClassifier class and the SGDRegressor class, which implement even more scalable versions of the linear models described here.

Another strength of linear models is that they make it relatively easy to understand how a prediction is made, using the formulas we saw earlier for regression and classification. Unfortunately, it is often not entirely clear why coefficients are the way they are. This is particularly true if your dataset has highly correlated features; in these cases, the coefficients might be hard to interpret.

Linear models often perform well when the number of features is large compared to the number of samples. They are also often used on very large datasets, simply because it’s not feasible to train other models. However, in lower-dimensional spaces, other models might yield better generalization performance. We will look at some examples in which linear models fail in Section 2.3.7.

Strengths, weaknesses, and parameters

MultinomialNB and BernoulliNB have a single parameter, alpha, which controls model complexity. The way alpha works is that the algorithm adds to the data alpha many virtual data points that have positive values for all the features. This results in a “smoothing” of the statistics. A large alpha means more smoothing, resulting in less complex models. The algorithm’s performance is relatively robust to the setting of alpha, meaning that setting alpha is not critical for good performance. However, tuning it usually improves accuracy somewhat.

GaussianNB is mostly used on very high-dimensional data, while the other two variants of naive Bayes are widely used for sparse count data such as text. MultinomialNB usually performs better than BernoulliNB, particularly on datasets with a relatively large number of nonzero features (i.e., large documents).

The naive Bayes models share many of the strengths and weaknesses of the linear models. They are very fast to train and to predict, and the training procedure is easy to understand. The models work very well with high-dimensional sparse data and are relatively robust to the parameters. Naive Bayes models are great baseline models and are often used on very large datasets, where training even a linear model might take too long.

Building decision trees

Let’s go through the process of building a decision tree for the 2D classification dataset shown in Figure 2-23. The dataset consists of two half-moon shapes, with each class consisting of 75 data points. We will refer to this dataset as two_moons.

Learning a decision tree means learning the sequence of if/else questions that gets us to the true answer most quickly. In the machine learning setting, these questions are called tests (not to be confused with the test set, which is the data we use to test to see how generalizable our model is). Usually data does not come in the form of binary yes/no features as in the animal example, but is instead represented as continuous features such as in the 2D dataset shown in Figure 2-23. The tests that are used on continuous data are of the form “Is feature i larger than value a?”

Figure 2-23. Two-moons dataset on which the decision tree will be built

To build a tree, the algorithm searches over all possible tests and finds the one that is most informative about the target variable. Figure 2-24 shows the first test that is picked. Splitting the dataset horizontally at x[1]=0.0596 yields the most information; it best separates the points in class 0 from the points in class 1. The top node, also called the root, represents the whole dataset, consisting of 50 points belonging to class 0 and 50 points belonging to class 1. The split is done by testing whether x[1] <= 0.0596, indicated by a black line. If the test is true, a point is assigned to the left node, which contains 2 points belonging to class 0 and 32 points belonging to class 1. Otherwise the point is assigned to the right node, which contains 48 points belonging to class 0 and 18 points belonging to class 1. These two nodes correspond to the top and bottom regions shown in Figure 2-24. Even though the first split did a good job of separating the two classes, the bottom region still contains points belonging to class 0, and the top region still contains points belonging to class 1. We can build a more accurate model by repeating the process of looking for the best test in both regions. Figure 2-25 shows that the most informative next split for the left and the right region is based on x[0].

Figure 2-24. Decision boundary of tree with depth 1 (left) and corresponding tree (right)

Figure 2-25. Decision boundary of tree with depth 2 (left) and corresponding decision tree (right)

This recursive process yields a binary tree of decisions, with each node containing a test. Alternatively, you can think of each test as splitting the part of the data that is currently being considered along one axis. This yields a view of the algorithm as building a hierarchical partition. As each test concerns only a single feature, the regions in the resulting partition always have axis-parallel boundaries.

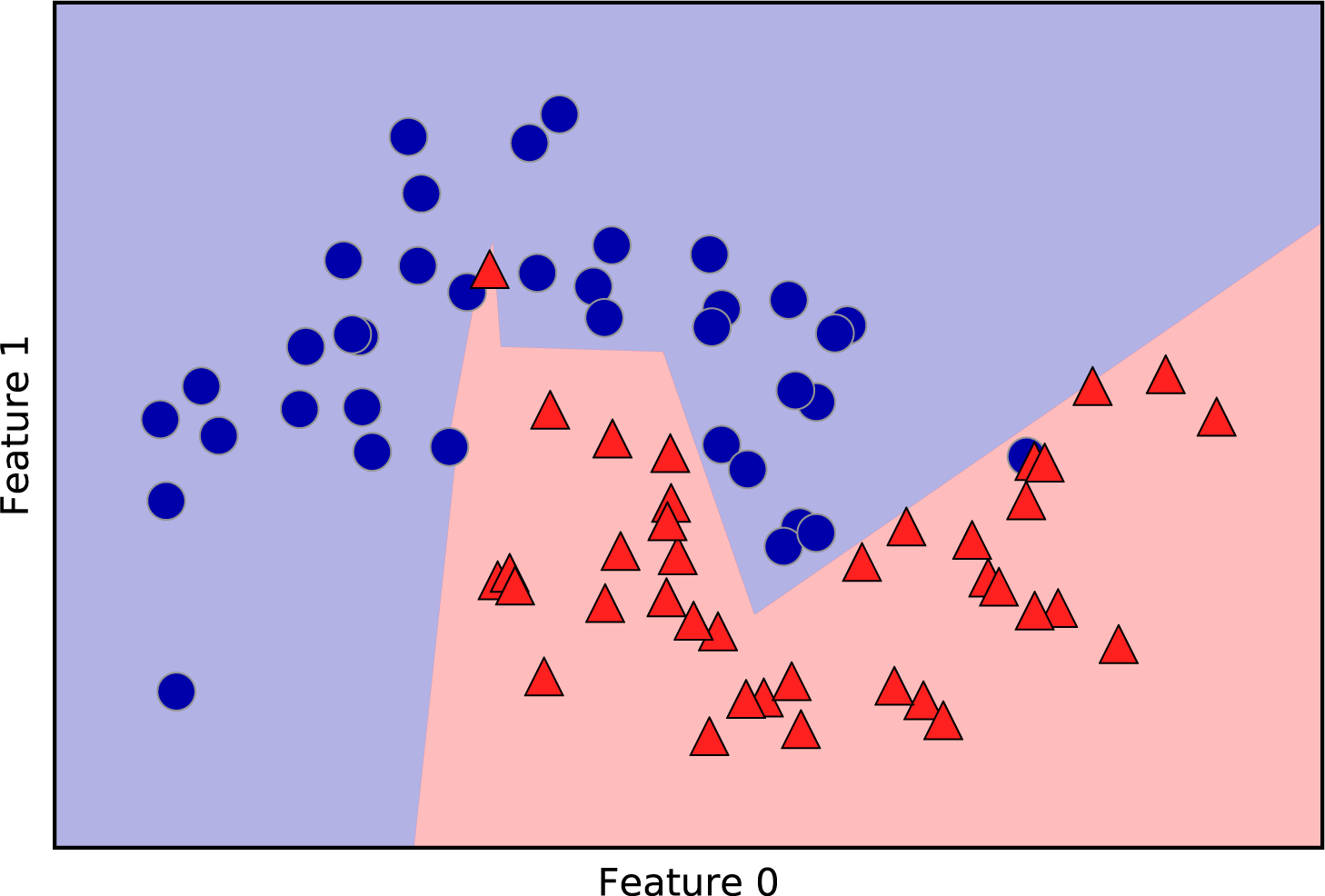
The recursive partitioning of the data is repeated until each region in the partition (each leaf in the decision tree) only contains a single target value (a single class or a single regression value). A leaf of the tree that contains data points that all share the same target value is called pure. The final partitioning for this dataset is shown in Figure 2-26.

Figure 2-26. Decision boundary of tree with depth 9 (left) and part of the corresponding tree (right); the full tree is quite large and hard to visualize

A prediction on a new data point is made by checking which region of the partition of the feature space the point lies in, and then predicting the majority target (or the single target in the case of pure leaves) in that region. The region can be found by traversing the tree from the root and going left or right, depending on whether the test is fulfilled or not.

It is also possible to use trees for regression tasks, using exactly the same technique. To make a prediction, we traverse the tree based on the tests in each node and find the leaf the new data point falls into. The output for this data point is the mean target of the training points in this leaf.

Controlling complexity of decision trees

Typically, building a tree as described here and continuing until all leaves are pure leads to models that are very complex and highly overfit to the training data. The presence of pure leaves mean that a tree is 100% accurate on the training set; each data point in the training set is in a leaf that has the correct majority class. The overfitting can be seen on the left of Figure 2-26. You can see the regions determined to belong to class 1 in the middle of all the points belonging to class 0. On the other hand, there is a small strip predicted as class 0 around the point belonging to class 0 to the very right. This is not how one would imagine the decision boundary to look, and the decision boundary focuses a lot on single outlier points that are far away from the other points in that class.

There are two common strategies to prevent overfitting: stopping the creation of the tree early (also called pre-pruning), or building the tree but then removing or collapsing nodes that contain little information (also called post-pruning or just pruning). Possible criteria for pre-pruning include limiting the maximum depth of the tree, limiting the maximum number of leaves, or requiring a minimum number of points in a node to keep splitting it.

Decision trees in scikit-learn are implemented in the DecisionTreeRegressor and DecisionTreeClassifier classes. scikit-learn only implements pre-pruning, not post-pruning.

Let’s look at the effect of pre-pruning in more detail on the Breast Cancer dataset. As always, we import the dataset and split it into a training and a test part. Then we build a model using the default setting of fully developing the tree (growing the tree until all leaves are pure). We fix the random_state in the tree, which is used for tie-breaking internally:

In[56]:

from sklearn.tree import DecisionTreeClassifier

cancer = load_breast_cancer()
X_train, X_test, y_train, y_test = train_test_split(
    cancer.data, cancer.target, stratify=cancer.target, random_state=42)
tree = DecisionTreeClassifier(random_state=0)
tree.fit(X_train, y_train)
print("Accuracy on training set: {:.3f}".format(tree.score(X_train, y_train)))
print("Accuracy on test set: {:.3f}".format(tree.score(X_test, y_test)))

Out[56]:

Accuracy on training set: 1.000
Accuracy on test set: 0.937

As expected, the accuracy on the training set is 100%—because the leaves are pure, the tree was grown deep enough that it could perfectly memorize all the labels on the training data. The test set accuracy is slightly worse than for the linear models we looked at previously, which had around 95% accuracy.

If we don’t restrict the depth of a decision tree, the tree can become arbitrarily deep and complex. Unpruned trees are therefore prone to overfitting and not generalizing well to new data. Now let’s apply pre-pruning to the tree, which will stop developing the tree before we perfectly fit to the training data. One option is to stop building the tree after a certain depth has been reached. Here we set max_depth=4, meaning only four consecutive questions can be asked (cf. Figures 2-24 and 2-26). Limiting the depth of the tree decreases overfitting. This leads to a lower accuracy on the training set, but an improvement on the test set:

In[57]:

tree = DecisionTreeClassifier(max_depth=4, random_state=0)
tree.fit(X_train, y_train)

print("Accuracy on training set: {:.3f}".format(tree.score(X_train, y_train)))
print("Accuracy on test set: {:.3f}".format(tree.score(X_test, y_test)))

Out[57]:

Accuracy on training set: 0.988
Accuracy on test set: 0.951

Analyzing decision trees

We can visualize the tree using the export_graphviz function from the tree module. This writes a file in the .dot file format, which is a text file format for storing graphs. We set an option to color the nodes to reflect the majority class in each node and pass the class and features names so the tree can be properly labeled:

In[58]:

from sklearn.tree import export_graphviz
export_graphviz(tree, out_file="tree.dot", class_names=["malignant", "benign"],
                feature_names=cancer.feature_names, impurity=False, filled=True)

We can read this file and visualize it, as seen in Figure 2-27, using the graphviz module (or you can use any program that can read .dot files):

In[59]:

import graphviz

with open("tree.dot") as f:
    dot_graph = f.read()
display(graphviz.Source(dot_graph))

Figure 2-27. Visualization of the decision tree built on the Breast Cancer dataset

The visualization of the tree provides a great in-depth view of how the algorithm makes predictions, and is a good example of a machine learning algorithm that is easily explained to nonexperts. However, even with a tree of depth four, as seen here, the tree can become a bit overwhelming. Deeper trees (a depth of 10 is not uncommon) are even harder to grasp. One method of inspecting the tree that may be helpful is to find out which path most of the data actually takes. The samples shown in each node in Figure 2-27 gives the number of samples in that node, while value provides the number of samples per class. Following the branches to the right, we see that worst radius > 16.795 creates a node that contains only 8 benign but 134 malignant samples. The rest of this side of the tree then uses some finer distinctions to split off these 8 remaining benign samples. Of the 142 samples that went to the right in the initial split, nearly all of them (132) end up in the leaf to the very right.

Taking a left at the root, for worst radius <= 16.795 we end up with 25 malignant and 259 benign samples. Nearly all of the benign samples end up in the second leaf from the left, with most of the other leaves containing very few samples.

Feature importance in trees

Instead of looking at the whole tree, which can be taxing, there are some useful properties that we can derive to summarize the workings of the tree. The most commonly used summary is feature importance, which rates how important each feature is for the decision a tree makes. It is a number between 0 and 1 for each feature, where 0 means “not used at all” and 1 means “perfectly predicts the target.” The feature importances always sum to 1:

In[60]:

print("Feature importances:")
print(tree.feature_importances_)

Out[60]:

Feature importances:
[0.    0.    0.    0.    0.    0.    0.    0.    0.    0.    0.01  0.048
 0.    0.    0.002 0.    0.    0.    0.    0.    0.727 0.046 0.    0.
 0.014 0.    0.018 0.122 0.012 0.   ]

We can visualize the feature importances in a way that is similar to the way we visualize the coefficients in the linear model (Figure 2-28):

In[61]:

def plot_feature_importances_cancer(model):
    n_features = cancer.data.shape[1]
    plt.barh(np.arange(n_features), model.feature_importances_, align='center')
    plt.yticks(np.arange(n_features), cancer.feature_names)
    plt.xlabel("Feature importance")
    plt.ylabel("Feature")
    plt.ylim(-1, n_features)

plot_feature_importances_cancer(tree)

Figure 2-28. Feature importances computed from a decision tree learned on the Breast Cancer dataset

Here we see that the feature used in the top split (“worst radius”) is by far the most important feature. This confirms our observation in analyzing the tree that the first level already separates the two classes fairly well.

However, if a feature has a low value in feature_importance_, it doesn’t mean that this feature is uninformative. It only means that the feature was not picked by the tree, likely because another feature encodes the same information.

In contrast to the coefficients in linear models, feature importances are always positive, and don’t encode which class a feature is indicative of. The feature importances tell us that “worst radius” is important, but not whether a high radius is indicative of a sample being benign or malignant. In fact, there might not be such a simple relationship between features and class, as you can see in the following example (Figures 2-29 and 2-30):

In[62]:

tree = mglearn.plots.plot_tree_not_monotone()
display(tree)

Out[62]:

Feature importances: [ 0.  1.]

Figure 2-29. A two-dimensional dataset in which the feature on the y-axis has a nonmonotonous relationship with the class label, and the decision boundaries found by a decision tree

Figure 2-30. Decision tree learned on the data shown in Figure 2-29

The plot shows a dataset with two features and two classes. Here, all the information is contained in X[1], and X[0] is not used at all. But the relation between X[1] and the output class is not monotonous, meaning we cannot say “a high value of X[1] means class 0, and a low value means class 1” (or vice versa).

While we focused our discussion here on decision trees for classification, all that was said is similarly true for decision trees for regression, as implemented in DecisionTreeRegressor. The usage and analysis of regression trees is very similar to that of classification trees. There is one particular property of using tree-based models for regression that we want to point out, though. The DecisionTreeRegressor (and all other tree-based regression models) is not able to extrapolate, or make predictions outside of the range of the training data.

Let’s look into this in more detail, using a dataset of historical computer memory (RAM) prices. Figure 2-31 shows the dataset, with the date on the x-axis and the price of one megabyte of RAM in that year on the y-axis:

In[63]:

import os
ram_prices = pd.read_csv(os.path.join(mglearn.datasets.DATA_PATH,
                                      "ram_price.csv"))

plt.semilogy(ram_prices.date, ram_prices.price)
plt.xlabel("Year")
plt.ylabel("Price in $/Mbyte")

Figure 2-31. Historical development of the price of RAM, plotted on a log scale

Note the logarithmic scale of the y-axis. When plotting logarithmically, the relation seems to be quite linear and so should be relatively easy to predict, apart from some bumps.

We will make a forecast for the years after 2000 using the historical data up to that point, with the date as our only feature. We will compare two simple models: a DecisionTreeRegressor and LinearRegression. We rescale the prices using a logarithm, so that the relationship is relatively linear. This doesn’t make a difference for the DecisionTreeRegressor, but it makes a big difference for LinearRegression (we will discuss this in more depth in Chapter 4). After training the models and making predictions, we apply the exponential map to undo the logarithm transform. We make predictions on the whole dataset for visualization purposes here, but for a quantitative evaluation we would only consider the test dataset:

In[64]:

from sklearn.tree import DecisionTreeRegressor
# use historical data to forecast prices after the year 2000
data_train = ram_prices[ram_prices.date < 2000]
data_test = ram_prices[ram_prices.date >= 2000]

# predict prices based on date
X_train = data_train.date[:, np.newaxis]
# we use a log-transform to get a simpler relationship of data to target
y_train = np.log(data_train.price)

tree = DecisionTreeRegressor(max_depth=3).fit(X_train, y_train)
linear_reg = LinearRegression().fit(X_train, y_train)

# predict on all data
X_all = ram_prices.date[:, np.newaxis]

pred_tree = tree.predict(X_all)
pred_lr = linear_reg.predict(X_all)

# undo log-transform
price_tree = np.exp(pred_tree)
price_lr = np.exp(pred_lr)

Figure 2-32, created here, compares the predictions of the decision tree and the linear regression model with the ground truth:

In[65]:

plt.semilogy(data_train.date, data_train.price, label="Training data")
plt.semilogy(data_test.date, data_test.price, label="Test data")
plt.semilogy(ram_prices.date, price_tree, label="Tree prediction")
plt.semilogy(ram_prices.date, price_lr, label="Linear prediction")
plt.legend()

Figure 2-32. Comparison of predictions made by a linear model and predictions made by a regression tree on the RAM price data

The difference between the models is quite striking. The linear model approximates the data with a line, as we knew it would. This line provides quite a good forecast for the test data (the years after 2000), while glossing over some of the finer variations in both the training and the test data. The tree model, on the other hand, makes perfect predictions on the training data; we did not restrict the complexity of the tree, so it learned the whole dataset by heart. However, once we leave the data range for which the model has data, the model simply keeps predicting the last known point. The tree has no ability to generate “new” responses, outside of what was seen in the training data. This shortcoming applies to all models based on trees.⁹

Strengths, weaknesses, and parameters

As discussed earlier, the parameters that control model complexity in decision trees are the pre-pruning parameters that stop the building of the tree before it is fully developed. Usually, picking one of the pre-pruning strategies—setting either max_depth, max_leaf_nodes, or min_samples_leaf—is sufficient to prevent overfitting.

Decision trees have two advantages over many of the algorithms we’ve discussed so far: the resulting model can easily be visualized and understood by nonexperts (at least for smaller trees), and the algorithms are completely invariant to scaling of the data. As each feature is processed separately, and the possible splits of the data don’t depend on scaling, no preprocessing like normalization or standardization of features is needed for decision tree algorithms. In particular, decision trees work well when you have features that are on completely different scales, or a mix of binary and continuous features.

The main downside of decision trees is that even with the use of pre-pruning, they tend to overfit and provide poor generalization performance. Therefore, in most applications, the ensemble methods we discuss next are usually used in place of a single decision tree.

Random forests

As we just observed, a main drawback of decision trees is that they tend to overfit the training data. Random forests are one way to address this problem. A random forest is essentially a collection of decision trees, where each tree is slightly different from the others. The idea behind random forests is that each tree might do a relatively good job of predicting, but will likely overfit on part of the data. If we build many trees, all of which work well and overfit in different ways, we can reduce the amount of overfitting by averaging their results. This reduction in overfitting, while retaining the predictive power of the trees, can be shown using rigorous mathematics.

To implement this strategy, we need to build many decision trees. Each tree should do an acceptable job of predicting the target, and should also be different from the other trees. Random forests get their name from injecting randomness into the tree building to ensure each tree is different. There are two ways in which the trees in a random forest are randomized: by selecting the data points used to build a tree and by selecting the features in each split test. Let’s go into this process in more detail.

Analyzing random forests

Let’s apply a random forest consisting of five trees to the two_moons dataset we studied earlier:

In[66]:

from sklearn.ensemble import RandomForestClassifier
from sklearn.datasets import make_moons

X, y = make_moons(n_samples=100, noise=0.25, random_state=3)
X_train, X_test, y_train, y_test = train_test_split(X, y, stratify=y,
                                                    random_state=42)

forest = RandomForestClassifier(n_estimators=5, random_state=2)
forest.fit(X_train, y_train)

The trees that are built as part of the random forest are stored in the estimator_ attribute. Let’s visualize the decision boundaries learned by each tree, together with their aggregate prediction as made by the forest (Figure 2-33):

In[67]:

fig, axes = plt.subplots(2, 3, figsize=(20, 10))
for i, (ax, tree) in enumerate(zip(axes.ravel(), forest.estimators_)):
    ax.set_title("Tree {}".format(i))
    mglearn.plots.plot_tree_partition(X_train, y_train, tree, ax=ax)

mglearn.plots.plot_2d_separator(forest, X_train, fill=True, ax=axes[-1, -1],
                                alpha=.4)
axes[-1, -1].set_title("Random Forest")
mglearn.discrete_scatter(X_train[:, 0], X_train[:, 1], y_train)

You can clearly see that the decision boundaries learned by the five trees are quite different. Each of them makes some mistakes, as some of the training points that are plotted here were not actually included in the training sets of the trees, due to the bootstrap sampling.

The random forest overfits less than any of the trees individually, and provides a much more intuitive decision boundary. In any real application, we would use many more trees (often hundreds or thousands), leading to even smoother boundaries.

Figure 2-33. Decision boundaries found by five randomized decision trees and the decision boundary obtained by averaging their predicted probabilities

As another example, let’s apply a random forest consisting of 100 trees on the Breast Cancer dataset:

In[68]:

X_train, X_test, y_train, y_test = train_test_split(
    cancer.data, cancer.target, random_state=0)
forest = RandomForestClassifier(n_estimators=100, random_state=0)
forest.fit(X_train, y_train)

print("Accuracy on training set: {:.3f}".format(forest.score(X_train, y_train)))
print("Accuracy on test set: {:.3f}".format(forest.score(X_test, y_test)))

Out[68]:

Accuracy on training set: 1.000
Accuracy on test set: 0.972

The random forest gives us an accuracy of 97%, better than the linear models or a single decision tree, without tuning any parameters. We could adjust the max_features setting, or apply pre-pruning as we did for the single decision tree. However, often the default parameters of the random forest already work quite well.

Similarly to the decision tree, the random forest provides feature importances, which are computed by aggregating the feature importances over the trees in the forest. Typically, the feature importances provided by the random forest are more reliable than the ones provided by a single tree. Take a look at Figure 2-34.

In[69]:

plot_feature_importances_cancer(forest)

Figure 2-34. Feature importances computed from a random forest that was fit to the Breast Cancer dataset

As you can see, the random forest gives nonzero importance to many more features than the single tree. Similarly to the single decision tree, the random forest also gives a lot of importance to the “worst radius” feature, but it actually chooses “worst perimeter” to be the most informative feature overall. The randomness in building the random forest forces the algorithm to consider many possible explanations, the result being that the random forest captures a much broader picture of the data than a single tree.

Gradient boosted regression trees (gradient boosting machines)

The gradient boosted regression tree is another ensemble method that combines multiple decision trees to create a more powerful model. Despite the “regression” in the name, these models can be used for regression and classification. In contrast to the random forest approach, gradient boosting works by building trees in a serial manner, where each tree tries to correct the mistakes of the previous one. By default, there is no randomization in gradient boosted regression trees; instead, strong pre-pruning is used. Gradient boosted trees often use very shallow trees, of depth one to five, which makes the model smaller in terms of memory and makes predictions faster. The main idea behind gradient boosting is to combine many simple models (in this context known as weak learners), like shallow trees. Each tree can only provide good predictions on part of the data, and so more and more trees are added to iteratively improve performance.

Gradient boosted trees are frequently the winning entries in machine learning competitions, and are widely used in industry. They are generally a bit more sensitive to parameter settings than random forests, but can provide better accuracy if the parameters are set correctly.

Apart from the pre-pruning and the number of trees in the ensemble, another important parameter of gradient boosting is the learning_rate, which controls how strongly each tree tries to correct the mistakes of the previous trees. A higher learning rate means each tree can make stronger corrections, allowing for more complex models. Adding more trees to the ensemble, which can be accomplished by increasing n_estimators, also increases the model complexity, as the model has more chances to correct mistakes on the training set.

Here is an example of using GradientBoostingClassifier on the Breast Cancer dataset. By default, 100 trees of maximum depth 3 and a learning rate of 0.1 are used:

In[70]:

from sklearn.ensemble import GradientBoostingClassifier

X_train, X_test, y_train, y_test = train_test_split(
    cancer.data, cancer.target, random_state=0)

gbrt = GradientBoostingClassifier(random_state=0)
gbrt.fit(X_train, y_train)

print("Accuracy on training set: {:.3f}".format(gbrt.score(X_train, y_train)))
print("Accuracy on test set: {:.3f}".format(gbrt.score(X_test, y_test)))

Out[70]:

Accuracy on training set: 1.000
Accuracy on test set: 0.958

As the training set accuracy is 100%, we are likely to be overfitting. To reduce overfitting, we could either apply stronger pre-pruning by limiting the maximum depth or lower the learning rate:

In[71]:

gbrt = GradientBoostingClassifier(random_state=0, max_depth=1)
gbrt.fit(X_train, y_train)

print("Accuracy on training set: {:.3f}".format(gbrt.score(X_train, y_train)))
print("Accuracy on test set: {:.3f}".format(gbrt.score(X_test, y_test)))

Out[71]:

Accuracy on training set: 0.991
Accuracy on test set: 0.972

In[72]:

gbrt = GradientBoostingClassifier(random_state=0, learning_rate=0.01)
gbrt.fit(X_train, y_train)

print("Accuracy on training set: {:.3f}".format(gbrt.score(X_train, y_train)))
print("Accuracy on test set: {:.3f}".format(gbrt.score(X_test, y_test)))

Out[72]:

Accuracy on training set: 0.988
Accuracy on test set: 0.965

Both methods of decreasing the model complexity reduced the training set accuracy, as expected. In this case, lowering the maximum depth of the trees provided a significant improvement of the model, while lowering the learning rate only increased the generalization performance slightly.

As for the other decision tree–based models, we can again visualize the feature importances to get more insight into our model (Figure 2-35). As we used 100 trees, it is impractical to inspect them all, even if they are all of depth 1:

In[73]:

gbrt = GradientBoostingClassifier(random_state=0, max_depth=1)
gbrt.fit(X_train, y_train)

plot_feature_importances_cancer(gbrt)

Figure 2-35. Feature importances computed from a gradient boosting classifier that was fit to the Breast Cancer dataset

We can see that the feature importances of the gradient boosted trees are somewhat similar to the feature importances of the random forests, though the gradient boosting completely ignored some of the features.

As both gradient boosting and random forests perform well on similar kinds of data, a common approach is to first try random forests, which work quite robustly. If random forests work well but prediction time is at a premium, or it is important to squeeze out the last percentage of accuracy from the machine learning model, moving to gradient boosting often helps.

If you want to apply gradient boosting to a large-scale problem, it might be worth looking into the xgboost package and its Python interface, which at the time of writing is faster (and sometimes easier to tune) than the scikit-learn implementation of gradient boosting on many datasets.

Linear models and nonlinear features

As you saw in Figure 2-15, linear models can be quite limiting in low-dimensional spaces, as lines and hyperplanes have limited flexibility. One way to make a linear model more flexible is by adding more features—for example, by adding interactions or polynomials of the input features.

Let’s look at the synthetic dataset we used in “Feature importance in trees” (see Figure 2-29):

In[74]:

X, y = make_blobs(centers=4, random_state=8)
y = y % 2

mglearn.discrete_scatter(X[:, 0], X[:, 1], y)
plt.xlabel("Feature 0")
plt.ylabel("Feature 1")

Figure 2-36. Two-class classification dataset in which classes are not linearly separable

A linear model for classification can only separate points using a line, and will not be able to do a very good job on this dataset (see Figure 2-37):

In[75]:

from sklearn.svm import LinearSVC
linear_svm = LinearSVC().fit(X, y)

mglearn.plots.plot_2d_separator(linear_svm, X)
mglearn.discrete_scatter(X[:, 0], X[:, 1], y)
plt.xlabel("Feature 0")
plt.ylabel("Feature 1")

Now let’s expand the set of input features, say by also adding feature1 ** 2, the square of the second feature, as a new feature. Instead of representing each data point as a two-dimensional point, (feature0, feature1), we now represent it as a three-dimensional point, (feature0, feature1, feature1 ** 2).¹⁰ This new representation is illustrated in Figure 2-38 in a three-dimensional scatter plot:

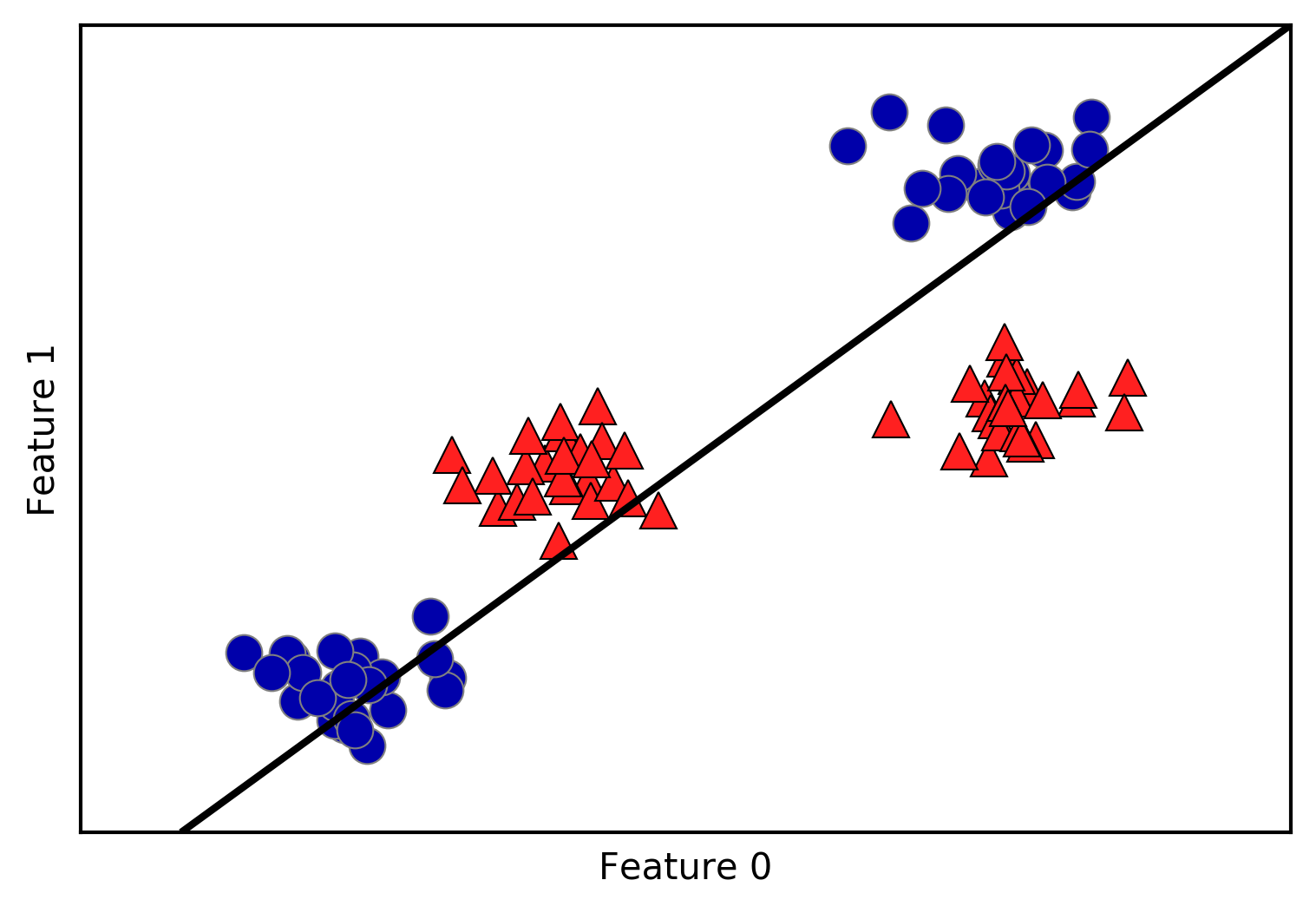
Figure 2-37. Decision boundary found by a linear SVM

In[76]:

# add the squared second feature
X_new = np.hstack([X, X[:, 1:] ** 2])

from mpl_toolkits.mplot3d import Axes3D, axes3d
figure = plt.figure()
# visualize in 3D
ax = Axes3D(figure, elev=-152, azim=-26)
# plot first all the points with y == 0, then all with y == 1
mask = y == 0
ax.scatter(X_new[mask, 0], X_new[mask, 1], X_new[mask, 2], c='b',
           cmap=mglearn.cm2, s=60, edgecolor='k')
ax.scatter(X_new[~mask, 0], X_new[~mask, 1], X_new[~mask, 2], c='r', marker='^',
           cmap=mglearn.cm2, s=60, edgecolor='k')
ax.set_xlabel("feature0")
ax.set_ylabel("feature1")
ax.set_zlabel("feature1 ** 2")

Figure 2-38. Expansion of the dataset shown in Figure 2-37, created by adding a third feature derived from feature1

In the new representation of the data, it is now indeed possible to separate the two classes using a linear model, a plane in three dimensions. We can confirm this by fitting a linear model to the augmented data (see Figure 2-39):

In[77]:

linear_svm_3d = LinearSVC().fit(X_new, y)
coef, intercept = linear_svm_3d.coef_.ravel(), linear_svm_3d.intercept_

# show linear decision boundary
figure = plt.figure()
ax = Axes3D(figure, elev=-152, azim=-26)
xx = np.linspace(X_new[:, 0].min() - 2, X_new[:, 0].max() + 2, 50)
yy = np.linspace(X_new[:, 1].min() - 2, X_new[:, 1].max() + 2, 50)

XX, YY = np.meshgrid(xx, yy)
ZZ = (coef[0] * XX + coef[1] * YY + intercept) / -coef[2]
ax.plot_surface(XX, YY, ZZ, rstride=8, cstride=8, alpha=0.3)
ax.scatter(X_new[mask, 0], X_new[mask, 1], X_new[mask, 2], c='b',
           cmap=mglearn.cm2, s=60, edgecolor='k')
ax.scatter(X_new[~mask, 0], X_new[~mask, 1], X_new[~mask, 2], c='r', marker='^',
           cmap=mglearn.cm2, s=60, edgecolor='k')

ax.set_xlabel("feature0")
ax.set_ylabel("feature1")
ax.set_zlabel("feature1 ** 2")

Figure 2-39. Decision boundary found by a linear SVM on the expanded three-dimensional dataset

As a function of the original features, the linear SVM model is not actually linear anymore. It is not a line, but more of an ellipse, as you can see from the plot created here (Figure 2-40):

In[78]:

ZZ = YY ** 2
dec = linear_svm_3d.decision_function(np.c_[XX.ravel(), YY.ravel(), ZZ.ravel()])
plt.contourf(XX, YY, dec.reshape(XX.shape), levels=[dec.min(), 0, dec.max()],
             cmap=mglearn.cm2, alpha=0.5)
mglearn.discrete_scatter(X[:, 0], X[:, 1], y)
plt.xlabel("Feature 0")
plt.ylabel("Feature 1")

Figure 2-40. The decision boundary from Figure 2-39 as a function of the original two features

The kernel trick

The lesson here is that adding nonlinear features to the representation of our data can make linear models much more powerful. However, often we don’t know which features to add, and adding many features (like all possible interactions in a 100-dimensional feature space) might make computation very expensive. Luckily, there is a clever mathematical trick that allows us to learn a classifier in a higher-dimensional space without actually computing the new, possibly very large representation. This is known as the kernel trick, and it works by directly computing the distance (more precisely, the scalar products) of the data points for the expanded feature representation, without ever actually computing the expansion.

There are two ways to map your data into a higher-dimensional space that are commonly used with support vector machines: the polynomial kernel, which computes all possible polynomials up to a certain degree of the original features (like feature1 ** 2 * feature2 ** 5); and the radial basis function (RBF) kernel, also known as the Gaussian kernel. The Gaussian kernel is a bit harder to explain, as it corresponds to an infinite-dimensional feature space. One way to explain the Gaussian kernel is that it considers all possible polynomials of all degrees, but the importance of the features decreases for higher degrees.¹¹

In practice, the mathematical details behind the kernel SVM are not that important, though, and how an SVM with an RBF kernel makes a decision can be summarized quite easily—we’ll do so in the next section.

Understanding SVMs

During training, the SVM learns how important each of the training data points is to represent the decision boundary between the two classes. Typically only a subset of the training points matter for defining the decision boundary: the ones that lie on the border between the classes. These are called support vectors and give the support vector machine its name.

To make a prediction for a new point, the distance to each of the support vectors is measured. A classification decision is made based on the distances to the support vector, and the importance of the support vectors that was learned during training (stored in the dual_coef_ attribute of SVC).

The distance between data points is measured by the Gaussian kernel:

• k_rbf(x₁, x₂) = exp (–ɣǁx₁ - x₂ǁ²)

Here, x₁ and x₂ are data points, ǁ x₁ - x₂ ǁ denotes Euclidean distance, and ɣ (gamma) is a parameter that controls the width of the Gaussian kernel.

Figure 2-41 shows the result of training a support vector machine on a two-dimensional two-class dataset. The decision boundary is shown in black, and the support vectors are larger points with the wide outline. The following code creates this plot by training an SVM on the forge dataset:

In[79]:

from sklearn.svm import SVC
X, y = mglearn.tools.make_handcrafted_dataset()
svm = SVC(kernel='rbf', C=10, gamma=0.1).fit(X, y)
mglearn.plots.plot_2d_separator(svm, X, eps=.5)
mglearn.discrete_scatter(X[:, 0], X[:, 1], y)
# plot support vectors
sv = svm.support_vectors_
# class labels of support vectors are given by the sign of the dual coefficients
sv_labels = svm.dual_coef_.ravel() > 0
mglearn.discrete_scatter(sv[:, 0], sv[:, 1], sv_labels, s=15, markeredgewidth=3)
plt.xlabel("Feature 0")
plt.ylabel("Feature 1")

Figure 2-41. Decision boundary and support vectors found by an SVM with RBF kernel

In this case, the SVM yields a very smooth and nonlinear (not a straight line) boundary. We adjusted two parameters here: the C parameter and the gamma parameter, which we will now discuss in detail.

Tuning SVM parameters

The gamma parameter is the one shown in the formula given in the previous section, which corresponds to the inverse of the width of the Gaussian kernel. Intuitively, the gamma parameter determines how far the influence of a single training example reaches, with low values meaning corresponding to a far reach, and high values to a limited reach. In other words, the wider the radius of the Gaussian kernel, the further the influence of each training example. The C parameter is a regularization parameter, similar to that used in the linear models. It limits the importance of each point (or more precisely, their dual_coef_).

Let’s have a look at what happens when we vary these parameters (Figure 2-42):

In[80]:

fig, axes = plt.subplots(3, 3, figsize=(15, 10))

for ax, C in zip(axes, [-1, 0, 3]):
    for a, gamma in zip(ax, range(-1, 2)):
        mglearn.plots.plot_svm(log_C=C, log_gamma=gamma, ax=a)

axes[0, 0].legend(["class 0", "class 1", "sv class 0", "sv class 1"],
                  ncol=4, loc=(.9, 1.2))

Figure 2-42. Decision boundaries and support vectors for different settings of the parameters C and gamma

Going from left to right, we increase the value of the parameter gamma from 0.1 to 10. A small gamma means a large radius for the Gaussian kernel, which means that many points are considered close by. This is reflected in very smooth decision boundaries on the left, and boundaries that focus more on single points further to the right. A low value of gamma means that the decision boundary will vary slowly, which yields a model of low complexity, while a high value of gamma yields a more complex model.

Going from top to bottom, we increase the C parameter from 0.1 to 1000. As with the linear models, a small C means a very restricted model, where each data point can only have very limited influence. You can see that at the top left the decision boundary looks nearly linear, with the misclassified points barely having any influence on the line. Increasing C, as shown on the bottom left, allows these points to have a stronger influence on the model and makes the decision boundary bend to correctly classify them.

Let’s apply the RBF kernel SVM to the Breast Cancer dataset. By default, C=1 and gamma=1/n_features:

In[81]:

X_train, X_test, y_train, y_test = train_test_split(
    cancer.data, cancer.target, random_state=0)

svc = SVC()
svc.fit(X_train, y_train)

print("Accuracy on training set: {:.2f}".format(svc.score(X_train, y_train)))
print("Accuracy on test set: {:.2f}".format(svc.score(X_test, y_test)))

Out[81]:

Accuracy on training set: 1.00
Accuracy on test set: 0.63

The model overfits quite substantially, with a perfect score on the training set and only 63% accuracy on the test set. While SVMs often perform quite well, they are very sensitive to the settings of the parameters and to the scaling of the data. In particular, they require all the features to vary on a similar scale. Let’s look at the minimum and maximum values for each feature, plotted in log-space (Figure 2-43):

In[82]:

plt.boxplot(X_train, manage_xticks=False)
plt.yscale("symlog")
plt.xlabel("Feature index")
plt.ylabel("Feature magnitude")

From this plot we can determine that features in the Breast Cancer dataset are of completely different orders of magnitude. This can be somewhat of a problem for other models (like linear models), but it has devastating effects for the kernel SVM. Let’s examine some ways to deal with this issue.

Figure 2-43. Feature ranges for the Breast Cancer dataset (note that the y axis has a logarithmic scale)

Preprocessing data for SVMs

One way to resolve this problem is by rescaling each feature so that they are all approximately on the same scale. A common rescaling method for kernel SVMs is to scale the data such that all features have 0 mean and unit variance, or that all features are between 0 and 1. We will see how to do this using the StandardScaler or MinMaxScaler preprocessing method in Chapter 3, where we’ll give more details. The best choice of preprocessing method depends on the properties of the dataset. For now, let’s do this “by hand”:

In[83]:

# compute the minimum value per feature on the training set
min_on_training = X_train.min(axis=0)
# compute the range of each feature (max - min) on the training set
range_on_training = (X_train - min_on_training).max(axis=0)

# subtract the min, and divide by range
# afterward, min=0 and max=1 for each feature
X_train_scaled = (X_train - min_on_training) / range_on_training
print("Minimum for each feature
", X_train_scaled.min(axis=0))
print("Maximum for each feature
", X_train_scaled.max(axis=0))

Out[83]:

Minimum for each feature
[0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
 0. 0. 0. 0. 0. 0.]
Maximum for each feature
 [1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
 1. 1. 1. 1. 1. 1.]

In[84]:

# use THE SAME transformation on the test set,
# using min and range of the training set (see Chapter 3 for details)
X_test_scaled = (X_test - min_on_training) / range_on_training

In[85]:

svc = SVC()
svc.fit(X_train_scaled, y_train)

print("Accuracy on training set: {:.3f}".format(
        svc.score(X_train_scaled, y_train)))
print("Accuracy on test set: {:.3f}".format(svc.score(X_test_scaled, y_test)))

Out[85]:

Accuracy on training set: 0.948
Accuracy on test set: 0.951

Scaling the data made a huge difference! Now we are actually in an underfitting regime, where training and test set performance are quite similar but less close to 100% accuracy. From here, we can try increasing either C or gamma to fit a more complex model. For example:

In[86]:

svc = SVC(C=1000)
svc.fit(X_train_scaled, y_train)

print("Accuracy on training set: {:.3f}".format(
    svc.score(X_train_scaled, y_train)))
print("Accuracy on test set: {:.3f}".format(svc.score(X_test_scaled, y_test)))

Out[86]:

Accuracy on training set: 0.988
Accuracy on test set: 0.972

Here, increasing C allows us to improve the model significantly, resulting in 97.2% accuracy.

Strengths, weaknesses, and parameters

Kernelized support vector machines are powerful models and perform well on a variety of datasets. SVMs allow for complex decision boundaries, even if the data has only a few features. They work well on low-dimensional and high-dimensional data (i.e., few and many features), but don’t scale very well with the number of samples. Running an SVM on data with up to 10,000 samples might work well, but working with datasets of size 100,000 or more can become challenging in terms of runtime and memory usage.

Another downside of SVMs is that they require careful preprocessing of the data and tuning of the parameters. This is why, these days, most people instead use tree-based models such as random forests or gradient boosting (which require little or no preprocessing) in many applications. Furthermore, SVM models are hard to inspect; it can be difficult to understand why a particular prediction was made, and it might be tricky to explain the model to a nonexpert.

Still, it might be worth trying SVMs, particularly if all of your features represent measurements in similar units (e.g., all are pixel intensities) and they are on similar scales.

The important parameters in kernel SVMs are the regularization parameter C, the choice of the kernel, and the kernel-specific parameters. Although we primarily focused on the RBF kernel, other choices are available in scikit-learn. The RBF kernel has only one parameter, gamma, which is the inverse of the width of the Gaussian kernel. gamma and C both control the complexity of the model, with large values in either resulting in a more complex model. Therefore, good settings for the two parameters are usually strongly correlated, and C and gamma should be adjusted together.

The neural network model

MLPs can be viewed as generalizations of linear models that perform multiple stages of processing to come to a decision.

Remember that the prediction by a linear regressor is given as:

• ŷ = w[0] * x[0] + w[1] * x[1] + ... + w[p] * x[p] + b

In plain English, ŷ is a weighted sum of the input features x[0] to x[p], weighted by the learned coefficients w[0] to w[p]. We could visualize this graphically as shown in Figure 2-44:

In[87]:

display(mglearn.plots.plot_logistic_regression_graph())

Figure 2-44. Visualization of logistic regression, where input features and predictions are shown as nodes, and the coefficients are connections between the nodes

Here, each node on the left represents an input feature, the connecting lines represent the learned coefficients, and the node on the right represents the output, which is a weighted sum of the inputs.

In an MLP this process of computing weighted sums is repeated multiple times, first computing hidden units that represent an intermediate processing step, which are again combined using weighted sums to yield the final result (Figure 2-45):

In[88]:

display(mglearn.plots.plot_single_hidden_layer_graph())

Figure 2-45. Illustration of a multilayer perceptron with a single hidden layer

This model has a lot more coefficients (also called weights) to learn: there is one between every input and every hidden unit (which make up the hidden layer), and one between every unit in the hidden layer and the output.

Computing a series of weighted sums is mathematically the same as computing just one weighted sum, so to make this model truly more powerful than a linear model, we need one extra trick. After computing a weighted sum for each hidden unit, a nonlinear function is applied to the result—usually the rectifying nonlinearity (also known as rectified linear unit or relu) or the tangens hyperbolicus (tanh). The result of this function is then used in the weighted sum that computes the output, ŷ. The two functions are visualized in Figure 2-46. The relu cuts off values below zero, while tanh saturates to –1 for low input values and +1 for high input values. Either nonlinear function allows the neural network to learn much more complicated functions than a linear model could:

In[89]:

line = np.linspace(-3, 3, 100)
plt.plot(line, np.tanh(line), label="tanh")
plt.plot(line, np.maximum(line, 0), label="relu")
plt.legend(loc="best")
plt.xlabel("x")
plt.ylabel("relu(x), tanh(x)")

Figure 2-46. The hyperbolic tangent activation function and the rectified linear activation function

For the small neural network pictured in Figure 2-45, the full formula for computing ŷ in the case of regression would be (when using a tanh nonlinearity):

• h[0] = tanh(w[0, 0] * x[0] + w[1, 0] * x[1] + w[2, 0] * x[2] + w[3, 0] * x[3] + b[0])
• h[1] = tanh(w[0, 1] * x[0] + w[1, 1] * x[1] + w[2, 1] * x[2] + w[3, 1] * x[3] + b[1])
• h[2] = tanh(w[0, 2] * x[0] + w[1, 2] * x[1] + w[2, 2] * x[2] + w[3, 2] * x[3] + b[2])
• ŷ = v[0] * h[0] + v[1] * h[1] + v[2] * h[2] + b

Here, w are the weights between the input x and the hidden layer h, and v are the weights between the hidden layer h and the output ŷ. The weights v and w are learned from data, x are the input features, ŷ is the computed output, and h are intermediate computations. An important parameter that needs to be set by the user is the number of nodes in the hidden layer. This can be as small as 10 for very small or simple datasets and as big as 10,000 for very complex data. It is also possible to add additional hidden layers, as shown in Figure 2-47:

In[90]:

mglearn.plots.plot_two_hidden_layer_graph()

Figure 2-47. A multilayer perceptron with two hidden layers

Having large neural networks made up of many of these layers of computation is what inspired the term “deep learning.”

Tuning neural networks

Let’s look into the workings of the MLP by applying the MLPClassifier to the two_moons dataset we used earlier in this chapter. The results are shown in Figure 2-48:

In[91]:

from sklearn.neural_network import MLPClassifier
from sklearn.datasets import make_moons

X, y = make_moons(n_samples=100, noise=0.25, random_state=3)

X_train, X_test, y_train, y_test = train_test_split(X, y, stratify=y,
                                                    random_state=42)

mlp = MLPClassifier(solver='lbfgs', random_state=0).fit(X_train, y_train)
mglearn.plots.plot_2d_separator(mlp, X_train, fill=True, alpha=.3)
mglearn.discrete_scatter(X_train[:, 0], X_train[:, 1], y_train)
plt.xlabel("Feature 0")
plt.ylabel("Feature 1")

Figure 2-48. Decision boundary learned by a neural network with 100 hidden units on the two_moons dataset

As you can see, the neural network learned a very nonlinear but relatively smooth decision boundary. We used solver='lbfgs', which we will discuss later.

By default, the MLP uses 100 hidden nodes, which is quite a lot for this small dataset. We can reduce the number (which reduces the complexity of the model) and still get a good result (Figure 2-49):

In[92]:

mlp = MLPClassifier(solver='lbfgs', random_state=0, hidden_layer_sizes=[10])
mlp.fit(X_train, y_train)
mglearn.plots.plot_2d_separator(mlp, X_train, fill=True, alpha=.3)
mglearn.discrete_scatter(X_train[:, 0], X_train[:, 1], y_train)
plt.xlabel("Feature 0")
plt.ylabel("Feature 1")

Figure 2-49. Decision boundary learned by a neural network with 10 hidden units on the two_moons dataset

With only 10 hidden units, the decision boundary looks somewhat more ragged. The default nonlinearity is relu, shown in Figure 2-46. With a single hidden layer, this means the decision function will be made up of 10 straight line segments. If we want a smoother decision boundary, we could add more hidden units (as in Figure 2-48), add a second hidden layer (Figure 2-50), or use the tanh nonlinearity (Figure 2-51):

In[93]:

# using two hidden layers, with 10 units each
mlp = MLPClassifier(solver='lbfgs', random_state=0,
                    hidden_layer_sizes=[10, 10])
mlp.fit(X_train, y_train)
mglearn.plots.plot_2d_separator(mlp, X_train, fill=True, alpha=.3)
mglearn.discrete_scatter(X_train[:, 0], X_train[:, 1], y_train)
plt.xlabel("Feature 0")
plt.ylabel("Feature 1")

In[94]:

# using two hidden layers, with 10 units each, now with tanh nonlinearity
mlp = MLPClassifier(solver='lbfgs', activation='tanh',
                    random_state=0, hidden_layer_sizes=[10, 10])
mlp.fit(X_train, y_train)
mglearn.plots.plot_2d_separator(mlp, X_train, fill=True, alpha=.3)
mglearn.discrete_scatter(X_train[:, 0], X_train[:, 1], y_train)
plt.xlabel("Feature 0")
plt.ylabel("Feature 1")

Figure 2-50. Decision boundary learned using 2 hidden layers with 10 hidden units each, with rect activation function

Figure 2-51. Decision boundary learned using 2 hidden layers with 10 hidden units each, with tanh activation function

Finally, we can also control the complexity of a neural network by using an l2 penalty to shrink the weights toward zero, as we did in ridge regression and the linear classifiers. The parameter for this in the MLPClassifier is alpha (as in the linear regression models), and it’s set to a very low value (little regularization) by default. Figure 2-52 shows the effect of different values of alpha on the two_moons dataset, using two hidden layers of 10 or 100 units each:

In[95]:

fig, axes = plt.subplots(2, 4, figsize=(20, 8))
for axx, n_hidden_nodes in zip(axes, [10, 100]):
    for ax, alpha in zip(axx, [0.0001, 0.01, 0.1, 1]):
        mlp = MLPClassifier(solver='lbfgs', random_state=0,
                            hidden_layer_sizes=[n_hidden_nodes, n_hidden_nodes],
                            alpha=alpha)
        mlp.fit(X_train, y_train)
        mglearn.plots.plot_2d_separator(mlp, X_train, fill=True, alpha=.3, ax=ax)
        mglearn.discrete_scatter(X_train[:, 0], X_train[:, 1], y_train, ax=ax)
        ax.set_title("n_hidden=[{}, {}]
alpha={:.4f}".format(
                      n_hidden_nodes, n_hidden_nodes, alpha))