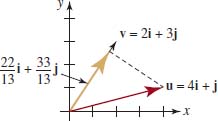5 Triangle Trigonometry
Chapter Outline
5.1 Right Triangle Trigonometry
5.2 Applications of Right Triangles
Introduction The word trigonometry (from the Greek trigonon meaning “triangle” and metria meaning “measurement”) refers to the measurement of triangles. In Section 4.2 we defined the trigonometric functions using coordinates of points on the unit circle and by using radian measure we were able to define the trigonometric functions of any angle. In this section we will show that the trigonometric functions of an acute angle in a right triangle have an equivalent definition in terms of the lengths of the sides of the triangle.
![]() Terminology In FIGURE 5.1.1(a)1 we have drawn a right triangle with sides labeled a, b, and c (indicating their respective lengths) and one of the acute angles denoted by θ. From the Pythagorean theorem we know that a2 + b2 = c2. The side opposite the right angle is called the hypotenuse; the remaining sides are referred to as the legs of the triangle. The legs labeled a and b are, in turn, said to be the side adjacent to the angle θ and the side opposite the angle θ. We will also use the abbreviations hyp, adj, and opp to denote the lengths of these sides.
Terminology In FIGURE 5.1.1(a)1 we have drawn a right triangle with sides labeled a, b, and c (indicating their respective lengths) and one of the acute angles denoted by θ. From the Pythagorean theorem we know that a2 + b2 = c2. The side opposite the right angle is called the hypotenuse; the remaining sides are referred to as the legs of the triangle. The legs labeled a and b are, in turn, said to be the side adjacent to the angle θ and the side opposite the angle θ. We will also use the abbreviations hyp, adj, and opp to denote the lengths of these sides.
FIGURE 5.1.1 In (a) and (b) the right triangles are the same
If we place θ in standard position and draw a unit circle centered at the origin, we see from Figure 5.1.1(b) that there are two similar right triangles containing the same angle θ. Since corresponding sides of similar triangles are proportional, it follows that
![]()
Also, we have
![]()
Then, applying the reciprocal identities (12) in Section 4.4, each trigonometric function of can be written as the ratio of the lengths of the sides of a right triangle as follows. See FIGURE 5.1.2.
FIGURE 5.1.2 Defining the trigonometric functions of θ
DEFINITION 5.1.1 Trigonometric Functions of u in a Right Triangle
For an acute angle in a right triangle as shown in FIGURE 5.1.2,

EXAMPLE 1 Values of the Six Trigonometric Functions
Find the exact values of the six trigonometric functions of the angle in the right triangle shown in FIGURE 5.1.3.
Solution From FIGURE 5.1.3 we see that the side opposite has length 8 and the side adjacent has length 15. From the Pythagorean theorem the hypotenuse c is
![]()
Thus from (1) the values of the six trigonometric functions are

FIGURE 5.1.3 Right triangle in Example 1
EXAMPLE 2 Using a Right Triangle Sketch
If θ is an acute angle and ![]() find the values of the other trigonometric functions of θ
find the values of the other trigonometric functions of θ
Solution We sketch a right triangle with an acute angle θ satisfying ![]() by making opp = 2 and hyp = 7 as shown in FIGURE 5.1.4. From the Pythagorean theorem we have
by making opp = 2 and hyp = 7 as shown in FIGURE 5.1.4. From the Pythagorean theorem we have

Thus,
The values of the remaining five trigonometric functions are obtained from the definitions in (1):

FIGURE 5.1.4 Right triangle in Example 2
![]() Solving Right Triangles Applications of right triangle trigonometry in fields such as surveying and navigation involve solving right triangles. The expression “to solve a triangle” means that we wish to find the length of each side and the measure of each angle in the triangle. We can solve any right triangle if we know either two sides or one acute angle and one side. As the following examples will show, sketching and labeling the triangle is an essential part of the solution process. It will be our general practice to label a right triangle as shown in FIGURE 5.1.5. The three vertices will be denoted by A, B, and C, with C at the vertex of the right angle. We denote the angles at A and B by and α and β the lengths of the sides opposite these angles by a and b, respectively. The length of the side opposite the right angle at C is denoted by c.
Solving Right Triangles Applications of right triangle trigonometry in fields such as surveying and navigation involve solving right triangles. The expression “to solve a triangle” means that we wish to find the length of each side and the measure of each angle in the triangle. We can solve any right triangle if we know either two sides or one acute angle and one side. As the following examples will show, sketching and labeling the triangle is an essential part of the solution process. It will be our general practice to label a right triangle as shown in FIGURE 5.1.5. The three vertices will be denoted by A, B, and C, with C at the vertex of the right angle. We denote the angles at A and B by and α and β the lengths of the sides opposite these angles by a and b, respectively. The length of the side opposite the right angle at C is denoted by c.
FIGURE 5.1.5 Standard labeling for a right triangle
EXAMPLE 3 Solving a Right Triangle
Solve the right triangle having a hypotenuse of 4![]() length and one 60° angle.
length and one 60° angle.
Solution First we make a sketch of the triangle and label it as shown in FIGURE 5.1.6. We wish to find a, b, and β. Since α and β are complementary angles, α + β = 90° yields
![]()
FIGURE 5.1.6 Right triangle in Example 3
We are given the length of the hypotenuse, namely, hyp = 4![]() To find a, the length of the side opposite the angle α = 60°, we select the sine function. From sin α = opp/hyp, we obtain
To find a, the length of the side opposite the angle α = 60°, we select the sine function. From sin α = opp/hyp, we obtain
![]()
Since sin60° ![]() /2, we have
/2, we have
![]()
Finally, to find the length b of the side adjacent to the 60° we select the cosine function. From cos α = odj/hyp, we obtain
![]()
Because cos60° = ![]() , we find
, we find
![]()
In Example 3 once we determined a, we could have found b by using either the Pythagorean theorem or the tangent function. In general, there are usually several ways to solve a triangle.
![]() Use of a Calculator If angles other than 30°, 45°, or 60° are involved in a problem, we can obtain approximations of the desired trigonometric function values with a calculator. For the remainder of this chapter, whenever an approximation is used, we will round the final results to the nearest hundredth unless the problem specifies otherwise. To take full advantage of the calculator’s accuracy, store the computed values of the trigonometric functions in the calculator for subsequent calculations. If, instead, a rounded version of a displayed value is written down and then later keyed back into the calculator, the accuracy of the final result may be diminished.
Use of a Calculator If angles other than 30°, 45°, or 60° are involved in a problem, we can obtain approximations of the desired trigonometric function values with a calculator. For the remainder of this chapter, whenever an approximation is used, we will round the final results to the nearest hundredth unless the problem specifies otherwise. To take full advantage of the calculator’s accuracy, store the computed values of the trigonometric functions in the calculator for subsequent calculations. If, instead, a rounded version of a displayed value is written down and then later keyed back into the calculator, the accuracy of the final result may be diminished.
EXAMPLE 4 Solving a Right Triangle
Solve the right triangle with legs of length 4 and 5.
Solution After sketching and labeling the triangle as shown in FIGURE 5.1.7, we see that we need to find c, α and β. From the Pythagorean theorem, the hypotenuse c is given by
![]()
To find β we use tan β = opp/adj. (By choosing to work with the given quantities, we avoid error due to previous approximations.) Thus we have
![]()
From a calculator set in degree mode, we find β ≈ 38.66°. since α = 90° − β, we obtain α ≈ 51.34°.
FIGURE 5.1.7 Right triangle in Example 4
5.1 Exercises Answers to selected odd-numbered problems begin on page ANS-16.
In Problems 1–10, find the values of the six trigonometric functions of the angle θ in the given triangle.
1. 
FIGURE 5.1.8 Triangle for Problem 1
2. 
FIGURE 5.1.9 Triangle for Problem 2
3. 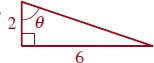
FIGURE 5.1.10 Triangle for Problem 3
4. 
FIGURE 5.1.11 Triangle for Problem 4
5. 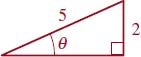
FIGURE 5.1.12 Triangle for Problem 5
6. 
FIGURE 5.1.13 Triangle for Problem 6
7. 
FIGURE 5.1.14 Triangle for Problem 7
8. 
FIGURE 5.1.15 Triangle for Problem 8
9. 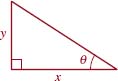
FIGURE 5.1.16 Triangle for Problem 9
10. 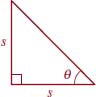
FIGURE 5.1.17 Triangle for Problem 10
In Problems 11–22, find the indicated unknowns. Each problem refers to the triangle shown in FIGURE 5.1.18.
11. a = 4, β = 27°; b, c
12. c = 10, β = 49°; a, b
13. b = 8, β = 34.33°; a, c
14. c = 25, α = 50°; a, b
15. b = 1.5, c = 3; α, β, a
16. a = 5, b = 2; α, β, c
17. a = 4, b = 10; α, β, c
18. b = 4, α = 58°; a, c
19. a = 9, c = 12; α, β, b
20. b = 3, c = 6; α, β, a
21. b = 20, α =23°; a, c
22. a = 11, α = 33.5°; b, c
FIGURE 5.1.18 Triangle for Problems 11–22
In Problems 23 and 24, solve for x in the given triangle.
23. 
FIGURE 5.1.19 Triangle for Problem 23
24. 
FIGURE 5.1.20 Triangle for Problem 24
For Discussion
For Problems 25 and 26, you should be familiar with the concepts and notation used in Section 4.11.
25. (a) A regular n-gon is an n-sided polygon inscribed in a circle; the polygon is formed by n equally spaced points on the circle. Suppose the polygon shown in FIGURE 5.1.21 represents a regular n-gon inscribed in a circle of radius r. Use right triangle trigonometry to show that the area A(n) of the n-gon is given by

(b) It stands to reason that the area A(n) approaches the area of the circle as the number of sides of the n-gon increases. Compute A100 and A1000.
FIGURE 5.1.21 Inscribed n-gon in Problem 25
(c) Let x = 2π /n in A(n) and note that as n → ∞ then x → 0. Use (1) of Section 4.11 to show that ![]() A(n) = πr2
A(n) = πr2
26. Consider a circle centered at the origin O with radius 1. As shown in FIGURE 5.1.22(a), let the shaded region OPR be a sector of the circle with central angle t such that 0 < t < π/2. We see from Figures 5.1.22(b)–(d) that
![]()
(a) Use right triangle trigonometry to show that the area of ΔOPR is ![]() sin t. and that the area of ΔOQR is
sin t. and that the area of ΔOQR is ![]() tan t.
tan t.
(b) Since the area of a sector of a circle is ![]() r2θ, where r is its radius and θ is measured in radians, it follows that the area of sector OPR is
r2θ, where r is its radius and θ is measured in radians, it follows that the area of sector OPR is ![]() t. Use this result, along with the areas in part (a), to show that the inequality in (2) yields
t. Use this result, along with the areas in part (a), to show that the inequality in (2) yields
![]()
(c) Discuss how the preceding inequality proves (1) of Section 4.11 when we let t → 0+.
FIGURE 5.1.22 Unit circle in Problem 26
FIGURE 5.1.23 Points in Problem 27
27. For the points P(x, y) and Q(x1, 0),x1 < x, in FIGURE 5.1.23, show that
![]()
[Hint: Use the identity in Problem 59 in Exercises 4.6.]
Introduction Right triangle trigonometry can be used to solve many practical problems, particularly those involving lengths, heights, and distances.
EXAMPLE 1 Finding the Height of a Tree
A kite is caught in the top branches of a tree. If the 90-ft kite string makes an angle of 22° with the ground, estimate the height of the tree by finding the distance from the kite to the ground.
Solution Let h denote the height of the kite. From FIGURE 5.2.1 we see that
![]()
A calculator set in degree mode gives h ≈ 33.71 ft
FIGURE 5.2.1 Tree in Example 1
EXAMPLE 2 Length of a Saw Cut
A carpenter cuts the end of a 4-in.-wide board on a bevel from the vertical, starting at a point 1![]() in. from the end of the board. Find the lengths of the diagonal cut and the remaining side. See FIGURE 5.2.2.
in. from the end of the board. Find the lengths of the diagonal cut and the remaining side. See FIGURE 5.2.2.
Solution Let x, y, and z be the (unknown) dimensions, as labeled in Figure 5.2.2. It follows from the definition of the tangent function that
![]()
To find y we observe that
![]()
![]()
FIGURE 5.2.2 Saw cut in Example 2
![]() Angles of Elevation and Depression The angle between an observer’s line of sight to an object and the horizontal is given a special name. As FIGURE 5.2.3 illustrates, if the line of sight is to an object above the horizontal, the angle is called an angle of elevation, whereas if the line of sight is to an object below the horizontal, the angle is called an angle of depression.
Angles of Elevation and Depression The angle between an observer’s line of sight to an object and the horizontal is given a special name. As FIGURE 5.2.3 illustrates, if the line of sight is to an object above the horizontal, the angle is called an angle of elevation, whereas if the line of sight is to an object below the horizontal, the angle is called an angle of depression.
FIGURE 5.2.3 Angles of elevation and depression
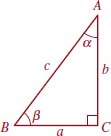
EXAMPLE 3 Using Angles of Elevation
A surveyor uses an instrument called a theodolite to measure the angle of elevation between ground level and the top of a mountain. At one point the angle of elevation is measured to be 41°. A half kilometer farther from the base of the mountain, the angle of elevation is measured to be 37°. How high is the mountain?
Solution Let h represent the height of the mountain. FIGURE 5.2.4 shows that there are two right triangles sharing the common side h, so we obtain two equations in two unknowns z and h:

We can solve each of these for h, obtaining, respectively,
h = (z + 0.5)tan 37° and h = ztan41°.
Equating the last two results gives an equation from which we can determine the distance z:
![]()
FIGURE 5.2.4 Mountain in Example 3
Solving for z gives us
![]()
Using h = z tan41° we find the height h of the mountain to be
![]()
EXAMPLE 4 Glide Path
Most airplanes approach San Francisco International Airport (SFO) on a straight glide path starting at a point 5.5 mi from the field. A few years ago, the FAA experimented with a computerized two-segment approach where a plane approaches the field on a 6° glide path starting at a point 5.5 mi out and then switches to a 3° glide path 1.5 mi from the point of touchdown. The point of this experimental approach was to reduce the noise of the planes over the outlying residential areas. Compare the height of a plane P′ using the standard 3° approach with the height of a plane P using the experimental approach when both planes are 5.5 mi from the airport.
Solution For purposes of illustration, the angles and distances shown in FIGURE 5.2.5 are exaggerated.
FIGURE 5.2.5 Glide paths in Example 4
First, suppose y is the height of plane P′ on the standard approach when it is 5.5 mi out from the airport. As we see in Figure 5.2.5(a),
![]()
Because distances from the airport are measured in miles, we convert y to feet
y = 5.5(5280) tan 3°ft ≈ 1522 ft.
Now, suppose z is the height of plane P on the experimental approach when it is 5.5 mi out from the airport. As shown in Figure 5.2.5(b), z = x + w, so we use two right triangles to obtain
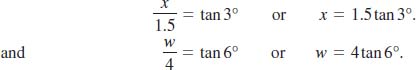
Hence the approximate height of plane P at a point 5.5 mi out from the airport is
z = x + w
= 1.5 tan3° + 4 tan6°
= 1.5(5280)tan 3° + 4(5280) tan 6° ≈ 2635 ft.
In other words, plane P is approximately 1113 ft higher than plane P′.
![]() Building a Function Section 2.8 was devoted to setting up or constructing functions that were described or expressed in words. As emphasized in that section, this is a task that you will surely face in a course in calculus. Our final example illustrates a recommended procedure of sketching a figure and labeling quantities of interest with appropriate variables.
Building a Function Section 2.8 was devoted to setting up or constructing functions that were described or expressed in words. As emphasized in that section, this is a task that you will surely face in a course in calculus. Our final example illustrates a recommended procedure of sketching a figure and labeling quantities of interest with appropriate variables.
EXAMPLE 5 Functions That Involve Trigonometry
A plane flying horizontally at an altitude of 2 miles approaches a radar station as shown in FIGURE 5.2.6.
(a) Express the distance d between the plane and the radar station as a function of the angle of elevation θ.
(b) Express the angle of elevation θ of the plane as a function of the horizontal separation x between the plane and the radar station.
Solution As shown in Figure 5.2.6, θ is an acute angle in a right triangle.
(a) We can relate the distance d and the angle θ by sin θ =2/d. Solving for d gives
![]()
Where 0 < θ ≤ 90°
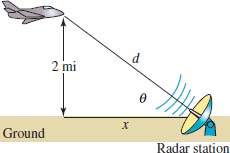
FIGURE 5.2.6 Plane in Example 5
(b) The horizontal separation x and θ are related by tan θ = 2/x. We make use of the inverse tangent function to solve for θ
![]()
where 0 < x < ∞
1. A building casts a shadow 20 m long. If the angle from the tip of the shadow to a point on top of the building is 69°, how high is the building?
2. Two trees are on opposite sides of a river, as shown in FIGURE 5.2.7. A baseline of 100 ft is measured from tree T1, and from that position the angle β to T2 is measured to be 29.7°. If the baseline is perpendicular to the line segment between T1 and T2, find the distance between the two trees.
3. A 50-ft tower is located on the edge of a river. The angle of elevation between the opposite bank and the top of the tower is 37°. How wide is the river?
4. A surveyor uses a geodometer to measure the straight-line distance from a point on the ground to a point on top of a mountain. Use the information given in FIGURE 5.2.8 to find the height of the mountain.
5. An observer on the roof of building A measures 27° a angle of depression between the horizontal and the base of building B. The angle of elevation from the same point to the roof of the second building is 41.42°. What is the height of building B if the height of building A is 150 ft? Assume buildings A and B are on the same horizontal plane.
FIGURE 5.2.7 Trees and river in Problem 2
FIGURE 5.2.8 Mountain in Problem 4
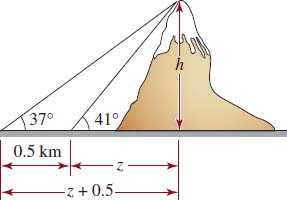
6. Find the height h of a mountain using the information given in FIGURE 5.2.9.
7. The top of a 20-ft ladder is leaning against the edge of the roof of a house. If the angle of inclination of the ladder from the horizontal is 51°, what is the approximate height of the house and how far is the bottom of the ladder from the base of the house?
8. An airplane flying horizontally at an altitude of 25,000 ft approaches a radar station located on a 2000-ft-high hill. At one instant in time, the angle between the radar dish pointed at the plane and the horizontal is 57°. What is the straight-line distance in miles between the airplane and the radar station at that particular instant?
9. A 5-mi straight segment of a road climbs a 4000-ft hill. Determine the angle that the road makes with the horizontal.
10. A box has dimensions as shown in FIGURE 5.2.10. Find the length of the diagonal between the corners P and Q. What is the angle θ formed between the diagonal and the bottom edge of the box?
11. Observers in two towns A and B on either side of a 12,000-ft mountain measure the angles of elevation between the ground and the top of the mountain. See FIGURE 5.2.11. Assuming that the towns and the mountaintop lie in the same vertical plane, find the horizontal distance between them.
12. A drawbridge* measures 7.5 m from shore to shore, and when completely open it makes an angle of 43° with the horizontal. See FIGURE 5.2.12(a). When the bridge is closed, the angle of depression from the shore to a point on the surface of the water below the opposite end is 27°. See Figure 5.2.12(b). When the bridge is fully open, what is the distance d between the highest point of the bridge and the water below?
FIGURE 5.2.9 Mountain in Problem 6
FIGURE 5.2.10 Box in Problem 10
FIGURE 5.2.11 Mountain in Problem 11
FIGURE 5.2.12 Drawbridge in Problem 12
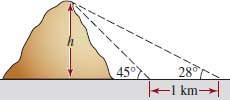
13. A flagpole is located at the edge of a sheer 50-ft cliff at the bank of a river of width 40 ft. See FIGURE 5.2.13. An observer on the opposite side of the river measures an angle of 9° between her line of sight to the top of the flagpole and her line of sight to the top of the cliff. Find the height of the flagpole.
14. From an observation site 1000 ft from the base of Mt. Rushmore the angle of elevation to the top of the sculpted head of George Washington is measured to be 80.05°, whereas the angle of elevation to the bottom of his head is 79.946°. Determine the height of George Washington’s head.
FIGURE 5.2.13 Flagpole in Problem 13

Bust of George Washington on Mt. Rushmore
15. The length of a Boeing 747 airplane is 231 ft. What is the plane’s altitude if it subtends an angle of 2° when it is directly above an observer on the ground? See FIGURE 5.2.14.
16. The height of a gnomon (pin) of a sundial is 4 in. If it casts a 6-in. shadow, what is the angle of elevation of the Sun?
17. Weather radar is capable of measuring both the angle of elevation to the top of a thunderstorm and its range (the horizontal distance to the storm). If the range of a storm is 90 km and the angle of elevation is 4°, can a passenger plane that is able to climb to 10 km fly over the storm?

Sundial
18. Cloud ceiling is the lowest altitude at which solid cloud is present. The cloud ceiling at airports must be sufficiently high for safe takeoffs and landings. At night the cloud ceiling can be determined by illuminating the base of the clouds with a searchlight pointed vertically upward. If an observer is 1 km from the searchlight and the angle of elevation to the base of the illuminated cloud is 8°, find the cloud ceiling. See FIGURE 5.2.15. (During the day cloud ceilings are generally estimated by sight. However, if an accurate reading is required, a balloon is inflated so that it will rise at a known constant rate. Then it is released and timed until it disappears into the cloud. The cloud ceiling is determined by multiplying the rate by the time of the ascent; trigonometry is not required for this calculation.)
19. Assuming that the Earth is a sphere, show that Cθ = Cecos θ, where Cθ is the circumference of the parallel of latitude at the latitude angle θ and Ce is the Earth’s circumference at the equator. See FIGURE 5.2.16. [Hint: Rcosθ = r. ]
FIGURE 5.2.14 Airplane in Problem 15
FIGURE 5.2.15 Searchlight in Problem 18
FIGURE 5.2.16 Earth in Problem 19
FIGURE 5.2.17 Angle in Problem 21
20. Use Problem 19 and the fact that the radius R of the Earth is 6400 km to find:
(a) the circumference of the Arctic Circle, which lies at 66°33′ N (66.55° N) latitude, and
(b) the distance “around the world” at the 58°40′ N (58.67° N) latitude.
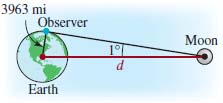
21. The distance between the Earth and the Moon varies as the Moon revolves around the Earth. At a particular time the geocentric parallax angle shown in FIGURE 5.2.17 is measured to be 1°. Calculate to the nearest hundred miles the distance between the center of the Earth and the center of the Moon at this instant. Assume that the radius of the Earth is 3963 miles.
22. The final length of a volcanic lava flow seems to decrease as the elevation of the lava vent from which it originates increases. An empirical study of Mt. Etna gives the final lava flow length L in terms of elevation h by the formula where L is measured in kilometers and h is measured in meters. Suppose that a Sicilian village at elevation 750 m is on a 10° slope directly below a lava vent at 2500 m. See FIGURE 5.2.18. According to the formula, how close will the lava flow get to the village?

Mt. Etna
FIGURE 5.2.18 Lava flow in Problem 22
FIGURE 5.2.19 Weather balloon in Problem 23
L = 23 − 0.0053h,
23. As shown in FIGURE 5.2.19, two tracking stations S1 and S2 sight a weather balloon between them at elevation angles α and β, respectively. Express the height h of the balloon in terms of α and β, and the distance c between the tracking stations.
24. An entry in a soapbox derby rolls down a hill. Using the information given in FIGURE 5.2.20, find the total distance d1 + d2 that the soapbox travels.
25. Find the height and area of the isosceles trapezoid shown in FIGURE 5.2.21.
FIGURE 5.2.20 Soapbox in Problem 24
FIGURE 5.2.21 Trapezoid in Problem 25
FIGURE 5.2.22 Escalator in Problem 26
FIGURE 5.2.23 Lighthouse in Problem 28
26. An escalator between the first and second floors of a department store is 58 ft long and makes an angle of 20° with the first floor. See FIGURE 5.2.22. Find the vertical distance between the floors.
27. Recent History According to the online encyclopedia Wikipedia, a French helicopter flown by Jean Boulet attained the world’s record height of 12,442 m in 1972. What would the angle of elevation to the helicopter have been from a point P on the ground 2000 m from the point directly beneath the helicopter?
28. Ancient History In an article from the online encyclopedia Wikipedia, the height h of the Lighthouse of Alexandria, one of the Seven Wonders of the Ancient World built between 280 and 247 B.C.E., is estimated to have been between 393 ft and 450 ft. The article goes on to say that there are ancient claims that the light could be seen on the ocean up to 29 miles away. Use the right triangle in FIGURE 5.2.23 along with the two given heights h to determine the accuracy of the 29 mile claim. Assume that the radius of the Earth is r = 3963 mi and s is distance measured in miles on the ocean. [Hint: Use 1 ft = 1/5280 mi and (7) of Section 4.1.]

Artist’s rendering of the Lighthouse of Alexandria
In Problems 29–32, proceed as in Example 5 and translate the words into an appropriate function.
29. A tracking telescope, located 1.25 km from the point of a rocket launch, follows a vertically ascending rocket. Express the height h of the rocket as a function of the angle of elevation θ.
30. A searchlight one-half mile offshore illuminates a point P on the shore. Express the distance d from the searchlight to the point of illumination P as a function of the angle θ shown in FIGURE 5.2.24.
31. A statue is placed on a pedestal as shown in FIGURE 5.2.25. Express the viewing angle θ as a function of the distance x from the pedestal.
FIGURE 5.2.24 Searchlight in Problem 30
FIGURE 5.2.25 Viewing angle in Problem 31
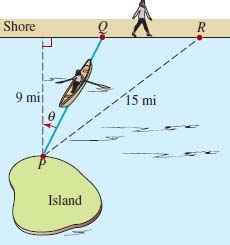
32. A woman on an island wishes to reach a point R on a straight shore on the mainland from a point P on the island. The point P is 9 mi from the shore and 15 mi from point R. See FIGURE 5.2.26. If the woman rows a boat at a rate of 3 mi/h to a point Q on the mainland, then walks the rest of the way at a rate of 5 mi/h, express the total time it takes the woman to reach point R as a function of the indicated angle θ. [Hint: Distance = rate × time.]
For Discussion
33. Consider the blue rectangle circumscribed around the red rectangle in FIGURE 5.2.27. With the aid of calculus it can be shown that the area of the blue rectangle is greatest when θ = π/4. Find this area in terms of a and b.
FIGURE 5.2.26 Woman rowing to shore in Problem 32
FIGURE 5.2.27 Rectangles in Problem 33
34. Home heating oil is often stored in a right circular cylindrical tank of diameter D that rests horizontally. As FIGURE 5.2.28 shows, the depth of the oil can be measured by inserting a dipstick down a vertical diameter. If the dipstick indicates that the depth of the oil is d inches, then show that the volume V of the oil is given by
![]()
where V0 is the volume of the tank. Although not necessary, assume for simplicity that the tank is less than half full as shown in the figure.
FIGURE 5.2.28 Oil tank in Problem 34
Introduction In Section 5.1 we saw how to solve right triangles. In this and the next section we consider two techniques for solving general triangles.
![]() Law of Sines Consider the triangle ABC, shown in FIGURE 5.3.1, with angles α, β, and γ, and corresponding opposite sides BC, AC, and AB. If we know the length of one side and two other parts of the triangle, we can then find the remaining three parts. One way of doing this is by the Law of Sines.
Law of Sines Consider the triangle ABC, shown in FIGURE 5.3.1, with angles α, β, and γ, and corresponding opposite sides BC, AC, and AB. If we know the length of one side and two other parts of the triangle, we can then find the remaining three parts. One way of doing this is by the Law of Sines.
FIGURE 5.3.1 General triangle
THEOREM 5.3.1 The Law of Sines
Suppose angles α, β, and γ, and opposite sides of length a, b, and c are as shown in FIGURE 5.3.1. Then
![]()
PROOF: Although the Law of Sines is valid for any triangle, we will prove it only for acute triangles—that is, a triangle in which all three angles α, β, and γ, are less than 90°. As shown in FIGURE 5.3.2, let h be the length of the altitude from vertex A to side BC. Since the altitude is perpendicular to the base BC it determines two right triangles. Consequently, we can write
FIGURE 5.3.2 Acute triangle
![]()
Thus (2) gives
![]()
Equating the two expressions in (3) gives c sin β = b sin γ so that
![]()
If we use the altitude from the vertex C to the side AB, it follows in the same manner that
![]()
Combining (4) and (5) yields the result in (1).
EXAMPLE 1 Determining the Parts of a Triangle
Find the remaining parts of the triangle shown in FIGURE 5.3.3.
FIGURE 5.3.3 Triangle in Example 1
Solution Let β = 20°, α = 130°, and b = 6. Because the sum of the angles in a triangle is 180° we have γ + 20° + 130 = 180° and so γ = 180° − 20° − 130° = 30°. From (1) we then see that
![]()
We use the first equality in (6) to solve for a:

The second equality in (6) gives c:
![]()
EXAMPLE 2 Height of a Building
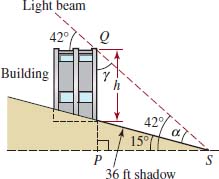
A building is situated on the side of a hill that slopes downward at an angle of 15°. The Sun is uphill from the building at an angle of elevation of 42°. Find the building’s height if it casts a shadow 36 ft long.
FIGURE 5.3.4 Triangle QPS in Example 2
Solution Denote the height of the building on the downward slope by h and construct a right triangle QPS as shown in FIGURE 5.3.4. Now α + 15° = 42° so that α = 27°. Since ΔQPS is a right triangle, γ + 42° = 90° gives γ = 90° − 42° = 48°. From the Law of Sines (1),
![]()
In Examples 1 and 2, where we were given two angles and a side opposite one of these angles, each triangle had a unique solution. However, this may not always be true for triangles where we know two sides and an angle opposite one of these sides. The next example illustrates the latter situation.
EXAMPLE 3 TWO Triangles
Find the remaining parts of the triangle with β = 50°, b = 5, and c = 6.
Solution From the Law of Sines, we have
![]()
From a calculator set in degree mode, we obtain γ ≈ 66.82°. At this point it is essential to recall that the sine function is also positive for second quadrant angles. In other words, there is another angle satisfying 0° ≤ γ ≤ 180° for which sin γ ≈ 0.9193. Using 66.82° as a reference angle we find the second quadrant angle to be 180° − 66.82° = 113.18°. Therefore, the two possibilities for γ are γ1 ≈ 66.82° and γ2 ≈ 113.18°. Thus, as shown in FIGURE 5.3.5, there are two possible triangles ABC1 and ABC2 satisfying the given three conditions.
FIGURE 5.3.5 Triangles in Example 3
To complete the solution of triangle ABC1 (Figure 5.3.5(a)), we first find α1 = 180° − γ1 − β or α1 ≈ 63.18°. To find the side opposite this angle we use
![]()
or a1 ≈ 5.82.
To complete the solution of triangle ABC2 (Figure 5.3.5(b)), we find α2 = 180° − γ2 − β or α2 < 16.82°. Then from
![]()
or a2 ≈ 1.89.
FIGURE 5.3.6 Horizontal base, the
![]() Ambiguous Case When solving triangles, the situation where two sides and an angle opposite one of these sides are given is called the ambiguous case. We have just seen in Example 3 that the given information may determine two different triangles. In the ambiguous case other complications can arise. For instance, suppose that the length of sides AB and AC (that is, c and b, respectively) and the angle β in triangle ABC are specified. As shown in FIGURE 5.3.6, we draw the angle β and mark off side AB with length c to locate the vertices A and B. The third vertex C is located on the base by drawing an arc of a circle of radius b (the length of AC) with center A. As shown in FIGURE 5.3.7, there are four possible outcomes of this construction:
Ambiguous Case When solving triangles, the situation where two sides and an angle opposite one of these sides are given is called the ambiguous case. We have just seen in Example 3 that the given information may determine two different triangles. In the ambiguous case other complications can arise. For instance, suppose that the length of sides AB and AC (that is, c and b, respectively) and the angle β in triangle ABC are specified. As shown in FIGURE 5.3.6, we draw the angle β and mark off side AB with length c to locate the vertices A and B. The third vertex C is located on the base by drawing an arc of a circle of radius b (the length of AC) with center A. As shown in FIGURE 5.3.7, there are four possible outcomes of this construction:
• The arc does not intersect the base and no triangle is formed.
• The arc intersects the base in two distinct points C1 and C2 and two triangles are formed (as in Example 3).
• The arc intersects the base in one point and one triangle is formed.
• The arc is tangent to the base and a single right triangle is formed.
FIGURE 5.3.7 Solution possibilities for the ambiguous case in the Law of Sines
EXAMPLE 4 Determining the Parts of a Triangle
Find the remaining parts of the triangle with β = 40°, b = 5, and c = 9.
Solution From the Law of Sines (1), we have
![]()
Since the sine of any angle must be between –1 and 1, sin γ ≈ 1.1570 is impossible. This means the triangle has no solution; the side with length b is not long enough to reach the base. This is the case illustrated in FIGURE 5.3.7(a).
5.3 Exercises Answers to selected odd-numbered problems begin on page ANS-16.
In Problems 1-16, refer to FIGURE 5.3.1. ![]()
In Problems 1–16, use the Law of Sines to solve the triangle.
1. α = 80°, β = 20°, b = 7
2. α = 60°, β = 15°, c = 30
3. β = 37°, b = 51°, a = 5
4. α = 30°, γ = 75°, a = 6
5. β = 72°, b = 12, c = 6
6. α = 120°, a = 9, c = 4
7. γ = 62°, b = 7, c= 4
8. β = 110°, γ = 25°, a = 14
9. γ = 62°, a = 8, c = 5
10. α = 55°, a = 20, c = 18
11. γ = 150°, b = 7, c = 5
12. α = 35°, a = 9, b = 12
13. β = 30°, a = 10, b = 7
14. α = 140°, γ = 20°, c =12
15. α = 20°, a = 8, c =27
16. α = 75°, γ = 45°, b =8
FIGURE 5.3.8 Pool in Problem 17
FIGURE 5.3.9 Telephone pole in Problem 19
Miscellaneous Applications
17. Length of a Pool A 10-ft rope that is available to measure the length between two points A and B at opposite ends of a kidney-shaped swimming pool is not long enough. A third point C is found such that the distance from A to C is 10 ft. It is determined that angle ACB is 115° and angle ABC is 35°. Find the distance from A to B. See FIGURE 5.3.8.
18. Width of a River Two points A and B lie on opposite sides of a river. Another point C is located on the same side of the river as B at a distance of 230 ft from B. If angle ABC is 105° and angle ACB is 20°, find the distance across the river from A to B.
19. Length of a Telephone Pole A telephone pole makes an angle of 82° with the level ground. As shown in FIGURE 5.3.9, the angle of elevation of the Sun is 76°. Find the length of the telephone pole if its shadow is 3.5 m. (Assume that the tilt of the pole is away from the Sun and in the same plane as the pole and the Sun.)
20. Not on the Level A man 5 ft 9 in. tall stands on a sidewalk that slopes down at a constant angle. A vertical street lamp directly behind him causes his shadow to be 25 ft long. The angle of depression from the top of the man to the tip of his shadow is 31°. Find the angle a, as shown in FIGURE 5.3.10, that the sidewalk makes with the horizontal.
21. How High? If the man in Problem 20 is 20 ft down the sidewalk from the street lamp, find the height of the light above the sidewalk.
22. Plane with an Altitude Angles of elevation to an airplane are measured from the top and the base of a building that is 20 m tall. The angle from the top of the building is 38°, and the angle from the base of the building is 40°. Find the altitude of the airplane.
23. Angle of Drive The distance from the tee to the green on a particular golf hole is 370 yd. A golfer hits his drive and paces its distance off at 210 yd. From the point where the ball lies, he measures an angle of 160° between the tee and the green. Find the angle of his drive off the tee measured from the dashed line from the tee to the green shown in FIGURE 5.3.11.
FIGURE 5.3.10 Sloping sidewalk in Problem 20
FIGURE 5.3.11 Angle of drive in Problem 23
24. In Problem 23, what is the distance from the ball to the green?
25. Help! One Coast Guard vessel is located 4 nautical miles due south of a second Coast Guard vessel when they receive a distress signal from a sailboat. To offer assistance, the first vessel sails on a bearing of S50°E at knots and the second vessel sails S10°E at 10 knots. Which one of the Coast Guard vessels reaches the sailboat first? [Hint: The concept of bearing is reviewed on page 297.]
Introduction Triangles for which we know either three sides or two sides and the included angle (that is, the angle formed by the given sides) cannot be solved directly using the Law of Sines. The method we consider next can be used to solve triangles in these two cases.
![]() Pythagorean Theorem In a right triangle, such as the one shown in FIGURE 5.4.1, the length c of the hypotenuse is related to the lengths a and b of the other two sides by the Pythagorean theorem
Pythagorean Theorem In a right triangle, such as the one shown in FIGURE 5.4.1, the length c of the hypotenuse is related to the lengths a and b of the other two sides by the Pythagorean theorem
![]()
This last equation is a special case of a general formula that relates the lengths of the sides of any triangle.
FIGURE 5.4.1 Right triangle
![]() Law of Cosines A generalization of (1) is called the Law of Cosines. Like the Law of Sines, (1) of Section 5.3, the Law of Cosines is valid for any triangle. But for convenience, we will prove the last two equations in (2) of Theorem 5.4.1 using again an acute triangle.
Law of Cosines A generalization of (1) is called the Law of Cosines. Like the Law of Sines, (1) of Section 5.3, the Law of Cosines is valid for any triangle. But for convenience, we will prove the last two equations in (2) of Theorem 5.4.1 using again an acute triangle.
THEOREM 5.4.1 The Law of Cosines
Suppose angles α, β, and γ, and opposite sides of lengths a, b, and c are as shown in FIGURE 5.3.1. Then

PROOF: Let P denote the point where the altitude from the vertex A intersects side BC. Then, since both ΔBPA and ΔCPA in FIGURE 5.4.2 are right triangles we have from (1),

FIGURE 5.4.2 Acute triangle
![]()
![]()
Now the length of BC is a = c cos β + b cos γ so that
![]()
Moreover, from (4),
![]()
Substituting (5) and (6) into (3) and simplifying yields the third equation in (2):

Note that equation (7) reduces to the Pythagorean theorem (1) when γ = 90°.
Similarly, if we use b cos γ = a − c cos β and h2 = c2 − (c cos β)2 to eliminate b cos γ and h2 in (4), we obtain the second equation in (2).
EXAMPLE 1 Determining the Parts of a Triangle
Find the remaining parts of the triangle shown in FIGURE 5.4.3.
FIGURE 5.4.3 Triangle in Example 1
Solution First, if we call the unknown side b and identify a = 12, c = 10, and β = 26°, then from the second equation in (2) we can write
b2 = (12)2 + (10)2 − 2(12)(10)cos 26°.
Therefore, b2 ≈ 28.2894 and so b ≈ 5.32.
Next, we use the Law of Cosines to determine the remaining angles in the triangle in FIGURE 5.4.3. If γ is the angle at the vertex C, then the third equation in (2) gives
![]()
With the aid of a calculator and the inverse cosine we find γ ≈ 55.51°. Note that since the cosine of an angle between 90° and 180° is negative, there is no need to consider two possibilities as we did in Example 3 in Section 5.3. Finally, the angle at the vertex A is α = 180° – β – γ or α ≈ 98.49°.
In Example 1, observe that after b is found, we know two sides and an angle opposite one of these sides. Hence we could have used the Law of Sines to find the angle γ.
In the next example we consider the case in which the lengths of the three sides of a triangle are given.
EXAMPLE 2 Determining the Angles in a Triangle
Find the angles α, β, and γ in the triangle shown in FIGURE 5.4.4.
Solution We use the Law of Cosines to find the angle opposite the longest side:
![]()
A calculator then gives γ ≈ 87.27°. Although we could use the Law of Cosines, we choose to find β by the Law of Sines:
![]()
FIGURE 5.4.4 Triangle in Example 2
Since γ is the angle opposite the longest side it is the largest angle in the triangle, so β must be an acute angle. Thus, sinβ ≈ 0.6659 yields β ≈ 41.75°. Finally, from α = 180° − β − γ we find α ≈ 50.98°.
![]() Bearing In navigation directions are given using bearings. A bearing designates the acute angle that a line makes with the north–south line. For example, FIGURE 5.4.5(a) illustrates a bearing of S40°W, meaning 40 degrees west of south. The bearings in Figures 5.4.5(b) and 5.4.5(c) are N65°E and S80°E, respectively.
Bearing In navigation directions are given using bearings. A bearing designates the acute angle that a line makes with the north–south line. For example, FIGURE 5.4.5(a) illustrates a bearing of S40°W, meaning 40 degrees west of south. The bearings in Figures 5.4.5(b) and 5.4.5(c) are N65°E and S80°E, respectively.
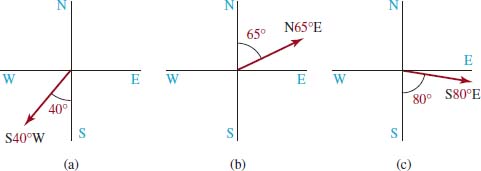
FIGURE 5.4.5 Three examples of bearings
EXAMPLE 3 Bearings of Two Ships
Two ships leave a port at 7:00 AM, one traveling at 12 knots (nautical miles per hour) and the other at 10 knots. If the faster ship maintains a bearing of N47°W and the other ship maintains a bearing of S20°W, what is their separation (to the nearest nautical mile) at 11:00 AM that day?
Solution Since the elapsed time is 4 hours, the faster ship has traveled 4. 12 = 48 nautical miles from port and the slower ship 4.10 = 40 nautical miles. Using these distances and the given bearings, we can sketch the triangle (valid at 11:00 AM) shown in FIGURE 5.4.6. In the triangle, c denotes the distance separating the ships and γ is the angle opposite that side. Since 47° + γ + 20° = 180° we find γ = 113°. Finally, the Law of Cosines
c2 = 482 + 402 – 2(48)(40)cos 113°,
gives c2 ≈ 5404.41 or c ≈ 73.51. Thus the distance between the ships (to the nearest nautical mile) is 74 nautical miles.
FIGURE 5.4.6 Ships in Example 3
5.4 Exercises Answers to selected odd-numbered problems begin on page ANS-16.
In Problems 1-16, refer to Figure 5.3.1. ![]()
In Problems 1–16, use the Law of Cosines to solve the triangle.
1. γ = 65°, a = 5, b = 8
2. β = 48°, a = 7, c = 6
3. α = 8, b = 10, c = 7
4. γ = 31.5°, a = 4, b = 8
5. γ = 97.33°, a = 3, b = 6
6. a = 7, b = 9, c, = 4
7. a = 11, b = 9.5, c, = 8.2
8. β = 162°, b = 11, c, = 8
9. α = 5, b = 7, c, = 10
10. a = 6, b = 5, c, = 7
11. a = 3, b = 4, c, = 5
12. a = 5, b = 12, c, = 13
13. a = 6, b = 8, c, = 12
14. β = 130°, a = 4, c, = 7
15. α = 22°, b = 3, c, = 9
16. β = 100°, a = 22.3, b, = 16.1
Miscellaneous Applications
17. How Far? A ship sails due west from a harbor for 22 nautical miles. It then sails S62°W for another 15 nautical miles. How far is the ship from the harbor?
18. How Far Apart? Two hikers leave their camp simultaneously, taking bearings of N42°W and S20°E, respectively. If they each average a rate of 5 km/h, how far apart are they after 1 h?
19. Bearings On a hiker’s map point A is 2.5 in. due west of point B and point C is 3.5 in. from B and 4.2 in. from A, respectively. See FIGURE 5.4.7. Find (a) the bearing of A from C, and (b) the bearing of B from C.
20. How Long Will It Take? Two ships leave port simultaneously, one traveling at 15 knots and the other at 12 knots. They maintain bearings of S42°W and S10°E, respectively. After 3 h the first ship runs aground and the second ship immediately goes to its aid.
(a) How long will it take the second ship to reach the first ship if it travels at 14 knots?
(b) What bearing should it take?
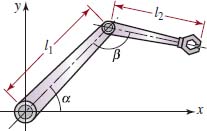
21. A Robotic Arm A two-dimensional robot arm “knows” where it is by keeping track of a “shoulder” angle α and an “elbow” angle β. As shown in FIGURE 5.4.8, this arm has a fixed point of rotation at the origin. The shoulder angle is measured counterclockwise from the x-axis, and the elbow angle is measured counterclockwise from the upper to the lower arm. Suppose that the upper and lower arms are both of length 2 and that the elbow angle β is prevented from “hyperextending” beyond 180°. Find the angles α and β that will position the robot’s hand at the point (1, 2).
22. Which Way? Two lookout towers are situated on mountain tops A and B, 4 mi from each other. A helicopter firefighting team is located in a valley at point C, 3 mi from A and 2 mi from B. Using the line between A and B as a reference, a lookout spots a fire at an angle of 40° from tower A and 82° from tower B. See FIGURE 5.4.9. At what angle, measured from CB, should the helicopter fly in order to head directly for the fire?
23. Making a Kite For the kite shown in FIGURE 5.4.10, use the Law of Cosines to find the lengths of the two dowels required for the diagonal supports.
24. Distance Across a Canyon From the floor of a canyon it takes 62 ft of rope to reach the top of one canyon wall and 86 ft to reach the top of the opposite wall. See FIGURE 5.4.11. If the two ropes make an angle of 123°, what is the distance d from the top of one canyon wall to the other?
FIGURE 5.4.7 Triangle in Problem 19
FIGURE 5.4.8 Robotic arm in Problem 21
FIGURE 5.4.9 Fire in Problem 22
FIGURE 5.4.10 Kite in Problem 23
FIGURE 5.4.11 Canyon in Problem 24
For Discussion
25. Use the Law of Cosines to derive the formula
![]()
for the area of a triangle with sides a, b, c where s = ![]() (a + b + c). This formula is named after the Greek mathematician an inventor Heron of Alexandria (c. 20–62 C.E.) but should actually be credited to Archimedes.
(a + b + c). This formula is named after the Greek mathematician an inventor Heron of Alexandria (c. 20–62 C.E.) but should actually be credited to Archimedes.
FIGURE 5.4.12 Corner lot in Problem 27
FIGURE 5.4.13 Blue man in Problem 29
26. Garden Plot Use Heron’s formula in Problem 25 to find the area of a triangular garden plot if the lengths of the three sides are 25, 32, and 41 m, respectively.
27. Corner Lot Find the area of the irregular corner lot shown in FIGURE 5.4.12. [Hint: Divide the lot into two triangular lots as shown and then find the area of each triangle. Use Heron’s formula in Problem 25 for the area of the acute triangle.]
28. Use Heron’s formula in Problem 25 to find the area of a triangle with vertices located at (3, 2), (–3, –6), and (0, 6) in a rectangular coordinate system.
29.Blue Man The effort in climbing a flight of stairs depends largely on the flexing angle of the leading knee. A simplified blue stick-figure model of a person walking up a staircase indicates that the maximum flexing of the knee occurs when the back leg is straight and the hips are directly over the heel of the front foot. See FIGURE 5.4.13. Show that
![]()
where θ is the knee joint angle, 2a is the length of the leg, R is the rise of a single stair step, and T is the width of a step. [Hint: Let h be the vertical distance from hip to heel of the leading leg, as shown in the figure. Set up two equations involving h: one by applying the Pythagorean theorem to the right triangle outlined in color and the other by using the Law of Cosines on the angle u. Then eliminate h and solve for cos θ.]
30. For a triangle with sides of lengths a, b, and c and γ is the angle opposite c we have seen on page 296 that when γ is a right angle the Law of Cosines reduces to the Pythagorean theorem c2 = a2 + b2. How is c2 related to a2 + b2 when
(a) γ is an acute angle (b) γ is an obtuse angle?
 Introduction Approximately the last one-third of a typical DDC/ICA/ course in calculus deals with the concept and applications of vectors in two and three dimensions. In order to describe certain physical quantities accurately, we must have two pieces of information: a magnitude and a direction. For example, when we discuss the flight of an airplane both its speed and its heading are important. Quantities that involve both magnitude and direction are represented by vectors. In this section we will survey some basic definitions and operations on vectors that lie in the coordinate plane or 2-space.
Introduction Approximately the last one-third of a typical DDC/ICA/ course in calculus deals with the concept and applications of vectors in two and three dimensions. In order to describe certain physical quantities accurately, we must have two pieces of information: a magnitude and a direction. For example, when we discuss the flight of an airplane both its speed and its heading are important. Quantities that involve both magnitude and direction are represented by vectors. In this section we will survey some basic definitions and operations on vectors that lie in the coordinate plane or 2-space.
![]() Terminology In science, mathematics, and engineering we distinguish two important quantities: scalars and vectors. A scalar is simply a real number and is generally represented by a lowercase italicized letter, such as a, k, or x. Scalars may be used to represent magnitudes and may have specific units attached to them; for example, 80 feet, 10 lb, or 20° Celsius. On the other hand, a vector, or displacement vector, may be thought of as an arrow or directed line segment (a line with a direction specified by an arrowhead) connecting points A and B in 2-space. The tail of the arrow is called the initial point and the tip of the arrow is called the terminal point. As shown in FIGURE 5.5.1, a vector is usually denoted by a boldfaced letter such as u or v, or if we wish to emphasize the initial and terminal points A and B, by the symbol
Terminology In science, mathematics, and engineering we distinguish two important quantities: scalars and vectors. A scalar is simply a real number and is generally represented by a lowercase italicized letter, such as a, k, or x. Scalars may be used to represent magnitudes and may have specific units attached to them; for example, 80 feet, 10 lb, or 20° Celsius. On the other hand, a vector, or displacement vector, may be thought of as an arrow or directed line segment (a line with a direction specified by an arrowhead) connecting points A and B in 2-space. The tail of the arrow is called the initial point and the tip of the arrow is called the terminal point. As shown in FIGURE 5.5.1, a vector is usually denoted by a boldfaced letter such as u or v, or if we wish to emphasize the initial and terminal points A and B, by the symbol ![]() . Thus, in contrast to a scalar which has only magnitude, a vector has both magnitude and direction. The magnitude of a vector is its length, that is, the distance between its initial and terminal points. The magnitude of vector is denoted by |u| or
. Thus, in contrast to a scalar which has only magnitude, a vector has both magnitude and direction. The magnitude of a vector is its length, that is, the distance between its initial and terminal points. The magnitude of vector is denoted by |u| or ![]() . Two vectors
. Two vectors ![]() and
and ![]() are said to be equal, written
are said to be equal, written ![]() CD, if they have both the same magnitude and the same direction, as shown in FIGURE 5.5.2. Thus vectors can be translated from one position to another so long as neither the magnitude nor the direction is changed.
CD, if they have both the same magnitude and the same direction, as shown in FIGURE 5.5.2. Thus vectors can be translated from one position to another so long as neither the magnitude nor the direction is changed.
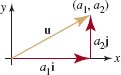
Because we can move a vector provided its magnitude and its direction are unchanged, we can place the initial point at the origin. Then, as shown in FIGURE 5.5.3, the terminal point P will have rectangular coordinates (x, y). Conversely, every ordered pair of real numbers (x, y) determines a vector ![]() , where P has rectangular coordinates (x, y). Thus we have a one-to-one correspondence between vectors and ordered pairs of real numbers. We say that u =
, where P has rectangular coordinates (x, y). Thus we have a one-to-one correspondence between vectors and ordered pairs of real numbers. We say that u = ![]() is the position vector of the point P(x, y) and is written
is the position vector of the point P(x, y) and is written
![]()
In general, any vector in the plane can be identified with a unique position vector u = ![]() . The numbers a1 and a2 are said to be the components of the position vector u and the notation
. The numbers a1 and a2 are said to be the components of the position vector u and the notation ![]() , a29 is called the component form of a vector.
, a29 is called the component form of a vector.
Since the magnitude of ![]() is the distance from the point (a1a2), to the origin, we define the magnitude |u| of the vector u
is the distance from the point (a1a2), to the origin, we define the magnitude |u| of the vector u ![]() to be
to be
![]()
The zero vector, denoted by 0, is defined by the component form 0 = ![]() . The magnitude of the zero vector is zero. The zero vector is not assigned any direction.
. The magnitude of the zero vector is zero. The zero vector is not assigned any direction.
FIGURE 5.5.1 Directed line segment in 2-space
FIGURE 5.5.2 Equal vectors
FIGURE 5.5.3 Position vector
Let u ![]() be a nonzero vector. If θ is an angle in standard position formed by u and the positive x-axis, as shown in FIGURE 5.5.4, then θ is called a direction angle for u. Also any angle coterminal with θ is also a direction angle for u. But for the sake of def-initeness we will choose θ such that in degrees 0° ≤ θ <, 360° or in radians 0 ≤ θ, <2π. Thus a vector u can be specified by giving either its components u =
be a nonzero vector. If θ is an angle in standard position formed by u and the positive x-axis, as shown in FIGURE 5.5.4, then θ is called a direction angle for u. Also any angle coterminal with θ is also a direction angle for u. But for the sake of def-initeness we will choose θ such that in degrees 0° ≤ θ <, 360° or in radians 0 ≤ θ, <2π. Thus a vector u can be specified by giving either its components u = ![]() or by its magnitude |u| and a direction angle. From trigonometry, we have the following relationships between the components, magnitude, and the direction angle of a vector u.
or by its magnitude |u| and a direction angle. From trigonometry, we have the following relationships between the components, magnitude, and the direction angle of a vector u.
FIGURE 5.5.4 Direction angle of a vector
DEFINITION 5.5.1 Direction Angle
For any nonzero vector u ![]() with direction angle θ:
with direction angle θ:
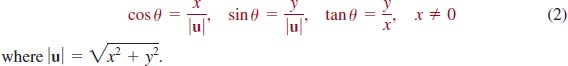
FIGURE 5.5.5 Vectors in Example 1
EXAMPLE 1 Direction Angle
Sketch each of the following vectors. Find the magnitude and the direction angle θ of each vector.
![]()
Solution The three vectors are sketched using different colors in FIGURE 5.5.5.
(a) From (1), the magnitude of u is
![]()
and from (2) its direction angle satisfies tanθ = 2/(–2) = –1. As we see in FIGURE 5.5.5, θ is a second quadrant angle and so we chose θ = arctan(–1) + π = –π/4 + π or θ = 3π/4.
(b) The magnitude of the vector v is ![]() and from FIGURE 5.5.5 we see immediately that its direction angle is θ = π/2.
and from FIGURE 5.5.5 we see immediately that its direction angle is θ = π/2.
(c) For the vector w we have |w| = ![]() . From tanθ = −
. From tanθ = −![]() we get arctan (2–
we get arctan (2–![]() ) = –π/3radians = –60°. Because we want 0 ≤ θ, < 360° we choose the direction angle to be θ = −60° + 360° or θ = 300°.
) = –π/3radians = –60°. Because we want 0 ≤ θ, < 360° we choose the direction angle to be θ = −60° + 360° or θ = 300°.
Vector Arithmetic Vectors can be combined with other vectors by the arithmetic operation of addition. In addition, vectors can be combined with scalars through multiplication. Using the component form of a vector we give next the algebraic definitions of the sum of two vectors, the scalar multiple of a vector, and equality of two vectors.
DEFINITION 5.5.2 Operations on Vectors
Let u = ![]() and v =
and v = ![]() be vectors, and let k be a real number. Then we define the
be vectors, and let k be a real number. Then we define the
![]()
![]()
![]()
![]() Subtraction Using (4), we define the negative of a vector
Subtraction Using (4), we define the negative of a vector ![]() by
by
![]()
We can then define subtraction, or the difference, of two vectors ![]() and v =
and v = ![]() as
as
![]()
EXAMPLE 2 Addition, Subtraction, and Scalar Multiplication
![]()
Solution From the definitions of addition, subtraction, and scalar multiples of vectors, we find

Operations (3), (4), and (6) possess the following properties.
THEOREM 5.5.1 Properties of Vector Operations
(i) u + v = v + u
(ii) u + (v + w) = (u + v) + w
(iii) k (u + v) = (ku + kv)
(iv) (k1 + k2) (u = k1u) + (k2u
(v) k1(k2 u) = (kik2)u
(vi) u + 0 = u
(vii) u + (−u) = 0
(viii) 0u = 0)
(ix) 1u = u
(x) |ku| = |k||u|
You should recognize properties (i) and (ii) of Theorem 5.5.1 as the commutative and associative laws of addition, respectively.
![]() Geometric Interpretations The sum u + v of two vectors can readily be interpreted geometrically in the plane using the concept of a position vector. If
Geometric Interpretations The sum u + v of two vectors can readily be interpreted geometrically in the plane using the concept of a position vector. If ![]() and v =
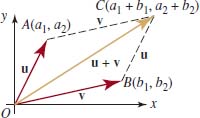
and v = ![]() , then the three vectors u, v, and u + v can be represented by directed line segments from the origin to the points A(a1, a2), B(b1, b2), and C(a1 + b1, a2 + b2), respectively. As shown in FIGURE 5.5.6, if the vector v is translated so that its initial point is A, then its terminal point will be C. Thus a geometric representation of the sum u + v can be obtained by placing the initial point of v on the terminal point of u and drawing the vector from the initial point of u to the terminal point of v. By examining the coordinates of the quadrilateral OACB in FIGURE 5.5.6, we see that it is a parallelogram formed by the vectors u and v, with u + v as one of its diagonals.
, then the three vectors u, v, and u + v can be represented by directed line segments from the origin to the points A(a1, a2), B(b1, b2), and C(a1 + b1, a2 + b2), respectively. As shown in FIGURE 5.5.6, if the vector v is translated so that its initial point is A, then its terminal point will be C. Thus a geometric representation of the sum u + v can be obtained by placing the initial point of v on the terminal point of u and drawing the vector from the initial point of u to the terminal point of v. By examining the coordinates of the quadrilateral OACB in FIGURE 5.5.6, we see that it is a parallelogram formed by the vectors u and v, with u + v as one of its diagonals.
We now consider a scalar multiple of the vector u = ![]() . If the symbol k represents any real number, then
. If the symbol k represents any real number, then

We have derived the property of scalar multiplication given in part (x) of Theorem 5.5.1, that is,
![]()
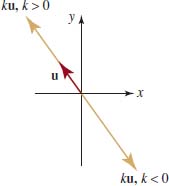
This property states that in the scalar multiplication of a vector u by a real number k, the magnitude of u is multiplied by |k|.As shown in FIGURE 5.5.7, if k. < 0, the direction of u does not change; but if k >.0, the direction of u is reversed. FIGURE 5.5.7 illustrates the case where |k| >. 1. A vector u and its negative −u have the same length but opposite direction.
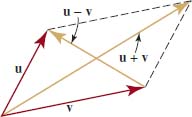
The geometric interpretation of the difference u – v of two vectors is obtained by observing that u = v + (u − v). Thus, u 2 v is the vector that when added to v yields u. As we see in FIGURE 5.5.8, the initial point of u − v will be at the terminal point of v, and the terminal point of u − v coincides with the terminal point of u. Hence the vector u − v is one diagonal of the parallelogram determined by u and v, with u + v being the other diagonal. See FIGURE 5.5.9.
FIGURE 5.5.6 Sum of two vectors u and v
FIGURE 5.5.7 Scalar multiple of a vector v
FIGURE 5.5.8 Difference of two vectors u and v
FIGURE 5.5.9 Sum and difference of vectors u and v as diagonals of a parallelogram
EXAMPLE 3 Sum and Difference
![]()
(a) Sketch the geometric interpretations of u + v and u − v.
(b) Sketch u + v and u − v as position vectors.
Solution (a) To interpret these vectors geometrically, we form the parallelogram with two sides determined by the vectors u and v and identify u + v and u − v as the diagonals shown in gold in FIGURE 5.5.10(a).
(b) From (3) and (6) we have, in turn,
![]()
As position vectors, we plot the points (2, 3) and (–4, –1)and then draw a vector (in red) stemming from the origin to each point. See Figure 5.5.10(b).
FIGURE 5.5.10 Sum and difference of vectors in Example 3
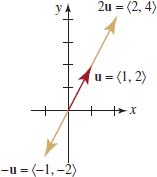
FIGURE 5.5.11 Scalar multiples and negative of the vector uin Example 4
EXAMPLE 4 Scalar Multiples
Let u = ![]() Find 2u and −u and give geometric interpretations of the vectors.
Find 2u and −u and give geometric interpretations of the vectors.
Solution The scalar multiple is ![]() . The negative of the vector u is
. The negative of the vector u is ![]() . Geometrically, the vector 2u has the same direction as u but is twice as long. The negative −u has the same length as u but has the opposite direction. See FIGURE 5.5.11.
. Geometrically, the vector 2u has the same direction as u but is twice as long. The negative −u has the same length as u but has the opposite direction. See FIGURE 5.5.11.
![]() Unit Vectors Any vector with magnitude 1 is called a unit vector. We can obtain a unit vector u in the same direction as a nonzero vector v by multiplying v by the positive scalar k = 1/|v;| (reciprocal of its magnitude). In this case we say that
Unit Vectors Any vector with magnitude 1 is called a unit vector. We can obtain a unit vector u in the same direction as a nonzero vector v by multiplying v by the positive scalar k = 1/|v;| (reciprocal of its magnitude). In this case we say that
![]()
is the normalization of the vector v. It follows from (7) that the normalization of a vector v is a unit vector because
![]()
EXAMPLE 5 Unit Vector
Given v = (2,−1), find a unit vector (a) in the same direction as v, and (b) in the opposite direction of v.
Solution First, we find the magnitude of the vector v:
![]()
(a) From (8), a unit vector in the same direction as v is then
![]()
(b) A unit vector in the opposite direction of v is the negative of u:
![]()
![]() i, j Vectors The unit vectors in the direction of the positive x- and y-axes, denoted by
i, j Vectors The unit vectors in the direction of the positive x- and y-axes, denoted by
![]()
are of special importance. See FIGURE 5.5.12. The two unit vectors in (9) are called the standard basis vectors for the vectors in 2-space because every vector can be expressed in terms of i and j. To see why this is so we use the definitions of vector addition and scalar multiplication to rewrite < ![]() as
as
![]()
FIGURE 5.5.12 The i
As shown in FIGURE 5.5.13, since i and j are unit vectors, the vectors a1i and a2 j are horizontal and vertical vectors of length and |a1| and |a2|, respectively. For this reason, a1 is called the horizontal component of u, and a2 is called the vertical component. The vector a1i + a2 j is often referred to as a linear combination of i and j. Using this notation for the vectors u = a1i + a2 j and v = b1i + b2 j, we can write the definition of the sum, difference, and scalar multiples of u and v in the following manner:
FIGURE 5.5.13 A vector u is a linear combination of i and j
![]()
![]()
![]()
EXAMPLE 6 Difference of Vectors
If u = 3i + j and v = 5i − 2j, find 4u − 2v.
Solution We use (12) followed by (11) to obtain

![]() Trigonometric Form of a Vector There is yet another way of representing vectors. For a nonzero vector u =
Trigonometric Form of a Vector There is yet another way of representing vectors. For a nonzero vector u = ![]() , with direction angle θ, we see from (2) that x = |u| cos° and y = |u| sinθ. Thus,
, with direction angle θ, we see from (2) that x = |u| cos° and y = |u| sinθ. Thus,
![]()
This latter representation is called the trigonometric form of the vector u.
EXAMPLE 7 Trigonometric Form
Express the vector u = ![]() in trigonometric form.
in trigonometric form.
FIGURE 5.5.14 Vector and direction angle in Example 7
Solution To write u in trigonometric form, we must find the magnitude |u| and its direction angle θ. From (1) and (2) we find

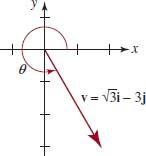
To determine θ, we sketch u and observe that the terminal side of the angle θ lies in the fourth quadrant. See FIGURE 5.5.14. Thus, with |u| = 2![]() and θ = 5π/3, (13) gives the trigonometric form of u:
and θ = 5π/3, (13) gives the trigonometric form of u:
![]()
EXAMPLE 8 Velocity as a Vector
Given that an airplane is flying at 200 mi/h on a bearing of N20°E, express its velocity as a vector.
Solution The desired velocity vector v is shown in FIGURE 5.5.15. Measured from the positive x-axis we see that the direction angle θ of v is θ = 90° − 20° = 70°. Then using |v| = 200, we have the vector
![]()
FIGURE 5.5.15 Velocity vector in Example 8
In Example 8 we see that velocity is a vector quantity. The magnitude |v| of the velocity v is a scalar quantity called speed.
In physics it is shown that when two forces act simultaneously at the same point P on an object, the object reacts as though a single force equal to the vector sum of the two forces is acting on the object at P. This single force is called the resultant force.
EXAMPLE 9 Resultant Force
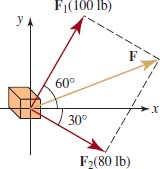
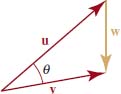
Two people push on a crate with forces F1 and F2, whose magnitudes and directions are shown in FIGURE 5.5.16. Find the magnitude and the direction of the resultant force.
Solution From the figure, we see that the direction angles for the two forces F1 and F2are θ1 = 60° and θ2 = 330°, respectively. Thus,
FIGURE 5.5.16 Resultant force (gold) in Example 9
The resultant force F can then be found by vector addition:
![]()
Thus the magnitude |F| of the resultant force is
![]()
If θ is a direction angle for F, then we know from (2) that
![]()
Since θ is a first quadrant angle, we find with the help of a calculator that θ ≈ 21.34°.
![]() Dot Product Up to now we have considered two kinds of vector operations on vectors, addition and scalar multiplication, which produced another vector. We now consider a special kind of product between vectors that originated in the study of mechanics. This product, known as the dot product, or inner product, of vectors u and v is denoted by u. v and is a real number, or scalar, defined in terms of the components of the vectors.
Dot Product Up to now we have considered two kinds of vector operations on vectors, addition and scalar multiplication, which produced another vector. We now consider a special kind of product between vectors that originated in the study of mechanics. This product, known as the dot product, or inner product, of vectors u and v is denoted by u. v and is a real number, or scalar, defined in terms of the components of the vectors.
DEFINITION 5.5.3 Dot Product
In 2-space the dot product of two vectors ![]() is the number
is the number
![]()
EXAMPLE 10 Do Product Using (14)
Suppose ![]() Find:
Find:
(a) u.v
(b) w.u
(c) v.w
Solution It follows form (14) that
(a)![]()
(b)![]()
(c)![]()
![]() Properties The dot product possesses the following properties.
Properties The dot product possesses the following properties.
THEOREM 5.5.2 Properties of the Dot Product

PROOF: We prove parts (ii) and (vi). The remaining proofs are straightforward and left for the reader. To prove part (ii) we let ![]() and v =
and v = ![]() . Then
. Then

To prove part (vi) we note that
![]()
EXAMPLE 11 Dot Products
Let ![]()
Solution (a) From (14),
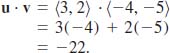
Because u·v is a scalar we have from (4) of Definition 5.5.2,
![]()
(b) From (iv) of Theorem 5.5.2 and part (a),
![]()
(c) Part (vi) of Theorem 5.5.2 relates the magnitude of a vector with the dot product. From (14) we have

![]() Alternative Form The dot product of two vectors can also be expressed in terms of the lengths of the vectors and the angle between them.
Alternative Form The dot product of two vectors can also be expressed in terms of the lengths of the vectors and the angle between them.
THEOREM 5.5.3 Alternative Form of the Dot Product
The dot product of two vectors u and v is
![]()
where u is the angle between the vectors such that 0 ≤ θ ≤ π
![]() This more geometric form is what is ? generally used as the definition of the dot product in a physics course.
This more geometric form is what is ? generally used as the definition of the dot product in a physics course.
PROOF: Suppose θ is the angle between the vectors u = a+i + a2j and v = b1i 1 b2j. Then the vector
w = v − u = (b1 − a1)i + (b2 2 a2)j
is the third side of the triangle indicated in FIGURE 5.5.17. By the Law of Cosines, (2) of Section 5.4, we can write
![]()
FIGURE 5.5.17 The vector w in the proof of Theorem 5.5.3
![]()
the right-hand side of the second equation in (16) simplifies to a1b1 + a2b2. Since this is the definition of the dot product given in (14), we see that |u||v| cosθ = u · v.
![]() Angle Between Vectors FIGURE 5.5.18 illustrates three cases of the angle θ in (15). If the vectors u and v are not parallel, then θ is the smaller of the two possible angles between them. Solving for cos u in (15) and then using the definition of the dot product in (14) we have a formula for the cosine of the angle between two vectors:
Angle Between Vectors FIGURE 5.5.18 illustrates three cases of the angle θ in (15). If the vectors u and v are not parallel, then θ is the smaller of the two possible angles between them. Solving for cos u in (15) and then using the definition of the dot product in (14) we have a formula for the cosine of the angle between two vectors:
![]()
FIGURE 5.5.18 The angle u in the dot product
EXAMPLE 12 Angle Between Two Vectors
Find the angle between u 2i + 5j and v = 5i − 4j.
Solution We have ![]()
Hence, (17) gives
![]()
FIGURE 5.5.19 Angle between the vectors in Example 12
and so ![]() radians or θ ∼ 106.86¯. See FIGURE 5.5.19.
radians or θ ∼ 106.86¯. See FIGURE 5.5.19.
![]() Orthogonal Vectors If u and v are nonzero vectors, then Theorem 5.5.3 implies that
Orthogonal Vectors If u and v are nonzero vectors, then Theorem 5.5.3 implies that
(i) u ·v> 0 if θ =0.
(ii) u ·v< 0 if θ is obtuse and
(iii) u ·v> 0 if cosθ = 0.
But in the last case, the only number in the interval [0, π] for which is cos θ, is θ = π/2. When θ = π/2, we say that the vectors are orthogonal or perpendicular. Thus, we are led to the following result.
THEOREM 5.5.4 Criterion for Orthogonal Vectors
Two nonzero vectors u and v are orthogonal if and only if u. v = 0.
As seen in FIGURE 5.5.12 the standard basis vectors i and j are orthogonal. Moreover, because ![]() we have
we have
![]()
and so from Theorem 5.5.4 the vectors i and j are orthogonal. Inspection of the result in part (c) of Example 10 shows that the two vectors ![]() , and are orthogonal.
, and are orthogonal.
EXAMPLE 13 Orthogonal Vectors
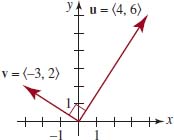
if u = (4,6) and v = (−3,2), then
![]()
From Theorem 5.5.4, we conclude that u and v are orthogonal. See FIGURE 5.5.20.
FIGURE 5.5.20 Orthogonal vectors in
![]() Component of u on v Parts (ii), (iii), and (vi) of Theorem 5.5.2 enable us to express the components of a vector u =a1i + a 2j in terms of a dot product: That is, u. i = a1. Similarly, u. j = a2 Symbolically, we write these components of u as.
Component of u on v Parts (ii), (iii), and (vi) of Theorem 5.5.2 enable us to express the components of a vector u =a1i + a 2j in terms of a dot product: That is, u. i = a1. Similarly, u. j = a2 Symbolically, we write these components of u as.
![]()
![]()
FIGURE 5.5.21 Component of vector u on vector v
We shall now see that the procedure indicated in (18) carries over to finding the component of u on a vector v. Note that in either of the two cases shown in FIGURE 5.5.21,
![]()

![]()
we see that
In other words:
To find the component of vector u on vector v, we dot u with a unit vector in the direction of v.
EXAMPLE 14 Component of a Vector on Another
Letu = 2i + 3j and v = i + j.find comp u
Solution We first form a unit vector in the direction of v:
![]()
Then from (20) we have
![]()
![]() Projection of u onto v The projection of a vector u in any of the directions determined by i and j, is the vector formed by multiplying the component of u = a1i + a2j in the specified direction with a unit vector in that direction; for example,
Projection of u onto v The projection of a vector u in any of the directions determined by i and j, is the vector formed by multiplying the component of u = a1i + a2j in the specified direction with a unit vector in that direction; for example,
![]()
and so on. FIGURE 5.5.22 shows the general case of the projection of u onto v:
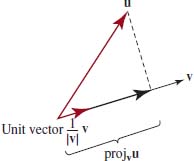
FIGURE 5.5.22 Projection of vector u onto vector v
That is,
To find the projection of vector u onto a vector v, we multiply a unit vector in the direction of v by the component of u on v.
If desired, the result in (21) can be expressed in terms of two dot products. Using (20)

EXAMPLE 15 Projection of u onto v
Find the projection of u = 4i + j onto the vectorv = 2i + 3j.Graph.
Solution First, we find the component of u on v. A unit vector in the direction of v is
![]()
and so the component of u on v is the number
![]()
Thus, from (21)

FIGURE 5.5.23 Projection of u onto v in Example 15
The graph of this vector is shown in gold color in FIGURE 5.5.23.
![]() Physical Interpretation of the Dot Product When a constant force of magnitude F moves an object a distance d in the same direction of the force, the work done is defined to be
Physical Interpretation of the Dot Product When a constant force of magnitude F moves an object a distance d in the same direction of the force, the work done is defined to be
![]()
However, if a constant force F applied to a body acts at an angle to the direction of motion, then the work done by F is defined to be the product of the component of F in the direction of the displacement and the distance | d | that the body moves:
![]()
See FIGURE 5.5.24. It follows from Theorem 5.5.3 that if F causes a displacement d of a body, then the work done is (23)
![]()
FIGURE 5.5.24 Work done by a force acting at an angle to the direction of motion
Note that (23) reduces to (22) when θ = 0.
EXAMPLE 16 Work Done by a Force at an Angle
Find the work done by a constant force F = 2i + 4j on a block that moves from P1(1, 1) to P2(4, 6). Assume that |F| is measured in pounds and |d| is measured in feet.
Solution The displacement vector of the block is given by
![]()
It follows from (23) that the work done is
![]()
NOTES FROM THE CLASSROOM

You should not draw the conclusion from the preceding discussion that all vector quantities can be pictured as arrows. Many applications of vectors in advanced mathematics do not lend themselves to this interpretation. However, for purposes in this text, we find this interpretation both convenient and useful.
5.5 Exercises Answers to selected odd-numbered problems begin on page ANS-16.
In Problems 1–8, sketch the given vector. Find the magnitude and the smallest positive direction angle of each vector.
1.![]()
2.![]()
3.![]()
4.![]()
5.![]()
6.![]()
7.![]()
8.![]()
In Problems 9–14, find u + v, – v, – 3u – 4v.
9.![]()
10.![]()
11.![]()
12.![]()
13.![]()
14.![]()
In Problems 15–20, find u – 4v and 2v + 5v
15. u = i – 2j, v = 8i + 3j
16. u = j, v = 4i – j
17. ![]()
18. u = 2i – 3j, v = 3i – 2j,
19. ![]()
20. u = 5i – 10j, v = –10i
In Problems 21–24, sketch the vectors u + v and u – v.
21. u = 2j + 3j, v = –i + 2j
22. u = 4i + j, v = 2i + 2j
23. u = 5i + j, v = 4i – 3j
24. u = 2i + 7j, v = –71 + 3j
In Problems 25–28, sketch the vectors 2v – v
25.![]()
26.![]()
27. v = 3i - 5j,
28.![]()
In Problems 29–32, if u = 3i – v = 2i + 4j, and, find the horizontal and the vertical components of the indicated vector.
29. 2u – v
30. 3(u + v)
31. v – 4u)
32. 4(u + 3v)
In Problems 33–36, express the given vector (a) in trigonometric form and (b) as a linear combination of the unit vectors i and j.
33.![]()
34.![]()
35.![]()
36.![]()
In Problems 37–40, find a unit vector (a) in the same direction as v,
37.![]()
38.![]()
39.![]()
40.![]()
In Problems 41 and 42, normalize the given vector when v = (2,8) and w = (3,4)
41.v + w
42.2v – 3w
43. Two forces F1 and F2 of magnitudes 4 N and 7 N, respectively, act on a point. If the angle between the forces is, find the magnitude of the resultant force F and the angle between F1 and F.
44. The resultant F of two forces F1 and F2 has a magnitude of 100 lb and direction as shown in FIGURE 5.5.25. If F1 = –200i, find the horizontal and the vertical components of F2.
In Problems 45–48, find the dot product u.v
45.![]()
46.![]()
47.![]()
48.![]()
FIGURE 5.5.25 Resultant in Problem 44
In Problems 49–62, ![]() . Find the indicated scalar or vector.
. Find the indicated scalar or vector.
49. u·v
50. v·w
51. u·w
52. v·v
53. w·w
54. u·(v + w)
55. u·(4v)
56. v·(u – w)
57. ![]()
58. (2u) · (u – 2v)
59. u · (u + v + w)
60. (2u) · (u – 2v)
61. ![]()
62. (w · v)u
In Problems 63 and 64, find the dot product u · v if the smaller angle between u and v is as given.
63. ![]()
64. ![]()
In Problems 65–68, find the angle between the given pair of vectors. Round your answer to two decimal places.
65.![]() 1, 4
1, 4![]() ,
, ![]() 2, -1
2, -1![]()
66.![]() 3, 5
3, 5![]() ,
, ![]() –4, –2
–4, –2![]()
67. i – j, 3i + j
68. 2i – j, 4i + j
In Problems 69–72, determine whether the given vectors are orthogonal.
69.![]()
70.![]()
71.![]()
72.![]()
In Problems 73 and 74, find a scalar c so that the given vectors are orthogonal.
73. u = 2i – cj, v= 3i + 2j
74. u = 4ci – 8jj, v= ci + 2j
75. Verify that the vector
![]()
is orthogonal to the vector u.
76. Find a scalar c so that the angle between the vectors and u = i + cj and v = i + j is 45·
In Problems 77–80, ![]() Find the indicated number.
Find the indicated number.
77. compv u
78. compu v
79.![]()
80.![]()
In Problems 81 and 82, find (a) projvu, and (b) projuv.
In Problems 83 and 84, u = 4i + 3j. and v = –i + j. Find the indicated vector.
83.![]()
84.![]()
85. A sled is pulled horizontally over ice by a rope attached to its front. A 20-lb force acting at an angle of with the horizontal moves the sled 100 ft. Find the work done.
86. A block with weight w is pulled along a frictionless horizontal surface by a constant force F of magnitude 30 lb in the direction by the vector d. See FIGURE 5.5.26.
(a) What is the work done by the weight w?
(b) What is the work done by the force F if d= 4i + 3j?
FIGURE 5.5.26 Block in Problem 86
FIGURE 5.5.27 Block in Problem 87
FIGURE 5.5.28 Hanging mass in Problem 89
87. A constant force F of magnitude 3 lb is applied to the block shown in FIGURE 5.5.27. The force F has the same direction as the vector u 3i + 4j. Find the work done in the direction of motion if the block moves from to p1(3,1)to p2 (9.3) Assume distance is measured in feet.
Miscellaneous Applications
88. Resultant Force A small boat is pulled along a canal by two tow ropes on opposite sides of the canal. The angle between the ropes is 50°. If one rope is pulled with a force of 250 lb and the other with a force of 400 lb, find the magnitude of the resultant force and the angle it makes with the 250-lb force.
89. Resultant Force A mass weighing 10 lb is hanging from a rope. A 2-lb force is applied horizontally to the weight, moving the rope from its horizontal position. See FIGURE 5.5.28. Find the resultant of this force and the force due to gravity.
90. In What Direction? As a freight train, traveling at 10 mi/h, passes a landing, a mail sack is tossed out perpendicular to the train with a velocity of 15 feet per second. In what direction does the mail sack slide on the landing?
91. Actual Direction The current in a river that is 0.5 mi across is 6 mi/h. A swimmer heads out from shore perpendicular to the current at 2 mi/h. In what direction is the swimmer actually going?
92. Getting One’s Bearings A hiker walks 1.0 mi to the northeast, then 1.5 mi to the east, and then 2.0 mi to the southeast. What are the hiker’s distance and bearing from the starting point? [Hint: Each part of the journey can be represented by a vector. Find the vector sum.]
93. What Is the Speed? In order for an airplane to fly due north at 300 mi/h, it must set a course 10° west of north (N10°W) because of a strong wind blowing due east. What is the speed of the wind?
For Discussion
94. A 200-lb traffic light supported by two cables hangs in static equilibrium. A condition of static equilibrium is that the object is at rest and that the sum of forces acting on the object is the zero vector 0. As shown in FIGURE 5.5.29(b), let the weight of the light be represented by w and forces in the two cables by F1 and F2. From the FIGURE 5.5.29(b) we then have
![]()
where the vectors on the left-hand side of the equality in trigonometric form are
![]()
Use (24) to determine the magnitude of F1 and F2. [Hint: Use (5) of Definition 5.5.2 and let v = 0 = (0.0).]
FIGURE 5.5.29 Hanging mass in Problem 94
A.Fill in the Blanks
In Problems 1–12, fill in the blanks.
1. To solve a triangle in which you know two angles and a side of opposite one of these angles, you would use the Law of ______ first.
2. The ambiguous case refers to solving a triangle when ______ are given.
3. To solve a triangle in which you know two sides and the included angle, you would use the Law of ______ first.
4. In an isosceles triangle, if a is the length of one of the two equal sides and is one of the two equal angles, then the area of the triangle in terms of a and is ______.
5. The largest angle in the triangle whose sides are 5.3, 4.4, and 4.1 is ______.
6. If θ is one of the acute angles in a right triangle and sinθ = ![]() , then tanθ ______.
, then tanθ ______.
7. A 6-ft-tall man walking along a level beach climbs onto a 4-ft-tall tree stump and looks over the water to the horizon. Assuming that the Earth is a perfect sphere of radius r = 3963 mi, then the distance measured along the surface of the Earth from the man to the horizon is ______ miles.
8. The difference between a scalar and vector is ______.
9. A unit vector in the opposite direction of is v = ![]() is ______.
is ______.
10. If u = 4i – 6j and v = – 3i + 10j then 5u – 6v ______.
11. The angle between the vectors u = 5i and v = – 2j is ______.
12. If |u| = 4,|v| = 3 and the angle between u and v is θ = 2π /3 then u. v= ______.
B. True/False____________
In Problems 1–12, answer true or false.
1. In a right triangle, if tanθ = ![]() then sinθ = 3 and cosθ = 4. ______
then sinθ = 3 and cosθ = 4. ______
2. In a right triangle, if sinθ = ![]() , then cotθ =
, then cotθ = ![]() . ______
. ______
3. For an acute angle θ in a right triangle, cscθ = ![]() ______
______
4. The Pythagorean theorem is a special case of the Law of Cosines. ______
5. In a right triangle, the hypotenuse is always the longest side. ______
6. If α and β are the acute angles in a right triangle, then sinα = cosβ. ______
7. If tanθ = ![]() for an acute angle θ in a right triangle, then cosθ = ______
for an acute angle θ in a right triangle, then cosθ = ______
8. A rowboat departs from a point on a straight beach that coincides with a north-south line. If the rowboat travels at a rate of 2.5 mi/h with a bearing of then after 4 h the rowboat is 10 mi from the beach. ______
9. A 20 ft extension ladder rests against the side of a vertical wall. If the base of the ladder is on flat ground 5.2 ft from the wall, then the angle the ladder makes with the ground is ______
10. The vector v = ![]() is twice as long as the vector u =
is twice as long as the vector u = ![]() ______
______
11. If u is a unit vector, then ______
12. If u and v are unit vectors, then are orthogonal. ______
C. Exercises_________
In Problems 1–4, solve the triangle satisfying the given conditions.
1. α = 30°, β = 70°, b = 10
2. γ = 145°, a = 25°, c = 20
3. α = 51°, b = 20, c = 10
4. γ = 4, b = 6, c = 3
5. A surveyor 100 m from the base of an overhanging cliff measures a
angle of elevation from that point to the top of the cliff. See FIGURE 5.R.1. If the cliff makes an angle of with the horizontal ground, determine its height h.
6. A rocket is launched from ground level at an angle of elevation of 43°. If the rocket hits a drone target plane flying at 20,000 ft, find the horizontal distance between the rocket launch site and the point directly beneath the plane. What is the straight-line distance between the rocket launch site and the target plane?
7. A competition water skier leaves a ramp at point R and lands at point S. See FIGURE 5.R.2. A judge at point J measures an ![]() RJS as 47° If the distance from the ramp to the judge is 110ft, find the length of the jump. Assume that
RJS as 47° If the distance from the ramp to the judge is 110ft, find the length of the jump. Assume that ![]() SRJ is 90°.
SRJ is 90°.
8. The angle between two sides of a parallelogram is If the lengths of the sides are 5 and 10 cm, find the lengths of the two diagonals.
9. A weather satellite orbiting the equator of the Earth at a height of H = 36,000 km spots a thunderstorm to the north at P at an angle of θ = 6.5° from its vertical. See FIGURE 5.R.3.
(a) Given that the Earth’s radius is approximately, R = 6370 km find the latitude ![]() of the thunderstorm.
of the thunderstorm.
(b) Show that angles θ and ![]() are related by
are related by
![]()
FIGURE 5.R.1 Cliff in Problem 5
FIGURE 5.R.2 Water skier in Problem 7
FIGURE 5.R.3 Satellite in Problem 9
10. It can be shown that a basketball of diameter d approaching the basket from an angle θ to the horizontal will pass through a hoop of diameter D if D sin θ > d, where 0° ≤ θ ≤ 90° See FIGURE 5.R.4. If the basketball has diameter 24.6 cm and the hoop has diameter 45 cm, what range of approach angles θ will result in a basket?
11. Each of the 24 NAVSTAR Global Positioning System (GPS) satellites orbits the Earth at an altitude of h = 20,200 km. Using this network of satellites, an inexpensive handheld GPS receiver can determine its position on the surface of the Earth to within 10 m. Find the greatest distance s (in km) on the surface of the Earth that can be observed from a single GPS satellite. See FIGURE 5.R.5. Take the radius of the Earth to be 6370 km. [Hint: Find the central angle θ subtended by s.]
12. An airplane flying horizontally at a speed of 400 miles per hour is climbing at an angle of from the horizontal. When the airplane passes directly over a car traveling 60 miles per hour, it is 2 miles above the car. Assuming that the airplane and the car remain in the same vertical plane, find the angle of elevation from the car to the airplane after 30 minutes.
13. A house measures 45 ft from front to back. The roof measures 32 ft from the front of the house to the peak and 18 ft from the peak to the back of the house. See FIGURE 5.R.6. Find the angles of elevation of the front and back parts of the roof.
14. The angle between two sides of a parallelogram is If the lengths of the sides are 5 and 10 cm, find the lengths of the two diagonals.
15. Help is Coming From two lifeguard towers A and B, a swimmer in distress is sighted on bearings of N46°E and N27°W respectively. If tower B is 250 ft due east of tower A, what is the distance from each tower to the swimmer?
16. Navigator’s Error An airplane is supposed to fly 500 mi due west to a refueling rendezvous point. If a 5° error is made in the heading, how far is the plane from the rendezvous point after flying 400 mi? Through what angle must the airplane turn in order to correct its course at that point?
In Problems 17–26, translate the words into an appropriate function.
17 A 20-ft-long water trough has ends in the form of isosceles triangles with sides that are 4 ft long. See FIGURE 2.8.21 in Exercises 2.8. As shown in FIGURE 5.R.7, let θ denote the angle between the vertical and one of the sides of a triangular end. Express the volume of the trough as a function of 2 θ
18. A person driving a car approaches a freeway sign as shown in FIGURE 5.R.8. Let θ be her viewing angle of the sign and let x represent her horizontal distance (measured in feet) to that sign. Express θ as a function of x.
19. As shown in FIGURE 5.R.9, a plank is supported by a sawhorse so that one end rests on the ground and the other end rests against a building. Express the length of the plank as a function of the indicated angle θ.
FIGURE 5.R.4 Basketball in Problem 10
FIGURE 5.R.5 GPS satellite in Problem 11
FIGURE 5.R.6 House in Problem 13
FIGURE 5.R.7 End of water trough in Problem 17
FIGURE 5.R.8 Freeway sign in Problem 18
FIGURE 5.R.9 Plank in Problem 19
20. A farmer wishes to enclose a pasture in the form of a right triangle using 2000 ft of fencing on hand. See FIGURE 5.R.10. Show that the area of the pasture as a function of the indicated angle is θ
21. Express the volume of the box shown in FIGURE 5.R.11 as a function of the indicated angle θ
22. A corner of an 8.5-in. × 11-in. piece of paper is folded over to the other edge of the paper as shown in FIGURE 5.R.12. Express the length L of the crease as a function of the angle θ shown in the figure.
FIGURE 5.R.10 Pasture in Problem 20
FIGURE 5.R.11 Box in Problem 21
FIGURE 5.R.12 Folded paper in Problem 22
23. A gutter is to be made from a sheet of metal 30 cm wide by turning up the edges of width 10 cm along each side so that the sides make equal angles with the vertical. See FIGURE 5.R.13. Express the cross-sectional area of the gutter as a function of the angle Ф.
24. A metal pipe is to be carried horizontally around a right-angled corner from a hallway 8 feet wide into a hallway that is 6 feet wide. See FIGURE 5.R.14. Express the length L of the pipe as a function of the angle shown in the figure.
25. In FIGURE 5.R.15 the blue, green, and red circles are of radii 3, 4, and 6, respectively. The dots represent the centers of the circles.
(a) Express the distance d between the centers of the blue and red circles as a function of the angle shown in the figure.
(b) Use the function is part (a) to determine the value of θ corresponding to d = 14.
26. The container shown in FIGURE 5.R.16 consists of an inverted cone (open at its top) attached to the bottom of a right circular cylinder (open at its top and bottom) of fixed radius R. The container has a fixed volume V. Express the total surface area S of the container as a function of the indicated angle. [Hint: See Appendix B for the lateral surface area of a cone.]
FIGURE 5.R.13 Gutter in Problem 23
FIGURE 5.R.14 Pipe in Problem 24
FIGURE 5.R.15 Circle in Problem 25
FIGURE 5.R.16 Container in Problem 26
27.![]()
28.![]()
29.![]()
30.![]()
31.![]()
32.![]()
33.![]()
34.![]()
35.![]()
36.![]()
37.![]()
38. |u + v|
39.trigonometric form of 2v
40. horizontal component of − (u + w
41. a unit vector in the opposite direction of w
42. the angle between v and w
43. Two forces F1 and F2 act at a point such that the resultant force F has a magnitude of 5 lb and is orthogonal to F1. If |F1| = 5 then find the magnitude of the vector F2 and the angle between F1 and F2 in degrees.
44. A baby elephant weighing 315 lb is standing still on a loading ramp shown in FIGURE 5.R.17. Assume that the origin of the rectangular coordinate system is at O and that the ramp makes an angle of with the horizontal.
(a) Express the vectors w = ![]() in u =
in u = ![]() trigonometric form. In each case use a direction angle that is positive and measured from the positive x-axis. The unknown quantities are the magnitudes of the |u| and |v| are the magnitudes of the components of the weight vector w =
trigonometric form. In each case use a direction angle that is positive and measured from the positive x-axis. The unknown quantities are the magnitudes of the |u| and |v| are the magnitudes of the components of the weight vector w = ![]() in the direction parallel to the ramp and perpendicular to the ramp, respectively.
in the direction parallel to the ramp and perpendicular to the ramp, respectively.
(b) Find |u| and |v| by using (20) of Section 5.5 to find compu w and compv w. 0v0 0u0
FIGURE 5.R.17 Elephant in Problem 44
* The drawbridge shown in FIGURE 5.2.12, where the span is continuously balanced by a counterweight, is called a bascule bridge.