Chapter 11
Two-Sample Hypothesis Testing
IN THIS CHAPTER
Testing differences between means of two samples
Testing means of paired samples
Testing hypotheses about variances
In business, in education, and in scientific research, the need often arises to compare one sample with another. Sometimes the samples are independent, and sometimes they’re matched in some way. Each sample comes from a separate population. The objective is to decide whether or not these populations are different from one another.
Usually, this involves tests of hypotheses about population means. You can also test hypotheses about population variances. In this chapter, I show you how to carry out these tests. I also discuss useful worksheet functions and data analysis tools that help you get the job done.
Hypotheses Built for Two
As in the one-sample case (refer to Chapter 10), hypothesis testing with two samples starts with a null hypothesis (H0) and an alternative hypothesis (H1). The null hypothesis specifies that any differences you see between the two samples are due strictly to chance. The alternative hypothesis says, in effect, that any differences you see are real and not due to chance.
It’s possible to have a one-tailed test, in which the alternative hypothesis specifies the direction of the difference between the two means, or a two-tailed test, in which the alternative hypothesis does not specify the direction of the difference.
For a one-tailed test, the hypotheses look like this:
H0: μ1 - μ2 = 0
H1: μ1 - μ2 > 0
or like this:
H0: μ1 - μ2 = 0
H1: μ1 - μ2 < 0
For a two-tailed test, the hypotheses are
H0: μ1 - μ2 = 0
H1: μ1 - μ2 ≠ 0
The zero in these hypotheses is the typical case. It’s possible, however, to test for any value — just substitute that value for zero.
To carry out the test, you first set α, the probability of a Type I error that you’re willing to live with (see Chapter 10). Then you calculate the mean and standard deviation of each sample, subtract one mean from the other, and use a formula to convert the result into a test statistic. Next, compare the test statistic to a sampling distribution of test statistics. If it’s in the rejection region that α specifies (see Chapter 10), reject H0. If not, don’t reject H0.
Revisited
In Chapter 9, I introduce the idea of a sampling distribution — a distribution of all possible values of a statistic for a particular sample size. In that chapter, I describe the sampling distribution of the mean. In Chapter 10, I show its connection with one-sample hypothesis testing.
For two-sample hypothesis testing, another sampling distribution is necessary. This one is the sampling distribution of the difference between means.
Within each pair, each sample comes from a different population. All the samples are independent of one another, so that picking individuals for one sample has no effect on picking individuals for another.
Figure 11-1 shows the steps in creating this sampling distribution. This is something you never do in practice. It’s all theoretical. As the figure shows, the idea is to take a sample out of one population and a sample out of another, calculate their means, and subtract one mean from the other. Return the samples to the populations, and repeat over and over and over. The result of the process is a set of differences between means. This set of differences is the sampling distribution.

FIGURE 11-1: Creating the sampling distribution of the difference between means.
Applying the Central Limit Theorem
Like any other set of numbers, this sampling distribution has a mean and a standard deviation. As is the case with the sampling distribution of the mean (see Chapters 9 and 10), the Central Limit Theorem applies here.
According to the Central Limit Theorem, if the samples are large, the sampling distribution of the difference between means is approximately a normal distribution. If the populations are normally distributed, the sampling distribution is a normal distribution even if the samples are small.
The Central Limit Theorem also has something to say about the mean and standard deviation of this sampling distribution. Suppose the parameters for the first population are μ1 and σ1, and the parameters for the second population are μ2 and σ2. The mean of the sampling distribution is
The standard deviation of the sampling distribution is
N1 is the number of individuals in the sample from the first population, and N2 is the number of individuals in the sample from the second.
Figure 11-2 shows the sampling distribution along with its parameters, as specified by the Central Limit Theorem.

FIGURE 11-2: The sampling distribution of the difference between means according to the Central Limit Theorem.
Z’s once more
Because the Central Limit Theorem says that the sampling distribution is approximately normal for large samples (or for small samples from normally distributed populations), you use the z-score as your test statistic. Another way to say “Use the z-score as your test statistic” is “Perform a z-test.” Here’s the formula:
The term (μ1-μ2) represents the difference between the means in H0.
This formula converts the difference between sample means into a standard score. Compare the standard score against a standard normal distribution — a normal distribution with μ = 0 and σ = 1. If the score is in the rejection region defined by α, reject H0. If it’s not, don’t reject H0.
You use this formula when you know the value of σ12 and σ22.
Here’s an example. Imagine a new training technique designed to increase IQ. Take a sample of 25 people and train them under the new technique. Take another sample of 25 people and give them no special training. Suppose that the sample mean for the new technique sample is 107, and for the no-training sample it’s 101.2. The hypothesis test is
H0: μ1 - μ2 = 0
H1: μ1 - μ2 > 0
I’ll set α at .05.
The IQ is known to have a standard deviation of 16, and I assume that standard deviation would be the same in the population of people trained on the new technique. Of course, that population doesn’t exist. The assumption is that if it did, it should have the same value for the standard deviation as the regular population of IQ scores. Does the mean of that (theoretical) population have the same value as the regular population? H0 says it does. H1 says it’s larger.
The test statistic is

With α = .05, the critical value of z — the value that cuts off the upper 5 percent of the area under the standard normal distribution — is 1.645. (You can use the worksheet function NORM.S.INV from Chapter 8 to verify this.) The calculated value of the test statistic is less than the critical value, so the decision is to not reject H0. Figure 11-3 summarizes this.

FIGURE 11-3: The sampling distribution of the difference between means, along with the critical value for α = .05 and the obtained value of the test statistic in the IQ example.
Data analysis tool: z-Test: Two Sample for Means
Excel provides a data analysis tool that makes it easy to do tests like the one in the IQ example. It’s called z-Test: Two Sample for Means. Figure 11-4 shows the dialog box for this tool along with sample data that correspond to the IQ example.

FIGURE 11-4: The z-Test data analysis tool and data from two samples.
To use this tool, follow these steps:
-
Type the data for each sample into a separate data array.
For this example, the data in the New Technique sample are in column E, and the data for the No Training sample are in column G.
- Select DATA | Data Analysis to open the Data Analysis dialog box.
- In the Data Analysis dialog box, scroll down the Analysis Tools list and select z-Test: Two Sample for Means.
- Click OK to open the z-Test: Two Sample for Means dialog box. (Refer to Figure 11-4.)
-
In the Variable 1 Range box, enter the cell range that holds the data for one of the samples.
For the example, the New Technique data are in $E$2:$E$27. (Note the $ signs for absolute referencing.)
-
In the Variable 2 Range box, enter the cell range that holds the data for the other sample.
The No Training data are in $G$2:$G$27.
-
In the Hypothesized Mean Difference box, type the difference between μ1 and μ2 that H0 specifies.
In this example, that difference is 0.
-
In the Variable 1 Variance (known) box, type the variance of the first sample.
The standard deviation of the population of IQ scores is 16, so this variance is 162= 256.
-
In the Variable 2 Variance (known) box, type the variance of the second sample.
In this example, the variance is also 256.
-
If the cell ranges include column headings, select the Labels check box.
I included the headings in the ranges, so I selected the box.
-
The Alpha box has 0.05 as a default.
I used the default value, consistent with the value of α in this example.
-
In the Output Options, select a radio button to indicate where you want the results.
I selected New Worksheet Ply to put the results on a new page in the worksheet.
-
Click OK.
Because I selected New Worksheet Ply, a newly created page opens with the results.
Figure 11-5 shows the tool’s results, after I expanded the columns. Rows 4, 5, and 7 hold values you input into the dialog box. Row 6 counts the number of scores in each sample.

FIGURE 11-5: Results of the z-Test data analysis tool.
The value of the test statistic is in cell B8. The critical value for a one-tailed test is in B10, and the critical value for a two-tailed test is in B12.
Cell B9 displays the proportion of area that the test statistic cuts off in one tail of the standard normal distribution. Cell B11 doubles that value — it’s the proportion of area cut off by the positive value of the test statistic (in the tail on the right side of the distribution) plus the proportion cut off by the negative value of the test statistic (in the tail on the left side of the distribution).
t for Two
The example in the preceding section involves a situation you rarely encounter — known population variances. If you know a population’s variance, you’re likely to know the population mean. If you know the mean, you probably don’t have to perform hypothesis tests about it.
Not knowing the variances takes the Central Limit Theorem out of play. This means that you can’t use the normal distribution as an approximation of the sampling distribution of the difference between means. Instead, you use the t-distribution, a family of distributions I introduce in Chapter 9 and apply to one-sample hypothesis testing in Chapter 10. The members of this family of distributions differ from one another in terms of a parameter called degrees of freedom (df). Think of df as the denominator of the variance estimate you use when you calculate a value of t as a test statistic. Another way to say “Calculate a value of t as a test statistic” is “Perform a t-test.”
Unknown population variances lead to two possibilities for hypothesis testing. One possibility is that although the variances are unknown, you have reason to assume they’re equal. The other possibility is that you cannot assume they’re equal. In the subsections that follow, I discuss these possibilities.
Like peas in a pod: Equal variances
When you don’t know a population variance, you use the sample variance to estimate it. If you have two samples, you average (sort of) the two sample variances to arrive at the estimate.
In this formula, sp2 stands for the pooled estimate. Notice that the denominator of this estimate is (N1-1) + (N2-1). Is this the df? Absolutely!
The formula for calculating t is

On to an example. FarKlempt Robotics is trying to choose between two machines to produce a component for its new microrobot. Speed is of the essence, so the company has each machine produce ten copies of the component and they time each production run. The hypotheses are
H0: μ1-μ2 = 0
H1: μ1-μ2 ≠ 0
They set α at .05. This is a two-tailed test because they don’t know in advance which machine might be faster.
Table 11-1 presents the data for the production times in minutes.
TABLE 11-1 Sample Statistics from the FarKlempt Machine Study
Machine 1 |
Machine 2 | |
|
Mean Production Time |
23.00 |
20.00 |
|
Standard Deviation |
2.71 |
2.79 |
|
Sample Size |
10 |
10 |
The pooled estimate of σ2 is

The estimate of σ is 2.75, the square root of 7.56.
The test statistic is

For this test statistic, df = 18, the denominator of the variance estimate. In a t-distribution with 18 df, the critical value is 2.10 for the right-side (upper) tail and –2.10 for the left-side (lower) tail. If you don’t believe me, apply T.INV.2T (see Chapter 10). The calculated value of the test statistic is greater than 2.10, so the decision is to reject H0. The data provide evidence that Machine 2 is significantly faster than Machine 1. (You can use the word significant whenever you reject H0.)
Like p’s and q’s: Unequal variances
The case of unequal variances presents a challenge. As it happens, when variances are not equal, the t-distribution with (N1-1) + (N2-1) degrees of freedom is not as close an approximation to the sampling distribution as statisticians would like.
Statisticians meet this challenge by reducing the degrees of freedom. To accomplish the reduction, they use a fairly involved formula that depends on the sample standard deviations and the sample sizes.
Because the variances aren’t equal, a pooled estimate is not appropriate. So you calculate the t-test in a different way:

You evaluate the test statistic against a member of the t-distribution family that has the reduced degrees of freedom.
T.TEST
The worksheet function T.TEST eliminates the muss, fuss, and bother of working through the formulas for the t-test.
Figure 11-6 shows the data for the FarKlempt machines example I show you earlier in the chapter. The figure also shows the Function Arguments dialog box for T.TEST.

FIGURE 11-6: Working with T.TEST.
Follow these steps:
-
Type the data for each sample into a separate data array and select a cell for the result.
For this example, the data for the Machine 1 sample are in column B and the data for the Machine 2 sample are in column D.
- From the Statistical Functions menu, select T.TEST to open the Function Arguments dialog box for
T.TEST. -
In the Function Arguments dialog box, enter the appropriate values for the arguments.
In the Array1 box, enter the sequence of cells that holds the data for one of the samples.
In this example, the Machine 1 data are in B3:B12.
In the Array2 box, enter the sequence of cells that holds the data for the other sample.
The Machine 2 data are in D3:D12.
The Tails box indicates whether this is a one-tailed test or a two-tailed test. In this example, it’s a two-tailed test, so I typed 2 in this box.
The Type box holds a number that indicates the type of t-test. The choices are 1 for a paired test (which you find out about in an upcoming section), 2 for two samples assuming equal variances, and 3 for two samples assuming unequal variances. I typed 2.
With values supplied for all the arguments, the dialog box shows the probability associated with the t value for the data. It does not show the value of t.
- Click OK to put the answer in the selected cell.
The value in the dialog box in Figure 11-6 is less than .05, so the decision is to reject H0.
By the way, for this example, typing 3 into the Type box (indicating unequal variances) results in a very slight adjustment in the probability from the equal variance test. The adjustment is small because the sample variances are almost equal and the sample sizes are the same.
Data analysis tool: t-Test: Two Sample
Excel provides data analysis tools that carry out t-tests. One tool works for the equal variance cases, and another for the unequal variances case. As you’ll see, when you use these tools, you end up with more information than T.TEST gives you.
Here’s an example that applies the equal variances t-test tool to the data from the FarKlempt machines example. Figure 11-7 shows the data along with the dialog box for t-Test: Two-Sample Assuming Equal Variances.

FIGURE 11-7: The equal variances t-Test data analysis tool and data from two samples.
To use this tool, follow these steps:
-
Type the data for each sample into a separate data array.
For this example, the data in the Machine 1 sample are in column B and the data for the Machine 2 sample are in column D.
- Select DATA | Data Analysis to open the Data Analysis dialog box.
- In the Data Analysis dialog box, scroll down the Analysis Tools list and select t-Test: Two Sample Assuming Equal Variances.
-
Click OK to open this tool’s dialog box.
This is the dialog box in Figure 11-7.
-
In the Variable 1 Range box, enter the cell range that holds the data for one of the samples.
For the example, the Machine 1 data are in $B$2:$B$12, including the column heading. (Note the $ signs for absolute referencing.)
-
In the Variable 2 Range box, enter the cell range that holds the data for the other sample.
The Machine 2 data are in $D$2:$D$12, including the column heading.
-
In the Hypothesized Mean Difference box, type the difference between μ1 and μ2 that H0 specifies.
In this example, that difference is 0.
-
If the cell ranges include column headings, select the Labels check box.
I included the headings in the ranges, so I selected the box.
- The Alpha box has 0.05 as a default. Change that value if you’re so inclined.
-
In the Output Options, select a radio button to indicate where you want the results.
I selected New Worksheet Ply to put the results on a new page in the worksheet.
-
Click OK.
Because I selected New Worksheet Ply, a newly created page opens with the results.
Figure 11-8 shows the tool’s results, after I expanded the columns. Rows 4 through 7 hold sample statistics. Cell B8 shows the H0-specified difference between the population means, and B9 shows the degrees of freedom.

FIGURE 11-8: Results of the Equal Variances t-Test data analysis tool.
The remaining rows provide t-related information. The calculated value of the test statistic is in B10. Cell B11 gives the proportion of area that the positive value of the test statistic cuts off in the upper tail of the t-distribution with the indicated df. Cell B12 gives the critical value for a one-tailed test: That’s the value that cuts off the proportion of the area in the upper tail equal to α.
Cell B13 doubles the proportion in B11. This cell holds the proportion of area from B11 added to the proportion of area that the negative value of the test statistic cuts off in the lower tail. Cell B14 shows the critical value for a two-tailed test: That’s the positive value that cuts off α/2 in the upper tail. The corresponding negative value (not shown) cuts off α/2 in the lower tail.
The samples in the example have the same number of scores and approximately equal variances, so applying the unequal variances version of the t-Test tool to that data set won’t show much of a difference from the equal variances case.
Instead I created another example, summarized in Table 11-2. The samples in this example have different sizes and widely differing variances.
TABLE 11-2 Sample Statistics for the Unequal Variances t-Test Example
Sample 1 |
Sample 2 | |
|
Mean |
100.125 |
67.00 |
|
Variance |
561.84 |
102.80 |
|
Sample Size |
8 |
6 |
To show you the difference between the equal variances tool and the unequal variances tool, I ran both on the data and put the results side by side. Figure 11-9 shows the results from both tools. To run the Unequal Variances tool, you complete the same steps as for the Equal Variances version, with one exception: In the Data Analysis Tools dialog box, you select t-Test: Two Sample Assuming Unequal Variances.

FIGURE 11-9: Results of the Equal Variances t-Test data analysis tool and the Unequal Variances t-Test data analysis tool for the data summarized in Table 11-2.
Figure 11-9 shows one obvious difference between the two tools: The Unequal Variances tool shows no pooled estimate of σ2, because the t-test for that case doesn’t use one. Another difference is in the df. As I point out earlier, in the unequal variances case, you reduce the df based on the sample variances and the sample sizes. For the equal variances case, the df in this example is 12, and for the unequal variances case, it’s 10.
The effects of these differences show up in the remaining statistics. The t values, critical values, and probabilities are different.
A Matched Set: Hypothesis Testing for Paired Samples
In the hypothesis tests I describe so far, the samples are independent of one another. Choosing an individual for one sample has no bearing on the choice of an individual for the other.
Sometimes, the samples are matched. The most obvious case is when the same individual provides a score under each of two conditions — as in a before-after study. For example, suppose ten people participate in a weight-loss program. They weigh in before they start the program and again after one month on the program. The important data is the set of before-after differences. Table 11-3 shows the data.
TABLE 11-3 Data for the Weight-Loss Example
Person |
Weight Before Program |
Weight After One Month |
Difference |
|
1 |
198 |
194 |
4 |
|
2 |
201 |
203 |
-2 |
|
3 |
210 |
200 |
10 |
|
4 |
185 |
183 |
2 |
|
5 |
204 |
200 |
4 |
|
6 |
156 |
153 |
3 |
|
7 |
167 |
166 |
1 |
|
8 |
197 |
197 |
0 |
|
9 |
220 |
215 |
5 |
|
10 |
186 |
184 |
2 |
|
Mean |
2.9 | ||
|
Standard Deviation |
3.25 |
The idea is to think of these differences as a sample of scores, and treat them as you would in a one-sample t-test. (See Chapter 10.)
You carry out a test on these hypotheses:
H0: μd ≤ 0
H1: μd > 0
The d in the subscripts stands for difference. Set α = .05.
The formula for this kind of t-test is
In this formula, ![]() is the mean of the differences. To find
is the mean of the differences. To find ![]() , you calculate the standard deviation of the differences and divide by the square root of the number of pairs:
, you calculate the standard deviation of the differences and divide by the square root of the number of pairs:
The df is N-1.
From Table 11-3,

With df = 9 (Number of pairs – 1), the critical value for α = .05 is 2.26. (Use T.INV to verify.) The calculated value exceeds this value, so the decision is to reject H0.
T.TEST for matched samples
Earlier, I describe the worksheet function T.TEST and show you how to use it with independent samples. This time, I use it for the matched samples weight-loss example. Figure 11-10 shows the Function Arguments dialog box for T.TEST along with data from the weight-loss example.

FIGURE 11-10: The Function Arguments dialog box for T.TEST along with matched sample data.
Here are the steps to follow:
-
Enter the data for each sample into a separate data array and select a cell.
For this example, the data for the Before sample are in column B and the data for the After sample are in column C.
- From the Statistical Functions menu, select T.TEST to open the Function Arguments dialog box for
T.TEST. -
In the Function Arguments dialog box, enter the appropriate values for the arguments.
In the Array1 box, type the sequence of cells that holds the data for one of the samples. In this example, the Before data are in B3:B12.
In the Array2 box, type the sequence of cells that holds the data for the other sample.
The After data are in C3:C12.
The Tails box indicates whether this is a one-tailed test or a two-tailed test. In this example, it’s a one-tailed test, so I type
1in the Tails box.The Type box holds a number that indicates the type of t-test to perform. The choices are 1 for a paired test, 2 for two samples assuming equal variances, and 3 for two samples assuming unequal variances. I typed
1.With values supplied for all the arguments, the dialog box shows the probability associated with the t value for the data. It does not show the value of t.
- Click OK to put the answer in the selected cell.
The value in the dialog box in Figure 11-10 is less than .05, so the decision is to reject H0.
If I assign the column headers in Figure 11-10 as names for the respective arrays, the formula in the Formula bar can be
=T.TEST(Before,After,1,1)
That format might be easier to explain if you had to show the worksheet to someone. (If you don’t remember how to define a name for a cell range, refer to Chapter 2.)
Data analysis tool: t-Test: Paired Two Sample for Means
Excel provides a data analysis tool that takes care of just about everything for matched samples. It’s called t-test: Paired Two Sample for Means. In this section, I use it on the weight-loss data.
Figure 11-11 shows the data along with the dialog box for t-Test: Paired Two Sample for Means.

FIGURE 11-11: The Paired Two Sample t-Test data analysis tool and data from matched samples.
Here are the steps to follow:
-
Enter the data for each sample into a separate data array.
For this example, the data in the Before sample are in column B and the data for the After sample are in column C.
- Select Data | Data Analysis to open the Data Analysis dialog box.
- In the Data Analysis dialog box, scroll down the Analysis Tools list, and select t-Test: Paired Two Sample for Means.
-
Click OK to open this tool’s dialog box.
This is the dialog box in Figure 11-11.
-
In the Variable 1 Range box, enter the cell range that holds the data for one of the samples.
For the example, the Before data are in $B$2:$B$12, including the heading. (Note the $ signs for absolute referencing.)
-
In the Variable 2 Range box, enter the cell range that holds the data for the other sample.
The After data are in $C$2:$C$12, including the heading.
-
In the Hypothesized Mean Difference box, type the difference between μ1 and μ2 that H0 specifies.
In this example, that difference is 0.
-
If the cell ranges include column headings, select the Labels check box.
I included the headings in the ranges, so I selected the check box.
- The Alpha box has 0.05 as a default. Change that value if you want to use a different α.
-
In the Output Options, select a radio button to indicate where you want the results.
I selected New Worksheet Ply to put the results on a new page in the worksheet.
-
Click OK.
Because I selected New Worksheet Ply, a newly created page opens with the results.
Figure 11-12 shows the tool’s results, after I expanded the columns. Rows 4 through 7 hold sample statistics. The only item that’s new is the number in cell B7, the Pearson Correlation Coefficient. This is a number between –1 and +1 that indicates the strength of the relationship between the data in the first sample and the data in the second.

FIGURE 11-12: Results of the Paired Two Sample t-Test data analysis tool.
If this number is close to 1 (as in the example), high scores in one sample are associated with high scores in the other, and low scores in one are associated with low scores in the other. If the number is close to –1, high scores in the first sample are associated with low scores in the second, and low scores in the first are associated with high scores in the second.
If the number is close to zero, scores in the first sample are unrelated to scores in the second. Because the two samples consist of scores on the same people, you expect a high value. (I describe this topic in much greater detail in Chapter 15.)
Cell B8 shows the H0-specified difference between the population means, and B9 shows the degrees of freedom.
The remaining rows provide t-related information. The calculated value of the test statistic is in B10. Cell B11 gives the proportion of area the positive value of the test statistic cuts off in the upper tail of the t-distribution with the indicated df. Cell B12 gives the critical value for a one-tailed test: That’s the value that cuts off the proportion of the area in the upper tail equal to α.
Cell B13 doubles the proportion in B11. This cell holds the proportion of area from B11 added to the proportion of area that the negative value of the test statistic cuts off in the lower tail. Cell B13 shows the critical value for a two-tailed test: That’s the positive value that cuts off α/2 in the upper tail. The corresponding negative value (not shown) cuts off α/2 in the lower tail.
Testing Two Variances
The two-sample hypothesis testing I describe thus far pertains to means. It’s also possible to test hypotheses about variances.
In this section, I extend the one-variance manufacturing example I use in Chapter 10. FarKlempt Robotics, Inc., produces a part that has to be a certain length with a very small variability. The company is considering two machines to produce this part, and it wants to choose the one that results in the least variability. FarKlempt Robotics takes a sample of parts from each machine, measures them, finds the variance for each sample, and performs a hypothesis test to see if one machine’s variance is significantly greater than the other’s.
The hypotheses are
H0: σ12 = σ22
H1: σ12 ≠ σ22
As always, an α is a must. As usual, I set it to .05.
When you test two variances, you don’t subtract one from the other. Instead, you divide one by the other to calculate the test statistic. Sir Ronald Fisher is a famous statistician who worked out the mathematics and the family of distributions for working with variances in this way. The test statistic is named in his honor. It’s called an F-ratio and the test is the F test. The family of distributions for the test is called the F-distribution.
Without going into all the mathematics, I’ll just tell you that, once again, df is the parameter that distinguishes one member of the family from another. What’s different about this family is that two variance estimates are involved, so each member of the family is associated with two values of df, rather than one as in the t-test. Another difference between the F-distribution and the others you’ve seen is that the F cannot have a negative value. Figure 11-13 shows two members of the F-distribution family.
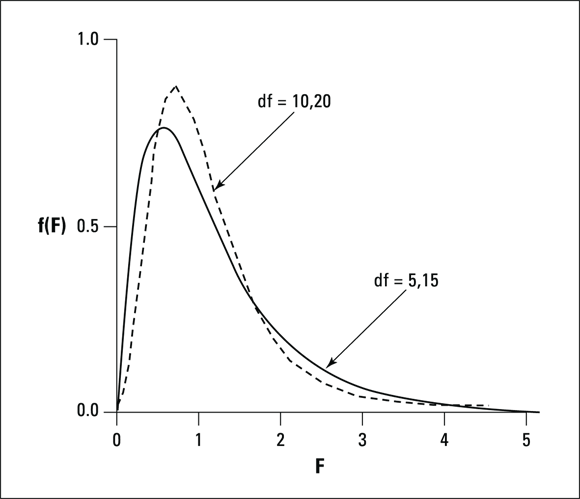
FIGURE 11-13: Two members of the F-distribution family.
The test statistic is
Suppose FarKlempt Robotics produces 10 parts with Machine 1 and finds a sample variance of .60 square inches. It produces 15 parts with Machine 2 and finds a sample variance of .44 square inches. Can the company reject H0?
Calculating the test statistic,
The df’s are 9 and 14: The variance estimate in the numerator of the F ratio is based on 10 cases, and the variance estimate in the denominator is based on 15 cases.
When the df’s are 9 and 14 and it’s a two-tailed test at α = .05, the critical value of F is 3.21. (In a moment, I show you an Excel function that finds the value for you.) The calculated value is less than the critical value, so the decision is to not reject H0.
Using F in conjunction with t
One use of the F-distribution is in conjunction with the t-test for independent samples. Before you do the t-test, you use F to help decide whether to assume equal variances or unequal variances in the samples.
In the equal variances t-test example I show you earlier, the standard deviations are 2.71 and 2.79. The variances are 7.34 and 7.78. The F-ratio of these variances is
Each sample is based on ten observations, so df = 9 for each sample variance. An F-ratio of 1.06 cuts off the upper 47 percent of the F-distribution whose df are 9 and 9, so it’s safe to use the equal-variances version of the t-test for these data.
In the sidebar at the end of Chapter 10, I mention that on rare occasions a high α is a good thing. When H0 is a desirable outcome and you’d rather not reject it, you stack the deck against rejecting by setting α at a high level so that small differences cause you to reject H0.
This is one of those rare occasions. It’s more desirable to use the equal variances t-test, which typically provides more degrees of freedom than the unequal variances t-test. Setting a high value of α (.20 is a good one) for the F-test enables you to be confident when you assume equal variances.
F.TEST
The worksheet function F.TEST calculates an F-ratio on the data from two samples. It doesn’t return the F-ratio. Instead, it provides the two-tailed probability of the calculated F-ratio under H0. This means that the answer is the proportion of area to the right of the F-ratio, and to the left of the reciprocal of the F-ratio (1 divided by the F-ratio).
Figure 11-14 presents the data for the FarKlempt machines example I just summarized for you. The figure also shows the Function Arguments dialog box for F.TEST.

FIGURE 11-14: Working with F.TEST.
Follow these steps:
-
Enter the data for each sample into a separate data array and select a cell for the answer.
For this example, the data for the Machine 1 sample are in column B and the data for the Machine 2 sample are in column D.
- From the Statistical Functions menu, select F.TEST to open the Function Arguments dialog box for
F.TEST. -
In the Function Arguments dialog box, enter the appropriate values for the arguments.
In the Array1 box, enter the sequence of cells that holds the data for the sample with the larger variance. In this example, the Machine 1 data are in B3:B12.
In the Array2 box, enter the sequence of cells that holds the data for the other sample. The Machine 2 data are in D3:D17.
With values entered for all the arguments, the answer appears in the dialog box.
- Click OK to put the answer in the selected cell.
The value in the dialog box in Figure 11-14 is greater than .05, so the decision is to not reject H0. Figure 11-15 shows the area that the answer represents.

FIGURE 11-15: F.TEST’s results.
Had I assigned names to those two arrays, the formula in the Formula bar could have been
=F.TEST(Machine_1,Machine_2)
If you don’t know how to assign names to arrays, see Chapter 2. In that chapter, you also find out why I inserted an underscore into each name.
F.DIST and F.DIST.RT
You use the worksheet function F.DIST or the function F.DIST.RT to decide whether or not your calculated F-ratio is in the region of rejection. For F.DIST, you supply a value for F, a value for each df, and a value (TRUE or FALSE) for an argument called Cumulative. If the value for Cumulative is TRUE, F.DIST returns the probability of obtaining an F-ratio of at most as high as yours if H0 is true. (Excel calls this the left-tail probability.) If that probability is greater than 1- α, you reject H0. If the value for Cumulative is FALSE, F.DIST returns the height of the F-distribution at your value of F. I use this option later in this chapter to create a chart of the F-distribution.
F.DIST.RT returns the probability of obtaining an F-ratio at least as high as yours if H0 is true. (Excel calls this the right-tail probability.) If that value is less than α, reject H0. In practice, F.DIST.RT is more straightforward.
Here, I apply F.DIST.RT to the preceding example. The F-ratio is 1.36, with 9 and 14 df.
The steps are:
- Select a cell for the answer.
- From the Statistical Functions menu, select F.DIST.RT to open the Function Arguments dialog box for
F.DIST.RT. (See Figure 11-16.) -
In the Function Arguments dialog box, enter the appropriate values for the arguments.
In the X box, type the calculated F. For this example, the calculated F is 1.36.
In the Deg_freedom1 box, type the degrees of freedom for the variance estimate in the numerator of the F. The degrees of freedom for the numerator in this example is 9 (10 scores – 1).
In the Deg_freedom2 box, I type the degrees of freedom for the variance estimate in the denominator of the F.
The degrees of freedom for the denominator in this example is 14 (15 scores – 1).
With values entered for all the arguments, the answer appears in the dialog box.
- Click OK to close the dialog box and put the answer in the selected cell.

FIGURE 11-16: The Function Arguments dialog box for F.DIST.RT.
The value in the dialog box in Figure 11-16 is greater than .05, so the decision is to not reject H0.
F.INV and F.INV.RT
The F.INV worksheet functions are the reverse of the F.DIST functions. F.INV finds the value in the F-distribution that cuts off a given proportion of the area in the lower (left) tail. F.INV.RT finds the value that cuts off a given proportion of the area in the upper (right) tail. You can use F.INV.RT to find the critical value of F.
Here, I use F.INV.RT to find the critical value for the two-tailed test in the FarKlempt machines example:
- Select a cell for the answer.
- From the Statistical Functions menu, select F.INV.RT to open the Function Arguments dialog box for
FINV.RT. -
In the Function Arguments dialog box, enter the appropriate values for the arguments.
In the Probability box, enter the proportion of area in the upper tail. In this example, that’s .025 because it’s a two-tailed test with α = .05.
In the Deg_freedom1 box, type the degrees of freedom for the numerator. For this example, df for the numerator = 9.
In the Deg_freedom2 box, type the degrees of freedom for the denominator. For this example, df for the denominator = 14.
With values entered for all the arguments, the answer appears in the dialog box. (See Figure 11-17.)
- Click OK to put the answer into the selected cell.

FIGURE 11-17: The Function Arguments dialog box for F.INV.RT.
Data analysis tool: F-test: Two Sample for Variances
Excel provides a data analysis tool for carrying out an F-test on two sample variances. I apply it here to the sample variances example I’ve been using. Figure 11-18 shows the data, along with the dialog box for F-Test: Two-Sample for Variances.

FIGURE 11-18: The F-Test data analysis tool and data from two samples.
To use this tool, follow these steps:
-
Enter the data for each sample into a separate data array.
For this example, the data in the Machine 1 sample are in column B and the data for the Machine 2 sample are in column D.
- Select Data | Data Analysis to open the Data Analysis dialog box.
- In the Data Analysis dialog box, scroll down the Analysis Tools list and select F-Test Two Sample For Variances.
-
Click OK to open this tool’s dialog box.
This is the dialog box shown in Figure 11-18.
-
In the Variable 1 Range box, enter the cell range that holds the data for the first sample.
For the example, the Machine 1 data are in $B$2:$B$12, including the heading. (Note the $ signs for absolute referencing.)
-
In the Variable 2 Range box, enter the cell range that holds the data for the second sample.
The Machine 2 data are in $D$2:$D$17, including the heading.
-
If the cell ranges include column headings, select the Labels check box.
I included the headings in the ranges, so I selected the box.
-
The Alpha box has 0.05 as a default. Change that value for a different α.
The Alpha box provides a one-tailed alpha. I want a two-tailed test, so I changed this value to .025.
-
In the Output Options, select a radio button to indicate where you want the results.
I selected New Worksheet Ply to put the results on a new page in the worksheet.
-
Click OK.
Because I selected New Worksheet Ply, a newly created page opens with the results.
Figure 11-19 shows the tool’s results, after I expanded the columns. Rows 4 through 6 hold sample statistics. Cell B7 shows the degrees of freedom.

FIGURE 11-19: Results of the F-Test data analysis tool.
The remaining rows present F-related information. The calculated value of F is in B8. Cell B9 gives the proportion of area the calculated F cuts off in the upper tail of the F-distribution. This is the right-side area shown earlier in Figure 11-15. Cell B10 gives the critical value for a one-tailed test: That’s the value that cuts off the proportion of the area in the upper tail equal to the value in the Alpha box.
Visualizing the F-Distribution
The F-distribution is extremely important in statistics, as you’ll see in the next chapter. In order to increase your understanding of this distribution, I show you how to graph it. Figure 11-20 shows the numbers and the finished product.

FIGURE 11-20: Visualizing the F-distribution.
Here are the steps:
-
Put the degrees of freedom in cells.
I put
10into cell B1, and15in cell B2. -
Create a column of values for the statistic.
In cells D2 through D42, I put the values 0 through 8 in increments of .2
-
In the first cell of the adjoining column, put the value of the probability density for the first value of the statistic.
Because I’m graphing an F-distribution, I use
F.DISTin cell E2. For the value of X, I click cell D2. For df1, I click B1 and press the F4 key to anchor this selection. For df2, I click B2 and press the F4 key. In the Cumulative box, I typeFALSEto return the height of the distribution for this value of t. Then I click OK. - Autofill the column with the values.
-
Create the chart.
Highlight both columns. On the Insert tab, in the Charts area, select Scatter with Smooth Lines.
-
Modify the chart.
I click inside the chart to open the Chart Elements tool (the plus sign) and use it to add the axis titles (F and f(F)). I also delete the chart title and the gridlines, but that’s a matter of personal taste. And I like to stretch out the chart.
-
Manipulate the chart.
To help you get a feel for the distribution, try different values for the df and see how the changes affect the chart.

 The sampling distribution of the difference between means is the distribution of all possible values of differences between pairs of sample means with the sample sizes held constant from pair to pair. (Yes, that’s a mouthful.) Held constant from pair to pair means that the first sample in the pair always has the same size, and the second sample in the pair always has the same size. The two sample sizes are not necessarily equal.
The sampling distribution of the difference between means is the distribution of all possible values of differences between pairs of sample means with the sample sizes held constant from pair to pair. (Yes, that’s a mouthful.) Held constant from pair to pair means that the first sample in the pair always has the same size, and the second sample in the pair always has the same size. The two sample sizes are not necessarily equal. If you’re looking at this test and thinking, “Hmmm… looks just like a one-sample t-test, but the one sample consists of the differences between pairs,” you’ve pretty much got it.
If you’re looking at this test and thinking, “Hmmm… looks just like a one-sample t-test, but the one sample consists of the differences between pairs,” you’ve pretty much got it.