CHAPTER 4
RELATIONS AND FUNCTIONS
4.1 RELATIONS
A relation is an association between objects. A book on a table is an example of the relation of one object being on another. It is especially common to speak of relations among people. For example, one person could be the niece of another. In mathematics, there are many relations such as equals and less-than that describe associations between numbers. To formalize this idea, we make the next definition.
![]() DEFINITION 4.1.1
DEFINITION 4.1.1
A set R is an (n-ary) relation if there exist sets A0, A1, ... , An−1 such that
![]()
In particular, R is a unary relation if n = 1 and a binary relation if n = 2. If R ⊆ A × A for some set A, then R is a relation on A and we write (A, R).
The relation on can be represented as a subset of the Cartesian product of the set of all books and the set of all tables. We could then write (dictionary, desk) to mean that the
dictionary is on the desk. Similarly, the set {(2, 4), (7, 3), (0, 0)} is a relation because it is a subset of Z × Z. The ordered pair (2, 4) means that 2 is related to 4. Likewise, R × Q is a relation where every real number is related to every rational number, and according to Definition 4.1.1, the empty set is also a relation because ∅ = ∅ × ∅.
![]() EXAMPLE 4.1.2
EXAMPLE 4.1.2
For any set A, define
![]()
Call this set the identity on A. In particular, the identity on R is
![]()
and the identity on Z is
![]()
Notice that ∅ is the identity on ∅.
![]() EXAMPLE 4.1.3
EXAMPLE 4.1.3
The less-than relation on Z is defined as
![]()
Another approach is to use membership in the set of positive integers as our condition. That is,
![]()
Hence, (4, 7) ∈ L because 7 − 4 ∈ Z+. See Exercise 1 for another definition of L.
When a relation R ⊆ A × B is defined, all elements in A or B might not be used. For this reason, it is important to identify the sets that comprise all possible values for the two coordinates of the relation.
![]() DEFINITION 4.1.4
DEFINITION 4.1.4
Let R ⊆ A × B. The domain of R is the set
![]()
and the range of R is the set
![]()
![]() EXAMPLE 4.1.5
EXAMPLE 4.1.5
If R = {(1, 3), (2, 4), (2, 5)}, then dom(R) = {1, 2} and ran(R) = {3, 4, 5}. We represent this in Figure 4.1 where A and B are sets so that {1, 2} ⊆ A and {3, 4, 5} ⊆ B. The ordered pair (1, 3) is denoted by the arrow pointing from 1 to 3. Also, both dom(R) and ran(R) are shaded.
Figure 4.1 R = {(1, 3), (2, 4), (2, 5)}.
![]() EXAMPLE 4.1.6
EXAMPLE 4.1.6
Let S = {(x, y) : |x| = y ∧ x, y ∈ R}. Notice that both (2, 2) and (−2, 2) are elements of S. Furthermore, dom(S) = R and ran(S) = [0, ∞).
The domain and range of a relation can be the same set as in the next two examples.
![]() EXAMPLE 4.1.7
EXAMPLE 4.1.7
If R = {(0, 1), (0, 2), (1, 0), (2, 0)}, then R is a relation on the set {0, 1, 2} with dom(R) = ran(R) = {0, 1, 2}.
![]() EXAMPLE 4.1.8
EXAMPLE 4.1.8
For the relation
![]()
both the domain and range equal R. First, note that it is clear by the definition of S that both dom(S) and ran(S) are subsets of R. For the other inclusion, take x ∈ R. Since (x, 1) ∈ S, x ∈ dom(S), and since (1, y) ∈ S, y ∈ ran(S).
Composition
Given the relations R and S, let us define a new relation. Suppose that (a, b) ∈ S and (b, c) ∈ R. Therefore, a is related to c through b. The new relation will contain the ordered pair (a, c) to represent this relationship.
![]() DEFINITION 4.1.9
DEFINITION 4.1.9
Let R ⊆ A × B and S ⊆ B × C. The composition of S and R is the subset of A × C defined as
![]()
As illustrated in Figure 4.2, the reason that (a, c) ∈ R ![]() S is because (a, b) ∈ S and (b, c) ∈ R. That is, a is related to c via R
S is because (a, b) ∈ S and (b, c) ∈ R. That is, a is related to c via R ![]() S because a is related to b via S and then b is related to c via R. The composition can be viewed as the direct path from a to c that does not require the intermediary b.
S because a is related to b via S and then b is related to c via R. The composition can be viewed as the direct path from a to c that does not require the intermediary b.

Figure 4.2 A composition of relations.
![]() EXAMPLE 4.1.10
EXAMPLE 4.1.10
To clarify the definition, let
![]()
and
![]()
We have that R ![]() S = {(0, 3), (0, 4), (0, 5)}. Notice that (0, 3) ∈ R
S = {(0, 3), (0, 4), (0, 5)}. Notice that (0, 3) ∈ R ![]() S because (0, 1) ∈ S and (1, 3) ∈ R. However, S
S because (0, 1) ∈ S and (1, 3) ∈ R. However, S ![]() R is empty since ran(R) and dom(S) are disjoint.
R is empty since ran(R) and dom(S) are disjoint.
![]() EXAMPLE 4.1.11
EXAMPLE 4.1.11
Define
![]()
and
![]()
Notice that R is the unit circle and S is the line with slope of 1 and y-intercept of (0, 1). Let us find R ![]() S.
S.

Therefore, R ![]() S is the circle with center (−1, 0) and radius 1.
S is the circle with center (−1, 0) and radius 1.
Example 4.1.10 shows that it is possible that S ![]() R ≠ R
R ≠ R ![]() S. However, we can change the order of the composition.
S. However, we can change the order of the composition.
![]() THEOREM 4.1.12
THEOREM 4.1.12
If R ⊆ A × B, S ⊆ B × C, and T ⊆ C × D, then T ![]() (S
(S ![]() R) = (T
R) = (T ![]() S)
S) ![]() R.
R.
PROOF
Assume that R ⊆ A × B, S ⊆ B × C, and T ⊆ C × D. Then,

Inverses
Let R ⊆ A × B. We know that R ![]() IA = R and IB
IA = R and IB ![]() R = R [Exercise 10(a)]. If we want IA = IB, we need A = B so that R is a relation on A. Then,
R = R [Exercise 10(a)]. If we want IA = IB, we need A = B so that R is a relation on A. Then,
![]()
For example, if we again define R = {(2, 4), (1, 3), (2, 5)} and view it as a relation on Z, then R composed on either side by IZ yields R. To illustrate, consider the ordered pair (1, 3). It is an element of R ![]() IZ because
IZ because
![]()
and it is also an element of IZ ![]() R because
R because
![]()
Notice that not every identity relation will have this property. Using the same definition of R as above,
![]()
but
![]()
Now let us change the problem. Given a relation R on A, can we find a relation S on A such that R ![]() S = S
S = S ![]() R = IA? The next definition is used to try to answer this question.
R = IA? The next definition is used to try to answer this question.
Let R be a binary relation. The inverse of R is the set
![]()
For a relation S, we say that R and S are inverse relations if R−1 = S.
![]() EXAMPLE 4.1.14
EXAMPLE 4.1.14
Let L be the less-than relation on R (Example 4.1.3). Then,

This shows that less-than and greater-than are inverse relations.
We now check whether R ![]() R−1 = R−1
R−1 = R−1 ![]() R = IA for any relation R on A. Consider R = {(2, 1), (4, 3)}, which is a relation on {1, 2, 3, 4}. Then,
R = IA for any relation R on A. Consider R = {(2, 1), (4, 3)}, which is a relation on {1, 2, 3, 4}. Then,
![]()
and we see that composing does not yield the identity on {1, 2, 3, 4} because
![]()
and
![]()
The situation is worse when we define S = {(2, 1), (2, 3), (4, 3)}. In this case, we have that
![]()
but
![]()
and
![]()
Neither of these compositions leads to an identity, but at least we have that
![]()
and
![]()
This can be generalized.
![]() THEOREM 4.1.15
THEOREM 4.1.15
Iran(R) ⊆ R ![]() R−1 and Idom(R) ⊆ R−1
R−1 and Idom(R) ⊆ R−1 ![]() R for any binary relation R.
R for any binary relation R.
The first inclusion is proved in Exercise 12. To see the second inclusion, let x ∈ dom(R). By definition, there exists y ∈ ran(R) so that (x, y) ∈ R. Hence, (y, x) ∈ R−1, which implies that (x, x) ∈ R−1 ![]() R.
R. ![]()
Exercises
1. Let L ⊆ Z × Z be the less-than relation as defined in Example 4.1.3. Prove that
![]()
2. Find the domain and range of the given relations.
(a) {(0, 1), (2, 3), (4, 5), (6, 7)}
(b) {((a, b), 1), ((a, c), 2), ((a, d), 3)}
(c) R × Z
(d) ∅ × ∅
(e) Q × ∅
(f) {(x, y) : x, y ∈ [0, 1] ∧ x < y}
(g) {(x, y) ∈ R2 : y = 3}
(h) {(x, y) ∈ R2 : y = |x|}
(i) {(x, y) ∈ R2 : x2 + y2 = 4}
(j) {(x, y) ∈ R2 : y ≤ ![]() ∧ x ≥ 0}
∧ x ≥ 0}
(k) {(f, g) : ∃a ∈ R(f(x) = ex ∧ g(x) = ax)}
(l) {((a, b), a + b) : a, b ∈ Z}
3. Write R ![]() S as a roster.
S as a roster.
(a) R = {(1, 0), (2, 3), (4, 6)}, S = {(1, 2), (2, 3), (3, 4)}
(b) R = {(1, 3), (2, 5), (3, 1)}, S = {(1, 3), (3, 1), (5, 2)}
(c) R = {(1, 2), (3, 4), (5, 6)}, S = {(1, 2), (3, 4), (5, 6)}
(d) R = {(1, 2), (3, 4), (5, 6)}, S = {(2, 1), (3, 5), (5, 7)}
4. Write R ![]() S using abstraction.
S using abstraction.
(a) R = {(x, y) ∈ R2 : x2 + y2 = 1}
S = R2
(b) R = {(x, y) ∈ R2 : x2 + y2 = 1}
S = Z × Z
(c) R = {(x, y) ∈ R2 : x2 + y2 = 1}
S = {(x, y) ∈ R2 : (x − 2)2 + y2 = 1}
(d) R = {(x, y) ∈ R2 : x2 + y2 = 1}
S = {(x, y) ∈ R2 : y = 2x − 1}
5. Write the inverse of each relation. Use the abstraction method where appropriate.
(a) ∅
(b) IZ
(c) {(1, 0), (2, 3), (4, 6)}
(e) Z × R
(f) {(x, sin x) : x ∈ R}
(g) {(x, y) ∈ R2 : x + y = 1}
(h) {(x, y) ∈ R2 : x2 + y2 = 1}
6. Let R ⊆ A × B and S ⊆ B × C. Show the following.
(a) R−1 ![]() S−1 ⊆ C × A.
S−1 ⊆ C × A.
(b) dom(R) = ran(R−1).
(c) ran(R) = dom(R−1).
7. Prove that if R is a binary relation, (R−1)−1 = R.
8. Prove that (S ![]() R)−1 = R−1
R)−1 = R−1 ![]() S−1 if R ⊆ A × B and S ⊆ B × C.
S−1 if R ⊆ A × B and S ⊆ B × C.
9. Let R, S ⊆ A × B. Prove the following.
(a) If R ⊆ S, then R−1 ⊆ S−1.
(b) (R ∪ S)−1 = R−1 ∪ S−1.
(c) (R ∩ S)−1 = R−1 ∩ S−1.
10. Let R ⊆ A × B.
(a) Prove R ![]() IA = R and IB
IA = R and IB ![]() R = R.
R = R.
(b) Show that if there exists a set C such that A and B are subsets of C, then R ![]() IC = IC
IC = IC ![]() R = R.
R = R.
11. Let R ⊆ A × B and S ⊆ B × C. Show that S ![]() R = ∅ if and only if dom(S) and ran(R) are disjoint.
R = ∅ if and only if dom(S) and ran(R) are disjoint.
12. For any relation R, prove Iran(R) ⊆ R ![]() R−1.
R−1.
13. Let R ⊆ A × B. Prove.
(a) ![]() {x ∈ A : (x, b) ∈ R} = dom(R).
{x ∈ A : (x, b) ∈ R} = dom(R).
(b) ![]() {y ∈ B : (a, y) ∈ R} = ran(R).
{y ∈ B : (a, y) ∈ R} = ran(R).
4.2 EQUIVALENCE RELATIONS
In practice we usually do not write relations as sets of ordered pairs. We instead write propositions like 4 = 4 or 3 < 9. To copy this, we will introduce an alternate notation.
![]() DEFINITION 4.2.1
DEFINITION 4.2.1
Let R be a relation on A. For all a, b ∈ A,
![]()
and
![]()
For example, the less-than relation L (Example 4.1.3) is usually denoted by <, and we write 2 < 3 instead of (2, 3) ∈ L or (2, 3) ∈ <.
Define the relation R on Z by
![]()
Therefore, for all a, b ∈ Z, a R b if and only if a divides b. Therefore, 4 R 8 but 8 ![]() 4.
4.
Relations can have different properties depending on their definitions. Here are three important examples using relations on A = {1, 2, 3}.
- {(1, 1), (2, 2), (3, 3)} has the property that every element of A is related to itself.
- {(1, 2), (2, 1), (2, 3), (3, 2)} has the property that if a is related to b, then b is related to a.
- {(1, 2), (2, 3), (1, 3)} has the property that if a is related to b and b is related to c, then a is related to c.
These examples lead to the following definitions.
![]() DEFINITION 4.2.3
DEFINITION 4.2.3
Let R be a relation on A.
- R is reflexive if a R a for all a ∈ A.
- R is symmetric when for all a, b ∈ A, if a R b, then b R a.
- R is transitive means that for all a, b, c ∈ A, if a R b and b R c, then a R c.
Notice that the relation in Example 4.2.2 is not reflexive because 0 does not divide 0 and is not symmetric because 4 divides 8 but 8 does not divide 4, but it is transitive because if a divides b and b divides c, then a divides c.
When a relation is reflexive, symmetric, and transitive, it behaves very much like an identity relation (Example 4.1.2). Such relations play an important role in mathematics, so we name them.
![]() DEFINITION 4.2.4
DEFINITION 4.2.4
A relation R on A is an equivalence relation if R is reflexive, symmetric, and transitive.
Observe that the relation in Example 4.2.2 is not an equivalence relation. However, any identity relation is an equivalence relation. We see this assumption at work in the next example.
Let R be a relation on Z × (Z {0}) so that for all a, c ∈ Z and b, d ∈ Z {0},
(a, b) R (c, d) if and only if ad = bc.
To see that this is an equivalence relation, let (a, b), (c, d), and (e, f) be elements of Z × (Z {0}).
- (a, b) R (a, b) since ab = ab.
- Assume (a, b) R (c, d). Then, ad = bc. This implies that cb = da, so (c, d) R (a, b).
- Let (a, b) R (c, d) and (c, d) R (e, f). This gives ad = bc and cf = de. Therefore, (a, b) R (e, f) because

![]() EXAMPLE 4.2.6
EXAMPLE 4.2.6
Take m ∈ Z+ and let a, b, and c be integers. Define a to be congruent to b modulo m and write
![]()
That is,
![]()
For example, we have that 7 ≡ 1 (mod 3), 1 ≡ 13 (mod 3), and 27 ≡ 0 (mod 3), but 2 ![]() 9 (mod 3) and 25
9 (mod 3) and 25 ![]() 0 (mod 3). Congruence modulo m defines the relation
0 (mod 3). Congruence modulo m defines the relation
![]()
Observe that
![]()
Prove that Rm is an equivalence relation.
- (a, a) ∈ Rm because a ≡ a (mod m).
- Assume (a, b) ∈ Rm. This implies that m | a − b. By Exercise 2.4.18, m | b − a. Hence, (b, a) ∈ Rm.
- Let (a, b), (b, c) ∈ Rm. Then a = b + mk and b = c + ml for some k, l ∈ Z. Substitution yields
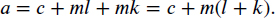
Since the sum of two integers is an integer, (a, c) ∈ Rm.
Equivalence Classes
Let R be a relation on {1, 2, 3, 4} such that
![]()
Observe that 1 is related to 2 and 3, 2 is related to 4, and 3 and 4 are not related to any number. Combining the elements that are related to a particular element results in a set named by the next definition.
![]() DEFINITION 4.2.7
DEFINITION 4.2.7
Let R be a relation on A with a ∈ A. The class of a with respect to R is the set
![]()
If R is an equivalence relation, [a]R is called an equivalence class. We often denote [a]R by [a] if the relation is clear from context.
Using R as defined in (4.1),
![]()
If R had been an equivalence relation on a set A, then [a]R would be nonempty for all a ∈ A because a would be an element of [a]R (Exercise 17).
![]() EXAMPLE 4.2.8
EXAMPLE 4.2.8
Let R be the equivalence relation from Example 4.2.5. We prove that
![]()
To see this, take (a, b) ∈ [(1, 3)]. This means that (1, 3) R (a, b), so b = 3a and a ≠ 0 because b ≠ 0. Hence, (a, b) = (a, 3a). Conversely, let n ≠ 0. Then, (1, 3) R (n, 3n) because 1 · 3n = 3 · n. Thus, (n, 3n) ∈ [(1, 3)].
![]() EXAMPLE 4.2.9
EXAMPLE 4.2.9
Using the notation of Example 4.2.6, let Rm be the relation defined by congruence modulo m. For all n ∈ Z, define
![]()
Therefore, when m = 5, the equivalence classes are:

![]()
The collection of all equivalence classes of a relation is a set named by the next definition.
![]() DEFINITION 4.2.10
DEFINITION 4.2.10
Let R be an equivalence relation on A. The quotient set of A modulo R is
![]()
Observe by Exercise 3 that it is always the case that
![]()
![]() EXAMPLE 4.2.11
EXAMPLE 4.2.11
Let m ∈ Z+. The quotient set Z/Rm is denoted by Zm. That is,
![]()
![]() EXAMPLE 4.2.12
EXAMPLE 4.2.12
Define the relation R on R2 by
![]()
R is an equivalence relation by Exercise 2. We note that for any (a, b) ∈ R2,

Therefore, the equivalence class of (a, b) is the line with a slope of 1 and a y-intercept equal to (0, b − a). The equivalence classes of (0, 1.5) and (0, −1) are illustrated in the graph in Figure 4.3. The quotient set R2/R is the collection of all such lines. Notice that
![]()
Partitions
In Example 4.2.12, we saw that R2 is the union of all the lines with slope equal to 1, and since the lines are parallel, they form a pairwise disjoint set. These properties can be observed in the other equivalence relations that we have seen. Each set is equal to the union of the equivalence classes, and the quotient set is pairwise disjoint. Generalizing these two properties leads to the next definition.
Figure 4.3 Two equivalence classes in R2 when (a, b) R (c, d) if and only if b − a = d − c.
![]() DEFINITION 4.2.13
DEFINITION 4.2.13
Let A be a nonempty set. The family ![]() is a partition of A if and only if
is a partition of A if and only if
 ⊆ P(A),
⊆ P(A),
 = A,
= A, is pairwise disjoint.
is pairwise disjoint.
To illustrate the definition, let A = {1, 2, 3, 4, 5, 6, 7} and define the elements of the partition to be A0 = {1, 2, 5}, A1 = {3}, and A2 = {4, 6, 7}. The family
![]()
is a subset of P(A), A = A0 ∪ A1 ∪ A2, and ![]() is pairwise disjoint. Therefore,
is pairwise disjoint. Therefore, ![]() is a partition of A. This is illustrated in Figure 4.4.
is a partition of A. This is illustrated in Figure 4.4.

Figure 4.4 A partition of the set A = {1, 2, 3, 4, 5, 6, 7}.
For each real number r ≥ 0, define Cr to be the circle with radius r centered at the origin. Namely,
![]()
Let ![]() = {Cr : r ∈ [0, ∞)}. We claim that
= {Cr : r ∈ [0, ∞)}. We claim that ![]() is a partition of R2.
is a partition of R2.
 ⊆ P(R2) because Cr ⊆ R2 for all r ≥ 0.
⊆ P(R2) because Cr ⊆ R2 for all r ≥ 0.- To prove that R2 =
 Cr, it suffices to show that R2 ⊆
Cr, it suffices to show that R2 ⊆  Cr, but this follows because if (a, b) ∈ R2, then
Cr, but this follows because if (a, b) ∈ R2, then

- To see that
 is pairwise disjoint, let r, s ≥ 0 and assume that (a, b) is an element of Cr ∩ Cs. Then,
is pairwise disjoint, let r, s ≥ 0 and assume that (a, b) is an element of Cr ∩ Cs. Then,

which implies that Cr = Cs.
The set Z5 is a family of subsets of Z, has the property that ![]() Z5 = Z, and is pairwise disjoint. Hence, Z5 is a partition for Z. We generalize this result to the next theorem. It uses an arbitrary equivalence relation on a given set to define a partition for that set. In this case, we say that the equivalence relation induces the partition.
Z5 = Z, and is pairwise disjoint. Hence, Z5 is a partition for Z. We generalize this result to the next theorem. It uses an arbitrary equivalence relation on a given set to define a partition for that set. In this case, we say that the equivalence relation induces the partition.
![]() THEOREM 4.2.15
THEOREM 4.2.15
If R is an equivalence relation on A, then A/R is a partition of A.
PROOF
Take a set A with an equivalence relation R.
- Since an equivalence class is a subset of A, we have A/R ⊆ P(A).
 A/R = A is (4.2).
A/R = A is (4.2).- Let [a], [b] ∈ A/R and assume that there exists y ∈ [a] ∩ [b]. In other words, a R y and b R y. Now take x ∈ [a]. This means that a R x. Since x R a and y R b by symmetry, we have that x R y, and then x R b by transitivity. Thus, x ∈ [b], which shows [a] ⊆ [b]. Similarly, [b] ⊆ [a], so [a] = [b].

The collection of equivalence relations forms a partition of a set. Conversely, if we have a partition of a set, the partition gives rise to an equivalence relation on the set. To see this, take any set A and a partition ![]() of A. For all a, b ∈ A, define
of A. For all a, b ∈ A, define
![]()
To show that R is an equivalence relation, take a, b, and c in A.
- Since a ∈ A and A =

 , there exists C ∈
, there exists C ∈  such that a ∈ C. Therefore, a R a.
such that a ∈ C. Therefore, a R a. - Assume a R b. This means that a, b ∈ C for some C ∈
 . This, of course, is the same as b, a ∈ C. Hence, b R a.
. This, of course, is the same as b, a ∈ C. Hence, b R a. - Suppose a R b and b R c. Then, there are sets C and D in
 so that a, b ∈ C and b, c ∈ D. This means that C ∩ D ≠ ∅. Since
so that a, b ∈ C and b, c ∈ D. This means that C ∩ D ≠ ∅. Since  is pairwise disjoint, C = D. So, a and c are elements of C, and we have a R c.
is pairwise disjoint, C = D. So, a and c are elements of C, and we have a R c.
This equivalence relation is said to be induced from the partition.
![]() EXAMPLE 4.2.16
EXAMPLE 4.2.16
The sets

form a collection that is a partition of Z. The equivalence relation that is induced from this partition is congruence modulo 5 (Example 4.2.9).
Exercises
1. For all a, b ∈ R {0}, let a R b if and only if ab > 0.
(a) Show that R is an equivalence relation on R {0}.
(b) Find [1] and [−3].
2. Define the relation S on R2 by (a, b) S (c, d) if and only if b − a = d − c. Prove that S is an equivalence relation.
3. Let S be an equivalence relation on A. Prove that A = ![]() .
.
4. Prove that if C is an equivalence class for some equivalence relation R and a ∈ C, then C = [a].
5. For all a, b ∈ Z, let a R b if and only if |a| = |b|.
(a) Prove R is an equivalence relation on Z.
(b) Sketch the partition of Z induced by this equivalence relation.
6. For all (a, b), (c, d) ∈ Z × Z, define (a, b) S (c, d) if and only if ab = cd.
(a) Show that S is an equivalence relation on Z × Z.
(b) What is the equivalence class of (1, 2)?
(c) Sketch the partition of Z × Z induced by this equivalence relation.
7. Let A be a set and a ∈ A. Show that the given relations are not equivalence relations on P(A).
(a) For all C, D ⊆ A, define C R D if and only if C ∩ D ≠ ∅.
(b) For all C, D ⊆ A, define C S D if and only if a ∈ C ∩ D.
8. Let z, z′ ∈ C and write z = a + bi and z′ = a′ + b′i. Define z = z′ to mean that a = a′ and b = b′. Prove that R is an equivalence relation.
9. Find.
(a) [3]5
(b) [12]6
(c) [2]5 ∪ [27]5
(d) [4]7 ∩ [5]7
10. Let r be the remainder obtained when n is divided by m. Prove [n]m = [r]m.
11. Let c, m ∈ Z and suppose that gcd(c, m) = 1. Prove.
(a) There exists b such that bc ≡ 1 (mod m). (Notice that b is that multiplicative inverse of c modulo m.)
(b) If ca ≡ cb (mod m), then a ≡ b (mod m).
(c) Prove that the previous implication is false if gcd(c, m) ≠ 1.
12. Prove that {(n, n + 1] : n ∈ Z} is a partition of R.
13. Prove that the following are partitions of R2.
(a) ![]() = {{(a, b)} : a, b ∈ R}.
= {{(a, b)} : a, b ∈ R}.
(b) ![]() = {{(r, y) : y ∈ R} : r ∈ R}.
= {{(r, y) : y ∈ R} : r ∈ R}.
(c) ![]() = {R × (n, n + 1] : n ∈ Z}.
= {R × (n, n + 1] : n ∈ Z}.
14. Is {[n, n + 1] × (n, n + 1) : n ∈ Z} a partition of R2? Explain.
15. Let R be a relation on A and show the following:
(a) R is reflexive if and only if R−1 is reflexive.
(b) R is symmetric if and only if R = R−1.
(c) R is symmetric if and only if (A × A) R is symmetric.
16. Let R and S be equivalence relations on A. Prove or show false.
(a) R ∪ S is an equivalence relation on A.
(b) R ∩ S is an equivalence relation on A.
17. Prove for all relations R on A.
(a) R is reflexive if and only if ∀a(a ∈ [a]).
(b) R is symmetric if and only if ∀a∀b(a ∈ [b] ↔ b ∈ [a]).
(c) R is transitive if and only if ∀a∀b∀c([b ∈ [a] ∧ c ∈ [b]] → c ∈ [a]).
(d) R is an equivalence relation if and only if ∀a∀b((a, b) ∈ R ↔ [a] = [b]).
18. Let R be a relation on A with the property that if a R b and b R c, then c R a. Prove that if R is also reflexive, R is an equivalence relation.
19. Define the relation R on C by a + bi R c + di if and only if
![]()
(a) Prove R is an equivalence relation on C.
(b) Graph [1 + i] in the complex plane.
(c) Describe the partition that R induces on C.
20. Let R and S be relations on A. The symmetric closure of R is S if R ⊆ S and for all symmetric relations T on A such that R ⊆ T, then S ⊆ T. Prove the following.
(a) R ∪ R−1 is the symmetric closure of R.
(b) A symmetric closure is unique.
4.3 PARTIAL ORDERS
While equivalence relations resemble equality, there are other common relations in mathematics that we can model. To study some of their attributes, we expand Definition 4.2.3 with three more properties.
![]() DEFINITION 4.3.1
DEFINITION 4.3.1
Let R be a relation on A.
- R is irreflexive if a
 a for all a ∈ A.
a for all a ∈ A. - R is asymmetric when for all a, b ∈ A, if a R b, then b
 a.
a. - R is antisymmetric means that for all a, b ∈ A, if a R b and b R a, then a = b.
Notice that a relation on a nonempty set cannot be both reflexive and irreflexive. However, many relations have neither property. For example, consider the relation R = {(1, 1)} on {1, 2}. Since (1, 1) ∈ R, the relation R is not irreflexive, and R is not reflexive because (2, 2) ∉ R. Likewise, a relation on a nonempty set cannot be both symmetric and asymmetric.
![]() EXAMPLE 4.3.2
EXAMPLE 4.3.2
The less-than relation on Z is irreflexive and asymmetric. It is also antisymmetric. To see this, let a, b ∈ Z. Since a < b and b < a is false, the implication
![]()
is true. The ≤ relation is also antisymmetric. However, ≤ is neither irreflexive nor asymmetric since 3 ≤ 3.
![]() EXAMPLE 4.3.3
EXAMPLE 4.3.3
Let R = {(1, 2)} and S = {(1, 2), (2, 1)}. Both are relations on {1, 2}. The first relation is asymmetric since 1 R 2 but 2 ![]() 1. It is also antisymmetric, but S is not antisymmetric because 2 S 1 and 1 S 2. Both the relations are irreflexive.
1. It is also antisymmetric, but S is not antisymmetric because 2 S 1 and 1 S 2. Both the relations are irreflexive.
Let R be a relation on a set A. We prove that
![]()
- Assume that R is antisymmetric and take (a, b) ∈ R ∩ R−1. This means that (a, b) ∈ R and (a, b) ∈ R−1. Therefore, (b, a) ∈ R, and since R is antisymmetric, a = b.
- Now suppose R ∩ R−1 ⊆ IA. Let (a, b), (b, a) ∈ R. We conclude that (a, b) ∈ R−1, which implies that (a, b) ∈ R ∩ R−1. Then, (a, b) ∈ IA. Hence, a = b.
As an equivalence relation is a generalization of an identity relation, the following relation is a generalization of ≤ on N. For this reason, instead of naming the relation R, it is denoted by the symbol ![]() .
.
![]() DEFINITION 4.3.5
DEFINITION 4.3.5
If a relation ![]() on a set A is reflexive, antisymmetric, and transitive,
on a set A is reflexive, antisymmetric, and transitive, ![]() is a partial order on A and the ordered pair (A,
is a partial order on A and the ordered pair (A, ![]() ) is called a partially ordered set (or simply a poset). Furthermore, for all a, b ∈ A, the notation a
) is called a partially ordered set (or simply a poset). Furthermore, for all a, b ∈ A, the notation a ![]() b means a
b means a ![]() b but a ≠ b.
b but a ≠ b.
For example, ≤ and = are partial orders on R, but < is not a partial order on R because the relation < is not reflexive. Although = is a partial order on any set, in general an equivalence relation is not a partial order (Example 4.2.6).
![]() EXAMPLE 4.3.6
EXAMPLE 4.3.6
Divisibility (Definition 2.4.2) is a partial order on Z+. To prove this, let a, b, and c be positive integers.
- a | a since a = a · 1 and a ≠ 0.
- Suppose that a | b and b | a. This means that b = ak and a = bl, for some k, l ∈ Z+. Hence, b = blk, so lk = 1. Since k and l are positive integers, l = k = 1. That is, a = b.
- Assume that we have a | b and b | c. This means that b = al and c = bk for some l, k ∈ Z+. By substitution, c = (al)k = a(lk): Hence, a | c.
![]() EXAMPLE 4.3.7
EXAMPLE 4.3.7
Let ![]() be a collection of symbols and let
be a collection of symbols and let ![]() * denote the set of all strings over
* denote the set of all strings over ![]() (as on page 5). Use the symbol
(as on page 5). Use the symbol ![]() to denote the empty string, the string of length zero. As with the empty set, the empty string is always an element of
to denote the empty string, the string of length zero. As with the empty set, the empty string is always an element of ![]() *. For example, if
*. For example, if ![]() = {a, b, c}, then abc, aaabbb, c, and
= {a, b, c}, then abc, aaabbb, c, and ![]() are elements of
are elements of ![]() *. Now, take σ, τ ∈
*. Now, take σ, τ ∈ ![]() *. The concatenation of σ and τ is denoted by
*. The concatenation of σ and τ is denoted by ![]() and is the string consisting of the elements of σ followed by those of τ. For example, if σ = 011 and τ = 1010, then
and is the string consisting of the elements of σ followed by those of τ. For example, if σ = 011 and τ = 1010, then ![]() = 0111010. Finally, for all σ, τ ∈
= 0111010. Finally, for all σ, τ ∈ ![]() *, define
*, define

Figure 4.5 A partial order defined on {0, 1}*.
![]()
It can be shown that ![]() is a partial order on
is a partial order on ![]() * (Exercise 8) with the structure seen in Figure 4.5 for
* (Exercise 8) with the structure seen in Figure 4.5 for ![]() = {0, 1}.
= {0, 1}.
The partial order ≤ on R has the property that for all a, b ∈ R, either a < b, b < a, or a = b. As we see in Figure 4.5, this is not the case for every partially ordered set. We do, however, have the following slightly weaker property.
![]() THEOREM 4.3.8 [Weak-Trichotomy Law]
THEOREM 4.3.8 [Weak-Trichotomy Law]
If ![]() is a partial order on A, for all a, b ∈ A, at most one of the following are true:
is a partial order on A, for all a, b ∈ A, at most one of the following are true:
a ![]() b, b
b, b ![]() a, or a = b.
a, or a = b.
PROOF
Let a, b ∈ A. We have three cases to consider.
- Suppose a
 b. This means that a
b. This means that a  b and a ≠ b. If in addition b
b and a ≠ b. If in addition b  a, by transitivity a
a, by transitivity a  a, which is a contradiction.
a, which is a contradiction. - That b
 a precludes both a
a precludes both a  b and a = b is proved like the first case.
b and a = b is proved like the first case. - If a = b, then by definition of
 it is impossible for a
it is impossible for a  b or b
b or b  a to be true.
a to be true. 
Technically, subset is not a relation, but in a natural way, it can be considered as one. Let ![]() be a family of sets. Define
be a family of sets. Define
![]()
Associate ⊆ with the relation S.
![]() EXAMPLE 4.3.9
EXAMPLE 4.3.9
Let A be a nonempty set. We show that (P(A), ⊆) is a partially ordered set. Let B, C, and D be subsets of A.
This example is in line with what we know about subsets. For instance, if A ⊂ B, then we conclude that B ⊄ A and A ≠ B, which is what we expect from the weak-trichotomy law (4.3.8).
Bounds
Let ![]() be a partial order on A with elements m and m′ such that a
be a partial order on A with elements m and m′ such that a ![]() m and a
m and a ![]() m′ for all a ∈ A. In particular, this implies that m
m′ for all a ∈ A. In particular, this implies that m ![]() m′ and m′
m′ and m′ ![]() m, so since
m, so since ![]() is antisymmetric, we conclude that m = m′. Similarly, if m
is antisymmetric, we conclude that m = m′. Similarly, if m ![]() a and m′
a and m′ ![]() a for all a ∈ A, then m = m′. This argument justifies the use of the word the in the next definition.
a for all a ∈ A, then m = m′. This argument justifies the use of the word the in the next definition.
![]() DEFINITION 4.3.10
DEFINITION 4.3.10
Let (A, ![]() ) be a poset and m ∈ A.
) be a poset and m ∈ A.
- m is the least element of A (with respect to
 ) if m
) if m  a for all a ∈ A.
a for all a ∈ A. - m is the greatest element of A (with respect to
 ) if a
) if a  m for all a ∈ A.
m for all a ∈ A.
There is no guarantee that a partially ordered set will have a least or a greatest element. In Example 4.3.9, the greatest element of P(A) with respect to ⊆ is A and the least element is ∅. However, in Example 4.3.7 (Figure 4.5), the least element of ![]() * is
* is ![]() , but there is no greatest element.
, but there is no greatest element.
![]() EXAMPLE 4.3.11
EXAMPLE 4.3.11
If A is a finite set of real numbers, A has a least and a greatest element with respect to ≤. Under the partial order ≤, the set Z+ also has a least element but no greatest element, and both {5n : n ∈ Z−} and Z− have greatest elements but no least elements. To show that B = {5n : n ∈ Z+} has a least element with respect to ≤, use the fact that the least element of Z+ is 1. Therefore, the least element of B is 5 because 5 ∈ B and 5(1) ≤ 5n for all n ∈ Z+.
Some sets will not have a least or greatest element with a given partial order but there will still be elements that are considered greater or lesser than every element of the set.
![]() DEFINITION 4.3.12
DEFINITION 4.3.12
Let ![]() be a partial order on A and B ⊆ A.
be a partial order on A and B ⊆ A.
- u ∈ A is an upper bound of B if b
 u for all b ∈ B. The element u is the least upper bound of B if it is an upper bound and for all upper bounds u′ of B, u
u for all b ∈ B. The element u is the least upper bound of B if it is an upper bound and for all upper bounds u′ of B, u  u′.
u′. - l ∈ A is a lower bound of B if l
 b for all b ∈ B. The element l is the greatest lower bound of B if it is a lower bound and for all lower bounds l′ of B, l′
b for all b ∈ B. The element l is the greatest lower bound of B if it is a lower bound and for all lower bounds l′ of B, l′  l.
l.
In the definition we can write the word the because the order is antisymmetric.
![]() EXAMPLE 4.3.13
EXAMPLE 4.3.13
The interval (3, 5) is a subset of R. Under the partial order ≤, both 5 and 10 are upper bounds of this interval, while 5 is a least upper bound. Also, 3 and −π are lower bounds, but 3 is the greatest lower bound.
![]() EXAMPLE 4.3.14
EXAMPLE 4.3.14
Assume that ![]() ⊆ P(Z). Since the elements of
⊆ P(Z). Since the elements of ![]() are subsets of Z, we conclude that
are subsets of Z, we conclude that ![]()
![]() ∈ P(Z) (Definition 3.4.8). If A ∈
∈ P(Z) (Definition 3.4.8). If A ∈ ![]() , then A ⊆
, then A ⊆ ![]()
![]() . Therefore,
. Therefore, ![]()
![]() is an upper bound of
is an upper bound of ![]() with respect to ⊆. To see that it is the least upper bound, let U be any upper bound of
with respect to ⊆. To see that it is the least upper bound, let U be any upper bound of ![]() . Take x ∈
. Take x ∈ ![]()
![]() . This means that there exists D ∈
. This means that there exists D ∈ ![]() such that x ∈ D. Since U is an upper bound of
such that x ∈ D. Since U is an upper bound of ![]() , D ⊆ U. Hence, x ∈ U, and we conclude that
, D ⊆ U. Hence, x ∈ U, and we conclude that ![]()
![]() ⊆ U.
⊆ U.
Comparable and Compatible Elements
In Figure 4.5, we see that 01 ![]() 010 and 01
010 and 01 ![]() 011. However, 010
011. However, 010 ![]() 011 and 011
011 and 011 ![]() 010. This means that in the poset of Example 4.3.7, there are pairs of elements that are related to each other and there are other pairs that are not.
010. This means that in the poset of Example 4.3.7, there are pairs of elements that are related to each other and there are other pairs that are not.
![]() DEFINITION 4.3.15
DEFINITION 4.3.15
Let (A, ![]() ) be a poset and a, b ∈ A. If a
) be a poset and a, b ∈ A. If a ![]() b or b
b or b ![]() a, then a and b are comparable with respect to
a, then a and b are comparable with respect to ![]() . Elements of A are incomparable if they are not comparable.
. Elements of A are incomparable if they are not comparable.
Continuing our review of the partially ordered set of Example 4.3.7, we note that the element ![]() has the property that no element is less than it, but as seen in Figure 4.5, for every element of
has the property that no element is less than it, but as seen in Figure 4.5, for every element of ![]() *, there exists an element of
*, there exists an element of ![]() * that is greater. However, that same relation defined on
* that is greater. However, that same relation defined on
![]()
has the property that 000, 001, 010, 011, 100, 101, 110, 111 have no elements greater than them. This leads to the next definition.
![]() DEFINITION 4.3.16
DEFINITION 4.3.16
Let (A, ![]() ) be a poset and m ∈ A.
) be a poset and m ∈ A.
- m is a minimal element of A (with respect to
 ) if a
) if a  m for all a ∈ A.
m for all a ∈ A. - m is a maximal element of A (with respect to
 ) if m
) if m  a for all a ∈ A.
a for all a ∈ A.
Therefore, the empty string is a minimal element of A (4.3), and 000, 001, 010, 011, 100, 101, 110, 111 are maximal. Notice that every least element is minimal and every greatest element is maximal.
Although not every pair of elements is comparable in the partially ordered set of Example 4.3.7, there are infinite sequences of comparable elements, such as
![]()
![]() DEFINITION 4.3.17
DEFINITION 4.3.17
A subset C of the poset (A, ![]() ) is a chain with respect to
) is a chain with respect to ![]() if a is comparable to b for all a, b ∈ C.
if a is comparable to b for all a, b ∈ C.
When Z is partially ordered by ≤, the sets {0, 1, 2, 3, ...}, {... , −3, −2, −1, 0}, and {... , −2, 0, 2, 4, ...} are chains. In P(Z), both
![]()
and
![]()
are chains with respect to ⊆.
![]() EXAMPLE 4.3.18
EXAMPLE 4.3.18
To see that {Ak : k ∈ Z+} where Ak = {x ∈ Z : (x − 1)(x − 2) · · · (x − k) = 0} is a chain with respect to ⊆, take m, n ∈ Z+. By definition,
![]()
and
![]()
If m ≤ n, then Am ⊆ An, otherwise An ⊆ Am.
![]() EXAMPLE 4.3.19
EXAMPLE 4.3.19
Let C0 and C1 be chains of A with respect to ![]() . Take a, b ∈ C0 ∩ C1. Then, a, b ∈ C0, so a
. Take a, b ∈ C0 ∩ C1. Then, a, b ∈ C0, so a ![]() b or b
b or b ![]() a. Therefore, C0 ∩ C1 is a chain. However, the union of two chains might not be a chain. For example, {{1}, {1, 2}} and {{1}, {1, 3}} are chains in (P(Z), ⊆), but {{1}, {1, 2}, {1, 3}} is not a chain because {1, 2}
a. Therefore, C0 ∩ C1 is a chain. However, the union of two chains might not be a chain. For example, {{1}, {1, 2}} and {{1}, {1, 3}} are chains in (P(Z), ⊆), but {{1}, {1, 2}, {1, 3}} is not a chain because {1, 2} ![]() {1, 3} and {1, 3}
{1, 3} and {1, 3} ![]() {1, 2}.
{1, 2}.
The sets Z, Q, and R are chains of R with respect to ≤. In fact, any subset of R is a chain of R because subsets of chains are chains. This motivates the next definition.
![]() DEFINITION 4.3.20
DEFINITION 4.3.20
The poset (A, ![]() ) is a linearly ordered set and
) is a linearly ordered set and ![]() is a linear order if A is a chain with respect to
is a linear order if A is a chain with respect to ![]() .
.
Since every subset A of R is a chain with respect to ≤, the relation ≤ is a linear order on A. Furthermore, since every pair of elements in a linear order are comparable, Theorem 4.3.8 can be strengthened.
![]() THEOREM 4.3.21 [Trichotomy Law]
THEOREM 4.3.21 [Trichotomy Law]
If ![]() is a linear order on A, for all a, b ∈ A, exactly one of the following are true: a
is a linear order on A, for all a, b ∈ A, exactly one of the following are true: a ![]() b, b
b, b ![]() a, or a = b.
a, or a = b.
Although it is not the case that every pair of elements of the poset defined in Example 4.3.7 is comparable, it is the case that for any given pair of elements, there exists another element that is related to the given elements. For example, for the pair 100 and 110, 1 ![]() 100 and 1
100 and 1 ![]() 110. Also, for the pair 101 and 10, 10
110. Also, for the pair 101 and 10, 10 ![]() 101 and 10
101 and 10 ![]() 10.
10.
![]() DEFINITION 4.3.22
DEFINITION 4.3.22
Let (A, ![]() ) be a poset. The elements a, b ∈ A are compatible if there exists c ∈ A such that c
) be a poset. The elements a, b ∈ A are compatible if there exists c ∈ A such that c ![]() a and c
a and c ![]() b. If a and b are not compatible, they are incompatible and we write a ⊥ b.
b. If a and b are not compatible, they are incompatible and we write a ⊥ b.
Observe that if a and b are comparable, they are also compatible. On the other hand, it takes some work to define a relation in which every pair of elements is incompatible.
![]() DEFINITION 4.3.23
DEFINITION 4.3.23
A subset D of a poset (A, ![]() ) is an antichain with respect to
) is an antichain with respect to ![]() when for all a, b ∈ D, if a ≠ b, then a ⊥ b.
when for all a, b ∈ D, if a ≠ b, then a ⊥ b.
The sets
![]()
and
![]()
are antichains of P(Z) with respect to ⊆.
Well-Ordered Sets
The notion of a linear order incorporates many of the properties of ≤ on N since ≤ is reflexive, antisymmetric, and transitive, and N is a chain with respect to ≤. However, there is one important property of (N, ≤) that is not included among those of a linear order. Because of the nature of the natural numbers, every subset of N that is nonempty has a least element. For example, 5 is the least element of {5, 7, 32, 99} and 2 is the least element of {2, 4, 6, 8, ... }. We want to be able to identify those partial orders that also have this property.
![]() DEFINITION 4.3.24
DEFINITION 4.3.24
The linearly ordered set (A, ![]() ) is a well-ordered set and
) is a well-ordered set and ![]() is a well-order if every nonempty subset of A has a least element with respect to
is a well-order if every nonempty subset of A has a least element with respect to ![]() .
.
According to Definition 4.3.24, (N, ≤) is a well-ordered set, but this fact about the natural numbers cannot be proved without making an assumption. Therefore, so that we have at least one well-ordered set with which to work, we assume the following.
![]() AXIOM 4.3.25
AXIOM 4.3.25
(N, ≤) is a well-ordered set.
Coupling Axiom 4.3.25 with the next theorem will yield infinitely many well-ordered sets.
![]() THEOREM 4.3.26
THEOREM 4.3.26
If (A, ![]() ) is well-ordered and B is a nonempty subset of A, then (B,
) is well-ordered and B is a nonempty subset of A, then (B, ![]() ) is well-ordered.
) is well-ordered.
PROOF
Let B ⊆ A and B ≠ ∅. To prove that B is well-ordered, let C ⊆ B and C ≠ ∅. Then, C ⊆ A. Since ![]() well-orders A, we know that C has a least element with respect to
well-orders A, we know that C has a least element with respect to ![]() .
. ![]()
Because Z ∩ [5, ∞) ⊆ Z+ ⊆ N, by Axiom 4.3.25 and Theorem 4.3.26, both (Z+, ≤) and (Z ∩ [5, ∞), ≤) are well-ordered sets.
![]() EXAMPLE 4.3.27
EXAMPLE 4.3.27
Let A = {nπ : n ∈ N}. To prove that A is well-ordered by ≤, let B ⊆ A such that B ≠ ∅. This means that there exists a nonempty subset I of N such that B = [nπ : n ∈ I}. Since N is well-ordered, I has least element m. We claim that mπ is the least element of B. To see this, take b ∈ B. Then, b = iπ for some i ∈ I. Since m is the least element of I, m ≤ i. Therefore, mπ ≤ iπ = b.
To prove that a set A is not well-ordered by ![]() , we must find a nonempty subset B of A that does not have a least element. This means that for every b ∈ B, there exists c ∈ B such that c
, we must find a nonempty subset B of A that does not have a least element. This means that for every b ∈ B, there exists c ∈ B such that c ![]() b. That is, there are elements bn ∈ B (n ∈ N) such that
b. That is, there are elements bn ∈ B (n ∈ N) such that
![]()
This informs the next definition.
![]() DEFINITION 4.3.28
DEFINITION 4.3.28
Let ![]() be a partial order on A and B = {ai : i ∈ N} be a subset of A.
be a partial order on A and B = {ai : i ∈ N} be a subset of A.
- B is increasing means i < j implies ai
 aj for all i, j ∈ N.
aj for all i, j ∈ N. - B is decreasing means i < j implies aj
 ai for all i, j ∈ N.
ai for all i, j ∈ N.
If a set is well-ordered, it has a least element, but the converse is not true. To see this, consider A = {0, 1/2, 1/3, 1/4, ...}. It has a least element, namely, 0, but A also contains the decreasing set
![]()
Therefore, A has a subset without a least element, so A is not well-ordered. We summarize this observation with the following theorem, and leave its proof to Exercise 23.
![]() THEOREM 4.3.29
THEOREM 4.3.29
(A, ![]() ) is not a well-ordered set if and only if (A,
) is not a well-ordered set if and only if (A, ![]() ) does not have a decreasing subset.
) does not have a decreasing subset.
Theorem 4.3.29 implies that any finite linear order is well-ordered.
![]() EXAMPLE 4.3.30
EXAMPLE 4.3.30
The decreasing sequence (4.4) with Theorem 4.3.29 shows that the sets (0, 1), [0, 1], Q, and {1/n : n ∈ Z+} are not well-ordered by ≤.
We close this section by proving two important results from number theory. Their proofs use Axiom 4.3.25. The strategy is to define a nonempty subset of a well-ordered set. Its least element r will be a number that we want. This least element also needs to have a particular property, say p(r). To show that it has the property, assume ¬p(r) and use this to find another element of the set that is less than r. This contradicts the minimality of r allowing us to conclude p(r).
![]() THEOREM 4.3.31 [Division Algorithm]
THEOREM 4.3.31 [Division Algorithm]
If m, n ∈ N with m ≠ 0, there exist unique q, r ∈ N such that r < m and n = mq + r.
PROOF
Uniqueness is proved in Example 2.4.14. To prove existence, take m, n ∈ N and define
![]()
Notice that n ∈ S, so S ≠ ∅. Therefore, S has a least element by Axiom 4.3.25. Call it r and write n = mq + r for some natural number q. Assume r ≥ m, which implies that r − m ≥ 0. Also,
![]()
because
![]()
so r − m ∈ S. Since r > r − m because m is positive, r cannot be the minimum of S, a contradiction. ![]()
The value q of the division algorithm (Theorem 4.3.31) is called the quotient and r is the remainder. For example, if we divide 5 into 17, the division algorithm returns a quotient of 3 and a remainder of 2, so we can write that 17 = 5(3) + 2. Notice that 2 < 3.
Call n ∈ Z a linear combination of the integers a and b if n = ua + vb for some u, v ∈ Z. Since 37 = 5(2) + 3(9), we see that 37 is a linear combination of 2 and 9. Furthermore, if d | a and d | b, then d | ua + vb. To see this, write a = dl and b = dk for some l, k ∈ Z. Then,
![]()
and this means d | ua + vb.
![]() THEOREM 4.3.32
THEOREM 4.3.32
Let a, b ∈ Z with not both equal to 0. If c = gcd(a, b), there exists m, n ∈ Z such that c = ma + nb.
PROOF
Define
![]()
Notice that T is not empty because a2 + b2 ∈ T. By Axiom 4.3.25, T has a least element d, so write d = ma + nb for some m, n ∈ Z.
- Since d > 0, the division algorithm (4.3.31) yields a = dq + r for some natural numbers q and r with r < d. Then,
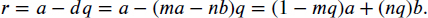
If r > 0, then r ∈ T, which is impossible because d is the least element of T. Therefore, r = 0 and d | a. Similarly, d | b.
- To show that d is the greatest of the common divisors, suppose s | a and s | b with s ∈ Z+. By definition, a = sk and b = sl for some k, l ∈ Z. Hence,

Thus, s ≤ d because s is nonzero and s divides d (Exercise 25).

Exercises
1. Is (∅, ⊆) a partial order, linear order, or well order? Explain.
2. For each relation on {1, 2}, determine if it is reflexive, irreflexive, symmetric, asymmetric, antisymmetric, or transitive.
(a) {(1, 2)}
(b) {(1, 2), (2, 1)}
(c) {(1, 1), (1, 2), (2, 1)}
(d) {(1, 1), (1, 2), (2, 2)}
(e) {(1, 1), (1, 2), (2, 1), (2, 2)}
(f) ∅
3. Give an example of a relation that is neither symmetric nor asymmetric.
4. Let R be a relation on A. Prove that R is reflexive if and only if (A × A) R is irreflexive.
5. Show that a relation R on A is asymmetric if and only if R ∩ R−1 = ∅.
6. Let (A, ![]() ) and (B, ≤) be posets. Define ~ on A × B by
) and (B, ≤) be posets. Define ~ on A × B by
![]()
Show that ~ is a partial order on A × B.
7. For any alphabet ![]() , prove the following.
, prove the following.
(a) For all σ, τ, ν ∈ ![]() *,
*, ![]() .
.
(b) There exists σ, τ ∈ ![]() * such that
* such that ![]() .
.
(c) ![]() * has an identity with respect to
* has an identity with respect to ![]() , but for all σ ∈
, but for all σ ∈ ![]() *, there is no inverse for σ if σ ≠
*, there is no inverse for σ if σ ≠ ![]() .
.
8. Prove that ![]() * from Example 4.3.7 is partially ordered by
* from Example 4.3.7 is partially ordered by ![]() .
.
9. Prove that (P(A), ⊆) is not a linear order if A has at least three elements.
10. Show that (![]() *,
*, ![]() ) is not a linear order if
) is not a linear order if ![]() has at least two elements.
has at least two elements.
11. Prove that the following families of sets are chains with respect to ⊆.
(a) {[0, n] : n ∈ Z+}
(b) {(2n)Z : n ∈ N} where (2n)Z = {2n · k : k ∈ Z}
(c) {Bn : n ∈ N} where Bn = ![]() {Ai : i ∈ N ∧ i ≤ n} and Ai is a set for all i ∈ N
{Ai : i ∈ N ∧ i ≤ n} and Ai is a set for all i ∈ N
12. Can a chain be disjoint or pairwise disjoint? Explain.
13. Suppose that {Ai : i ∈ N} is a chain of sets such that for all i ≤ j, Ai ⊆ Aj. Prove for all k ∈ N.
(a) ![]() {Ai : i ∈ N ∧ i ≤ k} = Ak
{Ai : i ∈ N ∧ i ≤ k} = Ak
(b) ![]() {Ai : i ∈ N ∧ i ≤ k} = A0
{Ai : i ∈ N ∧ i ≤ k} = A0
14. Let {An : n ∈ N} be a family of sets. For every m ∈ N, define Bm = ![]() . Show that {Bm : m ∈ N} is a chain.
. Show that {Bm : m ∈ N} is a chain.
15. Let ![]() i be a chain of the poset (A,
i be a chain of the poset (A, ![]() ) for all i ∈ I. Prove that
) for all i ∈ I. Prove that ![]() is a chain. Is
is a chain. Is ![]() necessarily a chain? Explain.
necessarily a chain? Explain.
16. Let (A, ![]() ) and (B, ≤) be linear orders. Define ~ on A × B by
) and (B, ≤) be linear orders. Define ~ on A × B by
![]()
if and only if
![]()
This relation is called a lexicographical order since it copies the order of a dictionary.
(a) Prove that (A × B, ~) is a linear order.
(b) Suppose that (a, b) is a maximal element of A × B with respect to ~. Show that a is a maximal element of A with respect to ![]() .
.
17. Let A be a set. Prove that B ⊆ P(A) {∅} is an antichain with respect to ⊆ if and only if B is pairwise disjoint.
18. Prove the following true or false.
(a) Every well-ordered set contains a least element.
(b) Every well-ordered set contains a greatest element.
(c) Every subset of a well-ordered set contains a least element.
(d) Every subset of a well-ordered set contains a greatest element.
(e) Every well-ordered set has a decreasing subset.
(f) Every well-ordered set has a increasing subset.
19. For each of the given sets, indicate whether or not it is well-ordered by ≤. If it is, prove it. If it is not, find a decreasing sequence of elements of the set.
(a) {![]() , 5, 6, 10.56, 17, −100}
, 5, 6, 10.56, 17, −100}
(b) {2n : n ∈ N}
(c) {π/n : n ∈ Z+}
(d) {π/n : n ∈ Z−}
(e) {−4, −3, −2, −1, ...}
(f) Z ∩ (π, ∞)
(g) Z ∩ (−7, ∞)
20. Prove that (Z ∩ (x, ∞), ≤) is a well-ordered set for all x ∈ R.
21. Show that a well-ordered set has a unique least element.
22. Let (A, ![]() ) be a well-ordered set. If B ⊆ A and there is an upper bound for B in A, then B has a greatest element.
) be a well-ordered set. If B ⊆ A and there is an upper bound for B in A, then B has a greatest element.
23. Prove Theorem 4.3.29.
24. Where does the proof of Theorem 4.3.31 go wrong if m = 0?
25. Prove that if a | b, then a ≤ b for all a, b ∈ Z.
26. Let a, b, c ∈ Z. Show that if gcd(a, c) = gcd(b, c) = 1, then gcd(a, bc) = 1.
27. Let a, b ∈ Z and assume that gcd(a, b) = 1. Prove.
(a) If a | n and b | n, then ab | n.
(b) gcd(a + b, b) = gcd(a + b, a) = 1.
(c) gcd(a + b, a − b) = 1 or gcd(a + b, a − b) = 2.
(d) If c | a, then gcd(b, c) = 1.
(e) If c | a + b, then gcd(a, c) = gcd(b, c) = 1.
(f) If d | ac and d | bc, then d | c.
28. Let a, b ∈ Z, where at least one is nonzero. Prove that S = T if
![]()
and
![]()
29. Prove that if d | a and d | b, then d | gcd(a, b) for all a, b, d ∈ Z.
4.4 FUNCTIONS
From algebra and calculus, we know what a function is. It is a rule that assigns to each possible input value a unique output value. The common picture is that of a machine that when a certain button is pushed, the same result always happens. In basic algebra a relation can be graphed in the Cartesian plane. Such a relation will be a function if and only if every vertical line intersects its graphs at most once. This is known as the vertical line test (Figure 4.6). This criteria is generalized in the next definition.
![]() DEFINITION 4.4.1
DEFINITION 4.4.1
Let A and B be sets. A relation f ⊆ A × B is a function means that for all (x, y), (x′, y′) ∈ A × B,
![]()
The function f is an n-ary function if there exists sets A0, A1, ... , An−1 such that A = A0 × A1 × · · · × An−1. If n = 1, then f is a unary function, and if n = 2, then f is a binary function,
![]() EXAMPLE 4.4.2
EXAMPLE 4.4.2
The set {(1, 2), (4, 5), (6, 5)} is a function, but {(1, 2), (1, 5), (6, 5)} is not since it contains (1, 2) and (1, 5). Also, ∅ is a function (Exercise 16).

Figure 4.6 Passing the vertical line test.
Define f = {(u, 1 + 2 cos πu) : u ∈ R}. Assume that both (x, 1 + 2 cos πx) and (x′, 1 + 2 cosπx′) are elements of f. Then, because cosine is a function,

Therefore, f is a function.
![]() EXAMPLE 4.4.4
EXAMPLE 4.4.4
The standard arithmetic operations are functions. For example, taking a square root is a unary function, while addition, subtraction, multiplication, and division are binary functions. To illustrate this, addition on Z is the set
![]()
Let f ⊆ A × B be a function. This implies that for all a ∈ A, either [a]f = ∅ or [a]f is a singleton (Definition 4.2.7). For example, if f = {(1, 2), (4, 5), (6, 5)}, then [1]f = {2} and [3]f = ∅. Because [a]f can contain at most one element, we typically simplify the notation.
![]() DEFINITION 4.4.5
DEFINITION 4.4.5
Let f be a function. For all a ∈ A, define
![]()
and write that f(a) is undefined if [a]f = ∅.
For example, using (4.5),
![]()
but A(5, π) is undefined. With ordered n-tuples, the outer parentheses are usually eliminated so that we write
![]()
Moreover, if D ⊆ A is the domain of the function f, write the function notation
![]()
and call B a codomain of f (Figure 4.7). Because functions are often represented by arrows that “send” one element to another, a function can be called a map. If f(x) = y, we can say that “f maps x to y.” We can also say that y is the image of x under f and x is a pre-image of y. For example, if
![]()
f maps 3 to 1, 2 is the image of 4, and 5 is a pre-image of 2 (Figure 4.8). If g is also a function with domain D and codomain B, we can use the abbreviation
![]()
to represent both functions. An alternate choice of notation involves referring to the functions as D → B.
![]() EXAMPLE 4.4.6
EXAMPLE 4.4.6
If f(x) = cos x, then f maps π to −1, 0 is the image of π/2, and π/4 is a pre-image of ![]() /2.
/2.
![]() EXAMPLE 4.4.7
EXAMPLE 4.4.7
Let A be any set. The identity relation on A (Definition 4.1.2) is a function, so call IA the identity map and write
![]()
Sometimes a function f is defined using a rule that pairs an element of the function's domain with an element of its codomain. When this is done successfully, f is said to be well-defined. Observe that proving that f is well-defined is the same as proving it to be a function.

Figure 4.8 The map f = {(3, 1), (4, 2), (5, 2)}.
Let f : R → R be defined by f(x) = 1 + 2 cos πx. This is the function
![]()
The work of Example 4.4.3 shows that f is well-defined.
Before we examine another example, let us set a convention on naming functions. It is partly for aesthetics, but it does help in organizing functions based on the type of elements in their domains and ranges.
- Use English letters (usually, f, g, and h) for naming functions that involve numbers. Typically, these will be lowercase, but there are occasions when we will choose them to be uppercase.
- Use Greek letters (often φ or ψ) for general functions or those with domains not consisting of numbers. They are also usually lowercase, but uppercase Greek letters like Φ and Ψ are sometimes appropriate. (See the appendix for the Greek alphabet.)
![]() EXAMPLE 4.4.9
EXAMPLE 4.4.9
Let n, m ∈ Z+ such that m | n. Define φ([a]n) = [a]m for all a ∈ Z. This means that
![]()
It is not clear that φ is well-defined since an equivalence class can have many representatives, so assume that [a]n = [b]n for a, b ∈ Z. Therefore, n | a − b. Then, by hypothesis, m | a − b, and this yields
![]()
![]() EXAMPLE 4.4.10
EXAMPLE 4.4.10
Let x ∈ R. Define the greatest integer function as
![]()
For example, ![]() 5
5![]() = 5,
= 5, ![]() 1.4
1.4![]() = 1, and
= 1, and ![]() −3.4
−3.4![]() = −4. The greatest integer function is a function R → Z. It is well-defined because the relation ≤ well-orders Z (Exercise 4.3.22).
= −4. The greatest integer function is a function R → Z. It is well-defined because the relation ≤ well-orders Z (Exercise 4.3.22).
If a relation on R is not a function, it will fail the vertical line test (Figure 4.9). To generalize, let φ ⊆ A × B. To show that φ is not a function, we must show that there exists (x, y1), (x, y2) ∈ φ such that y1 ≠ y2.
![]() EXAMPLE 4.4.11
EXAMPLE 4.4.11
The relation f = IR ∪ {(x, −x) : x ∈ R} is not a function since (4, 4) ∈ f and (4, −4) ∈ f.
Figure 4.9 The relation is not a function.
![]() EXAMPLE 4.4.12
EXAMPLE 4.4.12
Define φ ⊆ Z2 × Z3 by φ([a]2) = [a]3 for all a ∈ Z. Since 3 does not divide 2, φ is not well-defined. This is proved by noting that [0]2 = [2]2 but [0]3 ≠ [2]3.
There will be times when we want to examine sets of functions. If each function is to have the same domain and codomain, we use the following notation.
![]() DEFINITION 4.4.13
DEFINITION 4.4.13
If A and B are sets,
![]()
For instance, AB is a set of real-valued functions if A, B ⊆ R.
![]() EXAMPLE 4.4.14
EXAMPLE 4.4.14
If an is a sequence of real numbers with n = 0, 1, 2, ... , the sequence an is an element of NR. Illustrating this, the sequence
![]()
is a function and can be graphed as in Figure 4.10.
![]() EXAMPLE 4.4.15
EXAMPLE 4.4.15
Let A ⊆ R and fix a ∈ A. The evaluation map,
![]()
is defined as
![]()
Figure 4.10 an = (−1/2)n is a function.
For example, if g(x) = x2, then ![]() 3(g) = 9. Observe that the evaluation map is an element of
3(g) = 9. Observe that the evaluation map is an element of ![]() .
.
Equality
Since functions are sets, we already know that two functions are equal when they contain the same ordered pairs. However, there is a common test to determine function equality other than a direct appeal to Definition 3.3.7.
![]() THEOREM 4.4.16
THEOREM 4.4.16
Functions φ, ψ : A → B are equal if and only if φ(x) = ψ(x) for all x ∈ A.
PROOF
Sufficiency is clear, so to prove necessity suppose that φ(x) = ψ(x) for every x ∈ A. Take (a, b) ∈ φ. This means that φ(a) = b. By hypothesis, ψ(a) = b, which implies that (a, b) ∈ ψ. Hence, φ ⊆ g. The proof of ψ ⊆ φ is similar, so φ = g. ![]()
We use Theorem 4.4.16 in the next examples.
![]() EXAMPLE 4.4.17
EXAMPLE 4.4.17
Let f and g be functions R → R defined by
![]()
and
![]()
We show that f = g by taking x ∈ R and calculating
![]()
Let φ, ψ : Z → Z6 be functions such that
![]()
and
![]()
Take n ∈ Z. We show that [n + 12]6 = [n]6 by proceeding as follows:
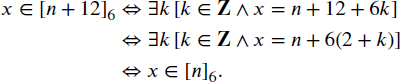
Therefore, φ = ψ.
![]() EXAMPLE 4.4.19
EXAMPLE 4.4.19
Define
![]()
by ψ(x) = ![]() x for all x ∈ R (Example 4.4.15). We show that ψ is well-defined. Take a, b ∈ R and assume that a = b. To show that ψ(a) = ψ(b), we prove
x for all x ∈ R (Example 4.4.15). We show that ψ is well-defined. Take a, b ∈ R and assume that a = b. To show that ψ(a) = ψ(b), we prove ![]() a =
a = ![]() b. Therefore, let f ∈ RR. Since f is a function and a, b ∈ dom(f), we have that f(a) = f(b). Thus,
b. Therefore, let f ∈ RR. Since f is a function and a, b ∈ dom(f), we have that f(a) = f(b). Thus,
![]()
By Theorem 4.4.16, we see that two functions f and g are not equal when either dom(f) ≠ dom(g) or f(x) ≠ g(x) for some x in their common domain. For example, f(x) = x2 and g(x) = 2x are not equal because f(3) = 9 and g(3) = 6. Although these two functions differ for every x ≠ 0 and x ≠ 2, it only takes one inequality to prove that the functions are not equal. For example, if we define

then f ≠ h since f(0) = 0 and h(0) = 7.
Composition
We now consider the composition of relations when those relations are functions.
![]() THEOREM 4.4.20
THEOREM 4.4.20
If φ : A → B and ψ : C → D are functions such that ran(φ) ⊆ C, then ψ ![]() φ is a function A → D and (ψ
φ is a function A → D and (ψ ![]() φ)(x) = ψ(φ(x)).
φ)(x) = ψ(φ(x)).
Because the range of φ is a subset of C, we know that φ ⊆ A × C and ψ ⊆ C × D. Let (a, d1), (a, d2) ∈ ψ ![]() φ. This means by Definition 4.1.9 that there exists c1, c2 ∈ C such that (a, c1), (a, c2) ∈ φ and (c1, d1), (c2, d2) ∈ ψ. Since φ is a function, c1 = c2, and then since ψ is a function, d1 = d2. Therefore, ψ
φ. This means by Definition 4.1.9 that there exists c1, c2 ∈ C such that (a, c1), (a, c2) ∈ φ and (c1, d1), (c2, d2) ∈ ψ. Since φ is a function, c1 = c2, and then since ψ is a function, d1 = d2. Therefore, ψ ![]() φ is a function, which is clearly A → D. Furthermore,
φ is a function, which is clearly A → D. Furthermore,

Hence, (ψ ![]() φ)(x) = ψ(φ(x)).
φ)(x) = ψ(φ(x)). ![]()
The ran(φ) ⊆ C condition is important to Theorem 4.4.20. For example, take the real-valued functions f(x) = x and g(x) = ![]() . Since f(−1) = −1 but g(−1) ∉ R, we conclude that (g
. Since f(−1) = −1 but g(−1) ∉ R, we conclude that (g ![]() f)(−1) is undefined.
f)(−1) is undefined.
![]() EXAMPLE 4.4.21
EXAMPLE 4.4.21
Define the two functions f : R → Z and g : R {0} → R by f(x) = ![]() x
x![]() and g(x) = 1/x. Since ran(f) = Z
and g(x) = 1/x. Since ran(f) = Z ![]() dom(g), there are elements of R for which g
dom(g), there are elements of R for which g ![]() f is undefined. However,
f is undefined. However,
![]()
so f ![]() g is defined and for all x ∈ R,
g is defined and for all x ∈ R,
![]()
![]() EXAMPLE 4.4.22
EXAMPLE 4.4.22
Let ψ : ZZ → Z be defined by ψ(f) = ![]() 3(f) and also let φ : Z → Z7 be φ(n) = [n]7. Since ran(ψ) ⊆ dom(φ), φ
3(f) and also let φ : Z → Z7 be φ(n) = [n]7. Since ran(ψ) ⊆ dom(φ), φ ![]() ψ is defined. Thus, if g : Z → Z is defined as g(n) = 3n,
ψ is defined. Thus, if g : Z → Z is defined as g(n) = 3n,
![]()
We should note that function composition is not a binary operation unless both functions are A → A for some set A. In this case, function composition is a binary operation on AA.
Restrictions and Extensions
There are times when a subset of a given function is required. For example, consider
![]()
If only positive values of x are required, we can define
![]()
so that g ⊆ f. We have notation for this.
![]() DEFINITION 4.4.23
DEFINITION 4.4.23
Let φ : A → B be a function and C ⊆ A.
- The restriction of φ to C is the function φ
 C : C → B so that
C : C → B so that

- The function ψ : D → E is an extension of φ if A ⊆ D, B ⊆ E, and ψ
 A = φ.
A = φ.
![]() EXAMPLE 4.4.24
EXAMPLE 4.4.24
Let f = {(1, 2), (2, 3), (3, 4), (4, 1)} and g = {(1, 2), (2, 3)}. We conclude that g = f ![]() {1, 2}, and f is an extension of g.
{1, 2}, and f is an extension of g.
![]() EXAMPLE 4.4.25
EXAMPLE 4.4.25
Let φ : U → V be a function and A, B ⊆ U. We conclude that
![]()
because

Binary Operations
Standard addition and multiplication of real numbers are functions R × R → R (Example 4.4.4). This means two things. First, given any two real numbers, their sum or product will always be the same number. For instance, 3+5 is 8 and never another number. Second, given any two real numbers, their sum or product is also a real number. Notice that subtraction also has these two properties when it is considered an operation involving real numbers, but when we restrict substraction to Z+, it no longer has the second property because the difference of two positive integers might not be a positive integer. That is, subtraction is not a function Z+ × Z+ → Z+.
A binary operation * on the nonempty set A is a function A × A → A.
The symbol that represents the addition function is +. It can be viewed as a function R → R. Therefore, using function notation, +(3, 5) = 8. However, we usually write this as 3 + 5 = 8. Similarly, since * represents an operation like addition, instead of writing * (a, b), we usually write a * b,
To prove that a relation * is a binary operation on A, we must show that it satisfies Definition 4.4.26. To do this, take a, a′, b, b′ ∈ A, and prove:
- a = a′ and b = b′ implies a * b = a′ * b′,
- A is closed under *, that is a * b ∈ A.
![]() EXAMPLE 4.4.27
EXAMPLE 4.4.27
Define x * y = 2x − y and take a, a′, b, b′ ∈ Z.
- Assume a = a′ and b = b′. Then,

The second equality holds because multiplication and subtraction are binary operations on Z.
- Because the product and difference of two integers is an integer, we have that a * b ∈ Z, so Z is closed under *.
Thus, * is a binary operation on Z.
![]() EXAMPLE 4.4.28
EXAMPLE 4.4.28
Let S = {e, a, b, c} and define * by the following table:

The table is read from left to right, so b * c = a. The table makes * into a binary operation since every pair of elements of S is assigned a unique element of S.
![]() EXAMPLE 4.4.29
EXAMPLE 4.4.29
Fix a set A. For any X, Y ∈ P(A), define X * Y = X ∪ Y.
This shows that * is a binary operation on P(A). Notice that * is a subset of [P(A) × P(A)] × P(A).
![]() EXAMPLE 4.4.30
EXAMPLE 4.4.30
Let m ∈ Z+ and define [a]m + [b]m = [a + b]m. We show that this is a binary operation on Zm.
- Let a1, a2, b1, b2 ∈ Z. Suppose [a1]m = [a2]m and [b1]m = [b2]m. This means that a1 = a2 + nk and b1 = b2 + nl for some k, l ∈ Z. Hence, a1 + b1 = a2 + b2 + n(k + l), and we have [a1 + b1]m = [a2 + b2]m.
- For closure, let [a]m, [b]m ∈ Zm where a and b are integers. Then, we have that [a]m + [b]m = [a + b]m ∈ Zm since a + b is an integer.
Many binary operations share similar properties with the operations of + and × on R. The next definition gives four of these properties.
![]() DEFINITION 4.4.31
DEFINITION 4.4.31
Let * be a binary operation on A.
- * is associative means that (a * b) * c = a * (b * c) for all a, b, c ∈ A.
- * is commutative means that a * b = b * a for all a, b ∈ A.
- The element e is an identity of A with respect to * when e ∈ A and e * a = a * e = a for all a ∈ A.
- Suppose that A has an identity e with respect to * and let a ∈ A. The element a′ ∈ A is an inverse of a with respect to * if a * a′ = a′ * a = e.
Notice that the identity, if it exists, must be unique. To prove this, suppose that both e and e′ are identities. These must be equal because e = e * e′ = e′. So, if a set has an identity with respect to an operation, we can refer to it as the identity of the set. Similarly, we can write the inverse if it exists for associative binary operations (Exercise 20).
![]() EXAMPLE 4.4.32
EXAMPLE 4.4.32
We assume that + and × are both associative and commutative on C and all subsets of C, that 0 is the identity with respect to + (the additive identity) and 1 is the identity with respect to × (the multiplicative identity), and that every complex number has an inverse with respect to + (an additive inverse) and every nonzero complex number has an inverse with respect to × (a multiplicative inverse).
The binary operation defined in Example 4.4.30 is both associative and commutative. To see that it is commutative, let a, b ∈ Z. Then,
![]()
where the second equality holds because + is commutative on Z. Its identity is [0]m [let b = 0 in (4.6)] and the additive inverse of [a]m is [−a]m.
![]() EXAMPLE 4.4.34
EXAMPLE 4.4.34
Since A ∪ B = B ∪ A and (A∪ B) ∪ C = A ∪ (B ∪ C) for all sets A, B, and C, the binary operation in Example 4.4.29 is both associative and commutative. Its identity is ∅, and only ∅ has an inverse.
Exercises
1. Indicate whether each of the given relations are functions. If a relation is not a function, find an element of its domain that is paired with two elements of its range.
(a) {(1, 2), (2, 3), (3, 4), (4, 5), (5, 1)}
(b) {(1, 1), (1, 2), (1, 3), (1, 4), (1, 5)}
(c) {(x, ![]() : x ∈ R}
: x ∈ R}
(d) {(x, ±![]() ) : x ∈ R}
) : x ∈ R}
(e) {(x, x2) : x ∈ R}
(f) {([a]5, b) : ∃k ∈ Z(a = b + 5k)}
(g) ψ : Z → Z5 if ψ(a) = [a]5
2. Prove that the given relations are functions.
(a) {(x, 1/x) : x ∈ R {0}}
(b) {(x, x + 1) : x ∈ Z}
(c) {(x |x|) : x ∈ R}
(d) {(x, ![]() ) : x ∈ [0, ∞)}
) : x ∈ [0, ∞)}
3. Let f = {(x, y) ∈ R2 : 2x + y = 1}. Show that f is a function with domain and codomain equal to the set of real numbers.
4. Let f, g : R → R be functions. Prove that φ(x, y) = (f(x), g(y)) is a function with domain and codomain equal to R × R.
5. Let A be a set and define ψ(A) = P(A). Show that ψ is a function.
6. Define

Show that f is well-defined with domain equal to R. What is ran(f)?
7. Let x be in the domain and y in the range of each relation. Explain why each of the given equations does not describe a function.
(a) y = 5 ± x
(b) x2 + y2 = 1
(c) x = 4y2 − 1
(d) y2 − x2 = 9
8. Let φ : Z → Z7 be defined by φ(a) = [a]7. Write the given images as rosters.
(a) φ(0)
(b) φ(7)
(c) φ(3)
(d) φ(−3)
9. Define φ([a]n) = [a]m for all a ∈ Z. Is φ being function sufficient for m | n? Explain.
10. Give an example of a function that is an element of the given sets.
(a) RR
(b) RZ
(c) NR
(d) R[0, ∞)
(e) Z(Z5)
11. Evaluate the indicated expressions.
(a) ![]() 4(f) if f(x) = 9x + 2
4(f) if f(x) = 9x + 2
(b) ![]() π(g) if g(θ) = sin θ
π(g) if g(θ) = sin θ
12. Since functions are sets, we can perform set operations on them. Let f(x) = x2 and g(x) = −x. Find the following.
(a) f ∪ g
(b) f ∩ g
(c) f g
(d) g f
13. Let ![]() be a chain of functions with respect to ⊆. Prove that
be a chain of functions with respect to ⊆. Prove that ![]()
![]() is a function.
is a function.
14. Let f and g be functions. Prove the following.
(a) If f and g are functions, f ∩ g is a function.
(b) f ∪ g is a function if and only if f(x) = g(x) for all x ∈ dom(f) ∩ dom(g).
15. Let f : A → B be a function. Define a relation S on A by a S b if and only if f(a) = f (b).
(a) Show S is an equivalence relation.
(b) Find [3]S if f : Z → Z is defined by f(n) = 2n.
(c) Find [2]S if f : Z → Z5 is given by f(n) = [n]5.
16. Show that ∅ is a function and find its domain and range.
17. Define * by x * y = x + y + 2 for all x, y ∈ Z.
(a) Show that * is a binary operation on Z.
(b) Prove that −2 is the identity of Z with respect to *.
(c) For every n ∈ Z, show that −n − 4 is the inverse of n with respect to *.
18. Define the binary operation * by x * y = 2x − y for all x, y ∈ Z.
(a) Is there an integer that serves as an identity with respect to *?
(b) Does every integer have an inverse with respect to *?
19. Let f, g : R → R be functions. Prove that f ![]() g is well-defined.
g is well-defined.
20. For an associative binary operation, prove that the inverse of an element is unique if it exists. Show that this might not be the case if the binary operation is not associative.
21. Prove that the given pairs of functions are equal.
(a) f(x) = (x − 1)(x − 2)(x + 3) and g(x) = x3 − 7x + 6
where f, g : R → R
(b) φ(a, b) = a + b and ψ(a, b) = b + a
where φ, ψ : Z × Z → Z
(c) φ(a, b) = ([a]5, [b + 7]5 and ψ(a, b) = ([a + 5]5, [b − 3]5)
where φ, ψ : Z × Z → Z5 × Z5
(d) φ(f) = f ![]() Z and ψ(f) = {(n, f(n)) : n ∈ Z}
Z and ψ(f) = {(n, f(n)) : n ∈ Z}
where φ, ψ : RR → ZR
22. Show that the given pairs of functions are not equal.
(a) f(x) = x and g(x) = 2x where f, g : R → R
(b) f(x) = x − 3 and g(x) = x + 3 where f, g : R → R
(c) φ(a) = [a]5 and ψ(a) = [a]4 where φ, ψ : Z → Z4 ∪ Z5
(d) φ(A) = A {0} and ψ(A) = A ∩ {1, 2, 3} where φ, ψ : P(Z) → P(Z)
23. Let ψ : R → RR be defined by ψ(a) = fa where fa is the function fa : R → R with fa(x) = ax. Prove that ψ is well-defined.
24. For each pair of functions, find the indicated values when possible.
(a) f : R → R and f(x) = 2x3
g : R → R and g(x) = x + 1
(f ![]() g)(2)
g)(2)
(g ![]() f)(0)
f)(0)
(b) f : [0, ∞) → R and f(x) = ![]()
g : R → R and g(x) = |x| − 1
(f ![]() g)(0)
g)(0)
(g ![]() f)(4)
f)(4)
(c) φ : Z → Z5 and φ(a) = [a]5
ψ : RR → R and ψ(f) = f(0)
(φ ![]() ψ)(.5x + 1)
ψ)(.5x + 1)
(ψ ![]() φ)(2)
φ)(2)
25. For each of the given functions, find the composition of the function with itself. For example, find f ![]() f for part (a).
f for part (a).
(a) f : R → R with f(x) = x2
(b) g : R → R with g(x) = 3x + 1
(c) φ : Z × Z → Z × Z with φ(x, y) = (2y, 5x − y)
(d) ψ : Zm → Zm with ψ([n]m) = [n + 2]m
26. Let φ : A → B be a function and ψ = φ ![]() C where C ⊆ A. Prove that if ι : C → A is defined by ι(c) = c (known as the inclusion map), then ψ = φ
C where C ⊆ A. Prove that if ι : C → A is defined by ι(c) = c (known as the inclusion map), then ψ = φ ![]() ι.
ι.
27. Write the given restrictions as rosters.
(a) {(1, 2), (2, 2), (3, 4), (4, 7)} ![]() {1, 3}
{1, 3}
(b) f ![]() {0, 1, 2, 3} where f(x) = 7x − 1 and dom(f) = R
{0, 1, 2, 3} where f(x) = 7x − 1 and dom(f) = R
(c) (g + h) ![]() {−3.3, 1.2, 7} where g(x) =
{−3.3, 1.2, 7} where g(x) = ![]() x
x![]() , h(x) = x + 1, and both dom(g) and dom(h) equal R
, h(x) = x + 1, and both dom(g) and dom(h) equal R
28. For functions f and g such that A, B ⊆ dom(f), prove the following.
(a) f ![]() A = f ∩ [A × ran(f)]
A = f ∩ [A × ran(f)]
(b) f ![]() (A ∩ B) = (f
(A ∩ B) = (f ![]() A) ∩ (f
A) ∩ (f ![]() B)
B)
(c) f ![]() (A B) = (f
(A B) = (f ![]() A) (f
A) (f ![]() B)
B)
(d) (g ![]() f)
f) ![]() A = g
A = g ![]() (f
(f ![]() A)
A)
29. Let f : U → V be a function. Prove that if A ⊆ U, then f ![]() A = f
A = f ![]() IA.
IA.
30. Let φ : AC → BC be defined by φ(f) = f ![]() B. Prove that φ is well-defined.
B. Prove that φ is well-defined.
31. A real-valued function f is periodic if there exists k > 0 so that f(x) = f(x + k) for all x ∈ dom(f). Let g, h : R → R be functions with period k. Prove that g ![]() h is periodic with period k.
h is periodic with period k.
32. Let (A, ![]() ) be a poset. A function φ : A → A is increasing means for all x, y ∈ A, if x
) be a poset. A function φ : A → A is increasing means for all x, y ∈ A, if x ![]() y, then φx
y, then φx ![]() φ(y). A decreasing function is defined similarly. Suppose that σ and τ are increasing. Prove that σ
φ(y). A decreasing function is defined similarly. Suppose that σ and τ are increasing. Prove that σ ![]() τ is increasing.
τ is increasing.
4.5 INJECTIONS AND SURJECTIONS
When looking at relations, we studied the concept of an inverse relation. Given R, obtain R−1 by exchanging the x- and y-coordinates. The same can be done with functions, but the inverse might not be a function. For example, given
![]()
its inverse is
![]()
However, if the original relation is a function, we often want the inverse also to be a function. This leads to the next definition.
φ : A → B is invertible means that φ−1 is a function B → A.
An immediate consequence of the definition is the next result.
![]() LEMMA 4.5.2
LEMMA 4.5.2
Let φ be invertible. Then, φ(x) = y if and only if φ−1(y) = x for all x ∈ dom(φ).
PROOF
Suppose that φ(x) = y. This means that (x, y) ∈ φ, so (y, x) ∈ φ−1. Since φ is invertible, φ−1 is a function, so write φ−1(y) = x. The converse is proved similarly. ![]()
We use Lemma 4.5.2 in the proof of the next theorem, which gives conditions for when a function is invertible.
![]() THEOREM 4.5.3
THEOREM 4.5.3
φ : A → B is invertible if and only if φ−1 ![]() φ = IA and φ
φ = IA and φ ![]() φ−1 = IB.
φ−1 = IB.
PROOF
Take a function φ : A → B. Then, φ−1 ⊆ B × A.
- Assume that φ−1 is a function B → A. Let x ∈ A and y ∈ B. By assumption, we have x0 ∈ A and y0 ∈ B such that φ(x) = y0 and φ−1(y) = x0. This implies that φ−1(y0) = x and φ(x0) = y by Lemma 4.5.2. Therefore,

and

- Now assume φ−1
 φ = IA and φ
φ = IA and φ  φ−1 = IB. To show that φ−1 is a function, take (y, x), (y, x′) ∈ φ−1. From this, we know that (x, y) ∈ φ. Therefore,
φ−1 = IB. To show that φ−1 is a function, take (y, x), (y, x′) ∈ φ−1. From this, we know that (x, y) ∈ φ. Therefore,

so x = x′. In addition, we know that dom(φ−1) ⊆ B, so to prove equality, let y ∈ B. Then,

Thus, there exists x ∈ A such that (y, x) ∈ φ−1, so y ∈ dom(φ−1).

![]() EXAMPLE 4.5.4
EXAMPLE 4.5.4
- Let f : R → R be the function given by f(x) = x + 2. Its inverse is g(x) = x − 2 by Theorem 4.5.3. This is because
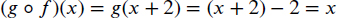

- If the function g : [0, ∞) → [0, ∞) is defined by g(x) = x2, then g−1 is a function [0, ∞) → [0, ∞) and is defined by g−1(x) =
 .
. - Let h : R → (0, ∞) be defined as h(x) = ex. By Theorem 4.5.3, we know that h−1(x) = ln x because elnx = x for all x ∈ [0, ∞) and ln ex = x for all x ∈ R.
Injections
Theorem 4.5.3 can be improved by finding a condition for the invertibility of a function based only on the given function. Consider the following. In order for a relation to be a function, it cannot look like Figure 4.9. Since the inverse exchanges the roles of the two coordinates, in order for an inverse to be a function, the original function cannot look like the graph in Figure 4.11. In other words, if f−1 is to be a function, there cannot exist x1 and x2 so that x1 ≠ x2 and f(x1) = f(x2). But then,
![]()
is equivalent to
![]()
which in turn is equivalent to
![]()
Hence, f being an invertible function implies that for every x1, x2 ∈ dom(f),
![]()

Figure 4.11 The inverse of a function might not be a function.
Figure 4.12 φ is a one-to-one function.
This means that the elements of the domain of f and the elements of the range of f form pairs of elements as illustrated in Figure 4.12. The sufficiency of (4.7) is the definition of a function, while necessity is the next definition.
![]() DEFINITION 4.5.5
DEFINITION 4.5.5
The function φ : A → B is one-to-one if and only if for all x1, x2 ∈ A,
![]()
A one-to-one function is sometimes called an injection.
![]() EXAMPLE 4.5.6
EXAMPLE 4.5.6
Define f : R → R by f(x) = 5x+1. To show that f is one-to-one, let x1, x2 ∈ R and assume f(x1) = f(x2). Then,

![]() EXAMPLE 4.5.7
EXAMPLE 4.5.7
Let φ : Z × Z → Z × Z × Z be the function
![]()
For any (a1, b1), (a2, b2) ∈ Z × Z, assume
![]()
This means that
![]()
Hence, a1 = a2 and b1 = b2, and this yields (a1, b1) = (a2, b2).
Figure 4.13 φ is not a one-to-one function.
If a function is not one-to-one, there must be an element of the range that has at least two pre-images (Figure 4.13). An example of a function that is not one-to-one is f(x) = x2 where both the domain and codomain of f are R. This is because f (2) = 4 and f(−2) = 4. Another example is g : R → R defined by g(θ) = cos θ. It is not an injection because g(0) = g(2π) = 1.
Although the original function might not be one-to-one, we can always restrict the function to a subset of its domain so that the resulting function is one-to-one. This is illustrated in the next two examples.
![]() EXAMPLE 4.5.8
EXAMPLE 4.5.8
Let f be the function {(1, 5), (2, 8), (3, 8), (4, 6)}. We observe that f is not one-to-one, but both
![]()
and
![]()
are one-to-one as in Figure 4.14.

Figure 4.14 Restrictions of f to A and B are one-to-one.
Let g : R → R be the function g(x) = x2. This function is not one-to-one, but g ![]() [0, ∞) and g
[0, ∞) and g ![]() (−10, −5) are one-to-one.
(−10, −5) are one-to-one.
Let f(x) = 3x + 6 and g(x) = ![]() . Both are injections. Notice that
. Both are injections. Notice that
![]()
and
![]()
are also injections. We can generalize this result to the next theorem.
![]() THEOREM 4.5.10
THEOREM 4.5.10
If φ : A → B and ψ : B → C are injections, ψ ![]() φ is an injection.
φ is an injection.
PROOF
Assume that φ : A → B and ψ : B → C are one-to-one. Let a1, a2 ∈ A and assume (ψ ![]() φ)(a1) = (ψ
φ)(a1) = (ψ ![]() φ)(a2). Then,
φ)(a2). Then,
![]()
Since ψ is one-to-one,
![]()
and since φ is one-to-one, a1 = a2. ![]()
Surjections
The function being an injection is not sufficient for it to be invertible since it is possible that not every element of the codomain will have a pre-image. In this case, the codomain cannot be the domain of the inverse. To prevent this situation, we will need the function to satisfy the next definition.
![]() DEFINITION 4.5.11
DEFINITION 4.5.11
A function φ : A → B is onto if and only if for every y ∈ B, there exists x ∈ A such that φ(x) = y. An onto function is also called a surjection.
This definition is related to the range (or image) of the function. The range of the function φ : A → B is
![]()
as illustrated in Figure 4.15. Thus, φ is onto if and only if ran(φ) = B.
![]() EXAMPLE 4.5.12
EXAMPLE 4.5.12
Define f : [0, ∞) → [0, ∞) by f(x) = ![]() . Its range is also [0, ∞), so it is onto.
. Its range is also [0, ∞), so it is onto.
Figure 4.15 The range of φ : A → B with y = φ(x).
![]() EXAMPLE 4.5.13
EXAMPLE 4.5.13
The ranges of the following functions are different from their codomains, so they are not onto.
- Let g : R → R be defined by g(x) = |x|. Then, ran(g) = [0, ∞).
- Define h : Z → Z by h(n) = 2n. Here, ran(h) = {2n : n ∈ Z}.
The functions illustrated in Figures 4.12, 4.13, and 4.14 are onto functions as are those in the next examples.
![]() EXAMPLE 4.5.14
EXAMPLE 4.5.14
Any linear function f : R → R that is not a horizontal line is a surjection. To see this, let f(x) = ax + b for some a ≠ 0. Take y ∈ R. We need to find x ∈ R so that ax + b = y. Choose
![]()
Then,

The approach in the example is typical. To show that a function is onto, take an arbitrary element of the codomain and search for a candidate to serve as its pre-image. When found, check it.
![]() EXAMPLE 4.5.15
EXAMPLE 4.5.15
Take a positive integer m and let φ : Z → Zm be defined as φ(k) = [k]m. To see that φ is onto, take [l]m ∈ Zm for some l ∈ Z. We then find that φ(l) = [l]m.
![]() EXAMPLE 4.5.16
EXAMPLE 4.5.16
Let m, n ∈ N with m > n. A function π : Rm → Rn defined by
![]()
is called a projection.. Such functions are not one-to-one, but they are onto. For instance, define π : R × R × R → R × R by
![]()
It is not one-to-one because π(1, 2, 3) = π(1, 2, 4) = (1, 2). However, if we take (a, b) ∈ R × R, then π(a, b, 0) = (a, b), so π is onto.
If a function is not onto, it has a diagram like that of Figure 4.16. Therefore, to show that a function is not a surjection, we must find an element of the codomain that does not have a pre-image.
![]() EXAMPLE 4.5.17
EXAMPLE 4.5.17
Define f : Z → Z by f(n) = 3n. This function is not onto because 5 does not have a pre-image in Z.
![]() EXAMPLE 4.5.18
EXAMPLE 4.5.18
The function
![]()
defined by φ(a, b) = (a, b, 0) is not onto because (1, 1, 1) does not have a pre-image in Z × Z.
We have the following analog of Theorem 4.5.10 for surjections.
![]() THEOREM 4.5.19
THEOREM 4.5.19
If φ : A → B and ψ : B → C are surjections, ψ ![]() φ is a surjection.
φ is a surjection.
PROOF
Assume that φ : A → B and ψ : B → C are surjections. Take c ∈ C. Then, there exists b ∈ B so that ψ(b) = c and a ∈ A such that φ(a) = b. Therefore,
![]()

Figure 4.16 φ is not a onto function.
Bijections
If we have a function that is both one-to-one and onto, then it is called a bijection or a one-to-one correspondence. Observe that ∅ is a bijection.
![]() EXAMPLE 4.5.20
EXAMPLE 4.5.20
As illustrated in Examples 4.5.6 and 4.5.14, every linear f : R → R with nonzero slope is a bijection.
![]() EXAMPLE 4.5.21
EXAMPLE 4.5.21
Both g : (−π/2, π/2) → R such that g(θ) = tan θ and h : R → (0, ∞) where h(x) = ex are bijections.
We are now ready to give the standard test for invertibility. Its proof requires both Lemma 4.5.2 and Theorem 4.5.3. The benefit of this theorem is that it provides a test for invertibility in which the given function is examined instead of its inverse.
![]() THEOREM 4.5.22
THEOREM 4.5.22
A function is invertible if and only if it is a bijection.
PROOF
Let φ : A → B be a function.
- Suppose that φ is invertible. To show that φ is one-to-one, let x1, x2 ∈ A and assume that φ(x1) = φ(x2). Then, by Theorem 4.5.3,
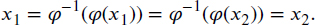
To see that φ is onto, take y ∈ B. Then, there exists x ∈ A such that φ−1(y) = x. Hence, φ(x) = y by Lemma 4.5.2.
- Assume that φ is both one-to-one and onto. To show that φ−1 is a function, let (y, x), (y, x′) ∈ φ−1. This implies that φ(x) = y = φ(x′). Since φ is one-to-one, x = x′. To prove that the domain of φ−1 is B, take y ∈ B. Since φ is onto, there exists x ∈ A such that φ(x) = y. By Lemma 4.5.2, we have that φ−1(y) = x, so y ∈ dom(φ−1).

By Theorem 4.5.22 the functions of Examples 4.5.20 and 4.5.21 are invertible.
![]() THEOREM 4.5.23
THEOREM 4.5.23
If φ : A → B and ψ : B → C are bijections, then φ−1 and ψ ![]() φ are bijections.
φ are bijections.
PROOF
Suppose φ is a bijection. By Theorem 4.5.22, it is invertible, so φ−1 is a function that has φ as its inverse. Therefore, φ−1 is a bijection by Theorem 4.5.22. Combining the proofs of Theorems 4.5.10 and 4.5.19 show that ψ ![]() φ is a bijection when ψ is a bijection.
φ is a bijection when ψ is a bijection. ![]()
Using the functions g and h from Example 4.5.21, we conclude from Theorem 4.5.23 that h ![]() g is a bijection with domain (−π/2, π/2) and range (0, ∞).
g is a bijection with domain (−π/2, π/2) and range (0, ∞).
Order Isomorphims
Consider the function
![]()
defined by φ(m, 0) = (0, m). It can be shown that φ is a bijection (compare Exercise 12). Define the linear orders ![]() on Z × {0} and
on Z × {0} and ![]() ′ on {0} × Z by
′ on {0} × Z by
![]()
and
![]()
Notice that (3, 0) ![]() (5, 0) and (0, 3)
(5, 0) and (0, 3) ![]() ′ (0, 5) because 3 ≤ 5. We can generalize this to conclude that
′ (0, 5) because 3 ≤ 5. We can generalize this to conclude that
![]()
and this implies that
![]()
This leads to the next definition.
![]() DEFINITION 4.5.24
DEFINITION 4.5.24
Let R be a relation on A and S be a relation on B.
- φ : A → B is an order-preserving function if for all a1, a2 ∈ A,

and we say that φ preserves R with S.
- An order-preserving bijection is an order isomorphism.
- (A, R) is order isomorphic to (B, S) and we write (A, R) ≅ (B, S) if there exists an order isomorphism φ : A → B preserving R with S. If (A, R) ≅ (B, S) and the relations R and S are clear from context, we can write A ≅ B. Sometimes (A, R) and (B, S) are said to have the same order type when they are order isomorphic.
An isomorphism pairs elements from two sets in such a way that the orders on the two sets appear to be the same.
Define f : R+ → R− by f(x) = −x (Example 3.1.12). Clearly, f is a bijection. Moreover, f preserved ≤ with ≥. To prove this, let x1, x2 ∈ R+. Then,
![]()
Therefore, (R+, ≤) ≅ (R−, ≥).
Observe that the inverse of (4.8) is the function
![]()
such that φ−1(0, m) = (m, 0). This function preserves ![]() ′ with
′ with ![]() . This result is generalized and proved in the next theorem.
. This result is generalized and proved in the next theorem.
![]() THEOREM 4.5.26
THEOREM 4.5.26
The inverse of an order isomorphism preserving R with S is an order isomorphism preserving S with R.
PROOF
Let φ : A → B be an order isomorphism preserving R with S. By Theorem 4.5.23, φ−1 is a bijection. Suppose that (b1, b2) ∈ S. Since φ is onto, there exists a1, a2 ∈ A such that φ(a1) = b1 and φ(a2) = b2. This implies that (φ(a1), φ(a2)) ∈ S. Since φ is an isomorphism preserving R with S, we have that (a1, a2) ∈ R. However, a1 = φ−1(b1) and a2 = φ−1(b2), so (φ−1(b1), φ−1(b2)) ∈ R. Therefore, φ−1 : B → A is an isomorphism preserving S with R. ![]()
Also, observe that g : R → (0, ∞) defined by g(x) = ex is an order isomorphism preserving ≤ with ≤. Using f from Example 4.5.25, the composition f ![]() g is an order isomorphism R → (−∞, 0) such that (f
g is an order isomorphism R → (−∞, 0) such that (f ![]() g)(x) = −ex. That this happens in general is the next theorem. Its proof is left to Exercise 25.
g)(x) = −ex. That this happens in general is the next theorem. Its proof is left to Exercise 25.
![]() THEOREM 4.5.27
THEOREM 4.5.27
If φ : A → B is an isomorphism preserving R with S and ψ : B → C is an isomorphism preserving S with T, then ψ ![]() φ : A → C is an isomorphism preserving R with T.
φ : A → C is an isomorphism preserving R with T.
![]() EXAMPLE 4.5.28
EXAMPLE 4.5.28
Let R be a relation on A, S be a relation on B, and T be a relation on C.
- Since the identity map is an order isomorphism, (A, R) ≅ (A, R).
- Suppose (A, R) ≅ (B, S). This means that there exists an order isomorphism φ : A → B preserving R with S. By Theorem 4.5.26, φ−1 is an order isomorphism preserving S with R. Therefore, (B, S) ≅ (A, R).
- Let (A, R) ≅ (B, S) and (B, S) ≅ (C, T). By Theorem 4.5.27, we conclude that (A, R) ≅ (C, T).
If an order-preserving function is one-to-one, even it is not a surjection, the function still provides an order isomorphism between its domain and range. This concept is named by the next definition.
![]() DEFINITION 4.5.29
DEFINITION 4.5.29
φ : A → B is an embedding if φ is an order isomorphism A → ran(φ).
For example, f : Z → Q such that f(n) = n is an embedding preserving ≤ and π : R2 → R3 such that ψ(x, y) = (x, y, 0) is an embedding preserving the lexicographical order (Exercise 4.3.16). Although R2 is not a subset of R3, we view the image of ψ as a copy of R2 in R3 that preserves the orders.
Exercises
1. Show that the given pairs of functions are inverses.
(a) f(x) = 3x + 2 and g(x) = ![]()
(b) φ(a, b) = (2a, b + 2) and ψ(a, b) = (![]() a, b − 2)
a, b − 2)
(c) f(x) = ax and g(x) = loga x, where a > 0
2. For each function, graph the indicated restriction.
(a) f ![]() (0, ∞), f(x) = x2
(0, ∞), f(x) = x2
(b) g ![]() [−5, −2], g(x) = |x|
[−5, −2], g(x) = |x|
(c) h ![]() [0, π/2], h(x) = cos x
[0, π/2], h(x) = cos x
3. Prove that the given functions are one-to-one.
(a) f : R → R, f(x) = 2x + 1
(b) g : R2 → R2, g(x, y) = (3y, 2x)
(c) h : R {9} → R {0}, h(x) = 1/(x − 9)
(d) φ : Z × R → Z × (0, ∞), φ(n, x) = (3n, ex)
(e) ψ : P(A) → P(B), ψ(C) = C ∪ {b} where A ⊂ B and b ∈ B A
4. Let f : (a, b) → (c, d) be defined by
![]()
Graph f and show that it is a bijection.
5. Let f and g be functions such that ran(g) ⊆ dom(f).
(a) Prove that if f ![]() g is one-to-one, g is one-to-one.
g is one-to-one, g is one-to-one.
(b) Give an example of functions f and g such that f ![]() g is one-to-one, but f is not one-to-one.
g is one-to-one, but f is not one-to-one.
6. Define φ : Z → Zm by φ(k) = [k]m. Show that φ is not one-to-one.
7. Show that the given functions are not one-to-one.
(a) f : R → R, f(x) = x4 + 3
(b) g : R → R, g(x)= |x − 2| + 4
(c) φ : P(A) → {{a}, ∅}, φ(B) = B ∩ {a}, where a ∈ A and A has at least two elements
(d) ![]() 5 : RR → R,
5 : RR → R, ![]() 5(f) = f(5)
5(f) = f(5)
8. Let f : R → R be periodic (Exercise 4.4.31). Prove that f is not one-to-one.
9. Show that the given functions are onto.
(a) f : R → R, f(x) = 2x + 1
(b) g : R → (0, ∞), g(x) = ex
(c) h : R {0} → R {0}, h(x) = 1/x
(d) φ : Z × Z → Z, φ(a, b) = a + b
(e) ![]() 5 : RR → R,
5 : RR → R, ![]() 5(f) = f(5)
5(f) = f(5)
10. Show that the given functions are not onto.
(a) f : R → R, f(x) = ex
(b) g : R → R, g(x) = |x|
(c) φ : Z × Z → Z × Z, φ(a, b) = (3a, b2)
(d) ψ : R → RR, ψ(a) = f, where f(x) = a for all x ∈ R
11. Let f and g be functions such that ran(g) ⊆ dom(f).
(a) Prove that if f ![]() g is onto, then f is onto.
g is onto, then f is onto.
(b) Give an example of functions f and g such that f ![]() g is onto, but g is not onto.
g is onto, but g is not onto.
12. Define φ : Q × Z → Z × Q by φ(x, y) = (y, x). Show that φ is a bijection.
13. Show that the function γ : A × B → C × D defined by
![]()
is a bijection if both φ : A → C and ψ : B → D are bijections.
14. Define γ : A × (B × C) → (A × B) × C by
![]()
Prove γ is a bijection.
15. Demonstrate that the inverse of a bijection is a bijection.
16. Prove that the empty set is a bijection with domain and range equal to ∅.
17. Let A ⊆ R and define φ : RR → AR by φ(f) = f ![]() A. Is φ always one-to-one? Is it always onto? Explain.
A. Is φ always one-to-one? Is it always onto? Explain.
18. A function f : A → B has a left inverse if there exists a function g : B → A such that g ![]() f = IA. Prove that a function is one-to-one if and only if it has a left inverse.
f = IA. Prove that a function is one-to-one if and only if it has a left inverse.
19. A function f : A → B has a right inverse if there exists a function g : B → A so that f ![]() g = IB. Prove a function is onto if and only if it has a right inverse.
g = IB. Prove a function is onto if and only if it has a right inverse.
20. Let (A, ![]() ) be a poset. For every bijection φ : A → A, φ is increasing (Exercise 4.4.32) if and only if φ−1 is increasing.
) be a poset. For every bijection φ : A → A, φ is increasing (Exercise 4.4.32) if and only if φ−1 is increasing.
21. Show that if a real-valued function is increasing, it is one-to-one.
22. Prove or show false this modification of Theorem 4.5.23: If φ : A → B and ψ : C → D are bijections with ran(φ) ⊆ C, then ψ ![]() φ is a bijection.
φ is a bijection.
23. Let A, B ⊆ R be two sets ordered by ≤. Let A be well-ordered by ≤. Prove that if f : A → B is an order-preserving surjection, B is well-ordered by ≤.
24. Let φ : A → B be an isomorphism preserving R with R′. Let C ⊆ A and D ⊆ B. Prove the following.
(a) (C, R ∩ [C × C]) ≅ (φ[C], R′ ∩ [φ [C] × φ [C]])
(b) (D, R′ ∩ [D × D]) ≅ (φ−1 [D], R ∩ [φ−1 [D] × φ−1 [D]])
25. Prove Theorem 4.5.27.
26. Define f : R → R by f(x) = 2x + 1. Prove that f is an order isomorphism preserving < with <.
27. Suppose that (A, R) and (B, S) are posets. Let φ : A → B be an order isomorphism preserving R with S and C ⊆ A. Prove that if m is the least element of C with respect to R, then φ(m) is the least element of φ[C] with respect to S.
28. Find linear orders (A, ![]() ) and (B,
) and (B, ![]() ′) such that each is isomorphic to a subset of the other but (A,
′) such that each is isomorphic to a subset of the other but (A, ![]() ) is not isomorphic to (B,
) is not isomorphic to (B, ![]() ′).
′).
29. Let (A, ![]() ) be a poset. Prove that there exists B ⊆ P(A) such that (A,
) be a poset. Prove that there exists B ⊆ P(A) such that (A, ![]() ) ≅ (B, ⊆).
) ≅ (B, ⊆).
4.6 IMAGES AND INVERSE IMAGES
So far we have focused on the image of single element in the domain of a function. Sometimes we will need to examine a set of images.
![]() DEFINITION 4.6.1
DEFINITION 4.6.1
Let φ : A → B be a function and C ⊆ A. The image of C (under φ) is
![]()
Notice that φ [C] ⊆ B (Figure 4.17) and φ [A] = ran(φ).
A similar definition can be made with subsets of the codomain.
![]() DEFINITION 4.6.2
DEFINITION 4.6.2
Let φ : A → B be a function and D ⊆ B. The inverse image of D (under φ) is
![]()
Figure 4.17 The image of C under φ.

Figure 4.18 The inverse image of D under φ.
Observe that φ−1 [D] ⊆ A (Figure 4.18) and φ−1 [ran(φ)] = A.
![]() EXAMPLE 4.6.3
EXAMPLE 4.6.3
Let f = {(1, 2), (2, 4), (3, 5), (4, 5)}. This set is a function. Its domain is {1, 2, 3, 4}, and its range is {2, 4, 5}. Then,
![]()
and
![]()
![]() EXAMPLE 4.6.4
EXAMPLE 4.6.4
Define f : R → R by f(x) = x2 + 1.
- To prove f [(1, 2)] = (2, 5), we show both inclusions. Let y ∈ f [(1, 2)]. Then, y = x2 + 1 for some x ∈ (1, 2). By a little algebra, we see that 2 < x2 + 1 < 5. Hence, y ∈ (2, 5). Conversely, let y ∈ (2, 5). Because

Figure 4.19 The image and inverse image of a set under f.
 ∈ (1, 2). Furthermore,
∈ (1, 2). Furthermore,
Therefore, y ∈ f [(1, 2)]. This is illustrated in Figure 4.19(a).
- Simply because f[(1, 2)] = (2, 5), we cannot conclude f−1[(2, 5)] equals (1, 2). Instead, f−1 [(2, 5)] = (−2, −1) ∪ (1, 2), as seen in Figure 4.19(b), because

- To show that f−1[(−2, −1)] is empty, take x ∈ f−1 [(−2, −1)]. This means that −2 < f(x) < −1, but this is impossible because f(x) is positive.
Let f = {(1, 3), (2, 3), (3, 4), (4, 5)}. This is a function {1, 2, 3, 4} → {3, 4, 5}. Notice that

![]()
This result concerning the interaction of images and inverse images with union and intersection is generalized in the next theorem.
![]() THEOREM 4.6.5
THEOREM 4.6.5
Let φ : A → B be a function with C, D ⊆ A and E, F ⊆ B.
- φ [C ∪ D] = φ [C] ∪ φ [D].
- φ [C ∩ D] ⊆ φ [C] ∩ φ [D].
- φ−1 [E ∪ F] = φ−1 [E] ∪ φ−1 [F].
- φ−1 [E ∩ F] = φ−1 [E] ∩ φ−1 [F].
PROOF
We prove the first and third parts, leaving the others for Exercise 7. By Exercise 3.2.8(d),

In addition,

It might seem surprising that we only have an inclusion in the second part of Theorem 4.6.5. To see that the other inclusion is false, let f = {(1, 3), (2, 3)}. Then,
![]()
but
![]()
Hence, f [{1}] ∩ f [{2}] ![]() f [{1} ∩ {2}]. However, if f had been a bijection, the inclusion would hold (Exercise 13).
f [{1} ∩ {2}]. However, if f had been a bijection, the inclusion would hold (Exercise 13).
Let f(x) = x2 + 1. We check the union results of Theorem 4.6.5.
- We have already seen in Example 4.6.4 that f[(1, 2)] = (2, 5). Since (1, 2) = (1, 1.5] ∪ [1.5, 2), apply f to both of these intervals and find that

Therefore, f [(1, 2)] = f[(1, 1.5]] ∪ f[[1.5, 2)].
- Also, from Example 4.6.4, f−1[(2, 5)] = (−2, −1) ∪ (1, 2). We can write (2, 5) as the union of (2, 4) and (3, 5). Since

we have that

Theorem 4.6.5 can be modified to arbitrary unions and intersections. The proof is left to Excercise 17.
![]() THEOREM 4.6.7
THEOREM 4.6.7
Let {Ai : i ∈ I} be a family of sets.
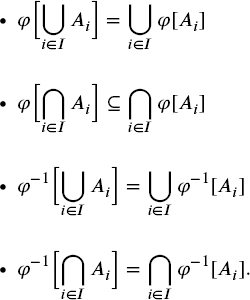
We know that the composition of a function and its inverse equals the identity map (Theorem 4.5.3). The last two results of the section show a similar result involving the image and inverse image using functions that are either one-to-one or onto.
Let φ : A → B be a function. Suppose C ⊆ A and D ⊆ B.
- If φ is one-to-one, then φ−1[φ[C]] = C.
- If φ is onto, then φ[φ−1[D]] = D.
PROOF
We prove the first part and leave the second to Exercise 8. Suppose that φ is an injection. We show that φ−1 [φ[C]] = C.
- Let x ∈ φ−1[φ[C]]. This means that there exists y ∈ φ[C] such that φ(x) = y. Furthermore, there is a z ∈ C so that φ(z) = y. Therefore, since φ is one-to-one, x = z, which means that x ∈ C.
- This step will work for any function. Take x ∈ C, so φ(x) ∈ φ[C]. By definition,

Since x is also an element of A, we conclude that x ∈ φ−1 [φ[C]].

Because we used the one-to-one condition only to prove φ−1[φ[C]] ⊆ C, we suspect that this inclusion is false if the function is not one-to-one. To see this, let f : R → R be defined as f(x) = x2. We know that f is not one-to-one. Choose C = {1}. Then,
![]()
Therefore, f−1[f[C]] ![]() C.
C.
When examining the example, we might conjecture that the function being one-to-one is necessary for equality. That this is the case is the following theorem.
![]() THEOREM 4.6.9
THEOREM 4.6.9
Let φ : A → B be a function.
- If φ−1 [φ[C]] = C for all C ⊆ A, then φ is one-to-one.
- If φ [φ−1[D]] = D for all D ⊆ B, then φ is onto.
PROOF
As with the previous theorem, we prove only the first part. The second part is Exercise 8. Assume
![]()
Take x1, x2 ∈ A and let φ(x1) = φ(x2). Now,
![]()
Because φ(x1) = φ(x2), we have that {x1, x2} ⊆ {z ∈ A : φ(z) = φ(x1)}, so we must have x1 = x2. ![]()
Exercises
1. Let f : R → R be defined by f(x) = 2x + 1. Find the images and inverse images.
(a) f [(1, 3]]
(b) f [(−∞, 0)]
(c) f−1[(−1, 1)]
(d) f −1[(0, 2) ∪ (5, 8)]
2. Let g : R → R be the function g(x) = x4 − 1. Find the images and inverse images.
(a) g[{0}]
(b) g[Z]
(c) g−1[{0, 15}]
(d) g−1[[−9, −5] ∪ [0, 5]]
3. Define φ : R × R → Z by φ(a, b) = ![]() a
a![]() +
+ ![]() b
b![]() . Find the images and inverse images.
. Find the images and inverse images.
(a) φ[{0} × R]
(b) φ[(0, 1) × (0, 1)]
(c) φ−1[{2, 4}]
(d) φ−1[N]
4. Let ψ : Z → Z be a function and define γ : P(Z) → P(Z) by γ (C) = ψ[C].
(a) Prove that γ is well-defined.
(b) Let ψ(n) = 2n. Find γ[{1, 2, 3}], γ[Z], γ−1[{1, 2, 3}], and γ−1[Z].
(c) Under what conditions is γ one-to-one?
(d) Under what conditions is γ onto?
5. For any function ψ, show that ψ[∅] = ∅ and ψ−1[∅] = ∅.
6. Prove for every B ⊆ A, IA[B] = B and (IA)−1 [B] = B.
7. Prove the remaining parts of Theorem 4.6.5.
8. Prove the unproven parts of Theorems 4.6.8 and 4.6.9.
9. Let φ : A → B be an injection and C ⊆ A.
(a) Prove φ(x) ∈ φ[C] if and only if x ∈ C.
(b) Show that Exercise 9(a) is false if the function is not one-to-one.
10. If ψ is a function, A ⊆ B ⊆ dom(ψ), and C ⊆ D ⊆ ran(ψ), show that both ψ[A] ⊆ ψ[B] and ψ−1[C] ⊆ ψ−1[D].
11. Let φ : A → B be a function and take disjoint sets U and V.
(a) Prove false: If U, V ⊆ A then φ[U] ∩ φ[V] = ∅.
(b) Prove false: If U, V ⊆ B, then φ−1 [U] ∩ φ−1 [V] = ∅.
(c) What additional assumption is needed to prove both of the implications?
12. Assume that φ and ψ are functions such that ran(ψ) ⊆ dom(φ). Let A be a subset of dom(ψ). Prove or show false with a counterexample: (φ ![]() ψ)[A] = φ[ψ[A]].
ψ)[A] = φ[ψ[A]].
13. Let φ : A → B be one-to-one. Prove the following.
(b) If C ⊆ A and D ⊆ B, then φ[C] = D if and only if φ−1[D] = C.
14. Prove that if φ : A → B is a bijection and C ⊆ A, then φ[A C] = B φ[C].
15. Find a function φ : A → B and a set D ⊆ B such that D ![]() φ[φ−1[D]].
φ[φ−1[D]].
16. Let ψ be an injection with A ⊆ dom(ψ) and B ⊆ ran(ψ). Prove that
![]()
17. Prove Theorem 4.6.7.










