CHAPTER 6
ORDINALS AND CARDINALS
6.1 ORDINAL NUMBERS
In Chapter 5, we defined certain sets to represent collections of numbers. Despite being sets themselves, the elements of those sets were called numbers. We continue this association with sets as numbers but for a different purpose. While before we defined ω, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() to represent N, Z, Q, R, and C, the definitions of this chapter are intended to be a means by which all sets can be classified according to a particular criterion. Specifically, in the later part of the chapter, we will define sets for the purpose of identifying the size of a given set, and we begin the chapter by defining sets that are used to identify whether two well-ordered sets have the same order type (Definition 4.5.24). A crucial tool in this pursuit is the following generalization of Theorem 5.5.1 to well-ordered infinite sets.
to represent N, Z, Q, R, and C, the definitions of this chapter are intended to be a means by which all sets can be classified according to a particular criterion. Specifically, in the later part of the chapter, we will define sets for the purpose of identifying the size of a given set, and we begin the chapter by defining sets that are used to identify whether two well-ordered sets have the same order type (Definition 4.5.24). A crucial tool in this pursuit is the following generalization of Theorem 5.5.1 to well-ordered infinite sets.
![]() THEOREM 6.1.1 [Transfinite Induction 1]
THEOREM 6.1.1 [Transfinite Induction 1]
Let (A, ![]() ) be a well-ordered set. If B ⊆ A and
) be a well-ordered set. If B ⊆ A and ![]() (A, x) ⊆ B implies x ∈ B for all x ∈ A, then A = B.
(A, x) ⊆ B implies x ∈ B for all x ∈ A, then A = B.
To show that A is a subset of B, suppose that A B is nonempty. Since A is well-ordered by ![]() , let m be the least element of A B. This implies that
, let m be the least element of A B. This implies that ![]() (A, m) ⊆ B, so m ∈ B by hypothesis, a contradiction.
(A, m) ⊆ B, so m ∈ B by hypothesis, a contradiction. ![]()
Note that transfinite induction restricted to ω is simply strong induction (Theorem 5.5.1). To see this, let the well-ordered set (A, ![]() ) of Theorem 6.1.1 be (ω, ≤). Define the set B = {k : p(k)} ⊆ ω for some formula p(k). The conditional
) of Theorem 6.1.1 be (ω, ≤). Define the set B = {k : p(k)} ⊆ ω for some formula p(k). The conditional
![]()
implies p(0) when n = 0 because seg≤(ω, 0) = ∅ and implies
![]()
when n > 0 because seg≤(ω, n) = n.
Our first use of transfinite induction is the following lemma. It uses the terminology of Exercise 4.4.32 and is the first of a sequence of lemmas that will play a critical role.
![]() LEMMA 6.1.2
LEMMA 6.1.2
Let (A, ![]() ) be well-ordered. If φ : A → A is increasing, then a
) be well-ordered. If φ : A → A is increasing, then a ![]() φ(a) for all a ∈ A.
φ(a) for all a ∈ A.
PROOF
Define B = {x ∈ A : x ![]() φ(x)}, where φ is an increasing function A → A. Let
φ(x)}, where φ is an increasing function A → A. Let ![]() (A, a) ⊆ B. We note that a is the least element of A
(A, a) ⊆ B. We note that a is the least element of A ![]() (A, a). Let y ∈
(A, a). Let y ∈ ![]() (A, a). This implies that y
(A, a). This implies that y ![]() φ(y)
φ(y) ![]() φ(a) by definition of B and because y
φ(a) by definition of B and because y ![]() a. Hence, φ(a) ∈ A seg
a. Hence, φ(a) ∈ A seg![]() (A, a). Thus, a
(A, a). Thus, a ![]() φ(a) and A = B by transfinite induction (Theorem 6.1.1).
φ(a) and A = B by transfinite induction (Theorem 6.1.1). ![]()
![]() LEMMA 6.1.3
LEMMA 6.1.3
For all well-ordered sets (A, ![]() ) and (A′,
) and (A′, ![]() ′), there exists at most one order isomorphism φ : A → A′.
′), there exists at most one order isomorphism φ : A → A′.
PROOF
Let φ : A → A′ and ψ : A → A′ be order isomorphisms. Since both φ−1 and ψ−1 are order isomorphisms A′ → A (Theorem 4.5.26), ψ−1 ![]() φ and φ−1
φ and φ−1 ![]() ψ are order isomorphisms A′ → A (Theorem 4.5.27). We note that for every b, c ∈ A, if b
ψ are order isomorphisms A′ → A (Theorem 4.5.27). We note that for every b, c ∈ A, if b ![]() c, then φ(b)
c, then φ(b) ![]() ′ φ(c) and then ψ−1(φ(b))
′ φ(c) and then ψ−1(φ(b)) ![]() ψ−1(φ(c)). This means that ψ−1
ψ−1(φ(c)). This means that ψ−1 ![]() φ is increasing. A similar argument proves that φ−1
φ is increasing. A similar argument proves that φ−1 ![]() ψ is increasing. To show that φ = ψ, let a ∈ A. By Lemma 6.1.2,
ψ is increasing. To show that φ = ψ, let a ∈ A. By Lemma 6.1.2,
![]()
and
![]()
Therefore, ψ(a) ![]() ′ φ(a) and φ(a)
′ φ(a) and φ(a) ![]() ′ ψ(a). Since
′ ψ(a). Since ![]() ′ is antisymmetric, we have that φ(a) = ψ(a).
′ is antisymmetric, we have that φ(a) = ψ(a). ![]()
No well-ordered set (A, ![]() ) is order isomorphic to any of its proper initial segments.
) is order isomorphic to any of its proper initial segments.
PROOF
Let (A, ![]() ) be a well-ordered set. Suppose that S is a proper initial segment of A. In order to obtain a contradiction, assume that φ : A → S is an order isomorphism. Take a ∈ A S. Since φ(a) ∈ S and φ is increasing, we have that a
) be a well-ordered set. Suppose that S is a proper initial segment of A. In order to obtain a contradiction, assume that φ : A → S is an order isomorphism. Take a ∈ A S. Since φ(a) ∈ S and φ is increasing, we have that a ![]() φ(a)
φ(a) ![]() a by Lemma 6.1.2.
a by Lemma 6.1.2. ![]()
The next result follows from Lemma 6.1.4 (Exercise 1).
![]() LEMMA 6.1.5
LEMMA 6.1.5
Distinct initial segments of a well-ordered set are not order isomorphic.
The lemmas lead to the following theorem.
![]() THEOREM 6.1.6
THEOREM 6.1.6
If (A, ![]() ) and (B,
) and (B, ![]() ′) are well-ordered sets, there exists an order isomorphism such that exactly one of the following holds.
′) are well-ordered sets, there exists an order isomorphism such that exactly one of the following holds.
- A ≅ B.
- A is order isomorphic to a proper initial segment of B.
- B is order isomorphic to a proper initial segment of A.
PROOF
Let (A, ![]() ) and (B,
) and (B, ![]() ′) be well-ordered sets. Appealing to Lemma 6.1.5, if x ∈ A, there is at most one y ∈ B such that seg
′) be well-ordered sets. Appealing to Lemma 6.1.5, if x ∈ A, there is at most one y ∈ B such that seg![]() (A, x) ≅
(A, x) ≅ ![]() (B, y), so define the function
(B, y), so define the function
![]()
We have a number of facts to prove.
- Let y1, y2 ∈ ran(φ) such that y1 = y2. Take x1, x2 ∈ A such that

and

Then, we have
 (A, x1) ≅
(A, x1) ≅  (A, x2), and x1 = x2 by Lemma 6.1.5. Therefore, φ is one-to-one.
(A, x2), and x1 = x2 by Lemma 6.1.5. Therefore, φ is one-to-one. - Take x1, x2 ∈ dom(φ) and assume that x1
 x2. This implies that
x2. This implies that

Then, by definition of φ, we have

and

Hence,
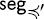 ,(B, φ(x1)) is order isomorphic to an initial segment S of
,(B, φ(x1)) is order isomorphic to an initial segment S of 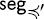 (B, φ(x2)) (Exercise 17). If S ≠
(B, φ(x2)) (Exercise 17). If S ≠ 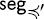 (B, φ(x1)), then B has two distinct isomorphic initial segments, contradicting Lemma 6.1.5. This implies that φ(x1)
(B, φ(x1)), then B has two distinct isomorphic initial segments, contradicting Lemma 6.1.5. This implies that φ(x1)  ′ φ(x2), so φ is order-preserving.
′ φ(x2), so φ is order-preserving. - Let x1, x2 ∈ A. Suppose that x1
 x2 and x2 ∈ dom(φ). This means that there exists y2 ∈ B such that
x2 and x2 ∈ dom(φ). This means that there exists y2 ∈ B such that

If x1 = x2, then x1 ∈ dom(φ), so assume that x1 ≠ x2. Since x1
 x2, we have that x1 ∈
x2, we have that x1 ∈  (A, x2). Because φ is order-preserving,
(A, x2). Because φ is order-preserving,
for some y1 ∈
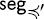 (B, y2) (Exercise 17). Therefore, (x1, y1) ∈ φ, so x1 ∈ dom(φ), proving that the domain of φ is an initial segment of A.
(B, y2) (Exercise 17). Therefore, (x1, y1) ∈ φ, so x1 ∈ dom(φ), proving that the domain of φ is an initial segment of A. - That the range of φ is an initial segment of B is proved like the previous case.
If φ is a surjection and dom(φ) = A, then φ is an order isomorphism A → B, else φ−1[B] is a proper initial segment of A. If φ is not a surjection, φ[A] is a proper initial segment of B. ![]()
Ordinals
Theorem 6.1.6 is a sort of trichotomy law for well-ordered sets. Two well-ordered sets look alike, or one has a copy of itself in the other. This suggests that we should be able to choose certain well-ordered sets to serve as representatives of all the different types of well-ordered sets. No two of the chosen sets should be order isomorphic, but it should be the case that every well-ordered set is order isomorphic to exactly one of them. That is, we should be able to classify all of the well-ordered sets. This will be our immediate goal and is the purpose behind the next definition.
![]() DEFINITION 6.1.7
DEFINITION 6.1.7
The set α is an ordinal number (or simply an ordinal) if (α, ⊆) is a well-ordered set and β = seg⊆(α, β) for all β ∈ α. For ordinals, define
![]()
Definition 6.1.7 implies that ω and every natural number is an ordinal because they are well-ordered by ⊆ and for all n ∈ ω {0},
![]()
and for all k ∈ n,
![]()
For example, 5 ∈ 7 and
![]()
We now prove a sequence of basic results about ordinals. The first is similar to Theorem 5.2.8, so its proof is left to Exercise 5.
![]() THEOREM 6.1.8
THEOREM 6.1.8
Ordinals are transitive sets.
![]() THEOREM 6.1.9
THEOREM 6.1.9
The elements of ordinals are transitive sets.
PROOF
Let α be an ordinal and β ∈ α. Take γ ∈ β and δ ∈ γ. Since α is transitive (Theorem 6.1.8), we have that γ ∈ α. Therefore, γ = seg(α, γ) and β = seg(α, β), so
![]()
which implies that β is transitive (Definition 5.2.7). ![]()
![]() THEOREM 6.1.10
THEOREM 6.1.10
Every element of an ordinal is an ordinal.
PROOF
Let α be an ordinal and β ∈ α. Notice that this implies that β is transitive (Theorem 6.1.9). Since β ⊆ α, we have that (β, ⊆) is a well-ordered set by a subset axiom (5.1.8) and Theorem 4.3.26. Now take δ ∈ β. Since δ ∈ α, we have that δ is transitive. Therefore, by Exercise 5.2.3,

From this, we conclude that δ = seg(β, δ). ![]()
Let α and β be ordinals. Then, α ⊂ β if and only if α ∈ β.
PROOF
If α ∈ β, then α ⊂ β because β is transitive (Theorem 6.1.8 and Exercise 5.2.3). Conversely, suppose that α ⊂ β. Let γ ∈ α and δ ⊂ γ with δ ∈ β. Since β is an ordinal, δ = seg(β, δ). Hence, δ = seg(γ, δ), which implies that δ ∈ γ because γ is an ordinal by Theorem 6.1.10. Therefore, δ ∈ α because α is transitive (Theorem 6.1.8). This shows that α is a proper initial segment of β with respect to ⊆ (Definition 5.6.1). From this, it follows by Lemma 5.6.3 that α = seg(β, ζ) for some ζ ∈ β. Hence, α ∈ β. ![]()
![]() THEOREM 6.1.12
THEOREM 6.1.12
Every ordinal is well-ordered by ∈.
The next theorem is an important part of the process of showing that the ordinals are the sets that classify all well-ordered sets according to their order types. It states that distinct ordinals are not order isomorphic with respect to ⊆.
![]() THEOREM 6.1.13
THEOREM 6.1.13
For all ordinals α and β, if (α, ⊆) ≅ (β, ⊆), then α = β.
PROOF
Let φ : α → β be an order isomorphism preserving ⊆. Define
![]()
Take δ ∈ α and assume that seg(α, δ) ⊆ A. Then,

The first equality follows because φ(δ) is an ordinal in β, the second follows because φ is an order isomorphism, and the fourth equation follows by the assumption. Therefore, by transfinite induction (Theorem 6.1.1), A = α, so φ is the identity map and α = β. ![]()
Because of Theorem 6.1.13, we are able to prove that there is a trichotomy law for the ordinals with respect to ⊆.
![]() THEOREM 6.1.14 [Trichotomy]
THEOREM 6.1.14 [Trichotomy]
For all ordinals α and β, exactly one of the following holds: α = β, α ⊂ β, or α ⊂ β.
Since (α, ⊆) and (β, ⊆) are well-ordered, by Theorem 6.1.6, exactly one of the following holds.
- α ≅ β, which implies that α = β by Theorem 6.1.13.
- There exists δ ∈ β such that α ≅ seg(β, δ). Since seg(β, δ) is an ordinal (Theorem 6.1.10), α = seg(β, δ), again by Theorem 6.1.13. Therefore, α ⊂ β.
- There exists γ ∈ α such that β ≅ seg(α, γ). As in the previous case, we have that β ⊂ α.

Because of Theorem 6.1.11, we can quickly conclude the following.
![]() COROLLARY 6.1.15
COROLLARY 6.1.15
For all ordinals α and β, exactly one of the following holds: α = β, α ∈ β, or α ∈ β.
In addition to the ordinals having a trichotomy law, the least upper bound with respect to ⊆ of a set of ordinals is also an ordinal (compare Example 4.3.14).
![]() THEOREM 6.1.16
THEOREM 6.1.16
If ![]() is a set of ordinals,
is a set of ordinals, ![]()
![]() is an ordinal.
is an ordinal.
PROOF
We show that ![]()
![]() satisfies the conditions of Definition 6.1.7. Since the elements of ordinals are ordinals,
satisfies the conditions of Definition 6.1.7. Since the elements of ordinals are ordinals, ![]()
![]() is a set of ordinals, and by Theorem 6.1.14, we see that (
is a set of ordinals, and by Theorem 6.1.14, we see that (![]()
![]() , ⊆) is a linearly ordered set. Let B ⊆
, ⊆) is a linearly ordered set. Let B ⊆ ![]()
![]() and take α ∈ B. We have two cases to consider.
and take α ∈ B. We have two cases to consider.
- Suppose α ∩ B = ∅. Let β ∈ B. Then, β ∉ α, so by Theorem 6.1.11 and Theorem 6.1.14, α ⊆ β. Hence, α is the least element of B.
- Let α ∩ B be nonempty. Since α is an ordinal, there exists an ordinal δ that is the least element of α ∩ B with respect to ⊆. Let β ∈ B. If β ⊂ α, then β ∈ α ∩ B, which implies that δ ⊆ β. Also, if α ⊆ β, then δ ⊂ β. Since these are the only two options (Theorem 6.1.14), this implies that δ is the least element of B.
We conclude that (![]()
![]() , ⊆) is a well-ordered set.
, ⊆) is a well-ordered set.
Next, let β ∈ ![]()
![]() . This means that there exists an ordinal α ∈ A such that β ∈ α. Since seg(
. This means that there exists an ordinal α ∈ A such that β ∈ α. Since seg(![]()
![]() , β) ⊆ β by definition, take δ ∈ β. Since α is transitive (Theorem 6.1.8), δ ∈ α. Therefore, δ ∈
, β) ⊆ β by definition, take δ ∈ β. Since α is transitive (Theorem 6.1.8), δ ∈ α. Therefore, δ ∈ ![]()
![]() , which implies that β ⊆ seg(
, which implies that β ⊆ seg(![]()
![]() , β).
, β). ![]()
Classification
Let α be an ordinal number. We check the two conditions of Definition 6.1.7 to show that α+ is an ordinal.
- Let B be a nonempty subset of α ∪ {α}. If B ∩ α ≠ ∅, then B has a least element with respect to ⊆ since (α, ⊆) is well-ordered. If B = {α}, then α is the least element of B.
- Let β ∈ α ∪ {α}. If β ∈ α, then β = seg(α, β) = seg(α+, β) because α is an ordinal number. Otherwise, β = α = seg(α+, α).
The ordinal α+ is called a successor ordinal because it has a predecessor. For example, every positive natural number is a successor ordinal.
Now assume that α ≠ ∅ and α is an ordinal that is not a successor.
- Let δ ∈ β ∈ α. Since α is transitive (Theorem 6.1.8), δ ∈ α. Thus, we conclude that
 {β : β ∈ α} ⊆ α.
{β : β ∈ α} ⊆ α. - Now take δ ∈ α. This implies that δ is an ordinal (Theorem 6.1.10), so δ ⊂ α by Theorem 6.1.11. Therefore, δ+ ⊆ α, so δ+ ⊂ α since α is not a successor. Thus, δ+ ∈ α, again by appealing to Theorem 6.1.11. Because δ ∈ δ+, we have that α ⊆
 {β : β ∈ α}.
{β : β ∈ α}.
We conclude that for every nonempty ordinal α that is not a successor,
![]()
Such an ordinal number is called a limit ordinal. For example, since every natural number is an ordinal, ω = ![]() {n : n ∈ ω} is a limit ordinal. Therefore, ω+, ω++, ω+++, ... are also ordinals, but they are successors.
{n : n ∈ ω} is a limit ordinal. Therefore, ω+, ω++, ω+++, ... are also ordinals, but they are successors.
All of this proves the following.
![]() THEOREM 6.1.17
THEOREM 6.1.17
A nonempty ordinal is either a successor or a limit ordinal.
Therefore, by Theorem 6.1.14 and Corollary 6.1.15, we can view the ordinals as sorted by ⊂ giving
![]()
and as sorted by ∈ giving
![]()
Characterizing every ordinal as being equal to 0, a successor ordinal, or a limit ordinal allows us to restate Theorem 6.1.1. The form of the theorem generalizes Theorem 5.4.1 to infinite ordinals. Its proof is left to Exercise 8.
![]() THEOREM 6.1.18 [Transfinite Induction 2]
THEOREM 6.1.18 [Transfinite Induction 2]
If α is an ordinal and A ⊆ α, then A = α if the following hold:
- 0 ∈ A.
- If β ∈ A, then β+ ∈ A.
- If β is a limit ordinal such that δ ∈ A for all δ ∈ β, then β ∈ A.
We use this second form of transfinite induction to prove the sought-after classification theorem for well-ordered sets.
![]() THEOREM 6.1.19
THEOREM 6.1.19
Let (A, ![]() ) be a well-ordered set. Then, (A,
) be a well-ordered set. Then, (A, ![]() ) ≅ (α, ⊆) for some ordinal α.
) ≅ (α, ⊆) for some ordinal α.
PROOF
Define
![]()
Let B = {y : ∃x [x ∈ A ∧ p(x, y)]}. By Theorem 6.1.13, p(x, y) defines a function, so by a replacement axiom (5.1.9), we conclude that B is a set. We have a number of items to prove.
Let D ⊆ B and D ≠ ∅. Let C = {a ∈ A : ∃α[α ∈ D ∧ p(a, α)]}. Observe that C is not empty. Therefore, there exists a least element m ∈ C with respect to ![]() . Take an ordinal δ0 ∈ D such that
. Take an ordinal δ0 ∈ D such that
![]()
Let δ ∈ D. This means that δ is an ordinal and
![]()
for some c ∈ C. Since m ![]() c, we have that
c, we have that
![]()
Hence, δ0 is isomorphic to a subset of δ, which implies that δ0 ⊆ δ (Theorem 6.1.13). We conclude that (B, ⊆) is a well-ordered set.
Let E = {β ∈ β : seg(B, β) = β}. Let seg(B, ![]() ) ⊆ E for
) ⊆ E for ![]() ∈ B.
∈ B.
- First, suppose that
 = γ+ for some ordinal γ. Then, seg(B, γ) = γ, so
= γ+ for some ordinal γ. Then, seg(B, γ) = γ, so

Also, γ+ ≅
 (A, a) for some a ∈ A. Let m be the greatest element of
(A, a) for some a ∈ A. Let m be the greatest element of  (A, a) (Exercise 9). This implies that γ ≅
(A, a) (Exercise 9). This implies that γ ≅  (A, a) {m}, so γ ∈ B. Hence,
(A, a) {m}, so γ ∈ B. Hence,
- Second, let
 =
=  {γ : γ ∈
{γ : γ ∈  }. This means that seg(B, γ) = γ for all γ ∈
}. This means that seg(B, γ) = γ for all γ ∈  . Therefore,
. Therefore,

and
 is again an element of E.
is again an element of E.
By transfinite induction (Theorem 6.1.18), E = B. This combined with (B, ⊆) being a well-ordered set means that B is an ordinal.
Define φ : A → B by φ(x) = y ⇔ p(x, y). Since φ is an order isomorphism (Exercise 10), B is an ordinal that is order isomorphic to (A, ![]() ), and because of Theorem 6.1.13, it is the only one.
), and because of Theorem 6.1.13, it is the only one. ![]()
For any well-ordered set (A, ![]() ), the unique ordinal α such that A ≅ α guaranteed by Theorem 6.1.19 is called the order type of A. Compare this definition with Definition 4.5.24. For example, the order type of ({2n : n > 5 ∧ n ∈
), the unique ordinal α such that A ≅ α guaranteed by Theorem 6.1.19 is called the order type of A. Compare this definition with Definition 4.5.24. For example, the order type of ({2n : n > 5 ∧ n ∈ ![]() }, ≤) is ω.
}, ≤) is ω.
Burali-Forti and Hartogs
Suppose ![]() = {0, 4, 6, 9}. Then,
= {0, 4, 6, 9}. Then, ![]()
![]() equals the ordinal 9, which is the least upper bound of
equals the ordinal 9, which is the least upper bound of ![]() . Also, assume that
. Also, assume that ![]() = {5, 100, ω}. Then,
= {5, 100, ω}. Then, ![]()
![]() = ω. However, the least upper bound of
= ω. However, the least upper bound of ![]() = {n ∈ ω: ∃k(k ∈ ω ∧ n = 2k)} is not an element of ω. Instead, the least upper bound of
= {n ∈ ω: ∃k(k ∈ ω ∧ n = 2k)} is not an element of ω. Instead, the least upper bound of ![]() is
is ![]()
![]() = ω. Moreover, notice that
= ω. Moreover, notice that ![]() ⊆ 10,
⊆ 10, ![]() ⊆ ω+, and
⊆ ω+, and ![]() ⊆ ω+. We generalize this to the next theorem.
⊆ ω+. We generalize this to the next theorem.
![]() THEOREM 6.1.20
THEOREM 6.1.20
If ![]() is a set of ordinals, there exists an ordinal α such that
is a set of ordinals, there exists an ordinal α such that ![]() ⊆ α.
⊆ α.
PROOF
Take ![]() to be a set of ordinals and let α ∈
to be a set of ordinals and let α ∈ ![]() . Then, α ⊆
. Then, α ⊆ ![]()
![]() and
and ![]()
![]() is an ordinal by Theorem 6.1.16. If α ⊂
is an ordinal by Theorem 6.1.16. If α ⊂ ![]()
![]() , then α ∈
, then α ∈ ![]()
![]() by Theorem 6.1.11. If α =
by Theorem 6.1.11. If α = ![]()
![]() , then α ∈ {
, then α ∈ {![]()
![]() }. Thus,
}. Thus, ![]() ⊆ (
⊆ (![]()
![]() )+.
)+. ![]()
Although every set of ordinals is a subset of an ordinal, there is no set of all ordinals, otherwise a contradiction would arise, as was first discovered by Cesare Burali-Forti (1897). This is why when we noted that ⊆ gives the ordinals a linear order, we did not claim that ⊆ is used to define a linearly ordered set containing all ordinals.
![]() THEOREM 6.1.21 [Burali-Forti]
THEOREM 6.1.21 [Burali-Forti]
There is no set that has every ordinal as an element.
PROOF
Suppose ![]() = {α : α is an ordinal} is a set. This implies that
= {α : α is an ordinal} is a set. This implies that ![]()
![]() is an ordinal by Theorem 6.1.16. However, for every α ∈
is an ordinal by Theorem 6.1.16. However, for every α ∈ ![]() , we have that α ∈ α+ ∈ A, showing that
, we have that α ∈ α+ ∈ A, showing that ![]() ⊆
⊆ ![]()
![]() . Since
. Since ![]()
![]() ∈
∈ ![]() , we also have
, we also have ![]()
![]() ∈
∈ ![]()
![]() , which contradicts Theorem 5.1.16.
, which contradicts Theorem 5.1.16. ![]()
The Burali-Forti theorem places a limit on what can be done with ordinals. One such example is a theorem of Friedrich Hartogs.
![]() THEOREM 6.1.22 [Hartogs]
THEOREM 6.1.22 [Hartogs]
For every set A, there exists an ordinal α such that there are no injections of α into A.
PROOF
Let A be a set. Define
![]()
Notice that for every α ∈ ![]() , there exists a bijection φα such that
, there exists a bijection φα such that
![]()
for some Bα ⊆ A. Define a well-order ![]() α on Bα by
α on Bα by
![]()
Then, φα is an order isomorphism preserving ⊆ with ![]() α. Next, define
α. Next, define
![]()
Since ![]() ⊆ P(A) × P(A × A), we have that
⊆ P(A) × P(A × A), we have that ![]() is a set by the Power Set Axiom (5.1.7) and a Subset Axiom (5.1.8). Let
is a set by the Power Set Axiom (5.1.7) and a Subset Axiom (5.1.8). Let
![]()
Suppose that p((B, ≤), α1) and p((B, ≤), α2). By Theorem 6.1.13, we have that α1 = α2, so p(x, y) defines a function with domain ![]() . Moreover,
. Moreover, ![]() is a subset of the range of this function because p((Bα,
is a subset of the range of this function because p((Bα, ![]() α), α) due to φα. Therefore,
α), α) due to φα. Therefore, ![]() is a set by a replacement axiom (5.1.9) and a subset axiom, and
is a set by a replacement axiom (5.1.9) and a subset axiom, and ![]() cannot contain all ordinals by the Burali-Forti theorem (6.1.21).
cannot contain all ordinals by the Burali-Forti theorem (6.1.21). ![]()
Transfinite Recursion
Theorem 6.1.19 only applies to well-ordered sets, so, for example, it does not apply to (![]() , ≤) or (
, ≤) or (![]() , ≤). However, if we change the order on
, ≤). However, if we change the order on ![]() from the standard ≤ to
from the standard ≤ to ![]() defined so as to put
defined so as to put ![]() into this order,
into this order,
![]()
then (![]() ,
, ![]() ) is a well-ordered set of order type ω. That this can be done even with sets like
) is a well-ordered set of order type ω. That this can be done even with sets like ![]() is due to a theorem first proved by Zermelo, which is often called the well-ordering theorem. Its proof requires some preliminary work.
is due to a theorem first proved by Zermelo, which is often called the well-ordering theorem. Its proof requires some preliminary work.
Let A be a set and α an ordinal. By Definition 4.4.13, αA is the set of all functions α → A. Along these lines, define
![]()
![]()
and
![]()
Also, f, g ∈ <ω![]() , but the identity function on ω is not an element of <ω
, but the identity function on ω is not an element of <ω![]() because its domain is ω. We should also note that for any set A,
because its domain is ω. We should also note that for any set A,
![]()
We use this notation in the following generalization of recursion to infinite ordinals.
![]() THEOREM 6.1.23 [Transfinite Recursion]
THEOREM 6.1.23 [Transfinite Recursion]
Let α be an ordinal. For every function ψ : <αA → A, there exists a unique function φ : α → A such that for every β ∈ α,
![]()
PROOF
To prove uniqueness, in addition to φ, let φ′ be a function α → A such that for all β ∈ α,
![]()
Define B = {β ∈ α : φ(β) = φ′(β)}. We use transfinite induction (Theorem 6.1.1) to show that B = α. Suppose seg(α, δ) ⊆ B with δ ∈ α. That is,
![]()
This implies that φ ![]() δ = φ′
δ = φ′ ![]() δ. Therefore,
δ. Therefore,
![]()
so δ ∈ B, and we conclude that φ = φ′.
We prove existence indirectly. Suppose that α is the least ordinal (Exercise 2) such that

Since the theorem is trivially true for α = 0, we have two cases to consider.
- Let α = δ+ for some ordinal δ. By minimality of α, we have a function φδ : δ → A such that for all β ∈ δ,

Extend φδ to
 δ : α → A by defining
δ : α → A by defining  δ (δ) = ψ0(φδ), so
δ (δ) = ψ0(φδ), so
This contradicts the minimality of α.
- Let α be a limit ordinal. For each δ ∈ α, there exists a unique φδ : δ → A such that

Notice that δ ∈ γ implies that φγ is an extension of φδ, otherwise φγ
 δ would have the property
δ would have the property
for all β ∈ δ yet φδ ≠ φγ
 δ. This contradicts the uniqueness of φδ. Therefore, {φδ : δ ∈ α} is a chain, so, as in Exercise 4.4.13, define the function φ : α → A by
δ. This contradicts the uniqueness of φδ. Therefore, {φδ : δ ∈ α} is a chain, so, as in Exercise 4.4.13, define the function φ : α → A by
To check that φ is the function given by the theorem, take β ∈ α. Since α is a limit ordinal, β+ ∈ α and

again contradicting the minimality of α.

Theorem 6.1.23 has a corollary that can be viewed as an extension of Theorem 5.2.14. Its proof is left to Exercise 18.
![]() COROLLARY 6.1.24
COROLLARY 6.1.24
Let A be a set and a ∈ A. For every ordinal α, if ψ is a function A → A, there exists a unique function φ : α → A such that
- φ(0) = a,
- φ(β+) = ψ(φ(α)) for all β ∈ α,
- φ(γ) =
 {φ(β) : β ∈ γ} for all limit ordinals γ ∈ α.
{φ(β) : β ∈ γ} for all limit ordinals γ ∈ α.
We are now ready to prove that every set can be well-ordered. The following theorem is equivalent to the axiom of choice (Exercise 20).
![]() THEOREM 6.1.25 [Zermelo]
THEOREM 6.1.25 [Zermelo]
For any set A, there exists a relation R on A such that (A, R) is a well-ordered set.
Take a set A and let ξ : P(A) → A be a choice function (Corollary 5.1.11). By Theorem 6.1.22, there is an ordinal α such that no injection α → A exists. Hence, we have φ : A → α that is one-to-one. Let B ⊆ A. Since every element of α is an ordinal, there exists an ordinal δ ⊆ α such that φ[B] = δ (Theorem 6.1.16). Define
![]()
Then, ![]() ∈ <α A. Let
∈ <α A. Let
![]()
and define
![]()
by h1(![]() ) = B. Also, define
) = B. Also, define
![]()
by h2 = ξ ![]() h1. Since P ⊆ <α A, extend h2 to some
h1. Since P ⊆ <α A, extend h2 to some
![]()
such that h ![]() P = h2. By transfinite recursion (Theorem 6.1.23), there exists a function f : α → A such that for all β ∈ α,
P = h2. By transfinite recursion (Theorem 6.1.23), there exists a function f : α → A such that for all β ∈ α,
![]()
Define Φ so that for all β ∈ α,

Notice that A ∉ A by Theorem 5.1.16. Let β0 be the least ordinal such that Φ(β0) = A. Then, Φ ![]() β0 is a bijection β0 → A [Exercise 19(a)]. Lastly, define the relation R on A by
β0 is a bijection β0 → A [Exercise 19(a)]. Lastly, define the relation R on A by
![]()
for all a, b ∈ A. Since ⊆ is a well-order on β0, R is a well-order on A [Exercise 19(b)]. ![]()
Exercises
1. Prove Lemma 6.1.5.
2. Does seg(![]() A, β) =
A, β) = ![]() α∈A seg(α, β) for all sets of ordinals A with β ∈ A? Explain.
α∈A seg(α, β) for all sets of ordinals A with β ∈ A? Explain.
3. Explain why {0, 2, 3, 4, 5} is not an ordinal.
4. Prove that ∅ is an element of every ordinal.
5. Prove that an ordinal is a transitive set (Theorem 6.1.8).
6. Let A be a set of ordinals. Prove.
(a) ![]() A is an ordinal.
A is an ordinal.
(b) A has a least element with respect to ⊆.
7. Let B be a nonempty subset of the ordinal α. Prove that there exists β ∈ B such that β and B are disjoint.
8. Prove Theorem 6.1.18.
9. From the proof of Theorem 6.1.19, prove that ![]() (A, a) has a greatest element.
(A, a) has a greatest element.
10. Prove that A is order isomorphic to B in the proof of Theorem 6.1.19.
11. The proof of Theorem 6.1.19 contains many isomorphisms without explicitly identifying the isomorphism. Find these functions and prove that they are order isomorphisms.
12. Let R be a well-ordering on A and suppose that A has no greatest element. Show the the order type of (A, R) is a limit ordinal.
13. Find a transitive set that is not an ordinal.
14. Theorem 6.1.21 comes from the Burali-Forti paradox. Like Russell's paradox (page 225), it arises when any formula is allowed to define a set. In this case, suppose that A = {α : α is an ordinal} and assume that A is a set. Prove that A is an ordinal that must include all ordinals as its elements.
15. Prove that there exists a function F such that F(n) is the nth Fibonacci number.
16. Prove that for every function h : <ω A → A, there is a unique function f : ω → A such that for all n ∈ ω, f(n) = h(f ![]() n).
n).
17. Let (A, ![]() ) and (B,
) and (B, ![]() ′) be well-ordered sets and φ : A → B be an order-preserving surjection. Prove that for every a ∈ A, there exists b ∈ B such that
′) be well-ordered sets and φ : A → B be an order-preserving surjection. Prove that for every a ∈ A, there exists b ∈ B such that
![]()
18. Prove Corollary 6.1.24.
19. Prove the following from the proof of Zermelo's theorem (6.1.25).
(a) Φ ![]() β0 is a bijection.
β0 is a bijection.
(b) R is a well-order on A.
20. Prove that Theorem 6.1.25 implies Axiom 5.1.10.
21. Prove that Zorn's lemma (5.1.13) implies Theorem 6.1.25 without using the axiom of choice.
6.2 EQUINUMEROSITY
How can we determine whether two sets are of the same size? One possibility is to count their elements. What happens, however, if the sets are infinite? We need another method. Suppose A = {12, 47, 84} and B = {17, 101, 200}. We can see that these two sets are the same size without counting. Define a function f : A → B so that f(12) = 17, f(47) = 101, and f(84) = 200. This function is a bijection. Since each element is paired with exactly one element of the opposite set, A and B must be the same size. This is the motivation behind our first definition.
![]() DEFINITION 6.2.1
DEFINITION 6.2.1
The sets A and B are equinumerous (written as A ≈ B) if there exists a bijection φ : A → B. If A and B are not equinumerous, write A ![]() B.
B.
![]() EXAMPLE 6.2.2
EXAMPLE 6.2.2
Take n ∈ ![]() such that n ≠ 0 and define
such that n ≠ 0 and define
![]()
We prove that ![]() ≈ n
≈ n![]() . To show this, we must find a bijection f :
. To show this, we must find a bijection f : ![]() → n
→ n![]() . Define f(k) = nk.
. Define f(k) = nk.
- Assume x1, x2 ∈
 , and let f(x1) = f(x2). Then nx1 = nx2, which yields x1 = x2 since n ≠ 0. Thus, f is one-to-one.
, and let f(x1) = f(x2). Then nx1 = nx2, which yields x1 = x2 since n ≠ 0. Thus, f is one-to-one. - Let y ∈ n
 . This means that y = nk for some k ∈
. This means that y = nk for some k ∈  , so y = f(k). This shows that f is onto and, hence, a bijection.
, so y = f(k). This shows that f is onto and, hence, a bijection.
![]() EXAMPLE 6.2.3
EXAMPLE 6.2.3
To see ![]() + ≈
+ ≈ ![]() , define a one-to-one correspondence so that each even integer is paired with a nonnegative integer and every odd integer is paired with a negative integer (Figure 6.1). Let g :
, define a one-to-one correspondence so that each even integer is paired with a nonnegative integer and every odd integer is paired with a negative integer (Figure 6.1). Let g : ![]() + →
+ → ![]() be defined by
be defined by

Notice that g(4) = 1 since 4 = 2(2), and g(5) = −3 because 5 = 2(3) − 1. This function is a bijection (Exercise 12).
Equinumerosity plays a role similar to that of equality of integers. This is seen in the next theorem. In fact, the theorem resembles Definition 4.2.4. Despite this, it does not demonstrate the existence of an equivalence relation. This is because an equivalence relation is a relation on a set, so, to define an equivalence relation, the next result would require a set of all sets, contradicting Corollary 5.1.17.
![]() THEOREM 6.2.4
THEOREM 6.2.4
Let A, B, and C be sets.
- A ≈ A. (Reflexive)
- If A ≈ B, then B ≈ A. (Symmetric)
- If A ≈ B and B ≈ C, then A ≈ C. (Transitive)
PROOF
- A ≈ A since the identity map is a bijection.
- Assume A ≈ B. Then, there exists a bijection φ : A → B. Therefore, φ−1 is a bijection. Hence, B ≈ A.
- By Theorem 4.5.23, the composition of two bijections is a bijection. Therefore, A ≈ B and B ≈ C implies A ≈ C.

The symmetric property allows us to conclude that n![]() ≈
≈ ![]() and
and ![]() ≈
≈ ![]() + from Examples 6.2.2 and 6.2.3. The transitivity part of Theorem 6.2.4 allows us to conclude from this that n
+ from Examples 6.2.2 and 6.2.3. The transitivity part of Theorem 6.2.4 allows us to conclude from this that n![]() ≈
≈ ![]() +.
+.
![]() EXAMPLE 6.2.5
EXAMPLE 6.2.5
Show (0,1) ≈ ![]() . We do this in two parts. First, let f : (0, 1) → (−π/2, π/2) be defined by f(x) = πx − π/2. This function is a one-to-one correspondence since its graph is a nonvertical, nonhorizontal line (Exercise 4.5.4). Second, define g : (−π/2, π/2) →
. We do this in two parts. First, let f : (0, 1) → (−π/2, π/2) be defined by f(x) = πx − π/2. This function is a one-to-one correspondence since its graph is a nonvertical, nonhorizontal line (Exercise 4.5.4). Second, define g : (−π/2, π/2) → ![]() to be the function g(x) = tan x. From trigonometry, we know that tangent is a bijection on (−π/2, π/2). Hence,
to be the function g(x) = tan x. From trigonometry, we know that tangent is a bijection on (−π/2, π/2). Hence,
![]()
and
![]()
Therefore, (0, 1) ≈ ![]() by Theorem 6.2.4.
by Theorem 6.2.4.
Order
If ≈ resembles equality, the following resembles the ≤ relation.
![]() DEFINITION 6.2.6
DEFINITION 6.2.6
The set B dominates the set A (written as A ![]() B) if there exists an injection φ : A → B. If B does not dominate A, write A
B) if there exists an injection φ : A → B. If B does not dominate A, write A ![]() B. Furthermore, define A
B. Furthermore, define A ![]() B to mean A
B to mean A ![]() B but A
B but A ![]() B.
B.
![]() EXAMPLE 6.2.7
EXAMPLE 6.2.7
If A ⊆ B, then A ![]() B. This is proved using the inclusion map (Exercise 4.4.26). For instance, let ι :
B. This is proved using the inclusion map (Exercise 4.4.26). For instance, let ι : ![]() + →
+ → ![]() be the inclusion map and f :
be the inclusion map and f : ![]() →
→ ![]() be defined as
be defined as
![]()
Then, ![]() +
+ ![]()
![]() because f
because f ![]() ι is an injection. Similarly,
ι is an injection. Similarly, ![]()
![]()
![]() . However, A ⊂ B does not imply A
. However, A ⊂ B does not imply A ![]() B. As an example, n
B. As an example, n![]() ≈
≈ ![]() , but n
, but n![]() ⊂
⊂ ![]() when n ≠ ±1.
when n ≠ ±1.
Another method used to prove that A ![]() B is to find a surjection B → A. Consider the sets A = {1, 2} and B = {3, 4, 5}. Define f : B → A to be the surjection given by f(3) = 1, f(4) = 2, and f(5) = 2. This is the inverse of the relation R in Figure 4.1. To show that B dominates A, we must find an injection A → B. To do this, modify f−1 by deleting (2, 4) and call the resulting function g. Observe that g(1) = 3 and g(2) = 5, which is an injection, so A
B is to find a surjection B → A. Consider the sets A = {1, 2} and B = {3, 4, 5}. Define f : B → A to be the surjection given by f(3) = 1, f(4) = 2, and f(5) = 2. This is the inverse of the relation R in Figure 4.1. To show that B dominates A, we must find an injection A → B. To do this, modify f−1 by deleting (2, 4) and call the resulting function g. Observe that g(1) = 3 and g(2) = 5, which is an injection, so A ![]() B.
B.
![]() THEOREM 6.2.8
THEOREM 6.2.8
If there exists a surjection φ : A → B, then B ![]() A.
A.
PROOF
Let φ : A → B be onto. Define a relation R ⊂ B × A by
![]()
Since φ is onto,
![]()
Corollary 5.1.11 yields a function f so that dom(f) = dom(R) and f ⊆ R. We claim that f is one-to-one. Indeed, let b1, b2 ∈ B. Assume that we have f(b1) = f(b2). Let a1 = f(b1) and a2 = f(b2) where a1, a2 ∈ A. This means a1 = a2. Also, φ(a1) = b1 and φ(a2) = b2 because f ⊆ R. Since φ is a function, b1 = b2. ![]()
![]() EXAMPLE 6.2.9
EXAMPLE 6.2.9
Let R be an equivalence relation on a set A. The map φ : A → A/R defined by φ(a) = [a]R is a surjection. Therefore, A/R ![]() A.
A.
We know that ![]() +
+ ![]()
![]() by Example 6.2.7. We can also prove this by using the function f :
by Example 6.2.7. We can also prove this by using the function f : ![]() →
→ ![]() + defined by f(x) = |
+ defined by f(x) = |![]() x
x![]() | + 1 and appealing to Theorem 6.2.8.
| + 1 and appealing to Theorem 6.2.8.
The next theorem states that ![]() closely resembles an antisymmetric relation (Definition 4.3.1). Cantor was the first to publish a statement of it (1888). He proved it using the axiom of choice, but it was later shown that it can be proved in ZF. It was proved independently by Ernst Schröder and Felix Bernstein around 1890. The proof given here follows that of Julius König (1906).
closely resembles an antisymmetric relation (Definition 4.3.1). Cantor was the first to publish a statement of it (1888). He proved it using the axiom of choice, but it was later shown that it can be proved in ZF. It was proved independently by Ernst Schröder and Felix Bernstein around 1890. The proof given here follows that of Julius König (1906).
![]() THEOREM 6.2.11 [Cantor–Schröder–Bernstein]
THEOREM 6.2.11 [Cantor–Schröder–Bernstein]
If A ![]() B and B
B and B ![]() A, then A ≈ B.
A, then A ≈ B.
PROOF
Let f : A → B and g : B → A be injections. To prove that A is equinumerous to B, we define a one-to-one correspondence h : A → B. To do this, we recursively define two sequences of sets by first letting
![]()
and
![]()
Then, for n ∈ ω,
![]()
and
![]()
This is illustrated in Figure 6.2. Note that both {Cn : n ∈ ω} and {Dn : n ∈ ω} are pairwise disjoint because f and g are one-to-one (Exercise 11). Define h by

We show that h is the desired function.
- Let x1, x2 ∈ A such that x1 ≠ x2. Since both f and g are one-to-one, we only need to check the case when x1 ∈ Ck for some k ∈ ω and x2 ∉ Cn for all n ∈ ω. Then, f(x1) ∈ Dk but g−l(x2) ∉ Dk, so f(x1) ≠ g−1 (x2). That is, h(x1) ≠ h(x2).
- Take y ∈ B. If y ∈ Dk for some k ∈ ω, then y = f(x) for some x ∈ Ck. That is, y = h(x). Now suppose y ∉
 n∈ ω Dn. Clearly, g(y) ∉ C0. If g(y) ∈ Ck for some k > 0, then y ∈ Dk−1, a contradiction. Hence, g(y) = x for some x ∈ ran(g)
n∈ ω Dn. Clearly, g(y) ∉ C0. If g(y) ∈ Ck for some k > 0, then y ∈ Dk−1, a contradiction. Hence, g(y) = x for some x ∈ ran(g)  n∈ω Cn. This implies that we have h(x) = g−1(x) = y.
n∈ω Cn. This implies that we have h(x) = g−1(x) = y.
Figure 6.2 The Cantor–Schröder–Bernstein theorem.
Because (0, 1) ⊆ [0, 1], we have that (0, 1) ![]() [0, 1], and because the function f : [0, 1] → (0, 1) defined by
[0, 1], and because the function f : [0, 1] → (0, 1) defined by
![]()
is an injection, we have that [0, 1] ![]() (0, 1), so we conclude by the Cantor–Schröder–Bernstein theorem (6.2.11) that (0, 1) ≈ [0, 1].
(0, 1), so we conclude by the Cantor–Schröder–Bernstein theorem (6.2.11) that (0, 1) ≈ [0, 1].
Diagonalization
The strict inequality A ![]() B is sometimes difficult to prove because we must show that there does not exist a bijection from A onto B. The next method was developed by Cantor (1891) to accomplish this for infinite sets. It is called diagonalization.
B is sometimes difficult to prove because we must show that there does not exist a bijection from A onto B. The next method was developed by Cantor (1891) to accomplish this for infinite sets. It is called diagonalization.
Let M be the set of all functions f : ω → {m, w}, where m ≠ w. To show that ω ![]() M, we prove two facts:
M, we prove two facts:
- There exists an injection ω → M.
- There is no one-to-one correspondence between ω and M.
Cantor's method does both of these at once. Let φ : ω → M be a function. Writing the functions of the range of φ as infinite tuples, let
![]()
where aij ∈ {m, w} for all i, j ∈ ω. For example,
![]()
Now, write the functions in order:

From this, a function f ∈ M that is not in the list can be found by identifying the elements on the diagonal and defining f(n) to be the opposite of ann. In other words, define for all i ∈ ω,

and f(n) = bn is an element of M not in the list because for all n ∈ ω,
![]()
Since the function φ mapping ω to M is arbitrary, there are injections ω → M but none of them are onto. Therefore,
![]()
Furthermore, note that the elements of [0, 1] can be uniquely represented as binary numbers of the form
![]()
where ai ∈ {0, 1} for each i ∈ ω. For example
![]()
and
![]()
Therefore,
![]()
Hence, we can conclude like Cantor that since [0, 1] ≈ ![]() (Examples 6.2.5 and 6.2.12),
(Examples 6.2.5 and 6.2.12),
![]()
Cantor's diagonalization argument can be generalized, but we first need a definition. Let A be a set and B ⊆ A. The function
![]()
is called a characteristic function and is defined by

For example, if A = ![]() and B = {0, 1, 3, 5}, then χB(1) = 1 but χB(2) = 0. Moreover, for every set A,
and B = {0, 1, 3, 5}, then χB(1) = 1 but χB(2) = 0. Moreover, for every set A,
![]()
The characteristic function plays an important role in the proof of the next theorem.
![]() THEOREM 6.2.13
THEOREM 6.2.13
If A is a set, A ![]() A2.
A2.
Since the function ψ : A → A2 defined by
![]()
is an injection, A2 dominates A. To show that A is not equinumerous with A2, we show that there is no surjection A → A2. Let φ : A → A2 be a function, and for all a ∈ A, write φ(a) = χBa for some Ba ⊆ A. Define χ so that

Therefore, χ ∉ ran(φ) because χBa (a) ≠ χ(a) for all a ∈ A. However, χ ∈ A2. To prove this, define
![]()
We conclude that χ(a) = χB(a) because if χBa (a) = 0, then a ∈ B, so χ(a) = 1 and χB(a) = 1, but if χBa(a) = 1, then a ∉ B, so χ(a) = 0 and χB(a) = 0. Therefore, χ = χB, and φ is not onto. ![]()
By Exercise 14,
![]()
This result combined with Theorem 6.2.13 quickly yield the following.
![]() COROLLARY 6.2.14
COROLLARY 6.2.14
If A is a set, A ![]() P(A).
P(A).
From the theorem, we conclude that there exists a sequence of sets
![]()
Thus, there are larger and larger magnitudes of infinity.
Exercises
1. Given χB : ![]() → {0, 1} with B = {2, 5, 19, 23}, find
→ {0, 1} with B = {2, 5, 19, 23}, find
(a) χB (1)
(b) χB (2)
(c) χB(−10)
(d) χB (19)
2. Find a surjection φ : ω × ω → ω showing that ω ![]() ω × ω.
ω × ω.
3. Prove the given equations.
(a) χA∪B = χA + χB − χAχB
(b) χA∩B = χAχB
4. Prove that there exists a bijection between the given pairs of sets.
(b) [−π/2, π/2] and [−1, 1]
(c) (0, ∞) and ![]()
(d) ω and ![]()
(e) ![]() + and
+ and ![]() −
−
(f) {(x, 0) : x ∈ ![]() } and
} and ![]()
(g) ![]() and
and ![]() ×
× ![]()
(h) {(x, y) ∈ ![]() ×
× ![]() : y = 2x + 4} and
: y = 2x + 4} and ![]()
5. Let a < b and c < d, where a, b, c, d ∈ ![]() . Prove.
. Prove.
(a) (a, b) ≈ (c, d)
(b) [a, b] ≈ [c, d]
(c) (a, b) ≈ [c, d]
(d) (a, b) ≈ (c, d]
6. Prove ![]() ≈
≈ ![]() .
.
7. Let A, B, C, and D be nonempty sets. Prove.
(a) ![]()
![]()
![]() −
−
(b) A ∩ B ![]() P(A)
P(A)
(c) A ![]() A × B
A × B
(d) [0, 2] ![]() [5, 7]
[5, 7]
(e) A ∩ B ![]() A
A
(f) AB ![]() A × B
A × B
(g) A × {0} ![]() (A ∪ B) × {1}
(A ∪ B) × {1}
(h) A × B × C ![]() A × B × C × D
A × B × C × D
(i) A B ![]() C × A
C × A
8. Prove.
(a) If A ![]() B and B ≈ C, then A
B and B ≈ C, then A ![]() C.
C.
(b) If A ≈ B and B ![]() C, then A
C, then A ![]() C.
C.
(c) If A ![]() B and B
B and B ![]() C, then A
C, then A ![]() C.
C.
(d) If A ![]() B and C
B and C ![]() D, then AC
D, then AC ![]() BD.
BD.
(e) If A ≈ B, then P(A) ≈ P(B).
(f) If A ≈ B and C ≈ D, then A × C ≈ B × D.
(g) If A ≈ B, a ∈ A, and b ∈ B, then A {a} ≈ B {b}.
(h) If A B ≈ B A, then A ≈ B.
(i) If A ⊆ B and A ≈ A ∪ C, then B ≈ A ∪ B ∪ C.
(j) If C ⊆ A, B ⊆ D, and A ∪ B ≈ B, then C ∪ D ≈ D.
9. Given the function φ : A → B, prove that φ ≈ A and φ ![]() ran(φ).
ran(φ).
10. Without appealing to the Cantor–Schröder–Bernstein theorem (6.2.11), prove that (0, 1) ≈ [0, 1].
11. Prove that the sets {Cn : n ∈ ω} and {Dn : n ∈ ω} from the proof of Theorem 6.2.11 are pairwise disjoint.
12. Show that g is a bijection, where g : ![]() + →
+ → ![]() is defined by
is defined by

13. Let A be an infinite set and {a1, a2, ... } be a set of distinct elements from A. Prove that A → A {a1} is a bijection, where

14. For any set A, prove that P(A) ≈ A2.
15. Prove that if f : A → B is a surjection, there exists a function g : B → A such that f ![]() g = IB.
g = IB.
16. Use the power set to prove that there is no set of all sets.
6.3 CARDINAL NUMBERS
Let A be a set. Define
![]()
By Zermelo's theorem (6.1.25), A can be well-ordered, so by Theorem 6.1.19, A is order isomorphic to some ordinal, so B is nonempty. Moreover, B is subset of an ordinal (Theorem 6.1.20). Therefore, (B, ⊆) has a least element, which has the property that it is not equinumerous to any of its elements. This allows us to define the second of our new types of number (page 283). This type will be used to denote the size of a set.
![]() DEFINITION 6.3.1
DEFINITION 6.3.1
An ordinal κ is a cardinal number (or simply a cardinal) if α ![]() κ for every α ∈ κ.
κ for every α ∈ κ.
Observe that every infinite cardinal is a limit ordinal. This is because α ≈ α+ for every infinite ordinal α. However, a limit ordinal might not be a cardinal.
Let κ and λ be cardinals. Suppose that A ≈ κ and A ≈ λ. By Theorem 6.2.4, we have that κ ≈ λ. If κ ∈ λ or λ ∈ κ, this would contradict the definition of a cardinal number. Therefore, κ = λ (Corollary 6.1.15), and we conclude that every set is equinumerous to exactly one cardinal.
The cardinality of a set A is denoted by |A| and defined as the unique cardinal equinumerous to A.
Observe that the cardinality of a cardinal κ is κ.
![]() EXAMPLE 6.3.3
EXAMPLE 6.3.3
Let ![]() be a set of cardinals. By Theorem 6.1.16, we know that
be a set of cardinals. By Theorem 6.1.16, we know that ![]()
![]() is an ordinal. Now we show that it is also a cardinal. Suppose that α is an ordinal such that α ≈
is an ordinal. Now we show that it is also a cardinal. Suppose that α is an ordinal such that α ≈ ![]()
![]() . By Definition 6.3.1, we must show that
. By Definition 6.3.1, we must show that ![]()
![]() ⊆ α. Suppose there exists an ordinal β ∈
⊆ α. Suppose there exists an ordinal β ∈ ![]()
![]() such that β ∉ α. This means that there exists a cardinal κ ∈
such that β ∉ α. This means that there exists a cardinal κ ∈ ![]() such that β ∈ κ. This is impossible because
such that β ∈ κ. This is impossible because
![]()
Finite Sets
Intuitively, we know what a finite set is. Both of the sets A = {0, 2, 3, 5, 8, 10} and B = {n ∈ ![]() : (n − 1)(n + 3) = 0} are examples because we can count all of their elements and find that there is only one ordinal equinumerous to A and only one ordinal equinumerous to B. That is, |A| = 6 and |B| = 2. This suggests the following definition.
: (n − 1)(n + 3) = 0} are examples because we can count all of their elements and find that there is only one ordinal equinumerous to A and only one ordinal equinumerous to B. That is, |A| = 6 and |B| = 2. This suggests the following definition.
![]() DEFINITION 6.3.4
DEFINITION 6.3.4
For every set A, if there exists n ∈ ω such that A ≈ n, then A is finite. If A is not finite, it is infinite.
As we will see, finite sets are fundamentally different from infinite sets. There are properties that finite sets have in addition to the number of their elements that infinite sets do not have. Let us consider some of those properties of finite sets.
![]() LEMMA 6.3.5
LEMMA 6.3.5
Let n be a positive natural number. If y ∈ n, then n {y} ≈ n−.
PROOF
We proceed by mathematical induction.
- When n = 1, it must be the case that y = 0, so n {y} = 0 = 1−.
- Take y ∈ n + 1. If y = n, then (n + 1) {n} = n, so suppose that y < n. By induction, there exists a bijection g : n {y} → n−. Then, define f : (n + 1) {y} → n by f(m) = g(m) for all m < n and f(n) = n. The function f is a bijection (Exercise 3).

Lemma 6.3.5 is used to prove a characteristic property of finite cardinals.
No natural number is equinumerous to a proper subset of itself.
PROOF
Let n ∈ ω be minimal such that there exists A ⊂ n and n ≈ A. Since ∅ has no proper subsets and the only proper subset of 1 is 0, we can assume that n ≥ 2. Let f : A → n be a bijection and x ∈ A and y ∈ n A such that f(x) = y. We check the following.
- Let a ∈ A {x}. If f(a) = y, then we contradict the hypothesis that f is one-to-one because f(x) = y and x ≠ a. Thus, f(a) ∈ n {y}.
- Take b ∈ n {y}. Since f is a surjection, there exists a ∈ A such that f(a) = b. If a = x, then {b, y} ⊆ [x]f (Definition 4.2.7), which is impossible because f is a function. Thus, a ∈ A {x}, and we conclude that f
 (A {x}) is onto n {y}.
(A {x}) is onto n {y}. - Since the restriction of a one-to-one function is one-to-one, f
 (A {x}) is one-to-one.
(A {x}) is one-to-one.
Hence, f0 = f ![]() (A {x}) is a bijection with range n {y}. We have two cases to consider.
(A {x}) is a bijection with range n {y}. We have two cases to consider.
- Suppose n− ∉ A. This implies that A {x} ⊆ n−. Since x ∈ A, we have that x ≠ n−, so x ∈ n−. Thus, A {x} ⊂ n−. By Lemma 6.3.5, there exists a bijection g : n {y} → n−, so we have A {x} ≈ n− because g
 f0 is a bijection, contradicting the minimality of n.
f0 is a bijection, contradicting the minimality of n. - Assume n− ∈ A. Define A′ = A {n−} ∪ {y}. Since y ∉ A, A′ ≈ A, which implies that A′ ≈ n. Replace A with A′ in the previous argument and use f
 (A′ {y}) to contradict the minimality of n.
(A′ {y}) to contradict the minimality of n. 
![]() COROLLARY 6.3.7
COROLLARY 6.3.7
Every finite set is equinumerous to exactly one natural number.
PROOF
Let A be finite. This means that A ≈ n for some n ∈ ω. Let m ∈ ω also have the property that A ≈ m. This implies that n ≈ m. Hence, by Theorem 6.3.6, we conclude that n = m because n ⊆ m or m ⊆ n. ![]()
There are many results that follow directly from Theorem 6.3.6. The following six corollaries are among them.
![]() COROLLARY 6.3.8 [Pigeonhole Principle]
COROLLARY 6.3.8 [Pigeonhole Principle]
Let A and B be finite sets with B ![]() A. There is no one-to-one function A → B.
A. There is no one-to-one function A → B.
There exists unique m, n ∈ ω such that A ≈ m and B ≈ n by Corollary 6.3.7. Assume that f : A → B is one-to-one. Then,
![]()
so m is equinumerous to a subset of n. This implies that m ⊆ n. However, n ⊂ m because B ![]() A, which contradicts Theorem 6.1.14.
A, which contradicts Theorem 6.1.14. ![]()
![]() COROLLARY 6.3.9
COROLLARY 6.3.9
No finite set is equinumerous to a proper subset of itself.
![]() COROLLARY 6.3.10
COROLLARY 6.3.10
A set equinumerous to a proper subset of itself is infinite.
Because f : ω → ω {0} defined by f(n) = n + 1 is a bijection, we have the next result by Corollary 6.3.10.
![]() COROLLARY 6.3.11
COROLLARY 6.3.11
ω is infinite.
The proofs of the last two corollaries are left to Exercise 5.
![]() COROLLARY 6.3.12
COROLLARY 6.3.12
If A is a proper subset of a natural number n, there exists m < n such that A ≈ m.
![]() COROLLARY 6.3.13
COROLLARY 6.3.13
Let A ⊆ B. If B is finite, A is finite, and if A is infinite, B is infinite.
Countable Sets
Since ω is the first infinite ordinal, it is also a cardinal. Therefore,
![]()
As sets go, finite sets and those equinumerous with ω are small, so we classify them together using the next definition.
![]() DEFINITION 6.3.14
DEFINITION 6.3.14
A set A is countable if A ![]() ω.
ω.
Sometimes countable sets are called discrete or denumerable. For example, the bijection f : ![]() + → ω defined by f(n) = n− shows that
+ → ω defined by f(n) = n− shows that ![]() + is countable. Moreover, a nonempty finite set is countable and can be written as
+ is countable. Moreover, a nonempty finite set is countable and can be written as
![]()
for some positive integer n. A countably infinite set can be written as
![]()
where there are infinitely many distinct elements of the set.
![]() EXAMPLE 6.3.15
EXAMPLE 6.3.15
The set of rational numbers is a countable set. To prove this, define a bijection f : ω → ![]() by first mapping the even natural numbers to the nonnegative rational numbers. The function is defined along the path indicated in Figure 6.3. When a rational number that previously has been used is encountered, it is skipped. To complete the definition, associate the odd naturals with the negative rational numbers using a path as in the diagram. This function is a bijection, so we conclude that
by first mapping the even natural numbers to the nonnegative rational numbers. The function is defined along the path indicated in Figure 6.3. When a rational number that previously has been used is encountered, it is skipped. To complete the definition, associate the odd naturals with the negative rational numbers using a path as in the diagram. This function is a bijection, so we conclude that ![]() is countable.
is countable.
We have defined countability in terms of bijections. Now let us identify a condition for countability using surjections.
![]() THEOREM 6.3.16
THEOREM 6.3.16
A set A is countable if and only if there exists a function from ω onto A.
PROOF
If φ : ω → A is a surjection, by Theorem 6.2.8, A ![]() ω. Conversely, suppose A is countable. We have two cases to check.
ω. Conversely, suppose A is countable. We have two cases to check.
If Ai is countable for all i = 0, 1, ... , n − 1, then A0 × A1 × · · · × An−1 is countable (Exercise 15). In particular, ω × ω and ![]() ×
× ![]() are countable. We also have the next theorem.
are countable. We also have the next theorem.
![]() THEOREM 6.3.17
THEOREM 6.3.17
The union of a countable family of countable sets is countable.
PROOF
Let {Aα : α ∈ I} be a family of countable sets with I countable. Since we have that ![]() ∅ = ∅ is countable (Example 3.4.12), we can assume that I is nonempty. For each α ∈ I, there exists a surjection in ω(Aα) by Theorem 6.3.16. Therefore, by Corollary 5.1.11, there exists
∅ = ∅ is countable (Example 3.4.12), we can assume that I is nonempty. For each α ∈ I, there exists a surjection in ω(Aα) by Theorem 6.3.16. Therefore, by Corollary 5.1.11, there exists
![]()
such that f(α) is a surjection ω → Aα for all α ∈ I. Because I is countable, we have a surjection g : ω → I, and since ω × ω is countable, we have another surjection h : ω → ω × ω. We now define
![]()
by ψ(m, n) = f(g(m))(n) and let
![]()
be defined by φ = ψ ![]() h. To check that φ is onto, let a ∈ Aα, some α ∈ I. Since g is onto, there exists i ∈ ω so that g(i) = α. Furthermore, since f(α) is onto, we have j ∈ ω such that f(α)(j) = a, and since h is onto, there exists k ∈ ω so that h(k) = (i, j). Therefore,
h. To check that φ is onto, let a ∈ Aα, some α ∈ I. Since g is onto, there exists i ∈ ω so that g(i) = α. Furthermore, since f(α) is onto, we have j ∈ ω such that f(α)(j) = a, and since h is onto, there exists k ∈ ω so that h(k) = (i, j). Therefore,
![]()
For example, ![]() {n
{n![]() : n ∈ ω} and
: n ∈ ω} and ![]() {
{![]() × {n} : n ∈ ω} are countable.
× {n} : n ∈ ω} are countable.
Alephs
Cantor denoted the first infinite cardinal ω by ![]() 0. The symbol
0. The symbol ![]() (aleph) is the first letter of the Hebrew alphabet. The next magnitude of infinity is
(aleph) is the first letter of the Hebrew alphabet. The next magnitude of infinity is ![]() 1, which seems to exist by Theorem 6.2.13. This continues and gives an increasing sequence of infinite cardinals, and since natural numbers must be less than any infinite cardinal, we have
1, which seems to exist by Theorem 6.2.13. This continues and gives an increasing sequence of infinite cardinals, and since natural numbers must be less than any infinite cardinal, we have
![]()
For instance, 4 ![]()
![]() 1,
1, ![]() 0
0 ![]()
![]() 0, and
0, and ![]() 3
3 ![]()
![]() 7.
7.
![]() EXAMPLE 6.3.18
EXAMPLE 6.3.18
Although he was unable to prove it, Cantor suspected that ![]() 1 = |
1 = |![]() |. This conjecture is called the continuum hypothesis (CH). However, it is possible that
|. This conjecture is called the continuum hypothesis (CH). However, it is possible that ![]() 1
1 ![]() |
|![]() |. It is also possible that
|. It is also possible that ![]() 1 = |
1 = |![]() |. Cantor was unable to prove CH because it is undecidable assuming the axioms of ZFC. In other words, it is an ST-sentence that can be neither proved nor disproved from ZFC.
|. Cantor was unable to prove CH because it is undecidable assuming the axioms of ZFC. In other words, it is an ST-sentence that can be neither proved nor disproved from ZFC.
Now to define the other alephs. Pick an ordinal α. Define the function h by

where g is a function with dom(g) ∈ α. For example, if α = 5 and
![]()
then h(g) is the least infinite cardinal not in {κ0, κ1, κ2, κ3, κ4}. By Transfinite Recursion (6.1.23), there exists a unique function f with domain α and
![]()
for all β ∈ α. Define
![]()
Since h(0) = ω, we have that ![]() 0 = ω. Moreover, the definition of f implies that
0 = ω. Moreover, the definition of f implies that

The question at this point is whether the alephs name all of the infinite cardinals. The next theorem answers the question.
For every infinite cardinal κ, there exists an ordinal α such that κ = ![]() α.
α.
PROOF
Suppose κ ≠ ![]() α for every ordinal α. We can assume that κ is the minimal such cardinal. Thus, for all cardinals λ ∈ κ, there exists an ordinal βλ such that λ =
α for every ordinal α. We can assume that κ is the minimal such cardinal. Thus, for all cardinals λ ∈ κ, there exists an ordinal βλ such that λ = ![]() βλ. Therefore, the least infinite cardinal not an element of
βλ. Therefore, the least infinite cardinal not an element of
![]()
is the next aleph, but this is κ. ![]()
![]() EXAMPLE 6.3.20
EXAMPLE 6.3.20
The generalized continuum hypothesis (GCH) states that for every ordinal α,
![]()
When α = 0, GCH implies that
![]()
which is CH (Example 6.3.18). Like CH, GCH is undecidable in ZFC.
Like the ordinals, the cardinals can be divided into two classes.
![]() DEFINITION 6.3.21
DEFINITION 6.3.21
Let κ be a nonzero cardinal number. If κ ∈ ω or there exists an ordinal α such that κ = ![]() α+, then κ is a successor cardinal. Otherwise, κ is a limit cardinal.
α+, then κ is a successor cardinal. Otherwise, κ is a limit cardinal.
For example, the positive natural numbers and ![]() 1 are successor cardinals, while
1 are successor cardinals, while ![]() 0 and
0 and ![]() ω are limit cardinals. Notice that if κ is a limit cardinal,
ω are limit cardinals. Notice that if κ is a limit cardinal,
![]()
Exercises
1. Prove that |α| = |α+| for every ordinal α.
2. Let p(x) be a formula. Prove that if p(α) is false for some ordinal α, then there exists a least ordinal β such that p(β) is false.
3. Prove that the function f in the proof of Lemma 6.3.5 is a bijection.
4. Show that the following attempted generalization of Lemma 6.3.5 is false: Let α be an ordinal and a ∈ A. If |A| = ![]() α+, then |A {a}| =
α+, then |A {a}| = ![]() α.
α.
5. Demonstrate Corollaries 6.3.12 and 6.3.13.
6. Let A and B be finite sets. Prove the following.
(a) |A ∪ B| = |A| + |B| − |A ∩ B|
(b) |A ∩ B| = |A| − |A B|
(c) |A × B| = |A| · |B|
7. Prove that the intersection and union of finite sets is finite is finite.
8. Prove that every finite set has a choice function without using the axiom of choice.
9. Let R and R−1 be well-orderings of a set A. Prove that A is finite.
10. Show that ![]() is countable.
is countable.
11. Let A be infinite. Find infinite sets B and C such that A = B ∪ C.
12. If B is countable, prove that |A × B| = |A|.
13. Let A and B be sets and A is countable. Prove that B is countable when A ≈ B.
14. Let A and B be countable sets. Show that the given sets are countable.
(a) A ∪ B
(b) A ∩ B
(c) A × B
(d) A B
15. Let A0, A1, ... , An−1 be countable sets. Prove that the given sets are countable.
(a) A0 ∪ A1 ∪ · · · ∪ An−1
(b) A0 ∩ A1 ∩ · · · ∩ An−1
(c) A0 × A1 × · · · × An−1
16. Prove.
(a) If A ∪ B is countable, A and B are countable.
(b) If A is countable, 2ω ≈ Aω
17. Let ![]() be a set of cardinals. Prove that
be a set of cardinals. Prove that ![]()
![]() is a cardinal.
is a cardinal.
18. A real number is algebraic if it is a root of a nonzero polynomial with integer coefficients. A real number that is not algebraic is transcendental. Prove that the set of algebraic numbers is countable and the set of transcendental numbers is uncountable.
19. Take a set A and define B = {α : α is an ordinal ∧ α ![]() A}. [See Hartogs' theorem (6.1.22).] Prove the following.
A}. [See Hartogs' theorem (6.1.22).] Prove the following.
(a) B is a cardinal.
(b) |A| ![]() B.
B.
(c) B is the least cardinal such that |A| ![]() B.
B.
20. Assuming GCH, find |P(P(P(P(P(![]() )))))|.
)))))|.
21. Prove that for all ordinals α and β, if α ∈ β, then ![]() α ∈
α ∈ ![]() β.
β.
22. Recursively define the following function using ![]() (beth), the second letter of the Hebrew alphabet. Let α be an ordinal.
(beth), the second letter of the Hebrew alphabet. Let α be an ordinal.

(a) Use ![]() to restate GCH.
to restate GCH.
(b) Use transfinite recursion (Corollary 6.1.24) to prove that ![]() defines a function.
defines a function.
6.4 ARITHMETIC
Since every natural number is both an ordinal and a cardinal, we want to extend the operations on ω to all of the ordinals and all of the cardinals. Since the purpose of the ordinals is to characterize well-ordered sets but the purpose of the cardinals is to count, we expect the two extensions to be different.
Ordinals
Definitions 5.2.15 and 5.2.18 define what it means to add and multiply finite ordinals. When generalizing these two definitions to the infinite ordinals, we must take care because addition and multiplication should be binary operations, but if we defined these operations on all ordinals, their domains would not be sets by the Burali-Forti Theroem (6.1.21), resulting in the operations not being sets. Therefore, we choose an ordinal and define addition and multiplication on it. Since 1 + 1 ∉ 2, the ordinal must be a limit ordinal.
![]() DEFINITION 6.4.1
DEFINITION 6.4.1
Let ζ be a limit ordinal. For all α, β ∈ ζ,
- α + 0 = α,
- α + β+ = (α + β)+,
- α + β =
 {α + δ : δ ∈ β} if β is a limit ordinal.
{α + δ : δ ∈ β} if β is a limit ordinal.
As with addition of natural numbers (Definition 5.2.15), to prove that Definition 6.4.1 gives a binary operation, let ψ : ζ → ζ be the successor function. By transfinite recursion (Corollary 6.1.24), there exist unique functions φα : α → ζ for all α ∈ ζ such that
Define A : ζ × ζ → ζ by A(α, β) = φα(β). By the uniqueness of each φα, the binary operation A is the function of Definition 6.4.1, so
![]()
Furthermore, take ζ′ to be a limit ordinal such that ζ ⊆ ζ′ and define ψ′ : ζ′ → ζ′ to be the successor function. As above, there are unique functions φ′α for all α ∈ ζ′ with the same properties as φα. Notice that
![]()
Otherwise, φ′α ![]() ζ would have the same properties as φα yet be a different function, contradicting the uniqueness given by transfinite recursion. Next, define the binary operation A′ : ζ′ × ζ′ → ζ′ by A′(α, β) = φ′α(β). Therefore,
ζ would have the same properties as φα yet be a different function, contradicting the uniqueness given by transfinite recursion. Next, define the binary operation A′ : ζ′ × ζ′ → ζ′ by A′(α, β) = φ′α(β). Therefore,
![]()
This implies that although addition is not defined as a binary operation on all ordinals, we can add any two ordinals and obtain the same sum independent of the ordinal on which the addition is defined.
Consider m ∈ ω. Since ω is a limit ordinal,
![]()
However,
![]()
and
![]()
Therefore, addition of infinite ordinals is not commutative. Moreover, an order isomorphism can be defined between ω + n and ({0} × ω)∪({1} × n) ordered lexicographically (Exercise 4.3.16) as

This means that ω + n looks like ω followed by a copy of n. Generalizing, the ordinal ω + ω looks like ω followed by a copy of ω. In particular,
![]()
which means that the proof its existence requires a replacement axiom (5.1.9). All of this suggests the next result.
Let ξ be a limit ordinal and α, β ∈ ξ. If x ∈ α + β, then x ∈ α or x ∈ α + b for some b ∈ β.
PROOF
Define
![]()
Clearly, 0 ∈ A, so take γ ∈ ζ such that seg(ζ, γ) ⊆ A.
- Let γ = δ+ for some ordinal δ. Take x ∈ α + δ+, which implies that x ∈ (α + δ)+. This means that x ∈ α + δ or x = α + δ. If x ∈ α + δ, then we are done. If x = α + δ, then x ∈ (α + δ)+ = α + δ+.
- Let γ be a limit ordinal. Take x ∈ α + γ. This means that x ∈ α + δ for some δ ∈ γ. Therefore, x ∈ α or x ∈ α + d for some d ∈ δ ⊂ γ.

Using Lemma 6.4.2, we can prove the next useful result.
![]() LEMMA 6.4.3
LEMMA 6.4.3
Let ζ be a limit ordinal. If α, β ∈ ζ, then α + β = α ∪ {α + b : b ∈ β}.
PROOF
Define
![]()
We have that 0 ∈ A, so assume seg(ζ, γ) ⊆ A, where γ ∈ ζ.
- Suppose γ = δ+. Then,

- Let γ be a limit ordinal. Take x ∈ α + γ. By Lemma 6.4.2, we have x ∈ α or x ∈ α + g for some g ∈ γ. If the former, we are done, so suppose the latter. In this case, the assumption gives

Thus, x = α + g′ for some g′ ∈ g ∈ γ. Conversely, if x ∈ α, then x ∈ α + 0, so x ∈ α + γ. For the other case, let x ∈ {α + g : g ∈ γ}. This implies that x ∈ (α + g)+ = α + g+ for some g ∈ γ. Since g+ ∈ γ,

Although ordinal addition is not commutative, it does have other familiar properties as noted in the next result.
Addition of ordinals is associative, and 0 is the additive identity.
PROOF
Let ζ be a limit ordinal. Define
![]()
Suppose γ is an ordinal such that seg(λ, γ) ⊆ A. We have two cases to check.
- Let γ = δ+ for some ordinal δ. Then,

- Let γ be a limit ordinal. We then have

In both cases, γ ∈ A, so by transfinite induction, A = ζ. Since we can also prove that
![]()
we conclude that 0 is the additive identity.
To prove that ordinal addition is associative, we proceed by transfinite induction. Let α, β, δ ∈ ζ. Define
![]()
Assume that seg(ζ, γ) ⊆ B. Then, γ ∈ B because by Lemma 6.4.3, we have

Note that Exercise 3.4.28(e) is used on the fourth equality. ![]()
![]() DEFINITION 6.4.5
DEFINITION 6.4.5
Let ζ be a limit ordinal. For all α, β ∈ ζ,
As with ordinal addition, ordinal multiplication is well-defined by transfinite recursion (Exercise 3). Also, as with addition of ordinals, certain expected properties hold, while others do not. The next two results are the analog of Lemma 6.4.3 and Theorem 6.4.4. Their proofs are Exercise 4.
![]() LEMMA 6.4.6
LEMMA 6.4.6
If α and β are ordinals, α · β = {α · b + a : b ∈ β ∧ a ∈ α}.
![]() THEOREM 6.4.7
THEOREM 6.4.7
Multiplication of ordinals is associative, and 1 is the multiplicative identity.
Observe that
![]()
Also, ω · 1 = 1 · ω = ω (Theorem 6.4.7), so multiplication on the right by a natural number behaves as we would expect in that
![]()
and
![]()
but
![]()
and
![]()
Hence, multiplication of ordinals is not commutative. Because of this, it is not surprising that there are issues with the distributive law. For ordinals, there is a left distributive law but not a right distributive law (Exercise 9).
![]() THEOREM 6.4.8 [Left Distributive Law]
THEOREM 6.4.8 [Left Distributive Law]
α · (β + δ) = α · + β + α · δ for all ordinals α, β, and δ.
Since addition of ordinals is an operation on a limit ordinal ζ, we know that for all ordinals α, β, δ ∈ ζ,
![]()
and
![]()
The next result gives information regarding how ordinal multiplication behaves with an inequality.
Let α, β, and δ be ordinals.
- If α ⊂ β, then δ + α ⊂ δ + β.
- If α ⊆ β, then α + δ ⊆ β + δ.
- If α ⊂ β and δ ≠ 0, then δ · α ⊂ δ · β.
- If α ⊆ β, then α · δ ⊆ β · δ.
PROOF
We prove the third part, leaving the others to Exercise 7. Let α ⊂ β and δ ≠ 0. Then, by Lemma 6.4.6,
![]()
Finally, we define exponentiation so that it generalizes exponentiation on ω (Exercise 5.2.17). It is a binary operation (Exercise 3).
![]() DEFINITION 6.4.10
DEFINITION 6.4.10
Let ζ be a limit ordinal and α, β ∈ ζ.
- α0 = 1
- αβ+ = αβ · α
- αβ =
 {αδ : δ ∈ β} if β is a limit ordinal.
{αδ : δ ∈ β} if β is a limit ordinal.
For example,
![]()
and
![]()
so raising an ordinal to a natural number appears to behave as expected. Also,
![]()
and
![]()
We leave the proof of the following properties of ordinal exponentiation to Exercise 11.
Let α, β, δ be ordinals.
- αβ+δ = αβ · αδ.
- (αβ)δ = αβ·δ.
Cardinals
Even though the finite cardinals are the same sets as the finite ordinals and every infinite cardinal is a limit ordinal, the arithmetic defined on the cardinals will only apply when the given sets are viewed as cardinals. The definitions for addition, multiplication, and exponentiation for cardinals are not given recursively.
![]() DEFINITION 6.4.12
DEFINITION 6.4.12
Let κ and λ be cardinals.
- κ + λ = |(κ × {0}) ∪ (λ × {1})|
- κ · λ = |κ × λ|
- κλ = |λκ|.
Since ordinal arithmetic was simply a generalization of the arithmetic of natural numbers, that the addition worked in the finite case was not checked. Here this is not the case, so let us check
![]()
Also,
![]()
This suggests that cardinal addition is commutative. This and other basic results are given in the next theorem. Some details of the proof are left to Exercise 14.
![]() THEOREM 6.4.13
THEOREM 6.4.13
Addition of cardinals is associative and commutative, and 0 is the additive identity.
PROOF
Let κ, λ, and μ be cardinals. Addition is associative because
![]()
is equinumerous to
![]()
![]()
and 0 is the additive identity because
![]()
Now let us multiply
![]()
and
![]()
As with cardinal addition, it seems that cardinal multiplication is commutative. This and other results are stated in the next theorem. Its proof is left to Exercise 15.
![]() THEOREM 6.4.14
THEOREM 6.4.14
Multiplication of cardinals is associative and commutative, and 1 is the multiplicative identity.
As with ordinal arithmetic (Theorem 6.4.8), cardinal arithmetic has a left distribution law, but since cardinal multiplication is commutative, cardinal arithmetic also has a right distribution law.
![]() THEOREM 6.4.15 [Distributive Law]
THEOREM 6.4.15 [Distributive Law]
Let κ, λ, and μ be cardinals.
- κ · (λ + μ) = κ · λ + κ · μ.
- (κ + λ) · μ = κ · μ + λ · μ.
PROOF
The left distribution law holds because
![]()
The remaining details of the proof are left to Exercise 16. ![]()
The last of the operations of Definition 6.4.12 is exponentiation. Let κ be a cardinal. Observe that since there is exactly one function 0 → κ (Exercise 4.4.16),
![]()
and if κ ≠ 0,
![]()
because there are no functions κ → 0, and by Theorem 6.2.13,
![]()
In addition, cardinal exponentiation follows other expected rules.
Let κ, λ, and μ be cardinals.
- κλ+μ = κλ · κμ.
- (κ · λ)μ = κμ · λμ.
- (κλ)μ = κλ · μ.
PROOF
We prove the last part and leave the rest to Exercise 17. Define
![]()
such that for all ψ ∈ μ(λκ), α ∈ λ and β ∈ μ,
![]()
We claim that φ is a bijection.
- Let ψ1, ψ2 ∈ μ(λκ). Assume that φ(ψ1) = φ(ψ2). Take α ∈ λ and β ∈ μ. Then,

Therefore, ψ1 = ψ2, and φ is one-to-one.
- Let ψ ∈ λ×μκ. For α ∈ λ and β ∈ μ, define ψ′(α)(β) = ψ(α, β). This implies that φ(ψ′) = ψ, so φ is onto.

Since every infinite cardinal number can be represented by an ![]() , let us determine how to calculate using this notation. We begin with a lemma.
, let us determine how to calculate using this notation. We begin with a lemma.
![]() LEMMA 6.4.17
LEMMA 6.4.17
If n ∈ ω and κ an infinite cardinal, n + κ = n · κ = κ.
PROOF
Let n be a natural number. Define φ : (n × {0}) ∪ (κ × {1}) → κ by
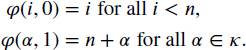
For example, if n = 5, then φ(4, 0) = 4, φ(0, 1) = 5, φ(6, 1) = 11, φ(ω, 1) = ω, and φ(ω + 1, 1) = ω + 1. Therefore, n + κ = κ because φ is a bijection. That n · κ = κ is left to Exercise 18. ![]()
Lemma 6.4.17 allows us to compute with alephs.
Let α and β be ordinals and n ∈ ω.

PROOF
The first part follows by Lemma 6.4.17. To prove the addition equation from the second part, let α and β be ordinals. Without loss of generality assume that α ⊆ β. By Definition 6.4.12,
![]()
Since ![]() β = |
β = |![]() β × {1}|,
β × {1}|,
![]()
Furthermore, because ![]() α ⊆
α ⊆ ![]() β,
β,

Because of Lemma 6.4.17, the last equality holds since ![]() β is infinite and {0, 1} is finite. Hence,
β is infinite and {0, 1} is finite. Hence,
![]()
by the Cantor–Schröder–Bernstein theorem (6.2.11). Since both ![]() α +
α + ![]() β and
β and ![]() β are cardinals,
β are cardinals, ![]() α +
α + ![]() β =
β = ![]() β.
β. ![]()
For example, ![]() 5 +
5 + ![]() 9 =
9 = ![]() 5 ·
5 · ![]() 9 =
9 = ![]() 9. More generally, we quickly have the following corollary by Theorem 6.3.19.
9. More generally, we quickly have the following corollary by Theorem 6.3.19.
![]() COROLLARY 6.4.19
COROLLARY 6.4.19
For every infinite cardinal κ, both κ + κ = κ and κ · κ = κ.
Exercises
1. Let ![]() = {A0, A1, ..., An−1} be a pairwise disjoint family of sets. Assuming that the sets are distinct, prove that the cardinality of
= {A0, A1, ..., An−1} be a pairwise disjoint family of sets. Assuming that the sets are distinct, prove that the cardinality of ![]()
![]() is equal to the sum
is equal to the sum
![]()
2. Let α and β be ordinals. Let φ : α → β be a function such that φ(δ) ∈ φ(γ) for all δ ∈ γ ∈ α (Compare Lemma 6.1.2). Prove the following.
(b) δ ⊆ φ(δ) for all δ ∈ α.
3. Let ζ be a limit ordinal. Use transfinite recursion to prove that ordinal multiplication (Definition 6.4.5) and ordinal exponentiation (Definition 6.4.10) are binary operations on ζ.
4. Prove Lemma 6.4.6 and Theorem 6.4.7.
5. For every ordinal α, prove that 0 · α = 0.
6. Prove that for all n ∈ ω, n + ω = n · ω as ordinals. Can this be generalized to α + β = α · β for ordinals α ∈ β with β being infinite? If so, is the α ∈ β required?
7. Prove the remaining parts of Theorem 6.4.9.
8. Find ordinals α, β, and δ such that the following properties hold.
(a) α ⊂ β but β + δ ⊆ α + δ.
(b) α ⊂ β but β · δ ⊆ α · δ.
9. Let α, β, and δ be ordinals.
(a) Prove that α · (β + δ) = α · β + α · δ.
(b) Show that it might be the case that (α + β) · δ ≠ α · δ + β · δ.
(c) For which ordinals does the right distribution law hold?
10. Let α, β, and δ be ordinals. Prove the following.
(a) α + β ∈ α · δ if and only if β ∈ δ.
(b) α + β = α + δ if and only if β = δ.
(c) If α + δ ∈ β + δ, then α ∈ β.
(d) α · β ∈ α · δ if and only if β ∈ δ and α ≠ 0.
(e) If α · β = α · δ, then β = δ or α = 0.
11. Prove Theorem 6.4.11.
12. Let α, β, and δ be ordinals. Prove the following.
(a) αβ ∈ αδ if and only if β ∈ α and 1 ∈ α.
(b) If α ∈ β, then αδ ⊆ βδ.
(c) If αδ ∈ βδ, then α ∈ β.
(d) If 1 ∈ α, then β ⊆ αβ.
(e) If α ∈ β, there exists a unique ordinal γ such that α + γ = β.
13. Prove that the ordinal ω + ω is not a cardinal.
14. Provide the details for the proof of Theorem 6.4.13.
15. Prove Theorem 6.4.14.
16. Provide the details to the proof of Theorem 6.4.15.
17. Prove the remaining parts of Theorem 6.4.16.
18. Prove that for any natural number n and infinite cardinal κ, n · κ = κ.
19. Prove that if κ is inifinte, (κ+)κ = 2κ.
20. Is there a cancellation law for ordinals or for cardinals?
21. Prove that κ + λ = κ · λ = λ, given that κ is a countable cardinal and λ is an infinite cardinal.
22. Generalize Exercise 21 by showing that if κ and λ are cardinals with λ infinite such that κ ![]() λ, then κ + λ = κ · λ = λ.
λ, then κ + λ = κ · λ = λ.
23. Let κ and λ be cardinals with ![]() 0
0 ![]() λ. Show that if 2
λ. Show that if 2 ![]() κ
κ ![]() λ, then κλ = 2λ.
λ, then κλ = 2λ.
24. Prove for all ordinals α that |α| ![]()
![]() α.
α.
25. For all ordinals α, define Hartogs' function by
![]()
Prove that Γ(α) is an ordinal and α ![]() Γ(α) for all ordinals α.
Γ(α) for all ordinals α.
26. Using Exercise 25, define an initial number ωα as follows.

Prove that initial numbers are limit ordinals and ω1 is the first uncountable ordinal.
27. Prove that there is no greatest initial number.
28. For all ordinals α, show that ![]() α = |ωα|. Can we write
α = |ωα|. Can we write ![]() α = ωα?
α = ωα?
29. For all countable ordinals α, show that ![]() =
= ![]() α+ implies that
α+ implies that ![]() =
= ![]() ω1 + 1.
ω1 + 1.
6.5 LARGE CARDINALS
Since every cardinal is a limit ordinal, every cardinal κ can be written in the form
![]()
In particular, for the limit cardinal ![]() ω+ω, we have that
ω+ω, we have that
![]()
Notice that (6.2) is the union of a set with ![]() ω+ω elements. However, we also have
ω+ω elements. However, we also have
![]()
and
![]()
Both (6.3) and (6.4) are unions of sets with ![]() 0 elements. The next definition is introduced to handle these differences. Since infinite cardinals are limit ordinals, the definition is given for limit ordinals.
0 elements. The next definition is introduced to handle these differences. Since infinite cardinals are limit ordinals, the definition is given for limit ordinals.
The cofinality of a limit ordinal α is denoted by cf(α) and defined as the least cardinal λ such that there exists ![]() ⊆ α with |
⊆ α with |![]() | = λ and α =
| = λ and α = ![]()
![]() .
.
Observe that cf(α) ![]() |α| because α =
|α| because α = ![]() α. There can be other sets B such that α =
α. There can be other sets B such that α = ![]() B, and they might have different cardinalities. Any set of ordinals B with this property is said to be cofinal in α. Moreover, we can write B = {βδ : δ ∈ κ} for some cardinal κ, so
B, and they might have different cardinalities. Any set of ordinals B with this property is said to be cofinal in α. Moreover, we can write B = {βδ : δ ∈ κ} for some cardinal κ, so
![]()
and when κ = cf(α),
![]()
![]() EXAMPLE 6.5.2
EXAMPLE 6.5.2
Since the finite union of a finite set is finite, the cofinality of any infinite set must be infinite. Therefore, because
![]()
we see that cf(ω) = ![]() 0. Also, since
0. Also, since
![]()
we conclude that cf(![]() ω) =
ω) = ![]() 0 and {
0 and {![]() n : n ∈ ω} is cofinal in
n : n ∈ ω} is cofinal in ![]() ω. However, cf(
ω. However, cf(![]() 1) =
1) = ![]() 1 because the countable union of countable sets is countable (Theorem 6.3.17).
1 because the countable union of countable sets is countable (Theorem 6.3.17).
Regular and Singular Cardinals
Since infinite cardinals are limit ordinals, we can classify the cardinals based on their cofinalities. We make the following definition.
![]() DEFINITION 6.5.3
DEFINITION 6.5.3
A cardinal κ is regular if κ = cf(κ), else it is singular.
Notice that Example 6.5.2 shows that ![]() 0 and
0 and ![]() 1 are regular but
1 are regular but ![]() ω is singular. This implies a direction to follow to characterize the cardinal numbers. We begin with the successors.
ω is singular. This implies a direction to follow to characterize the cardinal numbers. We begin with the successors.
![]() THEOREM 6.5.4
THEOREM 6.5.4
Successor cardinals are regular.
Let α be an ordinal and let ![]() ⊆
⊆ ![]() α + 1 such that
α + 1 such that ![]() α + 1 =
α + 1 = ![]()
![]() . This implies that |β|
. This implies that |β| ![]()
![]() α for all β ∈
α for all β ∈ ![]() . Thus,
. Thus,
![]()
By Theorem 6.4.18, we conclude that ![]() α + 1
α + 1 ![]() |
|![]() |, so cf(
|, so cf(![]() α+1) =
α+1) = ![]() α+1 by the Cantor–Schröder–Bernstein theorem (6.2.11).
α+1 by the Cantor–Schröder–Bernstein theorem (6.2.11). ![]()
Since ![]() 0 is regular, Theorem 6.5.4 tells us where to find the singular cardinals.
0 is regular, Theorem 6.5.4 tells us where to find the singular cardinals.
![]() COROLLARY 6.5.5
COROLLARY 6.5.5
A singular cardinal is an uncountable limit cardinal.
Because we have not proved the converse of Corollary 6.5.5, we investigate the cofinality of certain limit cardinals in an attempt to determine which limit cardinals are singular.
![]() THEOREM 6.5.6
THEOREM 6.5.6
If α is a limit ordinal, cf(![]() α) = cf(α).
α) = cf(α).
![]() PROOF
PROOF
The proof uses the Cantor–Schröder–Bernstein theorem (6.2.11). Let α be a limit ordinal.
- We first show that cf(
 α)
α)  cf(α). Let A be a cofinal subset of α such that |A| = cf(α). Notice that if β ∈ A, then
cf(α). Let A be a cofinal subset of α such that |A| = cf(α). Notice that if β ∈ A, then  β ∈
β ∈  α. On the other hand, take δ ∈
α. On the other hand, take δ ∈  α, which implies that |δ|
α, which implies that |δ| 
 α. Therefore, there exists γ ∈ α such that |δ| =
α. Therefore, there exists γ ∈ α such that |δ| =  γ. Since A is cofinal in α, there exists ζ ∈ A such that δ ∈ ζ. Hence, δ ∈
γ. Since A is cofinal in α, there exists ζ ∈ A such that δ ∈ ζ. Hence, δ ∈  ζ, which implies that δ ∈
ζ, which implies that δ ∈  {
{ β : β ∈ A}. Therefore,
β : β ∈ A}. Therefore,

from which follows,

- We now show cf(α)
 cf(
cf( α). Let A ⊆
α). Let A ⊆  α so that
α so that  α =
α =  A and |A| = cf(
A and |A| = cf( α). Define
α). Define

Then, β =

 is an ordinal by Theorem 6.1.16. For all ζ ∈ A, we have that ζ ∈
is an ordinal by Theorem 6.1.16. For all ζ ∈ A, we have that ζ ∈  β+1 because |ζ|
β+1 because |ζ| 
 β. Hence,
β. Hence,
from which follows that α ∈ β, which means that α ⊆

 . Therefore, since the elements of
. Therefore, since the elements of  are ordinals of α, we have that α =
are ordinals of α, we have that α = 
 , so
, so
Theorem 6.5.6 confirms the result of Example 6.5.2 because
![]()
Also,
![]()
so ![]() ω+ω is singular. Observe that by (6.5) and (6.6),
ω+ω is singular. Observe that by (6.5) and (6.6),
![]()
and
![]()
The next result generalizes this and proves that cf(cf(α)) = cf(α) for every limit ordinal α.
![]() THEOREM 6.5.7
THEOREM 6.5.7
For any limit ordinal α, cf(α) is a regular cardinal.
PROOF
Let α be a limit ordinal and write α = ![]() {Aγ : γ ∈ cf(α)}. For every ordinal γ ∈ cf(α), define αγ =
{Aγ : γ ∈ cf(α)}. For every ordinal γ ∈ cf(α), define αγ = ![]() δ∈γ Aδ. Then, {αγ : γ ∈ cf(α)} is a chain of ordinals (Theorem 6.1.16) and
δ∈γ Aδ. Then, {αγ : γ ∈ cf(α)} is a chain of ordinals (Theorem 6.1.16) and
![]()
Now write
![]()
Define
![]()
Let ζ ∈ α. This implies that ζ ∈ αγ0 for some γ0 ∈ cf(α). Then, γ0 ∈ βγ1 for some γ1 ∈ cf(cf (α)). Hence,
![]()
so ζ ∈ ![]() B. Therefore, α =
B. Therefore, α = ![]() B, and this implies that cf(α)
B, and this implies that cf(α) ![]() cf(cf (α)). Since the opposite inequality always holds, by the Cantor–Schröder–Bernstein theorem (6.2.11), cf(α) = cf(cf(α)), which means that cf(α) is regular.
cf(cf (α)). Since the opposite inequality always holds, by the Cantor–Schröder–Bernstein theorem (6.2.11), cf(α) = cf(cf(α)), which means that cf(α) is regular. ![]()
Although the Continuum Hypothesis cannot be proved, it is possible to discover some information about the value of ![]() . Notice how its proof resembles Cantor's diagonalization (page 303). It is due to König (1905).
. Notice how its proof resembles Cantor's diagonalization (page 303). It is due to König (1905).
![]() THEOREM 6.5.8 [König]
THEOREM 6.5.8 [König]
If κ is an infinite cardinal and cf(κ) ![]() λ, then κ
λ, then κ ![]() κλ.
κλ.
Suppose that κ is am infinite cardinal number and cf(κ) = λ. Write
![]()
Let ![]() = {fβ : β ∈ κ} be a subset of λκ. Define g : λ → κ such that
= {fβ : β ∈ κ} be a subset of λκ. Define g : λ → κ such that
![]()
For any α ∈ λ,
![]()
Therefore,
![]()
Since (6.7) is true for all α ∈ λ and {δα : α ∈ λ} is cofinal in κ, we conclude that g ≠ fβ for all β ∈ κ. Therefore, g ∉ ![]() , so κ
, so κ ![]() κλ. Note that the same argument leads to this conclusion if cf(κ)
κλ. Note that the same argument leads to this conclusion if cf(κ) ![]() λ (Exercise 4).
λ (Exercise 4). ![]()
![]() COROLLARY 6.5.9
COROLLARY 6.5.9
Let κ be an infinite cardinal. Then, κ ![]() cf(2κ).
cf(2κ).
PROOF
Suppose that cf (2κ) ![]() κ. By König's theorem (6.5.8), Theorem 6.4.16, and Corollary 6.4.19,
κ. By König's theorem (6.5.8), Theorem 6.4.16, and Corollary 6.4.19,
![]()
By Corollary 6.5.9,
![]()
but by Example 6.5.2, we know that cf(![]() ω) =
ω) = ![]() 0, so
0, so
![]()
Hence, even though we cannot prove what the cardinality of ![]() is, we do know that it is not
is, we do know that it is not ![]() ω.
ω.
Inaccessible Cardinals
As we have noted, ![]() 0 is both a regular and a limit cardinal. Are there any others with this property?
0 is both a regular and a limit cardinal. Are there any others with this property?
![]() DEFINITION 6.5.10
DEFINITION 6.5.10
A regular limit cardinal that is uncountable is called weakly inaccessible.
It is not possible using the axioms of ZFC to prove the existence of a weakly inaccessible cardinal. Here is another class of cardinals “beyond” the weakly inaccessible cardinals.
The cardinal κ is strongly inaccessible if it is an uncountable regular cardinal such that 2λ ![]() κ for all λ
κ for all λ ![]() κ.
κ.
Since every strongly inaccessible cardinal is weakly inaccessible (Exercise 1), it is not possible to prove from the axioms of ZFC that a strongly inaccessible cardinal exists. However, it is apparent that assuming GCH, κ is a weakly inaccessible cardinal if and only if κ is a strongly inaccessible cardinal (Exercise 10). Cardinal numbers such as these are known as large cardinals because assumptions beyond the axioms of ZFC are required to “reach” them.
Exercises
1. Prove that every strongly inaccessible cardinal is weakly inaccessible.
2. Let n ∈ ω. Show that cf(![]() n) =
n) = ![]() n.
n.
3. For all limit ordinals α, β, and δ, show that if α is cofinal in β and β is cofinal in δ, then α is cofinal in δ.
4. Rewrite the proof of König's theorem (6.5.8) assuming that cf(κ) ![]() λ.
λ.
5. Let α and β be limit ordinals. Prove that cf(α) = cf(α) if and only if (α, ⊆) and (β, ⊆) have order isomorphic cofinal subsets.
6. Let α be a countable limit ordinal. Show that cf(α) = ![]() 0.
0.
7. Let κ and λ be cardinals such that κ is infinite and 2 ![]() λ. Show the following.
λ. Show the following.
(a) κ ![]() cf(λκ).
cf(λκ).
(b) κ ![]() κcf(κ).
κcf(κ).
8. Assume GCH and let α and β be ordinals. Prove.
(a) If ![]() β
β ![]() cf(
cf(![]() α), then
α), then ![]() =
= ![]() α.
α.
(b) If cf(![]() α)
α) ![]()
![]() β
β ![]()
![]() α, then
α, then ![]() =
= ![]() α+.
α+.
9. Let α be a limit ordinal. Show that cf(![]() α) = cf(α). (See Exercise 6.3.22.)
α) = cf(α). (See Exercise 6.3.22.)
10. Prove that GCH implies that a cardinal is weakly inaccessible if and only if it is strongly inaccessible.
11. Let κ be a cardinal. Prove the following biconditionals.
(a) κ is weakly inaccessible if and only if κ is regular and ![]() κ = κ.
κ = κ.
(b) κ is strongly inaccessible if and only if κ is regular and ![]() κ = κ.
κ = κ.




