2
Location and Simple Linear Models
In statistical literature, various methods of estimation of the parameters of a given model are available, primarily based on the least squares estimator (LSE) and maximum likelihood estimator (MLE) principle. However, when uncertain prior information of the parameters is known, the estimation technique changes. The methods of circumvention, including the uncertain prior information, are of immense importance in the current statistical literature. In the area of classical approach, preliminary test (PT) and the Stein‐type (S) estimation methods dominate the modern statistical literature, side by side with the Bayesian methods.
In this chapter, we consider the simple linear model and the estimation of the parameters of the model along with their shrinkage version and study their properties when the errors are normally distributed.
2.1 Introduction
Consider the simple linear model with slope 
and intercept 
, given by
If 
, the model (2.1) reduces to
where 
is the location parameter of a distribution.
In the following sections, we consider the estimation and test of the location model, i.e. the model of (2.2), followed by the estimation and test of the simple linear model.
2.2 Location Model
In this section, we introduce two basic penalty estimators, namely, the ridge regression estimator (RRE) and the least absolute shrinkage and selection operator (LASSO) estimator for the location parameter of a distribution. The penalty estimators have become viral in statistical literature. The subject evolved as the solution to ill‐posed problems raised by Tikhonov (1963) in mathematics. In 1970, Hoerl and Kennard applied the Tikhonov method of solution to obtain the RRE for linear models. Further, we compare the estimators with the LSE in terms of 
‐risk function.
2.2.1 Location Model: Estimation
Consider the simple location model,
where 
, 
‐ 
‐tuple of 1's, and 
‐vector of i.i.d. random errors such that 
and 
, 
is the identity matrix of rank 
(
), 
is the location parameter, and, in this case, 
may be unknown.
The LSE of 
is obtained by
Alternatively, it is possible to minimize the log‐likelihood function when the errors are normally distributed:
giving the same solution (2.4) as in the case of LSE. It is known that the 
is unbiased, i.e. 
and the variance of 
is given by
The unbiased estimator of 
is given by
The mean squared error (MSE) of 
, any estimator of 
, is defined as
Test for 
when 
is known:
For the test of null‐hypothesis 
vs. 
, we use the test statistic
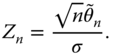
Under the assumption of normality of the errors, 
, where 
Hence, we reject 
whenever 
exceeds the threshold value from the null distribution. An interesting threshold value is 
.
For large samples, when the distribution of errors has zero mean and finite variance 
, under a sequence of local alternatives,
and assuming 
and 
(
), 
, the asymptotic distribution of 
is 
. Then the test procedure remains the same as before.
2.2.2 Shrinkage Estimation of Location
In this section, we consider a shrinkage estimator of the location parameter 
of the form
where 
. The bias and the MSE of 
are given by
Minimizing 
w.r.t. 
, we obtain
So that
Thus, 
is an increasing function of 
and the relative efficiency (REff) of 
compared to 
is
Further, the MSE difference is
Hence, 
outperforms the 
uniformly.
2.2.3 Ridge Regression–Type Estimation of Location Parameter
Consider the problem of estimating 
when one suspects that 
may be 0. Then following Hoerl and Kennard (1970), if we define
Then, we obtain the ridge regression–type estimate of 
as
or
Note that it is the same as taking 
in (2.8).
Hence, the bias and MSE of 
are given by
and
It may be seen that the optimum value of 
is 
and MSE at (2.18) equals
Further, the MSE difference equals
which shows 
uniformly dominates 
.
The REff of 
is given by
2.2.4 LASSO for Location Parameter
In this section, we define the LASSO estimator of 
introduced by Tibshirani (1996) in connection with the regression model.
Donoho and Johnstone (1994) defined this estimator as the “soft threshold estimator” (STE).
2.2.5 Bias and MSE Expression for the LASSO of Location Parameter
In order to derive the bias and MSE of LASSO estimators, we need the following lemma.
Using Lemma 2.1, we can find the bias and MSE expressions of 
.
2.2.6 Preliminary Test Estimator, Bias, and MSE
Based on Saleh (2006), the preliminary test estimators (PTEs) of 
under normality assumption of the errors are given by
Thus, we have the following theorem about bias and MSE.
2.2.7 Stein‐Type Estimation of Location Parameter
The PT heavily depends on the critical value of the test that 
may be zero. Thus, due to down effect of discreteness of the PTE, we define the Stein‐type estimator of 
as given here assuming 
is known
The bias of 
is 
, and the MSE of 
is given by
The value of 
that minimizes 
is 
, which is a decreasing function of 
with a maximum at 
and maximum value 
. Hence, the optimum value of MSE is
The REff compared to LSE, 
is
In general, the 
decreases from 
at 
, then it crosses the 1‐line at 
, and for 
, 
performs better than 
.
2.2.8 Comparison of LSE, PTE, Ridge, SE, and LASSO
We know the following MSE from previous sections:
Hence, the REff expressions are given by
Table 2.1 Table of relative efficiency.
 |
 |
 |
 |
 |
 |
| 0.000 | 1.000 |  |
4.184 | 2.752 | 9.932 |
| 0.316 | 1.000 | 11.000 | 2.647 | 2.350 | 5.694 |
| 0.548 | 1.000 | 4.333 | 1.769 | 1.849 | 3.138 |
| 0.707 | 1.000 | 3.000 | 1.398 | 1.550 | 2.207 |
| 1.000 | 1.000 | 2.000 | 1.012 | 1.157 | 1.326 |
| 1.177 | 1.000 | 1.721 | 0.884 | 1.000 | 1.046 |
| 1.414 | 1.000 | 1.500 | 0.785 | 0.856 | 0.814 |
| 2.236 | 1.000 | 1.200 | 0.750 | 0.653 | 0.503 |
| 3.162 | 1.000 | 1.100 | 0.908 | 0.614 | 0.430 |
| 3.873 | 1.000 | 1.067 | 0.980 | 0.611 | 0.421 |
| 4.472 | 1.000 | 1.050 | 0.996 | 0.611 | 0.419 |
| 5.000 | 1.000 | 1.040 | 0.999 | 0.611 | 0.419 |
| 5.477 | 1.000 | 1.033 | 1.000 | 0.611 | 0.419 |
| 6.325 | 1.000 | 1.025 | 1.000 | 0.611 | 0.419 |
| 7.071 | 1.000 | 1.020 | 1.000 | 0.611 | 0.419 |
It is seen from Table 2.1 that the RRE dominates all other estimators uniformly and LASSO dominates UE, PTE, and 
in an interval near 0. From Table 2.1, we find 
in the interval 
while outside this interval 
. Figure 2.1 confirms that.
Figure 2.1 Relative efficiencies of the estimators.
2.3 Simple Linear Model
In this section, we consider the model (2.1) and define the PT, ridge, and LASSO‐type estimators when it is suspected that the slope may be zero.
2.3.1 Estimation of the Intercept and Slope Parameters
First, we consider the LSE of the parameters. Using the model (2.1) and the sample information from the normal distribution, we obtain the LSEs of 
as
where
The exact distribution of 
is a bivariate normal with mean 
and covariance matrix
An unbiased estimator of the variance 
is given by
which is independent of 
, and 
follows a central chi‐square distribution with 
degrees of freedom (DF)
2.3.2 Test for Slope Parameter
Suppose that we want to test the null‐hypothesis 
vs. 
. Then, we use the likelihood ratio (LR) test statistic
where 
follows a noncentral chi‐square distribution with 1 DF and noncentrality parameter 
and 
follows a noncentral 
‐distribution with 
, where 
is DF and also the noncentral parameter is
Under 
, 
follows a central chi‐square distribution and 
follows a central 
‐distribution. At the 
‐level of significance, we obtain the critical value 
or 
from the distribution and reject 
if 
or 
; otherwise, we accept 
.
2.3.3 PTE of the Intercept and Slope Parameters
This section deals with the problem of estimation of the intercept and slope parameters 
when it is suspected that the slope parameter 
may be 
.
From (2.30), we know that the LSE of 
is given by
If we know 
to be 
exactly, then the restricted least squares estimator (RLSE) of 
is given by
In practice, the prior information that 
is uncertain. The doubt regarding this prior information can be removed using Fisher's recipe of testing the null‐hypothesis 
against the alternative 
. As a result of this test, we choose 
or 
based on the rejection or acceptance of 
. Accordingly, in case of the unknown variance, we write the estimator as
called the PTE, where 
is the 
‐level upper critical value of a central 
‐distribution with 
DF and 
is the indicator function of the set 
. For more details on PTE, see Saleh (2006), Ahmed and Saleh (1988), Ahsanullah and Saleh (1972), Kibria and Saleh (2012) and, recently Saleh et al. (2014), among others. We can write PTE of 
as
If 
, 
is always chosen; and if 
, 
is chosen. Since 
, 
in repeated samples, this will result in a combination of 
and 
. Note that the PTE procedure leads to the choice of one of the two values, namely, either 
or 
. Also, the PTE procedure depends on the level of significance 
.
Clearly, 
is the unrestricted estimator of 
, while 
is the restricted estimator. Thus, the PTE of 
is given by
Now, if 
, 
is always chosen; and if 
, 
is always chosen.
Since our interest is to compare the LSE, RLSE, and PTE of 
and 
with respect to bias and the MSE, we obtain the expression of these quantities in the following theorem. First we consider the bias expressions of the estimators.
Next, we consider the expressions for the MSEs of 
, 
, and 
along with the 
, 
, and 
.
2.3.4 Comparison of Bias and MSE Functions
Since the bias and MSE expressions are known to us, we may compare them for the three estimators, namely, 
, 
, and 
as well as 
, 
, and 
. Note that all the expressions are functions of 
, which is the noncentrality parameter of the noncentral 
‐distribution. Also, 
is the standardized distance between 
and 
. First, we compare the bias functions as in Theorem 2.4, when 
is unknown.
For 
or under 
,
Otherwise, for all 
and 
,
The absolute bias of 
is linear in 
, while the absolute bias of 
increases to the maximum as 
moves away from the origin, and then decreases toward zero as 
. Similar conclusions hold for 
.
Now, we compare the MSE functions of the restricted estimators and PTEs with respect to the traditional estimator, 
and 
, respectively. The REff of 
compared to 
may be written as
The efficiency is a decreasing function of 
. Under 
(i.e. 
), it has the maximum value
and 
, accordingly, as 
. Thus, 
performs better than 
whenever 
; otherwise, 
performs better 
.
The REff of 
compared to 
may be written as
where
Under the 
, it has the maximum value
and 
according as
Hence, 
performs better than 
if 
; otherwise, 
is better than 
. Since
we obtain
Figure 2.2 Graph of 
and 
for 
and 
.
As for the PTE of 
, it is better than 
, if
Otherwise, 
is better than 
. The
Under 
,
See Figure 2.2 for visual comparison between estimators.
2.3.5 Alternative PTE
In this subsection, we provide the alternative expressions for the estimator of PT and its bias and MSE. To test the hypothesis 
vs. 
, we use the following test statistic:
The PTE of 
is given by
where 
.
Hence, the bias of 
equals 
, and the MSE is given by
Next, we consider the Stein‐type estimator of 
as
The bias and MSE expressions are given respectively by
As a consequence, we may define the PT and Stein‐type estimators of 
given by
Then, the bias and MSE expressions of 
are
where
Similarly, the bias and MSE expressions for 
are given by
2.3.6 Optimum Level of Significance of Preliminary Test
Consider the REff of 
compared to 
. Denoting it by 
, we have
where
The graph of 
, as a function of 
for fixed 
, is decreasing crossing the 1‐line to a minimum at 
(say); then it increases toward the 1‐line as 
. The maximum value of 
occurs at 
with the value
for all 
, the set of possible values of 
. The value of 
decreases as 
‐values increase. On the other hand, if 
and 
vary, the graphs of 
and 
intersect at 
. In general, 
and 
intersect within the interval 
; the value of 
at the intersection increases as 
‐values increase. Therefore, for two different 
‐values, 
and 
will always intersect below the 1‐line.
In order to obtain a PTE with a minimum guaranteed efficiency, 
, we adopt the following procedure: If 
, we always choose 
, since 
in this interval. However, since in general 
is unknown, there is no way to choose an estimate that is uniformly best. For this reason, we select an estimator with minimum guaranteed efficiency, such as 
, and look for a suitable 
from the set, 
. The estimator chosen maximizes 
over all 
and 
. Thus, we solve the following equation for the optimum 
:
The solution 
obtained this way gives the PTE with minimum guaranteed efficiency 
, which may increase toward 
given by (2.61), and Table 2.2. For the following given data, we have computed the maximum and minimum guaranteed REff for the estimators of 
and provided them in Table 2.2.
Table 2.2 Maximum and minimum guaranteed relative efficiency.
 |
||||||
| 0.05 | 0.10 | 0.15 | 0.20 | 0.25 | 0.50 | |
 |
||||||
 |
4.825 | 2.792 | 2.086 | 1.726 | 1.510 | 1.101 |
 |
0.245 | 0.379 | 0.491 | 0.588 | 0.670 | 0.916 |
 |
8.333 | 6.031 | 5.005 | 4.429 | 4.004 | 3.028 |
 |
||||||
 |
4.599 | 2.700 | 2.034 | 1.693 | 1.487 | 1.097 |
 |
0.268 | 0.403 | 0.513 | 0.607 | 0.686 | 0.920 |
 |
7.533 | 5.631 | 4.755 | 4.229 | 3.879 | 3.028 |
 |
||||||
 |
4.325 | 2.587 | 1.970 | 1.652 | 1.459 | 1.091 |
 |
0.268 | 0.403 | 0.513 | 0.607 | 0.686 | 0.920 |
 |
6.657 | 5.180 | 4.454 | 4.004 | 3.704 | 2.978 |
 |
||||||
 |
4.165 | 2.521 | 1.933 | 1.628 | 1.443 | 1.088 |
 |
0.319 | 0.452 | 0.557 | 0.644 | 0.717 | 0.928 |
 |
6.206 | 4.955 | 4.304 | 3.904 | 3.629 | 2.953 |
2.3.7 Ridge‐Type Estimation of Intercept and Slope
In this section, we consider the ridge‐type shrinkage estimation of 
when it is suspected that the slope 
may be 0. In this case, we minimize the objective function with a solution as given here:
which yields two equations
Hence,
2.3.7.1 Bias and MSE Expressions
From (2.65), it is easy to see that the bias expression of 
and 
, respectively, are given by
Similarly, MSE expressions of the estimators are given by
where 
and
Hence, the REff of these estimators are given by
Note that the optimum value of 
is 
. Hence,
2.3.8 LASSO Estimation of Intercept and Slope
In this section, we consider the LASSO estimation of 
when it is suspected that 
may be 0. For this case, the solution is given by
Explicitly, we find
where 
and 
.
According to Donoho and Johnstone (1994), and results of Section 2.2.5, the bias and MSE expressions for 
are given by
where
Similarly, the bias and MSE expressions for 
are given by
Then the REff is obtained as
For the following given data, we have computed the REff for the estimators of 
and 
and provided them in Tables 2.3 and 2.4 and in Figures 2.3 and 2.4, respectively.
It is seen from Tables 2.3 and 2.4 and Figures 2.3 and 2.4 that the RRE dominates all other estimators but the restricted estimator uniformly and that LASSO dominates LSE, PTE, and SE uniformly except RRE and RLSE in a subinterval 
.
Table 2.3 Relative efficiency of the estimators for 
.
| Delta | LSE | RLSE | PTE | RRE | LASSO | SE |
| 0.000 | 1.000 |  |
2.987 | 9.426 | 5.100 | 2.321 |
| 0.100 | 1.000 | 10.000 | 2.131 | 5.337 | 3.801 | 2.056 |
| 0.300 | 1.000 | 3.333 | 1.378 | 3.201 | 2.558 | 1.696 |
| 0.500 | 1.000 | 2.000 | 1.034 | 2.475 | 1.957 | 1.465 |
| 1.000 | 1.000 | 1.000 | 0.666 | 1.808 | 1.282 | 1.138 |
| 1.177 | 1.000 | 0.849 | 0.599 | 1.696 | 1.155 | 1.067 |
| 2.000 | 1.000 | 0.500 | 0.435 | 1.424 | 0.830 | 0.869 |
| 5.000 | 1.000 | 0.200 | 0.320 | 1.175 | 0.531 | 0.678 |
| 10.000 | 1.000 | 0.100 | 0.422 | 1.088 | 0.458 | 0.640 |
| 15.000 | 1.000 | 0.067 | 0.641 | 1.059 | 0.448 | 0.638 |
| 20.000 | 1.000 | 0.050 | 0.843 | 1.044 | 0.447 | 0.637 |
| 25.000 | 1.000 | 0.040 | 0.949 | 1.036 | 0.447 | 0.637 |
| 30.000 | 1.000 | 0.033 | 0.986 | 1.030 | 0.447 | 0.637 |
| 40.000 | 1.000 | 0.025 | 0.999 | 1.022 | 0.447 | 0.637 |
| 50.000 | 1.000 | 0.020 | 1.000 | 1.018 | 0.447 | 0.637 |
Table 2.4 Relative efficiency of the estimators for 
.
| Delta | LSE | RLSE | PTE | RRE | LASSO | SE |
| 0.000 | 1.000 |  |
3.909 |  |
9.932 | 2.752 |
| 0.100 | 1.000 | 10.000 | 2.462 | 10.991 | 5.694 | 2.350 |
| 0.300 | 1.000 | 3.333 | 1.442 | 4.330 | 3.138 | 1.849 |
| 0.500 | 1.000 | 2.000 | 1.039 | 2.997 | 2.207 | 1.550 |
| 1.000 | 1.000 | 1.000 | 0.641 | 1.998 | 1.326 | 1.157 |
| 1.177 | 1.000 | 0.849 | 0.572 | 1.848 | 1.176 | 1.075 |
| 2.000 | 1.000 | 0.500 | 0.407 | 1.499 | 0.814 | 0.856 |
| 5.000 | 1.000 | 0.200 | 0.296 | 1.199 | 0.503 | 0.653 |
| 10.000 | 1.000 | 0.100 | 0.395 | 1.099 | 0.430 | 0.614 |
| 15.000 | 1.000 | 0.067 | 0.615 | 1.066 | 0.421 | 0.611 |
| 20.000 | 1.000 | 0.050 | 0.828 | 1.049 | 0.419 | 0.611 |
| 25.000 | 1.000 | 0.040 | 0.943 | 1.039 | 0.419 | 0.611 |
| 30.000 | 1.000 | 0.033 | 0.984 | 1.032 | 0.419 | 0.611 |
| 40.000 | 1.000 | 0.025 | 0.999 | 1.024 | 0.419 | 0.611 |
| 50.000 | 1.000 | 0.020 | 1.000 | 1.019 | 0.419 | 0.611 |
Figure 2.3 Relative efficiency of the estimators for 
.
Figure 2.4 Relative efficiency of the estimators for 
.
2.4 Summary and Concluding Remarks
This chapter considers the location model and the simple linear regression model when errors of the models are normally distributed. We consider LSE, RLSE, PTE, SE and two penalty estimators, namely, the RRE and the LASSO estimator for the location parameter for the location model and the intercept and slope parameter for the simple linear regression model. We found that the RRE uniformly dominates LSE, PTE, SE, and LASSO. However, RLSE dominates all estimators near the null hypothesis. LASSO dominates LSE, PTE, and SE uniformly.
Problems
- 2.1 Derive the estimate in (2.4) using the least squares method.
- 2.2
- Consider the simple location model
and show that for testing the null‐hypothesis 
against of 
, the test statistic is
and
where
is the unbiased estimator of 
. - What will be the distribution for
and 
under null and alternative hypotheses?
- Consider the simple location model
- 2.3
Show that the optimum value of ridge parameter
is 
and
- 2.4
Consider LASSO for location parameter
and show that
- 2.5 Prove Theorem 2.3.
- 2.6 Consider the simple linear model and derive the estimates given in (2.32) using the least squares method.
- 2.7 Consider the simple linear model and show that to test the null‐hypothesis
vs. 
. Then, we use the LR test statistic
where
follows a noncentral chi‐square distribution with 1 DF and noncentrality parameter 
and 
follows a noncentral 
‐distribution with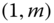 
, 
DF and noncentral parameter, - 2.8 Prove Theorems 2.4 and 2.5.
- 2.9
Consider the LASSO estimation of the intercept and slope models and show that the bias and MSE of
are, respectively,
- 2.10
Show that when
is known, LASSO outperforms the PTE whenever
