7
Partially Linear Regression Models
7.1 Introduction
In this chapter, the problem of ridge estimation is studied in the context of partially linear models (PLMs). In a nutshell, PLMs are smoothed models that include both parametric and nonparametric parts. They allow more flexibility compared to full/nonparametric regression models.
Consider the usual PLM with the form
where ![]() is a vector of explanatory variables,
is a vector of explanatory variables, ![]() is an unknown
is an unknown ![]() ‐dimensional parameter vector, the
‐dimensional parameter vector, the ![]() 's are known and nonrandom in some bounded domain
's are known and nonrandom in some bounded domain ![]() ,
, ![]() is an unknown smooth function, and
is an unknown smooth function, and ![]() 's are i.i.d. random errors with mean 0, variance
's are i.i.d. random errors with mean 0, variance ![]() , which are independent of
, which are independent of ![]() . PLMs are more flexible than standard linear models since they have both parametric and nonparametric components. They can be a suitable choice when one suspects that the response
. PLMs are more flexible than standard linear models since they have both parametric and nonparametric components. They can be a suitable choice when one suspects that the response ![]() linearly depends on
linearly depends on ![]() , but that it is nonlinearly related to
, but that it is nonlinearly related to ![]() .
.
Surveys regarding the estimation and application of the model (7.1) can be found in the monograph of Hardle et al. (2000). Raheem et al. (2012) considered absolute penalty and shrinkage estimators in PLMs where the vector of coefficients ![]() in the linear part can be partitioned as
in the linear part can be partitioned as ![]() ;
; ![]() is the coefficient vector of the main effects, and
is the coefficient vector of the main effects, and ![]() is the vector of the nuisance effects. For a more recent study about PLM, we refer to Roozbeh and Arashi (2016b). Since for estimation
is the vector of the nuisance effects. For a more recent study about PLM, we refer to Roozbeh and Arashi (2016b). Since for estimation ![]() , we need to estimate the nonparametric component
, we need to estimate the nonparametric component ![]() , we estimate it using the kernel smoothing method. Throughout, we do not further discuss the estimation of
, we estimate it using the kernel smoothing method. Throughout, we do not further discuss the estimation of ![]() in PLMs, since the main concern is the estimation of
in PLMs, since the main concern is the estimation of ![]() in the ridge context.
in the ridge context.
To estimate ![]() , assume that
, assume that ![]() ,
, ![]() satisfy the model (7.1). Since
satisfy the model (7.1). Since ![]() , we have
, we have ![]() for
for ![]() . Hence, if we know
. Hence, if we know ![]() , a natural nonparametric estimator of
, a natural nonparametric estimator of ![]() is given by
is given by

where the positive weight function ![]() satisfies the three regularity conditions given here:
satisfies the three regularity conditions given here:
 ,
, ,
,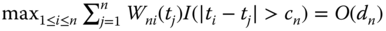 , where
, where  is the indicator function of the set
is the indicator function of the set  ,
,

These assumptions guarantee the existence of ![]() at the optimal convergence rate
at the optimal convergence rate ![]() , in PLMs with probability one. See Müller and Rönz (1999) for more details.
, in PLMs with probability one. See Müller and Rönz (1999) for more details.
7.2 Partial Linear Model and Estimation
Consider the PLM defined by
where ![]() 's are responses,
's are responses, ![]() ,
, ![]() , are covariates of the unknown vectors, namely,
, are covariates of the unknown vectors, namely, ![]() and also
and also ![]() , respectively, and
, respectively, and ![]() are design points,
are design points, ![]() is a real valued function defined on
is a real valued function defined on ![]() , and
, and ![]() are independently and identically distributed (i.i.d.) errors with zero mean and constant variance,
are independently and identically distributed (i.i.d.) errors with zero mean and constant variance, ![]() .
.
Our main objective is to estimate ![]() when it is suspected that the
when it is suspected that the ![]() ‐dimensional sparsity condition
‐dimensional sparsity condition ![]() may hold. In this situation, we first estimate the parameter
may hold. In this situation, we first estimate the parameter ![]() using's Speckman's (1988) approach of partial kernel smoothing method, which attains the usual parametric convergence rate
using's Speckman's (1988) approach of partial kernel smoothing method, which attains the usual parametric convergence rate ![]() without undersmoothing the nonparametric component
without undersmoothing the nonparametric component ![]() .
.
Assume that ![]() satisfy the model (7.3). If
satisfy the model (7.3). If ![]() is the true parameter, then
is the true parameter, then ![]() . Also, for
. Also, for ![]() , we have
, we have
Thus, a natural nonparametric estimator of ![]() given
given ![]() is
is

with the probability weight functions ![]() satisfies the three regularity conditions (i)–(iii).
satisfies the three regularity conditions (i)–(iii).
Suppose that we partitioned the design matrix,

and others as
where

To estimate ![]() , we minimize
, we minimize

with respect to ![]() . This yields the estimator of
. This yields the estimator of ![]() as
as

where

respectively.
If ![]() is true, then the restricted estimator is
is true, then the restricted estimator is

Further, we assume that ![]() are i.i.d. random variables and let
are i.i.d. random variables and let
Then, the conditional variance of ![]() given
given ![]() is
is ![]() , where
, where ![]() with
with ![]() . Then, by law of large numbers (LLN),
. Then, by law of large numbers (LLN),

and the matrix ![]() is nonsingular with probability 1. Readers are referred to Shi and Lau (2000), Gao (1995, 1997), and Liang and Härdle (1999), among others. Moreover, for any permutation
is nonsingular with probability 1. Readers are referred to Shi and Lau (2000), Gao (1995, 1997), and Liang and Härdle (1999), among others. Moreover, for any permutation ![]() of
of ![]() as
as ![]() ,
,

Finally, we use the following assumption:
The functions ![]() and
and ![]() satisfy the Lipchitz condition of order 1 on
satisfy the Lipchitz condition of order 1 on ![]() for
for ![]() . Then, we have the following theorem.
. Then, we have the following theorem.
As a result of Theorem 7.1, we have the following limiting cases:


 where
where  is the
is the  th diagonal element of
th diagonal element of  .
.
7.3 Ridge Estimators of Regression Parameter
Let the PLM be given as the following form
where
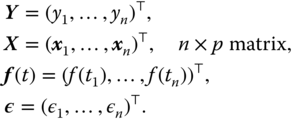
In general, we assume that ![]() is an
is an ![]() ‐vector of i.i.d. random variables with distribution
‐vector of i.i.d. random variables with distribution ![]() , where
, where ![]() is a symmetric, positive definite known matrix and
is a symmetric, positive definite known matrix and ![]() is an unknown parameter.
is an unknown parameter.
Using the model (7.20) and the error distribution of ![]() we obtain the maximum likelihood estimator (MLE) or generalized least squares estimator (GLSE) of
we obtain the maximum likelihood estimator (MLE) or generalized least squares estimator (GLSE) of ![]() by minimizing
by minimizing
to get
where ![]() ,
, ![]() ,
, ![]() , and
, and ![]() ,
, ![]() .
.
Now, under a restricted modeling paradigm, suppose that ![]() satisfies the following linear nonstochastic constraints
satisfies the following linear nonstochastic constraints
where ![]() is a
is a ![]() nonzero matrix with rank
nonzero matrix with rank ![]() and
and ![]() is a
is a ![]() vector of prespecified values. We refer restricted partially linear model (RPLM) to (7.20). For the RPLM, one generally adopts the well‐known GLSE given by
vector of prespecified values. We refer restricted partially linear model (RPLM) to (7.20). For the RPLM, one generally adopts the well‐known GLSE given by
The GLSE is widely used as an unbiased estimator. We refer to Saleh (2006) and Saleh et al. (2014) for more details and applications of restricted parametric or nonparametric models.
Now, in the line of this book, if there exists multicollinearity in ![]() , the
, the ![]() would be badly apart from the actual coefficient parameter in some directions of
would be badly apart from the actual coefficient parameter in some directions of ![]() ‐dimension space. Hence, instead of minimizing the GLSE objective function as in (7.21), following Roozbeh (2015), one may minimize the objective function where both
‐dimension space. Hence, instead of minimizing the GLSE objective function as in (7.21), following Roozbeh (2015), one may minimize the objective function where both ![]() and
and ![]() are penalty functions
are penalty functions
where ![]() is a vector of constants.
is a vector of constants.
The resulting estimator is the restricted generalized ridge estimator (GRE), given by
where

is the GRE and ![]() is the ridge parameter.
is the ridge parameter.
From Saleh (2006), the likelihood ratio criterion for testing the null hypothesis ![]() , is given by
, is given by

where ![]() ,
, ![]() , is an unbiased estimator of
, is an unbiased estimator of ![]() .
.
Note that ![]() follows a noncentral
follows a noncentral ![]() ‐distribution with
‐distribution with ![]() DF and noncentrality parameter
DF and noncentrality parameter ![]() given by
given by

Following Saleh (2006), we define three sorts of estimators using the test statistic ![]() . First, we consider the preliminary test generalized ridge estimator (PTGRE) defined by
. First, we consider the preliminary test generalized ridge estimator (PTGRE) defined by
where ![]() is the upper
is the upper ![]() ‐level critical value for the test of
‐level critical value for the test of ![]() and
and ![]() is the indicator function of the set
is the indicator function of the set ![]() .
.
This estimator has been considered by Saleh and Kibria (1993). The PTGRE has the disadvantage that it depends on ![]() , the level of significance, and also it yields the extreme results, namely,
, the level of significance, and also it yields the extreme results, namely, ![]() and
and ![]() depending on the outcome of the test.
depending on the outcome of the test.
A nonconvex continuous version of the PTGRE is the Stein‐type generalized ridge estimator (SGRE) defined by

The Stein‐type generalized ridge regression has the disadvantage that it has strange behavior for small values of ![]() . Also, the shrinkage factor
. Also, the shrinkage factor ![]() becomes negative for
becomes negative for ![]() . Hence, we define the positive‐rule Stein‐type generalized ridge estimator (PRSGRE) given by
. Hence, we define the positive‐rule Stein‐type generalized ridge estimator (PRSGRE) given by
Shrinkage estimators have been considered by Arashi and Tabatabaey (2009), Arashi et al. (2010, 2012), Arashi (2012), and extended to monotone functional estimation in multidimensional models just as the additive regression model, semi‐parametric PLM, and generalized linear model by Zhang et al. (2008).
7.4 Biases and  Risks of Shrinkage Estimators
Risks of Shrinkage Estimators
In this section, we give exact expressions of the bias and ![]() ‐risk functions for the estimators
‐risk functions for the estimators ![]() and
and ![]() . Since the properties of unrestricted, restricted, and preliminary test estimators have been widely investigated in the literature, we refer to Sarkar (1992) and Saleh and Kibria (1993) for the properties of unrestricted, restricted, and preliminary test generalized ridge regression estimator.
. Since the properties of unrestricted, restricted, and preliminary test estimators have been widely investigated in the literature, we refer to Sarkar (1992) and Saleh and Kibria (1993) for the properties of unrestricted, restricted, and preliminary test generalized ridge regression estimator.
For analytical comparison between the proposed estimators, we refer to Roozbeh (2015) and continue our study with numerical results.
7.5 Numerical Analysis
To examine the ![]() ‐risk performance of the proposed estimators, we adopted the Monte Carlo simulation study of Roozbeh (2015) for illustration.
‐risk performance of the proposed estimators, we adopted the Monte Carlo simulation study of Roozbeh (2015) for illustration.
To achieve different degrees of collinearity, following Kibria (2003) the explanatory variables were generated using the given model for ![]() :
:
where ![]() are independent standard normal pseudorandom numbers, and
are independent standard normal pseudorandom numbers, and ![]() is specified so that the correlation between any two explanatory variables is given by
is specified so that the correlation between any two explanatory variables is given by ![]() . These variables are then standardized so that
. These variables are then standardized so that ![]() and
and ![]() are in correlation forms. Three different sets of correlation corresponding to
are in correlation forms. Three different sets of correlation corresponding to ![]() , and 0.99 are considered. Then
, and 0.99 are considered. Then ![]() observations for the dependent variable are determined by
observations for the dependent variable are determined by

where ![]() , and
, and

which is a mixture of normal densities for ![]() and
and ![]() is the normal probability density function (p.d.f.) with mean
is the normal probability density function (p.d.f.) with mean ![]() and variance
and variance ![]() . The main reason for selecting such a structure for the nonlinear part is to check the efficiency of the nonparametric estimations for wavy function. This function is difficult to estimate and provides a good test case for the nonparametric regression method.
. The main reason for selecting such a structure for the nonlinear part is to check the efficiency of the nonparametric estimations for wavy function. This function is difficult to estimate and provides a good test case for the nonparametric regression method.
According to Roozbeh (2015), it is assumed ![]() , for which the elements of
, for which the elements of ![]() are
are ![]() and
and ![]() . The set of linear restrictions is assumed to have form
. The set of linear restrictions is assumed to have form ![]() , where
, where

For the weight function ![]() , we use
, we use

which is Priestley and Chao's weight with the Gaussian kernel. We also apply the cross‐validation (CV) method to select the optimal bandwidth ![]() , which minimizes the following CV function
, which minimizes the following CV function

where ![]() obtains by replacing
obtains by replacing ![]() and
and ![]() by
by

Here, ![]() is the predicted value of
is the predicted value of ![]() at
at ![]() with
with ![]() and
and ![]() left out of the estimation of the
left out of the estimation of the ![]() .
.
The ratio of largest eigenvalue to smallest eigenvalue of the design matrix in model (7.24) is approximately ![]() , and 14 495.28 for
, and 14 495.28 for ![]() , and 0.99, respectively.
, and 0.99, respectively.
In Tables 7.1–7.6, we computed the proposed estimators' ![]() risk,
risk,

for different values of ![]() and
and ![]() .
.
We found the best values of ![]() (
(![]() ) by plotting
) by plotting
vs. ![]() for each of the proposed estimators (see Figure 7.1).
for each of the proposed estimators (see Figure 7.1).
Figure 7.2 shows the fitted function by kernel smoothing after estimation of the linear part of the model using ![]() and
and ![]() , that are,
, that are, ![]() , respectively, for
, respectively, for ![]() , and 0.99. The minimum of CV approximately obtained was
, and 0.99. The minimum of CV approximately obtained was ![]() for the model (7.24) with
for the model (7.24) with ![]() . The diagram of CV vs.
. The diagram of CV vs. ![]() is also plotted in Figure 7.3.
is also plotted in Figure 7.3.
From the simulation, we found that at most ![]() for superiority of PRSGRE over SGLSE are 0.598, 0.792, and 0.844 for
for superiority of PRSGRE over SGLSE are 0.598, 0.792, and 0.844 for ![]() , and 0.99, respectively. It is realized that the ridge parameter
, and 0.99, respectively. It is realized that the ridge parameter ![]() is an increasing function of
is an increasing function of ![]() for superiority of PRSGRE over SGRE in
for superiority of PRSGRE over SGRE in ![]() ‐risk sense. These
‐risk sense. These ![]() values are 0.527, 0.697, and 0.730 for superiority of PRSGRE over PRSGLSE. Finally, the PRSGRE is better than SGRE for all values of
values are 0.527, 0.697, and 0.730 for superiority of PRSGRE over PRSGLSE. Finally, the PRSGRE is better than SGRE for all values of ![]() and
and ![]() in
in ![]() ‐risk sense.
‐risk sense.
Table 7.1 Evaluation of the Stein‐type generalized RRE at different ![]() values in model (7.24) with
values in model (7.24) with ![]() .
.
| Coefficients ( |
0 | 0.05 | 0.10 | 0.15 | 0.20 | 0.25 | 0.30 | |
| 1.986 | 1.986 | 1.986 | 1.986 | 1.987 | 1.987 | 2.004 | 1.987 | |
| 3.024 | 3.025 | 3.026 | 3.027 | 3.028 | 3.029 | 3.004 | 3.030 | |
| 3.999 | 4.002 | 4.005 | 4.008 | 4.011 | 4.013 | 3.996 | 4.016 | |
| 0.274 | 0.274 | 0.273 | 0.273 | 0.273 | 0.273 | 0.273 | 0.273 |
Table 7.2 Evaluation of PRSGRE at different ![]() values in model (7.24) with
values in model (7.24) with ![]() .
.
| Coefficients ( |
0 | 0.05 | 0.10 | 0.15 | 0.20 | 0.25 | 0.30 | |
| 2.008 | 2.007 | 2.006 | 2.006 | 2.005 | 2.005 | 2.004 | 2.004 | |
| 3.012 | 3.010 | 3.009 | 3.007 | 3.006 | 3.004 | 3.004 | 3.003 | |
| 4.016 | 4.012 | 4.008 | 4.004 | 4.000 | 3.997 | 3.996 | 3.993 | |
| 0.242 | 0.241 | 0.241 | 0.241 | 0.241 | 0.241 | 0.241 | 0.241 | |
| 0.027 | 0.027 | 0.027 | 0.028 | 0.028 | 0.028 | 0.028 | 0.028 |
Table 7.3 Evaluation of SGRE at different ![]() values in model (7.24) with
values in model (7.24) with ![]() .
.
| Coefficients ( |
0 | 0.10 | 0.20 | 0.30 | 0.40 | 0.50 | 0.60 | |
| 2.025 | 2.024 | 2.024 | 2.0232 | 2.022 | 2.022 | 2.021 | 2.020 | |
| 3.009 | 3.008 | 3.006 | 3.005 | 3.003 | 3.003 | 3.002 | 3.001 | |
| 3.992 | 3.989 | 3.985 | 3.982 498 | 3.979 | 3.979 | 3.975 | 3.972 | |
| 0.540 | 0.537 | 0.535 | 0.534 | 0.534 | 0.534 | 0.534 | 0.536 | |
| 0.090 | 0.090 | 0.089 | 0.089 | 0.089 | 0.089 | 0.088 | 0.088 |
Table 7.4 Evaluation of PRSGRE at different ![]() values in model (7.24) with
values in model (7.24) with ![]() .
.
| Coefficients ( |
0 | 0.10 | 0.20 | 0.30 | 0.40 | 0.50 | 0.60 | |
| 2.025 | 2.023 | 2.021 | 2.018 | 2.017 | 2.016 | 2.014 | 2.012 | |
| 3.009 | 3.005 | 3.000 | 2.996 | 2.994 | 2.991 | 2.987 | 2.983 | |
| 3.992 | 3.978 | 3.965 | 3.951 | 3.944 | 3.937 | 3.924 | 3.911 | |
| 0.476 | 0.474 | 0.472 | 0.471 787 | 0.471 | 0.471 | 0.472 | 0.474 | |
| 0.0903 | 0.0905 | 0.090 | 0.090 | 0.090 | 0.091 | 0.0912 | 0.091 |
Table 7.5 Evaluation of SGRE at different ![]() values in model (7.24) with
values in model (7.24) with ![]() .
.
| Coefficients ( |
0 | 0.10 | 0.20 | 0.30 | 0.40 | 0.50 | 0.60 | |
| 1.487 | 1.500 | 1.510 | 1.517 | 1.522 | 1.523 | 1.525 | 1.527 | |
| 3.046 | 3.024 | 3.001 | 2.977 | 2.954 | 2.949 | 2.930 | 2.906 | |
| 5.025 | 4.854 | 4.700 | 4.563 | 4.438 | 4.412 | 4.324 | 4.221 | |
| 5.748 | 5.391 | 5.179 | 5.082 | 5.076 | 5.085 | 5.142 | 5.265 | |
| 0.040 | 0.040 | 0.041 | 0.041 | 0.042 | 0.042 | 0.042 | 0.042 |
Table 7.6 Evaluation of PRSGRE at different ![]() values in model (7.24) with
values in model (7.24) with ![]() .
.
| Coefficients ( |
0 | 0.10 | 0.20 | 0.30 | 0.40 | 0.50 | 0.60 | |
| 1.487 | 1.496 | 1.501 | 1.503 | 1.503 | 1.503 | 1.500 | 1.496 | |
| 3.046 | 3.007 | 2.967 | 2.927 | 2.901 | 2.887 | 2.847 | 2.808 | |
| 5.025 | 4.786 | 4.572 | 4.379 | 4.264 | 4.205 | 4.046 | 3.901 | |
| 5.060 | 4.752 | 4.584 | 4.525 | 4.534 | 4.552 | 4.648 | 4.798 | |
| 0.040 | 0.041 | 0.042 | 0.042 | 0.043 | 0.043 | 0.044 | 0.045 |
7.5.1 Example: Housing Prices Data
The housing prices data consist of 92 detached homes in the Ottawa area that were sold during 1987. The variables are defined as follows. The dependent variable is sale price (SP), the independent variables include lot size (lot area; LT), square footage of housing (SFH), average neighborhood income (ANI), distance to highway (DHW), presence of garage (GAR), and fireplace (FP). The full parametric model has the form

Looking at the correlation matrix given in Table 7.7, there exists a potential multicollinearity between variables SFH & FP and DHW & ANI.
We find that the eigenvalues of the matrix ![]() are given by
are given by ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() . It is easy to see that the condition number is approximately equal to
. It is easy to see that the condition number is approximately equal to ![]() . So,
. So, ![]() is morbidity badly.
is morbidity badly.

Figure 7.1 Plots of  and risks vs.
and risks vs.  for different values of
for different values of  .
.

Figure 7.2 Estimation of the mixtures of normal p.d.fs by the kernel approach. Solid lines are the estimates and dotted lines are the true functions.

Figure 7.3 Plot of CV vs. 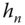 .
.
Table 7.7 Correlation matrix.
| Variable | SP | LT | SFH | FP | DHW | GAR | ANI |
| SP | 1.00 | 0.14 | 0.47 | 0.33 | 0.29 | 0.34 | |
| LT | 0.14 | 1.00 | 0.15 | 0.15 | 0.08 | 0.16 | 0.13 |
| SFH | 0.47 | 0.15 | 1.00 | 0.46 | 0.02 | 0.22 | 0.27 |
| FP | 0.33 | 0.15 | 0.46 | 1.00 | 0.10 | 0.14 | 0.38 |
| DHW | 0.08 | 0.02 | 0.10 | 1.00 | 0.05 | ||
| GAR | 0.29 | 0.16 | 0.22 | 0.14 | 0.05 | 1.00 | 0.02 |
| ANI | 0.34 | 0.13 | 0.27 | 0.38 | 0.02 | 1.00 |
An appropriate approach, as a remedy for multicollinearity, is to replace the pure parametric model with a PLM. Akdeniz and Tabakan (2009) proposed a PLM (here termed as semi‐parametric model) for this data by taking the lot area as the nonparametric component.

Figure 7.4 Plots of individual explanatory variables vs. dependent variable, linear fit (dash line), and local polynomial fit (solid line).
To realize the type of relation from linearity/nonlinearity viewpoint between dependent variable (SP) and explanatory variables (except for the binary ones), they are plotted in Figure 7.4. According to this figure, we consider the average neighborhood income (ANI) as a nonparametric part. So, the specification of the semi‐parametric model is

To compare the performance of the proposed restricted estimators, following Roozbeh (2015), we consider the parametric restriction ![]() , where
, where

The test statistic for testing ![]() , given our observations, is
, given our observations, is
where ![]() . Thus, we conclude that the null‐hypothesis
. Thus, we conclude that the null‐hypothesis ![]() is accepted.
is accepted.
Table 7.8 summarizes the results. The “parametric estimates” refer to a model in which ANI enters. In the “semiparametric estimates,” we have used the kernel regression procedure with optimal bandwidth ![]() for estimating
for estimating ![]() . For estimating the nonparametric effect, first we estimated the parametric effects and then applied the kernel approach to fit
. For estimating the nonparametric effect, first we estimated the parametric effects and then applied the kernel approach to fit ![]() on
on ![]() for
for ![]() , where
, where ![]() (Figure 7.5).
(Figure 7.5).
Table 7.8 Fitting of parametric and semi‐parametric models to housing prices data.
| Parametric estimates | Semiparametric estimates | |||
| Variable | Coef. | s.e. | Coef. | s.e. |
| Intercept | 62.67 | 20.69 | — | — |
| LT | 0.81 | 2.65 | 9.40 | 2.25 |
| SFH | 39.27 | 11.99 | 73.45 | 11.15 |
| FP | 6.05 | 7.68 | 5.33 | 8.14 |
| DHW | |
6.77 | |
7.28 |
| GAR | 14.47 | 6.38 | 12.98 | 7.20 |
| ANI | 0.56 | 0.28 | — | — |
| 798.0625 | 149.73 | |||
| 33 860.06 | 88 236.41 | |||
| 0.3329 | 0.86 | |||
The ratio of largest to smallest eigenvalues for the new design matrix in model (7.25) is approximately ![]() , and so there exists a potential multicollinearity between the columns of the design matrix. Now, in order to overcome the multicollinearity for better performance of the estimators, we used the proposed estimators for model (7.25).
, and so there exists a potential multicollinearity between the columns of the design matrix. Now, in order to overcome the multicollinearity for better performance of the estimators, we used the proposed estimators for model (7.25).
The SGRRE and PRSGRE for different values of the ridge parameter are given in Tables 7.9 and 7.10, respectively. As it can be seen, ![]() is the best estimator for the linear part of the semi‐parametric regression model in the sense of risk.
is the best estimator for the linear part of the semi‐parametric regression model in the sense of risk.

Figure 7.5 Estimation of nonlinear effect of ANI on dependent variable by kernel fit.
In Figure 7.6, the ![]() and
and ![]() of SGRE (solid line) and PRSGDRE (dash line) vs. ridge parameter
of SGRE (solid line) and PRSGDRE (dash line) vs. ridge parameter ![]() are plotted. Finally, we estimated the nonparametric effect (
are plotted. Finally, we estimated the nonparametric effect (![]() ) after estimation of the linear part by
) after estimation of the linear part by ![]() in Figure 7.7, i.e. we used kernel fit to regress
in Figure 7.7, i.e. we used kernel fit to regress ![]() on
on ![]() .
.
Table 7.9 Evaluation of SGRRE at different ![]() values for housing prices data.
values for housing prices data.
| Variable ( |
0.0 | 0.10 | 0.20 | 0.30 | 0.40 | 0.50 | 0.60 | |
| Intercept | — | — | — | — | — | — | — | — |
| LT | 9.043 | 9.139 | 9.235 | 9.331 | 9.427 | 9.250 | 9.524 | 9.620 |
| SFH | 84.002 | 84.106 | 84.195 | 84.270 | 84.334 | 84.208 | 84.385 | 84.425 |
| FP | 0.460 | 0.036 | 0.376 | 0.777 | 1.168 | 0.441 | 1.549 | 1.919 |
| DHW | ||||||||
| GAR | 4.924 | 4.734 | 4.548 | 4.367 | 4.190 | 4.519 | 4.017 | 3.848 |
| ANI | — | — | — | — | — | — | — | — |
| 257.89 | 254.09 | 252.62 | 252.59 | 253.35 | 256.12 | 260.82 | 267.31 | |
| 2241.81 | 2241.08 | 2240.50 | 2240.42 | 2240.12 | 2240.03 | 2240.02 | 2240.18 |
Table 7.10 Evaluation of PRSGRRE at different ![]() values for housing prices data.
values for housing prices data.
| Variable ( |
0.0 | 0.10 | 0.20 | 0.30 | 0.40 | 0.50 | 0.60 | |
| Intercept | — | — | — | — | — | — | — | — |
| LT | 9.226 | 9.355 | 9.476 | 9.481 | 9.604 | 9.725 | 9.843 | 9.958 |
| SFH | 78.614 | 77.705 | 76.860 | 76.820 | 75.959 | 75.120 | 74.303 | 73.506 |
| FP | 2.953 | 3.229 | 3.483 | 3.495 | 3.751 | 3.998 | 4.237 | 4.466 |
| DHW | ||||||||
| GAR | 9.042 | 9.112 | 9.176 | 9.179 | 9.242 | 9.303 | 9.362 | 9.417 |
| ANI | — | — | — | — | — | — | — | — |
| 234.02 | 230.68 | 229.67 | 230.82 | 232.68 | 234.02 | 239.12 | 246.00 | |
| 2225.762 | 2233.685 | 2240.480 | 2240.838 | 2248.805 | 2256.785 | 2264.771 | 2272.758 |

Figure 7.6 The diagrams of  and risk vs.
and risk vs.  for housing prices data.
for housing prices data.

Figure 7.7 Estimation of  (ANI) by kernel regression after removing the linear part by the proposed estimators in housing prices data.
(ANI) by kernel regression after removing the linear part by the proposed estimators in housing prices data.
7.6 High‐Dimensional PLM
In this section, we develop the theory proposed in the previous section for the high‐dimensional case in which ![]() . For our purpose, we adopt the structure of Arashi and Roozbeh (2016), i.e. we partition the regression parameter
. For our purpose, we adopt the structure of Arashi and Roozbeh (2016), i.e. we partition the regression parameter ![]() as
as ![]() , where the sub‐vector
, where the sub‐vector ![]() has dimension
has dimension ![]() ,
, ![]() and
and ![]() with
with ![]() . Hence, the model (7.20) has the form
. Hence, the model (7.20) has the form
where ![]() is partitioned according to
is partitioned according to ![]() in such a way that
in such a way that ![]() is a
is a ![]() sub‐matrix,
sub‐matrix, ![]() .
.
In this section, we consider the estimation of ![]() under the sparsity assumption
under the sparsity assumption ![]() . Hence, we minimize the objective function
. Hence, we minimize the objective function
where ![]() is a function of sample size
is a function of sample size ![]() and
and ![]() is a vector of constants.
is a vector of constants.
The resulting estimator of ![]() is the generalized ridge regression estimator (RRE), given by
is the generalized ridge regression estimator (RRE), given by

where ![]() and
and ![]() is the generalized restricted estimator of
is the generalized restricted estimator of ![]() given by
given by
Here, ![]() is the bandwidth parameter as a function of sample size
is the bandwidth parameter as a function of sample size ![]() , where we estimate
, where we estimate ![]() by
by ![]() ,
, ![]() with
with ![]() is a kernel function of order
is a kernel function of order ![]() with bandwidth parameter
with bandwidth parameter ![]() (see Arashi and Roozbeh 2016).
(see Arashi and Roozbeh 2016).
Note that the generalized (unrestricted) ridge estimators of ![]() and
and ![]() , respectively, have the forms
, respectively, have the forms

where

In order to derive the forms of shrinkage estimators, we need to find the test statistic for testing the null‐hypothesis ![]() . Thus, we make use of the following statistic
. Thus, we make use of the following statistic

where ![]() and
and
To find the asymptotic distribution of ![]() , we need to make some regularity conditions. Hence, we suppose the following assumptions hold
, we need to make some regularity conditions. Hence, we suppose the following assumptions hold
- (A1) (A1)
 , where
, where  is the
is the  th row of
th row of  .
. - (A2) (A2)
 as
as  ,
, - (A3) (A3) Let

Then, there exists a positive definite matrix
 such that
such that
- (A4) (A4)
 .
. - (A5) (A5)
 ,
,  .
.
Note that by (A2), (A4), and (A5), one can directly conclude that as ![]()
The test statistic ![]() diverges as
diverges as ![]() , under any fixed alternatives
, under any fixed alternatives ![]() . To overcome this difficulty, in sequel, we consider the local alternatives
. To overcome this difficulty, in sequel, we consider the local alternatives
where ![]() is a fixed vector.
is a fixed vector.
Then, we have the following result about the asymptotic distribution of ![]() . The proof is left as an exercise.
. The proof is left as an exercise.
Then, in a similar manner to that in Section 5.2, the PTGRE, SGRE, and PRSGRE of ![]() are defined respectively as
are defined respectively as


Under the foregoing regularity conditions (A1)–(A5) and local alternatives ![]() , one can derive asymptotic properties of the proposed estimators, which are left as exercise. To end this section, we present in the next section a real data example to illustrate the usefulness of the suggested estimators for high‐dimensional data.
, one can derive asymptotic properties of the proposed estimators, which are left as exercise. To end this section, we present in the next section a real data example to illustrate the usefulness of the suggested estimators for high‐dimensional data.
7.6.1 Example: Riboflavin Data
Here, we consider the data set about riboflavin (vitamin ![]() ) production in
) production in ![]() , which can be found in the R package “hdi”. There is a single real‐valued response variable which is the logarithm of the riboflavin production rate. Furthermore, there are
, which can be found in the R package “hdi”. There is a single real‐valued response variable which is the logarithm of the riboflavin production rate. Furthermore, there are ![]() explanatory variables measuring the logarithm of the expression level of 4088 genes. There is one rather homogeneous data set from
explanatory variables measuring the logarithm of the expression level of 4088 genes. There is one rather homogeneous data set from ![]() samples that were hybridized repeatedly during a fed batch fermentation process where different engineered strains and strains grown under different fermentation conditions were analyzed. Based on 100‐fold cross‐validation, the LASSO shrinks 4047 parameters to zero and remains
samples that were hybridized repeatedly during a fed batch fermentation process where different engineered strains and strains grown under different fermentation conditions were analyzed. Based on 100‐fold cross‐validation, the LASSO shrinks 4047 parameters to zero and remains ![]() significant explanatory variables.
significant explanatory variables.
To detect the nonparametric part of the model, for ![]() , we calculate
, we calculate
where ![]() is obtained by deleting the
is obtained by deleting the ![]() th column of matrix
th column of matrix ![]() . Among all 41 remaining genes, “
. Among all 41 remaining genes, “![]() ” had minimum
” had minimum ![]() value. We also use the added‐variable plots to identify the parametric and nonparametric components of the model. Added‐variable plots enable us to visually assess the effect of each predictor, having adjusted for the effects of the other predictors. By looking at the added‐variable plot (Figure 7.8), we consider “
value. We also use the added‐variable plots to identify the parametric and nonparametric components of the model. Added‐variable plots enable us to visually assess the effect of each predictor, having adjusted for the effects of the other predictors. By looking at the added‐variable plot (Figure 7.8), we consider “![]() ” as a nonparametric part. As it can be seen from this figure, the slope of the least squares line is equal to zero, approximately, and so, the specification of the sparse semi‐parametric regression model is
” as a nonparametric part. As it can be seen from this figure, the slope of the least squares line is equal to zero, approximately, and so, the specification of the sparse semi‐parametric regression model is
where ![]() and
and ![]() .
.

Figure 7.8 Added‐variable plot of explanatory variables  vs. dependent variable, linear fit (solid line) and kernel fit (dashed line).
vs. dependent variable, linear fit (solid line) and kernel fit (dashed line).
For estimating the nonparametric part of the model, ![]() , we use
, we use

which is Priestley and Chao's weight with the Gaussian kernel.
We also apply the CV method to select the optimal bandwidth ![]() and
and ![]() , which minimizes the following CV function
, which minimizes the following CV function

where ![]() is obtained by replacing
is obtained by replacing ![]() and
and ![]() with
with ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Table 7.11 shows a summary of the results. In this table, the RSS and ![]() , respectively, are the residual sum of squares and coefficient of determination of the model, i.e.
, respectively, are the residual sum of squares and coefficient of determination of the model, i.e. ![]() , and
, and ![]() . For estimation of the nonparametric effect, at first we estimated the parametric effects by one of the proposed methods and then the local polynomial approach was applied to fit
. For estimation of the nonparametric effect, at first we estimated the parametric effects by one of the proposed methods and then the local polynomial approach was applied to fit ![]() on
on ![]() ,
, ![]() .
.
Table 7.11 Evaluation of proposed estimators for real data set.
| Method | GRE | GRRE | SGRRE | PRSGRRE |
| RSS | 16.1187 | 1.9231 | 1.3109 | 1.1509 |
| 0.7282 | 0.9676 | 0.9779 | 0.9806 |
In this example, as can be seen from Figure 7.8, the nonlinear relation between dependent variable and ![]() can be detected, and so the pure parametric model does not fit the data; the semi‐parametric regression model fits more significantly. Further, from Table 7.11, it can be deduced that PRSGRE is quite efficient, in the sense that it has significant value of goodness of fit.
can be detected, and so the pure parametric model does not fit the data; the semi‐parametric regression model fits more significantly. Further, from Table 7.11, it can be deduced that PRSGRE is quite efficient, in the sense that it has significant value of goodness of fit.
7.7 Summary and Concluding Remarks
In this chapter, apart from the preliminary test and penalty estimators, we mainly concentrated on the Stein‐type shrinkage ridge estimators, for estimating the regression parameters of the partially linear regression models. We developed the problem of ridge estimation for the low/high‐dimensional case. We analyzed the performance of the estimators extensively in Monte Carlo simulations, where the nonparametric component of the model was estimated by the kernel method. The housing prices data used the low‐dimensional part and the riboflavin data used for the high‐dimensional part for practical illustrations, in which the cross‐validation function was applied to obtain the optimal bandwidth parameters.
Problems
- 7.1 Prove that the test statistic for testing
 is
is

and
 is the
is the  ‐level critical value. What would be the distribution of
‐level critical value. What would be the distribution of  under both null and alternative hypotheses?
under both null and alternative hypotheses? - 7.2 Prove that the biases of the Stein‐type and positive‐rule Stein‐type of generalized RRE are, respectively, given by

where
 and
and  are defined in Theorem 7.2.
are defined in Theorem 7.2. - 7.3
Show that the risks of the Stein‐type and positive‐rule Stein‐type of generalized RRE are, respectively, given by

- 7.4 Prove that the test statistic for testing
 is
is

where
 and
and
- 7.5 Prove Theorem 7.2.
- 7.6 Consider a real data set, where the design matrix elements are moderate to highly correlated, then find the efficiency of the estimators using unweighted risk functions. Find parallel formulas for the efficiency expressions and compare the results with that of the efficiency using weighted risk function. Are the two results consistent?
