Challenge Problem Solutions

(1) Let x and y be the lengths of the two randomly determined sides. That is, 0 < x < 1 and 0 < y < 1. Also, by the triangle inequality (a fancy way of saying that the shortest path between two points is along a straight line), we have x + y > 1. If we plot this inequality on the unit square (defining the triangular region above the diagonal from Y to X in Figure S1), then it is clear that all possible triangles (obtuse and acute) are associated with just the points in the upper diagonal triangle XYZ. That is, XYZ is the sample space of the problem, with area 1/2. For the triangle to be obtuse, we further require that x² + y² < 1, or , a condition that associates the points in the shaded region in Figure S1 with obtuse triangles. The area of the shaded region is

where the first term (the integral) is the area of the entire portion of the unit square below the curve and the second term is the area of the lower diagonal half of the unit square (which isn’t in the sample space). The probability we are after is then

The code obtuse1.m simulates this process. It randomly assigns values to x and y from 0 to 1 and, if x + y > 1, then it has a triangle and so further checks for the obtuse condition. It does this until a total of ten million triangles have been generated. When I ran the code several times, I got values for the probability of an obtuse triangle ranging from 0.5707 to 0.571, in fairly good agreement with theory.

Figure S1. Sample space for obtuse triangles.

(2) The geometric probability analysis in the Gazette assumes that the interior point is uniformly distributed over the interior of the entire equilateral triangle. One can certainly assume that, of course, but it isn’t part of the problem statement, and to simply say “we drop the rod and it breaks into three pieces” isn’t sufficient even to imply it. One could easily imagine the rod most likely to break in its middle, with the probability of breaking elsewhere diminishing in an infinity of different ways as one moves away from the rod’s midpoint. All the problem statement gives us are three values with a fixed sum (the lengths of the pieces), which means they are not even all independent. Three values do uniquely determine the location of an interior point, but uniformity over the interior of the equilateral triangle is a separate and distinct issue that needs to be established.

(3) We have two possible sets of triangle inequalities, which I’ll call I and II, for x < y and for x > y, respectively.

For I, these inequalities easily reduce to

and for II to

Plotting both sets of inequalities on the unit square (which is the sample space of the problem) in Figure S2 below, we see that set I gives us the upper triangular shaded area (in which x and y are such that triangles are possible from the broken pieces) and set II gives us the lower triangular shaded area (in which x and y are also such that triangles are possible from the broken pieces).

Figure S2. Sample space for broken glass rod.

Using the fundamental assumption of geometric probability (because x and y are both uniformly random), we have

This is the same answer arrived at in the Mathematical Gazette solution to Challenge Problem 2, with its (much) less specific definition of the meaning of breaking. Interesting! I won’t bother simulating this problem because Challenge Problem 4, using the same breaking procedure as here, starts where this problem leaves off; if something is wrong here we’ll see it with the simulation of Problem 4. As you’ll see, however, the Monte Carlo simulation in Problem 4 agrees quite well with theory.

(4) Suppose we are working with the lengths of x, y − x, and 1 − y (that is, with inequality set I from the previous problem). There can be only one obtuse angle in an obtuse triangle, and so there are just three equally likely choices for the side opposite the obtuse angle. Since the square of that side must be greater than the sum of the squares of the other two sides, we can write the following inequalities, one for each choice of side:

These inequalities quickly reduce to, in order,

All three of these inequalities are shown as shaded regions in Figure S3 (in the upper triangle, where set I applies), and if you repeat the above for set II you’ll see there are three more such regions in the lower triangle where the set II inequalities apply. The total probability associated with these six regions is the probability we have an obtuse triangle given that we have a triangle. The area of region (b), for example, is

Figure S3. Sample space for alternative broken glass rod.

and (perhaps initially, with just a bit of surprise) the area of region c is the same:

With a little thought, however, this shouldn’t be surprising, as all six areas are equal by symmetry: which of the three angles is the obtuse angle is arbitrary. The only remaining issue is whether or not these areas have any overlap. In fact, they don’t (for example, set 1/2(1 − x) = (1 − 2x ²)/(2(1 − x)) and solve; you’ll see this occurs only at x = 0). So, the total shaded area in the figure, representing obtuse triangles, is 6[3/8 − 1/2 ln(2)], and dividing by the area of the sample space gives us the probability for an obtuse triangle (given that we have a triangle after the breaking process):

The code obtuse2.m simulates this process until a total of ten million triangles have been generated, checking each triangle for the obtuse condition. When run several times, the code gave estimates for the probability ranging from 0.6819528 to 0.6825122.

(5) Let X be the random variable denoting the length of the shorter piece after the first break, and so 1 − X represents the length of the longer piece. Let Y be the random variable denoting the length of one of the pieces into which the piece of length 1 − X is then broken. We now have three pieces of lengths X, Y, and 1 − X − Y. The piece of length X is uniformly random from 0 to 1/2 (because the shorter piece would in fact be the longer piece if it were longer than 1/2), and Y is uniformly random from 0 to 1 − X. Let x and y be particular values for X and Y, respectively. Then, from the triangle inequalities we have the following required conditions for a triangle to exist:

x + y > 1 − x − y, x + (1 − x − y) > y, y + (1 − x − y) > x.

These quickly reduce to

or y > 1/2 − x and y < 1/2. In other words, y must be in the interval 1/2 − x < y < 1/2 for a triangle to exist. Since Y is uniform over 0 to 1 − X, the differential probability dP that Y has a particular value y somewhere in the interval 1/2 − x < y < 1/2 is

where f_X(x) is the probability density of X (which is 2 as X is uniform from 0 to 1/2) and f_X(x)dx is the probability X has a particular value in the differential interval x to x + dx. So the differential probability that Y has a particular value y somewhere in the interval 1/2 − x < y < 1/2 is

This differential probability for a triangle existing depends on X having the particular value of x: to find the total probability for a triangle to exist we simply integrate dP over all possible x. Thus, our probability (changing variable to u = 1 − x) is

The code long.m simulates this breaking process ten million times and, when run several times, produced estimates for the probability P ranging from 0.3861520 to 0.3866718.

(6) In Figure S4 I’ve drawn the dartboard (a circle centered on the origin, with the equation x² + y² = 1). We imagine the board has been rotated after the first dart has landed so the dart is on the x-axis a positive distance s from the origin, where s is in the interval 0 to 1. Because of the symmetry of the circle, we lose no generality in doing this. Next, imagine a thin circular band of radius s and very small width Δs centered on the origin. The probability the first dart has landed somewhere in that band is the area of the band divided by the area of dart board (because darts are uniform over the dartboard): (π(s + Δs)² − πs²)/= 2sΔs, where we ignore all powers of Δs higher than the first (because we are going to let Δs → 0, that is, let Δs → ds, in just a moment). Now, superimposed on the dartboard circle is another circle with unit radius, centered on the first dart, with equation (x − s)² + y² = 1. If the second dart lands outside this second circle (but inside the first circle, of course, as both darts hit the dartboard), then the second dart is at least unit distance from the first dart. That is, the second dart lands in the shaded, lune-shaped region that has area A(s), where A(0) = 0. The probability the second dart lands in the shaded region is (again) the area of the region divided by the area of the dartboard, that is, A(s)/π. Thus, the differential probability dP that the two darts are at least unit distance apart is the product of the probabilities of these two independent events:

Figure S4. Geometry of the two-dart problem.

The total probability we are after is simply the integral of dP over all s:

To do this integral, we first have to find A(s) which is itself an integral. Writing this integral as twice the area of that portion of the lune that is above the x-axis, we have

Using the integration formula (see any good set of math tables)

you can show (with just a bit of algebra) that

Thus,

or, changing the dummy variable of integration from s to x,

From the integration formulas (see your math tables again),

and

I’ll let you plug in the limits and do the arithmetic to confirm that P = 3/4π = 0.41349. … The code dd.m (for double-dart) simulates this process until it has generated ten million double hits on the dartboard, where the variable total is the number of double hits that are at least unit distance apart. The code achieves a uniform distribution of dart landing points by imagining the circular dartboard enclosed by a square centered on the origin with edge length 2 (the diameter of the dartboard). Pairs of darts are uniformly “tossed” at the square, and used in the rest of the simulation only if both darts of a pair land within the circular dartboard. (This technique, called the rejection method, for the obvious reason, has the disadvantage of being wasteful of the random number generator. A more sophisticated way to generate points uniformly distributed over a circle is discussed in my Digital Dice [Princeton 2008], pp. 16–18.) When run several times, the code’s estimate for P ranged from 0.4133726 to 0.4136745.

(7) Following the hint, I’ll create a simulation first and then, once you see the result, I think you will be immediately reminded of an earlier challenge problem. And that should let you see how to theoretically analyze the problem. The code inside.m has two distinct parts. The first is pretty straightforward, as it randomly selects three points on the circumference of a circle (a circle having, with no loss in generality, unit radius) that will be the vertices of a triangle. (Again following the hint, the first of these three random points is always the point (1, 0).) The second part of the inside.m code is bit trickier, as it has to answer the question, “Once the code has the vertex points, how does it determine if the origin is inside the triangle determined by the vertex points?”

For a human, of course, this is an easy task—just look! But, lacking eyes, a computer code can’t do that. There are several numerical ways to answer the question, but what I’ll now show you is perhaps the simplest in both computational demands and concept. In Figure S5 you see a representative case of a triangle with vertices at A = (X1, Y1), B = (X2, Y2), and C = (X3, Y3). The origin is shown as being inside the triangle ABC. Looking at this geometry, I think the following observation will make sense: a point P is inside the triangle if:

Figure S5. A point inside a triangle.

Any point in the exterior of ABC will not satisfy all three of these requirements. Now, here’s how to understand what the phrase “same side of” means.

The equation of the line through A and B is the well-known y = mx + b, where the constant m is the slope of the line given by

and the constant b is the y-axis intercept, given by

b = Y1 − m X1.

Thus,

If we insert x = X3 into this equation, then we’ll clearly get a y-value greater than Y3, just as we will if we insert the x-coordinate for P. That is, if we call the results of these two insertions check1 and check2, then we’ll get

check1 = Y3 − (m X3 + b) < 0

and

check2 = YP − (m XP + b) < 0,

where the coordinates of P are (XP, YP).

The importance of these calculations isn’t the particular values of check1 and check2, rather it is that check1 and check2 will have the same sign if P and C are on the “same side of” AB. That means that their product will be positive if P and C are on the same side of AB but negative if they are on opposite sides. If P and B, and if P and A, satisfy the requirements of (b) and of (a), respectively, in the same way, then the code “knows” that P is inside the triangle ABC. When inside.m was run several times, each time for ten million random ABC triangles, the probability the origin—that is, P = (0, 0)—was inside ABC ranged from 0.2499534 to 0.2501911.

Now, who could possibly look at such numerical results and not think, “I’ll bet the theoretical probability is exactly 1/4!”? And doesn’t that remind you of another challenge problem in which we also divided a finite length into three parts? Sure it does—Challenge Problem 3. In fact, Challenge Problem 7 is just a cleverly disguised version of that earlier problem. Here’s why.

In Challenge Problem 3 we randomly broke a stick of unit length (in a prescribed way) into three pieces of lengths x, y − x (= z), and 1 − y, or y, x − y (= z), and 1 − x. The mathematics of that problem said that if 0 < x < 1, 0 < y < 1, and 0 < z < 1, with all three lengths less than 1/2, such that Σ lengths = 1, then we can form a triangle, and that this happens with probability 1/4. In our current problem we are also breaking a length (the circumference of a circle) into three pieces using the same random procedure in the selection of the angles α and β (let’s now suppose we measure these angles not in radians but as revolutions, with 2π radians = 1 revolution). Now, the three angles that separate the vertex points (if β > α these angles are α, α − β, and 1 − β, and if β < α these angles are β, α − β, and 1 − α) satisfy the same relations as do x, y, and z (all the angles are between 0 and 1, and Σ angles = 1). Also, as a simple sketch or two should reveal, all the angles must be less than 1/2 (revolution) for the origin to be inside the triangle formed by the vertex points. So, we conclude that since the mathematical description of Challenge Problem 7 is identical to that of Challenge Problem 3, the answers are identical, too.

(8) Suppose there are k teams in the league (I’ll substitute k = 6 and k = 10 when we are ready to calculate numerical values). Let p(n) be the probability the trophy has not been retired at the end of year n. Clearly, p(1) = p(2) = 1. There are exactly two sequences of events that result in the trophy still being unretired at the end of year n. These two sequences flow from a recognition that the champion team that year either was or was not the champion team at the end of the previous year, year n − 1. Let’s consider each possibility separately. If the champs at the end of year n didn’t win the previous year (probability (k − 1)/k), and the team that was the championship team that year didn’t retire the trophy, we have this sequence occurring with a probability of (k − 1)/k p(n − 1). For the second sequence, the champs at the end of year n did win the previous year (probability 1/k) but did not win the year before (year n − 2) (probability (k − 1)/k). The probability for this sequence is (k − 1/k)(1/k) p(n − 2). So, we immediately have

This difference equation can be used to generate the numerical values of p(n) for any value of n we wish, and we can keep doing that until we get to the first value of n = n* such that p(n*) < 1/2. This is easy to do with a computer. For k = 6 we find that n* = 31, because p(30) = 0.5004 while p(31) = 0.4882. For k = 10 we find that n* = 78, because p(77) = 0.5008 while p(78) = 0.4962. To solve the difference equation analytically, try solutions of the form p(n) = caⁿ, where c and a are constants. The difference equation will then reduce to a quadratic in a (two values), and you can use the p(1) = p(2) = 1 conditions to solve for the two c’s that go with the two a’s. The general form of the solution is . I warn you, however, that doing this will be a long slog through an arithmetic swamp, and by the time you are through you’ll be sending your computer love notes.

(9) This problem appeared in the May 1930 issue of the British math journal The Mathematical Gazette. After an ingenious, geometry-only analysis, it was shown that the answer is (4 − 5)/3 = 0.2189514. … That analysis centered on the definition of a parabola as the locus of points equidistant from a given point (the center of the green) called the focus, and a given line (an edge of the green) call the directrix. While quite clever, the analysis is also very detailed, so I decided to simply simulate the problem with the code golf.m. The idea is simple: if the ball is at (x, y), then the four distances to the edges of a unit square (the green) are x, 1 − x, y, and 1 − y, and we need only compare the minimum of them to the distance between the ball and the hole. The code does this ten million times and, with several executions, it gave estimates for the probability ranging from 0.2188581 to 0.2191731.

A final comment: Some months after writing up this solution, I happened to come across the following in the June 2009 issue of Mathematics Magazine (pp. 228–229), the solution to a problem posed in the magazine a year earlier: “A point is selected at random from the region of a regular n-gon. What is the probability that the point is closer to the center of the n-gon than it is to the n-gon itself?” I immediately recognized this as a generalization of the 1930 problem, which is obviously the n = 4 special case. The 2009 solution does require the evaluation of an integral (the 1930 solution was pure geometry), but overall, the 2009 solution for all n is quite pretty. The answer is 1/12[4 − sec⁴(π/2n)] and, if you substitute n = 4 into it, you do indeed get 0.2189514. … Notice that if n → ∞ (the n-gon approaches a circle) this probability approaches 1/3 − 1/12 = 1/4, which is clearly correct as that is the probability the golf ball lands inside the circle (centered on the hole) that has radius one-half of the radius of the now circular green. If the green is triangular (n = 3), the probability is 5/27 = 0.185185. …

(10) The code black.m (which calls the subroutine function draw.m) simulates the process. When run for the various arbitrary values of b and w given in the table below (10,000 times for each row, repeated five times, with the low and high estimates given), you’ll notice that independent of b and w, the probability that the last ball is black remains remarkably constant, and indeed the table strongly suggests that the exact result is always 1/2. A theoretical proof of this conjecture (3 pages long!), involving a double-indexed difference equation, can be found in the paper by B. F. Oakley and R. L. Perry, “A Sampling Process” (Mathematical Gazette, February 1965), pp. 42–44.

	b	w	Probability (low/high)
	1	1	0.4971–0.5073
	2	3	0.4989–0.5061
	3	3	0.4966–0.5080
	5	4	0.4991–0.5078
	7	9	0.4875–0.5055
	18	13	0.4962–0.5126
	15	39	0.4896–0.5037

Here’s a brief walkthrough of the code. The main program, black.m, controls the 10,000 loops for given starting values of b (the initial number of black balls) and w (the initial number of white balls). Prior to starting the first loop, the variable total is set to 0; the value of total is the number of loops (to date) that have resulted in a black ball as the last ball in the urn. Then, in each loop, as long as there are still balls in the urn (as determined by the while loop), the code “goes off to” the function draw.m. That function accepts two input arguments, b and w, and once it has performed the drawing process it returns two output arguments to black.m, namely, blackball and whiteball. Those two arguments are the new number of black and white balls, respectively, remaining in the urn, and so the values of b and w are immediately updated. Then, if b has reached 0 (there are no black balls left in the urn), the code sets w to 0, which forces the while loop to terminate and a new execution to begin with the original values of b and w. If, on the other hand, draw.m has returned whiteball = 0 (and so w = 0), then there are only black balls left in the urn, and so total is incremented by 1 because the last ball then has to be black (and b is set to 0 to again terminate the while loop). Finally, if both b and w are not 0, the while loop is executed again (and so draw.m is again called). Eventually, all 10,000 loops are completed and the last line of black.m prints the code’s estimate for the probability that the last ball in the urn is black.

The operation of draw.m is as follows. It starts with the reception of the current values of b and w as its input arguments from black.m. The drawing of the first ball is randomly made by comparing the value of rand (a number returned by the random number generator) to the current probability for a black ball: if the ball is black then the variable fcolor (for “first color”) is set to 1 and b is decremented by 1 (that is, the first ball is discarded), or fcolor is set to 0 for white and w is decremented by 1. A while loop is then entered (controlled by the variable keepgoing, which is initially set to 1) that successively draws (and discards) balls as long as they match the color of the first ball. Now, one of two things will eventually occur: (1) a color mismatch happens or (2) all the balls matching the first color are exhausted. If a color mismatch occurs, then the control variable keepgoing is reset to 0 to terminate the while loop. If a color exhaustion occurs (see the ‘if b==0’ or ‘if w==0’ loops), then keepgoing is also reset to 0 to terminate the while loop. The output arguments blackball and whiteball are then set equal to the present values of b and w, respectively, and program execution is returned to black.m.

(11) For A to win on the kth turn, he must not have tossed an ace on his first k − 1 turns (and neither did B). The probability neither player tossed an ace on the first turn (one toss each) is (5/6)², the probability neither player tossed an ace on the second turn (two tosses each) is (5/6)⁴, …, and the probability neither player tossed an ace on the k − 1th turn (k − 1 tosses each) is (5/6)^{2k − 2}. So, the probability that the players arrive at the start of the kth turn both aceless is

For A to toss an ace during the kth turn (that is, on the first toss, or on the second toss, or on the third toss, or …) is

So, summing over all possible k, we have the probability that A wins, P(A), as

which is easily coded in MATLAB^® to give P(A) = 0.596794. … The Monte Carlo code jb.m (jb for “James Bernoulli”) simulates this game one million times, keeping track in the variable W of the number of times A wins. The logic of the simulation is pretty simple. At the start of each game, the variables A and B are each set to 0, and the variable turn is set to 1. Then, A tosses the die turn times and, if one or more aces occur, then A is set to 1; then B tosses the die turn times and, if one or more aces occur, then B is set to 1. This is, of course, not the way two humans would play, but the next step accounts for that. Once Player B is done, the code checks A and B. If A = 1, then, irrespective of the value of B, Player A won, W is incremented by 1, and a new game is started. If A = 0 and B = 1, then Player B won, and so W is unchanged, and a new game is started. (Look at the variable keepgoing that controls the while loop.) If A = 0 and B = 0, then neither player tossed an ace, and so turn is incremented by 1, and another round of tosses occurs. When run several times, jb.m produced estimates for P(A) ranging from 0.595163 to 0.596921, nicely bracketing the theoretical value.

(12) Since A^2/3 > 0 and B^2/3 > 0 for all A and B from −1 to 1, we can think of this problem as asking for the probability that X = A^2/3 and Y = B^2/3 are such that X + Y < 1, where X and Y are independently distributed (each from 0 to 1). X and Y are, however, not uniformly distributed as are A and B. Let’s write the probability density functions of X and Y, respectively, as f_X(x) and f_Y(y). Since X and Y are independent, their joint pdf is f_X,Y(x, y) = f_X(x) f_Y(y). Let Z = X + Y. We want to compute Prob(Z < 1) = Prob(X + Y < 1) = Prob(Y < 1 − X). This probability is the probability of the shaded region in Figure S6 (the lower left diagonal half of the unit square), which we calculate by integrating the joint pdf of X and Y over that region, that is,

Figure S6. Sample space for Challenge Problem 12.

To do these integrals we need to find f_X(x) and f_Y(y). Once we find f_X(x) we’ll of course also know f_Y(y) since X and Y are identically distributed. To find f_X(x), we first calculate the distribution function of X, F_X(x), and then differentiate it. So,

because A is uniform from −1 to 1. Thus,

Similarly,

So,

Call the integral I, so that Prob(X + Y < 1) = 3/2I. It should be obvious by inspection (but you can prove it by making the change of variable u = 1 − x) that

and so

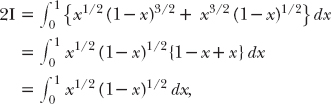
or

So,

Here’s an elementary way to evaluate the integral. The integral is the area under the curve y(x) = (x − x²)^1/2 as x varies from 0 to 1, and if you square this equation and do a little arranging, you’ll see it becomes (x − 1/2)² + y² = (1/2)². But this is simply the equation of a circle with radius 1/2 centered on the x-axis at x = 1/2. So the area in question (the value of the integral) is just the upper half of the area of that circle. The area of the circle is π/4 and so the integral is π/8, and thus

in excellent agreement with the code final.m.