3.1 The acceptance of incorrect answers

Binary floats can express very large and very small numbers, with a wide range of precisions. But they cannot express all real numbers. They can only represent rational numbers where the denominator is some power of 2. Some readers might be taken aback by this statement, since they have long ago gotten used to having floats represent square roots, π, decimals, and so on, and were even taught that floats were designed to represent real numbers. What is the problem?

The “original sin” of computer arithmetic is committed when a user accepts the following proposition:

And if anyone protests, they are typically told, “The only way to represent every real number is by using an infinite number of bits. Computers have only finite precision since they have finite memory. Accept it.”

There is no reason to accept it. The reasoning is flawed. Humans have had a simple, finite way of expressing the vast set of real numbers for hundreds of years. If asked, “What is the value of π?” an intelligent and correct reply is “3.14 …” where the “…” indicates there are more digits after the last one. If instead asked “What is seven divided by two?” then the answer can be expressed as “3.5” and the only thing after the last digit is a space. We sometimes need something more explicit than a space to show exactness.

Just as the sign bit positive (blank) or – is written to the left of the leftmost digit as a two-state indicator of the sign, exactness is a two-state indicator where the bit indicating exact (blank) or … is written just to the right of the rightmost digit. When we want to be more clear, we explicitly put a “+” in front of a positive number instead of a blank. Similarly, we can put the symbol “↓” after the digit sequence of an exact number, to emphasize “The digits stop here ↓.” Or put another way, all the bits after the last one shown are 0. It only takes one bit to store the sign of a number, and it only takes one bit, the ubit, to store whether it does or does not have more bits than the format is able to store.

If the bits in the fraction to the right of the last one shown are all 0, it is an exact value. If there is an infinite string of 1 bits, it is again exact and equal to the fraction that is one bit greater in the last place, the same way 5.999999 … is exactly the same as 6 if the number of 9s is infinite). If the ubit is set, then the quantity expressed is all real numbers between the exact value of an infinite string of 0s and the exact value of an infinite string of 1s. The closest thing to a historical precedent for the ubit is a “rounding to sticky bit” described by Pat Sterbenz in his long out-of-print book, Floating-Point Computation (1974). He used the bit to indicate “it is possible to calculate more bits”; he, too, put it at the end of the fraction.

There is a jargon term that numerical analysts use for the difference between a number and the number represented by the next larger fraction value: An ULP.

(Some texts use “Unit of Least Precision” as the abbreviated phrase.) For example, if we had the fixed-point binary number 1.0010, the ULP is the last 0, and a number that is one ULP larger would be 1.0011.

So we write 1.0010 ↓ if the number is exact, and 1.0010… to mean all values between 1.0010 and 1.0011, not including the endpoints. That is, it is an open interval, which is typically written with two numbers in parentheses like (1.0010, 1.0011). A closed interval includes the endpoints and is written with brackets, [1.0010, 1.0011], but that is not what we want here. If the ubit is set, it means an open interval one ULP wide. Here are the annotated bit fields, where the ubit is shown in magenta as a convention throughout this book:

The “h” represents the hidden bit: 0 if the exponent is all zero bits, and 1 otherwise. Suppose we again have only five bits for a float, but now use one bit for the sign, two bits for the exponent, one bit for the fraction (not counting the hidden bit), and use the last bit as the ubit. What values can we represent? Some examples:

• ■ 0 00 1 0 means exactly 12. (An all-zero exponent 00 means the hidden bit is zero.)

• ■ 0 00 1 1 means the open interval (12, 1). All real values x that satisfy 12 < x < 1.

• ■ 0 01 0 0 means the exact number 1.

The meanings increase monotonically, and neatly “tile” the real number line by alternating between exact numbers and the ranges between exact numbers. We no longer have to commit the “original sin” of substituting an incorrect exact number for the correct one. If you compute 2 ÷ 3, the answer with this five-bit format is “the open interval (12, 1)” which in this format is 0 00 1 1. That may be a very low-precision statement about the value 23, but at least it is the truth. If you instead use a float, you have to choose between two lies: 23=12 or 23=1.

The designers of hardware for floats and their math libraries have to jump through hoops to do “correct rounding,” by which they mean the requirement that rounding error never be more than 0.5 ULP. Imagine how many extra bits you have to compute, to figure out which way to round. For many common functions like e^x, there is no way to predict in advance how many digits have to be computed to round it correctly! At least the ubit eliminates the extra arithmetic needed for rounding. As soon as a computer can determine that there are nonzero bits beyond the rightmost bit in the fraction, it simply sets the ubit to 1 and is done.

The next section shows an unexpected payoff from the ubit: It provides an elegant way to represent the two kinds of NaNs.

3.2 “Almost infinite” and “beyond infinity”

Recall that we used the largest magnitude bit strings (all bits set to 1 in both the exponent and the fraction), with the sign bit, to mean positive and negative infinity. The largest magnitude finite numbers have a fraction just one ULP smaller, so their rightmost fraction bit is a 0. What does appending a ubit mean for those cases?

It may seem peculiar, but +∞ and –∞ are “exact” numbers, for our purposes. Sometimes people will say that some quantity, like the number of stars in the sky, is “almost infinite,” and the grammarian in the crowd will point out that “almost infinite” is contradictory, since it means “finite.” Actually, “almost infinite” is a useful computational concept, because it means a finite number that is too big to express.

With the ubit notation, it is possible to express the open intervals (maxreal, ∞) and (-∞, -maxreal), which mean “almost infinite.” That means every real number that is finite but too large in magnitude to express exactly with the available bits. This is a very different approach from extended-precision arithmetic, which uses software routines to express and perform arithmetic with oversize numbers by tacking on additional bits until memory is exhausted.

In terms of the five-bit examples of Section 2.5, where we presented a non-IEEE way to represent positive and negative infinity,

• 0 11 1 0 is + ∞ (sign bit = 0, so value is positive; all exponent and fraction bits are 1),

• 1 11 1 0 is – ∞ (sign bit = 1, so the value is negative).

The 0 ubit that ends the string marks the infinity values as exact. The largest magnitude finite values we can represent are one bit smaller in the fraction bits:

• 0 11 0 0 represents the number 4 by the rules for floats (hidden bit = 1), and

• 1 11 0 0 is –4. The maxreal and –maxreal values, one ULP less than ∞ and -∞.

When we turn the ubit on for the biggest finite numbers, it means “almost infinite.” That is, bigger than we can express, but still finite:

• 0 11 0 1 is the open interval (4, ∞), and

• 1 11 0 1 is the open interval (-∞, -4).

If setting the ubit means “a one ULP open interval beyond the number shown,” what does it mean to set the ubit for infinity? “Beyond infinity” makes us smile, because the phrase is nonsense. But we need a way to represent nonsense: NaN! So we can define “beyond positive infinity” as quiet NaN, and “beyond negative infinity” as signaling NaN. Sometimes we use red type to indicate signaling NaN, since it means “Stop computing!” In the five-bit case,

• 0 11 1 1 is quiet NaN, and

• 1 11 1 1 is signaling NaN.

There is an equivalent to maxreal at the opposite end of the dynamic range, which we call smallsubnormal.

Sometimes people use the expression “almost nothing,” and the same grammarians again might say, “That means ‘something’, so ‘almost nothing’ is an oxymoron, like ‘jumbo shrimp’.” However, the phrase “almost nothing” is just as useful as “almost infinite.” It means “not zero, but a smaller number than we can express.”

The ubit elegantly lets us represent that concept as well: Beyond zero. And it gives meaning to “negative zero” since that tells which direction to point the ULP interval that has zero as one end.

• 0 00 0 0 is exactly zero, and so is

• 1 00 0 0 because we do not care what the sign bit is for zero. But:

• 0 00 0 1 is the open interval (0, smallsubnormal) and

• 1 00 0 1 is the open interval (-smallsubnormal, 0).

Incidentally, meteorologists already use this idea when they write that the temperature is negative zero, –0°. That means a temperature between –0.5 ° and 0°, whereas writing 0° means a temperature between 0 ° and 0.5 °. For weathermen, it is obviously crucial to convey whether the temperature is above or below the freezing point of water (0° Celsius).

The smallest representable non-zero number has a 1 in the last bit of the fraction, and all other bits are 0. Because having all 0 bits in the exponent makes it a subnormal number, we call it smallsubnormal no matter how many exponent and fraction bits we are using. In this low-precision case of only five bits, that smallest nonzero number is 12, but of course it will usually be a much tinier quantity once we start using larger bit strings.

3.3 No overflow, no underflow, and no rounding

If a number becomes too large to express in a particular floating point precision (overflow), what should we do? The IEEE Standard says that when a calculation overflows, the value ∞ should be used for further calculations. However, setting the finite overflow result to exactly ∞ is infinitely wrong. Similarly, when a number becomes too small to express, the Standard says to use 0 instead. Both substitutions are potentially catastrophic things to do to a calculation, depending on how the results are used. The Standard also says that a flag bit should be set in a processor register to indicate if an overflow occurred. There is a different flag for underflow, and even one for “rounded.”

No one ever looks at these flags.

Computer languages provide no way to view the flags, and if a computing environment starts reporting intermediate underflow or overflow warnings even when the results look just fine, most users find out how to disable that reporting, which often improves the speed of the calculation. Chip designers are burdened with the requirement to put flags into the float arithmetic unit despite the fact that computer users find them useless at best, and annoying at worst.

We do not need overflow because instead we have “almost infinite” values (maxreal, ∞) and (-∞, -maxreal). We do not need underflow because we have the “almost nothing” values (-smallsubnormal, 0) and (0, smallsubnormal). A computation need never erroneously tell you, say, that 10^-100 000 is “equal to zero” but with a hidden (or intentionally disabled) underflow error. Instead, the result is marked strictly greater than zero but strictly less than the smallest representable number. Similarly, if you try to compute something like a billion to the billionth power, there is no need to incorrectly substitute infinity, and no need to set off an overflow alarm.

If you ask for the value of π, with five bits of fraction and a ubit, what you get is that the value lies in the open interval (3.125, 3.25), which is a true statement. There is no need to set a “rounded” flag in the processor, which is a “sticky” bit in that it stays set until something in the operating system resets it. It could happen, say, that a result like (3.125, 3.25) gets multiplied by zero and becomes exact again. The “rounded” flag is like a car with a “CHECK ENGINE” light that is always on, yet still seems to run fine.

One last comment about recording the exact-inexact description in the number format itself. If you enter a big positive number on a calculator and press the square root button over and over, eventually the display will show 1.0000000 exactly. Which is incorrect, of course. The error is very much like setting an overflow number to infinity or an underflow number to zero. With the ubit after the fraction, the answer can be “1.00000 …” with a “ …” that never goes away. The number is always marked as “greater than 1, but by an amount too small to express.” Traditional interval arithmetic cannot do this and makes the same mistake that floats do, accepting exact 1 as a possible result.

Here is some code that iterates until the square root is exactly 1, so mathematically, it should be an infinite loop:

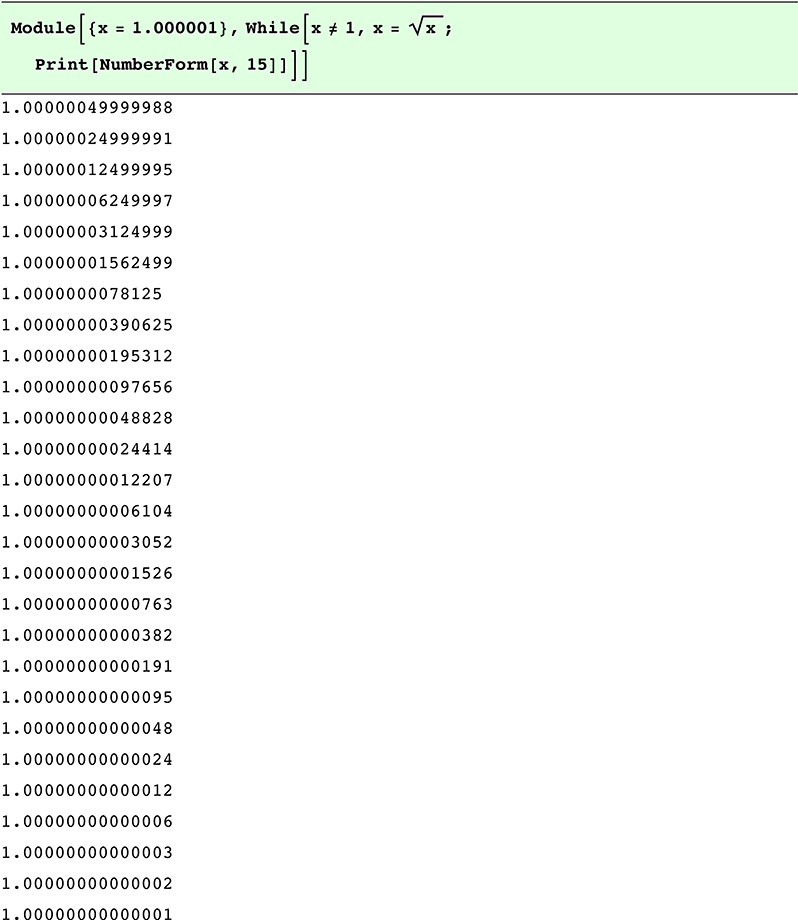
It stopped iterating. Double precision floats erroneously declared the last result exactly equal to 1. Many scientific calculations involve iteration and testing convergence, and the “stopping criterion” is a source of bugs and extra programming effort when using floating point representation. The ubit protects us from mistaking an exact number for a value that is asymptotically approaching it.

3.4 Visualizing ubit-enabled numbers

Floats were designed to allow calculations with (approximate) real numbers. For all formats discussed so far, bit strings could only represent discrete, exact values, so the value plots consisted of a series of points. With the ubit extension, we can now cover the entire real number line, as well as – ∞ and ∞, and the two NaN types.

For the five-bit case used previously, the represented values look like the value plot below, with dots for exact numbers and rectangles that have rounded corners to remind us that they are the open intervals between exact numbers (discrete values on the x axis are represented as having width if they represent an inexact range):

There are two subtle changes from previous graphs, other than the inclusion of open regions instead of just point values: The y coordinates where you might expect the numbers –5 and 5 instead have – ∞ and ∞ as exact values, and the arrows on the y axis point both directions to remind us that the entire real number line is now represented by the bit strings. We change the label for the y axis from “Decimal value” to “Represented value.”

The next question is whether things are better in terms of closure, when doing plus-minus-times-divide arithmetic. They are, but they are still not perfect. The reason is that we can only represent ranges that are one ULP wide, and many operations produce results that are wider than one ULP. For example, (0,12)+(0,12)=(0,1), but there is no way to express the interval (0, 1) in this format.

The closure plots with the ubit enabled look like the following, for a five-bit string:

Overflow and underflow cases have been eliminated. We are tantalizingly close to having a closed system, where the results of arithmetic are always representable without rounding or otherwise compromising correctness. Whenever we add something to accommodate a new type of value, we risk creating yet more cases that do not fit the format. Is this an endless process, or is it possible to create a closed system for honest arithmetic on real numbers with a limited number of bits?