11 Powers
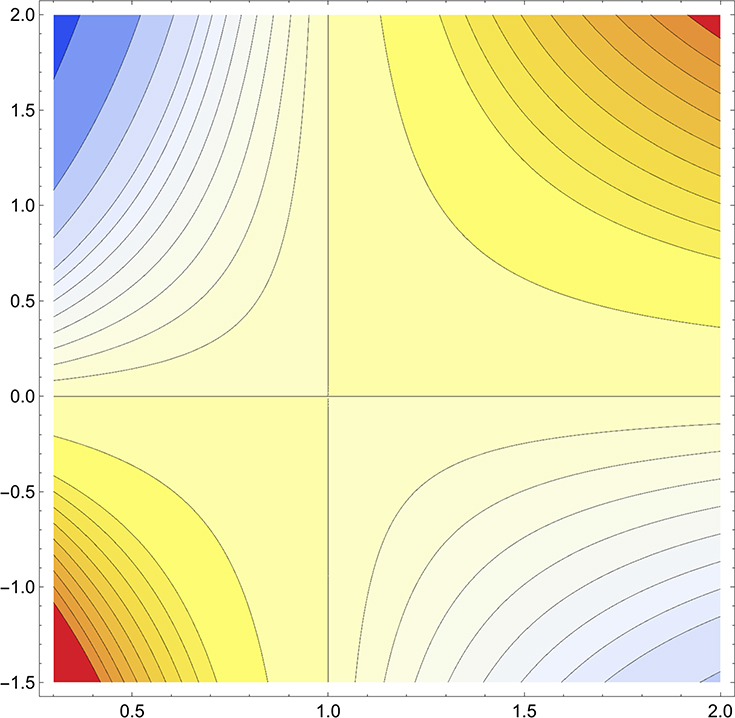
Section 10.1 showed a three-dimensional visualization of the saddle-shaped surface for multiplication, z = x × y. A similar saddle-shape occurs in the plot for z = xy, shown in a different way above, with a contour plot. The red corners are increasing values of the general power function xy and the blue corners are decreasing values. Computing the function means navigating a minefield of exception cases, as well as facing a previously unsolved math conundrum.
11.1 Square
Compared to the four basic arithmetic operations, finding xy for general values of x and y is a big jump up in effort. We start this chapter with a really soft toss, the creation of a routine for x2, just because squaring is such a common operation. Even that simple task provides a taste of a challenge that will be discussed in more detail in Part 2. Why not just evaluate the square of x by multiplying x times itself?
Suppose u is the unum representing [-1, 2). Here is why we should not simply use u⊗u to find the square of u. The square should be [0, 4], but a mindless multiplication lacks the information that the two values are the same variable, and produces the looser (albeit correct) bound (-2, 4]:

Squaring a number should never produce any negative numbers, but that is what the multiply routine will produce since it incorrectly assumes its input values are independent. So the code for squaring needs to watch for ranges that straddle zero. In a well-made unum environment, writing “x⊗x” should trigger an error and a question to the user, “Did you mean to square x?”
It is also still possible to get weird ties, as with the multiplication of general intervals: The square of (–2, 2] is [0, 4], not [0, 4). Closed endpoints “win” over open ones.
In the prototype, the g-layer function to square a general interval g is squareg [g], and the u-layer version is squareu [u]. The code for both is shown in Appendix C.14. Here is a quick test that shows squareg does the right thing:

The u-layer version is squareu [u ] where u is a unum or ubound. It tallies the numbers moved and bits moved; for unary operations (operations with one input), the count of numbers moved increases by two (one in, one out) and the cost of bits moved is the sum of the bits in the input and the output.

Exercise for the reader: What is the algorithm for finding the cube of a general interval?
The square function works on all real numbers and infinities. The hardware demands are no greater than that for multiplication. If we do higher integer powers of x like x3, x4 and so on, we will often need the extended-precision multiplier, or even the really big multiplier. Before we discuss that, consider another very common power function: x1/2, the square root of x.
11.2 Square root
Square roots that are not exact are irrational numbers; they cannot be expressed as a ratio of two integers . They are not, however, transcendental numbers, which may sound like a distinction that only mathematicians would ever care about. Square roots are algebraic numbers, defined as numbers that are roots of algebraic equations (polynomials with rational coefficients). Algebraic numbers are easy to evaluate to within one ULP, because there are plenty of fast ways to find the root of an algebraic equation. For the square root, there are techniques that double the number of correct digits with each iteration. It is really no harder to perform a square root in hardware than to compute the reciprocal of a number. That is why non-mathematicians might care about the difference between algebraic numbers and transcendental numbers: Speed.
The square root function will return NaN if used on a negative number, since we are restricting computations to real numbers. However, the square root allows an exact “negative zero” to work, instead of declaring the result imaginary, since the sign bit is ignored if the value is exactly zero. An inexact negative zero would always produce an imaginary result, though, because it includes numbers strictly less than zero. Hence, we have to return NaN for those cases. The unpacked unum format makes it simple and quick to check for values that trigger exceptions.
Incidentally, the IEEE Standard specifies that the square root of negative zero should be … negative zero. What in the world were they thinking?? It was Berkeley, and it was the 1980s, so perhaps some controlled substances were involved. Unum math ignores the sign of zero when it is an exact float.
In the prototype, the square root function in the g-layer is sqrtg [g] where g is a general interval. The square root in the u-layer is sqrtu [u], where u is a ubound. Try it on the square root of . The open end of the interval remains open, and because the closed end has an exact square root, it remains closed. As usual, the endpoint value of 1 is made open by setting its ubit (by adding ubitmask to the unum bit string.) The square root of should be :

Square roots on general intervals are easy because the function is monotone increasing. That means simply evaluating the square root of each endpoint like the example above; it preserves the less-than, greater-than ordering. That property did not hold for the square function, which caused complications.
Most square roots are numbers not expressible as exact floats, so just as with every other operation, we create an open interval that contains the true value. If an endpoint is closed and the square root is exact, the endpoint remains closed. Otherwise, ubound arithmetic finds the smallest possible ULP that contains the square root, and uses the unum for that to contain the correct value at that endpoint.
In the following example, we display the underlying unum machinery to show how the left endpoint is exact and compact (three bits in addition to the utag), whereas the endpoint demands all the fraction bits available and is marked inexact.

The square root of three is 1.7320508 ⋯ so the upper bound is accurate to over five decimal places. If we square this result, we will get a range slightly larger than the [1, 3 ] range that we started with.

Notice that the upper bound of the result is open. The correct answer [1, 3 ] is contained within the ubound result.
Exercise for the reader: The non-negative exact values of a {2, 2 } environment are listed in Section 4.10; how many of them have exact square roots?
Except for exception values, the endpoints represented by ubounds are like floats, a number of the form f 2e where f is a fraction in the interval [1, 2). Notice that we can always make e an even number by allowing f to be in the interval [1, 4) instead. So if the hardware sees that the exponent is an even integer, it evaluates ; if the exponent is odd, it instead evaluates , so the exponent is very easy to compute and is always representable. A unum square root operation differs from that of a float only in that unums automatically minimize the number of bits used to represent the exponent.
11.3 Nested square roots and “ULP straddling”
This may seem like a strange direction to take the discussion of xy, but there is a reason why we might want to find powers where as the next step to making the xy function general.
Since square root is such a well-behaved operation, can we use it to find , either as an exact number or the smallest ULP that contains it? The answer is yes, if you watch out for “ULP straddling” and correct it when it occurs. The first square root can produce an inexact unum, of course. The second square root then treats each endpoint separately, and the square roots of those might be different inexact unums, because the interval answer straddles an exact value instead of lying in the open interval between adjacent unums. Information loss could accumulate with each square root.
Fortunately, the problem is easily dispensed with, since squaring a number can be done exactly in the scratchpad. Here is a case where that happens in a {3, 3} environment when we try to find 2661/4 by taking its square root twice:
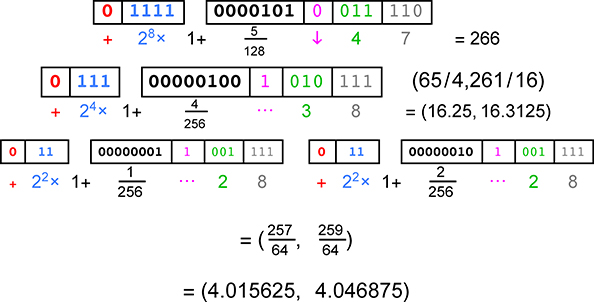
The result is two ULPs wide because the result of the second square root straddles the exact value . But only one of them can be correct. So raise the endpoints and the straddled point to the 4th power by squaring them twice to check (actually, we only need to do this for the midpoint, but we show the 4th power of all three values here for purposes of illustration):
Aha. Discard the lower ULP range, the one that goes from to , since its fourth power does not contain 266. The answer is the unum that represents .
This technique is easily extended to nested square roots:
Whenever a square root straddles an exact value and thus is two ULPs wide, just square the two ULPs repeatedly to see which one is the correct one, and continue. So our repertoire for finding xy is now “whenever y is an integer power of 2.” For positive powers of 2, do nested squaring. For negative powers of 2, do nested square roots with pruning of “bad ULPs” along the way. If the exponent is negative, simply compute with its absolute value and take the reciprocal at the end.
11.4 Taxing the scratchpad: Integers to integer powers
There is a reason it is called the power function. Just because an expression is easy to jot down does not mean it should be easy to compute. The factorial function n! = 1×2×…×n is a good example of this; even for a number as low as n = 70, n! is bigger than a googol. A googol is also easy to jot down with only five characters: 10100. The power function is in a whole different category from + – × ÷; it easily generates a gigantic amount of work to compute to the maximum precision. How big does the scratchpad have to be?
It is a large number of bits, but not as bad as it first looks because the separate storing of scale factors (exponents) means we only deal with integers expressed by the fraction bits. To get this down to numbers small enough to grasp, suppose the unum environment is {2, 2 }, so there are at most 22 = 4 bits to hold the fraction. With the hidden bit, the fraction represents integers 0 to 31, scaled by powers of 2. The scratchpad would need to hold integers as large as 3131 if we need the integer to be expressed exactly. That may look scary, but it only requires 155 bits at most. Expressing 31 takes five bits, so 312 takes ten bits, 313 takes 15 bits, and so on, therefore 3131 takes at most 5 × 31 = 155 bits.
If we built a unum environment with direct hardware support up to an environment of {4, 5 }, the maximum fraction length plus the hidden bit is 33 bits long. The integer represented by the fraction bits ranges from 0 to 233 - 1, or 0 to 8 589 934 591. The largest integer power would take (at most) this many bits to store:
In more common terms, about 33 gigabytes. In 2014, that much storage lies between the main memory size of a portable computer and that of a server.
So it is a big number, but such hardware exists. A current-generation microprocessor takes less than one second to read or write that much external data, quick enough by human standards but a billion times slower than an add or multiply. Power functions xy for general x and y are not operations we should demand casually if we want the same absolute standard of accuracy as the four arithmetic operations.
Now that we know what we are up against, try computing xy for a small environment.
11.5 A practice calculation of xy at low precision
We can express numbers x = 17 and exactly in a {2, 2} environment. Try = 173/8, byusing 173/8 = (173)1/8. The cube of 17 takes a couple of scratchpad multiplications, and then raising that to the power requires nested square roots as described in Section 12.4.
The number 17 occupies five bits, so 173 = 4913 can require no more than fifteen bits in the scratchpad. This is a small enough number of bits that we can actually look at the binary string for 4913:

With square roots, we needed the exponent to be an even number. To take the 8th root of a scale factor 2e, we need e to be an integer multiple of 8. So slide the bit string for 4913 eight places to the right:
Of course, the eighth root of 28 is simply 21. So to find 173/8, we seek an ULP-accurate value for (10 011.00110001)1/8 × 21. As a unum, the binary value 10011. ⋯ is

Now to perform three successive square root operations, checking each one for a straddle and pruning if necessary. (The notation “2^^” followed by zeros and ones allows direct entry of a bit string. They are color-coded with the usual system to make it easier to see the unum bit fields.)

That one landed inside an ULP, so no pruning is needed. The square root operation shrinks the relative width of a value by about half, so about half the time the new range does not straddle two ULPs. Perform the second square root:

Notice that the exponent field keeps shrinking. Again, it landed inside a smallest-possible ULP; for the final square root we will not be so lucky.

That straddles an exact value, since the fraction has less than four bits. There are two quick ways to know that a straddle has occurred: The fraction is not at its maximum length, or the ubound for the answer is a unum pair instead of a single unum. This is a case of the former, since the fraction field is only using three of its four bits maximum.
The computed range (1.375, 1.5) straddles the following exact unum:
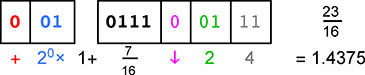
Find the 8th power of the straddled exact value by repeated squaring. If it is greater than the original number 10011.00110001 then we prune away the larger of the two ULPs; otherwise we prune the smaller one. Again for illustration, here are all three values raised to the 8th power:

The range {12.77 ⋯,18.23 ⋯} does not contain 10 011.00110001 = 19.19140625, so it is pruned away.
Exercise for the reader: If a straddle occurs every time when taking the 2k root of a number using k nested square roots, what is the total number of multiplications required for the pruning of the spurious ULP-wide ranges?
Finally, scale the final ULP-wide unum by the exponent, 21, to get 173/8 to the maximum available precision (all four bits of the fraction field in use):

In studying the problem of computing the power function, the author came across this extraordinary and oft-quoted statement in the literature on the subject:
“Nobody knows how much it would cost to compute y^w correctly rounded for every two floating-point arguments at which it does not over/underflow... No general way exists to predict how many extra digits will have to be carried to compute a transcendental expression and round it correctly to some preassigned number of digits. Even the fact (if true) that a finite number of extra digits will ultimately suffice may be a deep theorem.”
—William Kahan
Really??
The first part of that quotation is certainly no longer true, for anyone who has read this far. We just showed the maximum cost and the maximum time needed to compute a power function for two floats. The high cost of doing it that way makes us anxious to find a better way, but it is a predictable finite cost and time, guaranteed. It is just as deterministic a method as the ones for multiplying and adding bit strings.
The quotation is misleading, probably through omission. The “…” part of this quotation probably left out an explanation that yw is not a transcendental function if y and w are floats, because then the problem is algebraic, and Kahan knows that. The second part of the above quote remains true, and practical approaches for computing the transcendental function ⅇx will be discussed in Section 11.7.
11.6 Practical considerations and the actual working routine
11.6.1 Why the power function can be fast
At this point, some readers may be thinking: Is this guy insane?? Potentially computing hundreds of millions of digits exactly, just to guarantee the correctness of xy? That is not what is proposed here. The argument about the maximum number of digits and the maximum number of computational steps was to prove that there is a finite upper bound to both that is known in advance. That is not a practical way to compute xy, but something more like an “existence proof.”
In practice, we are willing to tolerate two things that can make the job of finding xy much easier:
We do not require that the routine always takes the same amount of execution time for any two input values.
We do not require provably minimum ULP width for every result.
Almost every operation with unums involves variable amounts of execution time; it would be ridiculous to find the maximum time, say, for a multiplication of any precision, and insist that the processor always allow that many clock cycles to pass even when multiplying a finite number by zero. Every operation should be allowed to go as fast as possible.
As for requiring “provably minimum ULP width,” there are efficient methods for computing xy that seem to do just that, but proving that they always are so accurate is tough. Unums offer the perfect solution to this, however, because they contain the accuracy information. If there is a very rare case where the calculation of xy is two ULPs wide instead of one, the ubound will say so. There is no possibility of being misled by the result, since the unum format allows communication of the width of a rigorous bound for the answer.
11.6.2 The prototype power function
The prototype approaches the power function similarly to the approach for multiplication. The contour plot that began the chapter shows a very similar need to do “left facing” and “right facing” endpoint calculations for a saddle-shaped surface. In this case, the flat point at the center of the saddle is not at the origin, but at x = 1, y = 0. The two tables below define what to do for general interval endpoints in the x-y plane where x
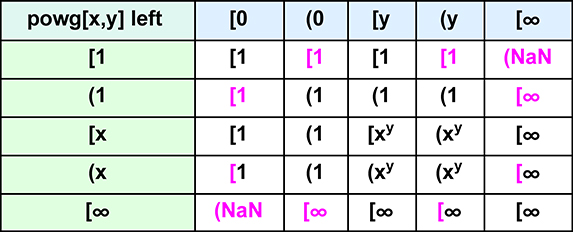

If 0 ≤ x < 1, we compute 1/(1/x)y instead, reversing the roles of left and right endpoints. If x or y is negative, the result is often a NaN (a complex number instead of a real) unless y is an integer. Here are some of the weird cases that can happen when computing the power function:
0-2 = ∞. It looks like it should be a NaN since we divide by zero, but for even negative integer powers of zero, the result is (±∞)2 = ∞.
1(maxreal,∞) = 1 but 1∞ = NaN.
(-∞)∞ = NaN but (-∞)-∞ = 0.
Exercise for the reader: In the g-layer, what is the correct value for ? (The contour plot at the beginning of the chapter may help answer this.)
Here is an example of the function powg evaluating in the g-layer:

The u-layer power function for uv is powu [u, v], and it tracks bits and numbers moved. The code for powg and powu is in Appendix C.15, and it probably has the record for complexity of all the operations in the prototype unum environment, because of all the special cases.
11.6.3 A challenge to the defenders of floats
Here is a challenge problem for people who think they have a slick way to find xy within 0.5 ULP using floats: Compute
Based on the way most math library routines work, the result with IEEE double precision will probably be something close to
and the library routine will round the result to that 15-decimal number. It will also set the “rounded” bit in the processor as required by IEEE rules, but guess what? It is incorrect to do so! The result is exact, something conventional methods of computing xy have no way to detect.
We only need a {3, 5} environment to get this result with the prototype:

Interval methods are often criticized for their tendency to produce overly conservative statements about a result. In this case, it is floats that deserve that criticism. There is a joke from the last century about someone asking an engineer “What is two times three?” He pulls out his slide rule and fiddles with it for a few seconds, then announces, “It’s about … six point zero.” If values can be posed exactly in the u-layer and an elementary function of them is also exactly expressible, it should be considered an error if the exact result is mislabeled as “approximate.”
Exercise for the reader: Construct another example like the one above where an exact exponent y has at least three nonzero digits to the right of the decimal and the base x has at least ten decimals when expressed exactly, and xy is also exact. Assume x and y are expressible as exact single-precision IEEE floats.
11.7 Exp(x) and a solution to “the Table-Maker’s Dilemma”
11.7.1 Another dilemma caused by the dishonesty of rounding
The exponential function is ⅇx, also written exp (x), where ⅇ is the base of the natural logarithm, 2.718281828 ⋯. Unlike xy where both x and y are floats, the exponential function is transcendental and cannot be computed as the root of a polynomial equation with rational coefficients. Fortunately, there are fast ways to evaluate it at any precision; the algorithms produce a tightening bound on the digit expansion until it finally falls within a minimum-sized ULP. However, the number of iterations needed could be anything, since it could just happen to be an irrational number that is very close to an exact value, forcing the evaluation to “go into overtime” to break the tie.
Here is an example of a transcendental calculation that shows this type of behavior in decimal form: looks an awful lot like an integer. If evaluated to thirty decimals accuracy, it is
If the uncertainty in the last place is even as small as 1012, it is unknown at that point whether the correct ULP to land the result in is just above the integer or just below it. Early makers of tables of logarithms first noticed that rounding for a few entries was extraordinarily hard to determine.
Professor Kahan coined the phrase “The Table-Maker’s Dilemma” for this phenomenon. It stems from the desire to assure the user of a table, “I promise you that none of the incorrect entries in this table are off by more than half an ULP.” The Table-Maker’s Dilemma is a direct consequence of the “original sin” of computer arithmetic that float users are asked to commit (Section 3.1).
Unums completely solve The Table-Maker’s Dilemma. Unums do not worry about “correctly rounding” a result because they do not round. If a value is not known to the smallest possible ULP size, it is simply returned with a larger ULP size (or a ubound) guaranteed to hold the value; unums label the size of the bound instead of returning an erroneous value, admitting what they do not know.
That said, there is certainly an easy way to make every single value of a function like ⅇx land in the smallest possible ULP size. Either tolerate variable-length calculations with the (very rare) occasional long evaluation time, as Thomas Lynch’s high-radix online arithmetic does, or simply identify in advance which floats are prone to the problem and handle those with a table.
Suppose the scratchpad computes a transcendental function with twice as many bits as there are in the fraction; the number of cases that happen to straddle two ULPs in the u-layer will be, statistically, about one at that precision. It is like keeping track of the “bad spots” on a hard disk drive. Find out where they are and work around them, making a small table part of the library function that has the handful of difficult tie cases precomputed so they do not have to be decided at run time.
11.7.2 The prototype exponential function
The code listings for the g-layer version expg and u-layer version expu are in Appendix C.15.Because it is a monotone increasing function, all the ubound logic has to do is evaluate the function at each boundary endpoint and track the open-closed properties. Here is an example of evaluating ⅇ(-∞,0]:

There are times that people get into the habit of using ⅇx when in some cases they could have used an exactly representable number for the base instead, like 10x or 2x. Those are available in the prototype by using powu or powu, for example. Doing so has the advantage that they have far more cases where the answer is exact. With the transcendental number ⅇ as the base, the only cases for which ⅇx is exact are when x is – ∞, 0, or ∞.
Exercise for the reader: If we put a limit of at most five bits to the left of the utag in a {2, 2 } environment, there are 66 nonnegative possible unum values:

If we include the negative versions of those, that makes 131 distinct exact unums. For which of those will 2x also be exact and in the above set? (Hint: It happens for more than ten percent of the values!)
