7 Fixed-size unum storage

Thomas Baines, Thomas Baines with Aborigines near the mouth of the Victoria River, N.T., 1857. Before the Warlpiri aborigines had much contact with other cultures, their counting system was “one, two, many.”
7.1 The Warlpiri unums
There are aboriginal hunter-gatherer people (such as the Warlpiri in Australia’s Northern Territory) whose language for numbers was limited to “one,” “two,” and “many” before they had contact with other cultures. Their original language is now almost lost, but we know they also had words for “none” (zero), “need” (negative), “junk” (NaN), and “all” (infinity), so in a sense their number vocabulary mapped very closely to the smallest possible float environment, augmented with a ubit. We can call this the “Warlpiri unum set.” Each number takes only four bits to express.
Definition: The Warlpiri unums use the smallest format possible, a {0, 0} environment. They have a sign bit, an exponent bit, a fraction bit, and a ubit.
Later we will show that such primitive four-bit values can be superior to even very high-precision floats at avoiding wrong answers. Better to say “Two times two is ‘many’” than to say “Two times two is overflow; let’s call it infinity.”
Hardware designers may be attracted to the fact that Warlpiri unums are fixed in size since they have no fields with which to express different esize and fsize values.
If you give up the economy of distinguishing between single and double ubounds and always use two unums per ubound, then every ubound can be represented with one byte. Imagine: A closed, mathematically unbreakable real number representation that requires only eight bits per value. Imagine how fast hardware could process such numbers.
There are sixteen four-bit strings, representing fifteen distinct values since we do not distinguish “negative zero” from zero. The precision may be ridiculously low, but given any real number or exception value, exactly one four-bit string will express it. Warlpiri unums can be useful in getting a very fast initial bound on an answer, or discovering that no answer exists. For example, in performing ray tracing for computer graphics, this low precision often suffices to prove that a ray cannot possibly hit the surface in question. The “maybe” cases that require more precision are surprisingly few. The three bits that form the “float” part of this tiny value obey IEEE rules for hidden bit, exponent bias, and so on, but remember that we deviate in selecting only two of the bit patterns to represent NaN: Signaling NaN and quiet NaN. Here is the Warlpiri number set, shown with four-bit strings in the top row, then conventional math notation for open intervals and exact numbers, then the real number line from – ∞ to ∞, and lastly, the English version of the way an aborigine might express the quantity:

The addition and multiplication tables taught in elementary school usually are for numbers 0 to 10. Beyond that, you need the pencil-pushing algorithms for multi-digit arithmetic that make most students hate math starting at an early age. Imagine: With Warlpiri real numbers, we can define + – × ÷ tables that encompass the entire real number line and make statements that are mathematically unassailable. If you ignore the NaN exceptions and “negative zero,” there are thirteen distinct unum input values, so each table has only 169 entries. Yet, they provide a closed mathematical system that covers all the real numbers and the exception cases like infinities and NaN. It is intriguing to think about a computer design that simply stores the tables and looks up results, which for some types of computer hardware can be faster than computing them with binary logic.
Exercise for the reader: Which Warlpiri unums are unchanged by the square root operation?
As a preview of issues to come, consider: What is the open interval (0, 1) divided by (0, 1)? Conventional computing says “There is a zero divided by zero in the ranges, so the answer is NaN.” Others might say “1 divided by 0 is infinity, so the answer is infinity.” But the open interval (0, 1) is never 0 and never 1; it is only the numbers in (0, 1)÷(0, 1) = (0, ∞). The result is somewhere between a number smaller than we can represent (but not zero), and a number larger than we can represent (but not infinity). The bound (0, ∞) is the best we can do, in the sense that having more bits of exponent or fraction would not change the answer. Whenever that happens, we say the result is “tight.” Notice that tight results are not necessarily reversible, because there is still possible loss of information. That is, addition and subtraction are not the inverse operations we would like them to be, where
and neither are multiplication and division, where we wish we could always guarantee that
Performing an operation on x followed by the inverse operation often gives a range that contains x but also contains other values. This can happen even when the operations are “tight,” because zero and infinity can destroy information about real number ranges.
If we ask what is 1 ÷ 2 in this ultra-low precision format, we must use the open interval (0, 1) since there is no string representing one-half. That is a “loose” result and information is always lost. It is still a true statement within the format, since one-half is contained in (0, 1), but if we had more bits, we could make the result tight. (Notice that if we use IEEE Standard float rules with no ubit, we get the false result that 1 ÷ 2 = 0 with three-bit floats, since it underflows!)
7.2 The Warlpiri ubounds
The ubound set has the 15 that are single unums, the set shown above, and 78 paired unums, for a total of 93 Warlpiri ubounds. As mentioned earlier, it might be more economical to always use pairs, where the single-unum entries store two copies of the same value; that way, there is no need for a “pair bit” and the Warlpiri ubounds always fit in an 8-bit byte. The following page shows them in three forms: Math (as a general interval), English, and as a 4-bit string or pair of 4-bit strings.

Here are a few examples of operations on Warlpiri ubounds:
If we attempt closure plots, they will be very boring: A solid 93 by 93 grid of dots, indicating that every operation on a Warlpiri ubound produces another Warlpiri ubound. This proves that closure under the four arithmetic operations is possible using a bit string of limited length. Designing real number formats with very few bits forces us to face up to all that is wrong with the current way we store real numbers on computers, and shows us how to fix the shortcomings before demanding more precision. If something is not worth doing, then it is not worth doing well.
Another thing we can do with the Warlpiri ubounds is create flawless elementary functions for them. For example:
Unlike math libraries for floats that strive to make almost all the results within half an ULP of the correct answer, there is no difficulty making every elementary function evaluation correct with Warlpiri ubounds. Ridiculously low precision, but correct. They can be used to prove the existence or nonexistence of an answer, which might save a lot of trouble. For example, if the mathematical question is “Does (continuous function of x) = 0 have any solutions for real numbers x?” then we can actually try every real number: Plug in (-∞, -2), -2, (-2, -1), -1, (-1, 0), 0, (0, 1), 1, (1, 2), 2, and (2, ∞) for x and see if any result ranges contain zero. If they do not, there is no reason to do a much more tedious root-finding algorithm. (More about this in Part 2.)
Exercise for the reader: Suppose we wish to create an “exact dot product” (Section 5.1.5) for Warlpiri ubounds that works for vectors up to length one billion. How many bits are needed for the accumulator in the g-layer?
Notice that standard hardware storage can handle Warlpiri ubounds, without the need to manage variable-length operands. They can be treated as 8-bit values packed into whatever power-of-2 bit size the computer memory level uses, and managed as an indexed array of integers.
Chapters 7 to 11 develop basic operations on unums and ubounds. In trying to get a feel for how things work with unums, it is helpful to keep the Warlpiri unums and ubounds in mind as test cases, since there are so few of them and the arithmetic is trivial to do in your head.
7.3 Hardware for unums: Faster than float hardware?
7.3.1 General comments about the cost of handling exceptions
With IEEE floats, there is usually hardware support up to some precision, and beyond that the operations must be done with software. A few years ago, the dividing line for many computers was between single and double precision. Currently, the dividing line is usually between double and quad precision. Hardware for unums can follow the same pattern, guaranteeing the availability of dedicated hardware up to some maximum length for the bit strings, and a number larger than that length triggers a trap to a software routine. The first exception to handle is “This computation is too large to fit into the hardware; use software instead.”
At some point, demanding too much precision or dynamic range will cause the system to run out of memory, as with all computer operations. The second exception to handle is “Even with software, there is not enough memory to perform this calculation.”
Once it is determined that a value fits into the allocated hardware, the processing of representations that could be NaN or infinity or subnormal involves testing for those situations. For hardware, exception handling is usually a painful thing to build and always seems to be a serial bottleneck getting in the way of high performance. (Which is why the Sun engineers tossed out hardware handling of NaN.)
Hardware for integer operations is very straightforward because the exception handling is so simple. To add a pair of n-bit signed integers, the hardware jumps into the task immediately, since the only thing that can go wrong is that the answer requires more than n bits, indicating underflow or overflow.
For IEEE floats, detecting exception cases is complicated and expensive. Is it a NaN? Is it an infinity? Is it negative? You might think “Is it negative” is just a matter of testing the sign bit, but remember “negative zero” is not actually negative. To figure out if a number is negative means testing all the bits in a float, because of the exception for negative zero. Suppose a chip designer is building a square root instruction, and decides to trigger a NaN if the sign bit is set, since the instruction does not allow negative inputs. That would give a NaN for , when the correct answer is 0. When the first version of a chip is tested, the errata sheets always seem to have quite a few cases similar to that one.
When the IEEE Standard for floats first came out, many chip designers grumbled that it was clearly not designed with circuit designers in mind since all the special values required tests. It is very much like decoding an instruction before a computer can begin to execute it. Float operations, unlike integer operations, involve crucial decisions that hinge on detecting special combinations of their bit patterns.
For example, if the logic for multiplication says “If x is infinity and y is strictly greater than zero, the product is positive infinity,” what does the hardware have to do to detect infinity? To be even more specific, imagine the simplest possible case: Half-precision IEEE floats. There is exactly one bit string representing infinity (by IEEE rules): 0 11111 0000000000. That string needs to be detected by hardware, which means every bit has to be tested.
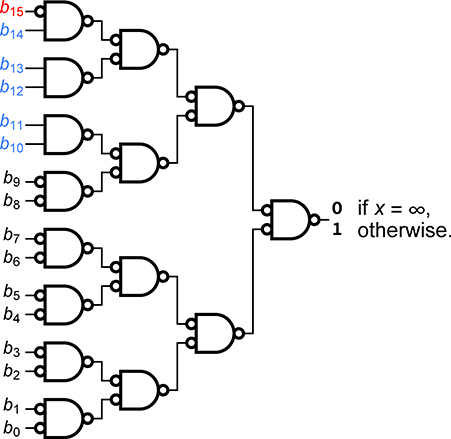
To do that quickly means building a tree of logic that collapses the state of all sixteen bits down to a single true-false bit. If the logic is composed of NAND gates (Not AND, meaning 0 if both inputs are 1, and 1 otherwise) and inverters (that turn 0 into 1 and 1 into 0), then the logic on the left (or something similar) is needed to test if x is the pattern representing the IEEE Standard representation of ∞. Even if you are not familiar with logic circuit symbols, this gives a flavor for the time and complexity involved.
If an inverter takes one gate delay and two transistors, and a NAND gate takes four transistors and one gate delay (CMOS technology), the tree of operations requires seven gate delays and 110 transistors. Imagine what it is like for a double-precision float; about four times as many transistors, and eleven gate delays. Of course, the way it is actually done is a little different. If the AND of all the bits in the exponent is 1, then the rest of the bits are checked to see if all of them are 0; otherwise, testing the other bits is not necessary. Is the hidden bit a 1? That test requires the OR of all the bits in the exponent, another tree structure like the one shown above.
There is a way that unums can make things easier for the hardware designer compared with IEEE floats. A simple principle can save chip area, execution time, energy, and design complexity all at once: Summary bits.
7.3.2 Unpacked unum format and the “summary bits” idea
If hardware dedicates 64-bit registers to unums, for example, environments up to {4, 5} will always fit, since maxubits is at most 59 for those combinations.
Exercise for the reader: The environment {5, 4} fits, but might be a bad idea. About how many decimals are needed to express maxreal in that environment?
The {4, 5} maximum environment provides up to 9.9 decimals of precision and a dynamic range as large as 109873 to 109864.
Since the floats that unums seek to replace often are 64-bit, using the same 64-bit hardware registers for unums seems like a good place to start. Requests for an environment with exponent fields larger than 16 bits or fraction fields larger than 32 bits trigger the use of software.
Because maxubits is always 59 or less for a {4, 5} environment, five bits of the 64-bit register are never used by unum bits. That suggests a use for them that makes the hardware faster, smaller, lower power, and easier to design: Maintain bits indicating if the unum is strictly less than zero, is NaN, is ±∞, is zero (exact or inexact), and whether this is not the last unum in a ubound (so the second unum is in another register). This information is already contained in the unum, but making it a single bit simplifies the circuitry required for processing.
Definition: A summary bit indicates a crucial feature of a unum that can otherwise be derived only by examining combinations of bits; it is used to save time and effort by “decoding” attributes of a unum.
The “hidden” bit can be unpacked into the “revealed bit,” displayed at last just to the left of the fraction. That eliminates much of the exception handling for subnormal numbers by allowing the fraction (starting with the revealed bit) to be treated as an ordinary unsigned integer.
We also would rather not make bit retrieval a two-step operation, where we have to use the exponent size and fraction size to find out how far to the left to look for the sign bit, the exponent, and so on. Instead, the six sub-fields that make up a unum are given dedicated locations within the 64-bit register, right-justified bit strings for those with adjustable size. Here is one example of a fixed-size unum format:
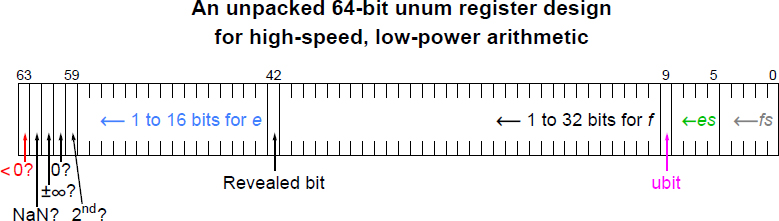
The creation of the summary bits occurs when a unum is unpacked from memory into a register by an instruction, or by the logic of an arithmetic operation. If someone mucks with individual bits in the above format, by using low-level instructions to set or reset them, it is perfectly easy to create a nonsensical, self-contradictory unpacked unum. The unpacked unum data type is not intended for programmer bittwiddling, only for use by the computing system.
The “<0?” summary bit: Many operations need to check the sign of a value as one of the first steps. As a convenience, we can store it in the leftmost bit so that existing signed integer computer instructions that check “If x < 0…” work for the unpacked unum register format. It will save a lot of grief that “negative zero” is accounted for, and in the register; that way, testing “If x < 0” is answered correctly by checking the first bit and not also having to check for all of the fraction and exponent bits and the ubit being 0. Of course, this assumes that the value represented is some kind of number, not a NaN; most of the arithmetic operations begin by checking for NaN, the second summary bit, but by putting the sign bit all the way to the left we get to use existing integer tests for “If i < 0” on the 64-bit unum string.
The “NaN?” summary bit: There really is only one type of NaN involved in any kind of operation: The quiet NaN. If it was a signaling NaN, there would not be any operation, because the task would have been stopped. There may be situations where a designer wants to use the unpacked format to indicate a signaling NaN, in which case the “< 0?” summary bit could, if set, indicate signaling NaN. We will here assume it is sufficient just to test bit 63, and if set, immediately return (quiet) NaN. Operations on NaN inputs should be the fastest execution of any possible inputs.
The rest of the bits of the register already store the unpacked form of NaN, providing a handy source for the bit string of the NaN answer. There is nothing to construct.
The “±∞?” summary bit: This summary bit is set if all the bits in esize, fsize, the fraction, and the exponent are 1. Notice that those four sub-fields have variable size and are right-justified within their dedicated location, so the environment settings still need to be taken into account when the unpacking is done.
![]()
Remember the 110-transistor logic tree to detect infinity for the half-precision IEEE float? Here is what the logic looks like for an unpacked unum. = ∞, 1 otherwise.
That represents about a 95% reduction in chip area and a 71% reduction in the time necessary to detect the infinity value, compared to the detection logic for every IEEE operation or for unum unpacking. Perhaps chip designers will not be as opposed to unums as has been previously suggested, given that the unpacked format is of fixed size, there is no need for rounding logic, and exception handling can be far faster and simpler. Unpacking is easily done concurrently with a sequence of memory fetches, since each fetch takes longer than the unpacking operation.
Exception testing like “Is x a NaN?” “Is x infinite?” can be processing while the rest of the hardware proceeds under the assumption that the answers will be “No.” That way, exception testing need not add time to the beginning of an operation for which actual arithmetic has to be done; it can overlap, and it can be very fast. When the answer turns out to be “Yes,” the hardware can interrupt any arithmetic processing, but energy is then wasted because of unnecessarily having started the calculation. A power-conscious design would not overlap the arithmetic with the exception testing, but would instead wait to find out the result of the NaN and infinity tests before doing any speculative work. With summary bits, the wait will not be long at all.
The “0?” summary bit: Arithmetic operations on zero tend to produce trivial results, or exception value results: 0 + x = x, 0 - x = -x, x÷0 = NaN, etc. There are many ways to express exact zero with a unum, and when zero is inexact, it represents different ULP sizes adjacent to zero. It is therefore extremely handy to be able to test a single bit since the decision is required so often by the arithmetic.
The “2nd?” summary bit: This is what we have sometimes called the “pair bit” for describing a ubound: If it is 1 (True), it means there is a second half to the ubound in the next register up. (With n registers, the highest numbered register wraps around to the lowest numbered one). Otherwise, this is a single-unum ubound.

The summary bits help to load the true-false scratchpad data area in the g- layer. Recall what the gbound structure looks like, left. The summary bits make it trivial to populate the Boolean ‘?’ entries with very few gate delays.
As an example, here is what the unpacked 64-bit register would look like representing the unum value for (-smallsubnormal, 0) in a {2, 3} environment, which is the open interval :
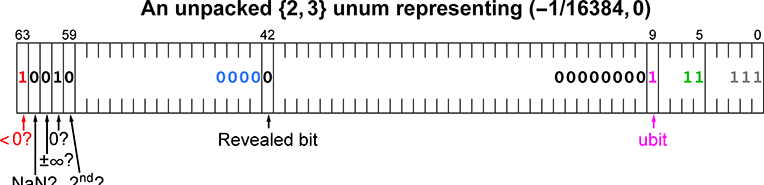
Chip designers, note: The blank register regions are “don’t care” bits that need not draw power while the environment stays at the same setting. Like snowplows at the airport during good weather; there is no need to keep their engines running.
Notice that the “<0?” summary bit is set, yet so is the “0?” summary bit. That is not a mistake; it is possible for inexact values of zero, of which this is an example, to be ULP-wide intervals on either side of exact zero.
Exercise for the reader: Create a similar unpacked format for a 32-bit register that works for environments up to {3, 3}. If you eliminate the “revealed bit” and the “2nd” bit, create an unpacked format for environments up to {2, 4}. How much logic is needed to determine the hidden bit, since it is not revealed?
