Chapter 3 The Integral

3.1 Introduction

• Integration can be thought of as a sum of an infinite number of objects or sections that are infinitesimally small. The integral can be used to calculate area under a curve, area of a region or surface, volume of an object, average value of a function, work done, pressure, as well as the change in a function when its rate of change is known. The last example uses the Fundamental Theorem of Calculus.

• Just as the derivative can be thought of as the limit of differences, the integral can be thought of as the limit of sums. On the graph of a function, the derivative can be represented by slope of the curve and the integral can be represented by area under the curve. The derivative of distance x is velocity v, and the area under the curve of v is x. The integral of velocity is distance and the integral of acceleration is velocity. The integral can be found by constructing sums or by calculating the antiderivative or definite integral using formulas, techniques, and tables.

3.2 Sums and Sigma Notation

• This section includes a brief review of sums, sigma notation, calculating sums, properties of sums, and changing limits.

• Sums are used in the estimation of integrals pertaining to area and volume. Because sums are used to represent integrals, the following brief review of sums and sigma notation is included.

• The Greek letter sigma Σ is used to describe a sequence of numbers that are combined in a sum. The following are examples of sums:

Sums do not have to begin at 1.

• The limits of the sum indicate the first and last numbers in the sum. For example:

The limits for are i = 1 to i = 3.

The letters i, j, and k are called dummy variables and represent the numbers in the sequence.

• Following are two examples of calculating sums:

(a.)

where the first and last numbers to be substituted are 2 and 5, respectively.

3(2) − 3 = 6 − 3 = 3

3(3) − 3 = 9 − 3 = 6

3(4) − 3 = 12 − 3 = 9

3(5) − 3 = 15 − 3 = 12

Therefore,

(b.)

• Properties of sums include:

(a.) If A_n and B_n each represent a sequence of numbers, then their sum can be written as:

This property can be demonstrated as follows:

(b.) If A_n represents a sequence and c represents a number that is multiplied with the sequence, then:

This property can be demonstrated as follows:

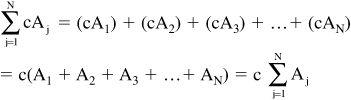
(c.) The sum of the first n terms in a sequence k can be calculated using the formula (n/2)(n + 1):

This formula can be demonstrated using the following two sums:

To find a solution that does not begin with 1 consider the sum:

where k is equivalent to

To calculate, subtract the formula for each sum:

[(10/2)(10 + 1)] − [(5/2)(5 + 1)] = 55 − 15 = 40

• Sometimes it is advantageous to change the variables and limits of a sum. This is possible as long as the changed sum is identical to the original sum. For example, the following notation represents the same sum:

This can be demonstrated as follows:

Because i and j are dummy variables, it is okay to use either i or j after substitution. However, it is important to perform a change of limits appropriately. Therefore:

• Products are represented by the capital Greek letter Pi or Π and are similar to sums except that once all the terms have been established by substituting the integers consecutively (from the lower integer to the upper integer), the terms are multiplied with each other rather than added.

3.3 The Antiderivative or Indefinite Integral and the Integral Formula

• This section includes the definition and notation for the antiderivative or indefinite integral, the integral formula, the constant of integration, families of antiderivatives, the indefinite integral of acceleration and velocity, and the indefinite integral of a constant alone.

• The antiderivative or indefinite integral is approximately equal to the reverse of the derivative. The antiderivative or indefinite integral of a function f(x) is written:

∫ f(x) dx

where ∫ is the integral symbol and f(x) is the integrand.

• If the derivative of the function f(x) is the function F(x) so that df(x)/dx = F(x), then the antiderivative of F(x) is f(x) plus a constant.

∫ F(x) dx = f(x) + c

where c represents an arbitrary constant of integration and dx indicates that integration occurs with respect to x.

• Remember the derivative formula:

dxⁿ/dx = nxⁿ⁻¹

Similarly, there is an integral formula for calculating antiderivatives or indefinite integrals:

∫ xⁿdx = (1/(n+1))xnⁿ⁺¹ + c

where c represents a constant value and is called the constant of integration.

Note: The integral formula is an important formula and is used frequently in calculus.

• The derivative of the antiderivative formula or integral formula can be evaluated using the derivative formula:

• A constant is added to the indefinite integral because the derivative of a constant is zero. Also, because the derivative is the rate of change of some function, it seems likely that several different functions could have the same rate of change. For example, calculating the derivatives using the derivative formula of the following three functions results in the same rate of change:

(d/dx)(2x² + 3) = 4x

(d/dx)(5^1/2 + 2x² + 2) = 4x

(d/dx)(2x² + π) = 4x

Then, take the indefinite integral of 4x using the integral formula to illustrate that each function is different even though they all have the same rate of change (derivative):

∫ 4x dx = (1/(1 + 1))4x¹⁺¹ + c = (1/2)4x² + c = 2x² + c

Therefore, in the three functions c represents 3, (5^1/2 + 2), and π.

• This example demonstrates that an indefinite integral represents a family of functions, each with a different value for c. A function and its family of antiderivatives can be represented graphically by raising or lowering the curve by the constant values.

The graph of df(x)/dx can be used to plot the graph of its antiderivatives f(x) because df(x)/dx is the slope of the curve represented by f(x) at any point along the curve. When df(x)/dx is positive (above the X-axis), f(x) is increasing, and when df(x)/dx is negative (below the X-axis), f(x) is decreasing. Also, when df(x)/dx is increasing along the X-axis, f(x) is concave up, and when df(x)/dx is decreasing along the X-axis, f(x) is concave down. Finally, when df(x)/dx crosses zero, f(x) has a local minimum or maximum.

For the graph below represented by df/dx, there is a family of curves represented by the graph of f(x):

The slope of the antiderivative f(x) at any point, should be the value df/dx at that point. A slope field of f(x) can be constructed by drawing short lines at multiple points on its graph that represent the slope of the curve at each point.

• Remember that the derivative can represent the rate of change of distance x(t) as velocity v(t) and the rate of change of velocity v(t) as acceleration a(t), such that

dx(t)/dt = v(t) and dv(t)/dt = a(t).

Conversely, the integral of acceleration is velocity and the integral of velocity is distance:

∫ a(t) dt = v(t) + c

∫ v(t) dt = x(t) + c

For example, using the integral formula,

∫ xⁿdx = (1/(n+1))xnⁿ⁺¹ + c

acceleration, velocity, and distance can be represented as:

v = ∫ a dt = at + v ₀

where v₀ represents a constant of integration.

Integrating again:

x = ∫ [at + v₀] dt = (1/2)at² + v₀t + x ₀

where x₀ represents a constant of integration.

• The integral of a constant c₁ alone is equal to the constant c₁ multiplied by the variable the integral is being integrated with respect to (which is indicated by dx), plus another constant c₂:

∫ c₁ dx = c₁x + c₂

3.4 The Definite Integral and the Fundamental Theorem of Calculus

• This section includes the definite integral, limits of integration, evaluating a definite integral using the Fundamental Theorem of Calculus, velocity and distance traveled, and calculating definite integrals using the integral formula and the Fundamental Theorem of Calculus.

• The indefinite integral represents a family of functions for different values of the constant of integration. Similarly, the definite integral represents a number pertaining to one of the functions of the indefinite integral such as the area under one of the curves. When the definite integral is evaluated, it is not necessary to add a constant of integration.

• If the endpoints of a function f(x) are set at specific values such as x = a and x = b, where they may be depicted on the graph of f(x), then the function is integrated as a definite integral. The endpoint values for a definite integral are called the limits of integration and are shown at the ends of the integral symbol _a∫^b.

If the integral of the function f(x) between x = a and x = b is the function F(x), then F(x) must be evaluated at x = a and x = b. The symbol for "evaluated at a and b”is and it describes subtraction of the function at the top value b minus the function at the bottom value a:

• The Fundamental Theorem of Calculus of a definite integral states that if f(x) is a continuous function between points x = a and x = b and f ’(x) is the derivative of f(x), then:

a ∫ ^bf ′(x) dx = f(b) − f(a)

Note: The Fundamental Theorem of Calculus is an important theorem and used frequently in calculus.

If F(x) is the antiderivative of f(x), so that:

∫ f(x) = F(x) + c, or F′(x) = f(x), then, the definite integral of f(x) between x = a and x = b is:

a ∫^b f(x) dx = F(b) − F(a)

• The constant of integration that results from an indefinite integral can be accounted for with respect to the definite integral as follows:

a ∫^b f(x) dx = [F(b) + c] − [F(a) + c] = F(b) − F(a)

• When the Fundamental Theorem is applied to a function defining velocity it provides a means to represent distance traveled in a designated time period by a definite integral. To analyze velocity and distance, the distance traveled can be represented by the definite integral of a velocity function. Because f ’(t) = v(t), where f represents position, v represents velocity, and t represents time. The change in position or distance traveled from point a to point b can be written:

f(b) − f(a) = a ∫^b f ’(t) dt

• The Fundamental Theorem is used when calculating many definite integrals. Applying the Fundamental Theorem is a shortcut to calculating the sums when the antiderivative can be found.

• The integral formula for the definite integral bounded by limits of integration x = a and x = b is used in conjunction with the Fundamental Theorem to calculate integrals:

For simple integrals the integral formula is used to integrate the function and the Fundamental Theorem is used to evaluate the result. For more complex integrals, the integral formula must be combined with techniques such as integration by parts, substitution, and integral tables. These are discussed in the last four sections of this chapter.

• Example: Find the area of the function f(x) = x² between x = 0 and x = 1 by integrating (using the integral formula) and evaluating at the two x boundaries (or limits of integration).

(See Section 3.6“The integral and the area under a curve".)

3.5 Improper Integrals

• This section includes the definition of an improper integral, convergence of an improper integral, and applying the comparison test for convergence of an improper integral.

• A definite integral is called an improper integral if the integrand is infinite or becomes infinite between its limits, or if one or both of the limits of integration are infinite. An improper integral is discontinuous or diverges at one or more points in a function between its limits of integration.

• Even though some part or region of an improper integral is infinite, the integral may converge and the area under the curve may be finite. Consider the following integral with an infinite boundary that still converges to an area of 1:

This can also be represented by:

As b approaches infinity, 1/b approaches zero and the integral converges to 1.

In general, an integral in the form:

1 ∫ ^∞ x^−P dx = 1 ∫ ^∞ 1/x^P dx where P > 1

defines a finite area and therefore converges.

• An improper integral may not converge. For example:

area under

When an integral does not converge, it is said to diverge.

• An integral that approaches positive or negative infinity at either boundary or has an integrand that is infinite somewhere between the limits may still converge. This can be shown by splitting the integral into a sum of two integrals within the original limits. For example, if the integrand is discontinuous at some point c between the limits, the integral can be rewritten as the sum of two integrals each with one finite limit and with an infinite limit at point c. Then the integral can be written as:

a ∫^b f(x) dx = a ∫^c f(x) dx + c ∫^b f(x) dx

If both of the integrals converge, the sum of the resulting integrals will also converge.

Similarly, if both of the limits of integration of an integral are infinite, the integral can be rewritten as the sum of two integrals, each with a finite limit:

−∞∫^∞ f(x)dx = −∞ ∫^a f(x) dx + a ∫^∞ f(x) dx

where a is finite. Then if both of the integrals converge, the sum of the resulting integrals will also converge.

• The Comparison Test can be used to evaluate whether an improper integral will converge. This Comparison Test operates using the same concept as the Comparison Test described for convergence of a series in Chapter 4. The Comparison Test can be performed by finding another similar integral that fulfills the condition that if 0 ≤ f(x) ≤ g(x), then the area under f(x) is less than the area under g(x):

If ∫ g(x) dx < ∞, then ∫ f(x) dx < ∞

In addition it follows that:

if ∫ f(x) dx = ∞, then ∫ g(x) dx = ∞

To use this strategy to determine whether f(x) converges, f(x) must not be negative and must also be less than the function g(x) that does converge.

• When the Comparison Test is applied to an infinite series with positive terms, the series is convergent if each term is less than or equal to each corresponding term in a series that is known to be convergent. Conversely, if each term in an unknown infinite series is greater than or equal to each corresponding term in a known divergent infinite series, then the unknown series is also divergent.

An example of a known convergent series that is used in the Comparison Test is the P Series:

1 + 1/2^P + 1/3^P + … + 1/n^P + …

This series converges when P > 1 and diverges when P ≤ 1.

An example of an integral that is used as a comparison is:

1 ∫ ^∞ 1/x^P dx

which converges when P > 1 and diverges when P ≤ 1.

3.6 The Integral and the Area Under a Curve

• This section includes a theoretical explanation of the relationship between the area under a curve, distance, sums, and the definite integral.

• Integration provides a means to obtain distance information from velocity information. For example, if a bicyclist travels from the east side of town to the west side of town and if the velocity at each point in time is known, the distance traveled at each point can be determined. If information about time and velocity are known:

time (hr): t₀ = 0, t₁ = 1, t₂ = 2, t₃ = 3

velocity (mi/hr): v₀ = 1, v₁ = 3, v₂ = 5, v₃ = 6

Then the distance traveled f(t) can be estimated using two slightly different approaches that give a lower and upper estimate for the actual value. The first calculates the velocity at the lower end of the time period and the second calculates the velocity at the end of each time period. This results in a lower and an upper estimate:

distance f(t) = v(t₀)Δt + v(t₁)Δt + v(t₂)Δt

distance f(t) = v(t₁)Δt + v(t₂)Δt + v(t₃)Δt

In this example the lower and upper estimates for distance f(t) are:

f(t) = (1 mi/h)(1 hr) + (3 mi/hr)(1 hr) + (5 mi/hr)(1 hr) = 9 mi

f(t) = (3 mi/h)(1 hr) + (5 mi/hr)(1 hr) + (6 mi/hr)(1 hr) = 14 mi

The difference in the high and low estimates is (14 − 9 = 5). If smaller time periods are chosen, such as 30 min., 5 min., 1 min., 1 sec., etc., then the difference between the upper and lower estimates becomes smaller and the overall estimate is better. The upper and lower estimates can be represented on a graph of velocity vs. time:

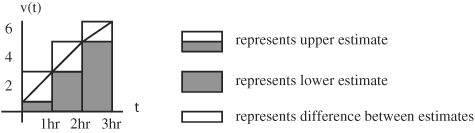
curve is drawn between upper and lower estimates

The area of each rectangle represents the distance traveled during each time period. The upper and lower rectangles of each period depicted represent the upper and lower estimates. The sum of the areas of the rectangles for all the time periods represents the total distance traveled (with the sum of the upper and lower rectangles representing the high and low estimates).

The difference between the estimates, as depicted on the graph, is the area of the rectangles that are between the upper and lower velocity values. The sum of the unshaded areas represents the total area of the differences. If the time period is reduced, the difference between the upper and lower estimates is proportionally reduced.

• The exact value of distance traveled in a given interval can be represented by taking the limit of the sum of the areas as the number of increments (rectangles) approaches infinity and, therefore, the rectangles become infinitesimally small. The estimates will converge to the accurate value of distance traveled as the number of increments measured approaches infinity. The limit of the sum as the number of increments in a defined region approaches infinity is the integral of the function defining the curve in that region.

In general, lower and upper sums (called Riemann sums) can be used to estimate an area. They both converge to the same integral and can be written in general terms as:

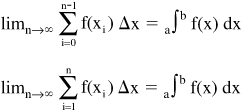
where a and b are the boundaries of a region that represents the area.

Note that the limit as n →∞ is used with sums representing an integral so that infinite sums are not used. The Riemann sum defines the definite integral as the limit of the number of terms approaches infinity. There are examples, however, where the function is not continuous or forms an asymptote and the integral (and sum) will blow up and the integral cannot be used to define the area under some region of a curve between designated points.

• In general, the integral is used to define the area under a curve on a graph of a function. To use the integral to define the area under some region of a curve between points x = a and x = b, the curve in this region must be continuous and not extend into a vertical asymptote. Consider the following graph of function f(x):

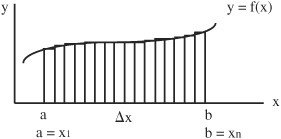
The striped pattern represents an approximation of the area under the curve of function y = f(x). The area under the curve between x = a and x = b is given by:

a ∫^b f(x) dx

This is the definite integral of f(x) between x = a and x = b.

In the interval between x = a and x = b on the graph of f(x), the X-axis is divided into n equal parts of width Δx such that the Δx segments extend from the X-axis to the f(x) curve so that the area is divided into vertical rectangular strips. (Δ represents a small change in x.)

Between x = a and x = b, for the n rectangular strips, each strip is called the ith strip. The width of each strip is Δx and the height of each strip is y_i. The area of each strip is width times height, given by: (y_i)(Δx) or (f(x_i))(Δx)

An approximation for the total area of f(x) between x = a and x = b is the sum of the areas of the n strips and is given by:

Or equivalently:

If the width of Δx shrinks and the number of strips increases, the sum of the strips will represent a better approximation of the actual area under the curve. By taking the limit as the number of increments approaches infinity:

Note that Δx can be equivalently written (b−a)/n.

Therefore, the area approximation can be written:

In the graph of a function, as the number of increments increases in a specified interval and the rectangular area increments approach the area under the curve, then the sum approaches the integral given by: ∫ f(x) dx.

3.7 Estimating Integrals Using Sums and the Associated Error

• This section is an extension of the previous section and discusses the error associated with sums. It includes the midpoint rule, the trapezoid rule, and Simpson’s rule.

• When integrals are estimated using upper and lower sums of rectangles, there is an error region above or below the curve. The total error for a curve bounded by two points is the sum of the error regions that lie between the upper and lower estimates. Lower and upper Riemann Sums (introduced in the previous section) used to estimate

_a ∫^b f(x) dx are:

f(x₀)Δx + f(x₁)Δx + f(x₂)Δx + ...+ f(x_n−1)Δx

f(x₁)Δx + f(x₂)Δx + f(x₃)Δx + ...+ f(x_n)Δx

The error associated with the sums can be depicted as:

blowup of y = f(x) depicting one Δx interval and error

The error resulting from summation can be reduced by increasing the number of increments (rectangles) and thus reducing their width.

• If integrals are estimated using sums of rectangles and the curve falls in the center (or midpoint) of each rectangle rather than the top or bottom, the error is reduced. Using this midpoint rule, the area estimated by the sum of rectangles (or increments) will be closer to the actual area under the curve. The Riemann sum using the midpoint rule is given by:

f(x_1/2)Δx + f(x_3/2)Δx + f(x_5/2)Δx + ...+ f(x_n−1/2)Δx

The error for the midpoint rule can be depicted as:

blowup of y = f(x) depicting one Δx interval and error

• Integrals estimated using upper and lower sums of rectangles can have the error reduced by using an average of the two sums. This is referred to as the trapezoid rule. Also note that trapezoids fit under sloping lines. Using this trapezoid rule, the area is estimated by the sum of rectangles (or increments) where the average values of the measurements at the top and bottom of each rectangle are combined in the sum. The area for the rectangle from f(x₀) to f(x₁) is (1/2)[f(x₀) + f(x₁)]Δx. The Riemann sum using the trapezoid rule is given by:

(1/2)[f(x₀)Δx + f(x₁)Δx + f(x₂)Δx + ... + f(x_n-1)Δx]

+ (1/2)[f(x₁)Δx + f(x₂)Δx + f(x₃)Δx + ... + f(x_n)Δx]

or Δx[(1/2)f(x₀) + f(x₁ + f(x₂) + ... + f(x_n−1) + (1/2)f(x_n)]

If the rectangles have different widths, the sum becomes:

(1/2)[f(x₀) + f(x₁)]Δx₁ + (1/2)[f(x₁) + f(x₂)]Δx₂

+ ... + (1/2)[f(x_n−1) + f(x_n)]Δx_n

where Δx_i = (x_i − x_{i −1})

The error for the trapezoid rule is depicted as:

blowup of y = f(x) depicting one Δx interval and error

• Example: Estimate ₀ ∫² x² dx using the trapezoid rule with 4 subdivisions.

Δx is equivalent to (b−a)/n or (2−0)/4 = 1/2. Therefore,

Δx[(1/2)f(x₀) + f(x₁) + f(x₂) + ...+ f(x_n−1) + (1/2)f(x_n)]

becomes:

(1/2)[(1/2)(0)² + (1/2)² + 1² + (3/2)² + (1/2)(2)²] =

(1/2)(1/2)(0)² + (1/2)(1/2)² + (1/2)1² + (1/2)(3/2)² + (1/2)(1/2)(2)²

= 0 + 1/8 + 1/2 + 9/8 + 1= 1/8 + 4/8 + 9/8 + 8/8 = 22/8 = 11/4

Therefore, ₀∫² x² dx is approximately equal to 11/4.

Comparing this result with calculating the definite integral directly:

Therefore, the error from using the trapezoid rule with

n = 4 is 8/3 − 11/4 = 1/12 or approximately 0.0833.

• Integrals can also be estimated using a method called Simpson’s rule, which gives a better approximation than the trapezoid and midpoint rules. Simpson’s rule combines the trapezoid and midpoint rules as a weighted average:

(1/3)[2 × (midpoint values) + (trapezoid values)]

The sum for Simpson’s rule can be written:

(2/3)Δx[f(x_1/2) + f(x_3/2) + f(x_5/2) + ... + f(x_n−1/2)]

+ (1/3)Δx[(1/2)f(x₀) + f(x₁) + f(x₂) + ...+ f(x_n−1) + (1/2)f(x_n)]

• For example, use Simpson’s rule to estimate ₀∫² x² dx, and compare it with the trapezoid rule above. Again, use 4 subdivisions.

Δx is equivalent to (b−a)/n or (2−0)/4 = 1/2

Therefore, Simpson’s rule is written:

(2/3)(1/2)[(1/4)² + (3/4)² + (5/4)² + (7/4)²]

+ (1/3)(1/2)[(1/2)(0)² + (1/2)² + 1² + (3/2)² + (1/2)(2)²]

= (2/3)(1/2)[(1/4)² + (3/4)² + (5/4)² + (7/4)²] + (1/3)(11/4)

= (1/3)[1/16 + 9/16 + 25/16 + 49/16] + 11/12

= 21/12 + 11/12 = 32/12 = 8/3

Therefore, ₀∫² x² dx is approximately equal to 8/3.

This value of 8/3 is the exact value of the integral and therefore shows Simpson’s rule to be an excellent estimate.

3.8 The Integral and the Average Value

• This section briefly discusses the relationship between the integral, the area under the curve, and the average value of a function in a defined interval.

• The integral not only represents the area under the curve on the graph of a function, but the integral also represents average value of a function in an interval.

The average value of f(x) in an interval a−b is the integral

_a∫^b f(x) dx divided by the length of the a−b interval, given by (b − a):

average value = [1/(b − a)] _a∫^b f(x) dx

The following figure depicts the average value where the integral represents the area under the curve, the average value of f is the height of the rectangle, and the width of the rectangle is (b − a).

3.9 Area Below the X-axis, Even and Odd Functions, and Their Integrals

• This section includes a brief review of integrals and the areas above and below the X-axis, as well as even functions and odd functions and their integrals.

• In functions where the curve falls below the X-axis the area between the X-axis and the curve is negative in value and subtracts from the area above the X-axis.

The graph of y = f(x) between x = −a and x = a is given by:

_−a ∫^a f(x) dx = (area A) + (area C) + (−area B) + (−area D)

where area B and area D are negative in value and subtracted from area A and area C.

• If the area below the X-axis is equal to the area above the X-axis, the resulting integral is equal to zero. The graph below of f between x = a and x = b is given by:

_a ∫^b f(x) dx = positive region + negative region = 0

where the positive region is equal to the negative region.

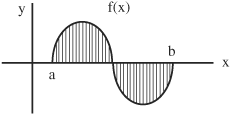
• By determining whether a function is even or odd, it is often possible to simplify the integral of the function to a more manageable form and solve using symmetry.

• A function is even if f(x) = f(−x) between x = −a and x = a. An example of a graph of an even function is:

From the graph, it is clear by symmetry that the section on the left of the Y-axis between x = −a and x = 0 is equivalent to the section on the right of the Y-axis between x = 0 and x = a. The integral for this even function can be written:

_−a ∫^a f(x) dx = 2 _−a ∫⁰ f(x) dx = 2 ₀∫^a f(x) dx

In an even function, the area for negative values of x is equal to the area for positive values of x.

Examples of even functions include:

f(x) = c, f(x) = x², f(x) = x⁴, f(x) = x²ⁿ

and f((−x)²) = (−x)(−x) = x².

• A function is odd if f(x) = −f(−x) between x = −a and x = a. An example of a graph of an odd function is:

From the graph it is clear by symmetry that the section on the left of the Y-axis between x = −a and x = 0 is equivalent but opposite to the section on the right of the Y-axis between x = 0 and x = a. The integral for this odd function can be written:

_−a∫^a f(x) dx = _−a∫⁰ f(x) dx + ₀∫^a f(x) dx = area P + area N = 0

Note that _−a∫⁰ f(x) dx = − ₀∫^a f(x) dx.

In an odd function, the area for negative values of x is equal but opposite to the area for positive values of x, and the two areas subtract and cancel each other out resulting in an integral equivalent to zero.

Examples of odd functions include:

f(x) = x, f(x) = x³, f(x) = x⁵, f(x) = x²ⁿ⁺¹

and f((−x)³) = (−x)(−x)(−x) = (−x)³

3.10 Integrating a Function and a Constant, the Sum of Functions, a Polynomial, and Properties of Integrals

• This section includes the integral of a function multiplied by a constant, the integral of the sum of functions, the integral of a polynomial function, switching limits of integration, equal limits, the integral over two subin-tervals, and comparing two integrals.

• The integral of a function multiplied by a constant is equal to the constant multiplied by the integral of the function. Therefore, if a function is multiplied by a constant or number, the constant can be brought out of the integral and multiplied with the resulting function.

_a∫^b C f(x) dx = C _a∫^b f(x) dx, where C is any real number.

• The graph of the area represented by _a∫^b f(x) dx will be elongated or narrowed along the X-axis when it is multiplied by a constant. For example:

∫ 2 f(x) dx = 2 ∫ f(x) dx

• The integral of a sum of functions is equal to the sum of the integrals. If an integral is of a sum of functions, the functions can be integrated together or as separate terms.

a ∫^b [f(x) + g(x)] dx = _a∫^b f(x) dx + _a∫^b g(x) dx

This can be represented using a sum:

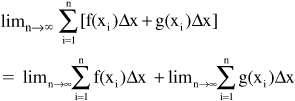
Similarly for the indefinite integral:

∫ [f(x) + g(x)] dx = ∫ f(x) dx + ∫ g(x) dx

When constants c₁ and c₂ are present, the sum of two functions is:

∫ [c₁ f(x) + c₂ g(x)] dx = c₁ ∫ f(x) dx + c₂ ∫ g(x) dx

• The integral of a polynomial function can be evaluated term-by-term. Therefore, to integrate a polynomial function, apply the integral formula term-by-term (as with differentiating). For example:

∫ (x³ + x² + x) dx = ∫ x³ dx + ∫ x² dx + ∫ x dx

= [(1/4)x⁴ + c₁] + [(1/3)x³ + c₂] + [(1/2)x² + c₃]

Combining the constants of integration results in:

(1/4)x⁴ + (1/3)x³ + (1/2)x² + C where C = c₁ + c₂ + c₃.

• Switching the limits of integration on a definite integral reverses the sign of the integral:

_a∫^b f(x) dx = − _b∫^a f(x) dx

This occurs because integration is moving across the area in the opposite direction which reverses the sign and can be demonstrated using sums. The area is given by:

where Δx = (b−a)/n.

In the negative direction, the integral is:

where −Δx = −(a−b)/n = +(b−a)/n.

• An integral that has both of its limits the same is equal to zero and represents an area over a point:

_a∫^a f(x) dx = 0

This integral is evaluated as:

F(a) − F(a) = 0

• An integral over an interval is equal to the sum of two integrals that represent two subintervals that when combined exactly equal the total original interval:

_a ∫^c f(x) dx = _a∫^b f(x) dx + _b∫^c f(x) dx providing a < b < c.

This is true because the entire area spans from x = a to x = c, where the two areas from x = a to x = b and from x = b to x = c sum to the entire area.

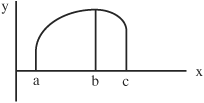
• When comparing integrals, the integral of function f(x) is greater than or equal to the integral of function g(x), if f(x) is greater than or equal to g(x):

_a ∫^b f(x) dx ≥ _a ∫^b g(x) dx providing f(x) ≥ g(x) and a ≤ x ≤ b.

The integrals can be compared when the area under f(x) and g(x) each lie on or above the X-axis and the area represented by f(x) is larger or smaller than the area represented by g(x).

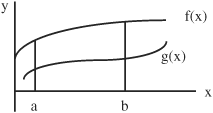
3.11 Multiple Integrals

• This section includes integrating double and triple definite and indefinite integrals; integral of a constant; and distance, velocity, and acceleration.

• Integration may be repeated multiple times. To take multiple definite integrals of a function, begin with the innermost integral and evaluate it at the limits of integration for the inside integral, then take the integral of the result and evaluate it at the next innermost limits of integration. Repeat this for the number of integrals specified by the number of ∫ symbols.

• To evaluate a double integral: _a∫^b _c∫^d f(x) dx dx

First take the integral of f(x) and evaluate it at its limits of integration c and d, then take the integral of the result and evaluate it at the limits of a and b.

• The integral of a constant alone is equal to the constant c₁ multiplied by the variable the integral is being integrated with respect to (indicated by dx), plus another constant c₂.

For example:

∫ c₁ dx = c₁x + c₂

• In examples where distance = x(t), velocity = v(t), and acceleration = a(t), the double integral of acceleration is:

∫∫ a(t) dt dt = ∫ v(t) + c₁ dt = x(t) + c₁t + c₂

• To evaluate a triple integral of a function containing three variables:

_a ∫^b _c ∫^d _e∫^f f(x,y,z) dz dy dx

First evaluate the function f(x,y,z) by taking the integral of f(x,y,z) dz and evaluating it at the limits of e and f, next take the integral of the result with respect to dy and evaluate it at the limits of c and d, then take the integral of the result with respect to dx and evaluate it at the limits of a and b. In problems where an integral is describing volume in a coordinate system, the limits a and b, c and d, and e and f, may correspond to the X-axis, the Y-axis, and the Z-axis respectively. In this example:

_a∫^b _c∫^d _e∫^f f(x, y, z) dz dy dx

The first integral performed is _e∫^f f(x, y, z) dz,

the second integral is _c∫^d (result of first integral) dy,

the third integral is _a∫^b (result of second integral) dx.

Notice that the innermost limits on the ∫ symbol correspond with the innermost dx, dy, or dz, and progress outward so that each ∫ symbol corresponds with its respective dx, dy, or dz. Also note that multiple integrals may be in the forms:

∫∫∫ f(x) dx dx dx

∫∫∫ f(x,y,z) dx dy dz

• In an example of a triple integral where the integral of f(x) is F(x), the integral of F(x) is g(x) and the integral of g(x) is G(x), then the triple integral of f(x) is:

∫∫∫ f(x) dx dx dx = ∫∫ F(x) + c₁ dx dx

= ∫ g(x) + c₁x + c₂ dx = G(x) + (c₁x²/2) + c₂x + c₃

3.12 Examples of Common Integrals

• This section includes examples of selected simple indefinite integrals commonly used in calculus:

∫ 0 dx = c

∫ 2 dx = 2x + c

∫ xⁿdx = xⁿ⁺¹/(n+1) + c, when n ≠ −1.

∫ 1/x dx = ln |x| + c

∫ 1/(2x+3) dx = (1/2) ln|2x+3| + c

∫ e ^x dx = e^x + c

∫ e ^2x dx = (1/2)e ^2x + c

∫ a^x dx = [a^x/ln a] + c, when a > 0 and a ≠ 1.

∫ e ^{2(x + 6)} dx = (1/2)e ^2(x+6) + c

∫ e ^u (du/dx) dx = e ^u(x) + c

∫ ln x dx = x ln x − x + c, when x > 0.

∫ cos x dx = sin x + c

∫ sin x dx = −cos x + c

∫ tan x dx = ln |sec x| + c

∫ sec x dx = ln(sec x + tan x) + c = log tan(u/2 + π/4) + c

∫ csc x dx = ln(csc x − cot x) + c = log tan(u/2) + c

∫ sec²x dx = tan x + c

∫ csc²x dx = −cot x + c

∫ cot x dx = ∫ (cos x / sin x) dx = | sin x | + c

∫ sinh x dx = cosh x + c

∫ cosh x dx = ∫ (sinh x / cosh x) dx = ln(cosh x) + c

∫ tanh x dx = sinh x + c

∫ [u(x) + v(x)] dx = ∫ u(x) dx + ∫ v(x) dx

3.13 Integrals Describing Length

• This section develops the integral that represents the length of a curve.

• The integral can be applied to determine the length of a curve. Using a rectangular coordinate system, a segment of a curve or an arc can be determined by dividing the segment or arc into sections such that each one is nearly a straight line. From geometry, it is known that the distance between two points (x₁,y₁) and (x₂,y₂) is a line given by:

Similarly, the length ds of a section of a curve can be represented as:

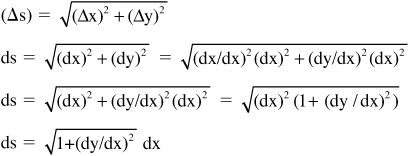
Therefore, the length of an interval of a curve can be represented as the limit of the sum of the sections ds. If the length of a curve is given by y = f(x) between points x = a and x = b, then the sum of the sections is:

3.14 Integrals Describing Area

• This section includes using single and double integrals to describe areas of circles, rectangular regions, regions bounded by and regions between two curves, triangular wedge regions, and surfaces of revolution.

• The integral applies to areas of circles as well as areas under curves. The area of a circle is πr² and the derivative of the area of a circle is circumference 2πr. Conversely, the integral of the circumference of a circle 2πr is the area πr².

Therefore, the area of a circle = ∫ (circumference) dr.

When applying the integral to a circle rather than a curve, the circle can be subdivided into rings of thickness Δr rather than rectangles, as depicted in the figure:

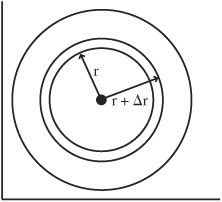
The sum of the rings can be represented by:

A = ₀∫^r 2πr dr = πr²

where the area of each ring is π(r + Δr)² − πr².

• Area can be represented using integrals of a two-variable function f(x,y) as well as a one-variable function f(x). Areas represented using two variables include rectangles in planes, areas in XY-planes that are bounded by closed curves, or areas that are two-dimensional slices of three-dimensional objects.

For example, a rectangular region can be measured within an XY-coordinate system where the area is defined between x = a and x = b and between y = c and y = d:

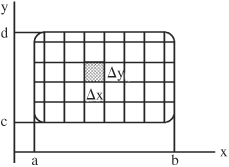
The area is divided into subintervals along each axis so that each interval has a rectangular shape and has x- and y-coordinates. The total area can be represented by the sum of this two-dimensional grid of rectangles. Each rectangle defining a subinterval of the total area has an area of ΔA =ΔxΔy, with Δx = (b−a)/n and Δy = (d−c)/m, where n is the number of subdivisions along the X-axis and m is the number of subdivisions along the Y-axis. If Δx_i = | x_i+1 − x_i| and Δy_j = | y_j+1 − y_j|, then the area of a subinterval can also be written ΔA_ij = Δx_iΔy_j. The sum of all the subinterval areas as i goes from 1 to n and as j goes from 1 to m approximates the total area. As the limits of n and m approach infinity and therefore Δx and Δy approach zero, the area can be written:

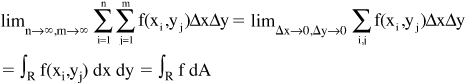
where R is the region bounded by the closed curve.

If the area of this region has part of the curve represented by y = f₁(x) and the other part of the curve represented by y = f₂(x), so that all of the curve is accounted for, the integral can be split:

∫_R f dA = _f1(x)∫^f2(x) _f1(x)∫^f2(x) dy dx

• For example, find the area bounded by two curves, between y = x² and y = 1 using a double integral:

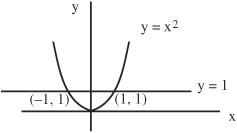
The area bounded by y = x², y = 1 is closed by the two intersection points (-1,1) and (1,1) where x = -1 and x = 1. The double integral describing these two curves is defined by where the two intersection points cross each other, which is where the two values of x and the two functions y = f(x) meet:

−1∫¹ [1−x²]0∫¹ dy dx = ₋₁∫¹ [1 − x²] dx = [x − x³/3 |₋₁¹

= [1 − 1/3] − [(−1) − (−1)^3/3] = [2/3] − [−1 − (−1/3)] = 4/3

Therefore, the area is 4/3 square units.

• If two curves represented by two functions don’t intersect, the area between the two curves can be described by the integral of the absolute value of the difference between the two functions in a defined interval. For example, if one curve is given by f(x), the second curve is given by g(x) and the interval is a-b, the integral is: _a∫^b f(x) − g(x)| dx

• The area of a triangular wedge section of a circle can be described by considering that the wedge section (Δθ/2π) is a part of the whole area of the circle πr² and can therefore be represented as: (Δθ/2π)(πr²) = (1/2)r²Δθ

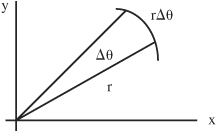
If a region contains numerous triangular wedge sections, then the total area can be represented by a sum of all the sections:

A = lim_Δθ→0 Σ (1/2) r² Δθ = (1/2)∫ r² dθ

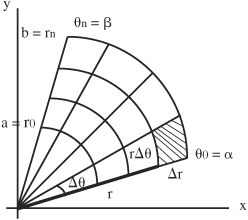
• To represent area in polar coordinates a grid can be constructed in a similar manner to sectioning an area in rectangular coordinates and summing the subsections. (See Section 1.9 on coordinate systems.) In polar coordinates the sections are defined by r rays at various θ values where a ≤ r ≤ b and α≤θ≤β, and there are n subsections in each of these directions:

The sum of the subsections is given by:

where ΔA ≈ r Δθ Δr and each subsection has an area defined by Δr along the r ray multiplied by r Δθ along the Δ direction (which is an arc).

The total area is:

• The integral can be applied to determine surface area using a surface of revolution. If the curve of a function y = f(x) is revolved around the X-axis, the surface area of the resulting surface can be determined. (Note that revolution can also occur around the Y-axis.)

• A surface that was revolved about the axis can be divided into sections similar in shape to a cylinder, where the area of an arced cylindrical surface S can be given by:

ΔS = 2πy Δs or dS = 2πy ds

The surface area of each section is the width of the cylindrical section (not the radius) multiplied by the circumference at the center of the section. Therefore, the surface area resulting from revolving curve y = f(x) around the X-axis between x = a and x = b is:

Or approximately,

where ds = dx (described in Section 3.13.)

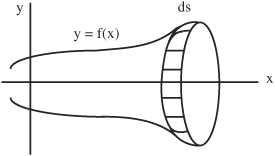
If the curve is revolved around the Y-axis instead, the surface area is:

Or approximately,

3.15 Integrals Describing Volume

• This section presents different techniques that may be applied to problems involving the volume of an object and includes: volume of revolution, volume by cylindrical shells, volume of spheres, volume by projecting a closed curve along the Z-axis and sectioning into columns or cubes, and volume in terms of cylindrical and spherical coordinates.

• When modeling a problem where volume must be determined, there are a variety of techniques to consider depending on the geometry of the object. The integral can also be used to define the volume of an object. Volume can be defined using single integral equations, double integral equations, and triple integral equations. Sums can be constructed by slicing or sectioning a three-dimensional object and adding up the sections.

• In the graph of a non-negative continuous function, the area under the curve of function y = f(x) is given by: _a∫^b f(x) dx. If the function is revolved about the X-axis between x = a and x = b, a volume is generated. This volume is called the volume of revolution. Each circular cross-section has an area of πy² and a thickness of dx. Therefore, the volume of a section is πy²dx. The volume of the“volume of revolution”between two vertical planes at x = a and x = b (see figure below) is given by:

V ≈ Σ πy² Δx = π_a∫^b f(x)² dx = π_a∫^b y² dx

• In the graph of a non-negative continuous function between x = a and x = b, the volume can be described using the method of volume by cylindrical shells. If the area bounded by x = a and x = b is revolved about the Y-axis generating a volume, this volume can be divided along the X-axis into n parts, each having a thickness of Δx and n vertical cylinders will result. The volume of each cylindrical shell is obtained by subtracting the volume of a smaller cylinder from the next larger cylinder πR²h − πr²h = πh(R² − r²), where R is the radius of the larger cylinder and r of the smaller and h is the length along the Y-axis.

More generally, if R = (x + dx) and r = x, then subtracting the cylinders gives:

π(x + dx)²h − πx²h = πh(x + dx)(x +dx) − πx²h

= πh[x² + 2x(dx) + (dx)²] − πx²h

= πhx² + 2xπh(dx) + πh(dx)² − πx²h = 2xπh(dx) + πh(dx)²

If the sum of the n shells is taken as n approaches infinity and the thickness of each shell approaches zero, the πh(dx)² term will quickly approach zero because of (dx)² or Δx². The volume depicted below can be described by:

As the number of shells approaches infinity, then the volume becomes:

V = _a∫^b 2πhx dx

• The integral can also be applied to the volume of spheres. The volume of a sphere can be divided up into nested spheres or shells, each having a thickness of Δr, where each shell can be measured from radius r to radius r + Δr. The measurement of each shell can be estimated by its surface area multiplied by Δr, or 4πr²Δr. Therefore, the volume is the sum of the volumes of the incremental shells:

V = ₀∫^r 4πr² dr = (4/3)πr³

which is the volume of a sphere.

• Volume of an object can be described by projecting a closed curve vertically along the Z-axis in an XYZ coordinate system into a three-dimensional solid. See figures below. This volume can be determined in terms of double or triple integration and summation. If the volume of this object is divided into columns in the direction of the Z-axis, where an area subdivision dydx in the XY plane is projected vertically along the Z-axis to the surface z = F(x,y), the volume of each column is F(x,y) dydx. The sum of all the columns as the number of columns approaches infinity, gives the total volume for the function F(x,y) and is described by:

where the "_R" defines a region of area.

An alternative method of describing this same volume is to divide it into cubes in the XYZ coordinate system so that the volume of each cube is dxdydz. Then the sum of all the cubes gives the total volume and can be described by:

V = _a∫^b _f1(x)∫^f2(x) _F1(x,y) ∫^F2(x,y) dy dx

where F₁(x,y) = z and F₂(x,y) = z describe the surfaces along z and f₁(x) = y and f₂(x) = y describe the closed curve. The interval along the X-axis is from x = a to x = b.

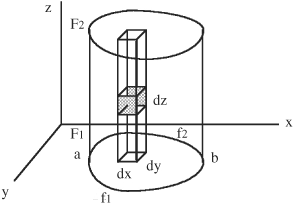
• In general, a volume in an XYZ coordinate system can be divided into cubes, such that each cube has a volume ΔxΔyΔz =ΔV and Δx = (b − a)/m, Δy = (c − d)/n, Δz = (e − f)/p and m, n, and p correspond to the number of subdivisions along the three axes. The sum of all the cubes gives the total volume and is described along the three axes by:

V = _a∫^b _c∫^d _e∫^f dz dy dx

• The volume of a rectangular solid can be determined by dividing it into many cubic or rectangular sections. Consider a rectangular solid positioned with its lower left corner at the vertex of an XYZ coordinate system:

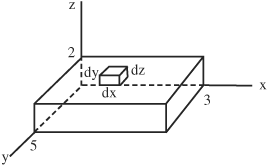
The rectangular solid spans from x = 0 to x = 3, y = 0 to y = 5, and z = 0 to z = 2. The integral describing volume is:

V = ₀∫³ ₀∫⁵ ₀∫² dz dy dx = ₀∫³ ₀∫⁵ 2 dy dx = ₀ ∫³ 2y |₀⁵ dx

= ₀∫³ 10 dx = 10x |³₀ = 30 cubic units

In this example, the volume can also be obtained by simple geometry as length × width × height, or

3 × 5 × 2 = 30 cubic units.

• In cylindrical coordinates, the volume of an object can be sectioned in a grid of subsections where the volume of each subsection is defined according to the coordinates. Then the subsections can be summed or integrated to find the total volume. (See Section 1.9 on coordinate systems.)

In cylindrical coordinates the sections are defined by r rays at various θ values and projected along the Z-axis with a ≤ r ≤ b, α≤θ≤β and c ≤ z ≤ d. The r component is measured from the Z-axis, the θ component measures the distance around the Z-axis and the z component measures along the Z-axis.

The following figure depicts a point P(r,θ,z) in a cylindrical coordinate system:

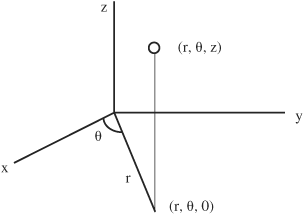
Where a ≤ r ≤ b, α≤β,c≤z ≤ d

• For example, the volume of a triangular wedge section that is projected vertically along the Z-axis can be represented in cylindrical coordinates.

The area of each subsection is ΔA ≈r Δθ Δr and is defined by Δr along the r-ray multiplied by rΔθ along the θ direction. Therefore, the volume of a subsection is ΔV ≈ r Δr Δθ Δz. For the total volume containing numerous triangular wedge sections where r = 2, θ = π, and z = 3, the volume can be represented by:

V = _c∫^d _α∫^β _a∫^b r dr dθ dz = ₀∫³ ₀ ∫ ^π ₀∫² r dr dθ dz

= ₀ ∫³ ₀∫^π 2²/2 dθ dz = ₀∫³ ₀∫^π 2 dθ dz = ₀∫³ 2π dz = 6π

To verify this answer, consider that both the top and bottom are level, therefore the volume should be equivalent to the area of one end multiplied by the z-dimension:

(Δθ/2π)πr²(z) = (1/2)r²Δθ(z) = (1/2)(4)π(3) = 6π

where (Δθ/2π)πr² defines a wedge of a circle.

• To represent volume in spherical coordinates, where x = ρ cos θ sin φ, y = φ sin θ sin φ, z = ρ cos φ, ρ = (x² + y² + z²)^1/2, a grid can be constructed in a similar manner to sectioning a volume in rectangular coordinates and summing the subsections. (See Section 1.9 on coordinate systems.) In spherical coordinates, the sections are expressed in terms of ρ, θ, and φ, where ρ can range from 0 to ∞ and originates from the origin, θ can range from 0 to 2π and measures the distance around the Z-axis, and φ can range from 0 to π and measures down from the Z-axis. Note that p is measured from the origin rather than the Z-axis as is the case with r in cylindrical coordinates. This figure depicts a point P(ρ,θ,φ) in a spherical coordinate system:

To find volume in spherical coordinates, divide the object into n subsections in each of the ρ, θ, and φ directions and integrate the volume of each subsection over 0 ≤ ρ ≤ ∞, 0 ≤θ≤ 2π, and 0 ≤φ≤π. Each subsection is a semi-rectangular volume element and is defined in terms of its (π θ,φ) coordinates as depicted on the next page. One edge of the element has a length of Δρ, one edge is defined by rotating ρ the length Δφ resulting in length ρΔφ, and one edge is defined by rotating in the θ direction measured out from the Z-axis at the length (ρ sin φ) resulting in a length of (ρsin φΔθ). Therefore, the volume of a subsection is:

ΔV = (Δρ)(ρΔφ) (ρsin φΔθ) = ρ²(sin φ) Δρ Δθ Δφ

The total volume is the sum of the subsections as the size of each subsection approaches zero, which is the integral:

V = ₀∫^π ₀∫^2π ₀∫^∞ ρ² sin φ dρ dθ dφ

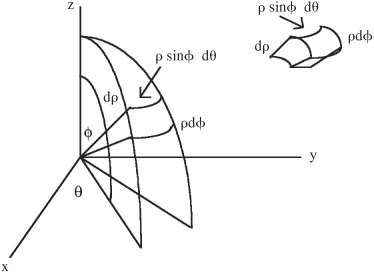
• For example, the volume of a sphere located at the origin of a spherical coordinate system, having a radius = R is given by:

V = ₀∫^π ₀∫^2π₀∫^R ρ² sin φ dρ dθ dφ

= ₀∫^π ₀∫^2π (1/3)R³ sin φ dθ dφ = ₀∫^π (2π)(1/3)R³ sin φ dφ

= (2π)(1/3)R³ [−cos π−− cos 0] = (2/3)πR³[+1+ 1]

= (4/3)πR³

which is the known volume of a sphere.

3.16 Changing Coordinates and Variables

• This section provides a brief summary of changing coordinates and variables including the volume of a sphere in rectangular, cylindrical, and spherical coordinates, and changing between coordinates using the Jacobian factor.

• When describing areas and volumes of circles, spheres, cylinders, and other non-rectangular shapes, it may be advantageous to evaluate integrals in polar or spherical coordinates rather than rectangular coordinates.

• For example, the volume of a sphere located at the origin given in Cartesian (rectangular), cylindrical, and spherical coordinates can be represented as follows:

(a.) In rectangular coordinates, the equation for a sphere is, x² + y² + z² = R². The sphere can be divided into sections such as octants with the volume of each octant further divided into small rectangular or cubic subsections. In an XYZ coordinate system, the volume of each cube is dxdydz. Then the sum of all the cubes in the octant multiplied by 8 gives the total volume of the sphere. Using this strategy, the volume of a sphere located at the origin of the coordinate system can be represented by:

The interval along the X-axis is from x = 0 to x = b.

(b.) In cylindrical coordinates, the equation for a sphere is, r² + z² = R². Again, the sphere can be divided into sections such as octants with the volume of each octant further divided into small subsections. If the sphere is located at the origin, the equation for volume is:

(c.) In spherical coordinates, the equation for a sphere is, p = R. If the sphere is divided into octants with the volume of each octant further divided into small subsections, and the sphere is located at the origin, then volume can be represented as:

V = (8) ₀∫^π/2 ₀∫^π/2 ₀∫^R ρ² sin φ dρ dθ dφ = (4/3)πR³

• To change between coordinate systems when evaluating an integral, the expressions for x, y, and z can be substituted from the original coordinates to the new coordinates. For example, to make a simple change from rectangular to polar coordinates for area, first substitute x = r cos θ and y = r sin θ in the integrand, then change the limits of integration to describe the dimensions within the new coordinate system. Finally, replace dA with r drdθ.

• A general method used to change variables uses the Jacobian J determinant for two or three variables. In this method, x, y, and z are related to new coordinates u, v, and w, such that x = x(u,v,w), y = y(u,v,w), and z = z(u,v,w). The Jacobian represents a factor that relates the original coordinate system to the new coordinate system.

For a single integral, changing from:

∫ f(x) dx to ∫ f(u) du,

the factor relating dx and du is simply the ratio dx/du. Therefore, the dx can be replaced with (dx/du)du. Similarly, (du/dx)dx is equivalent to du.

For a double integral, changing from:

∫∫ f(x,y) dx dy to ∫∫ f(u,v) du dv,

the factor given by J relates the area dxdy with area dudv such that dxdy becomes |J| dudv. The variables x and y are related in that x = x(u,v) and y = y(u,v), and each point in the x-y coordinate system is related to each point in the u-v coordinate system. Therefore, the integral in the x−y system corresponds to the integral in the u-v system as:

∫∫f(x,y) dx dy = ∫∫f(x(u,v),y(u,v))|J | du dv.

In a triple integral, when changing from:

∫∫∫ f(x,y,z) dx dy dz to ∫∫∫ f(u,v,w) du dv dw,

the factor relates the volume dxdydz with volume dudvdw such that dxdydz becomes |J | dudvdz. Therefore, the integral in the x-y-z system corresponds to the integral in the u-v-w system as:

∫∫∫ f(x,y,z) dxdydz = ∫∫∫ f(x(u,v,w),y(u,v,w),z(u,v,w) |J | dudvdw

• The J factor in two and three variable integrals, represents the Jacobian determinant and corresponds to the (dx/dy) factor in the one-variable integral. There are both two- and three-dimensional Jacobian determinants that correspond to two- and three-variable integrals. The Jacobian determinant for two variables is:

The Jacobian determinant for three variables is:

These determinants for two and three variables are sometimes represented by:

Also note that the δ represents a partial derivative. See Chapter 6 for a discussion of partial derivatives.

• The J factor represented by the Jacobian determinant can be derived by translating an element of the area or volume represented by a two-or three-variable integral from an XY (or XYZ) coordinate system to a UV (or UVW) coordinate system. Consider the relationship of a volume element in an XYZ coordinate system vs. a UVW coordinate system that represents a cylindrical or spherical system. Because a curved region in a rectangular coordinate system can correspond to a rectangular region in cylindrical or spherical coordinates, the volume element has curved sides in the rectangular coordinates and straight sides in cylindrical and spherical coordinates.

This figure represents only the x-y and u-v planes for simplicity. If the curved element in the XYZ coordinate system is represented in vector form such that the vector representing each curved line has an i component in the x-direction, a j component in the y-direction, and a k component in the z-direction (see Section 5.1 for explanation of i, j, k,), then:

The change in x is given by:

(x(u+Δu, v, w) − x(u, v, w ))i + (y(u+Δu, v, w) − y(u, v, w ))j

+ (z(u + Δu, v, w) − z(u, v, w))k

≈ [(∂x/∂u)Δu]i + [(∂y/∂u)Δu]j + [(∂z/∂u)Δu]k

The change in y is given by:

(x(u, v+Δv, w) − x(u, v, w ))i + (y(u, v+ Δv, w) − y(u, v, w ))j

+ (z(u, v+ Δv, w) − z(u, v, w))k

≈ [(∂x/∂v)Δv]i + [(∂y/∂v)Δv]j + [(∂z/∂v)Δv]k

The change in z is given by:

(x(u, v, w+Δw) − x(u, v, w ))i + (y(u, v, w + Δw) − y(u, v, w ))j

+ (z(u, v, w +Δw) − z(u, v, w))k

≈ [(∂x/∂w)Δw]i + [(∂y/∂w)Δw]j + [(∂z/∂w)Δw]k

The vector product (cross product) of the x, y, and z components is:

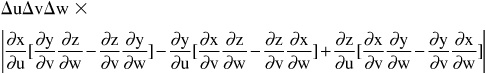
where the quantity within the absolute value symbol represents the determinant:

• In general, to change coordinate systems in an integral, express x, y, and z in terms of the new variables u, v, and w, convert the x–y–z element into a u–v–w element, and include the Jacobian determinant to factor in the change in the shape of the element.

• The Jacobian determinants can derive the conversion factors for polar, cylindrical, and spherical coordinate systems.

In polar coordinates:

x = r cos θ= u cos v

y = r sin θ= u sin v

The Jacobian in polar coordinates is:

In spherical coordinates:

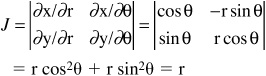
x = ρ cos θ sin φ = u cos v sin w

y = ρ sin θ sin φ = u sin v sin w

z = ρ cos φ = u cos w

The Jacobian in spherical coordinates is:

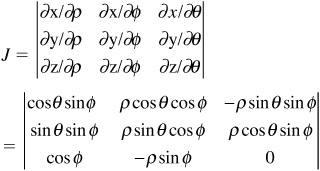
Calculating this determinant results in J = ρ² sin φ.

3.17 Applications of the Integral

• This section includes some applications of the integral including work, pressure, center of mass, and distributions.

Work and Pressure

• Work performed = force × distance. For example, if a particle or object is moved by a constant force F some distance x, then the work done is W = (F)(x). For a variable force F pushing or pulling a particle or object in the direction of motion along a straight line from x₁ to x₂, work can be represented by:

_x1∫^x2 F(x) dx

The motion is often described along an axis of a coordinate system. If the motion is along a curve ds from s₁ to s₂, then the total work done can be represented by:

_s1∫^s2 F(s) ds

• Example: What is the work required to lift an object weighing 1,000 pounds six feet off the ground?

₀∫⁶ (1,000) dx = (1,000)(6) − (1,000)(0) = 6,000 foot-pounds

(Note that pounds is the weight. If mass were given it would need to be multiplied with the acceleration of gravity in the proper units.)

Because this is a simple problem that does not require sectioning into subsections or elements and then summing as the size of each subsection approaches zero, this result of integration can be compared with simply multiplying.

W = (force)(distance)

W = (1,000 pounds)(6 feet) = 6,000 foot-pounds

• In more complicated work integrals, the geometry of what is being described is written into the integral. For example, to calculate the work required to pump fluid out of a cylindrical tank of height h, the integral could be designed to calculate the sum of disc-shaped sections of water that each need to be lifted out of the tank. The volume of each disc is πr²dz and the weight of a disc is the density p of the fluid multiplied by the volume of the disc, or ρπr²dz. (This is not the same ρ as described in polar coordinate systems.) If the distance each disc needs to be lifted is given by z (which will be slightly different for each disc because they are starting from different heights), the integral giving weight multiplied with distance is:

₀∫^h ρπr² z dz

• Pressure is force per unit area, P = F/A, and therefore force is pressure multiplied with area, F = PA. The pressure exerted by a liquid at a given point in the liquid or on an object that is submersed in the liquid, is the same in all directions at a given point. The pressure increases the deeper it is measured in a body of liquid and is given by:

P =ρgh = wh

where ρ is the density of the liquid (mass/volume);

g is the gravitational constant;

h is the height, or more specifically depth, from the surface of the liquid; and

w is the weight per volume of the liquid, or ρg.

The total pressure on an object or on a specified region of liquid can be represented as the sum of all the subdivisions of area at various depths. If a section of area is defined by the length of a horizontal section l at a given height h with a thickness dh, then the force on the section is:

ΔF = whl Δh

Therefore, the total force F on the object or region is the sum of the forces of all sections:

F = ∫ whl dh

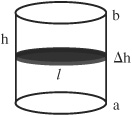
Consider the work required to pump water up and out of a tank that has a height of h and a diamter of l. If the tank is divided into sections having area A, thickness Δh, and each at a slightly different height, then this can be thought of as pumping each section out individually and summing:

W = _a ∫^b Awh dh

Center of Mass

• Integrals can be used to describe the center of mass. The center of mass is defined as the moment divided by the mass, where the moment is defined as the distance of the mass from a line or axis multiplied by the mass itself. For example, for a point mass m₁ located a certain distance x₁ from an axis, the moment of that point mass is x₁m₁. If there are many point masses located at specific distances from the axis, the sum of those moments is: Σx_im_i

If there is a continuous distribution of these masses at various lengths from the axis, the sum of the moments becomes: ∫ x dm

The center of mass is: ∫ x dm ÷ ∫ dm

where dm represents an element of mass.

• The center of mass can be measured from an axis or a plane in terms of one, two, or three dimensions. In one dimension, masses can behave as a single mass along a line or curve, such that the density ρ of each element of mass is described in terms of ρ = mass/volume, and the volume is represented in this one-dimensional situation as the length of the element of mass, so that the density at a point is dm/ds. Therefore, the mass is density multiplied by length, ρ ds. The total center of mass is:

moment/mass = ∫ ρx ds ÷ ∫ ds

In an XY coordinate system, the center of mass described according to x-and y-coordinates is:

∫ ρx ds ÷ ∫ ds and ∫ ρy ds ÷ ∫ ds

• For two-dimensions, center of mass is described in terms of density multiplied by area such that dm = ρ dA, and the masses are distributed in a plane rather than along a line or curve. The center of mass occurs where all the masses balance. There is a moment around the X-axis, Σy_im_i, and the Y-axis, Σx_im_i. Each element has x and y coordinates within the plane. Therefore:

dm =ρ dA = ρ(y₁ − y₂) dx = ρ(x₁ − x₂) dy

In an X-Y coordinate system, the center of mass described according to x- and y-coordinates is:

∫ ρ(y₁ − y₂) x dx ÷ ∫ ρ(y₁ − y₂) dx and

∫ ρ(x₁ − x₂) y dy ÷ ∫ ρ(x₁ − x₂) dy

• For three-dimensions, center of mass is described in terms of density multiplied by volume such that dm = ρdV, and the masses are distributed in three-dimensional space. If the volume is described in terms of a volume of revolution:

V = π _a∫^b f(x)² dx or V = π _a ∫ ^b y² dx

and sections are made perpendicular to the Y-axis, then:

dm = ρπx² dy

Each section is the same distance from the bottom plane, so that a first moment is given by:

∫ ρπx² y dy

The center of mass is described as the moment divided by the mass:

∫ ρx²y dy ÷ ∫ ρx² dy

• Note that moment of inertia is used in the description of physical systems such as rotating bodies. The moment of inertia is calculated similar to the first moment in the center of mass description above, except that the distance from the mass to the axis or plane is squared. For example, in the one-dimensional situation the first moment is:

∫ ρx ds and ∫ ρy ds

Using the square of distance, the moment of inertia is:

∫ ρx² ds and ∫ ρy² ds

Distributions, Probabilities, and Integration

• Integrals are often used to describe various statistical quantities. One example is the probability that some value of x will fall between two points, a and b, and is described in terms of a density function p(x) and the integral:

_a∫^b p(x) dx

Providing _−∞∫^∞ p(x) dx = 1 and p(x) ≥ 0 for all x values.

This can be represented as an area between points a and b.

• An example using two variables occurs where the two variables are distributed throughout a population. The density function can be given in terms of two variables p(x,y) and a volume is described on a graph such that x is between x = a and x = b and y is between y = c and y = d:

_a ∫^b _c ∫^d p(x,y) dydx

Providing _−∞∫^∞ _−∞∫^∞ p(x,y) dy dx = 1 and p(x) ≥ 0 for all x and y.

3.18 Evaluating Integrals Using Integration by Parts

• This section provides a summary of the method of integration by parts, which is a practical method used often to evaluate integrals. Included in this section is the formula for integration by parts for indefinite and definite integrals and its derivation.

• To evaluate complicated integrals, methods that go beyond simply applying the integral formula are often required. Some of the most common methods are integration by parts, substitution, partial fractions, and looking up integrals in integral tables.

• To evaluate certain complicated integrals, the method of integration by parts can be applied. Applying this method is often compared to applying the product rule for evaluating derivatives. To use this method, the integral must exist in the form or be arranged to fit the following formula:

∫ f(x) g’(x) dx = f(x) g(x) − ∫ f ’(x) g(x) dx

Or equivalently:

∫ f g’ dx = f g − ∫ f’ g dx

Note: The integration by parts formula is an important formula used frequently in calculus.

Using other notation, where u = f(x) and v = g(x), the integration by parts formula is written:

∫ u dv = uv − ∫ v du

• The integration by parts formula can be derived by integrating the product rule. The product rule is:

Integrate each term:

∫(fg)’ dx = ∫ f’g dx + ∫ fg’ dx

Rearrange:

∫ fg’ dx = ∫ (fg)’ dx − ∫ f ’g dx

Because ∫ (fg)’ dx = fg, this becomes:

∫ fg’ dx = fg − ∫ f’g dx

which is the integration by parts formula.

• When the integral is a definite integral, the f(x)g(x) term is also evaluated at the limits, and the integration by parts formula for a definite integral becomes:

_a∫^b f(x) g’(x) dx = f(b)g(b) − f(a)g(a) − _a∫^b f ’(x) g(x) dx

• To use integration by parts, the appropriate parts of the integral must be substituted for f ’(x) and g(x), (or equivalently u and dv). The choice should be dependent on how easy it will be to get f(x) from f’(x).

• Example: Integrate ∫ x cos x dx.

First arrange in a form that will fit the integration by parts formula and make the following substitutions:

u = x

du = dx

dv = cos x dx

From the substitution for dv, integrate v:

v = ∫ cos x dx = sin x

Substituting into the integration by parts formula:

∫ u dv = uv − ∫ v du

The integral becomes:

∫ x cos x dx = x sin x − ∫ sin x dx

Because ∫ sin x dx = − cos x, the integral becomes:

∫ x cos x dx = x sin x + cos x + c

• The integration by parts formula may need to be repeated during the evaluation of an integral.

For example, integrate: ∫ x²e^x dx:

Using the integration by parts formula: ∫ u dv = uv − ∫ v du

The substitutions are:

u = x², dv = e^x dx, therefore, v = e^x and du = 2x dx

Substitute into the formula:

∫ x²e^x dx = x²e^x − ∫ e^x 2x dx

Repeat integration by parts on ∫ e^x 2x dx

The substitutions are:

u = 2x, dv = e^x dx, therefore, v = e^x and du = 2 dx

Substitute into the formula:

∫ e^x 2x dx = 2xe^x − 2 ∫ e^x dx = 2xe^x − 2e^x + c

Therefore, substituting back into the original integral:

∫ x²e^x dx = x²e^x − (2xe^x − 2e^x) + c = e^x(x² − 2x + 2) + c

(See the end of Section 3.19 for simplifications that can be used to simplify integrals before applying integration by parts. These include using trigonometric identities, factoring, and some common derivatives.)

3.19 Evaluating Integrals Using Substitution

• This section provides a summary of the method of substitution, which is a practical method used often to evaluate integrals. Included in this section is a description of substitution, its relationship to the chain rule, using substitution for indefinite and definite integrals, and simplifying integrals before applying substitution using trigonometric identities, factoring, and common derivatives.

• Substitution of variables is used to translate a complicated integral into a more manageable form so that the integral can be solved using the integral formula or integral tables. Then the integral is translated back to its original variables. When using substitution or other methods, there are certain types of simplifications that may be particularly helpful to perform on the original integral before the more formal technique is employed. Such simplifications may involve using trigonometric identities, the Pythagorean theorem, and factoring.

• The method of substitution is sometimes referred to as change of variables. The substitution method is a general strategy involving substituting placeholder variables into a complicated integral, solving the integral in its simplified form, then substituting the original variables back into the resulting expression.

• Using substitution to solve integrals is often compared with using the chain rule to evaluate derivatives. In fact the substitution method is generally based on the chain rule from differentiation. To understand substitution it is helpful to review the chain rule. The chain rule is used often to determine the derivative of composite functions. To use the chain rule for differentiation, it is important to identify the outer function and the inner function in the equation or expression to be differentiated. The chain rule formula is:

[f(g(x))]’ = f’(g(x))(g’(x))

Or equivalently, for more complex functions:

The chain rule essentially states that the derivative of f(g(x)) equals the derivative of the outside function multiplied by the derivative of the inside function. For example, use the chain rule to differentiate:

(d/dx)(x² + 7)³ = 3(x² + 7)²(2x)

The chain rule results in the product of two factors, the derivative of the outside function and the derivative of the inside function. If the integral in question has a form similar to f’(g(x))(g’(x)), then its integral or antiderivative has the form f(g(x)).

• Substitution can generally be applied to integrals that have their integrand in a form similar to f ’(g(x))(g’(x)). The key to using the substitution method is identifying the“inside function”by looking at which factor is the derivative of the inside function. This generally involves guessing what the antiderivative could be by using the reverse of the chain rule and trying to identify the inside function and the outside function from the factors, then differentiating that result to check whether it was, in fact, the antiderivative. The substitution method may produce a result that is off by a constant factor which can be corrected, then checked by differentiation.

• A general form of an integral that lends itself to substitution is f (g(x))(g’(x)) = f (u)(g’(x)). If f(u) is a continuous function and g(x) is a function such that dg(x)/dx exists and g(x) = u = u(x) = the inside function, then:

∫ f(u) du = ∫ f(g(x))g’(x) dx

Equivalently:

where du = (du/dx)dx

• To use the substitution method to calculate an integral, first identify the inside function by looking at which factor is the derivative of the inside function, choose u and compute du/dx, identify and integrate f(u) du, then substitute u back into the antiderivative.

• Example: Find the integral

First, identify the inside function by looking at which factor is the derivative of the inside function.

Notice that the numerator (x + 1) is the derivative of the denominator (x² + 2x + 10), except for a factor of 2. Therefore, choose u = (x² + 2x + 10).

The derivative of u is: du/dx = (2x + 2) = 2(x + 1)

Rearranging gives: dx = du / 2(x + 1)

Next, substitute u and du into the integral so that (x² + 2x + 10) = u and dx = du / 2(x + 1), then evaluate the integral:

(Remember, ∫ 1/x dx = ln |x| + c.)

Finally, substitute the original expressions back into the evaluated integral, where u = (x² + 2x + 10):

(1/2) ln|(x² + 2x + 10)| + c

Therefore:

∫(x + 1)/(x² + 2x + 10) dx = (1/2) ln | (x² + 2x + 10) | + c

• Example: Find the integral ∫ f(x) dx = ∫ x(exp{x²}) dx.

First, identify the inside function by looking at which factor is the derivative of the inside function.

Notice that the factor x is the derivative of x², except for a factor of 2. Therefore choose u = x².

The derivative of u is: du/dx = 2x, or du = 2x dx

Rearranging gives: dx = du/2x

Next, substitute u and du into the integral so that x² = u and dx = du/2x, then evaluate the integral:

∫ x (exp{u}) du/2x = (1/2)∫ exp{u} du = (1/2) exp{u} + c

Finally, substitute the original expressions back into the evaluated integral, where u = x²:

(1/2) exp{x²} + c

Therefore, ∫ x (exp{x²}) dx = (1/2) exp{x²} + c.

• If the integral is a definite integral, the limits can be evaluated after the resulting antiderivative has been converted back to its original variables, or the original limits can be converted into new limits in terms of the new variables and the antiderivative can be evaluated in the new limits and does not need to be converted back to the original variables.

• Example: Find: ₀∫¹ f(x) = ₀∫¹ 2x(x² + 1)^1/2 dx.

First, identify the inside function by looking at which factor is the derivative of the inside function.

Notice that the factor 2x is the derivative of (x² + 1). Therefore, choose u = (x² + 1).

The derivative of u is: du/dx = 2x, or du = 2x dx

Rearranging gives: dx = du/2x

Also, transforming the limits: u(1) = 2 and u(0) = 1

Next, substitute u and du into the integral:

This is the final answer because the limits were transformed and the integral was evaluated in the new limits.

Alternatively, the antiderivative in this example can be solved using the substituted integrand, then the result transformed back into the original variables, and evaluated at the original limits:

₀∫¹ 2x(x² + 1)^1/2 dx = ₀∫¹ u^1/2 du = (2/3)u^3/2

Substitute the original expressions back into the evaluated integral, where u = (x² + 1):

(2/3)u^3/2 = (2/3)(x² + 1)^3/2

Then evaluate at original limits:

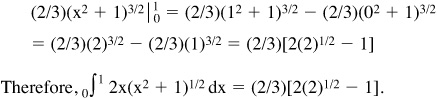
Simplifying Integrals Before Using Formal Techniques

• It may be helpful to simplify an integral before a more formal technique is employed. Simplifications may include factoring, substituting trigonometric identities, or using the Pythagorean theorem.

• Factoring can also be used to simplify an integral. Examples of factoring include:

x² + (m + n)x + mn → factors to → (x + m)(x + n)

x² + 2x + 1 → factors to → (x + 1)(x + 1)

pqx² + (pn + qm)x + mn → factors to → (px + m)(qx + n)

x² − y² → factors to → (x + y)(x − y)

x² + 2xy + y² → factors to → (x + y)²

x² − 2xy + y² → factors to → (x − y)²

x² − 2x + 2 → factors to → (x − 1)² + 1

Check this last example by working backward:

(x − 1)(x − 1) + 1 = (x² − 2x + 1) + 1 = x² − 2x + 2

• Examples of trigonometric functions and relations that can be used when making substitutions include:

sin²x + cos²x = 1

sin²x = 1 − cos²x

cos²x = 1 − sin²x

1 + tan²x = sec²x

sec²x − 1 = tan²x

1 + cot²x = csc²x

csc²x − 1 = cot²x

tan x = sin x / cos x = 1 / cot x

cot x = cos x / sin x = 1 / tan x = cos x csc x

sec x = 1 / cos x

csc x = 1 / sin x

sin 2x = 2 sin x cos x

cos 2x = cos²x − sin²x = 2 cos²x − 1 = 1 − 2 sin²x

sin(π − x) = sin x

cos(π − x) = −cos x

sin x = cos(x − π/2) = cos(π/2 − x)

cos x = sin(x + π/2) = sin(π/2 − x)

sin(x − y) = sin x cos y − cos x sin y

cos(x + y) = cos x cos y − sin x sin y

cos(x − y) = cos x cos y + sin x sin y

sin x cos y = (1/2)sin(x − y) + (1/2)sin(x + y)

cos x sin y = (1/2)sin(x + y) − (1/2)sin(x − y)

cos x cos y = (1/2)cos(x − y) + (1/2)cos(x + y)

sin x sin y = (1/2)cos(x − y) − (1/2)cos(x + y)

tan(x + y) = (tan x + tan y)/(1 − tan x tan y)

e ^ix = cos x + i sin x

e ^−ix = cos x − i sin x

e ^i(−x) = cos(−x) + i sin(−x)

cos x = (1/2)(e ^ix + e ^−ix)

sin x = (1/2i )(e ^ix − e ^−ix)

cosh x = (1/2)e ^x + (1/2)e ^−x

sinh x = (1/2)e ^x − (1/2)e ^−x

e ^x = cosh x + sinh x

e ^−x = cosh x − sinh x

sinh²x = (1/2)(cosh 2x − 1)

cosh²x = (1/2)(cosh 2x + 1)

sinh(x ± y) = sinh x cosh y ± cosh x sinh y

cosh(x ± y) = cosh x cosh y ± sinh x sinh y

• The following substitutions provide examples of simplifying integrals based on trigonometric identities for the particular selection of u and calculation of du used in the substitution method:

(a.) If an integral contains [u² − a²]^1/2, substitute for u, u = a csc θ, then [u² − a²]^1/2 becomes:

[a²csc²θ − a²]^1/2 = [a²(csc²θ− 1)]^1/2 = [a²cot²θ]^1/2 = a cot θ

Note that (du/dθ)(a csc θ) = − a csc θ cot θ.

(b.) Alternatively, if the integral contains [u² − a²]^1/2, substitute for u, u = a sec θ, then [u² − a²]^1/2 becomes:

[a²sec²θ − a²]^1/2 = [a²(sec²θ − 1)]^1/2 = [a²tan²θ]^1/2 = a tan θ

Note that (du/dθ)(a sec θ) = a sec θ tan θ.

(c.) If an integral contains [u² + a²]^1/2, substitute for u, u = a tan θ, then [u² + a²]^1/2 becomes:

[a²tan²θ + a²]^1/2 = [a²(tan²θ + 1)]^1/2 = [a²sec²θ)]^1/2

= a sec θ= a(1/(cos²x))

Note that (duAW)(a tan θ) = a sec²θ.

(d.) If the integral contains [a² − u²]^1/2, substitute for u, u = a sin θ, then [a² − u²]^1/2 becomes:

[(a² − a²sin²θ)]^1/2 = [a²(1 − sin²θ)]^1/2 = [a²cos²θ]^1/2 = a cos θ

Note that (du/dθ)(a sin θ) = a cos θ.

• Examples of derivatives to remember when using the substitution method and integration-by-parts:

(d/dx)sin x = cos x

(d/dx)cos x = −sin x

(d/dx)tan x = 1/(cos²x) = sec²x

(d/dx)cot x = −csc²x

(d/dx)csc x = −csc x cot x

(d/dx)sec x = sec x tan x

(d/dx)sin⁻¹x = 1/(1 − x²)^1/2

(d/dx)cos⁻¹x = −1/(1 − x²)^1/2

(d/dx)tan⁻¹x = 1/(1 + x²)

(d/dx)cot⁻¹x = −1/(1 + y²)

(d/dx)sec⁻¹y = 1/|y|(y² − 1)^1/2

(d/dx)csc⁻¹y = −1|y| (y² − 1)^1/2

y = uⁿ, (dy/dx) = nuⁿ⁻¹(du/dx), for positive n.

y = a^u, (dy/dx) = a^u(log a)(du/dx)

y = u^v, (dy/dx) = vu^v−1(du/dx) + u^v(log u)(dv/dx)

y = e ^u, (dy/dx) = e ^u(du/dx)

y = log_au, (dy/dx) = (1/u)log_ae (du/dx)

y = log u, (dy/dx) = (1/u)(du/dx), u ≠ 0.

y = cos u, (dy/dx) = −sin u(du/dx)

y = sin u, (dy/dx) = cos u(du/dx)

(d/dx)ln x = 1/x

• Example: Integrate ∫ sin³x dx using substitutions for sine and cosine.

Rearrange:

∫ sin³x dx = ∫ sin²x sin x dx = ∫ (1 − cos²x)sin x dx

= ∫ (sin x − cos²x sin x) dx = ∫ sin x dx − ∫ cos²x sin x dx

Integrate:

∫ sin x dx = cos x

Then solve ∫ cos²x sin x dx

by substituting cos x = u and sin x dx = du:

∫ cos²x sin x dx = ∫ u² du = u³/3 + c = (cos x)³/3 + c

Therefore:

∫ sin³x dx = ∫ sin x dx − ∫ cos²x sin x dx = cos x − (1/3)cos³x + c

• Note, the identity sin²x + cos²x = 1, is equivalent to sin²x = 1 − cos²x and cos²x = 1 − sin²x. These are particularly helpful because they can be applied to sine and cosine raised to other powers. For ∫ sin²x cos x dx and ∫ cos²x sin x dx, substitutions can be made such as u = sin x, du = cos x dx and u = cos x, du = -sin x dx. These substitutions result in integrals in the form ∫ u² du. Note that other powers of both cosine and sine can be treated similarly and integrated using the substitution method.

3.20 Evaluating Integrals Using Partial Fractions

• This section includes a brief explanation of the method of partial fractions. For a more comprehensive explanation, see a calculus textbook.

• The method of partial fractions is applicable when the integrand is a rational fraction such as a quotient of polynomials. In this method, the fraction is separated into a sum of simple fractions that can be easily integrated. The integral of simple fractions often involves the natural logarithm (except when the denominator is raised to a power). When using partial fractions for certain integrals, it may be helpful to remember that ∫ 1/x dx = ln | x | + c, or for a more complicated function, ∫ 2/(x + 1) dx = 2 ln|x + 1| + c.

• Following is a brief explanation of the method of partial fractions and how to use it to solve an integral:

(a.) First verify that the degree of the numerator is smaller than the degree of the denominator. If the degree of the numerator is equal or larger, divide the leading term of the denominator into the leading term of the numerator.

(b.) Next, factor the denominator.

(c.) Then separate the fractions into simpler fractions and insert unknown constants A, B, C, etc., into each numerator. Each factor will generally become a separate fraction. The new numerators will each contain the part of the original denominator (common denominator) that is absent from its new denominator. The constants make the original integral equal to the simpler fractions.

(d.) Then solve for the unknown constants A, B, C, etc., by setting the sum of the new numerators equal to the original numerator.

(e.) Finally, integrate each new fraction resulting in a sum of logarithms.

• A general relation that can be followed for a fraction with a simple binomial in the denominator and a numerator with its degree less than that of the denominator is:

where, (ax + b) = A(x − n) + B(x − m).

Using the constants A and B, solve as two integrals:

∫ [(ax − b)/(x − m)(x − n)] dx = ∫ A/(x − m) dx + ∫ B/(x − n) dx

= A ln |x − m| + B ln|x − n| + c

• The partial fractions method can be demonstrated in this simple example of the integral: ∫ 1/(x² + 3x + 2) dx

First factor the denominator:

∫ 1/[(x + 1)(x + 2)] dx

Translate this integral into two simple integrals:

∫ A/(x + 1) dx + ∫ B/(x + 2) dx

where A and B represent constants that make

1/[(x + 1)(x + 2)] equivalent to [A/(x + 1) + B/(x + 2)].

Determine the value of A and B by first combining [A/(x + 1) + B/(x + 2)] back into one fraction with a common denominator (the original denominator) with the proper multiplication steps in the numerators:

Then solve for A and B by setting the original numerator“1”equal to the new numerator:

1 = x(A + B) + 2A + 1B

In order for the expression on the right to equal 1, A + B must equal zero. If this is true, the resulting equation becomes, 1 = 2A + 1B. This leaves two equations and two unknowns:

A + B = 0 and 1 = 2A + B

A and B can be solved using substitution of the two unknown variables into the two equations. Rearrange (A + B = 0) to isolate A, then substitute the expression for A into (1 = 2A + B):

A = −B

1 = 2(−B) + B = − 2B + B = − B

1 = − B

Therefore, B = −1.

Substituting B into the A = − B:

A = − (−1)

Therefore, A = 1.

Check results by substituting into an original equation:

A = −B

1 = − (−1) = 1

Finally solve the simplified (split) integral using the A and B values:

∫ A/(x + 1) dx + ∫ B/(x + 2) dx = ∫ 1/(x + 1) dx − ∫ 1/(x + 2) dx

= ln | x + 1 | − ln | x + 2 | + c

Check this final answer by differentiating:

which is the original integral.

• A more complicated example using the partial fractions method is to solve the integral: ∫ (x + 2)/(x² + 2x − 3) dx

First factor the denominator:

∫ (x + 2)/[(x − 1)(x + 3)] dx

Translate this integral into two simple integrals:

∫ A/(x − 1) dx + ∫ B/(x + 3) dx

where A and B represent constants that make

(x + 2)/[(x − 1)(x + 3)] equivalent to [A/(x − 1) + B/(x + 3)].

Determine the value of A and B by first combining [A/(x − 1) + B/(x + 3)] back into one fraction with a common denominator (the original denominator) with the proper multiplication steps in the numerators:

To solve for A and B, set the original numerator“(x + 2)”equal to the new numerator:

(x + 2) = Ax + 3A + Bx − B

Rearranging:

2 = Ax + Bx − x + 3A − B

2 = x(A + B − 1) + 3A − B

Set A + B equal to 1 so the x term equals zero. If this is true, the resulting equation becomes (2 = 3A − B).

This leaves two equations and two unknowns:

A + B = 1 and 2 = 3A − B

A and B can be solved using substitution of the two unknown variables into the two equations. Rearrange (A + B = 1) to isolate A, then substitute the expression for A into (2 = 3A − B):

A = 1 − B

2 = 3(1 − B) − B

2 = 3 − 3B − 1B = 3 − 4B

−4B = −1

Therefore, B = 1/4.

Substituting B into the A = 1 − B:

A = 1 − 1/4 = 3/4

Therefore, A = 3/4.

Check results by substituting into an original equation:

A = 1 − B

3/4 = 4/4 − 1/4 = 3/4

Finally, solve the simplified (split) integral using the A and B values:

∫ A/(x − 1) dx + ∫ B/(x + 3) dx

= ∫ (3/4)/(x − 1) dx + ∫ (1/4)/(x + 3) dx

= (3/4) ln | x − 1| + (1/4) ln | x + 3 | + c

Check this final answer by differentiating:

which is the original integral.

3.21 Evaluating Integrals Using Tables

• Integral tables are used to solve integrals in forms that do not allow easy application of integration techniques. Integral tables are found in mathematical handbooks, calculus books, online integral tables, and the CRC Handbook of Chemistry and Physics.

• Integral tables contain solved integrals in various forms so that an unknown integral can be matched to or translated into the form in the integral table that is identical or most similar to it. If the unknown integral is not identical to a form in the table, a transformation of the integral must be made using substitution. For example, substitute y for ax. Specific substitutions are suggested within integral tables for certain integrals. In general, when making substitutions, a few points that may apply are to make a substitution of the dx terms, to express the limits of the definite integrals in the new dependent variable, and to perform reverse substitution to obtain the answer in terms of the original independent variable.

• In general when using integral tables, identify which type of integral best fits the integral in question. It may be helpful to peruse some integral tables to become familiar with the integrals and substitution suggestions and to read the introductory discussions at the beginning of the tables. Anyone using calculus will often need to look up integrals in the tables. It is worthwhile to become familiar with them. Remember to use laws of logarithms, trigonometric identities, factoring, etc., if necessary to transform an integral into a form that matches a solved integral in the tables. Also, note that sometimes a resulting integral in the tables will have another integral in its result. In these situations, repeat the formula on the resulting integral until there is a constant that results or no further integration is required.