D.1 Introduction

Identification of both steady state (SS) and transient state (TS) in noisy process signals is important. Steady‐state models are widely used in process control, online process analysis, and process optimization; and since manufacturing and chemical processes are inherently nonstationary, selected model parameter values need to be adjusted frequently to keep the models true to the process and functionally useful. But either the use or data‐based adjustment of SS models should only be triggered when the process is at SS. Additionally, detection of SS triggers the collection of data for process fault detection, the data reconciliation, the neural network training, the end of an experimental trial (collect data and implement the next set of conditions), etc.

Often, process owners, scientists, and engineers run a sequence of experiments to collect data throughout a range of operating conditions, and process operators sequence the next stage of a trial. Each sampling event is initiated when the operator observes that steady conditions are met. Then the operator implements the new set of operating conditions. Similarly, in batch operations the end of a stage is evidenced by signals reaching their equilibrium or completion values, and when operators observe that the stage is complete, they initiate the next step in the processing sequence. However, this visual method of triggering requires continual human attention, and it is subject to human error in the recognition of steady state. Features that can compromise the visual interpretation include noisy measurements, slow process changes, multiple dynamic trends, scheduled operator duties, upcoming lunch breaks, or change‐of‐shift timing.

Alternately, the experimental run or batch stage can be scheduled to go to the next set of conditions at preset time intervals. Unfortunately, this method can create inefficiency if the runs are scheduled for an unnecessarily long time, or the data can be worthless if the scheduled time is insufficient for any particular set of conditions to achieve steady state. Since the time to reach steady state varies with operating conditions, it is difficult to accurately predict the necessary hold time.

If SS detection were automated, process sampling or data recording would be initiated, and after, the computer could autonomously implement the next operational stage or set of experimental conditions. But likely on the first sampling after the new signals go to the process, the process will not have responded, and the process output signals will remain at their prior steady state. To prevent this past SS from triggering the next trial, the computer should first seek a TS after implementing new conditions and then seek the resulting SS.

An automated online, real‐time SS and TS identification would be useful to trigger the next stage of an experimental plan or process phase.

In the context of optimization, steady‐state identification is used several ways:

1. To identify that the optimization in nonlinear regression has converged
2. To identify that the optimization in stochastic applications has converged
3. To identify when an adequate number of realizations have been acquired to provide statistical confidence that the CDF is captured

If a process signal was noiseless, then SS or TS identification would be trivial. At steady state there is no change in data value. Alternately, if there is a change in data value, the process is in a transient state.

However, since process variables are usually noisy, the identification needs to “see” through the noise and would announce probable SS or probable TS situations, as opposed to definitive SS or definitive TS situations. Accordingly, a method also needs to consider more than the most recent pair of samples to confidently make any statement.

Since the noise could be a consequence of autocorrelated trends (of infinite types), varying noise amplitude (including zero), individual spikes, non‐Gaussian noise distributions, or spurious events, a useful technique also needs to be robust to such aspects. Fortunately, in applications to determining convergence in optimization, the signal is driven by independent random events (not autocorrelated), and an elementary (easy to understand, and implement, computationally fast) algorithm is applicable.

D.2 Conceptual Model

Begin with this conceptual model of the phenomena: The true process variable (PV) is at a constant value (at SS) and events create “noise,” independently distributed fluctuations on the measurement. In optimization, the noise on a measurement (the OF value) may arise from Monte Carlo stochastic functions or from randomized sampling of data. In observing experimental data, such measurement perturbations could be attributed to mechanical vibration, stray electromagnetic interference in signal transmission, electronic noise, flow turbulence, etc. In simulation, the “noise” represents realization‐to‐realization differences. Alternately, the concept includes a situation in which the true PV is averaging at a constant value, and internal spatial nonuniformity (resulting from nonideal fluid mixing or multiphase mixtures in a boiling situation) or an internal distribution of properties (crystal size, molecular weight) create temporal changes to the local measurement.

If the noise distribution and variance would be unchanging in time, then statistics would call this time series as stationary. However, for a process, the true value, nominal value, or average may be constant in time, but the noise distribution may change. So, SS does not necessarily mean stationary in a statistical sense of the term.

The first null hypothesis of this analysis is the conventional one where the process is at steady state, Ho: SS. For the approach recommended here, the statistic, a ratio of variances, the R‐statistic, will be developed. Due to the vagaries of noise, the R‐statistic will have a distribution of values at SS. As long as the R‐statistic value is within the normal range of a SS process, the null hypothesis cannot be rejected. When the R‐statistic has an extreme value, then the null hypothesis can be rejected with a certain level of confidence, and probable TS claimed.

By contrast, there is no single conceptual model of a transient state. A transient condition could be due to a ramp change in the true value, or an oscillation, or a first‐order transient to a new value, or a step change, etc. Each is a unique type of transient. Further, each single transient event type has unique characteristics such as ramp rate, cycle amplitude and frequency, and time constant and magnitude of change. Further, a transient could be comprised of any combination or sequence of the not‐at‐SS events. Since there is no unique model for TS, there can be no null hypothesis or corresponding statistic that can be used to reject the TS hypothesis and claim probable SS. Accordingly, an alternate approach needs to be used to claim probable SS.

The alternate approach used here is to take a transient condition that is barely detectable or decidedly inconsequential (per human judgment) and set the probably SS threshold for the R‐statistic as an improbable low value, but not so low as to be improbably encountered when the process is truly at SS.

D.3 Method Equations

This description is extracted from Nonlinear Regression Modeling for Engineering Applications: Modeling, Model Validation, and Enabling Design of Experiments, by R. R. Rhinehart, John Wiley & Sons, Inc., Hoboken, September 2016b.

The method of Cao and Rhinehart (1995) uses a ratio of two variances, as measured on the same set of data by two methods. Figure D.1 illustrates the concept. The value starts at a value of about 20, ramps to a value of about 5 at sample number 50, and then holds steady. The markers about that trend represent the measured data. The true trend is unknowable, only the measurements can be known, and they are infected with noise‐like fluctuations, masking the truth.

The method first calculates a filtered value of the process measurements, indicated by the solid line that lags behind the data. Then the variance in the data is measured by two methods. One deviation d₂ is the difference between measurement and the filtered trend. The deviation d₁ is the difference between sequential data measurements.

If the process is at SS, as illustrated in the 80–100 time period, the filtered value, X_f is almost the middle of the data. Then a process variance, σ², estimated by d₂ will ideally be equal to σ² estimated by d₁. Then the ratio of the variances, , will be approximately equal to unity, . Alternately, if the process is in a TS, then X_f is not the middle of data, the filtered value lags behind, and the variance as measured by d₂ will be much larger than the variance as estimated by d₁, , and ratio will be much greater than unity, .

In 2016, I became aware that von Neumann published an analysis of this ratio of variance concept in 1941. But I was not aware of that in the 1980s and seem to have rediscovered the concept and co‐analyzed with my PhD candidate Songling Cao. However, contrasting the von Neumann approach, to minimize computational burden, in this method a filtered value (not an average) provides an estimate of the data mean:

(D1)

where X is the process variable, X_f is the filtered value of X, λ₁ is the filter factor, and i is the time sampling index.

The first method to obtain a measure of the variance uses an exponentially weighted moving “variance” (another first‐order filter) based on the difference between the data and the “average”:

(D2)

where is the filtered value of a measure of variance based on differences between data and filtered values and is the previous filtered value.

Equation (D2) is a measure of the variance to be used in the numerator or the ratio statistic. The previous value of the filtered measurement is used instead of the most recently updated value to prevent autocorrelation from biasing the variance estimate, , keeping the equation for the ratio simple.

The second method to obtain a measure of variance is an exponentially weighted moving “variance” (another filter) based on sequential data differences:

(D3)

where is the filtered value of a measure of variance and is the previous filtered value.

This will be the denominator measure of the variance.

The ratio of variances, the R‐statistic, may now be computed by the following simple equation:

(D4)

The calculated value is to be compared with its critical values to determine SS or TS. Neither Equations (D2) nor (D3) computes the variance. They compute a measure of the variance. Accordingly, the coefficient in Equation (D4) is required to scale the ratio and to represent the variance ratio.

The essential assignment statements for Equations (D1)–(D4) are as follows:

nu2f := L2 * (measurement - xf) ^ 2 + cL2 * nu2f
xf := L1 * measurement + cL1 * xf
delta2f := L3 * (measurement - measurement_old) ^ 2 + cL3 * delta2f
measurement_old := measurement
R_Filter := (2 - L1) * nu2f / delta2f

The coefficients L1, L2, and L3 represent the lambda values, and the coefficients cL1, cL2, and cL3 represent the complementary values.

The five computational lines of code of this method require direct, no logic, low storage, and low computational operation calculations. In total there are four variables and seven coefficients to be stored, 10 multiplication or divisions, 5 additions, and 2 logical comparisons per observed variable.

Being a ratio of variances, the statistic is scaled by the inherent noise level in the data. It is also independent of the dimensional units chosen for the variable.

If the process is at steady state, then the R‐statistic will have a distribution of values near unity. Alternately, if the process is not at steady state, then the filtered value will lag behind the data, making the numerator term larger than the denominator, and the ratio will be larger than unity.

D.4 Coefficient, Threshold, and Sample Frequency Values

For simplicity and for balancing speed of response with surety of decision and robustness to noiseless periods, use filter values of λ₁ = λ₂ = λ₃ = 0.1. However, other users have recommended alternate values to optimize speed of response and type‐I and type‐II errors. The method works well for diverse combinations of filter coefficient values within the range of 0.05–0.2.

If R‐calculated > about 2.5, “reject” steady state with fairly high confidence and accept that the process is in a transient state. Alternately, if R‐calculated < about 0.85, “accept” that the process is at steady state and reject that it is in a transient state with fairly high confidence. If in‐between values for R‐calculated, hold the prior SS or TS state, because there is no confidence in changing the declaration.

The filter factors can be related to the number of data (the length of the time window) effectively influencing the average or variance calculation. Ideally, the number of data in a time window for the calculations is effectively N = 1/λ. However, based on a first‐order decay, roughly, the effective number of data in the window of observation that could still have an impact on the filtered value is about N = 3.5/λ.

Larger λ values mean that fewer data are involved in the analysis, which has a benefit of reducing the time for the identifier to catch up to a process change, reducing the average run length (ARL). But larger λ values have an undesired impact of increasing the variability on the statistic, confounding interpretation. The reverse is true: lower λ values undesirably increase the ARL to detection but increase precision (minimizing statistical errors).

The basis for this method presumes that there is no autocorrelation in the time series process data when at SS. Autocorrelation means that if a measurement is high (or low), the subsequent measurement will be related to it. For example, if a real process event causes a temperature measurement to be a bit high and the event has persistence, then the next measurement will also be influenced by the persisting event and will also be a bit high. Autocorrelation could be related to control action, thermal inertia, noise filters in sensors, etc. Autocorrelation would tend to make all R‐statistic distributions shift to the right, requiring a reinterpretation of critical values for each process variable.

For Monte Carlo simulations, the independent realizations in each trial return independent perturbations on the diversity of results (DV*, OF*, 95% limits, etc.). So realization‐to‐realization or iteration‐to‐iteration autocorrelation is not an issue. Similarly, when regression data are randomly sampled at each iteration, there is no autocorrelation.

Also, however, for measured process data, autocorrelation is commonly encountered due to persistence of perturbations or signal damping/filtering techniques. Here, it is more convenient to choose a sampling interval that eliminates autocorrelation than to model and compensate for autocorrelation in the test statistic. A plot of the current process measurement versus the previous sampling of the process measurement over a sufficiently long period of time (equaling several time constants) at steady state is required to establish the presence/absence of autocorrelation. To detect autocorrelation, visually choose a segment of data that is at steady state and plot the PV value versus its prior value.

Figure D.2 plots data with a lag of one sample (a measurement vs. the prior measurement) and shows autocorrelation. (Here, “lag” is used in the statistician’s sense and means “delay” in the process control sense. For process control, the term lag means a first‐order asymptotic response.) Figure D.3 plots the same data but with a lag of five samples and shows zero autocorrelation.

However, if the OF of the best player is being observed, it may not change for several iterations until a leap‐over finds a better spot. Accordingly, the iteration‐to‐iteration OF value would have autocorrelation. So, observe the OF of the worst player, not the best.

Generally, hydraulics (flow rates and levels) come to SS faster than gas pressure in large volumes, which is faster than temperature or composition. Further, noise in flow rate and level measurements will have little persistence; however, thermal inertia of temperature sensors may extend autocorrelation. So, a sampling interval for one variable might not be what is needed for another. The user might want to separate the process attributes into a set of hydraulic variables, another set of thermal and composition inventory (T, P, x) variables, and monitor the hydraulic state of the process and the thermal and composition states separately.

Summarizing, use λ₁ = λ₂ = λ₃ = 0.1. Use R‐critical = 2.5 to reject SS (accept TS) and R‐critical = 0.85 to accept SS (reject TS). Choose a sampling interval to eliminate autocorrelation from a visually determined SS period.

Figure D.4 illustrates the method. The process variable, PV, is connected to the left‐hand vertical axis (log 10‐scale) and is graphed with respect to sample interval. Initially it is at a steady state with a value of about 5. At a sample number 200, the PV begins a first‐order rise to a value of about 30. At sample number 700, the PV makes a step rise to a value of about 36. The ratio statistic is attached to the same left‐hand axis and shows an initial kick to a high value as variables are initialized and then relaxes to a value that wanders about the unity SS value. When the PV changes at sample 200, the R‐statistic value jumps up to values ranging between 4 and 11, which relaxes back to the unity value as the trend hits a steady value at a time of 500. Then when the small PV step occurs at sample 700, the R‐value jumps up to about 4 and then decays back to its nominal unity range. The SS value is connected to the right‐hand vertical axis and has values of either 0 or 1 that change when the R‐value exceeds the two limits of R_β,TS and R_1–α,SS.

D.5 Type‐I Error

If the null hypothesis is that a process is at SS, then a type‐I error is a claim of not‐at‐SS when the process is actually at SS. The concept is best understood by considering the distribution of the R‐statistic of a SS process. The statistical vagaries in the data create a distribution of the R‐statistic values. Figure D.5 represents the statistical distribution of the R‐statistic values at SS.

The R‐statistic will have some variability because of the random fluctuations in the sequential measured data. If the value of R is less than the upper 95% confidence value, the process may be at steady state, but if it is beyond (larger than) the 95% confidence value, then it is likely that the process is not at steady state. If the process is at steady state, there is a small, α = 5%, chance that R > R_0.95. The level of significance, α, is the probability of making a type‐I error of rejecting the SS hypothesis when it is true.

Five percent is the standard level of significance for economic decisions. However, if α = 5%, and the process is at SS, the identifier will make a false claim 5% of the time, about every 20th sample, which would render it nearly useless for automation.

Figure D.6 includes the distribution of the R‐statistic for a process that is not at steady state, one that is in a transient state, with its distribution of R‐statistic values greater that unity. For a process that is not at steady state, there is a high chance that R > R_0.95. As illustrated in Figure D.6, it is about a 70% chance.

So, if R > R_0.95, the likely explanation is that the process is in a transient state. As illustrated by the shaded areas to the right of the R_0.95 value, the probability that an excessive R‐value could come from the SS or the TS distribution, the odds are about 70–5% or 15 : 1 for being in the transient state. Claim TS.

There are several ways to reduce the probability of a T‐I error. An obvious one is to choose a smaller value for alpha, and in statistical process control (SPC), the value of α = 0.27% is normally accepted. But too small a level of significance means that a not‐at‐SS event might be missed—a T‐II error.

D.6 Type‐II Error

If the null hypothesis is that the process is at SS, then a type‐II error is claiming the process is at SS when it is actually in a TS. If R < R_0.95, this does not indicate the process is at steady state. Figure D.7 provides an illustration using the same two SS and TS distributions. As illustrated, the likelihood of R < R_0.95 if at steady state is 95%, and if not at steady state it is 30%. Here the odds are about 3 : 1 that the steady‐state conclusion is true. The 3 : 1 odds are not very definitive. So, to be confident that the process is at steady state, consider the left side of the distributions and an alternate T‐I error.

D.7 Alternate Type‐I Error

For a given transient state, R_β,TS is the lower β critical value and for a given steady state, R_1–α,SS is the 1 – α upper critical value. If R > R_1–α,SS, then it will reject SS (accept TS). And if R < R_1–α,SS, it will reject TS (accept SS).

If the process is at a transient state, then β is the probability of R < R_β,TS. Figure D.7 shows that the TS process has only about a 1% chance that R < R_β,TS. However, if the process is at steady state, then as illustrated, there is a 40% likelihood that R < R_β,TS. So, if R < R_1–α,SS, the odds are about 40 : 1 that process is at steady state. Claim SS.

However, if R_β,TS ≤ R ≤ R_1–α,SS, then there is a high likelihood of the process being either at steady or transient state. There is no adequate justification to make either claim. So retain the last claim.

Both type‐I and alternate type‐I errors are important. A type‐I error is the trigger of a “probable not at steady‐state” claim when the process is at steady state. An alternate type‐I error is the trigger of a “probable at steady‐state” claim when the process is in a transient state. In any statistical test, the user needs to choose the level of significance, α, the probability of a T‐I error, and power, β, the probability of an alternate T‐I error. Once decided, the R_1–α,SS critical value can be obtained from Cao and Rhinehart (1995) and the R_β,TS critical value from Shrowti et al. (2010).

However, it is more convenient and less dependent on idealizations to visually select data from periods that represent a transient or steady period and to find the R‐critical values that make the algorithm agree with the user interpretation. My experience recommends , for simplicity R_1–α,SS = 3–4 and R_β,TS = 0.8–0.9, chosen by visual inspection as definitive demarcations for a transient and steady process.

D.8 Alternate Array Method

I have been very pleased with the filter method described earlier when applied to detecting SS for convergence in either regression or stochastic functions. The rational for the three first‐order filters (for average and variances) is to reduce computational burden.

However, filters have the disadvantage of permitting a past event to linger with an exponentially weighted diminishing factor. This could extend the ARL to detect either SS or TS. Further, the filter structure is not as comfortable for many who are familiar with conventional sums in calculating variances. Further, the window of fixed length N is easier to grasp than the exponential weighted infinite window or the interpretation of the three lambda values. Alternately, in using a window of N data, the event is totally out of the window and out of the analysis after N samples, which provides a clearer user understanding of data window length.

Accordingly, this section describes an alternate calculation method for the R‐statistic ratio of variances.

Returning to the base concept with the R‐statistic as a ratio of variances, first calculate the average:

(D5)

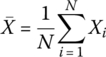
where i is the sample counter starting at the last sample and is counting back in time N data points in the window. Then the conventional variance can be expanded:

(D6)

And substituting for the average,

(D7)

Assuming no autocorrelation the variance can also be estimated as the differences between successive data. Since there are N – 1 data differences in a set of N data, there are N – 1 terms in the sum of differences in the data window and then N – 2 in the divisor:

(D8)

Then the ratio of variances is

(D9)

Note: Often, when I implement this, I normalize by the number in the sum, not the degrees of freedom (N not N – 1) and (N – 1 not N – 2).

This is essentially the von Neumann et al. (1941) approach. What appears to be a computationally expensive online calculation can be substantially simplified by using an array structure to the window of data and a pointer that indicates the array element to be replaced with the most recent measurement. With this concept, the sums are incrementally updated at each sampling.

Code for the array method with variances incrementally updated, including initialization on first call is revealed at the end of this Appendix. The method is as follows. First increment the counter to the next data storage location. Then decrement the sums with the data point to be removed. Then replace the data array element with the new value. Then increment the sums. Then recalculate the R‐statistic. In comparison with the filter method, this requires storage of the N data, the N squared data differences, and the three sums. The pointer updating adds a bit of extra computation. Our investigations indicate that the array approach takes about twice the execution time as the filter approach. Also, since it stores 2N data values, it has about that much more RAM requirement. The increased computer burden over the filter method may not be excessive in today’s online computing devices.

This approach calculates a true data variance from the average in the data window of N samples and has the additional benefit that the sensitivity of the R‐statistic to step changes in a signal is greater with the array method than with the filter method (about twice as sensitive from experience). The array approach can respond to changes of about 1.5σ. Accordingly, this defined window, array approach, is somewhat better in detecting small deviations from SS.

Further, the value of window length, N, explicitly defines the number of data after an event clears to fully pass through the data window and influence on the R‐value. By contrast, the filer method exponentially weights the past data, and the persisting influence ranges between about 3/λ and 4/λ number of samplings.

Additionally, the array methods seem less conflicted by autocorrelation and discretization flat spots in the time series of data.

However, the array method is computationally more burdensome than the filter method. Nominally, the filter method needs to store and manipulate seven values at each sampling. With λ = 0.1, this characterizes a window of about 35 samples. For the same characterization, the array method needs to store and manipulate over 180 variables at each sampling.

However, there is only one adjustable variable representing the data window, N. By contrast, the filter approach has three lambda values providing some flexibility in optimizing performance, as done by Bhat and Saraf (2004), but perhaps tripling the user confusion.

Today, my preference is to use the filter method. But if data vagaries (changes in autocorrelation, flat spots, coarse discretization, small shifts relative to noise) make it dysfunctional, then use the array method.

However, for optimization applications, which only need to determine SS (not TS), the filter method is fully adequate, much simpler to implement, and is my preference.

D.9 SSID and TSID VBA Code

Sub SSID_Filter() 'Cao-Rhinehart Filter Method

  If FirstCall THEN
               l1 = 0.1        'filter lambda values
               l2 = 0.1
               l3 = 0.1
               cl1 = 1 - l1
               cl2 = 1 - l2
               cl3 = 1 - l3
               n2f = 0               'initial values
               d2f = 0
               xf = 0
               xold = 0
               SS = 0.5            'indeterminate
Else
               x= 'acquire data
               n2f = l2 * (xf - x) ^ 2 + cl2 * n2f
               xf = l1 * x + cl1 * xf
               d2f = l3 * (x - xold) ^ 2 + cl3 * d2f
               xold = x
               If d2f > 0 Then
                     r = (2 - l1) * n2f / d2f
               End If
               If (2 - l1) * n2f <= lower * d2f Then SS = 1         'confidently @ SS
               If (2 - l1) * n2f > upper * d2f Then SS = 0          'confidently @TS
   End IF
End Sub

Sub SSID_Array()      'Rhinehart-Gore Array Method
  IF FIrstCall THEN
           Dim y(50)             'up to N=50 values in window
           Dim dy2(50)
           For j = 1 To 50   'initialize array
                y(j) = 0
               dy2(j) = 0
           Next j
           N = 10      'initialize
           sum1 = 0
           sum2 = 0
           sum3 = 0
           yold = 0
           j = 1
           SS = 0.5      'indeterminate
Else
                  j = j + 1       'counter for data array of N elements
                If j > N Then j = 1
                sum1 = sum1 - y(j) ^ 2          'decrement sums
                sum2 = sum2 - y(j)
                y(j) = 'acquire data
                sum1 = sum1 + y(j) ^ 2         'increment sums
                sum2 = sum2 + y(j)
                jj = jj + 1 'counter for difference array of N-1 elements
                If jj > N - 1 Then jj = 1
                sum3 = sum3 - dy2(jj)            'decrement
                dy2(jj) = (y(j) - yold) ^ 2
                yold = y(j)
                sum3 = sum3 + dy2(jj)            'increment
                If sum3 > 0 Then
                   r = 2 * ((N - 1) / N) * (sum1 - (sum2 ^ 2) / N) / sum3
                End If
                If 2 * (sum1 - (sum2 ^ 2) / N) <= 0.9 * sum3 Then SS = 1
                If 2 * (sum1 - (sum2 ^ 2) / N) > 2.5 * sum3 Then SS = 0
    End If
End Sub