CHAPTER 3

SOME DISCRETE DISTRIBUTIONS

In this chapter we present some frequently used discrete distributions.

3.1   DISCRETE UNIFORM, BINOMIAL AND BERNOULLI DISTRIBUTIONS

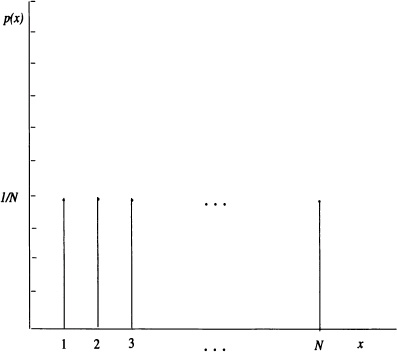
Definition 3.1 (Discrete Uniform Distribution) A random variable X has a discrete uniform distribution with N points, where N is a positive integer with possible distinct values x_i, i = 1,2, · · · , N, if its probability mass function is given by:

If in particular x_i = i, i = 1,2, · · · , N, the probability mass function is shown in Figure 3.1.

Theorem 3.1 (Properties of a Discrete Uniform Random Variable)
If X is a random variable having a discrete uniform distribution with N points, then:

Figure 3.1   Probability mass function for a discrete uniform distribution

1.

2.

3.

Corollary 3.1 If x_k = k, k = 1,2, · · · , N, then:

1.

2.

3.

Proof:

1. 
   
2. Left as an exercise for the reader.
3. Follows from the definition of the mgf.

EXAMPLE 3.1

A fair die is tossed. The sample space Ω = {1,2,3,4,5,6} and each event occurs with probability . Therefore we have a uniform distribution with:

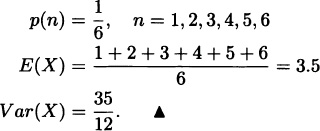
Definition 3.2 (Binomial and Bernoulli Distributions) A random variable X is said to have a binomial distribution with parameters n and p if its probability mass function is given by

where n is a positive integer and 0 < p < 1.

If n = 1, the binomial distribution is called a Bernoulli distribution with parameter p.

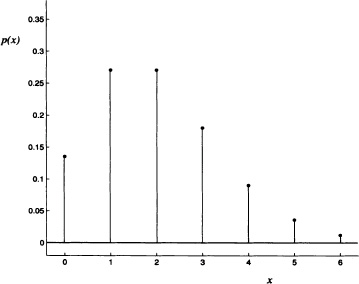
The probability mass function of a binomial distribution with parameters n = 6, p = 0.5 is shown in Figure 3.2.

Notation 3.1 We shall write X (n, p) to indicate that the random variable X has a binomial distribution with parameters n and p.

The binomial distribution is frequently used to describe experiments whose outcome can be regarded in terms of the occurrence or not of a certain phenomenon. If the random variable X denotes the number of successes achieved after carrying out n independent repetitions of the experiment, then X has a binomial distribution with parameters n and p, where p is the probability of success, that is, the probability that the desired phenomenon is observed; the probability of failure 1 – p is usually referred to with the letter q.

Figure 3.2   Probability mass function of a binomial distribution

EXAMPLE 3.2

A fair die is rolled five consecutive times. Let X be the random variable representing the number of times that the number 5 was obtained. Find the probability mass function of X.

Solution: The random variable X has a binomial distribution with parameters 5 and . Therefore:

EXAMPLE 3.3

A salesman from a travel agency knows from experience that the opportunity to sell a travel package is greater when he makes more contact with potential buyers. He has established that the probability that a costumer will buy a package after a visit is constant and equal to 0.01. If the set of visits done by the salesman constitute an independent set of trials, how many potential buyers must he visit in order to guarantee that the probability of selling at least a travel package will equal 0.85?

Solution: Let:

X := “Number of people that buy a travel package after the salesman’s visit”.

We have that X (n, 0.01) and wish to find n such that

P(X ≥ 1) = 0.85

or equivalently:

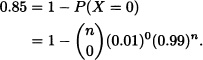
Therefore:

Consequently, the salesman must visit at least 189 people to achieve his goal.   

EXAMPLE 3.4

Paula’s best friend invited her to a party. Since Paula is still very young, her parents conditioned their consent to Paula’s brother going along with her. Paula’s brother proposes the following deal to her: “You pick a number, whichever you like, from 1 to 6; you then roll a fair die four times, and if the number you picked appears at least twice, then I will come with you. Otherwise, I won’t”. What is the probability that Paula is going to the party?

Solution: Let:

      X := “Number of times the number chosen by Paula appears”.

Clearly X (4, ). Then, the required probability equals:

EXAMPLE 3.5

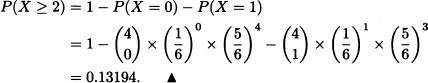
A player bets on a number from 1 to 6. Once he has bet, three fair dice are rolled. If the number chosen by the player appears i times, with i = 1,2,3, then the player is rewarded with 2i money tokens. If the number bet does not appear on any die, the player loses 3 tokens. Is this game fair to the player? Explain your answer.

Solution: Let X be the random variable representing the fortune of the player. The values X can take are –3,2,4 and 6. We have that:

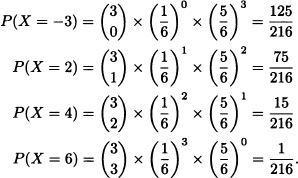
Accordingly:

This indicates that in the long run the player loses 159 tokens for every 216 games played. Therefore, the game does not favor him.    

EXAMPLE 3.6

(Hoel et al., 1971) Suppose that n balls are randomly distributed in r urns. Find the probability that exactly k balls were put in the first r₁ urns.

Solution: Let X := “number of balls in the first r₁ urns”. Since X (n,p) with p = then:

EXAMPLE 3.7

Consider the k-out-of-n structure which is a special case of parallel redundant system. This type of configuration requires that at least k components succeed out of the total n parallel components for the system to succeed. The problem is to compute the system reliability given the component reliabilities p_i. The reliability of a k-out-of-n structure of independent components, which all have the same reliability p, equals:

This formula holds since the sum of n random variables has a Bernoulli distribution with parameters n and p under given assumptions.   

Next, we present some properties of the binomial distribution.

Theorem 3.2 (Properties of the Binomial Distribution) Let X be a random variable having a binomial distribution with parameters n and p. Then:

1. E(X) = np.

2. Var(X) = npq, where q := 1 – p.

3. m_X(t) = (pe^t + q)ⁿ.

Proof:   In Example 2.54 we verified that the mgf of a random variable with binomial distribution of parameters n and p is given by m_X(t) = (pe^t + q)ⁿ. Thus:

Furthermore, we have:

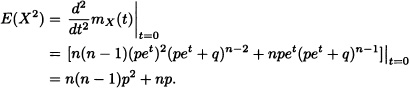
Hence, we obtain:

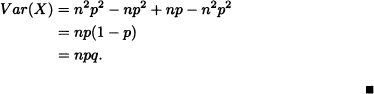
Note 3.1  Suppose that X is a random variable with a binomial distribution of parameters n and p. Let:

Seeing that

then for k = 1, · · · , n:

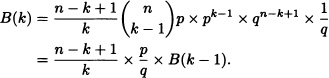
Hence, starting with B(0) = qⁿ the values of B(k) for k = 1, · · ·, n can be recursively obtained.

Algorithm 3.1

Input: p, n, where n is the number of terms.

Output: B(k) for k = 0(1)n.

Initialization: q := (1 – p),

B(0) := qⁿ.

Iteration: For k = 0(1)n – 1 do:

Using the last algorithm we obtain, for example, for n = 5 and p = 0.3:

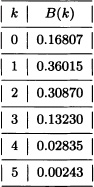
Note 3.2  From the previous remark, we have that:

That is:

B(k) > B(k – 1) if and only if (n + 1 )p > k.

Thus, if X (n, p), then P(X = k) increases monotonically until it reaches a maximum for k = ⌊(n + 1)p⌋ (where ⌊a⌋ denotes the integer part or floor of a) and, after this value, it decreases monotonically.

3.2   HYPERGEOMETRIC AND POISSON DISTRIBUTIONS

In Chapter 1, we saw that if an urn contains N balls, R of which are red and N – R white, and a sample of size n is extracted without substitution, then the probability P(A_k) that exactly k of the extracted balls are red equals:

If we are only interested in the number k of red balls among the n balls extracted, then P(k) := P(A_k) defines a probability measure over the set {0,1, ··· ,n} called the hypergeometric distribution with parameters n, R and N. More precisely, we have:

Definition 3.3 (Hypergeometric Distribution) A random variable X is said to have a hypergeometric distribution with parameters n, R and N if its probability mass function is given by

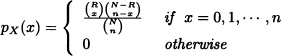
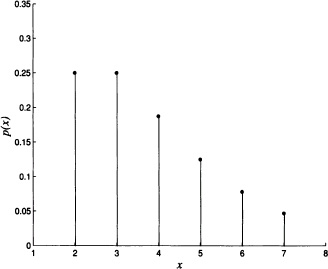
Figure 3.3   Probability mass function of a hypergeometric distribution

where N is a positive integer, R is a nonnegative integer less than or equal to N and n is a positive integer less than or equal to N.

The probability mass function of a hypergeometric distribution with parameters n = 4, R = 7 and N = 20 is shown in Figure 3.3.

Notation 3.2 The expression X Hg(n, R, N) means that the random variable X has a hypergeometric distribution with parameters n, R and N.

EXAMPLE 3.8

The surveillance division of a university has acquired 50 communication devices in order to optimize the security in the campus. Eight of them are randomly selected and tested to identify any possible flaws. If 3 of the 50 devices are defective, what is the probability that the sample contains at most two defective devices?

Solution: Let X := “number of defective devices found in the sample”. It follows that X Hg(8,3,50). Therefore:

EXAMPLE 3.9

A work team established by the Department of the Environment programmed inspection of 25 factories in order to investigate possible violations to the environmental contamination act. Nevertheless, cuts in budget have substantially reduced the work team size, so that only 5 out of 25 factories are going to be inspected. If it is known that 10 of the factories are working outside the environmental contamination act, find the probability that at least one of the factories sampled is working against the regulations.

Solution: Let X := “number of factories operating in contravention of the environmental contamination act”. It is straightforward that X Hg(5,10,25), whereupon we have:

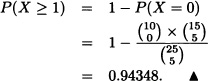
Note 3.3  Suppose that the size N of the population is unknown, but we wish to find it without counting one by one each individual. A way of doing this is the so-called capture-recapture method, which consists in capturing R individuals from the population, tagging them and then returning them to the population. Once the tagged and untagged individuals have mixed, a sample of size n is taken. Let X be the random variable representing the number of tagged individuals in the sample. Clearly X Hg(n,R,N). Suppose that the observed value of X is k. Then P_k(N) := P(X = k) represents the probability that the sample contains k tagged individuals when the population has size N. So we will estimate N as the value for which the probability that X equals k is maximum. Such a value is known as the maximum likelihood estimate of N. To find it, we observe that:

That is,

and thereby:

EXAMPLE 3.10

To establish the number of fishes in a lake the following procedure is followed: 2000 fishes are captured, tagged and then returned to the lake. Days after, 350 fishes are captured and it is observed that 50 of them are tagged. Then, according to the previous remark, the maximum likelihood estimate of the size N of the population is:

Below we present some of the properties of the hypergeometric distribution.

Theorem 3.3 (Properties of the Hypergeometric Distribution) Let X Hg(n,R,N). Then:

1.

2.

Proof:

1. 
   
   

   where we used the following identity:

   

2. Seeing that
   

   Var(X) = E(X(X – 1)) + E(X) – (E(X))²

   it suffices to find E(X(X – 1)). Thus:

   

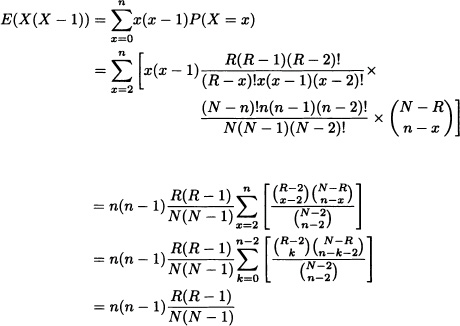
   Using the relation

   

   We obtain

   

Next we will see that if the population size N is large enough in comparison to the sample size n, then the hypergeometric distribution can be approximated by a binomial distribution. More precisely, we have the following result:

Theorem 3.4 Let 0 < p < 1. If N, R → ∞ in such a way that → p, then:

Proof:   Observing that → (1 – p) = q > 0 when N, R → ∞, we see that (N – R) → ∞ when N → ∞. Therefore:

EXAMPLE 3.11

In a city with 2 million inhabitants, 60% belong to political party A. One hundred people are randomly chosen from the inhabitants. The distribution of the number of people, among the 100 drawn who belong to party A is hypergeometric with parameters 100, 1200000 and 2000000. Applying the previous result we can approximate this distribution by a binomial with parameters n = 100 and p = 0.6. That way, for example, the probability that among the 100 people chosen exactly 40 belong to party A equals:

Figure 3.4   Probability mass function of a Poisson distribution

The following table compares the binomial and hypergeometric distributions:

Definition 3.4 (Poisson Distribution) A random variable X is said to have a Poisson distribution with parameter > 0 if its probability mass function is given by:

The probability mass function of a Poisson distribution with parameter = 2 is shown in Figure 3.4.

Notation 3.3 Let X be a random variable. We write to indicate that X has a Poisson distribution with parameter .

Note 3.4  Let and ()(k) := P(X = k). It is straightforward that, for k = 1,2, · · · :

Hence, starting with ()(0) = e ⁻ the values of ()(k) can be recursively obtained for k = 1,2, · · ·.

A simple algorithm to calculate the values of the Poisson distribution making use of the previous expression is given by:

Algorithm 3.2[Calculus of ()(k)]

Input: , n, with n being the number of terms.

Output: ()(k) for k = 0(1)n.

Initialization: ()(k) = e⁻.

Iteration: For k = 0(1)n – 1 do:

Analyzing the graph of the probability mass function from a random variable with Poisson distribution, we observe that the individual probabilities become smaller as the variable takes larger values. This is precisely one of the general characteristics of the Poisson distribution. Other properties of the Poisson distribution are given in the following theorem.

Theorem 3.5 Let X be a random variable with Poisson distribution of parameter . Then:

1. E(X) = .

2. Var(X) = .

3. m_X(t) = exp((e^t – 1)).

Proof:   We start by proving 3 and by applying the properties of the mgf we deduce 1 and 2. Accordingly:

Thus

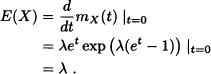
Also

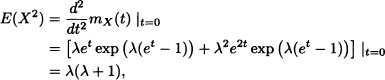
which yields

Var(X) = A.

The property E(X) = Var(X) holds only for Poisson distribution and is a characterizing property of the distribution.   

EXAMPLE 3.12

The number of patients who come daily to the emergency room (E.R.) of a certain hospital has a Poisson distribution with mean 10. What is the probability that, during a normal day, the number of patients admitted in the emergency room of the hospital will be less than or equal to 3? Solution: Let X := “number of patients who come daily to the E.R.”. From the data supplied by the statement of the problem, we know that X (10). Therefore:

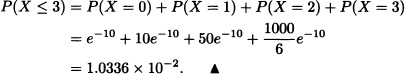
It will be proved below that for large enough n and suitably small p a binomial distribution with parameters n and p can be approximated by a Poisson distribution of parameter = np; that is, under these circumstances, the Poisson distribution is a limit of the binomial distribution.

Theorem 3.6 If p(n) is a sequence satisfying 0 < p(n) < 1 and n × (p(n)) , then:

Proof:   Let _n = n × (p(n)). Then:

Taking the limit when n → ∞ we see that the quotients , · · · , as well as the factor tend to 1, while the expression (1 – )ⁿ tends to e⁻. As a result:

The following table shows how good the approximation is when = np = 1:

Assume p(n) = p, i.e., the probability that the success in any trial is p and all the trials are independent for finite n. For large n, the sum of Bernoulli random variables with parameters n and p tends to Poisson random variable with parameter = np.

The preceding theorem implies that the Poisson distribution offers a good probabilistic model for those random experiments where there are independent repetitions and only two possible outcomes, success or failure, with small probability of success, and where the main interest lies on knowing the number of successes obtained after a large enough number of repetitions of the experiment. Empirically, it has been determined that the approximation can be safely used if n ≥ 100, p ≤ 0.01 and np ≤ 20.

EXAMPLE 3.13

There are 135 students inside a conference hall. The probability that one of the students celebrates his or her birthday today equals . What is the probability that two or more students from the conference hall are celebrating their birthdays today?

Solution: Let X := “number of students celebrating their birthdays today”. It is known that X (135, ); however, this distribution can be approximated by means of a Poisson distribution with parameter . Thereby

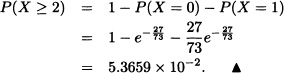
3.3   GEOMETRIC AND NEGATIVE BINOMIAL DISTRIBUTIONS

When working with a binomial distribution we proceeded as follows: a random experiment was repeated n times and the probability of obtaining exactly k successes was found. In this case, the number of repetitions remains constant while the number of successes is random. Instead suppose the question is the following: What is the probability that the experiment has to be repeated n times to obtain exactly k successes? That is, now the number of successes remains constant while the number of repetitions is a random variable X.

What is the probability that X takes the values j = k, k +1, · · · ? If X = j, then the jth result was necessarily a success and therefore the other k – 1 successes are obtained in the remaining j – 1 repetitions of the experiment. That is,

where 0 < p < 1 is the success probability.

Definition 3.5 (Geometric and Negative Binomial Distributions) A random variable X is said to have a negative binomial distribution with parameters k and p if its probability mass function is given by:

In the special case where k = 1 it is said that the random variable has a geometric distribution with parameter p.

The probability mass function of a negative binomial distribution with parameters k = 2 and P = is shown in Figure 3.5.

Notation 3.4 The expressions X _N (k,p) and X (p) mean that X has a negative binomial distribution with parameters k and p and X has a geometric distribution of parameter p.

Note 3.5  Suppose that we are interested not in the number of repetitions required to obtain k successes but in the number of failures Y that happened before we obtained exactly k successes. In this case we have that X = k + Y and therefore:

Figure 3.5   Probability mass function of a negative binomial distribution

Some authors call this last distribution the negative binomial and the one defined before as the Pascal distribution.

EXAMPLE 3.14

In a quality control department, units coming from an assembly line are inspected. If the proportion of defective units is 0.03, what is the probability that the twentieth unit inspected is the third one found defective?

Solution: Let X := “number of units necessary to inspect in order to obtain exactly three defective ones”. Clearly X _N (3,0.03). Hence:

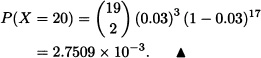
Below, we find the mean and variance of a random variable having a negative binomial distribution.

Theorem 3.7 Let X be a random variable having a negative binomial distribution with parameters k and p. Then:

1.

2.

3.

Proof:   The rth moment of X around the origin is given by

where Y _N (k + 1, p). Therefore

and

which yields:

On the other hand,

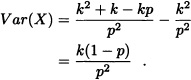
where:

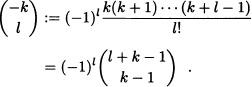
Using the Taylor series expansion of the function (x) := (1 – x) ^−k about the origin, we obtain:

Accordingly:

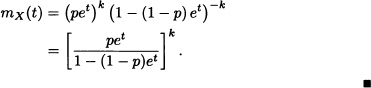
Corollary 3.2 If X is a random variable having a geometric distribution with parameter p, then:

1.

2.

3.

Note 3.6  For the random variable Y = X – k we have:

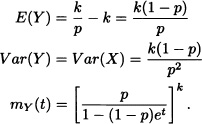
Note 3.7  Suppose that the size N of a population is unknown. We wish to determine N without counting each of the individuals. One way of doing this is the so-called inverse capture-recapture method, which consists in capturing R individuals from the population and returning them to it after they have been properly tagged. Once the tagged and nontagged individuals are homogeneously mixed, a new sample is taken from the population drawing one individual at a time until a predetermined number of tagged individuals k is reached. Let X be the random variable representing the number of necessary extractions to obtain k tagged individuals. Clearly X _N(k,p), where p = . Suppose that the observed value X equals j. Then P_k(N) := P(X = j) represents the probability that j extractions were required in order to obtain exactly k tagged individuals when the population size is N. Therefore, we can take as an estimator of N the value for which the probability that X equals j is maximum. Such an estimator is called a maximum likelihood estimate of N and equals:

EXAMPLE 3.15

To establish the number of fishes in a lake, it is proceeded as follows: 1000 fishes are captured and tagged, then returned to the lake. Days after, fishes are captured until 15 of them are tagged. If it was necessary to make 120 extractions to obtain the desired number of marked fishes, then according to the previous remark, the maximum likelihood estimate of the population size is:

Note 3.8  Let X be a random variable having a negative binomial distribution with parameters k and p, and let Y be a random variable having a binomial distribution with parameters n and p. Then:

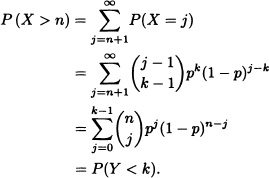
EXERCISES

3.1   A fair coin is flipped an even number of times. What is the probability that half the times the result obtained is a “head”?

3.2   In a national automobile club a telephonic campaign is started in order to increase the number of its members. From previous experience, it is known that one out of every 10 people called actually join the club. If in a day 20 people are called, what is the probability that at least two of them join the club? What is the expected number?

3.3   A fair die is rolled 10 consecutive times. Find the probability that the number 5 is obtained at least 3 times.

3.4   In the computer room of an educational center there are 20 computers. The probability that any given computer is being used in peak hours is 0.9. What is the probability that at least one computer is available in peak hours? What is the probability that all the computers are being used?

3.5   An airline knows that 5% of the people making reservations on a certain flight will not show up. Consequently, their policy is to sell 52 tickets for a flight that can hold only 50 passengers. Assume that passengers who come to the airport are independent with each other. What is the probability that there will be a seat available for every passenger who shows up?

3.6   Find the probability distribution of a binomial random variable X with parameters n and p truncated to the right at X = r, r > 0.

3.7   Let X be a random variable having a binomial distribution with parameters n and p. Suppose that E(X) = 12 and Var(X) = 4. Find n and p.

3.8   A coin is flipped as many times as needed to obtain a head for the first time.

a) Describe the sample space of this experiment.

b) Let X be the random variable representing the required number of tosses. Find P(X > 1) and P(X ≤ n).

3.9   Assume that the number of clients X arriving in an hour at a bank is a Poisson random variable and P(X = 0) = 0.02. Find the mean and variance of X.

3.10   Let X be a random variable having a Poisson distribution with parameter . If P(X = 0) = 0.4, find P(X ≤ 3).

3.11   Let X be a Poisson random variable with parameter . Assume P(X = 2) = 2P(X = 1). Find P(X = 0).

3.12   The quality control department of a factory inspects the units finished by the assembly line. It is believed that the proportion of defective units equals 0.01. What is the probability that the fifth unit inspected is the second defective one?

3.13   Casinos use roulettes with 38 pockets, of which 18 are black, 18 are red and 2 are green. Let X be the random variable representing the number of times it is necessary to spin the wheel to obtain a red number for the first time. Find the probability mass function of X.

3.14   A number from the interval (0,1) is randomly chosen. What is the probability that:

a) The first decimal digit is 1.

b) The second decimal digit is 5.

c) The first decimal digit of its square root is 3.

3.15   A multiple-choice test contains 30 questions, each with four possible options. Suppose that a student only guesses the answers:

a)   What is the probability that the student answers right more than 20 questions?

b)   What is the probability that the student answers less than 3 questions right?

c)   What is the probability that the student answers all the questions wrong?

3.16   Recent studies determined that the probability of dying due to a certain flu vaccine is 0.00001. If 200,000 people are vaccinated, and we assume that each person can be regarded as an independent trial, what is the probability that no one dies because of the vaccine?

3.17   A professor wishes to set up the final examination with multiple-choice test. The examination must have 15 questions, and on account of internal regulations, a student approves if he or she answers at least 10 questions right. To minimize the “risk” of a student approving the examination by guessing the answers, the teacher wishes to put k possible choices to each question with only one being correct. What value must k have so that a student randomly answering the test has a probability of passing equal to 0.001?

3.18   Fifteen daltonic people are required for a medical experiment. If it is known that only 0.1% of the population has this condition, what is the expected number of interviews that must be carried out to find the 15 people required?

3.19   There are N fishes in a lake from which R (≤ N) are tagged. Assume that n (≤ R) fishes are caught one by one without replacement and let T_i := “the ith fish captured is tagged” for i = 1,2, · · · , n. What is p(T_i) equal to? Are T₁ and T₃ independent?

3.20   At a certain governmental institution, the probability that a call is answered in less than 30 seconds is 0.25. Assume the calls to be independent.

a) If someone calls 10 times, what is the probability that 9 calls are answered in less than 30 seconds?

b) If someone calls 20 times, what is the average number of calls that are going to be answered in less than 30 seconds?

c) What is the average number of calls that have to be made in order to get an answer in less than 30 seconds?

d) What is the probability that 6 calls have to be made to get 2 of them answered in less than 30 seconds?

3.21   Suppose that 5% of the articles produced in a factory are defective. If 15 articles are randomly chosen and inspected, what is the probability that there are at most 3 defective articles in the sample?

3.22   Suppose that X is a random variable having a geometric distribution with parameter p. Find the probability mass function of X² and X + 3.

3.23   Three copies of the book “Get rich in less than 24 hours” in a library are lent to users for a day. The number of daily requests for a copy is a Poisson random variable with mean 5. Find:

a) The proportion of days wherein the demand of a copy of the book is zero.

b) The proportion of the days wherein the demand of a copy of the book surpasses the supply.

3.24   A certain system of a spacecraft must work correctly in order for the ship to make a safe entry to the atmosphere. A component of such a system operates without complications only 85% of the time. With the purpose of increasing the reliability of the system, four of these components are installed in such a way that the system will function properly if at least one of the components operates without complications.

a) What is the probability that the system will malfunction? Assume that the components operate independently from each other.

b) If the system fails, what can be inferred from the alleged 85% probability of success of a single component?

3.25   The records of an insurance company show that only 0.1% of the population suffers from a certain type of accident each year. If 10,000 people are randomly selected to be insured, what is the probability that no more than 5 of those clients have that type of accident next year?

3.26   There axe 20 spectacled bears in a forest, 5 of which are captured, tagged and then released. Weeks later 4 of the 20 bears are captured again. Find the probability that at most 2 of the captured bears are tagged.

3.27   A company analyzes the shipments from its suppliers to detect products that do not comply with the minimum quality specifications required. It is known that 3% of such products do not meet the quality standards of the company. What size must a sample have in order to have at least a 0.90 probability that at least one article selected does not comply with the quality requirements? Suppose that in this case the hypergeometric distribution can be approximated by a binomial distribution.

3.28   A 300-page book has 253 typographical errors. Assuming that each page has 5000 characters, what is the probability that there are no typos on the first page? What is the probability that there is at least one typo on the first page?

3.29   A factory makes ink cartridges for stylographic pens. One out of every 30 cartridges made by the factory turns out to be defective. The cartridges are packed in six-unit boxes. Find the expected number of boxes that contain, respectively, no defective cartridges, 1 defective cartridge, 2 or more defective cartridges, in a shipment of 1000 boxes.

3.30   The police suspect that in a truck loaded with 40 rice bundles there might be cocaine packages camouflaged. To confirm their suspicion, the police randomly pick 5 bundles to be inspected. If indeed, 10 from the 40 bundles contain cocaine camouflaged, what is the probability that at least 1 of the inspected bundles has cocaine?

3.31   At a TV contest the following game is played: the contestant must simultaneously extract 3 ballots from an urn containing 5 ballots marked with a prize and 9 unmarked ballots. If the 3 ballots drawn are marked, the contestant has two choices: he or she can either pick one of the marked prizes and retire or repeat the extraction three more times, and if in those repetitions all three extracted ballots are marked, then the contestant will win, in addition to all prizes marked in the ballots, a brand new car. If a contestant chooses this last alternative, what is the probability that he or she has of winning?

3.32   (Ross, 1998) The number of times a person suffers from a cold in a year is a random variable having a Poisson distribution with parameter = 3/year. Suppose that there is a new medicine (based on large quantities of vitamin C) that reduces the Poisson parameter to = 2/year on 85% of the population and has no major effects on preventing colds for the remaining 15%. If a given person takes the medicine throughout a year and during that time has 2 colds, what is the probability that the medicine did not have an effect on that person?

3.33   Determine the expected value and the variance of the number of times that is necessary to roll a fair die until the result “1” happens 4 consecutive times.

3.34   A player has the following strategy in the roulette: He bets two tokens to the red color. If on the first spin of the wheel appears a red number, he takes the money won and retires; if on the first spin of the wheel appears a black or green number, he spins the wheel two more times betting two tokens to the red color each time and then retires. Let X be the random variable representing the fortune of the player. Find E(X) (see Exercise 3.13).

3.35   To pay for his college fees, a young man has decided to sell cheese and ham sandwiches. The money needed to make each sandwich is $0.50 and he expects to sell them at $1.50 each. However, the sandwiches that are not sold on any day cannot be sold on the next day. If the daily demand of sandwiches is a random variable having a binomial distribution with parameters n = 20 and p = , how many sandwiches must he make to maximize his expected daily income?

3.36   A fair coin is flipped as many times as necessary to obtain “head” for the first time. Let X be the number of required flips.

a) Find E(X).

b) Find E(2^X) (if it exists).

3.37   A coin is biased in such a way that the probability of obtaining a “head” equals 0.4. Use Chebyschev’s inequality to determine how many times must the coin be flipped in order to have at least a 0.9 probability that the quotient between the number of heads and the number of total flips lies between 0.3 and 0.5.

3.38   Let X be a random variable having a Poisson distribution with parameter . Find the value of for which P(X = k) is maximum.

3.39   A company rents out time on a computer for periods of t hours, for which it receives $400 an hour. The number of times the computer breaks down during t hours is a random variable having the Poisson distribution with = (0.8)t, and if the computer breaks down x times it costs 50x dollars to fix it. How should the company select t in order to maximize its expected profit?

3.40   A film supplier produces 10 rolls of a specifically sensitized film each year. If the film is not sold within a year it must be discarded. Past experience indicates that D, the small demand for the film, is a Poisson-distributed random variable with parameter 8. If a profit of $7 is made on every roll which is sold, while a loss of $2 is incurred on every roll which must be discarded, compute the expected profit which the supplier may realize on the 10 rolls which he produces.

3.41   Let X be a random variable having a Poisson distribution with rameter . Prove the following:

3.42   Let X be a random variable having a binomial distribution with parameters n and p. Prove that:

3.43   Let X be a random variable having a binomial distribution with parameters n and p. Find the value of p that maximizes P(X = k) for k = 0,1,··· ,n.

3.44   Let X be a random variable having a hypergeometric distribution with parameters n, R and N.

a) Prove that:

b) Verify

   if and only if

3.45   Let X be a random variable having a Poisson distribution with rameter . Prove that:

3.46   Let X be a random variable having a geometric distribution with parameter p. Prove that:

P(X = n + k| X > n) = P(X = k).

3.47   Let X be a random variable having a geometric distribution with parameter p. Find E ().

3.48   Let X be a random variable having a Poisson distribution with parameter . Prove:

a) E(X²) = E(X + 1).

b) If = 1, then E(|X−1|) = .

3.49   Find the characteristic function of a random variable having a binomial distribution with parameters n and p.

3.50   Find the characteristic function of a random variable having a Poisson distribution with parameter .

3.51   How many children must a couple have so that, with a 0.95 probability, she gives birth to at least one boy and one girl?

3.52   A reputed publisher claims that in the handbooks published by them misprints occur at the rate of 0.0024 per page. What is the probability that in a randomly chosen handbook of 300 pages, the third misprint will occur after examining 100 pages?