CHAPTER 11
STOCHASTIC CALCULUS
Stochastic calculus plays an essential role in modern mathematical finance and risk management. The objective of this chapter is to develop conceptual ideas of stochastic calculus in order to provide a motivational framework. This chapter presents an informal introduction to martingales, Brownian motion, and stochastic calculus. Martingales were first defined by Paul Lévy (1886–1971). The mathematical theory of martingales has been developed by American mathematician Joseph Doob (1910–2004). We begin with the basic notions of martingales and its properties.
11.1 MARTINGALES
The martingale is a strategy in a roulette game in which, if a player loses a round of play, then he doubles his bet in the following games so that if he wins he would recover from his previous losses. Since it is true that a large losing sequence is a rare event, if the player continues to play, it is possible for the player to win, and thus this is apparently a good strategy. However, the player could run out of funds as the game progresses, and therefore the player cannot recover the losses he has previously accumulated. One must also take into account the fact that casinos impose betting limits.
Formally, suppose that a player starts a game in which he wins or loses with the same probability of ![]() . The player starts betting a single monetary unit. The strategy is progressive where the player doubles his bet after each loss in order to recoup the loses. A possible outcome for the game would be the following:
. The player starts betting a single monetary unit. The strategy is progressive where the player doubles his bet after each loss in order to recoup the loses. A possible outcome for the game would be the following:
Bet 1 2 4 8 16 1 1
Outcome F F F F W W F
Profit -1 -3 -7 -15 1 2 1
Here W denotes “Win” and F denotes “Failure”. This shows that every time the player wins, he recovers all the previous losses and it is also possible to increase his wealth to one monetary unit. Moreover, if he loses the first n bets and wins the (n + l)th, then his wealth after the nth bet is equal to:
![]()
This would indicate a win for the player. Nevertheless, as we shall see later, to carry out this betting strategy successfully, the player would need on average infinite wealth and he would have to bet infinitely often (Rincón, 2011).
In probability theory, the notion of a martingale describes a fair game. Suppose that the random variable Xm denotes the wealth of a player in the mth round of the game and the σ-field ![]() m has all the knowledge of the game at the mth round. The expectation of Xn (with n ≥ m), given the information in
m has all the knowledge of the game at the mth round. The expectation of Xn (with n ≥ m), given the information in ![]() m, is equal to the fortune of the player up to time m. Then the game is fair. Using probability terms, we have, with probability 1:
m, is equal to the fortune of the player up to time m. Then the game is fair. Using probability terms, we have, with probability 1:
E(Xn | ![]() m) = Xm for all m ≤ n.
m) = Xm for all m ≤ n.
A stochastic process {Xt;t ≥ 0} satisfying the above equation is called a discrete-time martingale. Formally we have the following definitions:
Definition 11.1 Let (Ω, ![]() , P) be a probability space. A filtration is a collection of sub-σ-algebras (
, P) be a probability space. A filtration is a collection of sub-σ-algebras (![]() n)n≥0 of
n)n≥0 of ![]() such that
such that ![]() m ⊆
m ⊆ ![]() n for all m ≤ n. We say that the sequence {Xn;n ≥ 0} is adapted to the filtration (
n for all m ≤ n. We say that the sequence {Xn;n ≥ 0} is adapted to the filtration (![]() n)n≥0 if for each n the random variable Xn is
n)n≥0 if for each n the random variable Xn is ![]() n-measurable, that is, {ω
n-measurable, that is, {ω ![]() Ω : Xn(ω) ≤ a}
Ω : Xn(ω) ≤ a} ![]()
![]() n for all a
n for all a ![]()
![]() .
.
Definition 11.2 Let {Xn;n ≥ 0} be a sequence of random variables defined on the probability space (Ω, ![]() , P) and (
, P) and (![]() n)n≥0 be a filtration in
n)n≥0 be a filtration in ![]() . Suppose that {Xn;n ≥ 0} is adapted to the filtration (
. Suppose that {Xn;n ≥ 0} is adapted to the filtration (![]() n)n≥0 and E(Xn) exists for all n. We say that:
n)n≥0 and E(Xn) exists for all n. We say that:
(a) {Xn;n ≥ 0} is a (![]() n)n-martingale if and only if E(Xn |
n)n-martingale if and only if E(Xn | ![]() m) = Xm a.s. for all m ≤ n.
m) = Xm a.s. for all m ≤ n.
(b) {Xn;n ≥ 0} is a (![]() n)n-submartingale if and only if E(Xn |
n)n-submartingale if and only if E(Xn | ![]() m) ≥ Xm a.s. for all m ≤ n.
m) ≥ Xm a.s. for all m ≤ n.
(c) {Xn;n ≥ 0} is a (![]() n)n-supermartingale if and only if E(Xn |
n)n-supermartingale if and only if E(Xn | ![]() m) ≤ Xm a.s. for all m ≤ n.
m) ≤ Xm a.s. for all m ≤ n.
Note 11.1 The sequence {Xn;n ≥ 0} is obviously adapted to the canonical filtration or natural filtration. That is to say that the filtration (![]() n)n≥0 is given by
n)n≥0 is given by ![]() n = σ (X1, X2, · · ·, Xn), where σ (X1, X2, · · ·, Xn) is the smallest σ-algebra with respect to which the random variables X1,X2,· · ·,Xn are
n = σ (X1, X2, · · ·, Xn), where σ (X1, X2, · · ·, Xn) is the smallest σ-algebra with respect to which the random variables X1,X2,· · ·,Xn are ![]() n-σ-measurable. When we speak of martingales, supermartingales and submartingales, with respect to the canonical filtration, we will not explicitly mention it. In other words, if we say: “(Xn)n is a (sub-, super-) martingale” and we do not reference the filtration, it is assumed that the filtration is the canonical filtration.
n-σ-measurable. When we speak of martingales, supermartingales and submartingales, with respect to the canonical filtration, we will not explicitly mention it. In other words, if we say: “(Xn)n is a (sub-, super-) martingale” and we do not reference the filtration, it is assumed that the filtration is the canonical filtration.
Note 11.2 If {Xn;n ≥ 0} is a (![]() n)n-martingale, it is enough to see that:
n)n-martingale, it is enough to see that:
E(Xn+1) | ![]() n) = Xn for all n
n) = Xn for all n ![]()
![]() .
.
Note 11.3 If {Xn;n ≥ 0} is a (![]() n)n-submartingale, then {−Xn;n ≥ 0} is a (
n)n-submartingale, then {−Xn;n ≥ 0} is a (![]() n)n-supermartingale. Thus, in general, with very few modifications, every proof made for submartingales is also valid for supermartingales and vice versa.
n)n-supermartingale. Thus, in general, with very few modifications, every proof made for submartingales is also valid for supermartingales and vice versa.
Let {Xn;n ≥ 0} be a martingale with respect to (![]() n)n≥0 and (
n)n≥0 and (![]() n)n≥0 be a filtration such that
n)n≥0 be a filtration such that ![]() n ⊆
n ⊆ ![]() n for all n. If Xn is
n for all n. If Xn is ![]() n-measurable, then {Xn;n ≥ 0} is a martingale with respect to (
n-measurable, then {Xn;n ≥ 0} is a martingale with respect to (![]() n)n. Indeed:
n)n. Indeed:

Therefore, every (![]() n)n-martingale is a martingale with respect to the canonical filtration.
n)n-martingale is a martingale with respect to the canonical filtration. ![]()
![]() EXAMPLE 11.2 Random Walk Martingale
EXAMPLE 11.2 Random Walk Martingale
Let Z1, Z2, · · · be a sequence of i.i.d. random variables on a probability space (Ω, ![]() , P) with finite mean μ = E (Z1), and let
, P) with finite mean μ = E (Z1), and let ![]() n = σ(Z1, · · ·, Zn), n ≥ 1. Let Xn = Z1 + · · · + Zn, n ≥ 1. Then, for all n ≤ 1,
n = σ(Z1, · · ·, Zn), n ≥ 1. Let Xn = Z1 + · · · + Zn, n ≥ 1. Then, for all n ≤ 1,
so that:
![]()
Thus, {Xn;n ≤ 1} is a martingale if μ = 0, a submartingale if μ > 0 and a supermart ingale if μ < 0. ![]()
![]() EXAMPLE 11.3 Second-Moment Martingale
EXAMPLE 11.3 Second-Moment Martingale
Let Z1, Z2, · · · be a sequence of i.i.d. random variables on a probability space (Ω, ![]() , P) with finite mean μ = E (Z1) and variance σ2 = Var(Z1). Let
, P) with finite mean μ = E (Z1) and variance σ2 = Var(Z1). Let ![]() n = σ(Z1,· · ·, Zn), n ≥ 1. Let
n = σ(Z1,· · ·, Zn), n ≥ 1. Let ![]() and
and ![]() . It is easily verified that {Yn;n ≥ 1} is a submartingale and
. It is easily verified that {Yn;n ≥ 1} is a submartingale and ![]() is a martingale. Assume:
is a martingale. Assume:

Let X1,X2,· · · be a sequence of independent random variables with E (Xn) = 1 for all n. Let {Yn;n ≥ 1} be:
![]()
If ![]() n = σ(X1,· · ·, Xn), it is clear that:
n = σ(X1,· · ·, Xn), it is clear that:
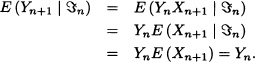
That is, {Yn;n ≥ 1} is a martingale with respect to (![]() n)n.
n)n. ![]()
Suppose that an urn has one red ball and one black ball. A ball is drawn at random from the urn and is returned along with a ball of the same color. The procedure is repeated many times. Let Xn denote the number of black balls in the urn after n drawings. Then X0 = 1 and {Xn;n ≥ 0} is a Markov chain with transitions

and
![]()
Let ![]() be the proportion of black balls after n drawings. Then {Mn;n ≥ 0} is a martingale, since:
be the proportion of black balls after n drawings. Then {Mn;n ≥ 0} is a martingale, since:

![]() EXAMPLE 11.6 Doob’s Martingale
EXAMPLE 11.6 Doob’s Martingale
Let X be a random variable with E(|X|) < ∞, and let {![]() n}n≥1 be a filtration. Define Xn = E(X |
n}n≥1 be a filtration. Define Xn = E(X | ![]() n) for n ≥ 1. Then {Xn,n ≥ 0} is a martingale with respect to {
n) for n ≥ 1. Then {Xn,n ≥ 0} is a martingale with respect to {![]() n}n≥0:
n}n≥0:


As we know that every martingale is also a submartingale and a supermartingale, the following theorem provides a method for getting a submartingale from a martingale.
Theorem 11.1 Let {Mn;n ≥ 0} be a martingale with respect to the filtration (![]() n)n≥0. If
n)n≥0. If ![]() (·) is a convex function with E(|
(·) is a convex function with E(|![]() (Mn)|) < ∞ for all n, then {
(Mn)|) < ∞ for all n, then {![]() (Mn);n ≥ 0} is a submartingale.
(Mn);n ≥ 0} is a submartingale.
Proof: By Jensen’s inequality (Jacod and Protter, 2004):
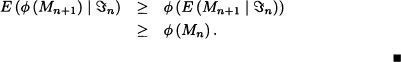
Let {Mn;n ≥ 0} be a nonnegative martingale with respect to the filtration (![]() n)n≥0. Then
n)n≥0. Then ![]() and {−log Mn;n ≥ 0} are submartingales.
and {−log Mn;n ≥ 0} are submartingales. ![]()
Let {Yn;n ≥ 1} be an arbitrary collection of random variables with E[|Yn|] < ∞ for all n ≥ l. Let ![]() n = σ (Y1, · · ·, Yn), n ≥ 1. For n ≥ 1, define
n = σ (Y1, · · ·, Yn), n ≥ 1. For n ≥ 1, define
where ![]() 0 = {
0 = {![]() ,Ω}. Then, for each n ≥ 1, Xn is
,Ω}. Then, for each n ≥ 1, Xn is ![]() n-measurable with E[|Xn|] < ∞. Also, for n ≥ 1:
n-measurable with E[|Xn|] < ∞. Also, for n ≥ 1:

Hence {Xn;n ≥ 1} is a martingale. Thus, it is possible to construct a martingale sequence starting from any arbitrary sequence of random variables. ![]()
Let {Xn;n ≥ 0} be a martingale with respect to the filtration (![]() n)n≥0 and let {Yn;n ≥ 0} be defined by:
n)n≥0 and let {Yn;n ≥ 0} be defined by:
Yn+1 := Xn+1 − Xn, n = 0,1,2, · · ·.
It is clear that:
![]()
Suppose that {Cn;n ≥ 1} is a predictable stochastic process, that is, Cn is a ![]() n−1-measurable random variable for all n. We define a new process {Zn;n ≥ 0} as:
n−1-measurable random variable for all n. We define a new process {Zn;n ≥ 0} as:

The process {Zn;n ≥ 0} is a martingale with respect to filtration {![]() n}n≥0 and is called a martingale transformation of the process Y, denoted by Z = C · Y. The martingale transforms are the discrete analogues of stochastic integrals. They play an important role in mathematical finance in discrete time (see Section 12.3).
n}n≥0 and is called a martingale transformation of the process Y, denoted by Z = C · Y. The martingale transforms are the discrete analogues of stochastic integrals. They play an important role in mathematical finance in discrete time (see Section 12.3). ![]()
Note 11.4 Suppose that {Cn;n ≥ 1} represents the amount of money a player bets at time n and Yn := Xn − Xn−1 is the amount of money he can win or lose in each round of the game. If the bet is a monetary unit and X0 is the initial wealth of the player, then Xn is the player’s fortune at time n and Zn represents the player’s fortune by using the game strategy {Cn;n ≥ 1}. The previous example shows that if {Xn;n ≥ 0} is a martingale and the game is fair, it will remain so no matter what strategy the player follows.
Let ξ1, ξ2 · · · be i.i.d. random variables and suppose that for a fixed t:
m(t) := E(etξ1) < ∞.
The sequence of random variables {Xn;n ≥ 0} with X0 := 1 and

Let ξ1,ξ2 · · · and Xn (t) be as in the example above. We define the random variables ![]() as:
as:
![]()
We have that ![]() is a martingale.
is a martingale. ![]()
Definition 11.3 A random variable ![]() with values {1,2, · · · }∪{∞} is a stopping time with respect to the filtration (
with values {1,2, · · · }∪{∞} is a stopping time with respect to the filtration (![]() n)n≥1 if {
n)n≥1 if {![]() ≤ n}
≤ n} ![]()
![]() n for each n ≥ 1.
n for each n ≥ 1.
Note 11.5 The condition given in the previous definition is equivalent to {![]() = n}
= n} ![]()
![]() n for each n ≥ 1.
n for each n ≥ 1.
![]() EXAMPLE 11.12 First Arrival Time
EXAMPLE 11.12 First Arrival Time
Let X1,X2, · · · be a sequence of random variables adapted to the filtration (![]() n)n≥1. Suppose that A is a Borel set of
n)n≥1. Suppose that A is a Borel set of ![]() and consider the random variable defined by
and consider the random variable defined by
τ := min {n ≥ 1 : Xn ![]() A}
A}
with min (![]() ) := ∞. It is clear that τ is a stopping time since:
) := ∞. It is clear that τ is a stopping time since:
![]()
In particular we have that, for the gambler’s ruin case, the time τ at which the player reaches the set A = {0, a} for the first time is a stopping time. ![]()
![]() EXAMPLE 11.13 Martingale Strategy
EXAMPLE 11.13 Martingale Strategy
Previously we observed that if a player who follows the martingale strategy loses the first n bets and wins the (n + l)th bet, then his wealth Xn+1 after the (n + l)th bet is:
![]()
Suppose that τ is the stopping time at which the player wins for the first time. It is of our interest to know what is, on average, his deficit for that time. That is, we want to determine the value E(Xτ−1) from the previous equation. We have:
![]()
Therefore, on average, a player must have an infinite capital to fulfill the strategy. ![]()
Let {Xn;n ≥ 1} be a martingale with respect to the filtration (![]() n)n≥1. We know that E(Xn) = E(X1) for any n ≥ 1. Nevertheless, if τ is a stopping time, it is not necessarily satisfied that τ. Our next objective is to determine the conditions under which τ, where τ is the stopping time.
n)n≥1. We know that E(Xn) = E(X1) for any n ≥ 1. Nevertheless, if τ is a stopping time, it is not necessarily satisfied that τ. Our next objective is to determine the conditions under which τ, where τ is the stopping time.
Definition 11.4 Let τ be a stopping time with respect to the filtration (![]() n)n≥0 and let {Xn;n ≥ 0} be a martingale with respect to the same filtration. We define the stopped process {XτΛn;n ≥ 0} as follows:
n)n≥0 and let {Xn;n ≥ 0} be a martingale with respect to the same filtration. We define the stopped process {XτΛn;n ≥ 0} as follows:
![]()
Theorem 11.2 If {Xn;n ≥ 1} is a martingale with respect to (![]() n)n≥0, and if τ is a stopping time with respect to (
n)n≥0, and if τ is a stopping time with respect to (![]() n)n≥0, then {XτΛn;n ≥ 0} is a martingale.
n)n≥0, then {XτΛn;n ≥ 0} is a martingale.
Proof: Refer to Jacod and Protter (2004). ![]()
Theorem 11.3 (Optional Stopping Theorem) Let {Xn;n ≥ 0} be a martingale with respect to the filtration (![]() n)n≥1 and let τ be a stopping time with respect to (
n)n≥1 and let τ be a stopping time with respect to (![]() n)n≥1. If
n)n≥1. If
1. τ < ∞ a.s.,
2. E(Xτ) and < ∞
3. ![]() ,
,
then E{Xτ) = E (Xn) for all n ≥ 1.
Proof: Since for any n ≥ 1 it is satisfied that
![]()
and since the process {Xn;n ≥ 0} and {XτΛn;n ≥ 0} are both martingales, we have:
On the other hand by the hypothesis
![]()
and
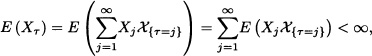
it follows that the tail of the series, which is ![]() , tends to zero as n tends to ∞. Therefore, taking the limit as n → ∞ in (11.2), we obtain:
, tends to zero as n tends to ∞. Therefore, taking the limit as n → ∞ in (11.2), we obtain:
E(Xτ) = E(Xn) for all n ≥ 1. ![]()
Note 11.6 Suppose that {Xn;n ≥ 0} is a symmetric random walk in ![]() with X0 := 0 and that N is a fixed positive integer and let τ be the stopping time defined by:
with X0 := 0 and that N is a fixed positive integer and let τ be the stopping time defined by:
τ := min {n ≥ 1 : |Xn| = N}.
It is easy to verify that the process {Xn;n ≥ 0} and the process ![]() are martingales. Moreover, it is possible to show that the stopping theorem hypotheses are satisfied. Consequently, we get
are martingales. Moreover, it is possible to show that the stopping theorem hypotheses are satisfied. Consequently, we get
![]()
from which we have:
![]()
That is, the random walk needs on average N2 steps to reach the level N.
The following results on convergence of martingales, which we state without proof, provide many applications in stochastic calculus and mathematical finance.
Theorem 11.4 Let{Xn;n ≤ 0} be a submartingale with respect to (![]() n)n≥0 such that supn E(|Xn|) < ∞. Then there exists a random variable X having E(|X|) < ∞ such that:
n)n≥0 such that supn E(|Xn|) < ∞. Then there exists a random variable X having E(|X|) < ∞ such that:
![]()
Note 11.7 There is a similar result for supermartingales because if {Xn;n ≥ 0} is a supermartingale with respect to (![]() n)n≥0, then {−Xn;n ≥ 0} is a submartingale with respect to (
n)n≥0, then {−Xn;n ≥ 0} is a submartingale with respect to (![]() n)n≥0. The previous theorem implies in addition that every nonnegative martingale converges almost surely. The following example shows that, in general, there is no convergence in the mean.
n)n≥0. The previous theorem implies in addition that every nonnegative martingale converges almost surely. The following example shows that, in general, there is no convergence in the mean.
Suppose that {Yn;n ≥ 1} is a sequence if i.i.d random variables with normal distribution eac having mean 0 and variance σ2. Let:

It is easy to prove that {Xn;n ≥ 0} is a nonnegative martingale. By using the strong law of large numbers we obtain that ![]() . Nevertheless,
. Nevertheless, ![]() since E (Xn) = 1 for all n.
since E (Xn) = 1 for all n. ![]()
Now we present a theorem which gives a sufficient condition to ensure the almost sure convergence and convergence in the r-mean. Its proof is beyond the scope of this text, (refer to Williams, 2006).
Theorem 11.5 If {Xn;n ≥ 0} is a martingale with respect to ![]() such that
such that ![]() E(|Xn|r) < ∞ for some r > 1, then there is a random variable X such that
E(|Xn|r) < ∞ for some r > 1, then there is a random variable X such that
Xn ![]() X
X
converges almost surely and in the r-mean.
Next, we give a brief account of continuous-time martingales. Many of the properties of martingales in discrete time are also satisfied in the case of martingales in continuous time.
Definition 11.5 Let (Ω, ![]() , P) be a probability space. A filtration is a family of sub-σ-algebras (
, P) be a probability space. A filtration is a family of sub-σ-algebras (![]() t)t
t)t![]() T such that
T such that ![]() s ⊆
s ⊆ ![]() t for all s ≤ t.
t for all s ≤ t.
Definition 11.6 A stochastic process {Xt;t ![]() T} is said to be adapted to the filtration (
T} is said to be adapted to the filtration (![]() t)t
t)t![]() T if Xt is
T if Xt is ![]() t-measurable for each t
t-measurable for each t ![]() T.
T.
Definition 11.7 Let ![]() ≠ T ⊆
≠ T ⊆ ![]() . A process {Xt;t
. A process {Xt;t ![]() T} is called a martingale with respect to the filtration (
T} is called a martingale with respect to the filtration (![]() t)t
t)t![]() T if:
T if:
1. {Xt;t ![]() T} is adapted to the filtration (
T} is adapted to the filtration (![]() t)t
t)t![]() T.
T.
2. E(|Xt|) < ∞ for all t ![]() T.
T.
3. E(Xt | ![]() s) = Xs a.s. for all s ≥ t.
s) = Xs a.s. for all s ≥ t.
a. If condition 3 is replaced by: E(Xt | ![]() s) ≥ Xs a.s. for all s ≤ t, then the process is called a submartingale.
s) ≥ Xs a.s. for all s ≤ t, then the process is called a submartingale.
b. If condition 3 is replaced by: E (Xt | ![]() s) ≤ Xs a.s. for all s ≤ t, then the process is called a supermartingale.
s) ≤ Xs a.s. for all s ≤ t, then the process is called a supermartingale.
Note 11.9 Condition 3 in the previous definition is equivalent to:
E (Xt − Xs | ![]() s) = 0 a.s. for all s ≤ t.
s) = 0 a.s. for all s ≤ t.
Note 11.10 The sequence {Xt;t ∈ T} is clearly adapted to the canonical filtration, that is, to the filtration (![]() t)t∈T, where
t)t∈T, where ![]() t = σ (Xs, s ≤ t) is the smallest σ-algebra with respect to which the random variables Xs with s ≤ t are measurable.
t = σ (Xs, s ≤ t) is the smallest σ-algebra with respect to which the random variables Xs with s ≤ t are measurable.
Let {Xt; t ≥ 0} be a process with stationary and independent increments. Assume ![]() t = σ (Xs, s ≤ t) and E (Xt) = 0 for all t ≥ 0. Then:
t = σ (Xs, s ≤ t) and E (Xt) = 0 for all t ≥ 0. Then:

That is, {Xt;t ≥ 0} is a martingale with respect to (![]() t)t≥0.
t)t≥0. ![]()
Note 11.11 If in the above example we replace the condition “E (Xt) = 0 for all t ≥ 0” by “E(Xt) ≥ 0 for all t ≥ 0” [“E (Xt) ≤ 0 for all t ≥ 0”] we find that the process is a submartingale (a supermartingale).
Let {Nt; t ≥ 0} be a Poisson process with parameter λ > 0. The process {Nt;t ≥ 0} has independent and stationary increments and in addition E(Nt) = λt ≥ 0. Hence, {Nt; t ≥ 0} is a submartingale.
However, the process {Nt − λt;t ≥ 0} is a martingale and is called a compensated Poisson process. ![]()
11.2 BROWNIAN MOTION
The Brownian motion is named after the English botanist Robert Brown (1773–1858) who observed that pollen grains suspended in a liquid moved irregularly. Brown, as his contemporaries, assumed that the movement was due to the life of these grains. However, this idea was soon discarded as the observations remained unchanged by observing the same movement with inert particles. Later it was found that the movement was caused by continuous particle collisions with molecules of the liquid in which it was embedded. The first attempt to mathematically describe the Brownian motion was made by the Danish mathematician and astronomer Thorvald N. Thiele (1838–1910) in 1880. Then in the early twentieth century, Louis Bachelier (1900), Albert Einstein (1905) and Norbert Wiener (1923) initiated independently the development of the mathematical theory of Brownian motion. Louis Bachelier (1870–1946) used this movement to describe the behavior of stock prices in the Paris stock exchange. Albert Einstein (1879–1955) in 1905 published his paper “Über die von dev molekularischen Theorie der Wärme gefordete Bewegung von in ruhenden Flüssigkeiten suspendierten Teilchen” in which he showed that at time t, the erratic movement a particle can be modeled by a normal distribution. The American mathematician Norbert Wiener (1894–1964) was the first to perform a rigorous construction of Einstein’s model of Brownian motion, which led to the definition of the so-called Wiener measure in the space of trajectories. In this section we introduce Brownian motion and present a few of its important properties.
Definition 11.8 The stochastic process B = {Bt,t ≥ 0} is called a standard Brownian motion or simply a Brownian motion if it satisfies the following conditions:
- B0 = 0.
- B has independent and stationary increments.
- For s < t, every increment {Bt − Bs} is normally distributed with mean 0 and variance (t − s).
- Sample paths are continuous with probability 1.
- The Brownian motion is a Gaussian process. This is because the distribution of a random vector of the form(Bt1, Bt2, … , Btn) is a linear combination of the vector (Bt1, Bt2 − Bt1, …, Btn − Btn−1) which has normal distribution.
- The Brownian motion is a Markov process with transition probability density function

for any x, y ∈
 and 0 < s < t.
and 0 < s < t.Figure 11.1 Sample path of Brownian motion
- The probability density function of Bt is given by:

In the following algorithm, we simulate the sample path for the Brownian motion. This involves repeatedly generating independent standard normal random variables.
Input: T, N where T is the length of time interval and N is the time steps.
Output: BM(k) for k = 0(1)N.
Initialization: BM(0) := 0
Iteration: For k = 0(1)N − 1 do:
Z(k + 1) = stdnormal(rand(0, 1))
BM(k +1) = BM(K) + ![]() × Z(k + 1)
× Z(k + 1)
where stdnormal(rand(0, 1)) is the value of the standard normal random variable using the random number generated in the interval (0, 1). Using this algorithm, we obtain the sample path of Brownian motion as shown in Figure 11.1 for T = 10 and N = 1000.
Now we will discuss some simple and immediate properties of the Brownian motion:
- E (Bt) = 0 for all t ≥ 0.
- E
 = t for all t ≥ 0.
= t for all t ≥ 0. - The covariance of Brownian motion C (s, t) = min (s, t). This is because, if s ≤ t, then:

Similarly, if t ≤ s, we get C(s, t) = t. Hence, the covariance of Brownian motion C(s, t) = min (s, t).
Theorem 11.6 Let {Bt;t ≥ 0} be a Brownian motion. Then the following processes are also Brownian motions:
- Shift Property: For any s > 0,
 = Bt+s − Bs is a Brownian motion.
= Bt+s − Bs is a Brownian motion. - Symmetry Property:
 = −Bt is a Brownian motion.
= −Bt is a Brownian motion. - Scaling Property: For any constant c > 0,
 is a Brownian motion.
is a Brownian motion. - Time Reversal Property:
 for t > 0 with B0 = 0 is a Brownian motion.
for t > 0 with B0 = 0 is a Brownian motion.
Proof: It is easy to check that {![]() ;t ≥ 0} for i = 1, 2, 3, 4 are processes with independent increments with
;t ≥ 0} for i = 1, 2, 3, 4 are processes with independent increments with ![]() = 0. Also the increments are normally distributed with mean 0 and variance (t − s).
= 0. Also the increments are normally distributed with mean 0 and variance (t − s). ![]()
Brownian Motion as a Limit of Random Walks Let {Xt,t ≥ 0} be the stochastic process representing the position of a particle at time t. We assume that the particle performs a random walk such that in a small interval of time of duration Δt the particle moves forward a small distance Δx with probability p or moves backward by a small distance Δx with probability q = 1 − p, where p is independent of x and t. Suppose that the random variable Yk denotes the length of the kth step taken by the particle in a small interval of time Δt and the Yk’s are independent and identically distributed random variables with P(Yk = +Δx) = p = 1 − P(Yk = −Δx).
Suppose that the interval of length t is divided into n equal subintervals of length Δt. Then n · (Δt) = t, and the total displacement Xt of the particle is the sum of n i.i.d. random variables Yk, so that
with n = [n(t)] and n(t) = t/Δt for each t ≥ 0. As a function of t, for each ω, Xt is a step function where steps occur every Δt units of time and steps are of magnitude Δx. We have:
E(Yi) = (p − q)Δx and Var(Yi) = 4pq(Δx)2.
Then:
E(Xt) = n(p − q)Δx and Var(Xt) = 4npq(Δx)2.
Substituting ![]() we have:
we have:
![]()
When we allow Δx → 0 and Δt → 0, the corresponding steps n tend to ∞.We assume that the following expressions have finite limits:
and
where μ and σ are constants. Since the Yk’s are i.i.d. random variables, using the central limit theorem, for large n = n(t) the sum ![]() is asymptotically normal with mean μt and variance σ2t. That is,
is asymptotically normal with mean μt and variance σ2t. That is,
where Z is a standard normal random variable.
Various Gaussian and non-Gaussian stochastic processes of practical relevance can be derived from Brownian motion. We introduce some of those processes which will find interesting applications in finance.
Let {Bt;t ≥ 0} be a Brownian motion. The stochastic process {Rt;t ≥ 0} defined by
![]()
is called a Brownian motion reflected at the origin. The mean and variance of Rt are given by:

Let {Bt;t ≥ 0} be a Brownian motion. The stochastic process {At;t ≥ 0} is defined by
![]()
where T0 = inf{t ≥ 0 : Bt = 0} is the hitting time at 0. Then At is called the absorbed Brownian motion. ![]()
The stochastic process {Ut; 0 ≤ t ≤ 1}, defined as
Ut = Bt − tB1,
is called a Brownian bridge or the tied-down Brownian motion.
The name Brownian bridge comes from the fact that it is tied down at both ends t = 0 and t = 1 since U0 = U1 = 0. In fact, the Brownian bridge {Ut;0 ≤ t ≤ 1} is characterized as being a Gaussian process with continuous sample paths and the covariance function
Cov (Us, Ut) = s(1 − t), 0 ≤ s ≤ t ≤ 1.
If{Ut;0 ≤ t ≤ 1} is a Brownian bridge, then it can be shown that the stochastic process
![]()
is the standard Brownian motion. ![]()
Let {Bt;t ≥ 0} be a Brownian motion. For μ ∈ ![]() and σ > 0, the process
and σ > 0, the process
![]()
is called a Brownian motion with drift μ. It is easy to check that ![]() is a Gaussian process with mean fit and covariance C(s, t) = σ2 min(s, t).
is a Gaussian process with mean fit and covariance C(s, t) = σ2 min(s, t). ![]()
Let {Bt;t ≥ 0} be a Brownian motion. For μ ∈ ![]() and σ > 0, the process
and σ > 0, the process
Xt = exp(μt + σBt), t ≥ 0,
is called a geometric Brownian motion. ![]()
This process has been used to describe stock price fluctuations (see next chapter for more details). It should be noted that Xt is not a Gaussian process. Now we will give the mean and covariance for the geometric Brownian motion.
Using the moment generating function of the normal random variable (4.2), we get:
Similarly we obtain the covariance of the geometric Brownian motion for s < t,
and the variance is given by:
The previous section discussed continuous-time martingales. Presently we will see a Brownian motion as an example of a continuous-time martingale.
Theorem 11.7 Suppose that {Bt;t ≥ 0} is a Brownian motion with respect to filtration ![]() t, where
t, where ![]() t := σ(Bs; s ≤ t). Then
t := σ(Bs; s ≤ t). Then
- {Bt} is a martingale,
- {
 − t} is a martingale and
− t} is a martingale and - for
 , {exp(σBt − (σ2/2)t)} is a martingale (called an exponential martingale).
, {exp(σBt − (σ2/2)t)} is a martingale (called an exponential martingale).
Proof:
- It is clear that, for every t ≥ 0, Bt is adapted to the filtration
 and E(Bt) exists. For any s, t ≥ 0 such that s < t:
and E(Bt) exists. For any s, t ≥ 0 such that s < t:
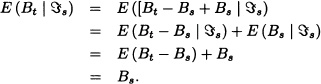
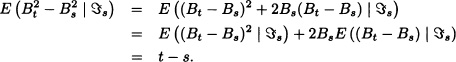
Thus:

- The moment generating function of {Bt; t ≥ 0} is given by:

Therefore
 and
and  is integrable. Now:
is integrable. Now:
Note 11.13 Let {Xt; t ≥ 0} be a stochastic process with respect to filtration ![]() . Then {Xt; t ≥ 0} is a Brownian motion if and only if it satisfies the following conditions:
. Then {Xt; t ≥ 0} is a Brownian motion if and only if it satisfies the following conditions:
- X0 = 0 a.s.
- {Xt; t ≥ 0} is a martingale with respect to filtration
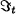 .
.  is a martingale with respect to filtration
is a martingale with respect to filtration 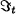 .
.- With probability 1, the sample paths are continuous.
The above result is known as Lévy’s characterization of a Brownian motion (see Mikosh, 1998).
The possible realization of a sample path’s structure and its properties play a crucial role and are the subject matter of deep study. Brownian motion has the continuity of the sample path by definition. Another important property is that it is nowhere differentiable with probability 1. The mathematical proof of this property is beyond the scope of this text. For rigorous mathematical proof, the reader may refer to Karatzas and Shreve (1991) or Breiman (1992).
Now we will see an important and interesting property of a Brownian motion called quadratic variation. In the following, we define the notion of quadratic variation for a real-valued function.
Definition 11.9 Let f (t) be a function defined on the interval [0, T]. The quadratic bounded variation of the function f is
![]()
where ![]() is a partition of the interval [0,T],
is a partition of the interval [0,T],
![]()
with:
![]()
Theorem 11.8 The quadratic variation of the sample path of a Brownian motion over the interval [0, T] converges in mean square to T.
Proof: Let ![]() be a partition of the interval [0, T] :
be a partition of the interval [0, T] :
![]()
Let
![]()

Also:

We conclude that:
![]()
Thus we have proved that Qn converges to T in mean square. ![]()
We can also prove Qn converges to T with probability 1. This proof can be found in Breiman (1992) and Karatzas and Shreve (1991) (see Chapter 8 for different types of convergence of random variables).
As we have seen in this section, the sample path of Brownian motion is nowhere differentiable. Because the stochastic processes which are driven by Brownian motion are also not differentiable, we cannot apply classical calculus. In the following section we introduce the stochastic integral or Itô integral with respect to Brownian motion and its basic rules. We will do so using an intuitive approach which is based on classical calculus. For a mathematically rigorous approach on this integral see Karatzas and Shreve (1991) or Oksendal (2006).
11.3 ITÔ CALCULUS
The stochastic calculus or Itô calculus was developed during the year 1940 by Japanese mathematician K. Itô and is similar to the classical calculus of Newton which involves differentials and integrals of deterministic functions. In this section, we will study the stochastic integral of the process {Xt; t ≥ 0} with respect to a Brownian motion, that is, we adequately define the following expression:
In the classical calculus, the equations which consist of the expressions of the form dx are known as differential equations. If we replace the term dx by an expression of the form dXt, the equations are known as stochastic differential equations. Formally, a stochastic differential equation has the form
where μ(x, t) and σ(x, t) are given functions. Equation (11.10) can be written in integral form:
The first integral is a Riemann integral. How can we interpret the second integral? Initially we could take our inspiration from ordinary calculus in defining this integral as a limit of partial sums, such as
![]()
provided the sum exists. Unlike the Riemann sums, the value of the sum here depends on the choice of the chosen points ti’s. In the case of stochastic integrals, the key idea is to consider the Riemann sums where the integrand is evaluated at the left endpoints of the subintervals. That is:
![]()
Observing that the sum of random variables will be another random variable, the problem is to show that the limit of the above sum exists in some suitable sense. The mean square convergence (see Chapter 8 for the definition) is used to define the stochastic integral. We establish the family of stochastic processes for which the Itô integral can be defined.
Definition 11.10 Let L2 be the set of all the stochastic processes {Xt; t ≥ 0} such that:
(a.) The process X = {Xt; t ≥ 0} is progressively measurable with respect to the given filtration ![]() . This means that, for every t, the mapping (s, ω) → Xs(ω) on every set [0, t] × Ω is measurable.
. This means that, for every t, the mapping (s, ω) → Xs(ω) on every set [0, t] × Ω is measurable.
(b.) ![]() for all T > 0.
for all T > 0.
Now we give the definition of the Itô integral for any process {Xt; t ≥ 0} ∈ L2.
Definition 11.11 Let {Xt; t ≥ 0} be a stochastic process in L2 and T > 0 fixed. We define the stochastic integral or Itô integral of Xt with respect to Brownian motion Bt over the interval [0, T] as
where ![]() is a partition of the interval [0, T] such that
is a partition of the interval [0, T] such that
![]()
with:
![]()
Notation:
![]()
Consider the stochastic integral
![]()
where Bt is a Brownian motion. Let 0 = t0 < t1 < t2 < … < tn = T be a partition of the interval [0, T]. From the definition of the stochastic integral, we have:
![]()
By the use of the identity
![]()
We get:
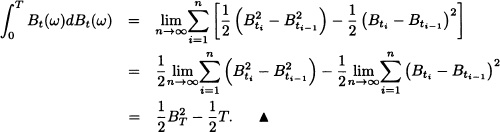
The stochastic integral (11.12) for all T > 0 satisfies the following properties:
- Zero mean:

- Itô isometry:

- Martingale: For t ≤ T,

- Linearity: For {Xt; t ≥ 0}, {Yt; t ≥ 0} ∈ L2,
![]()
Proof: We now prove only the martingale property of the Itô integral. For proofs of the remaining properties, the reader may refer to Karatzas and Shreve (1991). Consider

where the above equality follows by the zero mean property. ![]()
Let ![]() be an Itô integral. We have E (Xt) = 0 by property (11.22). The variance is calculated by use of the mgf of Brownian motion and Itô isometry. We have:
be an Itô integral. We have E (Xt) = 0 by property (11.22). The variance is calculated by use of the mgf of Brownian motion and Itô isometry. We have:
![]()
In the context of ordinary calculus, the Itô formula is also known as the change of variable or chain rule for the stochastic calculus.
Theorem 11.9 (Itô’s Formula) Let ![]() be a twice-differentiable function and let B = {Bt; t ≥ 0} be a Brownian motion that starts at x0, that is, B0 = x0. Then
be a twice-differentiable function and let B = {Bt; t ≥ 0} be a Brownian motion that starts at x0, that is, B0 = x0. Then
![]()
or in the differential form:
![]()
Proof: Fix t > 0. Let ![]() be a partition of [0, t]. By Taylor’s theorem, we have:
be a partition of [0, t]. By Taylor’s theorem, we have:

Taking the limit n → ∞ when Δt → 0, we find that the first sum of the right- hand side converges to the Itô integral and the second sum on the right-hand side converges to ![]() because of mean square convergence. We get:
because of mean square convergence. We get:
![]()
Thus:
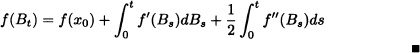
Let f (x) = x2 and B = {Bt; t ≥ 0} be a standard Brownian motion. The Itô formula establishes that:
![]()
That is:
![]()
Let f (x) = x3 and B = {Bt; t ≥ 0} be a standard Brownian motion. The Itô formula establishes that:
![]()
That is:
![]()
Let ![]() for a Brownian motion {Bt; t ≥ 0} with B0 = 0. Prove that
for a Brownian motion {Bt; t ≥ 0} with B0 = 0. Prove that
![]()
and hence find ![]() and
and ![]() .
.
Solution. By the Itô’s formula, we have:
![]()
Taking expectation we have:
![]()
Since β2(t) = t, we get:

Definition 11.12 For a fixed T > 0, the stochastic process {Xt;0≤ t ≤ T} is called an Itô process if it has the form
where X0 is ![]() -measurable and the processes Yt and Zt are
-measurable and the processes Yt and Zt are ![]() -adapted such that, for all t ≥ 0, E(|Yt|) < ∞ and E(|Zt|2) < ∞. An Itô process has the differential form
-adapted such that, for all t ≥ 0, E(|Yt|) < ∞ and E(|Zt|2) < ∞. An Itô process has the differential form
We now give the Itô formula for an Itô process.
Theorem 11.10 (Itô’s Formula for the General Case) Let {Xt; t ≥ 0} be an Itô process given in (11.14). Suppose that f (t, x) is a twice continuously differentiable function with respect to x and t. Then f(t, Xt) is also an Itô process and:

Proof: See Oksendal (2006). ![]()
Note 11.14 We introduce the notation
![]()
which is computed using the following multiplication rules:
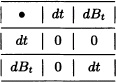
The Itô formula then can be expressed in the following form:

Note 11.15 Itô’s formula can also be expressed in differentials as:
![]()
Let Xt = t and f(t, x) = g (x) be a twice-differentiable function. It is easy to see that:
![]()
Thus, applying Itô’s formula, we get:
![]()
That is, the fundamental theorem of calculus is a particular case of Itô’s formula. ![]()
Let Xt = h (t) where h is a differentiable function and let f (t, x) = g (x) be a twice-differentiable function. It is easy to check that:
![]()
Applying Itô’s formula, we obtain :
![]()
In this case also, the substitution theorem of calculus is a particular case of Itô’s formula. ![]()
Let {Bt; t ≥ 0} be a Brownian motion and consider the following differential equation:
Let Zt = log(yt). Then, by Itô’s formula, we have:
![]()
Thus:
![]()
Integrating we get
![]()
so that the solution of equation (11.15) is:
![]()
Consider the Langevin equation
dXt = −βXtdt + αdBt
where ![]() and β > 0. The process {Xt; t ≥ 0} with X0 = x0 can be written as:
and β > 0. The process {Xt; t ≥ 0} with X0 = x0 can be written as:
![]()
Let f (t, x) = eβtx. Applying Itô’s formula, we get:

Integration of the above equation gives for s ≤ t:
![]()
The solution of the Langevin equation with initial condition X0 = xo is called an Ornstein-Uhlenbeck process. ![]()
We complete this chapter with the Itô formula for functions of two or more variables.
Multidimensional Itô Formula
We now give the Itô formula for functions of two variables. Consider a two-dimensional process
where ![]() and
and ![]() are two Brownian motions with their covariances given by
are two Brownian motions with their covariances given by
where ρ is the correlation coefficient of the two Brownian motions. Let g(t, x, y) be a twice-differentiable function and let Zt = g(t, Xt, Yt). Then Zt is also an Itô process and satisfies:

For the proof, the reader may refer to Karatzas and Shreve (1991).
Note 11.16 For any two Itô processes, {Xt; t ≥ 0} and {Yt; t ≥ 0}, we have the following product rule for the differention:
Theorem 11.11 Let Xt and Yt be two Itô processes such that ![]() and
and ![]() . Then:
. Then:
![]()
Proof: Let ![]() and
and ![]() .
.
By using the identity
![]()
and taking expectation, we get:
![]()
By use of Itô’s isometry property we get the desired result. ![]()
Suppose that Xt = tBt. Use of product rule (11.19) gives us:
dXt = tdBt + Btdt. ![]()
Suppose that Xt = tBt and Yt satisfies the stochastic differential equation
![]()
We know that Yt = eBt is a geometric Brownian motion. Then the use of product rule (11.19) gives us:
d (XtYt) = XtdYt + YtdXt + tYtdt.
![]()
Suppose that
with X0 = 0, α, β ![]()
![]() and {Bt; t ≥ 0} and {Wt; t ≥ 0} are two Brownian motions. Let f(t, x) = x2. Then, from Itô’s formula,
and {Bt; t ≥ 0} and {Wt; t ≥ 0} are two Brownian motions. Let f(t, x) = x2. Then, from Itô’s formula,
with ![]() . Note that Xt = αBt + βWt and:
. Note that Xt = αBt + βWt and:
From equations (11.21) and (11.22), we get:
![]()
Using the relation
![]()
we have the following interesting result:
![]()
Without recourse to measure theory, we have presented various tools necessary in dealing with financial models with the use of stochastic calculus. This chapter does not make a full-fledged analysis and is intended as a motivation for the further study. For a more rigorous treatment, the reader may refer to Grimmett and Stirzaker (2001), Oksendal (2005), Mikosch (2002), Shreve (2004), and Karatzas and Shreve (1991).
EXERCISES
11.1 In Example 11.11 verify
![]()

11.2 Let {Xn; n ≥ 0} be a martingale (supermartingale) with respect to the filtration ![]() . Prove that
. Prove that
![]()
for all k ≥ 0.
11.3 Let {Xn; n ≥ 0} be a martingale (supermartingale) with respect to the filtration ![]() . Prove that:
. Prove that:
E(Xn) = E(Xk) (≤ for supermantingale)
for all 0 ≤ k ≤ n
11.4 Let {Xn; n ≥ 0} be a martingale with respect to the filtration ![]() and assume f to be a convex function. Prove that {f(Xn); n ≥ 0} is a submartingale with respect to the filtration
and assume f to be a convex function. Prove that {f(Xn); n ≥ 0} is a submartingale with respect to the filtration ![]() .
.
11.5 If {Xt; t ≥ 0} is a martingale with respect to ![]() if
if ![]() is a convex function such that E(|h(Xt)|) < ∞ for all t ≥ 0, show that {h(Xt); t ≥ 0} is a submartingale with respect to
is a convex function such that E(|h(Xt)|) < ∞ for all t ≥ 0, show that {h(Xt); t ≥ 0} is a submartingale with respect to ![]() .
.
11.6 Let ξ1, ξ2, … be i.i.d. random variables, such that P (ξn = 1) = p and P (ξn = −1) = 1 − p for some p in (0,1). Prove that {Mn; n ≥ 0} with

is a martingale with respect to ![]() , where
, where ![]() and
and ![]() for n ≥ 1.
for n ≥ 1.
11.7 Let X1, X2, … be a sequence of i.i.d. random variables satisfying
![]()
Let M0 := 0, Mn := X1X2 … Xn and ![]() . Is {Mn; n ≥ 0} a martingale with respect to
. Is {Mn; n ≥ 0} a martingale with respect to ![]() ? Explain.
? Explain.
11.8 Let X1, X2, … be a sequence of random variables such that E (Xn) = 0 for all n = 1,2, … and suppose E (eXn) exists for all n = 1,2, … .
a) Is the sequence {Yn; n ≥ 1} with ![]() a submartingale with respect to
a submartingale with respect to ![]() , where
, where ![]() for n ≥ 1? Explain.
for n ≥ 1? Explain.
b) Find (if possible) constants αn such that the sequence {Zn; n ≥ 1} with ![]() is a martingale with respect to
is a martingale with respect to ![]() , where
, where ![]() for n ≥ 1.
for n ≥ 1.
11.9 (Doob’s descomposition) Let {Yn; n ≥ 0} be a submartingale with respect to the filtration ![]() . Show that
. Show that
![]()
for n = 1,2, … is a martingale with respect to ![]() and that the sequence An := Yn − Mn, n = 1,2,…, satisfies 0 ≤ A1 ≤ A1 ≤ …. Is An measurable with respect to
and that the sequence An := Yn − Mn, n = 1,2,…, satisfies 0 ≤ A1 ≤ A1 ≤ …. Is An measurable with respect to ![]() ? Explain.
? Explain.
11.10 Let X1, X2, … be a sequence of independent random variables such that ![]() exists for all n = 1,2, … and suppose Sn := X1+…+Xn, n = 1, 2, …. Is
exists for all n = 1,2, … and suppose Sn := X1+…+Xn, n = 1, 2, …. Is ![]() a submartingale? If it is so, then determine the process {An; n ≥ 1} as in the exercise above.
a submartingale? If it is so, then determine the process {An; n ≥ 1} as in the exercise above.
11.11 Let {Xn; n ≥ 1} be a sequence of random variables adapted to the filtration ![]() . Suppose that
. Suppose that ![]() is the time at which the process {Xn; n ≥ 1} reaches for the first time the set A and let:
is the time at which the process {Xn; n ≥ 1} reaches for the first time the set A and let:
![]()
Show that ![]() is a stopping time. What does
is a stopping time. What does ![]() represent?
represent?
11.12 Let τ be a stopping time with respect to the filtration ![]() and k be a fixed positive integer. Show that the following random variables are stopping times:
and k be a fixed positive integer. Show that the following random variables are stopping times: ![]() .
.
11.13 Let {Xn; n ≥ 1} be the independent random variables with E[Xn] = 0 and Var(Xn) = σ2 for all n ≥ 1. Set M0 = 0 and ![]() , where Sn = X1 + X2 + … + Xn. Is {Mn; n ≥ 1} a martingale with respect to the sequence Xn?
, where Sn = X1 + X2 + … + Xn. Is {Mn; n ≥ 1} a martingale with respect to the sequence Xn?
11.14 Let {Nt; t ≥ 0} be a Poisson process with rate λ and ![]() is a filtration associated with Nt. Write down the conditional distribution of Nt+s − Nt given
is a filtration associated with Nt. Write down the conditional distribution of Nt+s − Nt given ![]() , where s > 0, and use your answer to find
, where s > 0, and use your answer to find ![]() .
.
11.15 (Lawler, 1996) Consider the simple symmetric random walk model Yn = X1 + X2 + … + Xn + with Y0 = 0, where the steps Xi’s are independent and identically distributed with P[Xk = 1] = 1/2 and P[Xk = −1] = 1/2 for all k. Let T := inf{n : Yn = −1} denote the hitting time of −1. We know that P[T < ∞] = 1. Show that if s > 0, then ![]() with M0 = 1 is a martingale, where
with M0 = 1 is a martingale, where ![]() .
.
11.16 Let X1, X2, … be independent random variables such that

where a1 = 2 and ![]() . Is
. Is ![]() a martingale?
a martingale?
11.17 Let Bt be a Brownian motion. Find E ((Bt − Bs)4).
11.18 Let {Bt; t ≥ 0} and ![]() be two independent Brownian motions. Show that
be two independent Brownian motions. Show that
![]()
is also a Brownian motion. Find the correlation between Bt and Xt.
11.19 Let Bt be a Brownian motion. Find the distribution of B1 + B2 + B3 + B4.
11.20 Let {Bt; t ≥ 0} be a Brownian motion. Show that e−αtBe2αt is a Gaussian process. Find its mean and covariance functions.
11.21 Let {Bt; t ≥ 0} be a Brownian motion. Find the distribution for the integral
![]()
11.22 St has the following differential equations:
dSt = μStdt + σStdBt.
Find the equation for the process ![]() .
.
11.23 Use the Itô formula to write down the stochastic differential equations for the following equations. {Bt; t ≥ 0} is a Brownian motion process.
a) ![]() .
.
b) Yt = tBt.
c) Zt = exp(ct + αBt).
![]()
Find E(It(B)) and E(It(B)2).
![]()
![]()
11.27 Suppose that Xt satisfies:
![]()
Let Yt = f (t, Xt) = (2t + 3)Xt + 4t2. Find Yt.
11.28 Use Itô’s formula to show that:
![]()
11.29 Consider the stochastic differential equation
![]()
with X0 = 0.
a) Find Xt.
b) Let Zt = eXt. Find the stochastic differential equation for Zt using Itô’s formula
11.30 Find the solution of the stochastic differential equation
dZt = Ztdt + 2ZtdBt.
11.31 Solve the following stochastic differential equation for the spot rate of interest:
drt = (b − rt)dt + σdBt
where rt is an interest rate, ![]() and σ ≥ 0.
and σ ≥ 0.
11.32 Suppose that Xt follows the process dXt = 0.05Xtdt + 0.25XtdBt. Using Itô’s lemma find the equation for process ![]() .
.


