Chapter 22. Clustering
Clustering, which plays a big role in modern machine learning, is the partitioning of data into groups. This can be done in a number of ways, the two most popular being K-means and hierarchical clustering. In terms of a data.frame, a clustering algorithm finds out which rows are similar to each other. Rows that are grouped together are supposed to have high similarity to each other and low similarity with rows outside the grouping.
22.1. K-means
One of the more popular algorithms for clustering is K-means. It divides the observations into discrete groups based on some distance metric. For this example, we use the wine dataset from the University of California–Irvine Machine Learning Repository, available at http://archive.ics.uci.edu/ml/datasets/Wine.
> wine <- read.table("data/wine.csv", header = TRUE, sep = ",")
> head(wine)
Cultivar Alcohol Malic.acid Ash Alcalinity.of.ash Magnesium
1 1 14.23 1.71 2.43 15.6 127
2 1 13.20 1.78 2.14 11.2 100
3 1 13.16 2.36 2.67 18.6 101
4 1 14.37 1.95 2.50 16.8 113
5 1 13.24 2.59 2.87 21.0 118
6 1 14.20 1.76 2.45 15.2 112
Total.phenols Flavanoids Nonflavanoid.phenols Proanthocyanins
1 2.80 3.06 0.28 2.29
2 2.65 2.76 0.26 1.28
3 2.80 3.24 0.30 2.81
4 3.85 3.49 0.24 2.18
5 2.80 2.69 0.39 1.82
6 3.27 3.39 0.34 1.97
Color.intensity Hue OD280.OD315.of.diluted.wines Proline
1 5.64 1.04 3.92 1065
2 4.38 1.05 3.40 1050
3 5.68 1.03 3.17 1185
4 7.80 0.86 3.45 1480
5 4.32 1.04 2.93 735
6 6.75 1.05 2.85 1450
Because the first column is the cultivar, and that might be too correlated with group membership, we exclude that from the analysis.
> wineTrain <- wine[, which(names(wine) != "Cultivar")]
For K-means we need to specify the number of clusters, and then the algorithm assigns observations into that many clusters. There are heuristic rules for determining the number of clusters, which we will get to later. In R, K-means is done with the aptly named kmeans function. Its first two arguments are the data to be clustered, which must be all numeric (K-means does not work with categorical data), and the number of centers (clusters). Because there is a random component to the clustering, we set the seed to generate reproducible results.
> set.seed(278613)
> wineK3 <- kmeans(x = wineTrain, centers = 3)
Printing the K-means objects displays the size of the clusters, the cluster mean for each column, the cluster membership for each row and similarity measures.
> wineK3
K-means clustering with 3 clusters of sizes 62, 47, 69
Cluster means:
Alcohol Malic.acid Ash Alcalinity.of.ash Magnesium
1 12.92984 2.504032 2.408065 19.89032 103.59677
2 13.80447 1.883404 2.426170 17.02340 105.51064
3 12.51667 2.494203 2.288551 20.82319 92.34783
Total.phenols Flavanoids Nonflavanoid.phenols Proanthocyanins
1 2.111129 1.584032 0.3883871 1.503387
2 2.867234 3.014255 0.2853191 1.910426
3 2.070725 1.758406 0.3901449 1.451884
Color.intensity Hue OD280.OD315.of.diluted.wines Proline
1 5.650323 0.8839677 2.365484 728.3387
2 5.702553 1.0782979 3.114043 1195.1489
3 4.086957 0.9411594 2.490725 458.2319
Clustering vector:
[1] 2 2 2 2 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 1 1 1 2 2 1 1 2 2 1 2 2 2
[33] 2 2 2 1 1 2 2 1 1 2 2 1 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 3 1 3 1 3
[65] 3 1 3 3 1 1 1 3 3 2 1 3 3 3 1 3 3 1 1 3 3 3 3 3 1 1 3 3 3 3 3 1
[97] 1 3 1 3 1 3 3 3 1 3 3 3 3 1 3 3 1 3 3 3 3 3 3 3 1 3 3 3 3 3 3 3
[129] 3 3 1 3 3 1 1 1 1 3 3 3 1 1 3 3 1 1 3 1 1 3 3 3 3 1 1 1 3 1 1 1
[161] 3 1 3 1 1 3 1 1 1 1 3 3 1 1 1 1 1 3
Within cluster sum of squares by cluster:
[1] 566572.5 1360950.5 443166.7
(between_SS / total_SS = 86.5 %)
Available components:
[1] "cluster" "centers" "totss" "withinss"
[5] "tot.withinss" "betweenss" "size"
Plotting the result of K-means clustering can be difficult because of the high dimensional nature of the data. To overcome this, the plot.kmeans function in useful performs multidimensional scaling to project the data into two dimensions, and then color codes the points according to cluster membership. This is seen in Figure 22.1.
> require(useful)
> plot(wineK3, data = wineTrain)
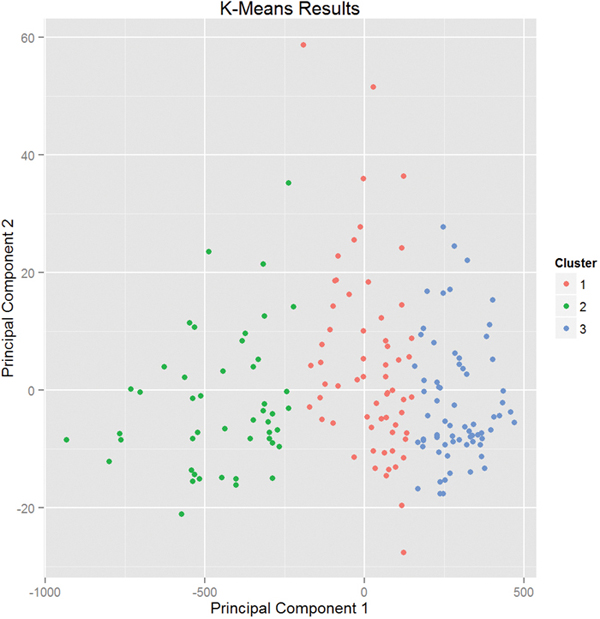
Figure 22.1 Plot of wine data scaled into two dimensions and color coded by results of K-means clustering.
If we pass the original wine data and specify that Cultivar is the true membership column, the shape of the points will be coded by Cultivar, so we can see how that compares to the colors in Figure 22.2. A strong correlation between the color and shape would indicate a good clustering.
> plot(wineK3, data = wine, class = "Cultivar")
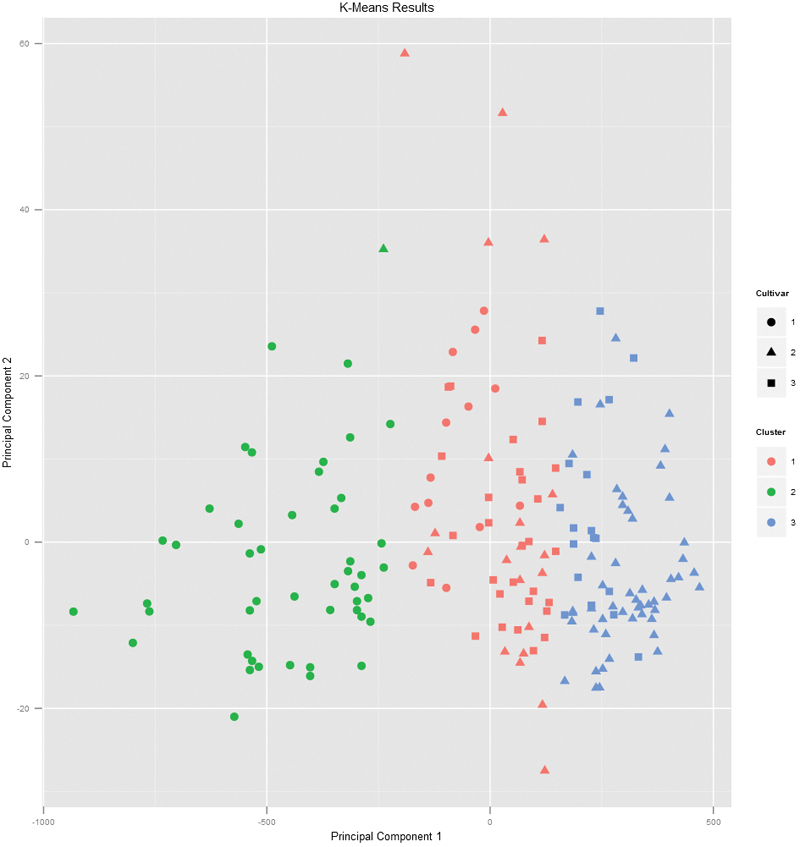
Figure 22.2 Plot of wine data scaled into two dimensions and color coded by results of K-means clustering. The shapes indicate the cultivar. A strong correlation between the color and shape would indicate a good clustering.
K-means can be subject to random starting conditions, so it is considered good practice to run it with a number of random starts. This is accomplished with the nstart argument.
> set.seed(278613)
> wineK3N25 <- kmeans(wineTrain, centers = 3, nstart = 25)
> # see the cluster sizes with 1 start
> wineK3$size
[1] 62 47 69
> # see the cluster sizes with 25 starts
> wineK3N25$size
[1] 62 47 69
For our data the results did not change. For other datasets the number of starts can have a significant impact.
Choosing the right number of clusters is important in getting a good partitioning of the data. According to David Madigan, the chair of the Department of Statistics, Columbia University, a good metric for determining the optimal number of clusters is Hartigan’s Rule ( J. A. Hartigan is one of the authors of the most popular K-means algorithm). It essentially compares the ratio of the within-cluster sum of squares for a clustering with k clusters and one with k + 1 clusters, accounting for the number of rows and clusters.
If that number is greater than 10, then it is worth using k + 1 clusters. Fitting this repeatedly can be a chore and computationally inefficient if not done right. The useful package has the FitKMeans function for doing just that. The results are plotted in Figure 22.3.
> wineBest <- FitKMeans(wineTrain, max.clusters=20, nstart=25,
+ seed=278613)
> wineBest
Clusters Hartigan AddCluster
1 2 505.429310 TRUE
2 3 160.411331 TRUE
3 4 135.707228 TRUE
4 5 78.445289 TRUE
5 6 71.489710 TRUE
6 7 97.582072 TRUE
7 8 46.772501 TRUE
8 9 33.198650 TRUE
9 10 33.277952 TRUE
10 11 33.465424 TRUE
11 12 17.940296 TRUE
12 13 33.268151 TRUE
13 14 6.434996 FALSE
14 15 7.833562 FALSE
15 16 46.783444 TRUE
16 17 12.229408 TRUE
17 18 10.261821 TRUE
18 19 -13.576343 FALSE
19 20 56.373939 TRUE
> PlotHartigan(wineBest)
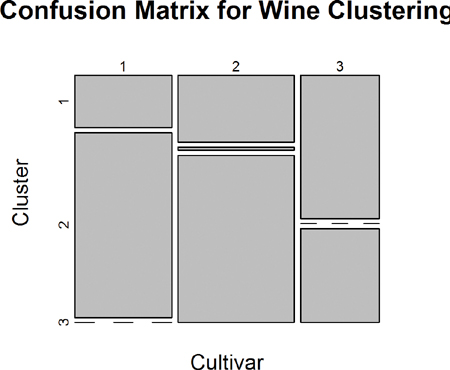
According to this metric we should use 13 clusters. Again, this is just a rule of thumb and should not be strictly adhered to. Because we know there are three cultivars it would seem natural to choose three clusters. Then again, the results of the clustering with three clusters did only a fairly good job of aligning the clusters with the cultivars, so it might not be that good of a fit. Figure 22.4 shows the cluster assignment going down the left side and the cultivar across the top. Cultivar 1 is mostly alone in its own cluster, and cultivar 2 is just a little worse, while cultivar 3 is not clustered well at all. If this were truly a good fit, the diagonals would be the largest segments.
> table(wine$Cultivar, wineK3N25$cluster)
1 2 3
1 13 46 0
2 20 1 50
3 29 0 19
> plot(table(wine$Cultivar, wineK3N25$cluster),
+ main="Confusion Matrix for Wine Clustering",
+ xlab="Cultivar", ylab="Cluster")
An alternative to Hartigan’s Rule is the Gap statistic, which compares the within-cluster dissimilarity for a clustering of the data with that of a bootstrapped sample of data. It is measuring the gap between reality and expectation. This can be calculated (for numeric data only) using clusGap in cluster. It takes a bit of time to run because it is doing a lot of simulations.
> require(cluster)
> theGap <- clusGap(wineTrain, FUNcluster = pam, K.max = 20)
> gapDF <- as.data.frame(theGap$Tab)
> gapDF
logW E.logW gap SE.sim
1 9.655294 9.947093 0.2917988 0.03367473
2 8.987942 9.258169 0.2702262 0.03498740
3 8.617563 8.862178 0.2446152 0.03117947
4 8.370194 8.594228 0.2240346 0.03193258
5 8.193144 8.388382 0.1952376 0.03243527
6 7.979259 8.232036 0.2527773 0.03456908
7 7.819287 8.098214 0.2789276 0.03089973
8 7.685612 7.987350 0.3017378 0.02825189
9 7.591487 7.894791 0.3033035 0.02505585
10 7.496676 7.818529 0.3218525 0.02707628
11 7.398811 7.750513 0.3517019 0.02492806
12 7.340516 7.691724 0.3512081 0.02529801
13 7.269456 7.638362 0.3689066 0.02329920
14 7.224292 7.591250 0.3669578 0.02248816
15 7.157981 7.545987 0.3880061 0.02352986
16 7.104300 7.506623 0.4023225 0.02451914
17 7.054116 7.469984 0.4158683 0.02541277
18 7.006179 7.433963 0.4277835 0.02542758
19 6.971455 7.401962 0.4305071 0.02616872
20 6.932463 7.369970 0.4375070 0.02761156
Figure 22.5 shows the Gap statistic for a number of different clusters. The optimal number of clusters is the smallest number producing a gap within one standard deviation of the number of clusters that minimizes the gap.

Figure 22.5 Gap curves for wine data. The blue curve is the observed within-cluster dissimilarity, and the green curve is the expected within-cluster dissimilarity. The red curve represents the Gap statistic (expected-observed) and the error bars are the standard deviation of the gap.
> # logW curves
> ggplot(gapDF, aes(x=1:nrow(gapDF))) +
+ geom_line(aes(y=logW), color="blue") +
+ geom_point(aes(y=logW), color="blue") +
+ geom_line(aes(y=E.logW), color="green") +
+ geom_point(aes(y=E.logW), color="green") +
+ labs(x="Number of Clusters")
>
> # gap curve
> ggplot(gapDF, aes(x=1:nrow(gapDF))) +
+ geom_line(aes(y=gap), color="red") +
+ geom_point(aes(y=gap), color="red") +
+ geom_errorbar(aes(ymin=gap-SE.sim, ymax=gap+SE.sim), color="red") +
+ labs(x="Number of Clusters", y="Gap")
22.2. PAM
Two problems with K-means clustering are that it does not work with categorical data and it is susceptible to outliers. An alternative is K-medoids. Instead of the center of a cluster being the mean of the cluster, the center is one of the actual observations in the cluster. This is akin to the median, which is likewise robust against outliers.
The most common K-medoids algorithm is Partitioning Around Medoids (PAM). The cluster package contains the pam function. For this example, we look at some data from the World Bank, including both numerical measures such as GDP and categorical information such as region and income level.
Now we use the country codes to download a number of indicators from the World Bank using WDI.
> indicators <- c("BX.KLT.DINV.WD.GD.ZS", "NY.GDP.DEFL.KD.ZG",
+ "NY.GDP.MKTP.CD", "NY.GDP.MKTP.KD.ZG",
+ "NY.GDP.PCAP.CD", "NY.GDP.PCAP.KD.ZG",
+ "TG.VAL.TOTL.GD.ZS")
> require(WDI)
>
> # pull info on these indicators for all countries in our list
> # not all countries have information for every indicator
> # some countries do not have any data
> wbInfo <- WDI(country="all", indicator=indicators, start=2011,
+ end=2011, extra=TRUE)
> # get rid of aggregated info
> wbInfo <- wbInfo[wbInfo$region != "Aggregates", ]
> # get rid of countries where all the indicators are NA
> wbInfo <- wbInfo[which(rowSums(!is.na(wbInfo[, indicators])) > 0), ]
> # get rid of any rows where the iso is missing
> wbInfo <- wbInfo[!is.na(wbInfo$iso2c), ]
The data have a few missing values, but fortunately pam handles missing values well. Before we run the clustering algorithm we clean up the data some more, using the country names as the row names of the data.frame and ensuring the categorical variables are factors with the proper levels.
> # set rownames so we can know the country without using that for
> # clustering
> rownames(wbInfo) <- wbInfo$iso2c
> # refactorize region, income and lending to account for any changes
> # in the levels
> wbInfo$region <- factor(wbInfo$region)
> wbInfo$income <- factor(wbInfo$income)
> wbInfo$lending <- factor(wbInfo$lending)
Now we fit the clustering using pam from the cluster package. Figure 22.6 shows a silhouette plot of the results. Each line represents an observation, and each grouping of lines is a cluster. Observations that fit the cluster well have large positive lines and observations that do not fit well have small or negative lines. A bigger average width for a cluster means a better clustering.
> # find which columns to keep
> # not those in this vector
> keep.cols <- which(!names(wbInfo) %in% c("iso2c", "country", "year",
+ "capital", "iso3c"))
> # fit the clustering
> wbPam <- pam(x=wbInfo[, keep.cols], k=12, keep.diss=TRUE,
+ keep.data=TRUE)
>
> # show the medoid observations
> wbPam$medoids
BX.KLT.DINV.WD.GD.ZS NY.GDP.DEFL.KD.ZG NY.GDP.MKTP.CD
PT 5.507851973 0.6601427 2.373736e+11
HT 2.463873387 6.7745103 7.346157e+09
BY 7.259657119 58.3675854 5.513208e+10
BE 19.857364384 2.0299163 5.136611e+11
MX 1.765034004 5.5580395 1.153343e+12
GB 1.157530889 2.6028860 2.445408e+12
IN 1.741905033 7.9938177 1.847977e+12
CN 3.008038634 7.7539567 7.318499e+12
DE 1.084936891 0.8084950 3.600833e+12
NL 1.660830419 1.2428287 8.360736e+11
JP 0.001347863 -2.1202280 5.867154e+12
US 1.717849686 2.2283033 1.499130e+13
NY.GDP.MKTP.KD.ZG NY.GDP.PCAP.CD NY.GDP.PCAP.KD.ZG
PT -1.6688187 22315.8420 -1.66562016
HT 5.5903433 725.6333 4.22882080
BY 5.3000000 5819.9177 5.48896865
BE 1.7839242 46662.5283 0.74634396
MX 3.9106137 10047.1252 2.67022734
GB 0.7583280 39038.4583 0.09938161
IN 6.8559233 1488.5129 5.40325582
CN 9.3000000 5444.7853 8.78729922
DE 3.0288866 44059.8259 3.09309213
NL 0.9925175 50076.2824 0.50493944
JP -0.7000000 45902.6716 -0.98497734
US 1.7000000 48111.9669 0.96816270
TG.VAL.TOTL.GD.ZS region longitude latitude income lending
PT 58.63188 2 -9.135520 38.7072 2 4
HT 49.82197 3 -72.328800 18.5392 3 3
BY 156.27254 2 27.576600 53.9678 6 2
BE 182.42266 2 4.367610 50.8371 2 4
MX 61.62462 3 -99.127600 19.4270 6 2
GB 45.37562 2 -0.126236 51.5002 2 4
IN 40.45037 6 77.225000 28.6353 4 1
CN 49.76509 1 116.286000 40.0495 6 2
DE 75.75581 2 13.411500 52.5235 2 4
NL 150.41895 2 4.890950 52.3738 2 4
JP 28.58185 1 139.770000 35.6700 2 4
US 24.98827 5 -77.032000 38.8895 2 4
>
> # make a silhouette plot
> plot(wbPam, which.plots=2, main="")
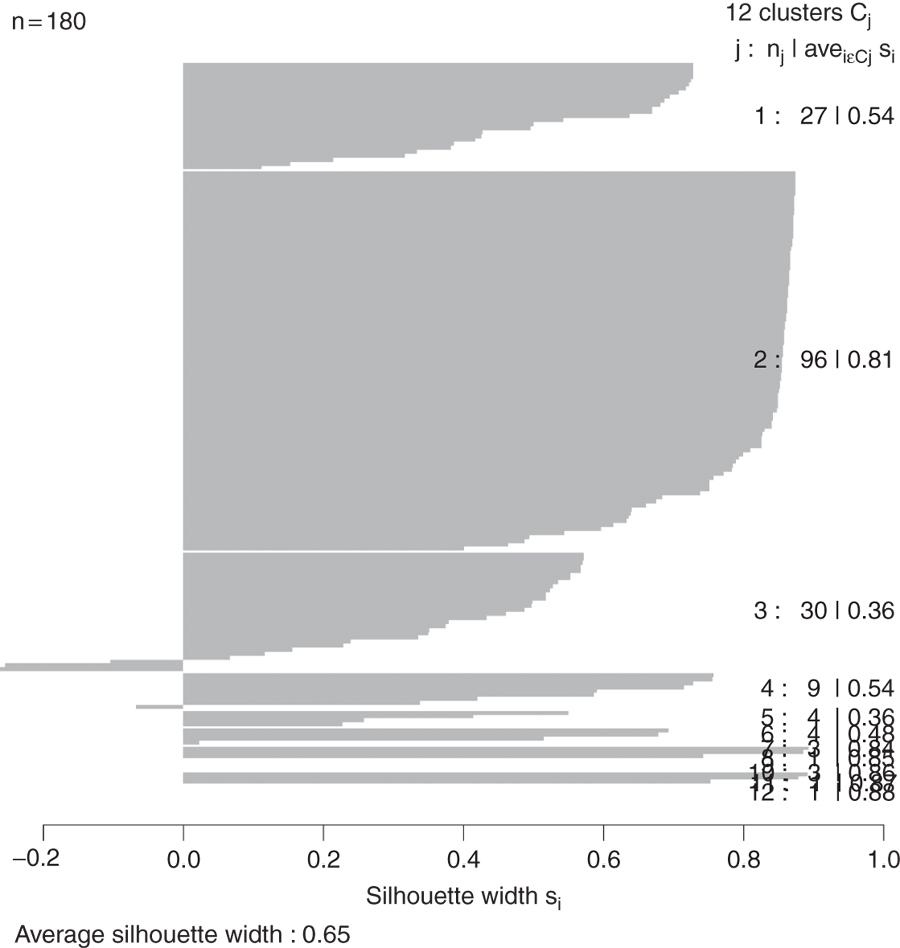
Figure 22.6 Silhouette plot for country clustering. Each line represents an observation, and each grouping of lines is a cluster. Observations that fit the cluster well have large positive lines and observations that do not fit well have small or negative lines. A bigger average width for a cluster means a better clustering.
Because we are dealing with country level information, it would be informative to view the clustering on a world map. As we are working with World Bank data, we will use the World Bank shapefile of the world available at http://maps.worldbank.org/overlays/2712. It can be downloaded in a browser as any other file or using R. While this is slower than using a browser, it can be nice if we have to programmatically download many files.
> download.file(url="http://jaredlander.com/data/worldmap.zip",
+ destfile="data/worldmap.zip", method="curl")
The file needs to be unzipped, which can be done through the operating system or in R.
> unzip(zipfile = "data/worldmap.zip", exdir = "data")
Of the four files, we only need to worry about the one ending in .shp because R will handle the rest. We read it in using readShapeSpatial from maptools.
name CntryName FipsCntry
0 Fips Cntry: Aruba AA
1 Fips Cntry: Antigua & Barbuda AC
2 Fips Cntry: United Arab Emirates AE
3 Fips Cntry: Afghanistan AF
4 Fips Cntry: Algeria AG
5 Fips Cntry: Azerbaijan AJ
> require(maptools)
> world <- readShapeSpatial(
+ "data/world_country_admin_boundary_shapefile_with_fips_codes.shp"
+ )
> head(world@data)
There are some blatant discrepancies between the two-digit code in the World Bank shapefile and the two-digit code in the World Bank data pulled using WDI. Notably, Austria should be “AT,” Australia “AU,” Myanmar (Burma) “MM,” Vietnam “VN” and so on.
> require(plyr)
> world@data$FipsCntry <- as.character(
+ revalue(world@data$FipsCntry,
+ replace=c(AU="AT", AS="AU", VM="VN", BM="MM", SP="ES",
+ PO="PT", IC="IL", SF="ZA", TU="TR", IZ="IQ",
+ UK="GB", EI="IE", SU="SD", MA="MG", MO="MA",
+ JA="JP", SW="SE", SN="SG"))
+ )
In order to use ggplot2 we need to convert this shapefile object into a data.frame, which requires a few steps.
> # make an id column using the rownames
> world@data$id <- rownames(world@data)
> # fortify it, this is a special ggplot2 function that converts
> # shapefiles to data.frames
> require(ggplot2)
> require(rgeos)
> world.df <- fortify(world, region = "id")
> head(world.df)
long lat order hole piece group id
1 -69.88223 12.41111 1 FALSE 1 0.1 0
2 -69.94695 12.43667 2 FALSE 1 0.1 0
3 -70.05904 12.54021 3 FALSE 1 0.1 0
4 -70.05966 12.62778 4 FALSE 1 0.1 0
5 -70.03320 12.61833 5 FALSE 1 0.1 0
6 -69.93224 12.52806 6 FALSE 1 0.1 0
Before we can join this to the clustering, we need to join FipsCntry back into world.df.
> world.df <- join(world.df,
+ world@data[, c("id", "CntryName", "FipsCntry")],
+ by="id")
> head(world.df)
long lat order hole piece group id CntryName FipsCntry
1 -69.88223 12.41111 1 FALSE 1 0.1 0 Aruba AA
2 -69.94695 12.43667 2 FALSE 1 0.1 0 Aruba AA
3 -70.05904 12.54021 3 FALSE 1 0.1 0 Aruba AA
4 -70.05966 12.62778 4 FALSE 1 0.1 0 Aruba AA
5 -70.03320 12.61833 5 FALSE 1 0.1 0 Aruba AA
6 -69.93224 12.52806 6 FALSE 1 0.1 0 Aruba AA
Now we can take the steps of joining in data from the clustering and the original World Bank data.
> clusterMembership <- data.frame(FipsCntry=names(wbPam$clustering),
+ Cluster=wbPam$clustering,
+ stringsAsFactors=FALSE)
> head(clusterMembership)
FipsCntry Cluster
AE AE 1
AF AF 2
AG AG 2
AL AL 2
AM AM 2
AO AO 3
> world.df <- join(world.df, clusterMembership, by="FipsCntry")
> world.df$Cluster <- as.character(world.df$Cluster)
> world.df$Cluster <- factor(world.df$Cluster, levels=1:12)
> 1
[1] 1
Building the plot itself requires a number of ggplot2 commands to format it correctly. Figure 22.7 shows the map, color coded by cluster membership; the gray countries either do not have World Bank information or were not properly matched up between the two datasets.
> ggplot() +
+ geom_polygon(data=world.df, aes(x=long, y=lat, group=group,
+ fill=Cluster, color=Cluster)) +
+ labs(x=NULL, y=NULL) + coord_equal() +
+ theme(panel.grid.major=element_blank(),
+ panel.grid.minor=element_blank(),
+ axis.text.x=element_blank(), axis.text.y=element_blank(),
+ axis.ticks=element_blank(), panel.background=element_blank())

Figure 22.7 Map of PAM clustering of World Bank data. Gray countries either do not have World Bank information or were not properly matched up between the two datasets.
Much like with K-means, the number of clusters in a K-medoids clustering must be specified. Something similar to Hartigan’s Rule can be built using the dissimilarity information returned by pam.
> wbPam$clusinfo
size max_diss av_diss diameter separation
[1,] 27 122871463849 46185193372 200539326122 1.967640e+10
[2,] 96 22901202940 7270137217 31951289020 3.373324e+09
[3,] 30 84897264072 21252371506 106408660458 3.373324e+09
[4,] 9 145646809734 59174398936 251071168505 4.799168e+10
[5,] 4 323538875043 146668424920 360634547126 2.591686e+11
[6,] 4 327624060484 152576296819 579061061914 3.362014e+11
[7,] 3 111926243631 40573057031 121719171093 2.591686e+11
[8,] 1 0 0 0 1.451345e+12
[9,] 1 0 0 0 8.278012e+11
[10,] 3 61090193130 23949621648 71848864944 1.156755e+11
[11,] 1 0 0 0 1.451345e+12
[12,] 1 0 0 0 7.672801e+12
22.3. Hierarchical Clustering
Hierarchical clustering builds clusters within clusters, and does not require a prespecified number of clusters like K-means and K-medoids do. A hierarchical clustering can be thought of as a tree and displayed as a dendrogram; at the top there is just one cluster consisting of all the observations, and at the bottom each observation is an entire cluster. In between are varying levels of clustering.
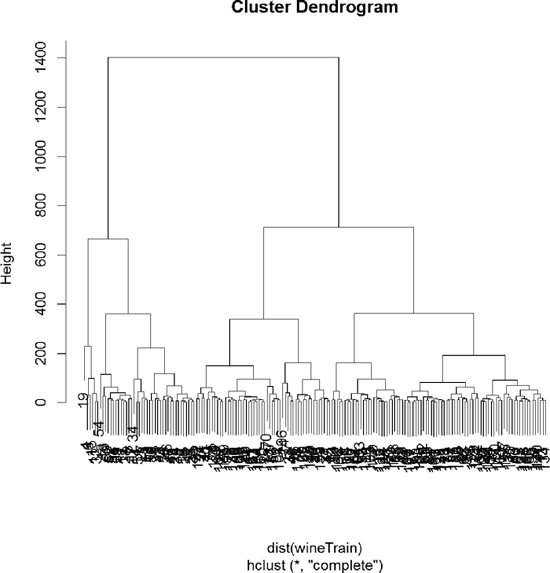
Using the wine data, we can build the clustering with hclust. The result is visualized as a dendrogram in Figure 22.8. While the text is hard to see, it labels the observations at the end nodes.
> wineH <- hclust(d = dist(wineTrain))
> plot(wineH)
Hierarchical clustering also works on categorical data like the country information data. However, its dissimilarity matrix must be calculated differently. The dendrogram is shown in Figure 22.9.
> # calculate distance
> keep.cols <- which(!names(wbInfo) %in% c("iso2c", "country", "year",
+ "capital", "iso3c"))
> wbDaisy <- daisy(x=wbInfo[, keep.cols])
>
> wbH <- hclust(wbDaisy)
> plot(wbH)
There are a number of different ways to compute the distance between clusters and they can have a significant impact on the results of a hierarchical clustering. Figure 22.10 shows the resulting tree from four different linkage methods: single, complete, average and centroid. Average linkage is generally considered the most appropriate.
> wineH1 <- hclust(dist(wineTrain), method = "single")
> wineH2 <- hclust(dist(wineTrain), method = "complete")
> wineH3 <- hclust(dist(wineTrain), method = "average")
> wineH4 <- hclust(dist(wineTrain), method = "centroid")
>
> plot(wineH1, labels = FALSE, main = "Single")
> plot(wineH2, labels = FALSE, main = "Complete")
> plot(wineH3, labels = FALSE, main = "Average")
> plot(wineH4, labels = FALSE, main = "Centroid")
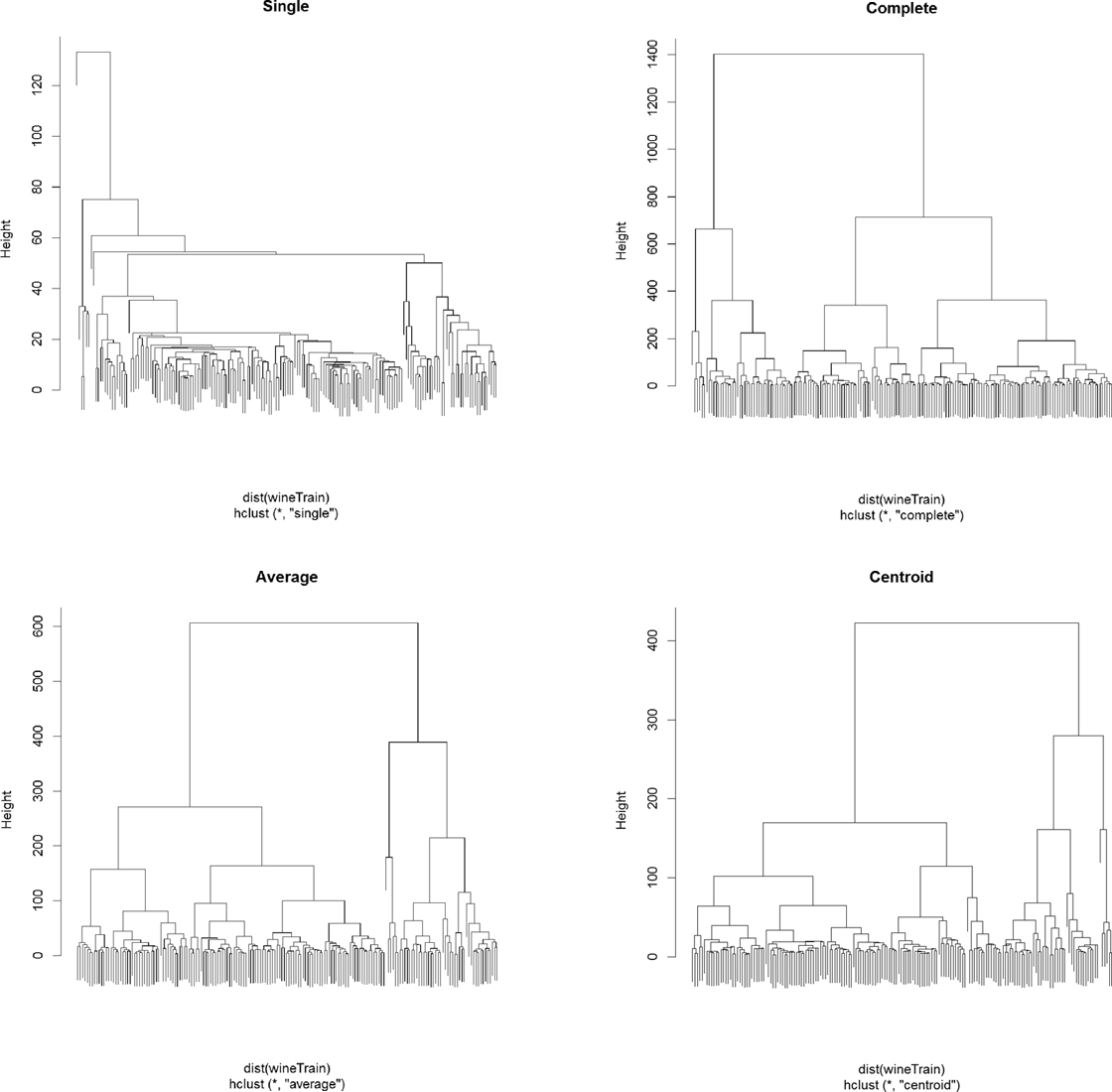
Figure 22.10 Wine hierarchical clusters with different linkage methods. Clockwise from top left: single, complete, centroid, average.
Cutting the resulting tree produced by hierarchical clustering splits the observations into defined groups. There are two ways to cut it, either specifying the number of clusters, which determines where the cuts take place, or specifying where to make the cut, which determines the number of clusters. Figure 22.11 demonstrates cutting the tree by specifying the number of clusters.
> # plot the tree
> plot(wineH)
> # split into 3 clusters
> rect.hclust(wineH, k = 3, border = "red")
> # split into 13 clusters
> rect.hclust(wineH, k = 13, border = "blue")
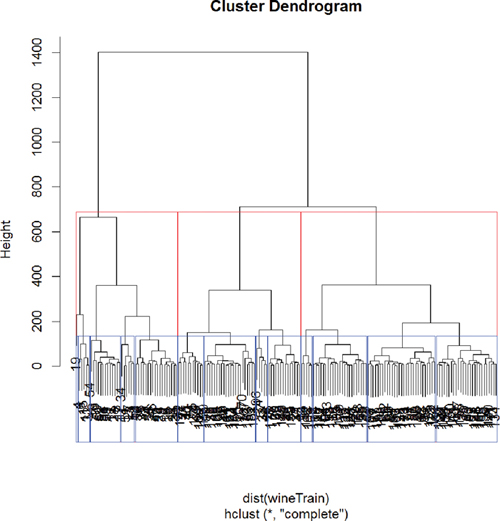
Figure 22.11 Hierarchical clustering of wine data split into three groups (red) and 13 groups (blue).
Figure 22.12 demonstrates cutting the tree by specifying the height of the cuts.
> # plot the tree
> plot(wineH)
> # split into 3 clusters
> rect.hclust(wineH, h = 200, border = "red")
> # split into 13 clusters
> rect.hclust(wineH, h = 800, border = "blue")
22.4. Conclusion
Clustering is a popular technique for segmenting data. The primary options for clustering in R are kmeans for K-means, pam in cluster for K-medoids and hclust for hierarchical clustering. Speed can sometimes be a problem with clustering, especially hierarchical clustering, so it is worth considering replacement packages like fastcluster, which has a drop-in replacement function, hclust, which operates just like the standard hclust, only faster.