9
Worked Out Examples
In this chapter, three simple examples on real image data will be presented. It is the intention that readers who are new to PRTools just get some flavour about building and applying a recognition system. Then three worked out examples of the topics discussed in this book will be given: classification, parameter estimation and state estimation. They will take the form of a step-by-step analysis of datasets obtained from real-world applications. The examples demonstrate the techniques treated in the previous chapters. Furthermore, they are meant to illustrate the standard approach to solve these types of problems. Obviously, the Matlab® and PRTools algorithms presented in the previous chapters will be used. The datasets used here are available through the website accompanying this book and www.37steps.com.
9.1 Example on Image Classification with PRTools
9.1.1 Example on Image Classification
In this section an example on real-world colour images will be presented. We will go through the program step by step. If possible, copy the lines in Matlab® and look at the response in the command window or in a graphical window elsewhere on the screen. This example deals with a set of 256 colour images, the Delft Image Database (delft_idb) stored in a datafile (see Figure 9.1). They are organized in nine classes named books, chess, coffee, computers, mug, phone, plant, rubbish and sugar. First it should be checked to see whether the data are available:
prdatafiles
Figure 9.1 The Delft Image Database, 10 pictures of 40 subjects each. Source: The Delft Image Database.

Figure 9.2 The ATT face database (formerly the ORL database), 10 pictures of 40 subjects each. Source: The ATT face Database.

Figure 9.3 The eigenfaces corresponding to the first 25 eigenvectors.

Figure 9.4 Projections on the first two eigenvectors.

Figure 9.5 The classification error by the 1NN rule as a function of the number of eigenvectors.
This command checks whether the so-called prdatafiles are available on your system. This is a collection of datafile examples and the Matlab® commands to load the data. If needed the commands are automatically downloaded from the PRTools website. By the following statement the data itself is downloaded if needed and all details of the datafile, such as filenames and class labels are stored into a variable.
A = delft_idband PRTools responds with a number of details about the datafile:
Delft Image Database, raw datafile with 256 objects in 9 crisp classes:
[19 44 33 35 41 30 18 9 27]The images can be shown by
show(A)The display may take some time, especially if the datafile is stored elsewhere in the network, as all images are stored in separate files. We split the set of images at random in 80% for training (i.e. building the classification system) and 20% for testing (i.e. evaluating its performance).
[A_train, A_test] = gendat (A, 0.8)In this example the images will be characterized by their histograms. For real-world applications much more preprocessing, like denoising and normalization on image size, intensity and contrast, may be needed. Moreover, features other than histograms may be desired. For many of them PRTools commands are available.
W_preproc = histm ([], [1:10:256])By this command histograms with a bin size of 10 are defined. As the images have three colour bands (red, green and blue), in total 3*26 = 78 feature values will be computed. Note that the command is just a definition of the operation. It will now be applied to the data:
B_train = A_train*W_preproc*datasetmThe execution of this statement takes time as all 256 images have to be processed. If switched on, a wait-bar is displayed reporting the progress. In PRTools the ‘*’ operator means: ‘use the variable on the left of the “*” operator as input for the procedure defined on the right-hand side of it.’ The routine datasetm (a PRTools mapping) converts the pre-processed datafile into a dataset, which is the PRTools construction of a collections of objects (here images) represented by vectors of the same length (here the histograms with size 78). A 78-dimensional space is too large for most classifiers to distinguish classes with at most some tens of objects. We therefore reduce the space by PCA to 8 dimensions:
W_featred = pca (B_train, 8)W_featred is not the set of objects in the reduced space, but it is the operator, trained by the PCA algorithm on the training set, which can map objects from the 78-dimensional space to the 8-dimensional space. This operator is needed explicitly as it has to be applied on the training objects as well as on all future objects to be classified.
W_classf = fisherc (B_train*W_featred)Herewith the PCA mapping stored in W_featred is applied on the training set and in the reduced space the Fisher classifier is computed. This is possible as all class information of the objects is still stored, as well as in B_train, as in the mapped (transformed) dataset B_train*W_featred. The total classification system is now the sequence of pre-processing, dataset conversion, feature reduction and classification. All these operations are defined in variables and the sequence can be defined by:
W_class_sys = W_preproc*datasetm*W_featred*W_classfA test set can be classified by this system by
D = A_test*W_class_sysAll results are stored in the 256 ×9 classification matrix D. This is also a dataset. It stores class confidences or distances for all objects (256) to all classes (9). A routine labelled may be used to find for every object the most confident or nearest class by D*labeld. As D also contains the original, true labels may be retrieved by getlabels(D). These may be displayed together with the estimated labels:
disp([getlabels(D) D*labeld])Finally, the fraction of erroneously classified objects can be found by
D*testdDepending on the actual split in training and test sets the result is about 50% error. This is not very good, but it should be realized that it is a nine-class problem, and finding the correct class out of nine in 50% of the times is still better than random. The individual classification results can be analysed by:
delfigs
for i=1:47
figure
imagesc(imread(A_test,i))
axis off
truelab = getlabels(D(i,:));
estilab = D(i,:)*labeld;
title([truelab ' - -> ' estilab])
if ∼strcmp(truelab,estilab)
set(gcf,'Colour',[0.9 0.4 0.4]);
end
end
showfigsIt can be concluded that many errors (red frames) are caused by confusing backgrounds. The backgrounds of the objects are unrelated to the object classes. Taking histograms of the entire images is thereby not very informative.
Finally, the entire example is listed for readers who want to run it in a single flow or store it for future inspection.
delfigs
echo on
% load the delft_idb image collection
A = delft_idb
% split it in a training set (80%) and a test set (20%)
[A_train,A_test] = gendat(A,0.8)
% define the preprocessing for the training set
W_preproc = histm([],[1:10:256])
% and convert it to a dataset
B_train = A_train*W_preproc*datasetm
% define a PCA mapping to 5 features
W_featred = pca(B_train,8)
% apply it to the training set and compute a classifier
W_classf = fisherc(B_train*W_featred)
% define the classification system
W_class_sys = W_preproc*datasetm*W_featred*W_classf
% classify the unlabeled testset
D = A_test*W_class_sys
% show the true and estimated labels
disp([getlabels(D) D*labeld])
% show its performance
fprintf('Classification error: %6.3f
',D*testd)
input('Hit the return to continue …');
% show all individual test results
delfigs
for i=1:47
figure
imagesc(imread(A_test,i))
axis off
truelab = getlabels(D(i,:));
estilab = D(i,:)*labeld;
title ([truelab ' –> ' estilab])
if ∼strcmp(truelab,estilab)
set (gcf,'Colour',[0.9 0.4 0.4]);
end
end
showfigs
echo off9.1.2 Example on Face Classification
This example shows how to do face recognition using the nearest neighbour rule based on eigenfaces. We will make use of the ATT face database (formerly the ORL database). It is heavily used in publications as an example of an easy set of images as the pictures are taken under very similar conditions. The database is stored in prdatafiles. As in the previous example, it should be verified first whether this repository is available or should be downloaded.
prdatafilesNow the data itself can be read from disk. If not available it is downloaded from the PRTools website first. For historical reasons the command is still called orl.
a = orlWe now have a datafile. It points to a set of 400 images (faces) stored on disk. It is constructed in such a way that the labels of the images for the 40 classes are stored in the datafile construct. Here a class is a set of 10 faces belonging to the same person.
% Convert to dataset and show
a = dataset (a);
a = setprior(a,0);
show (a,20);
pauseWith these statements the datafile is converted to a dataset, using every pixel as a feature. As the images have a size of 112 × 92 the feature vectors have a length of 10 304.
% Compute eigenfaces
w = pca(a);
% show first 24 eigenfaces
figure;
show (w(:,1:24),6)The PCA (principal components) mapping is computed and the first 24 components, called eigenfaces, are shown as images.
%project eigenfaces
b = a*w;
figure;
scatterd(b);
title('Scatterplot of 10 face images of 40 subjects')
xlabel('Projection on eigenface 1')
ylabel('Projection on eigenface 2')
fontsize(16)This is a scatterplot of all 400 images as points in a two-dimensional space constructed by the first two eigenfaces.
% Compute error curve as function of number of eigenfaces
e = zeros (1, 16);
featsizes = [1 2 3 5 7 10 15 20 30 50 70 100 150 200 300 399];
for n = 1:length(featsizes)
e(n) = testk(b(:,1:featsizes(n)));
end
figure
semilogx(featsizes,e)
axis ([1 400 0 1])The classification error using the nearest neighbour rule is shown as a function of the number of eigenfaces used. It shows that about 40 components are sufficient. This corresponds to the number of classes to be distinguished. This is caused by the fact that interclass differences (between the classes) are much larger than intraclass differences (between the images in the same class).
% Annotate error curve
title('1NN classification error of the ATT face database')
xlabel('Number of Eigenfaces')
ylabel('1NN error')
fontsize(16)
linewidth(2)Proper annotation of figures is needed for documentation and presentations.
showfigsThe showfigs command is a command that comes with PRTools and that makes an attempt to show all images on the screen. Its counterpart, delfigs, deletes all images. Figure 9.5 illustrate the face database and recognition results.
9.1.3 Example on Silhouette Classification
We will start with loading a simple, well-known dataset of silhouettes, the Kimia dataset (see Figure 9.6). It consists of a set of binary (0/1) images, representing the outlines of simple objects (e.g. toys). In the original dataset the images have different sizes. The version that is used in this example has been normalized to images of 64 × 64 pixels.

Figure 9.6 The total Kimia dataset.
The dataset is stored in the repository prdatasets. First it is checked whether it exists. If not, it is automatically down-loaded.
prdatasetsNow a command to load the data itself should be available and the example can be started.
delfigs;
a = kimia;
show (1-a,18)The first command, delfigs, just takes care that all existing figures (if any) are deleted.
As the dataset is too large to serve as a simple illustration we will select just the classes 1, 3, 5, 7 and 13 (see Figure 9.7).
b = seldat(a,[1 3 5 7,13]);
figure; show(1-b);
Figure 9.7 The selected classes.
Now two features (properties) will be computed for these objects: their sizes (number of pixels in an image with value 1) and the perimeter. The latter is found by two simple convolutions to compute the horizontal and vertical gradients, followed by a logical ‘or’ of the absolute values. The contour pixels will have a value 1 and all others are 0 (see Figure 9.8). The perimeter is found by a summation of all pixel values over an image.
area = im_stat(b,'sum');
bx = abs(filtim(b,'conv2',{[-1 1],'same'}));
by = abs(filtim(b,'conv2',{[-1 1]','same'}));
bor = or(bx,by);
figure; show(1-bor);
Figure 9.8 The computed contours.
The perimeter can be estimated by a summation of all pixel values over an image.
perimeter = im_stat(bor,'sum');The two features, area and perimeter, are combined into a dataset that contains just these two values for every object. Some additional properties will be stored in the dataset as well: all classes are given the same prior probability (0.2, as there are five classes) and the names of the features.
c = dataset([area perimeter]);
c = setprior(c,0);
c = setfeatlab(c,char('area','perimeter'));This two-dimensional dataset can be visualized:
figure; scatterd(c,'legend');The name of the dataset is still known and shown in Figure 9.9. It was stored in the dataset a and transferred by PRTools to b, area and perimeter. The same holds for the class names, shown in the legend. Finally, we will compute a classifier and show its decision boundary in the scatterplot. Different regions assigned to the various classes are given different colours.
w = ldc(c);
plotc(w,'col');
showfigs
Figure 9.9 Scatterplot.
Note that there are some small regions that did not obtain a colour. This is a numeric problem. Later it will be explained how to circumvent it. Can you identify the objects with almost no area and a large perimeter? Can you also identify the objects with a relatively small perimeter and a large area? The scatterplot shows a representation based on features of the original objects, the silhouettes. It enables the training and usage of classifiers, which is an example of a generalization. The showfigs command distributes all figures over the screen in order to have a better display. Finally, two classification errors are computed and displayed:
train_error = c*w*testc;
test_error = crossval(c,ldc,2);
disp([train_error test_error])The error in the training set, train_error, corresponds to the fraction of objects that are in the wrong class region in the scatter plot. The test error is estimated by twofold cross validation, a concept to be discussed later.
9.2 Boston Housing Classification Problem
9.2.1 Dataset Description
The Boston Housing dataset is often used to benchmark data analysis tools. It was first described in Harrison and Rubinfield (1978). This paper investigates which features are linked to the air pollution in several areas in Boston. The dataset can be downloaded from the UCI Machine Learning repository at http://www.ics.uci.edu/∼mlearn/MLRepository.html.
Each feature vector from the set contains 13 elements. Each feature element provides specific information on an aspect of an area of a suburb. Table 9.1 gives a short description of each feature element.
Table 9.1 The features of the Boston Housing dataset
| Feature name | Description | Feature range and type |
| 1 CRIME | Crime rate per capita | 0–89, real valued |
| 2 LARGE | Proportion of area dedicated to lots larger than 25 000 square feet | 0–100, real valued, but many have value 0 |
| 3 INDUSTRY | Proportion of area dedicated to industry | 0.46–27.7, real valued |
| 4 RIVER | 1 = borders the Charles River, 0 = does not border the Charles River | 0–1, nominal values |
| 5 NOX | Nitric oxides concentration (in parts per 10 million) | 0.38–0.87, real valued |
| 6 ROOMS | Average number of rooms per house | 3.5–8.8, real valued |
| 7 AGE | Proportion of houses built before 1940 | 2.9–100, real valued |
| 8 WORK | Average distance to employment centres in Boston | 1.1–12.1, real valued |
| 9 HIGHWAY | Highway accessibility index | 1–24, discrete values |
| 10 TAX | Property tax rate (per $10 000) | 187–711, real valued |
| 11 EDUCATION | Pupil–teacher ratio | 12.6–22.0, real valued |
| 12 AA | 1000(A – 0.63)2 where A is the proportion of African-Americans | 0.32–396.9, real valued |
| 13 STATUS | Percentage of the population which has lower status | 1.7–38.0, real valued |
The goal we set for this section is to predict whether the median price of a house in each area is larger than or smaller than $20 000. That is, we formulate a two-class classification problem. In total, the dataset consists of 506 areas, where for 215 areas the price is lower than $20 000 and for 291 areas it is higher. This means that when a new object has to be classified using only the class prior probabilities, assuming the dataset is a fair representation of the true classification problem, it can be expected that in (215/506) × 100% = 42.5% of the cases we will misclassify the area.
After the very first inspection of the data, by just looking what values the different features might take, it appears that the individual features differ significantly in range. For instance, the values for the feature TAX varies between 187 and 711 (a range of more than 500), while the feature values of NOX are between 0.38 and 0.87 (a range of less than 0.5). This suggests that some scaling might be necessary. A second important observation is that some of the features can only have discrete values, like RIVER and HIGHWAY. How to combine real-valued features with discrete features is already a problem in itself. In this analysis we will ignore this problem and we will assume that all features are real valued. (Obviously, we will lose some performance using this assumption.)
9.2.2 Simple Classification Methods
Given the varying nature of the different features and the fact that further expert knowledge is not given, it will be difficult to construct a good model for these data. The scatter diagram of Figure 9.10 shows that an assumption of Gaussian distributed data is clearly wrong (if only by the presence of the discrete features), but when just classification performance is considered, the decision boundary might still be good enough. Perhaps more flexible methods such as the Parzen density or the κ-nearest neighbour method will perform better after a suitable feature selection and feature scaling.

Figure 9.10 Scatterplots of the Boston Housing dataset. The left subplot shows features STATUS and INDUSTRY, where the discrete nature of INDUSTRY can be spotted. In the right subplot, the dataset is first scaled to unit variance, after which it is projected on to its first two principal components.
Let us start with some baseline methods and train a linear and quadratic Bayes classifier, ldc and qdc.
Listing 9.1
% Load the housing dataset, and set the baseline performance
prload housing.mat;
z % Show what dataset we have
w = ldc; % Define an untrained linear classifier
err_ldc_baseline = % Perform 5-fold cross-validation
crossval(z,w,5)
err_qdc_baseline = % idem for the quadratic classifier
crossval(z,qdc,5)The fivefold cross-validation errors of ldc and qdc are 13.0% and 17.4%, respectively. Note that by using the function crossval, we avoided having to use the training set for testing. If we had done that, the errors would be 11.9% and 16.2%, but this estimate would be biased and too optimistic. The results also depend on how the data are randomly split into batches. When this experiment is repeated, you will probably find slightly different numbers. Therefore, it is advisable to repeat the entire experiment a number of times (say, 5 or 10) to get an idea of the variation in the cross-validation results. However, for many experiments (such as the feature selection and neural network training below), this may lead to unacceptable training times; therefore, the code given does not contain any repetitions. For all the results given, the standard deviation is about 0.005, indicating that the difference between ldc and qdc is indeed significant. Notice that we use the word ‘significant’ here in a slightly loose sense. From a statistical perspective it would mean that for the comparison of the two methods, we should state a null hypothesis that both methods perform the same and define a statistical test (for instance a t-test) to decide if this hypothesis holds or not. In this discussion we use the simple approach in which we just look at the standard deviation of the classifier performances and call the performance difference significant when the averages differ by more than two times their standard deviations.
Even with these simple models on the raw, not pre-processed data, a relative good test error of 13.0% can be achieved (with respect to the simplest approach by looking at the class probabilities). Note that qdc, which is a more powerful classifier, gives the worst performance. This is due to the relatively low sample size: two covariance matrices, with ![]() free parameters each, have to be estimated on 80% of the data available for the classes (i.e. 172 and 233 samples, respectively). Clearly, this leads to poor estimates.
free parameters each, have to be estimated on 80% of the data available for the classes (i.e. 172 and 233 samples, respectively). Clearly, this leads to poor estimates.
9.2.3 Feature Extraction
It might be expected that more flexible methods, like the κ-nearest neighbour classifier (knnc, with κ optimized using the leave-one-out method) or the Parzen density estimator (parzenc), give better results. Surprisingly, a quick check shows that then the errors become 19.6% and 21.9% (with a standard deviation of about 1.1% and 0.6%, respectively), clearly indicating that some overtraining occurs and/or that some feature selection and feature scaling might be required. The next step, therefore, is to rescale the data to have zero mean and unit variance in all feature directions. This can be performed using the PRTools function scalem ([], ‘variance’).
Listing 9.2
prload housing.mat;
% Define an untrained linear classifier w/scaled input data
w_sc = scalem ([], ‘variance’);
w = w_sc*ldc;
% Perform 5-fold cross-validation
err_ldc_sc = crossval (z, w, 5)
% Do the same for some other classifiers
err_qdc_sc = crossval (z, w_sc*qdc, 5)
err_knnc_sc = crossval (z, w_sc*knnc, 5)
err_parzenc_sc = crossval (z, w_sc*parzenc, 5)First note that, when we introduce a pre-processing step, this step should be defined inside the mapping w. The obvious approach, to map the whole dataset z_sc = z*scalem (a, ‘variance’) and then to apply the cross-validation to estimate the classifier performance, is incorrect. In that case, some of the testing data are already used in the scaling of the data, resulting in an overtrained classifier, and thus in an unfair estimate of the error. To avoid this, the mapping should be extended from ldc to w_sc*ldc. The routine crossval then takes care of fitting both the scaling and the classifier.
By scaling the features, the performance of the first two classifiers, ldc and qdc, should not change. The normal density-based classifiers are insensitive to the scaling of the individual features, because they already use their variance estimation. The performance of knnc and parzenc, on the other hand, improve significantly, to 14.1% and 13.1%, respectively (with a standard deviation of about 0.4%). Although parzenc approaches the performance of the linear classifier, it is still slightly worse. Perhaps feature extraction or feature selection will improve the results.
As discussed in Chapter 7, principal component analysis (PCA) is one of the most often used feature extraction methods. It focuses on the high-variance directions in the data and removes low-variance directions. In this dataset we have seen that the feature values have very different scales. Applying PCA directly to these data will put high emphasis on the feature TAX and will probably ignore the feature NOX. Indeed, when PCA pre-processing is applied such that 90% of the variance is retained, the performance of all the methods significantly decreases. To avoid this clearly undesired effect, we will first rescale the data to have unit variance and apply PCA on the resulting data. The basic training procedure now becomes as shown below.
Listing 9.3
prload housing.mat;
% Define a preprocessing
w_pca = scalem([],‘variance’)*pca([],0.9);
% Define the classifier
w = w_sc*ldc;
% Perform 5-fold cross-validation
err_ldc_pca = crossval(z,w,5)It appears that, compared with normal scaling, the application of pca ([], 0.9) does not significantly improve the performances. For some methods, the performance increases slightly (16.6% (±0.6%) error for qdc, 13.6% (±0.9%) for knnc), but for other methods it decreases. This indicates that the high-variance features are not much more informative than the low-variance directions.
9.2.4 Feature Selection
The use of a simple supervised feature extraction method, such as Bhattacharrya mapping (implemented by replacing the call to pca by bhatm([])), also decreases the performance. We will therefore have to use better feature selection methods to reduce the influence of noisy features and to gain some performance.
We will first try branch-and-bound feature selection to find five features, with the simple inter–intraclass distance measure as a criterion, finding the optimal number of features. Admittedly, the number of features selected, five, is arbitrary, but the branch-and-bound method does not allow for finding the optimal subset size.
Listing 9.4
% Load the housing dataset
prload housing.mat;
% Construct scaling and feature selection mapping
w_fsf = featselo ([], ‘in-in’, 5)*scalem ([], ‘variance’);
% calculate cross-validation error for classifiers
% trained on the optimal 5-feature set
err_ldc_fsf = crossval (z, w_fsf*ldc, 5)
err_qdc_fsf = crossval (z, w_fsf*qdc, 5)
err_knnc_fsf = crossval (z, w_fsf*knnc, 5)
err_parzenc_fsf = crossval (z, w_fsf*parzenc, 5)The feature selection routine often selects features STATUS, AGE and WORK, plus some others. The results are not very good: the performance decreases for all classifiers. Perhaps we can do better if we take the performance of the actual classifier to be used as a criterion, rather than the general inter–intraclass distance. To this end, we can just pass the classifier to the feature selection algorithm. Furthermore, we can also let the algorithm find the optimal number of features by itself. This means that branch-and-bound feature selection can now no longer be used, as the criterion is not monotonically increasing. Therefore, we will use the forward feature selection, featself.
Listing 9.5
% Load the housing dataset
prload housing.mat;
% Optimize feature set for ldc
w_fsf = featself ([], ldc, 0)*scalem ([], ‘variance’);
err_ldc_fsf = crossval (z, w_fsf*ldc, 5)
% Optimize feature set for qdc
w_fsf = featself ([], qdc, 0)*scalem ([], ‘variance’);
err_qdc_fsf = crossval (z, w_fsf*qdc, 5)
% Optimize feature set for knnc
w_fsf = featself ([], knnc, 0)*scalem ([], ‘variance’);
err_knnc_fsf = crossval (z, w_fsf*knnc, 5)
% Optimize feature set for parzenc
w_fsf = featself ([], parzenc, 0)*scalem ([], ‘variance’);
err_parzenc_fsf = crossval (z, w_fsf*parzenc, 5)This type of feature selection turns out to be useful only for ldc and qdc, whose performances improve to 12.8% (±0.6%) and 14.9% (±0.5%), respectively. knnc and parzenc, on the other hand, give 15.9% (±1.0%) and 13.9% (±1.7%), respectively. These results do not differ significantly from the previous ones. The featself routine often selects the same rather large set of features (from most to least significant): STATUS, AGE, WORK, INDUSTRY, AA, CRIME, LARGE, HIGHWAY, TAX. However, these features are highly correlated and the set used can be reduced to the first three with just a small increase in error of about 0.005. Nevertheless, feature selection in general does not seem to help much for this dataset.
9.2.5 Complex Classifiers
The fact that ldc already performs so well on the original data indicates that the data are almost linearly separable. A visual inspection of the scatterplots in Figure 9.1 seems to strengthen this hypothesis. It becomes even more apparent after the training of a linear support vector classifier (svc([], ‘p’, 1)) and a Fisher classifier (fisherc), both with a cross-validation error of 13.0%, the same as for ldc.
Given that ldc and parzenc thus far performed best, we might try to train a number of classifiers based on these concepts, for which we are able to tune classifier complexity. Two obvious choices for this are neural networks and support vector classifiers (SVCs). Starting with the latter, we can train SVCs with polynomial kernels of degree close to 1 and with radial basis kernels of radius close to 1. By varying the degree or radius, we can vary the resulting classifier's nonlinearity
Listing 9.6
prload housing.mat; % Load the housing dataset
w_pre = scalem ([], `variance'); % Scaling mapping
degree = 1:3; % Set range of parameters
radius = 1:0.25:3;
for i = 1:length(degree)
err_svc_p (i) = ... % Train polynomial SVC
crossval (z,w_pre*svc([],`p',degree(i)),5);
end;
for i = 1:length(radius)
err_svc_r (i) = ... % Train radial basis SVC
crossval (z,w_pre*svc([], `r',radius(i)),5);
end;
figure; clf; plot(degree,err_svc_p);
figure; clf; plot(radius,err_svc_r);The results of a single repetition are shown in Figure 9.11 the optimal polynomial kernel SVC is a quadratic one (a degree of 2), with an average error of 12.5%, and the optimal radial basis kernel SVC (a radius of around 2) is slightly better, with an average error of 11.9%. Again, note that we should really repeat the experiment a number of times to get an impression of the variance in the results. The standard deviation is between 0.2% and 1.0%. This means that the minimum in the right subfigure is indeed significant and that the radius parameter should indeed be around 2.0. On the other hand, in the left subplot the graph is basically flat and a linear SVC is therefore probably to be preferred.

Figure 9.11 Performance of a polynomial kernel SVC (left, as a function of the degree of the polynomial) and a radial basis function kernel SVC (right, as a function of the basis function width).
For the sake of completeness, we can also train feedforward neural networks with varying numbers of hidden layers and units. In PRTools, there are three routines for training feedforward neural networks. The bpxnc function trains a network using the backpropagation algorithm, which is slow but does not often overtrain it. The lmnc function uses a second-order optimization routine, Levenberg–Marquardt, which speeds up training significantly but often results in overtrained networks. Finally, the neurc routine attempts to counteract the overtraining problem of lmnc by creating an artificial tuning set of 1000 samples by perturbing the training samples (see gendatk) and stops training when the error on this tuning set increases. It applies lmnc three times and returns the neural network, giving the best result on the tuning set. Here, we apply both bpxnc and neurc
Listing 9.7
prload housing.mat; % Load the housing dataset
w_pre = scalem([], ‘variance’); % Scaling mapping
networks = {bpxnc, neurc}; % Set range of parameters
nlayers = 1:2;
nunits = [4 8 12 16 20 30 40];
for i = 1:length(networks)
for j = 1:length(nlayers)
for k = 1:length(nunits)
% Train a neural network with nlayers(j) hidden layers
% of nunits(k) units each, using algorithm network{i}
err_nn(i,j,k) = crossval(z, …
w_pre*networks{i}([],ones(1,nlayers(j))*nunits(k)),5);
end;
end;
figure; clear all; % Plot the errors
plot (nunits,err_nn(i,1,:), ‘-’); hold on;
plot (nunits,err_nn(i,2,:), ‘- -’);
legend (‘1 hidden layer’, ‘2 hidden layers’);
end;Training neural networks is a computationally intensive process and here they are trained for a large range of parameters, using cross-validation. The algorithm above takes more than a day to finish on a modern workstation, although per setting just a single neural network is trained.
The results, shown in Figure 9.12, seem to be quite noisy. After repeating the algorithm several times, it appears that the standard deviation is of the order of 1%. Ideally, we would expect the error as a function of the number of hidden layers and units per hidden layer to have a clear global optimum. For bpxnc, this is roughly the case, with a minimal cross-validation error of 10.5% for a network with one hidden layer of 30 units and 10.7% for a network with two hidden layers of 16 units. Normally, we would prefer to choose the network with the lowest complexity as the variance in the error estimate would be lowest. However, the two optimal networks here have roughly the same number of parameters. Therefore, there is no clear best choice between the two.

Figure 9.12 Performance of neural networks with one or two hidden layers as a function of the number of units per hidden layer, trained using bpxnc (left) and neurc (right).
The cross-validation errors of networks trained with neurc show more variation (Figure 9.12). The minimal cross-validation error is again 10.5% for a network with a single hidden layer of 30 units. Given that the graph for bpxnc is much smoother than that of neurc, we would prefer to use a bpxnc-trained network.
9.2.6 Conclusions
The best overall result on the housing dataset was obtained using a bpxnc-trained neural network (10.5% cross-validation error), slightly better than the best SVC (11.9%) or a simple linear classifier (13.0%). However, remember that neural network training is a more noisy process than training an SVC or linear classifier: the latter two will find the same solution when run twice on the same dataset, whereas a neural network may give different results due to the random initialization. Therefore, using an SVC in the end may be preferable.
Of course, the analysis above is not exhaustive. We could still have tried more exotic classifiers, performed feature selection using different criteria and search methods, searched through a wider range of parameters for the SVCs and neural networks, investigated the influence of possible outlier objects and so on. However, this will take a lot of computation, and for this application there seems to be no reason to believe we might obtain a significantly better classifier than those found above.
9.3 Time-of-Flight Estimation of an Acoustic Tone Burst
The determination of the time of flight (ToF) of a tone burst is a key issue in acoustic position and distance measurement systems. The length of the acoustic path between a transmitter and receiver is proportional to the ToF, that is the time evolved between the departure of the waveform from the transmitter and the arrival at the receiver (Figure 9.13). The position of an object is obtained, for instance, by measuring the distances from the object to a number of acoustic beacons (see also Figure 1.2).

Figure 9.13 Setup of a sensory system for acoustic distance measurements.
The quality of an acoustic distance measurement is directly related to the quality of the ToF determination. Electronic noise, acoustic noise, atmospheric turbulence and temperature variations are all factors that influence the quality of the ToF measurement. In indoor situations, objects in the environment (wall, floor, furniture, etc.) may cause echoes that disturb the nominal response. These unwanted echoes can cause hard-to-predict waveforms, thus making the measurement of the ToF a difficult task.
The transmitted waveform can take various forms, for instance, a frequency modulated (chirped) continuous waveform (CWFM), a frequency or phase shift-keyed signal or a tone burst. The latter is a pulse consisting of a number of periods of a sine wave. An advantage of a tone burst is that the bandwidth can be kept moderate by adapting the length of the burst. Therefore, this type of signal is suitable for use in combination with piezoelectric transducers, which are cheap and robust, but have a narrow bandwidth.
In this section, we design an estimator for the determination of the ToFs of tone bursts that are acquired in indoor situations using a setup as shown in Figure 9.13. The purpose is to determine the time delay between sending and receiving a tone burst. A learning and evaluation dataset is available that contains 150 records of waveforms acquired in different rooms, different locations in the rooms, different distances and different heights above the floor. Figure 9.13 shows an example of one of the waveforms. Each record is accompanied by a reference ToF indicating the true value of the ToF. The standard deviation of the reference ToF is estimated at 10 μs. The applied sampling period is Δ = 2 μs.
The literature roughly mentions three concepts to determine the ToF, that is thresholding, data fitting (regression) and ML (maximum likelihood) estimation (Heijden van der et al., 2003). Many variants of these concepts have been proposed. This section only considers the main representatives of each concept:
- Comparing the envelope of the wave against a threshold that is proportional to the magnitude of the waveform.
- Fitting a one-sided parabola to the foot of the envelope of the waveform.
- Conventional matched filtering.
- Extended matched filtering based on a covariance model of the signal.
The first one is a heuristic method that does not optimize any criterion function. The second one is a regression method, and as such a representative of data fitting. The last two methods are ML estimators. The difference between these is that the latter uses an explicit model of multiple echoes. In the former case, such a model is missing.
The section first describes the methods. Next, the optimization of the design parameters using the dataset is explained and the evaluation is reported. The dataset and the Matlab® listings of the various methods can be found on the accompanying website.
9.3.1 Models of the Observed Waveform
The moment of time at which a transmission begins is well defined since it is triggered under full control of the sensory system. The measurement of the moment of arrival is much more involved. Due to the narrow bandwidth of the transducers the received waveform starts slowly. A low SNR makes the moment of arrival indeterminate. Therefore, the design of a ToF estimator requires the availability of a model describing the arriving waveform. This waveform w(t) consists of three parts: the nominal response ah(t − τ) to the transmitted wave, the interfering echoes ar(t − τ) and the noise v(t):
We assume that the waveform is transmitted at time t = 0, so that τ is the ToF. Equation (9.1) simply states that the observed waveform equals the nominal response h(t), but now time-shifted by τ and attenuated by a. Such an assumption is correct for a medium like air because, within the bandwidth of interest, the propagation of a waveform through air does not show a significant dispersion. The attenuation coefficient a not only depends on many factors but also on the distance, and thus also on τ. However, for the moment we will ignore this fact. The possible echoes are represented by ar(t − τ). They share the same time shift τ because no echo can occur before the arrival of the nominal response. The additional time delays of the echoes are implicitly modelled within r(t). The echoes and the nominal response also share a common attenuation factor. The noise v(t) is considered white.
The actual shape of the nominal response h(t) depends on the choice of the tone burst and on the dynamic properties of the transducers. Sometimes a parametric empirical model is used, for instance:
where f is the frequency of the tone burst, cos(2πft + ϕ) is the carrier and tm exp (−t/T) is the envelope. The factor tm describes the rise of the waveform (m is empirically determined, usually between 1 and 3). The factor exp(−t/T) describes the decay. Another possibility is to model h(t) non-parametrically. In that case, a sampled version of h(t), obtained in an anechoic room where echoes and noise are negligible, is recorded. The dataset contains such a record (see Figure 9.14).

Figure 9.14 A record of the nominal response h(t).
Often the existence of echoes is simply ignored, r(t) = 0. Sometimes a single echo is modelled, r(t) = d1h(t − τ1), where τ1 is the delay of the echo with respect to t = τ. The most extensive model is when multiple echoes are considered, ![]() . The sequences dk and τk are hardly predictable and are therefore regarded as random. In that case, r(t) also becomes random and the echoes are seen as disturbing noise with non-stationary properties.
. The sequences dk and τk are hardly predictable and are therefore regarded as random. In that case, r(t) also becomes random and the echoes are seen as disturbing noise with non-stationary properties.
The observed waveform z = [z0⋅⋅⋅zN − 1]T is a sampled version of w(t):
where Δ is the sampling period and N is the number of samples. Hence, NΔ is the registration period. With that, the noise v(t) manifests itself as a random vector v, with zero mean and covariance matrix Cv = σ2vI.
9.3.2 Heuristic Methods for Determining the ToF
Some applications require cheap solutions that are suitable for direct implementation using dedicated hardware, such as instrumental electronics. For that reason, a popular method to determine the ToF is simply thresholding the observed waveform at a level T. The estimated ToF ![]() is the moment at which the waveform crosses a threshold level T.
is the moment at which the waveform crosses a threshold level T.
Due to the slow rising of the nominal response, the moment ![]() of level crossing appears just after the true τ, thus causing a bias. Such a bias can be compensated afterwards. The threshold level T should be chosen above the noise level. The threshold operation is simple to realize, but a disadvantage is that the bias depends on the magnitude of the waveform. Therefore, an improvement is to define the threshold level relative to the maximum of the waveform, that is T = α max (w(t)), where α is a constant set to, for instance, 30%.
of level crossing appears just after the true τ, thus causing a bias. Such a bias can be compensated afterwards. The threshold level T should be chosen above the noise level. The threshold operation is simple to realize, but a disadvantage is that the bias depends on the magnitude of the waveform. Therefore, an improvement is to define the threshold level relative to the maximum of the waveform, that is T = α max (w(t)), where α is a constant set to, for instance, 30%.
The observed waveform can be written as g(t) cos (2πft + ϕ) + n(t), where g(t) is the envelope. The carrier cos (2πft + ϕ) of the waveform causes a resolution error equal to 1/f. Therefore, rather than applying the threshold operation directly, it is better to apply it to the envelope. A simple, but inaccurate method to get the envelope is to rectify the waveform and to apply a low-pass filter to the result. The optimal method, however, is much more involved and uses quadrature filtering. A simpler approximation is as follows. First, the waveform is band-filtered to reduce the noise. Next, the filtered signal is phase-shifted over 90° to obtain the quadrature component q(t) = g(t) sin (2πft + ϕ) + nq(t). Finally, the envelope is estimated using ![]() . Figure 9.15 provides an example.
. Figure 9.15 provides an example.

Figure 9.15 ToF measurements based on thresholding operations.
The design parameters are the relative threshold α, the bias compensation b and the cut-off frequencies of the band-filter.
9.3.3 Curve Fitting
In the curve-fitting approach, a functional form is used to model the envelope. The model is fully known except for some parameters, one of which is the ToF. As such, the method is based on the regression techniques introduced in Section 4.3.3. On adoption of an error criterion between the observed waveform and the model, the problem boils down to finding the parameters that minimize the criterion. We will use the SSD criterion discussed in Section 4.3.1. The particular function that will be fitted is the one-sided parabola defined by

The final estimate of the ToF is ![]() .
.
The function must be fitted to the foot of the envelope. Therefore, an important task is to determine the interval tb < t < te that makes up the foot. The choice of tb and te is critical. If the interval is short, then the noise sensitivity is large. If the interval is too large, modelling errors become too influential. The strategy is to find two anchor points t1 and t2 that are stable enough under the various conditions.
The first anchor point t1 is obtained by thresholding a low-pass filtered version gfiltered(t) of the envelope just above the noise level. If σv is the standard deviation of the noise in w(t), then gfiltered(t) is thresholded at a level ![]() , thus yielding t1. The standard deviation σv is estimated during a period preceding the arrival of the tone. A second suitable anchor point t2 is the first location just after t1 where gfiltered(t) is maximal, that is the location just after t1 where gfiltered(t)/dt = 0; te is defined midway between t1 and t2 by thresholding gfiltered(t) at a level
, thus yielding t1. The standard deviation σv is estimated during a period preceding the arrival of the tone. A second suitable anchor point t2 is the first location just after t1 where gfiltered(t) is maximal, that is the location just after t1 where gfiltered(t)/dt = 0; te is defined midway between t1 and t2 by thresholding gfiltered(t) at a level ![]() . Finally, tb is calculated as tb = t1 − β (te − t1). Figure 9.16 provides an example.
. Finally, tb is calculated as tb = t1 − β (te − t1). Figure 9.16 provides an example.

Figure 9.16 ToF estimation by fitting a one-sided parabola to the foot of the envelope.
Once the interval of the foot has been established, the curve can be fitted to the data (which in this case is the original envelope ![]() ). Since the curve is non-linear in x, an analytical solution, such as in the polynomial regression in Section 4.3.3 cannot be applied. Instead a numerical procedure, for instance using Matlab®'s
). Since the curve is non-linear in x, an analytical solution, such as in the polynomial regression in Section 4.3.3 cannot be applied. Instead a numerical procedure, for instance using Matlab®'s fminsearch, should be applied.
The design parameters are α, β and the cut-off frequency of the low-pass filter.
9.3.4 Matched Filtering
This conventional solution is achieved by neglecting the reflections. The measurements are modelled by a vector z with N elements:
The noise is represented by a random vector v with zero mean and covariance matrix Cv = σ2vI. Upon introduction of a vector h(τ) with elements h(nΔ − τ), the conditional probability density of z is

Maximization of this expression yields the maximum likelihood estimate for t. In order to do so, we only need to minimize the L2 norm of z − ah(τ):
The term zTz does not depend on τ and can be ignored. The second term is the signal energy of the direct response. A change of τ only causes a shift of it. However, if the registration period is long enough, the signal energy is not affected by such a shift. Thus, the second term can be ignored as well. The maximum likelihood estimate boils down to finding the τ that maximizes azTh(τ). A further simplification occurs if the extent of h(t) is limited to, say, KΔ with K ≪ N. In that case azTh(τ) is obtained by cross-correlating zn by ah(nΔ + τ):

The value of τ that maximizes y(τ) is the best estimate. The operator expressed by Equation (9.8) is called a matched filter or a correlator. Figure 9.17 shows a result of the matched filter. Note that apart from its sign, the amplitude a does not affect the outcome of the estimate. Hence, the fact that a is usually unknown does not matter much. Actually, if the nominal response is given in a non-parametric way, the matched filter does not have any design parameters.

Figure 9.17 Matched filtering.
9.3.5 ML Estimation Using Covariance Models for the Reflections
The matched filtered is not designed to cope with interfering reflections. Especially, if an echo partly overlaps the nominal response, the results are inaccurate. In order to encompass situations with complex interference patterns the matched filter must be extended. A possibility is to model the echoes explicitly. A tractable model arises if the echoes are described by a non-stationary autocovariance function.
9.3.5.1 Covariance Models
The echoes are given by ![]() . The points in time, τk, are a random sequence. Furthermore, we have τk > 0 since all echoes appear after the arrival of the direct response. The attenuation factors dk have a range of values. We will model them as independent Gaussian random variables with zero mean and variance σ2d. Negative values of dk are allowed because of the possible phase reversal of an echo. We limit the occurrence of an echo to an interval 0 < τk < T, and assume a uniform distribution. Then the autocovariance function of a single echo is
. The points in time, τk, are a random sequence. Furthermore, we have τk > 0 since all echoes appear after the arrival of the direct response. The attenuation factors dk have a range of values. We will model them as independent Gaussian random variables with zero mean and variance σ2d. Negative values of dk are allowed because of the possible phase reversal of an echo. We limit the occurrence of an echo to an interval 0 < τk < T, and assume a uniform distribution. Then the autocovariance function of a single echo is

If there are K echoes, the autocovariance function of r(t) is

because the factors dk and random points τk are independent.
For arbitrary τ, the reflections are shifted accordingly. The sampled version of the reflections is r(nΔ − τ), which can be brought in as vector r(τ). The elements Cr|τ(n, m) of the covariance matrix Cr|τ of r (τ), conditioned on τ, become
If the registration period is sufficiently large, the determinant |Cr|τ| does not depend on τ.
The observed waveform w(t) = a(h(t − τ) + r(t − τ)) + v(t) involves two unknown factors, the amplitude a and the ToF τ. The prior probability density of the latter is not important because the maximum likelihood estimator that we will apply does not require it. However, the first factor a is a nuisance parameter. We deal with it by regarding a as a random variable with its own density p(a). The influence of a is integrated in the likelihood function by means of Bayes’ theorem for conditional probabilities, that is p(z|τ) = ∫p(z|τ)p(a)da.
Preferably, the density p(a) reflects our state of knowledge that we have about a. Unfortunately, taking this path is not easy, for two reasons. It would be difficult to assess this state of knowledge quantitatively. Moreover, the result will not be very tractable. A more practical choice is to assume a zero mean Gaussian density for a. With that, conditioned on τ, the vector ah (τ) with elements ah(nΔ − τ) becomes zero mean and Gaussian with covariance matrix:
where σ2a is the variance of the amplitude a.
At first sight it seems counterintuitive to model a as a zero mean random variable since small and negative values of an are not very likely. The only reason for doing so is that it paves the way to a mathematically tractable model. In Section 9.2.4 we noticed already that the actual value of a does not influence the solution. We simply hope that in the extended matched filter a does not have any influence either. The advantage is that the dependence of τ on z is now captured in a concise model, that is a single covariance matrix:
This matrix completes the covariance model of the measurements. In the sequel, we assume a Gaussian conditional density for z. Strictly speaking, this holds true only if sufficient echoes are present since in that case the central limit theorem applies.
9.3.5.2 Maximum Likelihood Estimation of the Time-of-Flight
With the measurements modelled as a zero mean, Gaussian random vector with the covariance matrix given in Equation (9.13), the likelihood function for τ becomes

The maximization of this probability with respect to τ yields the maximum likelihood estimate (see Section 4.1.4). Unfortunately, this solution is not practical because it involves the inversion of the matrix Cz|τ. The size of Cz|τ is N × N where N is the number of samples of the registration (which can easily be of the order of 104).
9.3.5.3 Principal Component Analysis
Economical solutions are attainable by using PCA techniques (Section 8.1.1). If the registration period is sufficiently large, the determinant |Cz|τ| will not depend on τ. With that, we can safely ignore this factor. What remains is the maximization of the argument of the exponential:
The functional Λ (z|τ) is a scaled version of the log-likelihood function.
The first computational savings can be achieved if we apply a principal component analysis to Cz|τ. This matrix can be decomposed as follows:

where λn (τ) and un(τ) are eigenvalues and eigenvectors of Cz|τ. Using Equation (9.16), the expression for Λ(z|τ) can be moulded into the following equivalent form:

The computational savings are obtained by discarding all terms in Equation (9.17) that do not capture much information about the true value of τ. Suppose that λn and un are arranged according to their importance with respect to the estimation and that above some value of n, say J, the importance is negligible. With that, the number of terms in Equation (9.17) reduces from N to J. Experiments show that J is of the order of 10. A speed-up by a factor of 1000 is feasible.
9.3.5.4 Selection of Good Components
The problem addressed now is how to order the eigenvectors in Equation (9.17) such that the most useful components come first, and thus will be selected. The eigenvectors un(τ) are orthonormal and span the whole space. Therefore:

Substitution in Equation (9.17) yields

The term containing ‖z‖ does not depend on τ and can be omitted. The maximum likelihood estimate for τ appears to be equivalent to the one that maximizes

The weight γn(τ) is a good criterion to measure the importance of an eigenvector. Hence, a plot of the γn versus n is helpful to find a reasonable value of J such that J ≪ N. Hopefully, γn is large for the first few n and then drops down rapidly to zero.
9.3.5.5 The Computational Structure of the Estimator Based on a Covariance Model
A straightforward implementation of Equation (9.20) is not very practical. The expression must be evaluated for varying values of τ. Since the dimension of Cz|τ is large, this is not computationally feasible.
The problem will be tackled as follows. First, we define a moving window for the measurements zn. The window starts at n = i and ends at n = i + I − 1. Thus, it comprises I samples. We stack these samples into a vector x(i) with elements xn(i) = zn+i. Each value of i corresponds to a hypothesized value τ = iΔ. Thus, under this hypothesis, the vector x(i) contains the direct response with τ = 0, that is xn(i) = ah(nΔ) + ar(nΔ) + v(nΔ). Instead of applying operation (9.20) for varying τ, τ is fixed to zero and z is replaced by the moving window x(i):

If ![]() is the index that maximizes y(i), then the estimate for τ is found as
is the index that maximizes y(i), then the estimate for τ is found as ![]() .
.
The computational structure of the estimator is shown in Figure 9.18. It consists of a parallel bank of J filters/correlators, one for each eigenvector un(0). The results of that are squared, multiplied by weight factors γn(0) and then accumulated to yield the signal y(i). It can be proven that if we set σ2d = 0, i.e. a model without reflection, the estimator degenerates to the classical matched filter.

Figure 9.18 ML estimation based on covariance models.
The design parameters of the estimators are the ![]() , the duration of echo generation T, the echo strength
, the duration of echo generation T, the echo strength ![]() , the number of correlators J and the window size I.
, the number of correlators J and the window size I.
Example 9.1
In this example, the selected design parameters are SNR = 100, T = 0.8 ms, Sr = 0.2 and I = 1000. Using Equations (9.11) and (9.13), we calculate Cz|τ, and from that the eigenvectors and corresponding eigenvalues and weights are obtained. Figure 9.19 shows the result. As expected, the response of the first filter/correlator is similar to the direct response, and this part only implements the conventional matched filter. From the seventh filter on, the weights decrease, and from the fifteenth filter on the weights are near zero. Thus, the useful number of filters is between 7 and 15. Figure 9.20 shows the results of application of the filters to an observed waveform.

Figure 9.19 Eigenvalues, weights and filter responses of the covariance model-based estimator.

Figure 9.20 Results of the estimator based on covariance models.
9.3.6 Optimization and Evaluation
In order to find the estimator with the best performance the best parameters of the estimators must be determined. The next step then is to assess their performances.
9.3.6.1 Cross-validation
In order to prevent overfitting we apply a threefold cross-validation procedure to the data set consisting of 150 records of waveforms. The corresponding Matlab® code is given in Listing 9.8. Here, it is assumed that the estimator under test is realized in a Matlab® function called ToF_estimator().
The optimization of the operator using a training set occurs according to the procedure depicted in Figure 9.21. In Listing 9.8 this is implemented by calling the function opt_ToF_estimator(). The actual code for the optimization, given in Listing 9.9, uses the Matlab® function fminsearch().

Figure 9.21 Training the estimators.
We assume here that the operator has a bias that can be compensated for. The value of the compensation is just another parameter of the estimator. However, for its optimization the use of the function fminsearch() is not needed. This would unnecessarily increase the search space of the parameters. Instead, we simply use the (estimated) variance as the criterion to optimize, thereby ignoring a possible bias for a moment. As soon as the optimal set of parameters has been found, the corresponding bias is estimated afterwards by applying the optimized estimator once again to the learning set.
Note, however, that the uncertainty in the estimated bias causes a residual bias in the compensated ToF estimate. Thus, the compensation of the bias does not imply that the estimator is necessarily unbiased. Therefore, the evaluation of the estimator should not be restricted to assessment of the variance alone.
Listing 9.8 Matlab® listing for cross-validation.
prload tofdata.mat; % Load tof dataset containing 150 waveforms
Npart = 3; % Number of partitions
Nchunk = 50; % Number of waveforms in one partition
% Create 3 random partitions of the data set
p = randperm(Npart*Nchunk); % Find random permutation of 1:150
for n = 1:Npart
for i = 1:Nchunk
Zp{n,i} = Zraw{p((n−1)*Nchunk + i)};
Tp(n,i) = TOFindex(p((n−1)*Nchunk + i));
end
end
% Cross-validation
for n = 1:Npart
% Create a learn set and an evaluation set
Zlearn = Zp;
Tlearn = Tp;
for i = 1:Npart
if (i ==n)
Zlearn(i,:) = []; Tlearn(i,:) = [];
Zeval = Zp(i,:); Teval = Tp(i,:);
end
end
Zlearn = reshape(Zlearn,(Npart-1)*Nchunk,1);
Tlearn = reshape(Tlearn,1,(Npart-1)*Nchunk);
Zeval = reshape(Zeval ,1, Nchunk);
% Optimize a ToF estimator
[parm,learn_variance,learn_bias] = …
opt_ToF_estimator(Zlearn,Tlearn);
% Evaluate the estimator
for i = 1:Nchunk
index(i) = ToF_estimator(Zeval{i},parm);
end
variance(n) = var(Teval-index);
bias(n) = mean(Teval-index-learn_bias);
endListing 9.9 Matlab® listing for the optimization of a ToF estimator.
function [parm,variance,bias] = …
opt_ToF_estimator(Zlearn,Tlearn)
% Optimize the parameters of a ToF estimator
parm = [0.15, 543, 1032]; % Initial parameters
parm = fminsearch(@objective,parm,[],Zlearn,Tlearn);
[variance,bias] = objective(parm,Zlearn,Tlearn);
return;
% Objective function:
% estimates the variance (and bias) of the estimator
function [variance,bias] = objective(parm,Z,TOFindex)
for i = 1:length(Z)
index(i) = ToF_estimator(Z{i},parm);
end
variance = var(TOFindex - index);
bias = mean(TOFindex - index);
return9.3.6.2 Results
Table 9.2 shows the results obtained from the cross-validation. The first row of the table gives the variances directly obtained from the training data during optimization. They are obtained by averaging over the three variances of the three partitions. The second row tabulates the variances obtained from the evaluation data (also obtained by averaging over the three partitions). Inspection of these results reveals that the threshold method is overfitted. The reason for this is that some of the records have a very low signal-to-noise ratio. If – by chance – these records do not occur in the training set, then the threshold level will be set too low for these noisy waveforms.
Table 9.2 Results of threefold cross-validation of the four ToF estimators
| Envelope | Curve | Matched | CVM-based | |
| thresholding | fitting | filtering | estimator | |
| Variance (learn data) (μs2) | 356 | 378 | 14 339 | 572 |
| Variance (test data) (μs2) | 181 010 | 384 | 14 379 | 591 |
| corrected variance (μs2) | 180 910 | 284 | 14 279 | 491 |
| Bias (μs) | 35 | 2 | 10 | 2 |
| RMS (μs) | 427 ± 25 | 17 ± 1.2 | 119 ± 7 | 22 ± 1.4 |
The reference values of the ToFs in the dataset have an uncertainty of 10 ms. Therefore, the variance estimated from the evaluation sets has a bias of 100 μs2. The third row in the table shows the variances after correction for this effect.
Another error source to account for is the residual bias. This error can be assessed as follows. The statistical fluctuations due to the finite dataset cause uncertainty in the estimated bias. Suppose that σ2 is the variance of a ToF estimator. Then, according to Equation (6.11), the bias estimated from a training set of NS samples has a variance of σ2/NS. The residual bias has an order of magnitude of ![]() . In the present case, σ2 includes the variance due to the uncertainty in the reference values of the ToFs. The calculated residual biases are given in the fourth row in Table 9.2.
. In the present case, σ2 includes the variance due to the uncertainty in the reference values of the ToFs. The calculated residual biases are given in the fourth row in Table 9.2.
The final evaluation criterion must include both the variance and the bias. A suitable criterion is the mean square error or, equivalently, the root mean square error (RMS), defined as ![]() . The calculated RMSs are given in the fifth row.
. The calculated RMSs are given in the fifth row.
9.3.6.3 Discussion
Examination of Table 9.2 reveals that the four methods are ranked according to curve fitting, covariance model (CVM) based, matched filtering and finally thresholding. The performance of the threshold method is far behind the other methods. The reason for the failure of the threshold method is a lack of robustness. The method fails for a few samples in the training set. The robustness is simply improved by increasing the relative threshold, but at the cost of a larger variance. For instance, if the threshold is raised to 50%, the variance becomes around 900 μs2.
The poor performance of the matched filter is due to the fact that it is not able to cope with the echoes. The covariance model clearly helps to overcome this problem. The performance of the CVM method is just below that of curve fitting. Apparently, the covariance model is an important improvement over the simple white noise model of the matched filter, but is still too inaccurate to beat the curve-fitting method.
One might argue that the difference between the performances of curve fitting and CVM is not a statistically significant one. The dominant factor in the uncertainty of the RMSs is brought forth by the estimated variance. Assuming Gaussian distributions for the randomness, the variance of the estimation error of the variance is given by (see Equation (6.13))
where NS = 150 is the number of samples in the dataset. This error propagates into the RMS with a standard deviation of ![]() . The corresponding margins are shown in Table 9.2. It can be seen that the difference between the performances is larger than the margins, thus invalidating the argument.
. The corresponding margins are shown in Table 9.2. It can be seen that the difference between the performances is larger than the margins, thus invalidating the argument.
Another aspect of the design is the computational complexity of the methods. The threshold method and the curve-fitting method both depend on the availability of the envelope of the waveform. The quadrature filtering that is applied to calculate the envelope requires the application of the Fourier transform. The waveforms in the dataset are windowed to N = 8192 samples. Since N is a power of two, Matlab®'s implementations of the fast Fourier transforms, fft () and ifft (), have a complexity of 2N2 log2 N. The threshold method does not need further substantial computational effort. The curve-fitting method needs an additional numerical optimization, but since the number of points of the curve is not large, such an optimization is not very expensive.
A Fourier-based implementation of a correlator also has a complexity of 2N2 log2 N. Thus, the computational cost of the matched filter is in the same order as the envelope detector. The CVM-based method uses J correlators. Its complexity is (J + 1) N2 log2 N. Since typically J = 10, the CVM method is about 10 times more expensive than the other methods.
In conclusion, the most accurate method for ToF estimation appears to be the curve-fitting method with a computational complexity that is of the order of 2N2 log2 N. With this method, ToF estimation with an uncertainty of about 17 μs is feasible. The maximum likelihood estimator based on a covariance model follows the curve-fitting method closely with an uncertainty of 22 μs. Additional modelling of the occurrence of echoes is needed to improve its performance.
9.4 Online Level Estimation in a Hydraulic System
This third example considers the hydraulic system, which consists of two identical tanks connected by a pipeline with flow q1(t). The input flow q0(t) is acting on the first tank. q2(t) is the output flow from the second tank. Figure 9.22 shows an overview of the system. The relation between the level and the net input flow of a tank is C∂h = q∂t. C is the capacity of the tank. If the horizontal cross-sections of the tanks are constant, the capacity does not depend on h. The capacity of both tanks is C = 420 cm2. The order of the system is at least two, the two states being the levels h1(t) and h2(t). The goal is to design an online state estimator for the two levels h1(t) and h2(t), and for the input flow q0.

Figure 9.22 A simple hydraulic system consisting of two connected tanks.
The model that appeared to be best is Torricelli's model. In discrete time, with ![]() and
and ![]() , the model is
, the model is

where R1 and R2 are two constants that depend on the areas of the cross-sections of the pipelines of the two tanks and C is the capacity of the two tanks. These parameters are determined during the system identification and Δ = 5 s is the sampling period.
The system in Equation (9.23) is observable with only one level sensor. However, in order to allow consistency checks (which are needed to optimize and to evaluate the design) the system is provided with two level sensors. The redundancy of sensors is only needed during the design phase, because once a consistently working estimator has been found, one level sensor suffices.
The experimental data that are available for the design is a record of the measured levels as shown in Figure 9.23. The levels are obtained by means of pressure measurements using the Motorola MPX2010 pressure sensor. Some of the specifications of this sensor are given in Table 9.3. The full-scale span VFSS corresponds to Pmax = 10 kPa. In turn, this maximum pressure corresponds to a level of hmax = Pmax/ρg ≈ 1000 cm. Therefore, the linearity is specified between −10 cm and +10 cm. This specification is for the full range. In our case, the swing of the levels is limited to 20 cm and the measurement system was calibrated at 0 cm and 25 cm. Therefore, the linearity will be much less. The pressure hysteresis is an error that depends on whether the pressure is increasing or decreasing. The pressure hysteresis can induce a maximal level error between −1 cm and +1 cm. Besides these sensor errors, the measurements are also contaminated by electronic noise modelled by white noise v(i) with a standard deviation of σv = 0.04 cm. The model of the sensory system the becomes

or, more concisely, z(i) = Hx(i) + e(i) + v(i) with H = I. The error e(i) represents the linearity and hysteresis error.

Figure 9.23 Measured levels of two interconnected tanks.
Table 9.3 Specifications of the MPX2010 pressure sensor
| Characteristic | Symbol | Min | Typ | Max | Unit |
| Pressure range | P | 0 | — | 10 | kPa |
| Full-scale span | VFSS | 24 | 25 | 26 | mV |
| Sensitivity | ΔV/ΔP | — | 2.5 | — | mV/kPa |
| Linearity error | — | −1.0 | — | 1.0 | %VFSS |
| Pressure hysteresis | — | — | ±0.1 | — | %VFSS |
In the next sections, the linearized Kalman filter, the extended Kalman filter and the particle filter will be examined. In all three cases a model is needed for the input flow q0 (i). The linearized Kalman filter can only handle linear models. The extended Kalman filter can handle non-linear models, but only if the non-linearities are smooth. Particle filtering offers the largest freedom of modelling. All three models need parameter estimation in order to adapt the model to the data. Consistency checks must indicate which estimator is most suitable.
The prior knowledge that we assume is that the tanks at i = 0 are empty.
9.4.1 Linearized Kalman Filtering
The simplest dynamic model for q0(i) is the first-order AR model:
where ![]() is a constant input flow that maintains the equilibrium in the tanks. The Gaussian process noise w(i) causes random perturbations around this equilibrium. The factor α regulates the bandwidth of the fluctuations of the input flow. The design parameters are
is a constant input flow that maintains the equilibrium in the tanks. The Gaussian process noise w(i) causes random perturbations around this equilibrium. The factor α regulates the bandwidth of the fluctuations of the input flow. The design parameters are ![]() , σw and α.
, σw and α.
The augmented state vectors are x(i) = [x1(i) x2(i) q0 (i)]. Equations (9.23) and (9.25) make up the augmented state equation x(i + 1) = f(x(i), w(i)), which is clearly non-linear. The equilibrium follows from equating ![]() :
:

The next step is to calculate the Jacobian matrix of f():

The linearized model arises by application of a truncated Taylor series expansion around the equilibrium
with G = [0 0 1]T.
The three unknown parameters ![]() , α and σw must be estimated from the data. Various criteria can be used to find these parameters, but in most of these criteria the innovations play an important role. For a proper design the innovations are a white Gaussian sequence of random vectors with zero mean and known covariance matrixes, that is the innovation matrix. In the sequel we will use the NIS (normalized innovations squared). For a consistent design, the NIS must have a χ2N distribution. In the present case N = 2. The expectation of a χ2N-distributed variable is N. Thus, here, ideally the mean of the NIS is 2. A simple criterion is one that drives the average of the calculated NIS to 2. A possibility is
, α and σw must be estimated from the data. Various criteria can be used to find these parameters, but in most of these criteria the innovations play an important role. For a proper design the innovations are a white Gaussian sequence of random vectors with zero mean and known covariance matrixes, that is the innovation matrix. In the sequel we will use the NIS (normalized innovations squared). For a consistent design, the NIS must have a χ2N distribution. In the present case N = 2. The expectation of a χ2N-distributed variable is N. Thus, here, ideally the mean of the NIS is 2. A simple criterion is one that drives the average of the calculated NIS to 2. A possibility is

The values of ![]() , α and σw that minimize J are considered optimal.
, α and σw that minimize J are considered optimal.
The strategy is to realize a Matlab® function J = flinDKF(y) that implements the linearized Kalman filter, applies it to the data, calculates Nis(i) and returns J according to Equation (9.29). The input argument y is an array containing the variables ![]() , α and σw. Their optimal values are found by one of Matlab®'s optimization functions, for example
, α and σw. Their optimal values are found by one of Matlab®'s optimization functions, for example [parm, J] = fminsearch(@flinDKF, [20 0.95 5]).
Application of this strategy revealed an unexpected phenomenon. The solution of (![]() , α, σw) that minimizes J is not unique. The values of α and σw do not influence J as long as they are both sufficiently large. For instance, Figure 9.24 shows the results for α = 0.98 and σw = 1000 cm3/s. But any value of α and σw above this limit gives virtually the same results and the same minimum. The minimum obtained is J = 25.6. This is far too large for a consistent solution. Also the NIS, shown in Figure 9.24, does not obey the statistics of a χ22 distribution. During the transient, in the first 200 seconds, the NIS reaches extreme levels, indicating that some unmodelled phenomena occur there. However, during the remaining part of the process the NIS also shows some unwanted high peaks. Clearly the estimator is not consistent.
, α, σw) that minimizes J is not unique. The values of α and σw do not influence J as long as they are both sufficiently large. For instance, Figure 9.24 shows the results for α = 0.98 and σw = 1000 cm3/s. But any value of α and σw above this limit gives virtually the same results and the same minimum. The minimum obtained is J = 25.6. This is far too large for a consistent solution. Also the NIS, shown in Figure 9.24, does not obey the statistics of a χ22 distribution. During the transient, in the first 200 seconds, the NIS reaches extreme levels, indicating that some unmodelled phenomena occur there. However, during the remaining part of the process the NIS also shows some unwanted high peaks. Clearly the estimator is not consistent.

Figure 9.24 Results from the linearized Kalman filter.
Three modelling errors might explain the anomalous behaviour of the linearized Kalman filter. First, the linearization of the system equation might fail. Second, the AR model of the input flow might be inappropriate. Third, the ignorance of possible linearization errors of the sensors might not be allowed. In the next two sections, the first two possible explanations will be examined.
9.4.2 Extended Kalman Filtering
Linearization errors of the system equation are expected to be influential when the levels deviate largely from the equilibrium state. The abnormality during the transient in Figure 9.24 might be caused by this kind of error because there the non-linearity is strongest. The extended Kalman filter is able to cope with smooth linearity errors. Therefore, this method might give an improvement.
In order to examine this option, a Matlab® function J = fextDKF(y) was realized that implements the extended Kalman filter. Again, y is an array containing the variables ![]() , α and σw. Application to the data, calculation of J and minimization with
, α and σw. Application to the data, calculation of J and minimization with fminsearch() yields estimates as shown in Figure 9.25.

Figure 9.25 Results from the extended Kalman filter.
The NIS of the extended Kalman filter, compared with that of the linearized Kalman filter, is much better now. The optimization criterion J attains a minimal value of 3.6 instead of 25.6; a significant improvement has been reached. However, the NIS still does not obey a χ22 distribution. Also, the optimization of the parameters ![]() , α and σw is not without troubles. Again, the minimum is not unique. Any solution of α and σw satisfies as long as both parameters are sufficiently large. Moreover, it now appears that the choice of
, α and σw is not without troubles. Again, the minimum is not unique. Any solution of α and σw satisfies as long as both parameters are sufficiently large. Moreover, it now appears that the choice of ![]() does not have any influence at all.
does not have any influence at all.
The explanation of this behaviour is as follows. First of all, we observe that in the prediction step of the Kalman filter a large value of σw induces a large uncertainty in the predicted input flow. As a result, the prediction of the level in the first tank is also very uncertain. In the next update step, the corresponding Kalman gain will be close to one, and the estimated level in the first tank will closely follow the measurement, ![]() . If α is sufficiently large, so that the autocorrelation in the sequence q0(i) is large, the estimate
. If α is sufficiently large, so that the autocorrelation in the sequence q0(i) is large, the estimate ![]() is derived from the differences of succeeding samples
is derived from the differences of succeeding samples ![]() and
and ![]() . Since
. Since ![]() and
and ![]() , the estimate
, the estimate ![]() only depends on measurements. The value of
only depends on measurements. The value of ![]() does not influence that. The conclusion is that the AR model does not provide useful prior knowledge for the input flow.
does not influence that. The conclusion is that the AR model does not provide useful prior knowledge for the input flow.
9.4.3 Particle Filtering
A visual inspection of the estimated input flow in Figure 9.25 indeed reveals that an AR model does not fit well. The characteristic of the input flow is more like that of a random binary signal modelled by two discrete states {qmin, qmax} and a transition probability Pt(q0(i) |q0(i − 1)) (see Section 4.3.1). The estimated flow in Figure 9.25 also suggests that qmin = 0. This actually models an on/off control mechanism of the input flow. With this assumption, the transition probability is fully defined by two probabilities:

The unknown parameters of the new flow model are qmax, Pup and Pdown. These parameters must be retrieved from the data by optimizing some consistency criterion of an estimator. Kalman filters cannot cope with binary signals. Therefore, we now focus on particle filtering, because this method is able to handle discrete variables (see Section 4.4).
Again, the strategy is to realize a Matlab® function J = fpf(y) that implements a particle filter, applies it to the data and returns a criterion J. The input argument y contains the design parameters qmax, Pup and Pdown. The output J must express how well the result of the particle filter is consistent. Minimization of this criterion gives the best attainable result.
An important issue is how to define the criterion J. The NIS, which was previously used, exists within the framework of Kalman filters, that is for linear-Gaussian systems. It is not trivial to find a concept within the framework of particle filters that is equivalent to the NIS. The general idea is as follows. Suppose that, using all previous measurements Z(i − 1) up to time i − 1, the probability density of the state x(i) is p(x(i)|Z(i − 1)). Then the probability of z(i) is
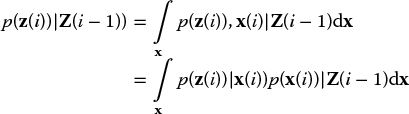
The density p(z(i)|x(i)) is simply the model of the sensory system and as such known. The probability p(x(i)|Z(i − 1)) is represented by the predicted samples. Therefore, using Equation (9.31) the probability p(z(i)|Z(i − 1)) can be calculated. The filter is consistent only if the sequence of observed measurements z(i) obeys the statistics prescribed by the sequence of densities p(z(i)|Z(i − 1)).
A test of whether all z(i) comply with p(z(i)|Z(i − 1)) is not easy, because p(z(i)|Z(i − 1)) depends on i. The problem will be tackled by treating each scalar measurement separately. We consider the nth element zn(i) of the measurement vector and assume that pn(z, i) is its hypothesized marginal probability density. Suppose that the cumulative distribution of zn(i) is Fn(z, i) = ∫z− ∞pn(ζ, i)dζ. Then the random variable un(i) = Fn(zn(i), i) has a uniform distribution between 0 and 1. The consistency check boils down to testing whether the set {un(i)|i = 0, …, I − 1 and n = 1, …, N} indeed has such a uniform distribution.
In the literature, the statistical test of whether a set of variables has a given distribution function is called a goodness-of-fit test. There are various methods for performing such a test. A particular one is the chi-square test and is as follows (Kreyszig, 1970).
Algorithm 9.1 Goodness-of-fit test (chi-square test for the uniform distribution)
Input: a set of variables that are within the interval [0, 1]. The size of the set is B.
- Divide the interval [0, 1] into a number of L equally spaced containers and count the number of times that the random variable falls in the ℓth container. Denote this count by bℓ. Thus, ∑Lℓ = 1bℓ = B. (Note: L must be such that bℓ > 5 for each ℓ.)
- Set e = B/L. This is the expected number of variables in one container.
- Calculate the test variable J = ∑Lℓ = 1(bℓ − e)2/e.
- If the set is uniformly distributed, then J has a χ2L − 1 distribution. Thus, if J is too large to be compatible with the χ2L − 1 distribution, the hypothesis of a uniform distribution must be rejected. For instance, if L = 20, the probability that J > 43.8 equals 0.001.
The particular particle filter that was implemented is based on the condensation algorithm described in Section 5.4.3. The Matlab® code is given in Listing 9.10. Some details of the implementation follow next (see Algorithm 5.4).
- The prior knowledge that we assume is that at i = 0 both tanks are empty, that is x1(0) = x2(0) = 0. The probability that the input flow is ‘on’ or ‘off’ is 50/50.
- During the update, the importance weights should be set to w(k) = p(z(i)|x(k)). Assuming a Gaussian distribution of the measurement errors, the weights are calculated as
 . The normalizing constant of the Gaussian can be ignored because the weights are going to be normalized anyway.
. The normalizing constant of the Gaussian can be ignored because the weights are going to be normalized anyway. - ‘Finding the smallest j such that w(j)cum ≥ r(k)’ is implemented by the bisection method of finding a root using the golden rule.
- In the prediction step, ‘finding the samples x(k) drawn from the density p(x(i)|x(i − 1) = x(k)selected)’ is done by generating random input flow transitions from ‘on’ to ‘off’ and from ‘off’ to ‘on’ according to the transition probabilities Pdown and Pup, and to apply these to the state equation (implemented by
f(Ys, R1,R2)). However, the time-discrete model only allows the transitions to occur at exactly the sampling periods ti = iΔ. In the real-time–continuous world, the transitions can take place anywhere in the time interval between two sampling periods. In order to account for this effect, the level of the first tank is randomized with a correction term randomly selected between 0 and qmaxΔ/C. Such a correction is only needed for samples where a transition takes place. - The conditional mean, approximated by
 , is used as the final estimate.
, is used as the final estimate. - The probability density p(z(i)|Z(i − 1)) is represented by samples z(k), which are derived from the predicted samples x(k) according to the model z(k) = Hx(k) + v(k), where v(k) is Gaussian noise with covariance matrix Cv. The marginal probabilities pn(z, i) are then represented by the scalar samples z(k)n. The test variables un(i) are simply obtained by counting the number of samples for which z(k)n < zn(i) and dividing it by K, the total number of samples.
Listing 9.10 Matlab® listing of a function implementing the condensation algorithm.
function J = fpf (y)
prload hyddata.mat; % Load the dataset (measurements in Z)
I = length (Z); % Length of the sequence
R1 = 105.78; % Friction constant (cm^5/s^2)
R2 = 84.532; % Friction constant (cm^5/s^2)
qmin = 0; % Minimal input flow
delta = 5; % Sampling period (s)
C = 420; % Capacity of tank (cm^2)
sigma_v = 0.04; % Standard deviation sensor noise (cm)
Ncond = 1000; % Number of particles
M = 3; % Dimension of state vector
N = 2; % Dimension of measurement vector
% set the design parameters
qmax = y(1); % Maximum input flow
Pup = y(2); % Transition probability up
Pdn = y(3); % Transition probability down
% Initialisation
hmax = 0; hmin = 0; % Margins of levels at i = 0
H = eye (N, M); % Measurement matrix
invCv = inv(sigma_v^2 * eye(N)); % Inv. cov. Of sensor noise
% Generate the samples
Xs(1,:) = hmin + (hmax−hmin)*rand(1,Ncond);
Xs(2,:) = hmin + (hmax−hmin)*rand(1,Ncond);
Xs(3,:) = qmin + (qmax−qmin)*(rand(1,Ncond)> 0:5);
for i = 1:I
% Generate predicted meas. representing p(z(i)<y>|</y>Z(i-1))
Zs = H*Xs + sigma_v*randn(2,Ncond);
% Get uniform distributed rv
u(1,i) = sum((Zs(1,:) < Z(1,i)))/Ncond;
u(2,i) = sum((Zs(2,:) < Z(2,i)))/Ncond;
% Update
res = H*Xs−Z(:,i)*ones(1,Ncond); % Residuals
W = exp (−0:5*sum (res.*(invCv*res)))’; % Weights
if (sum(W) == 0), error(’process did not converge’); end
W = W/sum (W); CumW = cumsum (W);
xest(:,i) = Xs(:,:)*W; % Sample mean
% Find an index permutation using golden rule root finding for
j = 1:Ncond
R = rand; ja = 1; jb = Ncond;
while (ja < jb−1)
jx = floor(jb–0:382*(jb–ja));
fa = R−CumW(ja); fb = R−CumW(jb); fxx = R−CumW(jx);
if (fb*fxx < 0), ja = jx; else, jb = jx; end
end
ind(j) = jb;
end
% Resample
for j = 1:Ncond, Ys(:,j) = Xs(:,ind(j)); end
% Predict
Tdn = (rand(1,Ncond)<Pdn); % Random transitions
Tup = (rand(1,Ncond)<Pup); % idem
kdn = find((Ys(3,:) == qmax) & Tdn); % Samples going down
kup = find((Ys(3,:) == qmin) & Tup); % Samples going up
Ys(3,kdn) = qmin; % Turn input flow off
Ys(1,kdn) = Ys(1,kdn) + … % Randomize level 1
(qmax−qmin)*delta*rand(1,length(kdn))/C;
Ys(3,kup) = qmax; % Turn input flow on
Ys(1,kup) = Ys(1,kup) − … % Randomize level 1
(qmax qmin)*delta*rand(1,length(kup))/C;
Xs = f(Ys,R1,R2); % Update samples
end
e = I/10; % Expected number of rv in one bin
% Get histograms (10 bins) and calculate test variables
for i = 1:2, b = hist(u(i,:)); c(i) = sum((b−e).^2/e); end
J = sum(c); % Full test (chi-square with 19 DoF)
returnFigure 9.26 shows the results obtained using particle filtering. With the number of samples set to 1000, minimization of J with respect to qmax, Pup and Pdown yielded a value of about J = 1400; this is a clear indication that the test variables u1(i) and u2(i) are not uniformly distributed because J should have a χ219 distribution. The graph in Figure 9.26, showing these test variables, confirms this statement. The values of Pup and Pdown that provided the minimum were about 0.3. This minimum was, however, very flat.

Figure 9.26 Results from particle filtering.
The large transition probabilities that are needed to minimize the criterion indicate that we still have not found an appropriate model for the input flow. After all, large transition probabilities mean that the particle filter has much freedom in selecting an input flow that fits with the data.
9.4.4 Discussion
Up to now we have not succeeded in constructing a consistent estimator. The linearized Kalman filter failed because of the non-linearity of the system, which is simply too severe. The extended Kalman filter was an improvement, but its behaviour was still not regular. The filter could only be put in action if the model for the input flow was unrestrictive, but the NIS of the filter was still too large. The particle filter that we tested used quite another model for the input flow than the extended Kalman filter, but yet this filter also needed an unrestrictive model for the input flow.
At this point, we must face another possibility. We have adopted a linear model for the measurements, but the specifications of the sensors mention linearity and hysteresis errors e(i) which can – when measured over the full-scale span – become quite large. Until now we have ignored the error e(i) in Equation (9.24), but without really demonstrating that doing so is allowed. If it is not, that would explain why both the extended Kalman filter and the particle filter only work out with unrestrictive models for the input signal. In trying to get estimates that fit the data from both sensors the estimators cannot handle any further restrictions on the input signal.
The best way to cope with the existence of linearity and hysteresis errors is to model them properly. A linearity error – if reproducible – can be compensated by a calibration curve. A hysteresis error is more difficult to compensate because it depends on the dynamics of the states. In the present case, a calibration curve can be deduced for the second sensor using the previous results. In the particle filter of Section 9.3.3 the estimate of the first level is obtained by closely following the measurements in the first tank. The estimates of the second level are obtained merely by using the model of the hydraulic system. Therefore, these estimates can be used as a reference for the measurements in the second tank.
Figure 9.27 shows a scatter diagram of the errors versus estimated levels of the second tank. Of course, the data are contaminated by measurement noise, but nevertheless the trend is appreciable. Using Matlab®'s polyfit () and polyval (), polynomial regression has been applied to find a curve that fits the data. The resulting polynomial model is used to compensate the linearity errors of the second sensor. The results, illustrated in Figure 9.28, show test variables that are much more uniformly distributed than the same variables in Figure 9.26. The chi-square test gives a value of J = 120. This is a significant improvement, but nevertheless still too much for a consistent filter. However, Figure 9.28 only goes to show that the compensation of the linearity errors of the sensors do have a large impact.

Figure 9.27 Calibration curve for the second sensor.

Figure 9.28 Results from particle filtering after applying a linearity correction.
For the final design, the errors of the first sensor should also be compensated. Additional measurements are needed to obtain the calibration curve for that sensor. Once this curve is available, the design procedure as described above starts over again, but this time with compensation of linearity errors included. There is no need to reconsider the linearized Kalman filter because we have already seen that its linearization errors are too severe.
9.5 References
- Harrison, D. and Rubinfeld, D.L., Hedonic prices and the demand for clean air, Journal of Environmental Economics and Management, 5, 81–102, 1978.
- Heijden, F. van der Túquerres, G. and Regtien, P.P.L., Time-of-flight estimation based on covariance models, Measurement Science and Technology, 14, 1295–304, 2003.
- Kreyszig, E., Introductory Mathematical Statistics – Principles and Methods, John Wiley & Sons, Inc., New York, 1970.
