Whereas Appendix A deals with general linear spaces and linear operators, the current appendix restricts attention to linear spaces with finite dimension, that is ℝ^N and ℂ^N. Therefore, all that has been said in Appendix A also holds true for the topics of this appendix.

B.1 Vectors and Matrices

Vectors in ℝ^N and ℂ^N are denoted by bold-faced letters, for example f and g. The elements in a vector are arranged either vertically (a column vector) or horizontally (a row vector). For example:

(B.1)

The superscript ^T is used to convert column vectors to row vectors. Vector addition and scalar multiplication are defined as in Section A.1.

A matrix H with dimension N × M is an arrangement of NM numbers h_n,m (the elements) on an orthogonal grid of N rows and M columns:

(B.2)

The elements are real or complex. Vectors can be regarded as N × 1 matrices (column vectors) or 1 × M matrices (row vectors). A matrix can be regarded as a horizontal arrangement of M column vectors with dimension N, for example:

(B.3)

Of course, a matrix can also be regarded as a vertical arrangement of N row vectors.

The scalar–matrix multiplication αH replaces each element in H with αh_n,m. The matrix–addition H = A + B is only defined if the two matrices A and B have equal size N × M. The result H is an N × M matrix with elements h_n,m = a_n,m + b_n,m. These two operations satisfy the axioms of a linear space (Section A.1). Therefore, the set of all N × M matrices is another example of a linear space.

The matrix–matrix product H = AB is defined only when the number of columns of A equals the number of rows of B. Suppose that A is an N × P matrix and that B is a P × M matrix; then the product H = AB is an N × M matrix with elements:

(B.4)

Since a vector can be regarded as an N × 1 matrix, this also defines the matrix–vector product g = Hf with f an M-dimensional column vector, H an N = M matrix and g an N-dimensional column vector. In accordance with these definitions, the inner product between two real N-dimensional vectors introduced in Section A.1.2 can be written as

(B.5)

It is easy to show that a matrix–vector product g = Hf defines a linear operator from ℝ^N into ℝ^N and ℂ^M into ℂ^N. Therefore, all definitions and properties related to linear operators (Section A.4) also apply to matrices.

Some special matrices are:

• The null matrix O. This is a matrix fully filled with zero. It corresponds to the null operator: Of = 0.
• The unit matrix I. This matrix is square (N = M), fully filled with zero, except for the diagonal elements, which are unit:
  
• This matrix corresponds to the unit operator: If = f.
• A diagonal matrix is a square matrix, fully filled with zero, except for its diagonal elements λ_n,n:
  
  Often, diagonal matrices are denoted by upper case Greek symbols.
• The transposed matrix H^T of an N × M matrix H is an M × N matrix; its elements are given by h^T_{m, n} = h_{n, m}.
• A symmetric matrix is a square matrix for which H^T = H.
• The conjugated of a matrix H is a matrix the elements of which are the complex conjugated of the one of H.
• The adjoint of a matrix H is a matrix H^* which is the conjugated and the transposed of H, that is: . A matrix H is self-adjoint or Hermitian if H^* = H. This is the case only if H is square and .
• The inverse of a square matrix H is the matrix H^–1 that satisfies H^–1 H = I. If it exists, it is unique. In that case the matrix H is called regular. If H^–1 does not exist, H is called singular.
• A unitary matrix U is a square matrix that satisfies U^–1 = U*. A real unitary matrix is called orthonormal. These matrices satisfy U^–1 = U^T.
• A square matrix H is Toeplitz if its elements satisfy h_n,m = g_(n–m) in which g_n is a sequence of 2N – 1 numbers.
• A square matrix H is circulant if its elements satisfy h_n,m = g_(n–m)%N. Here, (n – m)%N is the remainder of (n – m)/N.
• A matrix H is separable if it can be written as the product of two vectors: H = fg^T.

Some properties with respect to the matrices mentioned above:

(B.6)

(B.7)

(B.8)

(B.9)

(B.10)

The relations hold if the size of the matrices are compatible and the inverses exist. Property (B.10) is known as the matrix inversion lemma.

B.2 Convolution

Defined in a finite interval, the discrete convolution between a sequence f_k and g_k:

(B.11)

can be written economically as a matrix–vector product g = Hf. The matrix H is a Toeplitz matrix:

(B.12)

If this ‘finite interval’ convolution is replaced with a circulant (wrap-around) discrete convolution, then (B.11) becomes

(B.13)

In that case, the matrix–vector relation g = Hf still holds. However, the matrix H is now a circulant matrix:

(B.14)

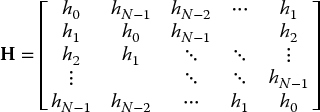
The Fourier matrix W is a unitary N × N matrix with elements given by

(B.15)

The (row) vectors in this matrix are the complex conjugated of the basis vectors given in (A.24). Note that W* = W^–1 because W is unitary. It can be shown that the circulant convolution in (B.13) can be transformed into an element-by-element multiplication provided that the vector g is represented by the orthonormal basis of (A.24). In this representation the circulant convolution g = Hf becomes (see Equation (A.36))

(B.16)

Writing W = [w₀ w₁ ⋅⋅⋅ w_{N − 1}] and carefully examining Hw_k reveals that the basis vectors w_k are the eigenvectors of the circulant matrix H. Therefore, we may write Hw_k = λ_kw_k with k = 0, 1, …, N − 1. The numbers λ_k are the eigenvalues of H. If these eigenvalues are arranged in a diagonal matrix:

(B.17)

the N equations Hw_k = λ_kw_k can be written economically as HW = W. Right-sided multiplication of this equation by W^–1 yields H = WW^–1. Substitution in Equation (B.16) gives

(B.18)

Note that the multiplication Λ with the vector W^–1f is an element-by-element multiplication because the matrix Λ is diagonal. The final result is obtained if we perform a left-sided multiplication in (b.18) by W:

(B.19)

The interpretation of this result is depicted in Figure B.1.

B.3 Trace and Determinant

The trace trace(H) of a square matrix H is the sum of its diagonal elements:

(B.20)

Properties related to the trace are (A and B are N × N matrices, f and g are N-dimensional vectors)

(B.21)

(B.22)

The determinant |H| of a square matrix H is recursively defined with its co-matrices. The co-matrix H_n,m is an (N – 1) × (N – 1) matrix that is derived from H by exclusion of the nth row and the mth column. The following equations define the determinant:

(B.23)

Some properties related to the determinant:

(B.24)

(B.25)

(B.26)

(B.27)

(B.28)

If λ_n are the eigenvalues of a square matrix A, then

(B.29)

The rank of a matrix is the maximum number of column vectors (or row vectors) that are linearly independent. The rank of a regular N × N matrix is always N. In that case, the determinant is always non-zero. The reverse also holds true. The rank of a singular N × N matrix is always less than N and the determinant is zero.

B.4 Differentiation of Vector and Matrix Functions

Suppose f(x) is a real or complex function of the real N-dimensional vector x. Then the first derivative of f(x) with respect to x is an N-dimensional vector function (the gradient):

(B.30)

If f (x) = a^Tx (i.e. the inner product between x and a real vector a), then

(B.31)

Likewise, if f(x) = x^THx (i.e. a quadratic form defined by the matrix H), then

(B.32)

The second derivative of f(x) with respect to x is an N × N matrix called the Hessian matrix:

(B.33)

The determinant of this matrix is called the Hessian.

The Jacobian matrix of an N-dimensional vector function f(): ℝ^M → ℝ^N is defined as an N × M matrix:

(B.34)

Its determinant (only defined if the Jacobian matrix is square) is called the Jacobian.

The differentiation of a function of a matrix, for example f(H), with respect to this matrix is defined similar to the differentiation in (B.30). The result is a matrix:

(B.35)

Suppose that we have a square, invertible R × R matrix function F(H) of an N × M matrix H, that is F(): ℝ^N × ℝ^M → ℝ^R × ℝ^R; then the derivative of F(H) with respect to one of the elements of H is

(B.36)

From this the following rules can be derived:

(B.37)

(B.38)

(B.39)

Suppose that A, B and C are square matrices of equal size. Then some properties related to the derivatives of the trace and the determinant are

(B.40)

(B.41)

(B.42)

(B.43)

(B.44)

In Equation (B.44), [A^–1]_m,n is the m, nth element of A^–1.

B.5 Diagonalization of Self-Adjoint Matrices

Recall from Section B.1 that an N × N matrix H is called self-adjoint or Hermitian if H* = H. From the discussion on self-adjoint operators in Section A.4 it is clear that associated with H there exists an orthonormal basis V = {v₀ v₁ ⋅⋅⋅ v_{N − 1}} that we now arrange in a unitary matrix V = [v₀ v₁ ⋅⋅⋅ v_{N − 1}]. Each vector v_k is an eigenvector with corresponding (real) eigenvalue λ_k. These eigenvalues are now arranged as the diagonal elements in a diagonal matrix Λ.

The operation Hf can be written as (see Equations (A.42) and (B.5))

(B.45)

Suppose that the rank of H equals R. Then there are exactly R non-zero eigenvalues. Consequently, the number of terms in Equation (B.45) can be replaced with R. From this, it follows that H is a composition of its eigenvectors according to

(B.46)

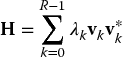
The summation on the right-hand side can be written more economically as VΛV*. Therefore:

(B.47)

The unitary matrix V* transforms the domain of H such that H becomes the diagonal matrix in this new domain. The matrix V accomplishes the inverse transform. In fact, Equation (B.47) is the matrix version of the decomposition shown in Figure A.2.

If the rank R equals N, there are exactly N non-zero eigenvalues. In that case, the matrix Λ is invertible and so is H:

(B.48)

It can be seen that the inverse H^–1 is also self-adjoint.

A self-adjoint matrix H is positive definite if its eigenvalues are all positive. In that case the expression satisfies the conditions of a distance measure (Section A.2). To show this it suffices to prove that satisfies the conditions of a norm (see Section A.2). These conditions are given in Section A.1. We use the diagonal form of H (see Equation (B.47):

(B.49)

Since V is a unitary matrix, the vector V*f can be regarded as the representation of f with respect to the orthonormal basis defined by the vectors in V. Let this representation be denoted by: ϕ = V*f. The expression f*Hf equals

(B.50)

Written in this form, it is easy to show that all conditions of a norm are met.

With the norm , the sets of points equidistant to the origin, that is the vectors that satisfy f*Hf = constant, are ellipsoids (see Figure B.2). This follows from Equation (B.50):

Hence, if we introduce a new vector u with elements defined as , we must require that:

We conclude that in the u domain the ordinary Euclidean norm applies. Therefore, the solution space in this domain is a sphere (Figure B.2(a)). The operation is merely a scaling of the axes by factors . This transforms the sphere into an ellipsoid. The principal axes of this ellipsoid line up with the basis vectors u (and ) (see Figure B.2(b)). Finally, the unitary transform f = V rotates the principal axes, but without affecting the shape of the ellipsoid (Figure B.2(c)). Hence, the orientation of these axes in the f domain is along the directions of the eigenvectors v_n of H.

The metric expressed by is called a quadratic distance. In pattern classification theory it is usually called the Mahalanobis distance.

B.6 Singular Value Decomposition (SVD)

The singular value decomposition theorem states that an arbitrary N × M matrix H can be decomposed into the product

(B.51)

where U is an orthonormal N × R matrix, Σ is a diagonal R × R matrix and V is an orthonormal M × R matrix. R is the rank of the matrix H. Therefore, R ≤ min (N, M).

The proof of the theorem is beyond the scope of this book. However, its connotation can be clarified as follows. Suppose, for a moment, that R = N = M. We consider all pairs of vectors of the form y = Hx, where x is on the surface of the unit sphere in ℝ^M, that is ‖x‖ = 1. The corresponding y must be on the surface in ℝ^N defined by the equation y^Ty = x^TH^THx. The matrix H^TH is a symmetric M × M matrix. By virtue of Equation (B.47) there must be an orthonormal matrix V and a diagonal matrix S such that¹

(B.52)

The matrix V = [v₀ ⋅⋅⋅ v_{M − 1}] contains the (unit) eigenvectors v_i of H^TH. The corresponding eigenvalues are all on the diagonal of the matrix S. Without loss of generality we may assume that they are sorted in descending order. Thus, S_i,i ≥ S_i+1,i+1.

With , the solutions of the equation y^Ty = x^TH^THx with ‖x‖ = 1 is the same set as the solutions of . Clearly, if x is a unit vector, then so is because V is orthonormal. Therefore, the solutions of y^Ty = ^TS is the set

where

(B.53)

is the matrix that is obtained by taking the square roots of all (diagonal) elements in S. The diagonal elements of are usually denoted by the singular values . With that, the solutions become a set:

(B.54)

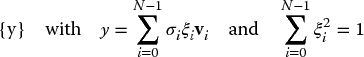
Equation (B.54) reveals that the solutions of y^Ty = x^TH^THx with ‖x‖ = 1 are formed by a scaled version of the sphere ‖x‖ = 1. Scaling takes place with a factor σ_i in the direction of v_i. In other words, the solutions form an ellipsoid.

Each eigenvector v_i gives rise to a principal axis of the ellipsoid. The direction of such an axis is the one of the vector Hv_i. We form the matrix HV = [Hv₀ ⋅⋅⋅ Hv_{M − 1}], which contains the vectors that point in the directions of all principal axes. Using Equation (B.52):

Consequently, the column vectors in the matrix U that fulfils

(B.55)

successively points in the directions of the principal axes. Since S is a diagonal matrix, we conclude from Equation (B.47) that U must contain the eigenvectors u_i of the matrix HH^T, that is U = [u₀ ⋅⋅⋅ u_{M − 1}]. The diagonal elements of S are the corresponding eigenvalues and U is an orthonormal matrix.

The operator H maps the vector v_i to a vector Hv_i whose direction is given by the unit vector u_i and whose length is given by σ_i. Therefore, Hv_i = σ_iu_i. Representing an arbitrary vector x as a linear combination of v_i, that is ξ = V^Tx, gives us finally the SVD theorem stated in Equation (B.51).

In the general case, N can differ from M and R ≤ min (N, M). However, Equations (B.51), (B.52), (B.54) and (B.55) are still valid, except that the dimensions of the matrices must be adapted. If R < M, then the singular values from σ_R up to σ_M–1 are zero. These singular values and the associated eigenvectors are then discarded. The ellipsoid mentioned above becomes an R-dimensional ellipsoid that is embedded in ℝ^N.

The process is depicted graphically in Figure B.3. The operator = V^Tx aligns the operand to the suitable basis {v_i} by means of a rotation. This operator also discards all components v_R up to v_M–1 if R < M. The operator stretches the axes formed by the {v_i} basis. Finally, the operator y = U hangs out each v_i component in ℝ^M as a u_i component in ℝ^N.

An important application of the SVD is matrix approximation. For that purpose, Equation (B.51) is written in an equivalent form:

(B.56)

We recall that the sequence σ₀, σ₁, ... is in descending order. Also, σ_i > 0. Therefore, if the matrix must be approximated by less then R terms, then the best strategy is to nullify the last terms. For instance, if the matrix H must be approximated by a vector product, that is H = fg^T, then the best approximation is obtained by nullifying all singular values except σ₀, that is H ≈ σ₀u₀v^T₀.

The SVD theorem is useful to find the pseudo inverse of a matrix:

(B.57)

The pseudo inverse gives the least squares solution to the equation y = Hx. In other words, the solution is the one that minimizes ‖Hx − y‖²₂. If the system is underdetermined, R < M, it provides a minimum norm solution, that is is the smallest solution of y = Hx.

The SVD is also a good departure point for a stability analysis of the pseudo inverse, for instance by studying the ratio between the largest and smallest singular values. This ratio is a measure of the sensitivity of the inverse to noise in the data. If this ratio is too high, we may consider regularizing the pseudo inverse by discarding all terms in Equation (B.57) whose singular values are too small.

Besides matrix approximation and pseudo inverse calculation the SVD finds application in image restoration, image compression and image modelling.

B.7 Selected Bibliography

1. Bellman, R.E., Introduction to Matrix Analysis, McGraw-Hill, New York, 1970.
2. Strang, G., Linear Algebra and Its Applications, Third Edition, Harcourt Brace Jovanovich, San Diego, CA, 1989.