8
Unsupervised Learning
In Chapter 6 we discussed methods for reducing the dimension of the measurement space in order to decrease the cost of classification and to improve the ability to generalize. In these procedures it was assumed that for all training objects, class labels were available. In many practical applications, however, the training objects are not labelled, or only a small fraction of them are labelled. In these cases it can be worthwhile to let the data speak for itself. The structure in the data will have to be discovered without the help of additional labels.
An example is colour-based pixel classification. In video-based surveillance and safety applications, for instance, one of the tasks is to track the foreground pixels. Foreground pixels are pixels belonging to the objects of interest, for example cars on a parking place. The RGB representation of a pixel can be used to decide whether a pixel belongs to the foreground or not. However, the colours of neither the foreground nor the background are known in advance. Unsupervised training methods can help to decide which pixels of the image belong to the background and which to the foreground.
Another example is an insurance company, which might want to know if typical groups of customers exist, such that it can offer suitable insurance packages to each of these groups. The information provided by an insurance expert may introduce a significant bias. Unsupervised methods can then help to discover additional structures in the data.
In unsupervised methods, we wish to transform and reduce the data such that a specific characteristic in the data is highlighted. In this chapter we will discuss two main characteristics that can be explored: the subspace structure of data and its clustering characteristics. The first tries to summarize the objects using a smaller number of features than the original number of measurements; the second tries to summarize the dataset using a smaller number of objects than the original number. Subspace structure is often interesting for visualization purposes. The human visual system is highly capable of finding and interpreting structure in 2D and 3D graphical representations of data. When higher dimensional data are available, a transformation to 2D or 3D might facilitate its interpretation by humans. Clustering serves a similar purpose, interpretation, but also data reduction. When very large amounts of data are available, it is often more efficient to work with cluster representatives instead of the whole dataset. In Section 8.1 we will treat feature reduction; in Section 8.2 we discuss clustering.
8.1 Feature Reduction
The most popular unsupervised feature reduction method is principal component analysis (Jolliffe, 1986). This will be discussed in Section 8.1.1. One of the drawbacks of this method is that it is a linear method, so non-linear structures in the data cannot be modelled. In Section 8.1.2 multidimensional scaling is introduced, which is a non-linear feature reduction method. Another classical non-linear feature reduction method is kernel principal component analysis (Schölkopf, 1998), which will be described in Section 8.1.3.
8.1.1 Principal Component Analysis
The purpose of principal component analysis (PCA) is to transform a high-dimensional measurement vector z to a much lower-dimensional feature vector y by means of an operation:
such that z can be reconstructed accurately from y.
Here ![]() is the expectation of the random vector z. It is constant for all realizations of z. Without loss of generality, we can assume that
is the expectation of the random vector z. It is constant for all realizations of z. Without loss of generality, we can assume that ![]() because we can always introduce a new measurement vector,
because we can always introduce a new measurement vector, ![]() , and apply the analysis to this vector. Hence, under that assumption, we have
, and apply the analysis to this vector. Hence, under that assumption, we have
The D × N matrix WD transforms the N-dimensional measurement space to a D-dimensional feature space. Ideally, the transform is such that y is a good representation of z despite of the lower dimension of y. This objective is strived for by selecting WD such that an (unbiased) linear MMSE estimate1
![]() for z based on y yields a minimum mean square error (see Section 4.1.5):
for z based on y yields a minimum mean square error (see Section 4.1.5):
It is easy to see that this objective function does not provide a unique solution for WD. If a minimum is reached for some WD, then any matrix AWD is another solution with the same minimum (provided that A is invertible) as the transformation A will be inverted by the linear MMSE procedure. For uniqueness, we add two requirements. First, we require that the information carried in the individual elements of y add up individually. With that we mean that if y is the optimal D-dimensional representation of z, then the optimal D – 1 dimensional representation is obtained from y, simply by deleting its least informative element. Usually the elements of y are sorted in decreasing order of importance, so that the least informative element is always the last element. With this convention, the matrix WD–1 is obtained from WD simply by deleting the last row of WD.
The requirement leads to the conclusion that the elements of y must be uncorrelated. If not, then the least informative element would still carry predictive information about the other elements of y which conflicts with our requirement. Hence, the covariance matrix Cy of y must be a diagonal matrix, say ![]() . If Cz is the covariance matrix of z, then
. If Cz is the covariance matrix of z, then
For D = N it follows that CZWTN = WTN∧N because WN is an invertible matrix (in fact, an orthogonal matrix) and WTNWN must be a diagonal matrix (see Appendix B.5 and C.3.2). As ![]() N is a diagonal matrix, the columns of WTN must be eigenvectors of Cz. The diagonal elements of
N is a diagonal matrix, the columns of WTN must be eigenvectors of Cz. The diagonal elements of ![]() N are the corresponding eigenvalues.
N are the corresponding eigenvalues.
The solution is still not unique because each element of y can be scaled individually without changing the minimum. Therefore, the second requirement is that each column of WTN has unit length. Since the eigenvectors are orthogonal, this requirement is fulfilled by WNWTN = I with I the N × N unit matrix. With that, WN establishes a rotation on z. The rows of the matrix WN, that is the eigenvectors, must be sorted such that the eigenvalues form a non-ascending sequence. For arbitrary D, the matrix WD is constructed from WN by deleting the last N – D rows.
The interpretation of this is as follows (see Figure 8.1). The operator WN performs a rotation on z such that its orthonormal basis aligns with the principal axes of the ellipsoid associated with the covariance matrix of z. The coefficients of this new representation of z are called the principal components. The axes of the ellipsoid point in the principal directions. The MMSE approximation of z using only D coefficients is obtained by nullifying the principal components with least variances. Hence, if the principal components are ordered according to their variances, the elements of y are formed by the first D principal components. The linear MMSE estimate is
Figure 8.1 Principal component analyses.
PCA can be used as a first step to reduce the dimension of the measurement space. In practice, the covariance matrix is often replaced by the sample covariance estimated from a training set (see Section 5.2.3).
Unfortunately, PCA can be counterproductive for classification and estimation problems. The PCA criterion selects a subspace of the feature space such that the variance of z is conserved as much as possible. However, this is done regardless of the classes. A subspace with large variance is not necessarily one in which classes are well separated.
A second drawback of PCA is that the results are not invariant to the particular choice of the physical units of the measurements. Each element of z is individually scaled according to its unit in which it is expressed. Changing a unit from, for instance, m (metre) to μm (micrometre) may result in dramatic changes of the principal directions. Usually this phenomenon is circumvented by scaling the vector z such that the numerical values of the elements all have unit variance.
Example 8.1 Image compression
Since PCA aims at the reduction of a measurement vector in such a way that it can be reconstructed accurately, the technique is suitable for image compression. Figure 8.2 shows the original image. The image plane is partitioned into 32 × 32 regions each having 8 × 8 pixels. The grey levels of the pixels are stacked in 64-dimensional vectors zn from which the sample mean and the sample covariance matrix have been estimated. The figure also shows the fraction of the cumulative eigenvalues, that is ![]() where γi is the ith diagonal element of Γ. The first eight eigenvectors are depicted as 8 × 8 images. The reconstruction based on these eight eigenvectors is also shown. The compression is about 96%. PRTools code for this PCA compression algorithm is given in Listing 8.1.
where γi is the ith diagonal element of Γ. The first eight eigenvectors are depicted as 8 × 8 images. The reconstruction based on these eight eigenvectors is also shown. The compression is about 96%. PRTools code for this PCA compression algorithm is given in Listing 8.1.

Figure 8.2 Application of PCA to image compression.
Listing 8.1 PRTools code for finding a set of PCA basis vectors for image compression and producing output similar to Figure 8.2.
im = double(imread(‘car.tif’)); % Load image
figure; clf; imshow(im, [0 255]); % Display image
x = im2col(im,[8 8],‘distinct’); % Extract 8x8 windows
z = dataset(x’); % Create dataset
z.featsize = [8 8]; % Indicate window size
% Plot fraction of cumulative eigenvalues
v = pca(z,0); figure; clf; plot(v);
% Find 8D PCA mapping and show basis vectors
w = pca(z,8); figure; clf; show(w)
% Reconstruct image and display it
z_hat = z*w*w’;
im_hat = col2im (+z_hat’,[8 8], size(im),‘distinct’);
figure; clf; imshow (im_hat, [0 255]);The original image blocks are converted into vectors, a dataset is created and a PCA base is found. This base is then shown and used to reconstruct the image. Note that this listing also uses the Matlab® Image Processing toolbox, specifically the functions im2col and co12im. The function pca is used for the actual analysis.
8.1.2 Multidimensional Scaling
Principal component analysis is limited to finding linear combinations of features on which to map the original data. This is sufficient for many applications, such as discarding low-variance directions in which only noise is suspected to be present. However, if the goal of a mapping is to inspect data in a two- or three-dimensional projection, PCA might discard too much information. For example, it can project two distinct groups in the data on top of each other or it might not show whether data are distributed non-linearly in the original high-dimensional measurement space.
To retain such information, a non-linear mapping method is needed. As there are many possible criteria to fit a mapping, there are many different methods available. Here we will discuss just one: multidimensional scaling (MDS) (Kruskal and Wish, 1977) or Sammon mapping (Sammon, 1969). The self-organizing map, discussed in Section 8.2.5, can be considered as another non-linear projection method.
MDS is based on the idea that the projection should preserve the distances between objects as well as possible. Given a dataset containing N-dimensional measurement vectors (or feature vectors) zi, i = 1, …, NS, we try to find new D-dimensional vectors yi, i = 1, …, NS according to this criterion. Usually, D ≪ N; if the goal is to visualize the data, we choose D = 2 or D = 3. If δij denotes the known distance between objects zi and zj, and dij denotes the distance between projected objects yi and yj, then distances can be preserved as well as possible by placing the yi such that the stress measure

is minimized. To do so, we take the derivative of (8.5) with respect to the objects y. It is not hard to derive that, when Euclidean distances are used, then

There is no closed-form solution setting this derivative to zero, but a gradient descent algorithm can be applied to minimize Equation (8.5). The MDS algorithm is then as follows.
Algorithm 8.1 Multidimensional scaling
- Initialization: randomly choose an initial configuration of the projected objects y(0). Alternatively, initialize y(0) by projecting the original dataset on its first D principal components. Set t = 0.
- Gradient descent
- For each object y(t)i, calculate the gradient according to Equation (8.6).
- Update: y(t + 1)i = yi(t) − α∂ES/∂y(t)i, where α is a learning rate.
- As long as ES significantly decreases, set t = t + 1 and go to step 2.
Figures 8.3(a) to (c) show examples of two-dimensional MDS mapping. The dataset, given in Table 8.1, consists of the geodesic distances of 13 world cities. These distances can only be fully brought in accordance with the true three-dimensional geographical positions of the cities if the spherical surface of the Earth is accounted for. Nevertheless, MDS has found two-dimensional mappings that resemble the usual Mercator projection of the Earth's surface on the tangent plane at the North Pole.

Figure 8.3 MDS applied to a matrix of geodesic distances of world cities.
Table 8.1 Distance matrix of 13 cities (in km)
| 0 | 3290 | 7280 | 10100 | 10600 | 9540 | 13300 | 7350 | 7060 | 13900 | 16100 | 17700 | 4640 | Bangkok |
| 0 | 7460 | 12900 | 8150 | 8090 | 10100 | 9190 | 5790 | 11000 | 17300 | 19000 | 2130 | Beijing | |
| 0 | 7390 | 14000 | 3380 | 12100 | 14000 | 2810 | 8960 | 9950 | 12800 | 9500 | Cairo | ||
| 0 | 18500 | 9670 | 16100 | 10300 | 10100 | 12600 | 6080 | 7970 | 14800 | Capetown | |||
| 0 | 11600 | 4120 | 8880 | 11200 | 8260 | 13300 | 11000 | 6220 | Honolulu | ||||
| 0 | 8760 | 16900 | 2450 | 5550 | 9290 | 11700 | 9560 | London | |||||
| 0 | 12700 | 9740 | 3930 | 10100 | 9010 | 8830 | Los Angeles | ||||||
| 0 | 14400 | 16600 | 13200 | 11200 | 8200 | Melbourne | |||||||
| 0 | 7510 | 11500 | 14100 | 7470 | Moscow | ||||||||
| 0 | 7770 | 8260 | 10800 | New York | |||||||||
| 0 | 2730 | 18600 | Rio | ||||||||||
| 0 | 17200 | Santiago | |||||||||||
| 0 | Tokyo |
Since distances are invariant to translation, rotation and mirroring, MDS can result in arbitrarily shifted, rotated and mirrored mappings. The mapped objects in Figures 8.3 have been rotated such that New York and Beijing lie on a horizontal line with New York on the left. Furthermore, the vertical axis is mirrored such that London is situated below the line New York–Beijing.
The reason for the preferred projection on the tangent plane near the North Pole is that most cities in the list are situated in the Northern hemisphere. The exceptions are Santiago, Rio, Capetown and Melbourne. The distances for just these cities are least preserved. For instance, the true geodesic distance between Capetown and Melbourne is about 10 000 (km), but they are mapped opposite to each other with a distance of about 18 000 (km).
For specific applications, it might be fruitful to focus more on local structure or on global structure. A way of doing so is by using the more general stress measure, where an additional free parameter q is introduced:

For q = 0, Equation (8.7) is equal to (8.5). However, as q is decreased, the (δij – dij)2 term remains constant but the δqij term will weigh small distances heavier than large ones. In other words, local distance preservation is emphasized, whereas global distance preservation is less important. This is demonstrated in Figure 8.3(a) to (c), where q = –2, q = 0 and q = +2 have been used, respectively. Conversely, if q is increased, the resulting stress measure will emphasize preserving global distances over local ones. When the stress measure is used with q = 1, the resulting mapping is also called a Sammon mapping.
The effects of using different values of q are demonstrated in Table 8.2. Here, for each city in the list, the nearest and the furthest cities are given. For each pair, the true geodesic distance from Table 8.1 is shown together with the corresponding distances in the MDS mappings. Clearly, for short distances, q = –2 is more accurate. For long distances, q = +2 is favourable. In Figure 8.3(a) to (c) the nearest cities (according to the geodesic distances) are indicated by solid thin lines. In addition, the nearest cities according to the MDS maps are indicated by dotted thick lines, Clearly, if q = –2, the nearest neighbours are best preserved. This is expected because the relations between nearest neighbours are best preserved if the local structure is best preserved.
Table 8.2 Results of MDS mapping

Figure 8.3 also shows a three-dimensional MDS mapping of the world cities. For clarity, a sphere is also included. MDS is able to find 2D to 3D mapping such that the resulting map resembles the true geographic position on the Earth's surface. The positions are not exactly on the surface of a sphere because the input of the mapping is a set of geodesic distances, while the output map measures distances according to a three-dimensional Euclidean metric.
The MDS algorithm has the same problems any gradient-based method has: it is slow and it cannot be guaranteed to converge to a global optimum. Another problem the MDS algorithm in particular suffers from is the fact that the number of distances in a dataset grows quadratically with NS. If the datasets are very large, then we need to select a subset of the points to map in order to make the application tractable. Finally, a major problem specific to MDS is that there is no clear way of finding the projection ynew of a new, previously unseen point znew. The only way of making sure that the new configuration {yi, i = 1, …, NS; ynew} minimizes Equation (8.5) is to recalculate the entire MDS mapping. In practice, this is infeasible. A crude approximation is to use triangulation: to map down to D dimensions, search for the D + 1 nearest neighbours of znew among the training points zi. A mapping ynew for znew can then be found by preserving the distances to the projections of these neighbours exactly. This method is fast, but inaccurate: because it uses nearest neighbours, it will not give a smooth interpolation of originally mapped points. A different, but more complicated solution is to use an MDS mapping to train a neural network to predict the yi for given zi. This will give smoother mappings, but brings with it all the problems inherent in neural network training. An example of how to use MDS in PRTools is given in Listing 8.2.
Listing 8.2 PRTools code for performing an MDS mapping.
prload worldcities; % Load dataset D
options. q=2;
w=mds(D,2,options); % Map to 2D with q=2
figure; clf; scatterd(D*w,‘both’); % Plot projections8.1.3 Kernel Principal Component Analysis
Kernel principal component analysis (KPCA) is a technique for non-linear feature extraction, closely related to methods applied in Support Vector Machines. It has been proved useful for various applications, such as de-noising and as a pre-processing step in regression problems. KPCA has also been applied, by Romdhani et al., to the construction of non-linear statistical shape models of faces. To understand the utility of kernel PCA, particularly for clustering, observe that, while N points cannot in general be linearly separated in d < N dimensions, they can almost always be linearly separated in d ≥ N dimensions. That is, given N points, xi if we map them to an N-dimensional space with Φ(xi) where Φ: Rd → RN, it is easy to construct a hyperplane that divides the points into arbitrary clusters. Of course, this Φ creates linearly independent vectors, so there is no covariance on which to perform eigen decomposition explicitly as we would in linear PCA.
Instead, in kernel PCA, a non-trivial, arbitrary Φ function is ‘chosen’ that is never calculated explcitly, allowing the possibility to use very-high-dimensional Φ’s if we never have to actually evaluate the data in that space. Since we generally try to avoid working in the Φ-space, which we will call the ‘feature space’, we can create the N-by-N kernel
which represents the inner product space (see Gramian matrix) of the otherwise intractable feature space. The dual form that arises in the creation of a kernel allows us to mathematically formulate a version of PCA in which we never actually solve the eigenvectors and eigenvalues of the covariance matrix in the Φ(x) space (see the kernel trick). The N-elements in each column of K represent the dot product of one point of the transformed data with respect to all the transformed points (N points). Some well-known kernels are shown in the example below.
Because we are never working directly in the feature space, the kernel formulation of PCA is restricted in that it computes not the principal components themselves but the projections of our data on to those components. To evaluate the projection from a point in the feature space Φ(x) on to the kth principal component Vk (where the superscript k means the component k, not powers of k)
We note that Φ(xi)TΦ(x) denotes the dot product, which is simply the elements of the kernel K. It seems all that is left is to calculate and normalize the aki which can be done by solving the eigenvector equation
where N is the number of data points in the set, and λ and a are the eigenvalues and eigenvectors of K. Then to normalize the eigenvectors ak we require that
Care must be taken regarding the fact that, whether or not χ has zero mean in its original space, it is not guaranteed to be centred in the feature space (which we never compute explicitly). Since centred data is required to perform an effective principal component analysis, we ‘centralize’ K to become K'$: ? >
where 1N denotes an N-by-N matrix for which each element takes value ![]() We use K' to perform the kernel PCA algorithm described above.
We use K' to perform the kernel PCA algorithm described above.
One caveat of kernel PCA should be illustrated here. In linear PCA, we can use the eigenvalues to rank the eigenvectors based on how much of the variation of the data is captured by each principal component. This is useful for data dimensionality reduction and it could also be applied to KPCA. However, in practice there are cases that all variations of the data are the same. This is typically caused by a wrong choice of kernel scale.
Example 8.1a Consider three concentric clouds of points (shown in Figure 8.4); we wish to use kernel PCA to identify these groups (see Figure 8.5). The colour of the points is not part of the algorithm, but are only there to show how the data groups together before and after the transformation.
First, consider the kernel
Applying this to kernel PCA yields the next image.
Now consider a Gaussian kernel:
That is, this kernel is a measure of closeness, equal to 1 when the points coincide and equal to 0 at infinity (see Figure 8.6).
Note in particular that the first principal component is enough to distinguish the three different groups, which is impossible using only linear PCA, because linear PCA operates only in the given (in this case two-dimensional) space, in which these concentric point clouds are not linearly separable.

Figure 8.4 Input points before kernel PCA.

Figure 8.5 Output after kernel PCA with k(x, y) = (xTy + 1)2. The three groups are distinguishable using the first component only (https://en.wikipedia.org/wiki/File:Kernel_pca_output.png).

Figure 8.6 Output after kernel PCA with a Gaussian kernel (https://en.wikipedia.org/wiki/File:Kernel_pca_output_gaussian.png). Source: Lei, https://en.wikipedia.org/wiki/Kernel_principal_component_analysis. Used under CC-BY-SA 3.0 https://en.wikipedia.org/wiki/Wikipedia:Text_of_ Creative_Commons_Attribution-ShareAlike_3.0_Unported_License.
Example 8.1b (Dambreville et al., 2008) KPCA can be considered to be a generalization of linear PCA. This technique has proven to be a powerful method to extract non-linear structures from a dataset. The idea behind KPCA consists of mapping a dataset from an input space I into a feature space F via a non-linear function ϕ. Then PCA is performed in F to find the orthogonal directions (principal components) corresponding to the largest variation in the mapped dataset. The first l principal components account for as much of the variance in the data as possible by using l directions. In addition, the error in representing any of the elements of the training set by its projection on to the first l principal components is minimal in the least squares sense (see Figure 8.7).

Figure 8.7 Kernel PCA methodology. A training set is mapped from input space I to feature space F via a non-linear function ϕ. PCA is performed in F to determine the principal directions defining the kernel PCA space (learned space): oval area. Any element of I can then be mapped to F and projected on the kernel PCA space via Plϕ, where l refers to the first l eigenvectors used to build the KPCA space.

Figure 8.8 The example of reducing dimensionality of a 2D circle by using KPCA.
Example 8.1c This example describes an implemented code to reduce the dimensionality of a two-dimensional circle by using the KPCA function in the Matlab® Startool toolbox (see Figure 8.8). We can get the satisfactory results as follows:
% Kernel Principal Component Analysis
clc
clear
close all
% generate circle data
X = gencircledata([1;1],5,250,1);
% compute kernel PCA
options.ker = 'rbf'; % use RBF kernel
options.arg = 4; % kernel argument
options.new_dim = 2; % output dimension
model = kpca(X,options);
XR = kpcarec(X,model); % compute reconstruced data
% Visualization
figure;
h1 = ppatterns(X);
h2 = ppatterns(XR, '+r');
legend([h1 h2],'Input vectors','Reconstructed');8.2 Clustering
Instead of reducing the number of features, we now focus on reducing the number of objects in the dataset. The aim is to detect ‘natural’ clusters in the data, that is clusters that agree with our human interpretation of the data. Unfortunately, it is very hard to define what a natural cluster is. In most cases, a cluster is defined as a subset of objects for which the resemblance between the objects within the subset is larger than the resemblance with other objects in other subsets (clusters).
This immediately introduces the next problem: how is the resemblance between objects defined? The most important cue for the resemblance of two objects is the distance between the objects, that is their dissimilarity. In most cases the Euclidean distance between objects is used as a dissimilarity measure, but there are many other possibilities. The Lp norm is well known (see Appendix A.1.1 and A.2):

The cosine distance uses the angle between two vectors as a dissimilarity measure. It is often used in the automatic clustering of text documents:

In PRTools the basic distance computation is implemented in the function proxm. Several methods for computing distances (and similarities) are defined. Next to the two basic distances mentioned above, some similarity measures are also defined, like the inner product between vectors and the Gaussian kernel. The function is implemented as a mapping. When a mapping w is trained on some data z, the application y*w then computes the distance between any vector in z and any vector in y. For the squared Euclidean distances a short-cut function distm is defined.
Listing 8.3 PRTools code for defining and applying a proximity mapping.
z = gendatb(3); % Create some train data
y = gendats(5); % and some test data
w = proxm(z,‘d’,2); % Squared Euclidean distance to z
D = y*w; % 5 × 3 distance matrix
D = distm(y,z); % The same 5 × 3 distance matrix
w = proxm(z,‘o’); % Cosine distance to z
D = y*w; % New 5 × 3 distance matrixThe distance between objects should reflect the important structures in the dataset. It is assumed in all clustering algorithms that distances between objects are informative. This means that when objects are close in the feature space, they should also resemble each other in the real world. When the distances are not defined sensibly and remote objects in the feature space correspond to similar real-world objects, no clustering algorithm will be able to give acceptable results without extra information from the user. In these sections it will therefore be assumed that the features are scaled such that the distances between objects are informative. Note that a cluster does not necessarily correspond directly to a class. A class can consist of multiple clusters or multiple classes may form a single cluster (and will therefore probably be hard to discriminate between).
By the fact that clustering is unsupervised, it is very hard to evaluate a clustering result. Different clustering methods will yield a different set of clusters and the user has to decide which clustering is to be preferred. A quantitative measure of the quality of the clustering is the average distance of the objects to their respective cluster centre. Assume that the objects zi (i = 1… NS) are clustered in K clusters, Ck (k = 1… K) with cluster center ![]() k and to each of the clusters Nk objects are assigned:
k and to each of the clusters Nk objects are assigned:

Other criteria, such as the ones defined in Chapter 5 for supervised learning, can also be applied.
With these error criteria, different clustering results can be compared provided that K is kept constant. Clustering results found for varying K cannot be compared. The pitfall of using criteria like Equation (8.10) is that the optimal number of clusters is K = NS, that is the case in which each object belongs to its own cluster. In the average-distance criterion it will result in the trivial solution: J = 0.
The choice of the number of clusters K is a very fundamental problem. In some applications, an expected number of clusters is known beforehand. Using this number for the clustering does not always yield optimal results for all types of clustering methods: it might happen that, due to noise, a local minimum is reached. Using a slightly larger number of clusters is therefore sometimes preferred. In most cases the number of clusters to look for is one of the research questions in the investigation of a dataset. Often the data are repeatedly clustered using a range of values of K and the clustering criterion values are compared. When a significant decrease in a criterion value appears, a ‘natural’ clustering is probably found. Unfortunately, in practice, it is very hard to objectively say when a significant drop occurs. True automatic optimization of the number of clusters is possible in just a very few situations, when the cluster shapes are given.
In the coming sections we will discuss four methods for performing a clustering: hierarchical clustering, K-means clustering, mixtures of Gaussians and finally self-organizing maps.
8.2.1 Hierarchical Clustering
The basic idea of hierarchical clustering (Johnson, 1977) is to collect objects into clusters by combining the closest objects and clusters to larger clusters until all objects are in one cluster. An important advantage is that the objects are not just placed in K distinct groups, but are placed in a hierarchy of clusters. This gives more information about the structure in the dataset and shows which clusters are similar or dissimilar. This makes it possible to detect subclusters in large clusters or to detect outlier clusters.
Figure 8.9 provides an example. The distance matrix of the 13 world cities given in Table 8.1 are used to find a hierarchical cluster structure. The figure shows that at the highest level the cities in the southern hemisphere are separated from the ones in the northern part. At a distance level of about 5000 km we see the following clusters: ‘East Asiatic cities’, ‘European/Arabic cities’, ‘North American cities’, ‘African city’, ‘South American cities’, ‘Australian city’.

Figure 8.9 Hierarchical clustering of the data in Table 8.1.
Given a set of NS objects zi to be clustered and an NS × NS distance matrix between these objects, the hierarchical clustering involves the following steps.
Algorithm 8.2 Hierarchical clustering
- Assign each object to its own cluster, resulting in NS clusters, each containing just one object. The initial distances between all clusters are therefore just the distances between all objects.
- Find the closest pair of clusters and merge them into a single cluster, so that the number of clusters reduces by one.
- Compute the distance between the new cluster and each of the old clusters, where the distance between two clusters can be defined in a number of ways (see below).
- Repeat steps 2 and 3 until all items are clustered into a single cluster of size NS or until a predefined number of clusters K is achieved.
In step 3 it is possible to compute the distances between clusters in several different ways. We can distinguish single-link clustering, average-link clustering and complete-link clustering. In single-link clustering, the distance between two clusters Ci and Cj is defined as the shortest distance from any object in one cluster to any object in the other cluster:
For average-link clustering, the minimum operator is replaced by the average distance and for the complete-link clustering it is replaced by the maximum operator.
In Figure 8.10 the difference between single link and complete link is shown for a very small toy dataset (NS = 6). At the start of the clustering, both single-link (left) and complete-link clustering (right) combine the same objects in clusters. When larger clusters appear, in the lower row, different objects are combined. The different definitions for the intercluster distances result in different characteristic cluster shapes. For single-link clustering, the clusters tend to become long and spidery, while for complete-link clustering the clusters become very compact.

Figure 8.10 The development from K = NS clusters to K = 1 cluster. (a) Single-link clustering. (b) Complete-link clustering.
The user now has to decide on what the most suitable number of clusters is. This can be based on a dendrogram. The dendrogram shows at which distances the objects or clusters are grouped together. Examples for single- and complete-link clustering are shown in Figure 8.11. At smaller distances, pairs of single objects are combined, at higher distances complete clusters. When there is a large gap in the distances, as can be seen in the single-link dendrogram, it is an indication that the two clusters are far apart. Cutting the dendrogram at height 1.0 will then result in a ‘natural’ clustering, consisting of two clusters. In many practical cases, the cut is not obvious to define and the user has to guess an appropriate number of clusters.

Figure 8.11 Hierarchical clustering with two different clustering types. (a) Single-link clustering. (b) Complete-link clustering.
Note that this clustering is obtained using a fixed dataset. When new objects become available, there is no straightforward way to include it in an existing clustering. In these cases, the clustering will have to be constructed from the beginning using the complete dataset.
In PRTools, it is simple to construct a hierarchical clustering. Listing 8.4 shows an example. Note that the clustering operates on a distance matrix rather than the dataset. A distance matrix can be obtained with the function distm.
Listing 8.4 PRTools code for obtaining a hierarchical clustering.
z = gendats(5); % Generate some data
figure; clf; scatterd(z); % and plot it
dendr = hclust(distm(z),‘s’); % Single link clustering
figure; clf; plotdg(dendr); % Plot the dendrogram8.2.2 K-Means Clustering
K-means clustering (Bishop, 1995) differs in two important aspects from hierarchical clustering. First, K-means clustering requires the number of clusters K beforehand. Second, it is not hierarchical; instead it partitions the dataset into K disjoint subsets. Again the clustering is basically determined by the distances between objects. The K-means algorithm has the following structure.
Algorithm 8.3 K-means clustering
- Assign each object randomly to one of the clusters k = 1, … , K.
- Compute the means of each of the clusters:
(8.19)

- Reassign each object zi to the cluster with the closest mean
 k.
k. - Return to step 2 until the means of the clusters do not change any more.
The initialization step can be adapted to speed up the convergence. Instead of randomly labelling the data, K randomly chosen objects are taken as cluster means. Then the procedure enters the loop in step 3. Note again that the procedure depends on distances, in this case between the objects zi and the means ![]() k. Scaling the feature space will here also change the final clustering result. An advantage of K-means clustering is that it is very easy to implement. On the other hand, it is unstable: running the procedure several times will give several different results. Depending on the random initialization, the algorithm will converge to different (local) minima. In particular, when a high number of clusters is requested, it often happens that some clusters do not gain sufficient support and are ignored. The effective number of clusters then becomes much less than K.
k. Scaling the feature space will here also change the final clustering result. An advantage of K-means clustering is that it is very easy to implement. On the other hand, it is unstable: running the procedure several times will give several different results. Depending on the random initialization, the algorithm will converge to different (local) minima. In particular, when a high number of clusters is requested, it often happens that some clusters do not gain sufficient support and are ignored. The effective number of clusters then becomes much less than K.
In Figure 8.12 the result of a K-means clustering is shown for a simple 2D dataset. The means are indicated by the circles. At the start of the optimization, that is at the start of the trajectory, each mean coincides with a data object. After 10 iteration steps, the solution converged. The result of the last iteration is indicated by ‘×’. In this case, the number of clusters in the data and the predefined K = 3 match. A fairly stable solution is found.

Figure 8.12 The development of the cluster means during 10 update steps of the K-means algorithm.
Example 8.2 Classification of mechanical parts, K-means clustering Two results of the K-means algorithm applied to the unlabelled dataset of Figure 5.1(b) are shown in Figure 8.13. The algorithm is called with K = 4. The differences between the two results are solely caused by the different realizations of the random initialization of the algorithm. The first result, Figure 8.13(a), is more or less correct (compare with the correct labelling as given in Figure 5.1(a). Unfortunately, the result in Figure 8.13(b) indicates that this success is not reproducible. The algorithm is implemented in PRTools with the function kmeans (see Listing 8.5).

Figure 8.13 Two results of K-means clustering applied to the ‘mechanical parts’ dataset.
Listing 8.5 PRTools code for fitting and plotting a K-means clustering, with K = 4.
prload nutsbolts_unlabeled; % Load the data set z
lab = kmeans(z,4); % Perform k-means clustering
y = dataset(z,lab); % Label by cluster assignment
figure; clf; scatterd(y); % and plot it8.2.3 Mixture of Gaussians
In the K-means clustering algorithm, spherical clusters were assumed by the fact that the Euclidean distance to the cluster centres ![]() k is computed. All objects on a circle or hypersphere around the cluster centre will have the same resemblance to that cluster. However, in many cases clusters have more structure than that. In the mixture of Gaussians model (Dempster et al., 1977; Bishop, 1995), it is assumed that the objects in each of the K clusters are distributed according to a Gaussian distribution. This means that each cluster is not only characterized by a mean
k is computed. All objects on a circle or hypersphere around the cluster centre will have the same resemblance to that cluster. However, in many cases clusters have more structure than that. In the mixture of Gaussians model (Dempster et al., 1977; Bishop, 1995), it is assumed that the objects in each of the K clusters are distributed according to a Gaussian distribution. This means that each cluster is not only characterized by a mean ![]() k but also by a covariance matrix Ck. In effect, a complete density estimate of the data is performed, where the density is modelled by
k but also by a covariance matrix Ck. In effect, a complete density estimate of the data is performed, where the density is modelled by

N(z|![]() k,Ck) stands for the multivariate Gaussian distribution and πk are the mixing parameters (for which
k,Ck) stands for the multivariate Gaussian distribution and πk are the mixing parameters (for which ![]() ). The mixing parameter πk can be regarded as the probability that z is produced by a random number generator with probability density N(z|
). The mixing parameter πk can be regarded as the probability that z is produced by a random number generator with probability density N(z|![]() k, Ck).
k, Ck).
The parameters to be estimated are the number K of mixing components, the mixing parameters π1, … , πK, the mean vectors ![]() k and the covariance matrices Ck. We will denote this set of free parameters by
k and the covariance matrices Ck. We will denote this set of free parameters by ![]() . This increase in the number of free parameters, compared to the K-means algorithm, leads to the need for a higher number of training objects in order to reliably estimate these cluster parameters. On the other hand, because more flexible cluster shapes are applied, fewer clusters might have to be used to approximate the structure in the data.
. This increase in the number of free parameters, compared to the K-means algorithm, leads to the need for a higher number of training objects in order to reliably estimate these cluster parameters. On the other hand, because more flexible cluster shapes are applied, fewer clusters might have to be used to approximate the structure in the data.
One method for fitting the parameters of Equation (8.20) to the data is to use the maximum likelihood estimation (see Section 4.1.4), i.e. to optimize the log-likelihood:

with ![]() . The optimization of L(Z|Ψ) w.r.t. Ψ is complicated and cannot be done directly with this equation. Fortunately, there exists a standard ‘hill-climbing’ algorithm to optimize the parameters in this equation. The expectation-maximization (EM) algorithm is a general procedure that assumes the following problem definition. We have two data spaces: the observed data Z and the so-called missing data (hidden data)
. The optimization of L(Z|Ψ) w.r.t. Ψ is complicated and cannot be done directly with this equation. Fortunately, there exists a standard ‘hill-climbing’ algorithm to optimize the parameters in this equation. The expectation-maximization (EM) algorithm is a general procedure that assumes the following problem definition. We have two data spaces: the observed data Z and the so-called missing data (hidden data) ![]() . Let Y be the complete data in which each vector yn consists of a known part zn and a missing part xn. Thus, the vectors yn are defined by yTn = [znT xTn]. Only zn is available in the training set; xn is missing and as such is unknown. The EM algorithm uses this model of ‘incomplete data’ to iteratively estimate the parameters Ψ of the distribution of zn. It tries to maximize the log-likelihood L(Z|Ψ). In fact, if the result of the ith iteration is denoted by Ψ (i), then the EM algorithm ensures that L(Z|Ψ (i+1)) ≥ L(Z|Ψ (i)).
. Let Y be the complete data in which each vector yn consists of a known part zn and a missing part xn. Thus, the vectors yn are defined by yTn = [znT xTn]. Only zn is available in the training set; xn is missing and as such is unknown. The EM algorithm uses this model of ‘incomplete data’ to iteratively estimate the parameters Ψ of the distribution of zn. It tries to maximize the log-likelihood L(Z|Ψ). In fact, if the result of the ith iteration is denoted by Ψ (i), then the EM algorithm ensures that L(Z|Ψ (i+1)) ≥ L(Z|Ψ (i)).
The mathematics behind the EM algorithm is rather technical and will be omitted. However, the intuitive idea behind the EM algorithm is as follows. The basic assumption is that with all data available, that is if we had observed the complete data Y, the maximization of L(Y|Ψ) would be simple, and the problem could be solved easily. Unfortunately, only Z is available and X is missing. Therefore, we maximize the expectation E[L(Y|Ψ)|Z] instead of L (Y|Ψ). The expectation is taken over the complete data Y, but under the condition of the observed data Z. The estimate from the ith iteration follows from

The integral extends over the entire Y space. The first step is the E step; the last one is the M step.
In the application of EM optimization to a mixture of Gaussians (with predefined K; see also the discussion in Section 8.2.1) the missing part xn, associated with zn, is a K-dimensional vector and xn indicates which one of the K Gaussians generated the corresponding object zn. The xn are called indicator variables. They use position coding to indicate the Gaussian associated with zn. In other words, if zn is generated by the kth Gaussian, then xn,k = 1 and all other elements in xn are zero. From that, the prior probability that xn,k = 1 is πk.
In this case, the complete log-likelihood of Ψ can be written as

Under the condition of a given Z, the probability density p(Y|Z, Ψ) = p(X, Z|Z, Ψ) can be replaced with the marginal probability P(X|Z, Ψ). Therefore in Equation (8.22), we have

However, since in Equation (8.23) L(Y|Ψ) is linear in X, we conclude that
where ![]() is the expectation of the missing data under the condition of Z and Ψ(i):
is the expectation of the missing data under the condition of Z and Ψ(i):

The variable ![]() is called the ownership because it indicates to what degree sample zn is attributed to the kth component.
is called the ownership because it indicates to what degree sample zn is attributed to the kth component.
For the M step, we have to optimize the expectation of the log-likelihood, that is ![]() . We do this by substituting
. We do this by substituting ![]() for xn,k into Equation (8.23), taking the derivative with respect to Ψ and setting the result to zero. Solving the equations will yield expressions for the parameters Ψ = {πk,
for xn,k into Equation (8.23), taking the derivative with respect to Ψ and setting the result to zero. Solving the equations will yield expressions for the parameters Ψ = {πk, ![]() k, Ck} in terms of the data zn and
k, Ck} in terms of the data zn and ![]() .
.
Taking the derivative of ![]() with respect to
with respect to ![]() k gives
k gives

Rewriting this gives the update rule for ![]() k:
k:

The estimation of Ck is somewhat more complicated. With the help of Equation (B.39), we can derive
This results in the following update rule for Ck:
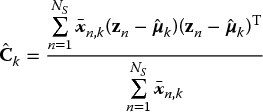
Finally, the parameters πk cannot be optimized directly because of the extra constraint, namely that![]() . This constraint can be enforced by introducing a Lagrange multiplier λ and extending the log-likelihood (8.23) by
. This constraint can be enforced by introducing a Lagrange multiplier λ and extending the log-likelihood (8.23) by

Substituting ![]() for xn,k and setting the derivative with respect to πk to zero yields
for xn,k and setting the derivative with respect to πk to zero yields

Summing Equation (8.32) over all clusters, we get

Further note that summing ![]() over all clusters gives the total number of objects NS; thus it follows that λ = NS. By substituting this result back into Equation (8.32), the update rule for πk becomes
over all clusters gives the total number of objects NS; thus it follows that λ = NS. By substituting this result back into Equation (8.32), the update rule for πk becomes

Note that with Equation (8.34), the determination of ![]() k and Ck in Equations (8.28) and (8.30) can be simplified to
k and Ck in Equations (8.28) and (8.30) can be simplified to

The complete EM algorithm for fitting a mixture of Gaussian model to a dataset is as follows.
Algorithm 8.4 EM algorithm for estimating a mixture of Gaussians Input: the number K of mixing components and the data zn.
- Initialization: select randomly (or heuristically) Ψ(0). Set i = 0.
- Expectation step (E step): using the observed data set zn and the estimated parameters Ψ(i), calculate the expectations
 of the missing values xn using Equation (8.26).
of the missing values xn using Equation (8.26). - Maximization step (M step): optimize the model parameters
 by maximum likelihood estimation using the expectation
by maximum likelihood estimation using the expectation  calculated in the previous step (see Equations (8.34) and (8.35)).
calculated in the previous step (see Equations (8.34) and (8.35)). - Stop if the likelihood did not change significantly in step 3. Else, increment i and go to step 2.
Clustering by EM results in more flexible cluster shapes than K-means clustering. It is also guaranteed to converge to (at least) a local optimum. However, it still has some of the same problems of K-means: the choice of the appropriate number of clusters, the dependence on initial conditions and the danger of convergence to local optima.
Example 8.3 Classification of mechanical parts, EM algorithm for mixture of Gaussians Two results of the EM algorithm applied to the unlabelled dataset of Figure 5.1(b) are shown in Figure 8.14. The algorithm is called with K = 4, which is the correct number of classes. Figure 8.14(a) is a correct result. The position and size of each component is appropriate. With random initializations of the algorithm, this result is reproduced with a probability of about 30%. Unfortunately, if the initialization is unlucky, the algorithm can also get stuck in a local minimum, as shown in Figure 8.14(b). Here, the components are at the wrong position.

Figure 8.14 Two results of the EM algorithm for the mixture of Gaussians estimation.
The EM algorithm is implemented in PRTools by the function emclust. Listing 8.6 illustrates its use.
Listing 8.6 Matlab® code for calling the EM algorithm for the mixture of Gaussians estimation.
prload nutsbolts_unlabeled; % Load the data set z
z = setlabtype(z,‘soft’); % Set probabilistic labels
[lab,w] = emclust(z,qdc,4); % Cluster using EM
figure; clf; scatterd(z);
plotm(w,[],0.2:0.2:1); % Plot results8.2.4 Mixture of probabilistic PCA
An interesting variant of the mixture of Gaussians is the mixture of probabilistic principal component analysers (Tipping and Bishop, 1999). Each single model is still a Gaussian like that in Equation (8.20), but its covariance matrix is constrained:
where the D × N matrix Wk has D eigenvectors corresponding to the largest eigenvalues of Ck as its columns and the noise level outside the subspace spanned by Wk is estimated using the remaining eigenvalues:

The EM algorithm to fit a mixture of probabilistic principal component analysers proceeds just as for a mixture of Gaussians, using C′k instead of Ck. At the end of the M step, the parameters Wk and σ2k are re-estimated for each cluster k by applying normal PCA to Ck and Equation (8.37), respectively.
The mixture of probabilistic principal component analysers introduces a new parameter, the subspace dimension D. Nevertheless, it uses far fewer parameters (when D ≪ N) than the standard mixture of Gaussians. Still it is possible to model non-linear data that cannot be done using normal PCA. Finally, an advantage over normal PCA is that it is a full probabilistic model, that is it can be used directly as a density estimate.
In PRTools, probabilistic PCA is implemented in qdc: an additional parameter specifies the number of subspace dimensions to use. To train a mixture, one can use emclust, as illustrated in Listing 8.8.
Listing 8.7 Matlab® code for calling the EM algorithm for a mixture of probabilistic principal component analyer estimation.
prload nutsbolts_unlabeled; % Load the data set z
z = setlabtype(z, ‘soft’); % Set probabilistic labels
[lab,w] = emclust(z,qdc([],[],[],1),4);
% Cluster 1D PCAs using EM
figure; clf; scatterd(z);
plotm(w, [],0.2:0.2:1); % Plot results8.2.5 Self-Organizing Maps
The self-organizing map (SOM; also known as self-organizing feature map, Kohonen map) is an unsupervised clustering and feature extraction method in which the cluster centres are constrained in their placing (Kohonen, 1995). The construction of the SOM is such that all objects in the input space retain as much as possible of their distance and neighbourhood relations in the mapped space. In other words, the topology is preserved in the mapped space. The method is therefore strongly related to multidimensional scaling.
The mapping is performed by a specific type of neural network, equipped with a special learning rule. Assume that we want to map an N-dimensional measurement space to a D-dimensional feature space, where D ≪ N. In fact, often D = 1 or D = 2. In the feature space, we define a finite orthogonal grid with M1 × M2 × ··· × MD grid points. At each grid point we place a neuron. Each neuron stores an N-dimensional vector that serves as a cluster centre. By defining a grid for the neurons, each neuron does not only have a neighbouring neuron in the measurement space but also has a neighbouring neuron in the grid. During the learning phase, neighbouring neurons in the grid are enforced to also be neighbours in the measurement space. By doing so, the local topology will be preserved.
The SOM is updated using an iterative update rule, which honours the topological constraints on the neurons. The iteration runs over all training objects zn, n = 1, … , NS, and at each iteration the following steps are taken.
Algorithm 8.5 Training a self-organizing map
- Initialization: choose the grid size, M1, …, MD, and initialize the weight vectors w(0)j (where j = 1, … , M1 × ··· × MD) of each neuron, for instance, by assignment of the values of M1 × ··· × MD different samples from the dataset and that are randomly selected. Set i = 0.
- Iterate:
- 2.1 Find, for each object zn in the training set, the most similarneuron w(i)k:
(8.38)
- This is called the best-matching or winning neuron for thisinput vector.
- 2.2 Update the winning neuron and its neighbours using theupdate rule:
(8.39)

- 2.3 Repeat steps 2.1 and 2.2 for all samples zn in the dataset.
- 2.4 If the weights in the previous steps did not change signif-icantly, then stop. Else, increment i and go to step 2.1.
Here η(i) is the learning rate and h(i)(|k(zn) – j|) is a weighting function. Both can depend on the iteration number i. This weighting function weighs how much a particular neuron in the grid is updated. The term |k(zn) – j| indicates the distance between the winning neuron k(zn) and neuron j, measured over the grid. The winning neuron (for which j = k(zn)) will get the maximal weight, because h(i)( ) is chosen such that
Thus, the winning neuron will get the largest update. This update moves the neuron in the direction of zn by the term (zn – wj).
The other neurons in the grid will receive smaller updates. Since we want to preserve the neighbourhood relations only locally, the further the neuron is from the winning neuron, the smaller the update. A commonly used weighting function that satisfies these requirements is the Gaussian function:

For this function a suitable scale σ(i) over the map should be defined. This weighting function can be used for a grid of any dimension (not just one-dimensional) when we realize that |k(zn) – j| means in general the distance between the winning neuron k(zn) and neuron j over the grid.
Let us clarify this with an example. Assume we start with data zn uniformly distributed in a square in a two-dimensional measurement space and we want to map these data into a one-dimensional space. Therefore, K = 15 neurons are defined. These neurons are ordered such that neuron j – 1 is the left neighbour of neuron j and neuron j + 1 is the right neighbour. In the weighting function σ = 1 is used, in the update rule η = 0:01; these are not changed during the iterations. The neurons have to be placed as objects in the feature space such that they represent the data as best as possible. Listing 8.8 shows an implementation for training a one-dimensional map in PRTools.
Listing 8.8 PRTools code for training and plotting a self-organizing map.
z = rand(100,2); % Generate the data set z
w = som(z,15); % Train a 1D SOM and show it
figure; clf; scatterd(z); plotsom(w);In Figure 8.15 four scatterplots of this dataset with the SOM (K = 15) are shown. In the left subplot, the SOM is randomly initialized by picking K objects from the dataset. The lines between the neurons indicate the neighbouring relationships between the neurons. Clearly, neighbouring neurons in feature space are not neighbouring in the grid. In the fourth subplot it is visible that after 100 iterations over the dataset, the one-dimensional grid has organized itself over the square. This solution does not change in the next 500 iterations.

Figure 8.15 The development of a one-dimensional self-organizing map, trained on a two-dimensional uniform distribution: (a) initialization; (b) to (d) after 10, 25 and 100 iterations, respectively.
With one exception, the neighbouring neurons in the measurement space are also neighbouring neurons in the grid. Only where the one-dimensional string crosses do neurons far apart in the grid become close neighbours in the feature space. This local optimum, where the map did not unfold completely in the measurement space, is often encountered in SOMs. It is very hard to get out of this local optimum. The solution would be to restart the training with another random initialization.
Many of the unfolding problems, and the speed of convergence, can be solved by adjusting the learning parameter η(i) and the characteristic width in the weighting function h(i)(|k(zn) – j|) during the iterations. Often, the following functional forms are used:

This introduces two additional scale parameters that have to be set by the user.
Although the SOM offers a very flexible and powerful tool for mapping a dataset to one or two dimensions, the user is required to make many important parameter choices: the dimension of the grid, the number of neurons in the grid, the shape and initial width of the neighbourhood function, the initial learning rate and the iteration dependencies of the neighbourhood function and learning rate. In many cases a two-dimensional grid is chosen for visualization purposes, but it might not fit the data well. The retrieved data reduction will therefore not reflect the true structure in the data and visual inspection only reveals an artificially induced structure. Training several SOMs with different settings might provide some stable solution.
Example 8.4 SOM of the RGB samples of an illuminated surface Figure 8.16(a) shows the RGB components of a colour image. The imaged object has a spherical surface that is illuminated by a spot illuminator. The light–material interaction involves two distinct physical mechanisms: diffuse reflection and specular (mirror-like) reflection. The RGB values that result from diffuse reflection are invariant to the geometry. Specular reflection only occurs at specific surface orientations determined by the position of the illuminator and the camera. Therefore, specular reflection is seen in the image as a glossy spot, a so-called highlight. The colour of the surface is determined by its spectral properties of the diffuse reflection component. Usually, specular reflection does not depend on the wavelength of the light so that the colour of the highlight is solely determined by the illuminator (usually white light).

Figure 8.16 A SOM that visualizes the effects of a highlight. (a) RGB image of an illuminated surface with a highlight (= glossy spot). (b) Scatter diagram of RGB samples together with a one-dimensional SOM.
Since light is additive, an RGB value z is observed as a linear combination of the diffuse component and the off-specular component: z = αzdiff + βzspec. The variables α and β depend on the geometry. The estimation of zdiff and zspec from a set of samples of z is an interesting problem. Knowledge of zdiff and zspec would, for instance, open the door to ‘highlight removal’.
Here, a one-dimensional SOM of the data is helpful to visualize the data. Figure 8.16(b) shows such a map. The figure suggests that the data forms a one-dimensional manifold, i.e. a curve in the three-dimensional RGB space. The manifold has the shape of an elbow. In fact, the orientation of the lower part of the elbow corresponds to data from an area with only diffuse reflection, that is to αzdiff. The upper part corresponds to data from an area with both diffuse and specular reflection, that is to αzdiff + βzspec.
8.2.6 Generative Topographic Mapping
We conclude this chapter with a probabilistic version of the self-organizing map, the generative topographic mapping (or GTM) (Bishop et al., 1998). The goal of the GTM is the same as that of the SOM: to model the data by clusters with the constraint that neighbouring clusters in the original space are also neighbouring clusters in the mapped space. Contrary to the SOM, a GTM is fully probabilistic and can be trained using the EM algorithm.
The GTM starts from the idea that the density p(z) can be represented in terms of a D-dimensional latent variable q, where in general D ≪ N. For this, a function z = ![]() (q; W) with weights W has to be found. The function maps a point q into a corresponding object z =
(q; W) with weights W has to be found. The function maps a point q into a corresponding object z = ![]() (q; W). Because in reality the data will not be mapped perfectly, we assume some Gaussian noise with variance σ2 in all directions. The full model for the probability of observing a vector z is
(q; W). Because in reality the data will not be mapped perfectly, we assume some Gaussian noise with variance σ2 in all directions. The full model for the probability of observing a vector z is

In general, the distribution of z in the high-dimensional space can be found by integration over the latent variable q:
In order to allow an analytical solution of this integral, a simple grid-like probability model is chosen for p(q), just like in the SOM:

That is a set of Dirac functions centred on grid nodes qk. The log-likelihood of the complete model can then be written as

However, the functional form for the mapping function ![]() (q; W) still has to be defined. This function maps the low-dimensional grid to a manifold in the high-dimensional space. Therefore, its form controls how non-linear the manifold can become. In the GTM, a regression on a set of fixed basis functions is used:
(q; W) still has to be defined. This function maps the low-dimensional grid to a manifold in the high-dimensional space. Therefore, its form controls how non-linear the manifold can become. In the GTM, a regression on a set of fixed basis functions is used:
where ![]() (q) is a vector containing the output of M basis functions, which are usually chosen to be Gaussian with means on the grid points and a fixed width σϕ. W is an N × M weight matrix.
(q) is a vector containing the output of M basis functions, which are usually chosen to be Gaussian with means on the grid points and a fixed width σϕ. W is an N × M weight matrix.
Given settings for K, M and σϕ, the EM algorithm can be used to estimate W and σ2. Let the complete data be yTn = [znT xTn], with xn the hidden variables; xn is a K-dimensional vector. The element xn,k codes the membership of zn with respect to the kth cluster. After proper initialization, the EM algorithm proceeds as follows.
Algorithm 8.6 EM algorithm for training a GTM
- E step: estimate the missing data:
(8.48)using Bayes’ theorem.

- M step: re-estimate the parameters:
(8.49)
 (8.50)
(8.50)
- Repeat steps 1 and 2 until no significant changes occur.
G is a K × K diagonal matrix with ![]() as elements. Γ is a K × M matrix containing the basis functions: Γk,m = γm(qk).
as elements. Γ is a K × M matrix containing the basis functions: Γk,m = γm(qk). ![]() is an NS × K matrix with the
is an NS × K matrix with the ![]() as elements. Z is a NS × N matrix, which contains the data vectors zTn as its rows. Finally, λ is a regularization parameter, which is needed in cases where ΓTGΓ becomes singular and the inverse cannot be computed.
as elements. Z is a NS × N matrix, which contains the data vectors zTn as its rows. Finally, λ is a regularization parameter, which is needed in cases where ΓTGΓ becomes singular and the inverse cannot be computed.
The GTM can be initialized by performing PCA on the dataset, projecting the data to D dimensions and finding W such that the resulting latent variables qn approximate as well as possible the projected data. The noise variance σ2 can be found as the average of the N – D smallest eigenvalues, as in probabilistic PCA.
Training the GTM is usually quick and converges well. However, it suffers from the standard problem of EM algorithms in that it may converge to a local optimum. Furthermore, its success depends highly on the choices for K (the number of grid points), M (the number of basis functions for the mapping), σϕ (the width of these basis functions) and λ (the regularization term). For inadequate choices, the GTM may reflect the structure in the data very poorly. The SOM has the same problem, but needs to estimate somewhat less parameters.
An advantage of the GTM over the SOM is that the parameters that need to be set by the user have a clear interpretation, unlike in the SOM where unintuitive parameters such as learning parameters and time parameters have to be defined. Furthermore, the end result is a probabilistic model, which can easily be compared to other models (e.g. in terms of likelihood) or combined with them.
Figure 8.17 shows some examples of GTMs (D = 1) trained on uniformly distributed data. Figure 8.17(a) clearly shows how the GTM can be overtrained if too many basis functions – here 10 – are used. In Figure 8.17(b), less basis functions are used and the manifold found is much smoother. Another option is to use regularization, which also gives a smoother result, as shown in Figure 8.17(c), but cannot completely prevent extreme non-linearities.

Figure 8.17 Trained generative topographic mappings. (a) K = 14, M = 10, σϕ = 0.2 and λ = 0. (b) K = 14, M = 5, σϕ = 0.2 and λ = 0. (c) K = 14, M = 10, σϕ = 0.2 and λ = 0.01.
Listing 8.9 shows how a GTM can be trained and displayed in PRTools.
Listing 8.9 PRTools code for training and plotting generative topographic mapping.
z = rand(100,2); % Generate the data set z
w = gtm(z,15); % Train a 1D GTM and show it
figure; clf; scatterd(z); plotgtm(w);8.3 References
- Bishop, C.M., Neural Networks for Pattern Recognition, Oxford University Press, Oxford, UK, 1995.
- Bishop, C.M., Svensén, M. and Williams, C.K.I., GTM: the generative topographic mapping, Neural Computation, 10(1), 215–234, 1998.
- Dambreville, S., Rathi, Y. and Tannenbaum, A., A framework for image segmentation using shape models and kernel space shape priors, IEEE Transactions on PAMI, 30(8), 1385–1399, 2008.
- Dempster, N.M., Laird, A.P. and Rubin, D.B., Maximum likelihood from incomplete data via the EM algorithm, Journal of the Royal Statististical Society B, 39, 185–197, 1977.
- Johnson, S.C., Hierarchical clustering schemes, Psychometrika, 2, 241–254, 1977.
- Jolliffe, I.T., Principal Component Analysis, Springer-Verlag, New York, 1986.
- Kohonen, T., Self-organizing Maps, Springer-Verlag, Heidelberg, Germany, 1995.
- Kruskal, J.B. and Wish, M., Multidimensional Scaling, Sage Publications, Beverly Hills, CA, 1977.
- Sammon, Jr, J.W., A nonlinear mapping for data structure analysis, IEEE Transactions on Computers, C-18, 401–409, 1969.
- Schölkopf, B., Smola, A. and Müller, K.R., Nonlinear component analysis as a kernel eigenvalue problem, Neural Computation, 10(5), 1299–1319, 1998.
- Tipping, M.E. and Bishop, C.M., Mixtures of probabilistic principal component analyzers, Neural Computation, 11 (2), 443–482, 1999.
Exercises
-
Generate a two-dimensional dataset z uniformly distributed between 0 and 1. Create a second dataset y uniformly distributed between –1 and 2. Compute the (Euclidean) distances between z and y, and find the objects in y that have a distance smaller than 1 to an object in z. Make a scatterplot of these objects. Using a large number of objects in z, what should be the shape of the area of objects with a distance smaller than 1? What would happen if you change the distance definition to the city-block distance (Minkowski metric with q = 1)? What would happen if the cosine distance is used? (0)
-
Create a dataset
z = gendatd(50, 50, 4,2);. Make a scatterplot of the data. Is the data separable? Predict what would happen if the data are mapped to one dimension. Check your prediction by mapping the data usingpca(z,1)and training a simple classifier on the mapped data (such asldc). (0) -
Load the
worldcitiesdataset and experiment using different values for q in the MDS criterion function. What is the effect? Can you think of another way of treating close sample pairs differently from far-away sample pairs? (0) -
Derive Equations (8.28), (8.30) and (8.34). (*)
-
Discuss in which datasets it can be expected that the data are distributed in a subspace or in clusters. In which cases will it not be useful to apply clustering or subspace methods? (*)
-
What is a desirable property of a clustering when the same algorithm is run multiple times on the same dataset? Develop an algorithm that uses this notion to estimate the number of clusters present in the data. (**)
-
In terms of scatter matrices (see the previous chapter), what does the K-means algorithm minimize? (0)
-
Under which set of assumptions does the EM algorithm degenerate to the K-means algorithm? (**)
-
What would be a simple way to lower the risk of ending up in a poor local minimum with the K-means and EM algorithms? (0)
-
Which parameter(s) control(s) the generalization ability of the self-organizing map (for example its ability to predict the locations of previously unseen samples) and that of the generative topographic mapping? (*)
