This appendix summarizes concepts from probability theory. This summary only concerns those concepts that are part of the mathematical background required for understanding this book. Mathematical peculiarities that are not relevant here are omitted. At the end of the appendix references to detailed treatments are given.

C.1 Probability Theory and Random Variables

The axiomatic development of probability involves the definitions of three concepts. Taken together these concepts are called an experiment. The three concepts are:

1. A set Ω consisting of outcomes ω_i. A trial is the act of randomly drawing a single outcome. Hence, each trial produces one ω ∈ Ω.
2. A is a set of certain¹ subsets of Ω. Each subset α ∈ A is called an event. The event {ω_i}, which consists of a single outcome, is called an elementary event. The set Ω is called the certain event. The empty subset Ø is called the impossible event. We say that an event α occurred if the outcome ω of a trial is contained in α, that is if ω ∈ α.

3. A real function P(α) is defined on A. This function, called probability, satisfies the following axioms:

   I: P(α) ≥ 0

   II: P(Ω) = 1

   III: If α, β ∈ A and α∩β = Ø then P(α∪β) = P(α) + P(β)

Example The space of outcomes corresponding to the colours of a traffic light is Ω = {red, green, yellow}. The set A may consist of subsets like Ø, red, green, yellow, red ∪ green, red ∩ green, red ∪ green ∪ yellow, etc. Thus, P(green) is the probability that the light will be green. P(green ∪ yellow) is the probability that the light will be green or yellow or both. P(green ∩ yellow) is the probability that at the same time the light is green and yellow.

A random variable is a mapping of Ω on to a set of numbers, for instance integer numbers, real numbers, complex numbers, etc. The distribution function is the probability of the event that corresponds to :

(C.1)

A note on the notation

In the notation , the variable is the random variable of interest. The variable x is the independent variable. It can be replaced by other independent variables or constants. Therefore, , and are all valid notations. However, to avoid lengthy notations the abbreviation F(x) will often be used if it is clear from the context that is meant. Also, the underscore notation for a random variable will be omitted frequently.

The random variable is said to be discrete if a finite number (or infinite countable number) of events x₁, x₂, … exists for which

(C.2)

Notation If the context is clear, the notation P(x_i) will be used to denote . The random variable is continuous if a function exists for which

(C.3)

The function is called the probability density of . The discrete case can be included in the continuous case by permitting to contain Dirac functions of the type P_iδ(x − x_i).

If the context is clear, the notation p(x) will be used to denote .

Examples We consider the experiment consisting of tossing a (fair) coin. The possible outcomes are {head, tail}. The random variable is defined according to:

This random variable is discrete. Its distribution function and probabilities are depicted in Figure C.1(a).

An example of a continuous random variable is the round-off error that occurs when a random real number is replaced with its nearest integer number. This error is uniformly distributed between −0.5 and 0.5. The distribution function and associated probability density are shown in Figure C.1(b).

Since F(x) is a non-decreasing function of x, and F(∞) = 1, the density must be a non-negative function with ∫p(x)dx = 1. Here, the integral extends over the real numbers from −∞ to ∞.

C.1.1 Moments

The moment of order n of a random variable is defined as

(C.4)

Formally, the notation should be , but as said before we omit the underscore if there is no fear of ambiguity. Another notation of E[xⁿ] is .

The first-order moment is called the expectation. This quantity is often denoted by μ_x or (if confusion is not to be expected) briefly μ. The central moments of order n are defined as

(C.5)

The first central moment is always zero. The second central moment is called variance:

(C.6)

The (standard) deviation of x denoted by σ_x, or briefly σ, is the square root of the variance:

(C.7)

C.1.2 Poisson Distribution

The act of counting the number of times that a certain random event takes place during a given time interval often involves a Poisson distribution. A discrete random variable that obeys the Poisson distribution has the probability function:

(C.8)

where λ is a parameter of the distribution. It is the expected number of events. Thus, E[n] = λ. A special feature of the Poisson distribution is that the variance and the expectation are equal: Var[n] = E[n] = λ. Examples of this distribution are shown in Figure C.2.

Example Radiant energy is carried by a discrete number of photons. In daylight situations, the average number of photons per unit area is of the order of 10¹² 1/(s mm²). However, in fact the real number is Poisson distributed. Therefore, the relative deviation σ_n/E[n] is . An image sensor with an integrating area of 100 μm², an integration time of 25 ms and an illuminance of 250 lx receives about λ = 10⁶ photons. Hence, the relative deviation is about 0.1%. In most imaging sensors this deviation is almost negligible compared to other noise sources.

C.1.3 Binomial Distribution

Suppose that we have an experiment with only two outcomes, ω₁ and ω₂. The probability of the elementary event {ω₁} g is denoted by P. Consequently, the probability of {ω₂} is 1 − P. We repeat the experiment N times and form a random variable by counting the number of times that {ω₁} g occurred. This random variable is said to have a binomial distribution with parameters N and P.

The probability function of is

(C.9)

The expectation of appears to be and its variance is .

Example The error rate of a classifier is E. The classifier is applied to N objects. The number of misclassified objects, n_error, has a binomial distribution with parameters N and E.

C.1.4 Normal Distribution

A well-known example of a continuous random variable is the one with a Gaussian (or normal) probability density:

(C.10)

The parameters μ and σ² are the expectation and the variance, respectively. Two examples of the probability density with different μ and σ² are shown in Figure C.3.

Gaussian random variables occur whenever the underlying process is caused by the outcomes of many independent experiments and the associated random variables add up linearly (the central limit theorem). An example is thermal noise in an electrical current. The current is proportional to the sum of the velocities of the individual electrons. Another example is the Poisson distributed random variable mentioned above. The envelope of the Poisson distribution approximates the Gaussian distribution as λ tends to infinity. As illustrated in Figure C.3, the approximation already looks quite reasonable when λ > 10.

Also, the binomial distributed random variable is the result of an addition of many independent outcomes. Therefore, the envelope of the binomial distribution also approximates the normal distribution as NP(1 − P) tends to infinity. In practice, the approximation is already reasonably good if NP(1 − P) > 5.

C.1.5 The Chi-Square Distribution

Another example of a continuous distribution is the χ²_n distribution. A random variable y is said to be χ²_n distributed (chi-square distributed with n degrees of freedom) if its density function equals

(C.11)

with Γ() the so-called gamma function. The expectation and variance of a chi-square distributed random variable appear to be

(C.12)

Figure C.4 shows some examples of the density and distribution.

The χ²_n distribution arises if we construct the sum of the square of normally distributed random variables. Suppose that with j = 1, …, n are n Gaussian random variables with and .

In addition, assume that these random variables are mutually independent;² then the random variable:

(C.13)

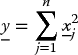
is χ²_n distributed.

C.2 Bivariate Random Variables

In this section we consider an experiment in which two random variables x and y are associated. The joint distribution function is the probability that and , that is

(C.14)

The function p(x, y) for which

(C.15)

is called the joint probability density. Strictly speaking, definition (C.15) holds true only when F(x, y) is continuous. However, by permitting p(x, y) to contain Dirac functions, the definition also applies to the discrete case.

From definitions (C.14) and (C.15) it is clear that the marginal distribution F(x) and the marginal density p(x) are given by

(C.16)

(C.17)

Two random variables and are independent if

(C.18)

This is equivalent to

(C.19)

Suppose that h( ·, ·) is a function . Then is a random variable. The expectation of equals

(C.20)

The joint moments m_ij of two random variables and are defined as the expectations of the functions :

(C.21)

The quantity i + j is called the order of m_ij. It can easily be verified that m₀₀ = 1, m₁₀ = E[x] = μ_x and m₀₁ = E[y] = μ_y.

The joint central moments μ_ij of order i + j are defined as

(C.22)

Clearly, μ₂₀ = Var[x] and μ₀₂ = Var[y]. Furthermore, the parameter μ₁₁ is called the covariance (sometimes denoted by Cov[x, y]). This parameter can be written as μ₁₁ = m₁₁ − m₁₀m₀₁. Two random variables are called uncorrelated if their covariance is zero. Two independent random variables are always uncorrelated. The reverse is not necessarily true.

Two random variables and are Gaussian if their joint probability density is

(C.23)

The parameters μ_x and μ_y are the expectations of and , respectively. The parameters σ_x and σ_y are the standard deviations. The parameter r is called the correlation coefficient, defined as

(C.24)

Figure C.5 shows a scatter diagram with 121 realizations of two Gaussian random variables. In this figure, a geometrical interpretation of Equation (C.23) is also given. The set of points (x, y) that satisfy

(i.e. the 1σ-level contour) turns out to form an ellipse. The centre of this ellipse coincides with the expectation. The eccentricity, size and orientation of the 1σ contour describe the scattering of the samples around this centre. and are the standard deviations of the samples projected on the principal axes of the ellipse. The angle between the principal axis associated with λ₀ and the x axis is θ. With these conventions, the variances of and , and the correlation coefficient r, are

(C.25)

Consequently, r = 0 whenever λ₀ = λ₁ (the ellipse degenerates into a circle) or whenever θ is a multiple of π/2 (the ellipse lines up with the axes). In both cases the random variables are independent. The conclusion is that two Gaussian random variables that are uncorrelated are also independent.

The situation r = 1 or r = −1 occurs only if λ₀ = 0 or λ₁ = 0. The ellipse degenerates into a straight line. Therefore, if two Gaussian random variables are completely correlated, then this implies that two constants a and b can be found for which .

The expectation and variance of the random variable defined by are

(C.26)

(C.27)

The expectation appears to be a linear operation, regardless of the joint distribution function. The variance is not a linear operation. However, Equation (C.27) shows that if two random variables are uncorrelated, then σ²_{x + y} = σ_x² + σ²_y.

Another important aspect of two random variables is the concept of conditional probabilities and moments. The conditional distribution (or in shorthand notation F(x∣y)) is the probability that given that . Written symbolically:

(C.28)

The conditional probability density associated with is denoted by or p(x∣y). Its definition is similar to Equation (C.3). An important property of conditional probability densities is Bayes’ theorem for conditional probabilities:

(C.29)

or in shorthand notation:

Bayes’ theorem is very important for the development of a classifier or an estimator (see Chapters 2 and 3).

The conditional moments are defined as

(C.30)

The shorthand notation is E[xⁿ|y]. The conditional expectation and conditional variance are sometimes denoted by μ_x|y and σ²_x|y, respectively.

C.3 Random Vectors

In this section, we discuss a finite sequence of N random variables: . We assume that these variables are arranged in an N-dimensional random vector x. The joint distribution function F(x) is defined as

(C.31)

The probability density p(x) of the vector x is the function that satisfies

(C.32)

with

The expectation of a function is

(C.33)

Similar definitions apply to vector-to-vector mappings and vector-to-matrix mappings . Particularly, the expectation vector and the covariance matrix are frequently used.

A Gaussian random vector has a probability density given by

(C.34)

The parameters (expectation vector) and C_x (covariance matrix) fully define the probability density.

A random vector is called uncorrelated if its covariance matrix is a diagonal matrix. If the elements of a random vector x are independent, the probability density of x is the product of the probability densities of the elements:

(C.35)

Such a random vector is uncorrelated. The reverse holds true in some specific cases, for example for all Gaussian random vectors.

The conditional probability density p(x∣y) of two random vectors x and y is the probability density of x if y is known. Bayes’ theorem for conditional probability densities becomes

(C.36)

The definitions of the conditional expectation vector and the conditional covariance matrix are similar.

C.3.1 Linear Operations on Gaussian Random Vectors

Suppose the random vector y results from a linear (matrix) operation y = Ax. The input vector of this operator x has expectation vector and covariance matrix C_x, respectively. Then, the expectation of the output vector and its covariance matrix are:

(C.37)

These relations hold true regardless of the type of distribution function. In general, the distribution function of y may be of a type different from the one of x. For instance, if the elements from x are uniformly distributed, then the elements of y will not be uniform except for trivial cases (e.g. when A = I). However, if x has a Gaussian distribution, then so has y.

Example Figure C.6 shows the scatter diagram of a Gaussian random vector x, the covariance matrix of which is the identity matrix I. Such a vector is called white. Multiplication of x by a diagonal matrix Λ^1/2 yields a vector y with covariance matrix . This vector is still uncorrelated. Application of a unitary matrix V to z yields the random vector z, which is correlated.

C.3.2 Decorrelation

Suppose a random vector z with covariance matrix C_z is given. Decorrelation is a linear operation A, which, when applied to z, will give a white random vector x. (The random vector x is called white if its covariance matrix C_x = T.) The operation A can be found by diagonalization of the matrix C_z. To see this, it suffices to recognize that the matrix C_z is self-adjoint, that is C_z = C^T_z. According to Section B.5, a unitary matrix V and a (real) diagonal matrix must exist such that . The matrix V consists of the normalized eigenvectors v_n of C_z, that is V = [v₀⋅⋅⋅v_{N − 1}]. The matrix contains the eigenvalues λ_n at the diagonal. Therefore, application of the unitary transform V^T yields a random vector y = V^T_z, the covariance matrix of which is . Furthermore, the operation applied to y gives the white vector . Hence, the decorrelation/whitening operation A equals . Note that the operation is the inverse of the operations shown in Figure C.6.

We define the 1σ-level contour of a Gaussian distribution as the solution of

(C.38)

The level contour is an ellipse (N = 2), an ellipsoid (N = 3) or a hyperellipsoid (N > 3). A corollary of the above is that the principal axes of these ellipsoids point in the direction of the eigenvectors of C_z and that the ellipsoids intersect these axes at a distance from equal to the square root of the associated eigenvalue (see Figure C.6).

C.4 Selected Bibliography

1. Papoulis, A., Probability, Random Variables and Stochastic Processes, McGraw-Hill, New York, 1965 (Third Edition: 1991).