In the course of history, human beings communicated with each other using their ears and eyes, by transmitting their messages via voice, sound, light, smoke, signs, paintings, and so on.[1] The invention of writing made written communications also possible. Telecommunications refers to the transmission of messages in the form of voice, image or data by using electrical signals and/or electromagnetic waves. As these messages modulate the amplitude, the phase or the frequency of a sinusoidal carrier, electrical signals are characterized both in time and frequency domains. The behavior of these signals in time and frequency domains are closely related to each other. Therefore, the design of telecommunication systems takes into account both the time‐ and the frequency‐characteristics of the signals.

In the time‐domain, modulating the amplitude, the phase and/or the frequency at high rates may become challenging because of the limitations in the switching capability of electronic circuits, clocks, synchronization and receiver performance. On the other hand, the frequency‐domain behavior of signals is of critical importance from the viewpoint of the bandwidth they occupy and the interference they cause to signals in the adjacent frequency channels. Frequency‐domain analysis provides valuable insight for the system design and efficient usage of the available frequency spectrum, which is a scarce and valuable resource. Distribution of the energy or the power of a transmitted signal with frequency, measured in terms of energy spectral density (ESD) or power spectral density (PSD), is important for the efficient use of the available frequency spectrum. ESD and PSD are determined by the Fourier transform, which relates time‐ and frequency‐domain behaviors of a signal, and the autocorrelation function, which is a measure of the similarity of a signal with a delayed replica of itself in the time domain. Spectrum efficiency provides a measure of data rate transmitted per unit bandwidth at a given transmit power level. It also determines the interference caused to adjacent frequency channels.

Signals are classified based on several parameters. A signal is said to be periodic if it repeats itself with a period, for example, a sinusoidal signal. A signal is said to be aperiodic if it does not repeat itself in time. The signals may also be classified as being analog or discrete (digital). An analog signal varies continuously with time while a digital signal is defined by a set of discrete values. For example, a digital signal may be defined as a sequence of 1 s and 0 s, which are transmitted by discrete voltage levels, for example, ±V volts. A signal is said to be deterministic if its behavior is predictable in time‐ and frequency‐domains. However, a random signal, for example, noise, can not be predicted beforehand and is therefore characterized statistically. [2][3][4][5][6][7][8][9]

In this book, we will deal with both baseband and passband signals. The spectrum of a baseband signal is centered around f = 0, while the spectrum of a passband signal is located around a sufficiently large carrier frequency f_c, such that the transmission bandwidth remains in the region f > 0. The baseband signals, though their direct use is limited, facilitate the analysis and design of the passband systems. A baseband signal may be up‐converted to become a passband signal by a frequency‐shifting operation, that is, multiplying the baseband signal with a sinusoidal carrier of sufficiently high carrier frequency f_c. Shifting the spectrum of a baseband signal, with spectral components for f < 0 and f > 0, to around a carrier frequency f_c, implies that the bandwidth of a passband signal is doubled compared to a baseband signal. Most telecommunication systems employ passband signals, that is, the messages to be transmitted modulate carriers with sufficiently large carrier frequencies. Bandpass transmission has numerous advantages, for example, ease of radiation/reception by antennas, noise and interference mitigation, frequency‐channel assignment by multiplexing and transmission of multiple message signals using a single carrier. In addition, passband transmission has the cost advantage, since it usually requires smaller, more cost‐effective and power‐efficient equipments.

This chapter will deal with analog/digital, periodic/aperiodic, deterministic/random and baseband/passband signals. Noting that the fundamental concepts can be explained by analogy to analog systems, this chapter will mostly be focused on analog baseband signals unless otherwise stated. The conversion of an analog signal into digital and the characterization of a digital signal will be treated in the subsequent chapters. Since the characteristics of passband signals can easily be derived from those of the baseband signals, the focus will be on the baseband signals. Telecommunication systems operate usually with random signals due to the presence of the system noise and/or fading and shadowing in wireless channels. [4][5][6][7]

Assuming that the student is familiar with probabilistic concepts, a short introduction is presented on random signals and processes. One may refer to Appendix F, Probability and Random Variables, for further details. Diverse applications of these concepts will be presented in the subsequent chapters.

1.1 Relationship Between Time and Frequency Characteristics of Signals

Fourier series and Fourier transform provide useful tools for characterizing the relationship between time‐ and frequency‐domain behaviors of signals. For spectral analysis, we generally use the Fourier series for periodic signals and the Fourier transform for aperiodic signals. These two will be observed to merge as the period of a periodic signal approaches infinity. [3][9]

1.1.1 Fourier Series

The Fourier series expansion of a periodic function with period T₀ = 1/f₀ is given by

(1.1)

Using the orthogonality between cos(nw₀t) and sin(nw₀t), the coefficients a_n and b_n are found as

(1.2)

where a₀ denotes the average value of . Using the Euler’s identity , the Fourier series expansion given by (1.1) may be rewritten as a complex Fourier series expansion:

(1.3)

From the equivalence of (1.1) and (1.3), one may easily show that

(1.4)

According to the Parseval’s theorem, the power of a periodic signal may be expressed in terms of the Fourier series coefficients:

(1.5)

One may also observe from (1.5) that the power of a periodic signal is equal to the sum of the powers |c_n|² of its spectral components, located at nf₀, and its PSD is discrete with values |c_n|². Hence, the signal power is the same irrespective of whether it is calculated in time‐ or frequency‐domains.

1.1.2 Fourier Transform

As T₀ goes to infinity as shown in Figure 1.1(b), tends to become an aperiodic signal, which will be shown hereafter as s(t). Then, f₀ = 1/T₀ approaches zero, spectral lines at nf₀ merge and form a continuous spectrum. The Fourier transform S(f) of an aperiodic continuous function s(t) is defined by [2][3][9]

(1.10)

This Fourier transform relationship will also be denoted as

(1.11)

Unless otherwise stated, small‐case letters will be used to denote time‐functions while capital letters will denote their Fourier transforms. It is evident from (1.10) that the value of S(f) at the origin gives the mean value of the signal:

(1.12)

while s(0) denotes the average value of S(f).

The so‐called Rayleigh’s energy theorem states that the energy of an aperiodic signal found in time‐ and frequency‐domains are identical to each other:

(1.13)

In view of the integration over −∞ < f < ∞ in (1.13), the energy of s(t) is equal to the area under the energy spectral density Ψ_s(f) of s(t), that is, the energy per unit bandwidth:

(1.14)

One may observe from (1.10) that the Fourier transform, hence the ESD, of a real signal s(t) with even symetry s(t) = s(−t), has also even symmetry with respect to f = 0.

1.1.2.1 Impulses and Transforms in the Limit

Dirac delta function does not exist physically, but is widely used in many areas of engineering. Some functions are used to approximate the Dirac delta function. For example, the rectangular pulse shown in Figure 1.2 approximates Dirac delta function in the time domain as T approaches zero. As the area under a Dirac delta function should be equal to unity, the amplitude of the rectangular pulse is chosen as A = 1/T. Figure 1.2(c) also shows that a Dirac delta function in the time domain has a flat spectrum, that is, its PSD is uniform. Similarly, the Fourier transform of a rectangular pulse approximates a Dirac delta function located at f = 0 as T → ∞ (see also Figure 1.2(b)), which implies that the Dirac delta function in the frequency domain implies a time‐invariant signal.

Some alternative definitions of the Dirac delta function are listed below: [2][3][9]

(1.17)

Some properties of the Dirac delta function are summarized below:

1. Area under the Dirac delta function is unity:
   (1.18)
2. Sampling of an ordinary function s(t) which is continuous at t₀:
   (1.19)
3. Relation with the unit step function
   (1.20)
4. Multiplication and convolution with a continuous function:
   (1.21)
5. Scaling
   (1.22)
6. Fourier transform
   (1.23)

1.1.2.2 Signals with Even and Odd Symmetry and Causality

Assuming that s(t) is a real‐valued function, its Fourier transform S(f) may be decomposed into its even and odd components as follows: [2]

(1.24)

It is clear from (1.24) that

(1.25)

When the signal has an even symmetry with respect to t = 0, that is, s(t) = s(−t), then S(f) becomes a real and even function of frequency:

(1.26)

When the signal has an odd symmetry with respect to t = 0, that is, s(t) = −s(−t), then S(f) becomes a purely imaginary and odd function of frequency:

(1.27)

A causal system is defined as a system where the output at time t₀ depends on only past and current values but not on future values of the input. In other words, the output y(t₀) depends only on the input x(t) for values of t ≤ t₀. Therefore, the output of a causal system has no time symmetry and its spectrum has both real and imaginary components.

1.1.2.3 Fourier Transform Relations

Some properties of the Fourier transform are listed below: [2][3][9]

1. Superposition

   If , then using the linearity property of the Fourier transform in (1.10),

   (1.34)
2. Time and frequency shift

   If , then

   (1.35)

   Proof: The use of variable transformations in the following equations lead to

   (1.36)

1.1.3 Fourier Transform of Periodic Functions

Fourier transform of a periodic function, of period T₀, with a complex Fourier series expansion given by (1.3) is given by [4]

(1.65)

The Fourier transform (1.65) is hence a discrete function of frequency, that is, is non‐zero at only the discrete frequencies nf₀. The PSD may be written as the square of the magnitude of its Fourier transform:

(1.66)

The power of a periodic signal is given by the area under the PSD:

(1.67)

Similarly, as given by (1.6) and shown in Figure 1.1, the coefficients of the complex Fourier series expansion of a periodic rectangular pulse train, with period T₀ = 1/f₀, also exhibit discrete frequency lines. One may observe from (1.6) that the coefficients satisfy where S(f) denotes the Fourier transform of a single rectangular pulse centered at the origin (see (1.15), (1.16) and the pulse train as T₀ → ∞ in Figure 1.1(b)). The PSD and the power of a periodic signal, given by (1.5), determined by the Fourier series analysis, are in complete with agreement with (1.66) and (1.67), found by the Fourier transform approach.

The PSD of an aperiodic signal s(t) with finite power can not be expressed by a Fourier series expansion. Instead, it may be written as

(1.68)

where S(f) denotes the Fourier transform of s(t) over the time interval [−T/2, T/2].

1.2 Power Spectal Density (PSD) and Energy Spectral Density (ESD)

1.2.1 Energy Signals Versus Power Signals

The energy of a signal s(t) is defined as

(1.75)

The power of a signal is defined as

(1.76)

As a special case when the power signal is periodic with a period T₀, the signal power defined by (1.76) simplifies to

(1.77)

Based on (1.75)−(1.77), signals may be classified as

1. An energy signal is defined as a signal with finite energy and zero power:
   (1.78)

   Aperiodic signals are typically energy signals as they have a finite energy and zero power.

2. A power signal has finite power and infinite energy:
   (1.79)

   Periodic signals are typically power signals since they have finite power and infinite energy. [4][5][6][7]

1.2.2 Autocorrelation Function and Spectral Density

ESD and PSD are employed to describe the distribution of, respectively, the signal energy and the signal power over the frequency spectrum. ESD/PSD is defined as the Fourier transform of the autocorrelation function of an energy/power signal. [4][5][6][7]

1.2.2.1 Energy Signals

Autocorrelation of a function s(t) provides a measure of the degree of similarity between the signal s(t) and a delayed replica of itself. The autocorrelation function of an energy signal s(t) is defined by

(1.87)

Note that τ, that varies in the interval (−∞,∞), measures the time shift between s(t) and its delayed replica. The sign of the time shift τ shows whether the delayed version of s(t) leads or lags s(t). If the time shift τ becomes zero, then s(t) will overlap with itself and the resemblence between them will be perfect. Consequently, the value of the autocorrelation function at the origion is equal to the energy of the signal:

(1.88)

It is logical to expect that the resemblence between a signal and its delayed replica to decrease with increasing values of τ. The properties of the autocorrelation function of a real valued energy signal may be listed as follows:

1. Symmetry about τ = 0:
   (1.89)
2. Maximum value occurs at τ = 0:
   (1.90)
3. Autocorrelation and ESD are related to each other by the Fourier transform:
   (1.91)

   where ESD is defined in (1.14) as the variation of the energy E of s(t) with frequency. One can prove the relationship given by (1.91) by taking the Fourier transform of the autocorrelation function of an energy signal, given by (1.87):

   (1.92)

1.2.2.2 Power Signals

The autocorrelation function of a power signal s(t) is defined by

(1.96)

If the power signal is periodic with a period T₀, then the autocorrelation can be computed by integration over a single period:

(1.97)

The value of the autocorrelation function at the origin is equal to the power of s(t):

(1.98)

The properties of the autocorrelation function of a real‐valued power signal s(t) are given by

1. Symmetry about τ = 0:
   (1.99)
2. Maximum value occurs at τ = 0:
   (1.100)
3. Autocorrelation and power spectral density (PSD) are related to each other by Fourier transform:
   (1.101)

   PSD, the variation of the power P of s(t) with frequency, is given by (1.66) and (1.68) for respectively periodic and aperiodic power signals.

Based on (1.87), (1.92), (1.96) and (1.101), the PSD and ESD of a signal may be obtained either by taking the magnitude‐square of its Fourier transform or the Fourier transform of the autocorrelation function (see Figure 1.11):

1.3 Random Signals

In a digital communication system, one of the M symbols is transmitted, in a finite symbol duration, using a pre‐defined M‐ary alphabet. These symbols are unknown to the receiver when they are transmitted. At the receiver, these signals bear a random character in AWGN, fading or shadowing channels. Since a random signal can not be predicted before reception, a receiver processes the received random signal in order to estimate the transmitted symbol. In view of the above, the performance of telecommunication systems can be evaluated by characterizing the random signals statistically.

This section aims to provide a short introduction to random signals and processes encountered in telecommunication systems. The reader may refer to Appendix F for further details about the random signals and their characterization. [3][9]

1.3.1 Random Variables

Given a sample space S and elements s∈S, we define a function X(s) whose domain is S and whose range is a set of numbers on the real line (see Figure 1.12). The function X(s) is called a random variable (rv). For example, if we consider coin flipping with outcomes head (H) and tail (T), the sample space is defined by S = {H, T} and the rv may be assumed to be X(s) = 1 for s = H and −1 for s = T. Note that a rv, which is unknown and unpredictable beforehand, is known completely once it occurs. For example, one does not know the outcome before flipping a coin. However, once the coin is flipped, the outcome (head or tail) is known.

A rv is characterized by its probability density function (pdf) or cumulative distribution function (cdf), which are interrelated. The cdf F_X(x) of a rv X is defined by

(1.105)

which specifies the probability with which the rv X is less than or equal to a real number x. The pdf of a rv X is defined as the derivative of the cdf.

(1.106)

Conversely, the cdf is defined as the integral of the pdf:

(1.107)

In view of (1.105)−(1.107), a rv is characterized by the following properties:

1. and the area under f_X(x) is always equal to unity: .
2. 0 ≤ F_X(x) ≤ 1 since and .
3. The cdf of a continuous rv X is a non‐decreasing and smooth function of X. Therefore, for x₂ ≥ x₁, .
4. When a rv X is discrete or mixed, its cdf is still a non‐decreasing function of X but contains discontinuities.

A rv is characterized by its moments. The n‐th moment of a rv X is defined as

(1.108)

where E[.] denotes the expectation. The rv’s encountered in telecommunication systems are mostly characterized by their first two moments, namely the mean (expected) value m_X and the variance :

(1.109)

When X is discrete or of a mixed type, the pdf contains impulses at the points of discontinuity of F_X(x). In such cases, the discrete part of f_X(x) may be expressed as

(1.110)

where the rv X may assume one of the N values, x₁, x₂,…, x_N at the discontinuities. For example, in case of coin flipping, two outcomes may be represented as x₁ for head and x₂ for tail. Then, P(X = x₁) = p ≤ 1 shows the probability of head, while P(X = x₂) = 1 − p denotes the probability of tail.

Mean value and the variance of a discrete rv is found by inserting (1.110) into (1.109):

(1.111)

For the special case of equally‐likely probabilities, that is, , then (1.111) simplifies to the well‐known expression

(1.112)

Now consider two rv’s X₁ and X₂, each of which may be continuous, discrete or mixed. The joint cdf is defined as

(1.113)

and is related to the joint pdf as follows:

(1.114)

The marginal pdf’s are found as follows:

(1.115)

The conditional pdf f(x_i|x_j), which gives the pdf of x_i for a given deterministic value of the rv x_j, has the following properties

(1.116)

Generalization of (1.113)‐(1.116) to more than two rv’s is straightforward. Statistical independence of random events has the following implications: If the experiments result in mutually exclusive outcomes, then the probability of an outcome in one experiment is independent of an outcome in any other experiment. The joint pdf’s (cdf’s) may then be written as the product of the pdf’s (cdf’s) corresponding to each outcome.

1.3.2 Random Processes

Future values of a deterministic signal can be predicted from its past values. For example, Acos(wt + Φ) shows a deterministic signal as long as A, w and Φ are deterministic and known; its future values can be determined exactly using its value at a certain time. However, it describes a random signal if any of A, w or Φ is random. For example, a noise generator generates a noise with a random amplitude and phase at any instant of time and these values change randomly with time. Similarly, amplitude and phase of a multipath fading signal vary randomly not only at a given instant of time but also with time. Hence, a random signal changes randomly not only at an instant of time but also with time. Therefore, future values of random signals cannot be predicted by using their observed past values. [4][6][7]

A rv may be used to describe a random signal at a given instant of time. Random process extends the concept of a rv to include also the time dimension. Such a rv then becomes a function of the possible outcomes s of a random event (experiment) and time t. In other words, every outcome s will be associated with a time (sample) function. The family (ensemble) of all such sample functions is called a random process and denoted as X(s, t). [3][4][9]

A random process does not need to be a function of a deterministic argument. For example, the terrain height between transmitter and receiver may be a random process of the distance, since the location and the height of the obstacles may change randomly. The random process may be continuous or discrete either in time or in the value of the rv.

For example, consider L Gaussian noise generators. The time variation of the noise voltages at the output of each of the noise generators is called as a sample function, or a realization of the process. Thus, each of the L sample functions, corresponding to a specific event s_j, changes randomly with time; noise voltages at any two instants are independent from each other (see Figure 1.13). The totality of sample functions is called an ensemble. On the other hand, at an instant of time t_k, the value of the rv X(s, t_k) depends on the event. For a specific event and time t_k, X(s_j, t_k) = X_j(t_k) is a real number. The properties of X(s,t) is summarized below: [3]

1. X(S, t) represents a family (ensemble) of sample functions, where .
2. X(s_j, t) represents a sample function for the event s_j (an outcome of S or a realization of the process).
3. X(S, t_k) is a rv at time t_k.
4. X(s_j, t_k) is a non‐random number.

For the sake of convenience, we will denote a random process by X(t) where the presence of the event is implicit.

1.3.2.1 Statistical Averages

Empirical determination of the pdf of a random process is neither practical nor easy since it may change with time. For example, the pdf of a Gaussian noise voltage may change with time as the temperature of the noise generator (a resistor) increases; then, the noise variance would be higher. Nevertheless, the mean and the autocorrelation function adequately describe the random processes encountered in telecommunication systems. The mean of a random process X(t) at time t_k is defined as

(1.118)

where the pdf of X(t_k) is defined over the ensemble of events at time t_k. Evidently, the mean would be time‐invariant if the pdf is time‐invariant. On the other hand, identical time variations of the mean and the variance of two random processes do not imply that these process are equivalents. For example, one of these processes may be changing faster than the other, and hence have higher spectral components. Therefore, autocorrelation functions (and corresponding PSDs) of these processes should also be compared with each other. The autocorrelation function of a random process X(t) provides a measure of the degree of similarity between the rv’s X(t_j) and X(t_k):

(1.119)

A random process X(t) is said to be stationary in the strict sense, if none of its statistics changes with time, but they depend only on the time difference t_k−t_j. This implies that the joint pdf satisfies the following:

(1.120)

Here, (1.120) should be read as the joint pdf of at times . For example, a strict sense stationary process satisfies the following for L = 1 and 2:

(1.121)

A random process X(t) is said to be wide sense stationary (WSS), if only its mean and autocorrelation function are unaffected by a shift in the time origin. This implies that the mean is a constant and the autocorrelation function depends only on the time difference t_k−t_j:

(1.122)

Note that strict‐sense stationarity implies wide‐sense stationarity, but the reverse is not true. In most applications, the analysis based on WSS assumption provides sufficiently accurate results at least over some time intervals of interest. The autocorrelation function of WSS random processes, which is an even function of τ, provides a measure of the degree of correlation between the random values of a process withτ seconds time shift from each other.

The properties of the autocorrelation function of a real‐valued WSS random process are listed below:

1. An even function of τ:
   (1.123)
2. Maximum value occurs at τ = 0:
   (1.124)
3. The value of the autocorrelation function at the origin is equal to the average power of the signal
   (1.125)
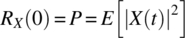
4. Autocorrelation and PSD are related to each other by the Fourier transform:
   (1.126)

1.3.2.2 Time Averaging and Ergodicity

The computation of the mean and the autocorrelation function of a random process by ensemble averaging is often not practical since it requires the use of all sample functions. For the so‐called ergodic processes, ensemble averaging may be replaced by time averaging. This means that the mean and the autocorrelation function of an ergodic process may be determined by using a single sample function. [3][4][5][7][8]

A random process is said to be ergodic in the mean if its mean can be calculated using a sample function, that is, using time averaging instead of ensemble averaging (see (1.118)):

(1.133)

A random process is said to be ergodic in the autocorrelation function, if R_X(x) is correctly described through the use of a sample function, that is, time averaging instead of ensemble averaging (see (1.119)):

(1.134)

It is not easy to test whether a random process is ergodic or not. However, in most applications, it is reasonable to assume that time and ensemble averaging are interchangeable.

1.3.2.3 PSD of a Random Process

Random processes are generally classified as power signals with a PSD as given by (1.68) and with the following properties:

1. The PSD is positive real‐valued function of frequency:
   (1.142)
2. The PSD has even symmetry with frequency:
   (1.143)
3. The PSD and autocorrelation function are Fourier transform pairs:
   (1.144)
4. The average normalized power of a random process is given by the area under the PSD:
   (1.145)

1.3.2.4 Noise

The thermal noise voltage n(t) that we encounter in telecommunication systems is a random process with zero mean and an autocorrelation function described by Dirac delta function:

(1.150)

The formula (1.150) implies that any two different noise samples are uncorrelated with each other, no matter how close the time difference between the samples is. Using the Fourier transform relationship between the autocorrelation function and the PSD, the two‐sided noise PSD is given by

(1.151)

The PSD of the Gaussian noise is flat in the frequency bands of interest for telecommunication applications; hence it is called as white noise. White Gaussian noise is characterized by Gaussian pdf with zero mean:

(1.152)

where denotes the noise variance. Figure 1.15 shows a sample function of a Gaussian noise process, which is white with zero mean and unity variance. The pdf of the noise voltage is depicted on the left‐hand side.

1.4 Signal Transmission Through Linear Systems

The telecommunication systems are mostly linear. Therefore, we will focus our attention on signal transmission through linear systems. The systems generally consist of cascade‐connected subsystems. The signal y(t) at the output of a linear system may be written as the convolution of the input signal x(t) with the impulse response h(t) of the system (see Figure 1.16): [4][5][7][8][9]

(1.153)

Impulse response represents the response of a linear system to an impulse at its input, that is, (see (1.21) and Figure 1.16(b)):

(1.154)

Using the convolution property of the Fourier transform, the Fourier transform of (1.153) leads to

(1.155)

where is called as the channel transfer function or the channel frequency response. H(f), which is generally complex, can be expressed in terms of the channel amplitude response and the phase response. Note that the PSD of the output signal is not the same as that of the input signal but modified by the channel frequency response.

For distortionless transmission of signals through a system, the output signal is desired to be the same as the input signal. A close look at (1.153) shows that this is possible only when the channel impulse response (CIR) is a delta function, that is, . However, this is not physical since the response of a system to an input signal at t = 0 is delayed by τ seconds by electronic equipments/processors and the propagation time in a channel. Then, to account for the delay, the CIR may be written in the form of a delayed delta function with channel amplitude gain α and channel phase θ:

(1.156)

Since , we conclude from (1.155) and (1.156) that, apart from a constant amplitude change due to α, such a channel does not cause any distortion on the PSD of the input signal. However, the channel induces a frequency‐ and delay‐dependent change in the phase of the output signal. A CIR with a flat frequency response as in (1.156) is not physically realizable since any physical channel has a non‐flat frequency response with a finite bandwidth. For example, electronic devices do not respond identically to all frequency components of the input signals. Similarly, both wired and wireless channels behave differently at different frequency bands. The analysis of (1.153) becomes even more complicated for channels where the channel gain α, the phase θ and the delay τ vary with time. Moreover, the channel may provide multiple replicas of the same signal with different gains, phases and delays due to scattering from different obstacles in wireless channels and reflections in discontinuities in wired channels. These issues will be discussed in detail in the subsequent chapters.

The definition of the bandwidth is not unique. Nevertheless, the PSD G_Y(f) of the output signal determines the bandwidth occupied by the signal in the channel. As one may observe from (1.155), the signal bandwidth is determined by G_X(f), while |H(f)|² is responsible for the channel (coherence) bandwidth. A channel with a bandwidth narrower than that of the signal distorts the signal transmitted through this channel. In other words, the channel bandwidth is required to be sufficiently larger than the signal bandwidth for signal transmission with minimal distortion. On the other hand, bearing in mind that the frequency spectrum is a scarce and valuable resource, the signals at the transmitter output are usually filtered so as the minimize the bandwidth requirements at the expense of some acceptable distortion. Hence, the transmission bandwidth of a signal is determined by the signal bandwidth, the channel bandwidth and filtering at the transmitter output.

Noting that the PSD of a real‐valued random process is even and has zero‐mean, the following definition of the rms baseband bandwidth is commonly used:

(1.157)

The spectrum of a passband signal is obtained by shifting its equivalent baseband spectrum to around the carrier frequency f_c along the frequency axis. Shifting a baseband spectrum to a passband frequency brings the negative frequency portions of the baseband spectrum to positive frequencies around f_c, hence leads to doubling the bandwidth (see Figure 1.5). Therefore, the passband rms bandwidth is simply the twice the baseband rms bandwidth:

(1.158)

For the sake of simplicity, assume . The rms baseband bandwidth is found using (1.157) as

(1.159)

References

1. [1] P. Chakravarthi, The history of communications from cave drawings to mail messages, IEEE AES Magazine, pp. 30−35, April 1992.
2. [2] A. B. Carlson, P. B. Crilly and J. C. Rutledge, Communication Systems (4th ed.), McGraw Hill: Boston, 2002.
3. [3] A. Papoulis and S. U. Pillai, Probability, Random Variables and Stochastic Processes (4th ed.), McGraw Hill: Boston, 2002.
4. [4] B. Sklar, Digital Communications: Fundamentals and Applications (2nd ed.), Prentice Hall PTR: New Jersey, 2003.
5. [5] S. Haykin, Communication Systems (3rd ed.), J. Wiley: New York, 1994.
6. [6] A. Goldsmith, Wireless Communications, Cambridge University Press: Cambridge, 2005.
7. [7] J. G. Proakis, Digital Communications (3rd ed.), McGraw Hill: New York, 1995.
8. [8] P. Beckmann, Probability in Communication Engineering, Harcourt, Brace and World, Inc.: New York, 1967.
9. [9] P. Z. Peebles, Jr., Probability, Random Variables, and Random Signal Principles (3rd ed.), McGraw Hill: New York, 1993.

Problems

1. Determine the complex exponential Fourier series for
   
2. Determine the Fourier series expansion of
   
3. Using Parseval’s energy theorem and the properties of the Fourier transform, determine
   
4. Using (1.166) and (1.167), determine the signal power and the SNR at the LPF output.
5. Determine the autocorrelation function of s(t) + w(t), where s(t) denotes the signal and w(t) Gaussian white noise.
6. Show that the cross‐correlation function between x(t) and y(t), which is defined by
   
   satisfies .
7. Prove (1.98) for a power signal, for example, cosw_ct.
8. Determine the Fourier transform of the function
   
   by using the properties of the Fourier transform only.
9. Determine the Fourier transform of a triangular pulse Λ(t/T) by using and the properties of the Fourier transform only.
10. Evaluate
    
11. Determine the convolution Π(t/T) ⊗ Π(t/2 T).
12. Determine the Fourier transform of
    
    Determine the time waveform and its Fourier transform if a unit step function u(t + t₀) is at the input of a system described by the above impulse response.
13. Draw the block diagram for and determine the Fourier transform of
    
14. Determine the Fourier transform of the following:

    

15. Determine the impulse response and the Fourier transform of the following:

    

16. A raised‐cosine pulse, which is defined by the following
    
    is commonly used for intersymbol interference (ISI) mitigation, instead of the so‐called Nyquist filter:
    
    Determine the impulse response of P(f) and compare with that of P_N(f).
17. Using the Fourier transform of s(t) and s(t) ± s(−t) from (1.28) and (1.31) and the Rayleigh energy theorem, show that