Chapter 5
Dual Pricing Algorithms by Wireless Network Duality for Utility Maximization
CHEE WEI TAN and LIANG ZHENG
5.1 Introduction
As wireless networks are becoming more heterogeneous and ubiquitous in our life, it is also becoming more difficult to allocate wireless resources and price them. A wireless service provider, through the dynamic measurement of network conditions, for example, interference, channel variation, number of users, and users’ mobility, can put in place a data pricing policy that determines a price for wireless resource allocation according to the type of demand for these resources. Recently, smart wireless data pricing has become an important topic of research [1–11]. An effective pricing algorithm can lead to more efficient use of the limited resources in the system and increase the overall utility or revenue [12–14]. A pareto optimal utility can be achieved using suitable pricing that reflects the amount of resources being consumed [11]. The goal of pricing is thus to encourage users to adopt a social behavior that maximizes social welfare rather than a purely noncooperative, that is, myopic and greedy, approach to resource allocation, which can lead to unfairness or unstable network conditions. How should wireless resources in large-scale heterogeneous wireless networks be analyzed and designed with clearly defined fairness and optimality in mind?
Wireless network optimization optimally matches the demand and supply of wireless resources subject to network constraints [15, 16]. Roughly speaking, it requires solving a constrained optimization problem to maximize a system objective subject to the demand and supply constraints of data services in addition to the diverse QoS constraints, interference, congestion, fairness, heterogeneity in wireless technologies, market power factors, and so on. It is common to specify the objective as the total social welfare of all the users, and a widely used social welfare is the sum of utilities. Another possible objective is the egalitarian fairness of the system. If only a portion of the users experiences better network conditions than other users, the pricing algorithm can drive the prices very high for users in the system at a time of congestion and high interference, exposing some users to unfairness. It is thus important that an optimal data pricing algorithm be designed through a judicious optimization of the wireless networkutility.
Wireless network utility maximization is intimately related to the signal-to-interference-and-noise-ratio (SINR) assignment for all users. A shadow price associated with SINR assignment constraints determines the performance received by the user. Given a set of power budget and interference temperature constraints, the SINR assignment of all users must be jointly coordinated, but there are two major hurdles that need to be overcome. First, algorithms that adapt the transmit power and interference temperature based on allocated SINR targets assume that the SINR targets are within the feasibility region, which, however, requires a centralized admission controller. Second, the algorithms have to be decentralized, practical to deploy, and be fast enough with minimal or, preferably, no parameter tuning. This is especially important because secondary users can arrive and depart in a dynamic setting, and so resources have to be adapted fast enough to converge to a new optimal operating point whenever the network conditions change. This, however, is challenging because of the tight coupling between primary and secondary users in the SINR assignment. It is desirable that the resource allocation for primary and secondary users be distributed with minimal overhead.
There are several works that partially address these two challenges in the literature. Hande et al. [17] study the SINR assignment in the context of wireless cellular networks by a reparameterization of the feasible SINR region and propose a load and spillage algorithm that jointly updates the SINR assignment and power. This algorithm, however, confines the optimality by considering a reduced feasible SINR region. Huang et al. [18] propose algorithms to coordinate the secondary users by sensing a feedback signal from the primary users’ interference temperature condition to reduce outage but do not address the joint optimal SINR assignment and power allocation. Lotfinezhad et al. [19] propose a radio admission control and scheduling policy, which, however, does not handle the interference temperature constraint. To coordinate the interference temperature by controlling the SINR assignment, Ragan and Madan [20] propose a belief propagation framework by wireless scheduling to solve a nonconvex utility maximization problem. Utility maximization algorithms using fractional frequency reuse have been proposed in References 21 and 22 for wireless cellular networks. Krishnan and Luss [23] consider a joint SINR assignment and power control to maximize the worst-case SINR with an interference temperature constraint. In Reference 24, this optimization of the egalitarian fairness of SINR is solved for individual power constraints using a nonlinear Perron–Frobenius theory.
The main contributions of this chapter are summarized as follows.
- We solve the wireless network utility maximization problem by parameterizing the global optimality in terms of SINR assignment, power and interference temperature allocation as optimization problems having spectral radius constraints. These spectral radiusconstraints capture fundamental characteristics of the underlying competition for resources. A special case that maximizes the egalitarian fairness of all the SINRs as the utility is solved optimally using a tuning-free geometrically fast convergent algorithm.
- We develop a wireless network duality and characterize analytically the power and interference temperature of the primal and dual networks. The relationship between them and the gradients of the spectral radius constraints in the utility maximization problem is established. The wireless network duality is thus useful for the computation of shadow price for SINR assignment.
- The utility maximization problem is solved using an optimization technique that can be interpreted as iteratively minimizing the interference load in the network. In particular, the egalitarian fairness SINR problem is adapted iteratively to solve the general utility maximization problem, which can further be solved distributively by leveraging the wireless network duality.
- Our algorithms can be practically implemented in today's wireless networks (3GPP systems) as they reuse a power control submodule already widely implemented. Numerical evaluations show that our algorithms have good performance, often yielding the optimal solution in tens of iterations even for a large number of users.
The rest of this chapter is organized as follows. In Section 5.2, we present the system model and reformulate our utility maximization problem in the SINR domain with spectral radius constraints. Then, using the nonlinear Perron–Frobenius theory, we first solve a special case of the utility maximization problem, the weighted max–min SINR, in Section 5.3.1. Next, using nonnegative matrix theory, we present the wireless network duality that we use to design a distributed algorithm to solve the utility maximization problem. We evaluate the performance of our algorithms numerically in Section 5.4. Finally, we conclude the chapter in Section 5.5. All the proofs can be found in our paper [25].
The following notation is used. We let ![]() denote the lth unit coordinate vector and
denote the lth unit coordinate vector and ![]() denote the identity matrix. The superscripts
denote the identity matrix. The superscripts ![]() denotes transpose. We denote
denotes transpose. We denote ![]() as a Schur product of
as a Schur product of ![]() and
and ![]() , that is,
, that is, ![]() , and denote
, and denote ![]() as the component-wise division between
as the component-wise division between ![]() and
and ![]() , that is,
, that is, ![]() . Let
. Let ![]() . For a vector
. For a vector ![]() ,
, ![]() is its diagonal matrix
is its diagonal matrix ![]() . Let
. Let ![]() denote
denote ![]() and
and ![]() denote
denote ![]() . The Perron–Frobenius eigenvalue of an irreduciblenonnegative matrix
. The Perron–Frobenius eigenvalue of an irreduciblenonnegative matrix ![]() is denoted as
is denoted as ![]() , and the Perron right and left eigenvector of
, and the Perron right and left eigenvector of ![]() associated with
associated with ![]() are denoted by
are denoted by ![]() and
and ![]() , respectively. An equality involving eigenvectors is true up to a scaling constant.
, respectively. An equality involving eigenvectors is true up to a scaling constant.
5.2 Utility Maximization
The network utility is a network-wide quality-of-service (QoS) measurement that quantifies the efficiency of the wireless resource allocation. Before talking about the pricing strategies that serve to maximize the network utility, in this section, we first introduce the concept of utility function and its dependence on all the users’ resource allocation.
We consider wireless networks with L users transmitting simultaneously on a shared spectrum. Owing to the shared nature of the wireless medium, the interference is unavoidable when users are transmitting simultaneously, that is, each user's transmission leads to interference for other users. The signal-to-interference-and-noise ratio (SINR) is an important performance metric used to measure the quality of wireless transmission. Let ![]() represent the channel gain, where
represent the channel gain, where ![]() is the channel gain from the kth transmitter to the lth receiver, and
is the channel gain from the kth transmitter to the lth receiver, and ![]() , where
, where ![]() is the noise power at the lth user. The vector
is the noise power at the lth user. The vector ![]() is the transmit power vector. Now, the SINR of the lth user in the primary network can be given in terms of
is the transmit power vector. Now, the SINR of the lth user in the primary network can be given in terms of ![]() :
:
From Eq. (5.1), we can observe the intimate connection between the SINR and users’ transmit power: a user would like to achieve a high SINR by increasing its transmit power, while this increase, in turn, gives rise to a higher interference level for other users. We also define a nonnegative matrix ![]() with entries:
with entries:
and the vector
Assuming that ![]() is irreducible, that is, each link has at least an interferer, we denote vector
is irreducible, that is, each link has at least an interferer, we denote vector ![]() as the SINR for all users for brevity and its equivalent form is given by
as the SINR for all users for brevity and its equivalent form is given by
where we use ![]() and
and ![]() in Eqs. (5.2) and (5.3), respectively. Thus, the utility function can be expressed as
in Eqs. (5.2) and (5.3), respectively. Thus, the utility function can be expressed as

which is a sum of individual utility of each user. The positive vector ![]() is used to reflect a priority of the utility of each user. For example, the utility function can be the weighted sum rate [26–28] and the
is used to reflect a priority of the utility of each user. For example, the utility function can be the weighted sum rate [26–28] and the ![]() -fairness utility [29].
-fairness utility [29].
As the SINR is a nontrivial nonlinear function of power, the joint SINR assignment and power control is a great challenge of resource allocation policy. It is also important to consider the power constraints for the system that reflect the available resource budget in the wireless networks. A general power constraint set ![]() is given by
is given by
where ![]() and
and ![]() are, respectively, the upper bound and positive weight vector for the weighted power constraints. In particular, when
are, respectively, the upper bound and positive weight vector for the weighted power constraints. In particular, when ![]() , we have the individual power constraint
, we have the individual power constraint ![]() for all l, and when
for all l, and when ![]() , we have a single total power constraint
, we have a single total power constraint ![]() . Next, let q denote the interference temperature vector, consisting of the total interference and the noise for each user, i.e., q = diag(v)(Fp + n). To mitigate the interference coming from the other users in the wireless networks, we also impose an individual interference temperature constraint to each user, and the interference temperature constraint set
. Next, let q denote the interference temperature vector, consisting of the total interference and the noise for each user, i.e., q = diag(v)(Fp + n). To mitigate the interference coming from the other users in the wireless networks, we also impose an individual interference temperature constraint to each user, and the interference temperature constraint set ![]() is given by
is given by
Using the system model introduced above, the utility maximization problem is then given by
Denote the optimal ![]() in Eq. (5.8) as
in Eq. (5.8) as ![]() . To proceed further, we reformulate Eq. (5.8) as an equivalent optimization problem in the SINR domain with a set of spectral radius constraints, whose problem structure is useful for developing the wireless network duality and proposing a distributed pricing algorithm.
. To proceed further, we reformulate Eq. (5.8) as an equivalent optimization problem in the SINR domain with a set of spectral radius constraints, whose problem structure is useful for developing the wireless network duality and proposing a distributed pricing algorithm.
Then, we have the following result.
Using a logarithmic mapping of a variable, Eq. (5.9) can be transformed to an optimization problem with a convex constraint set. For ![]() , let
, let
That is, ![]() . Then, Eq. (5.9) is equivalent to
. Then, Eq. (5.9) is equivalent to
Let us denote the optimal solution of Eq. (5.14) by ![]() . Note that
. Note that ![]() for all l.
for all l.
Now, we make the following assumption on the objective function that is useful in our proposed distributed pricing algorithm later in Section 5.3.8.
We briefly introduce the concept of Pareto optimality and Pareto dominance on the utility feasible set and then propose a pricing algorithm that is Pareto optimal. An SINR vector ![]() Pareto dominates the another SINR vector
Pareto dominates the another SINR vector ![]() if
if ![]() is greater than
is greater than ![]() for all l, and at least one of these inequalities is strict. In this case, the network utility computed by
for all l, and at least one of these inequalities is strict. In this case, the network utility computed by ![]() is sure to be greater than the network utility computed by
is sure to be greater than the network utility computed by ![]() . An SINR vector
. An SINR vector ![]() is Pareto optimal if there does not exist any
is Pareto optimal if there does not exist any ![]() that Pareto dominates it. In other words, no user can increase its utility without hurting any other users when the current resource allocation is Pareto optimal. Notably, the optimal resource allocation is Pareto optimal; however, it does not Pareto dominate all the resource allocation. Figure 5.1 illustrates the concept of Pareto optimality and Pareto dominance by a two-user example. The gray region in Figure 5.1 is the utility feasible region. Any points above the dashed line in the utility feasible region dominate the resource allocation vector
that Pareto dominates it. In other words, no user can increase its utility without hurting any other users when the current resource allocation is Pareto optimal. Notably, the optimal resource allocation is Pareto optimal; however, it does not Pareto dominate all the resource allocation. Figure 5.1 illustrates the concept of Pareto optimality and Pareto dominance by a two-user example. The gray region in Figure 5.1 is the utility feasible region. Any points above the dashed line in the utility feasible region dominate the resource allocation vector ![]() , for example, the feasible point
, for example, the feasible point ![]() . The resource allocation vector
. The resource allocation vector ![]() is Pareto optimal; however, although
is Pareto optimal; however, although ![]() and
and ![]() , it Pareto dominates neither
, it Pareto dominates neither ![]() nor
nor ![]() . An optimal pricing algorithm can coordinate the users to maximize the overall network utility based on a feedback signal to balance between the change (increase or decrease) of its own utility and the impact on other users’ utility caused by this change. In the next section, we use the wireless network duality to yield such a pareto optimal pricing algorithm.
. An optimal pricing algorithm can coordinate the users to maximize the overall network utility based on a feedback signal to balance between the change (increase or decrease) of its own utility and the impact on other users’ utility caused by this change. In the next section, we use the wireless network duality to yield such a pareto optimal pricing algorithm.

Figure 5.1 Illustration of the Pareto optimality and Pareto dominance. The utility feasible region is for a two-user example with the utility function  , that is,
, that is,  and
and  , respectively. The channel gains are given by
, respectively. The channel gains are given by  ,
,  ,
,  , and
, and  . The weights and upper bound for the weighted power constraints are
. The weights and upper bound for the weighted power constraints are  ,
,  , and
, and  .
.
5.3 The Wireless Network Duality
The heterogeneity of a wireless network further complicates the network optimization as our wireless network technologies such as cellular networks, cognitive radio networks, and femtocell networks are changing rapidly. An important feature in wireless networks that can be exploited for utility maximization is the notion of wireless network duality. Network duality is a fundamental concept in multiuser communication [32, 33]. Network dualities for wireless cellular and ad-hoc networks were investigated in References 34 and 35 for a total power minimization problem (a convex problem) using linear programming duality. A network duality was later developed for a max–min weighted SINR problem (a nonconvex problem) in References 26, 36, and 37 using nonnegative matrix theory and geometric programming duality. These network dualities (including the one in this chapter) assert that two different networks, respectively, a primal network and a dual network, can be construed to attain an identical SINR performance. For example, the well-known uplink–downlink duality in cellular network states that the uplink network reverses the link directions in the downlink network, as illustrated in Figure 5.2. Hence, a feasible SINR for one is also feasible for the other. There are many applications for the uplink–downlink duality, for example, beamforming and power control optimization in Reference 34 and optimizing the energy-robustness trade-off in cellular network in Reference 38.

Figure 5.2 Uplink–downlink duality. (a) The uplink network. (b) The downlink network.

Figure 5.3 Wireless network duality. (a) The primal network. (b) The dual network.
In this section, we develop a wireless network duality involving the primary network and the dual network, as illustrated in Figure 5.3(a) and (b), respectively, which facilitates a distributed pricing algorithm design. The primary network and the dual network, comprising the wireless network duality, are constructed to attain identical SINR performance. In particular, the dual network reverses the link directions in the primary network (cf. Figure 5.3), that is, the channel gain from the kth transmitter to the lth receiver is ![]() in the dual network. This will be used to propose and analyze distributed algorithms for jointly optimal SINR assignment, power and interference temperature control. Our algorithms are based on a novel wireless network duality that decouples SINR assignment, power and interference temperature. Further, the power and interference temperature in the primal and the dual networks are jointly optimized to solve the utility maximization problem formulated for the primal network subject to the power budget and interference temperature constraints. Through this wireless network duality, the egalitarian SINR fairness problem can be interpreted as solving the general utility maximization problem in a distributed manner when the weights in the egalitarian SINR fairness problem are tuned appropriately.
in the dual network. This will be used to propose and analyze distributed algorithms for jointly optimal SINR assignment, power and interference temperature control. Our algorithms are based on a novel wireless network duality that decouples SINR assignment, power and interference temperature. Further, the power and interference temperature in the primal and the dual networks are jointly optimized to solve the utility maximization problem formulated for the primal network subject to the power budget and interference temperature constraints. Through this wireless network duality, the egalitarian SINR fairness problem can be interpreted as solving the general utility maximization problem in a distributed manner when the weights in the egalitarian SINR fairness problem are tuned appropriately.
5.3.1 Wireless Network Duality and Algorithms
In this section, we consider Eq. (5.14) for both smooth and nonsmooth utility functions. In particular, in Section 5.3.3, a max–min weighted SINR problem (for egalitarian SINR fairness) will be first solved using a nonlinear Perron–Frobenius theory.1 This is then used together with the wireless network duality in Section 5.3.4 to solve Eq. (5.14). It will be shown that the transmit power and interference temperature can be analytically expressed as the Perron right eigenvectors of the specially constructed matrices associated with the spectral radius constraints in Eq. (5.14). This leads to the development of a wireless network duality involving the dual network as illustrated in Figure 5.3b, which facilitates a distributed algorithm design to maximize the primal network utility.
5.3.2 Smooth and Nonsmooth Utility
The reformulation introduced in Section 5.2 allows us to decompose the utility maximization problem in Eq. (5.8) into first optimizing ![]() , that is, optimizing the SINR assignment and then optimizing the power
, that is, optimizing the SINR assignment and then optimizing the power ![]() and interference temperature
and interference temperature ![]() . In this section, we discuss the assumption for the objectivefunction, which will also be useful in our proposed distributed algorithm in Section 5.3.6 to solve Eq. (5.8) for both smooth and nonsmooth utility functions.
. In this section, we discuss the assumption for the objectivefunction, which will also be useful in our proposed distributed algorithm in Section 5.3.6 to solve Eq. (5.8) for both smooth and nonsmooth utility functions.
For example, the ![]() -fairness utility [29] satisfies Assumption 5.2, given by
-fairness utility [29] satisfies Assumption 5.2, given by

Note that Eq. (5.14) includes the sum rate maximization problem studied in References 27 and 28, when ![]() , but this objective function does not satisfy Assumption 5.2, and henceforth, it is a nonconvex problem that requires global optimization techniques, for example, those studied in References 27 and 28.
, but this objective function does not satisfy Assumption 5.2, and henceforth, it is a nonconvex problem that requires global optimization techniques, for example, those studied in References 27 and 28.
If ![]() is differentiable and separable, that is,
is differentiable and separable, that is, ![]() , let
, let ![]() and
and ![]() denote the first-order and second-order derivatives of
denote the first-order and second-order derivatives of ![]() with respect to
with respect to ![]() , respectively. Then,
, respectively. Then, ![]() is concave in
is concave in ![]() if and only if the curvature is sufficiently large [17]:
if and only if the curvature is sufficiently large [17]:
In the general case (when ![]() can be nonsmooth), we consider the subgradient of
can be nonsmooth), we consider the subgradient of ![]() , whose definition is given as follows.
, whose definition is given as follows.
5.3.3 Nonsmooth Special Case: 
In this section, let us consider the max–min weighted SINR problem (for egalitarian SINR fairness), which is a special case of Eq. (5.9) that has a nonsmooth concave objective function:
where ![]() is a positive vector with the entry
is a positive vector with the entry ![]() used to reflect a priority of the lth link. A larger
used to reflect a priority of the lth link. A larger ![]() indicates a higher priority.
indicates a higher priority.
Let us define the following set of nonnegative matrices:
By applying the nonnegative matrix theory and the nonlinear Perron–Frobenius theory, we obtain a closed-form solution to Eq. (5.16) as well as the corresponding optimal solution in Eq. (5.8), which is unique.
We next give an intriguingly simple algorithm to compute the analytical solution in Lemma 5.1. In particular, by applying the nonlinear Perron–Frobenius theory in Reference 39, the following algorithm computes ![]() given in Lemma 5.1.
given in Lemma 5.1.
Interestingly, using the Friedland–Karlin inequalities in References 43 and 27, Eq. (5.16) is equivalent to Eq. (5.9) with a smooth objective function given by
where ![]() is the matrix defined for the mth user with m given in Eq. (5.20): if the optimal value for Eq. (5.16) is
is the matrix defined for the mth user with m given in Eq. (5.20): if the optimal value for Eq. (5.16) is ![]() for m in Eq. (5.20), then
for m in Eq. (5.20), then ![]() ; if the optimal value for Eq. (5.16) is
; if the optimal value for Eq. (5.16) is ![]() for m in Eq. (5.20), then
for m in Eq. (5.20), then ![]() .
.
5.3.4 Wireless Network Duality
In this section, we develop a dual network having identical SINR performance as the primal network but with all the link directions reversed. The concept of the dual network is actually a virtual network using the same topology of the primal network. Thus, we use ![]() as the channel fading matrix in the dual network (because of the reversed link directions).
as the channel fading matrix in the dual network (because of the reversed link directions).
We now turn to solve Eq. (5.14) for general utility functions that satisfy Assumption 5.2 using a projected subgradient method [40]. Interestingly, this method can be made distributed by connecting the gradients of the spectral radius functions in Eq. (5.14) with the power and the interference temperature in both the primal and the dual networks (cf. Figure 5.3). This is achieved by applying the wireless network duality that exploits the structure of the spectral radius functions in Eq. (5.14).
Recall that we have already defined the nonnegative matrices ![]() and
and ![]() given in Eqs. (5.17) and (5.18), respectively. The gradients
given in Eqs. (5.17) and (5.18), respectively. The gradients ![]() of
of ![]() and
and ![]() at
at ![]() are given, respectively, by [27, 43]
are given, respectively, by [27, 43]
and
normalized such that ![]() . We already know from the reformulation in Section 5.2 that the Perron right eigenvectors of the matrices in Eqs. (5.10) and (5.12) are the optimal transmit power
. We already know from the reformulation in Section 5.2 that the Perron right eigenvectors of the matrices in Eqs. (5.10) and (5.12) are the optimal transmit power ![]() and the optimal interference temperature
and the optimal interference temperature ![]() of the primal network, respectively, which also appear in Eq. (5.24) for
of the primal network, respectively, which also appear in Eq. (5.24) for ![]() in Eqs. (5.11) and (5.25) for
in Eqs. (5.11) and (5.25) for ![]() in Eq. (5.13), respectively. Observe that the gradient for the spectral radius function is the Schur product of the Perron right and left eigenvectors (recall that the Schur product is the component-wise product of two vectors). This interesting characterization leads naturally to the development of a dual network, where a physical interpretation can be given to the Perron left eigenvectors of the matrices in Eqs. (5.10) and (5.12). It enables a distributed method to compute
in Eq. (5.13), respectively. Observe that the gradient for the spectral radius function is the Schur product of the Perron right and left eigenvectors (recall that the Schur product is the component-wise product of two vectors). This interesting characterization leads naturally to the development of a dual network, where a physical interpretation can be given to the Perron left eigenvectors of the matrices in Eqs. (5.10) and (5.12). It enables a distributed method to compute ![]() in Eqs.(5.24) and (5.25). As shown in Figure 5.3b, the dual network reverses the link direction of the primal network, that is, the channel gain from the kth transmitter to the lth receiver is
in Eqs.(5.24) and (5.25). As shown in Figure 5.3b, the dual network reverses the link direction of the primal network, that is, the channel gain from the kth transmitter to the lth receiver is ![]() in the dual network.
in the dual network.
Observe that the channel matrix in Eq. (5.1) is replaced by its transpose in Eq. (5.28). However, this dual network must achieve all possible SINR values that are feasible in the primal network. Combining Eqs. (5.26) and (5.27), we have
and
Corresponding to the primal network power and interference temperature constraints, the dual network power and interference temperature constraints can be given, respectively, by (note the use of ![]() , where
, where ![]() can be i in Eq. (5.11) or
can be i in Eq. (5.11) or ![]() can be j in Eq. (5.13))
can be j in Eq. (5.13))
and
Moreover, it is still true that either the dual network power constraint or the dual network interference temperature constraint is tight at optimality. We then have the following result that connects the transmit powers and interference temperatures of both the primal and dual networks, which is used in a distributed algorithm design in Section 5.3.6.
Finally, Table 5.1 summarizes the wireless network duality that characterizes the transmit power and interference temperature in the primal and the dual networks as the Perron right and left eigenvectors of appropriately constructed nonnegative matrices.
Table 5.1 The Wireless Network Duality Illustrates the Connection between the Primal and the Dual Networks in Terms of Both the Perron Right and Left Eigenvectors of the Nonnegative Matrices Associated with the Spectral Radius Constraints in Eq. utilityTildeGamma
| Wireless Network Duality | ||||
| Primal Network | Dual Network | |||
 |
 |
 |
||
 |
 |
 |
5.3.5 Interference Load Minimization
In Section 5.2, the constraints of the utility maximization problem in Eq. (5.8) can be succinctly reformulated as spectral radius constraints, that is, ![]() and
and ![]() , where
, where ![]() and
and ![]() are given in Eqs. (5.17) and (5.18), respectively. These spectral radius functions capture the effect of interference on the feasibility of SINR assignment. The spectral radius thus plays the role of a useful measure for interference, which we call the interference load. This means that a smaller
are given in Eqs. (5.17) and (5.18), respectively. These spectral radius functions capture the effect of interference on the feasibility of SINR assignment. The spectral radius thus plays the role of a useful measure for interference, which we call the interference load. This means that a smaller ![]() or
or ![]() indicates a smaller interference load on the network, which leads to a larger feasible SINR region that can be optimized. On the other hand, the interference load increases with interference and, therefore, reduces the feasible SINR region. This connection between the interference load and our utility maximization problem in Section 5.2 is made precise in the following. By leveraging both the wireless network duality in Section 5.3.4 and the interference load minimization problem (to be introduced in the following), a distributed algorithm will then be proposed to solve the utility maximization problem in Eq. (5.9).
indicates a smaller interference load on the network, which leads to a larger feasible SINR region that can be optimized. On the other hand, the interference load increases with interference and, therefore, reduces the feasible SINR region. This connection between the interference load and our utility maximization problem in Section 5.2 is made precise in the following. By leveraging both the wireless network duality in Section 5.3.4 and the interference load minimization problem (to be introduced in the following), a distributed algorithm will then be proposed to solve the utility maximization problem in Eq. (5.9).
First, let us consider the following convex optimization problem given by
where ![]() and
and ![]() are given in Eqs. (5.17) and (5.18), respectively,
are given in Eqs. (5.17) and (5.18), respectively, ![]() is the logarithmic mapping by
is the logarithmic mapping by ![]() , and
, and ![]() is a given probability vector that is used to approximate
is a given probability vector that is used to approximate ![]() using its Taylor series expansion up to the first-order terms (cf. proof of Theorem 5.3).
using its Taylor series expansion up to the first-order terms (cf. proof of Theorem 5.3).
In the following, it is fruitful to consider the interference load minimization problem that is intimately related to Eq. (5.35) and instead minimizes a spectral radius function subject to a single linear constraint:
where ![]() is the logarithmic transformation:
is the logarithmic transformation: ![]() .The following result connects Eqs. (5.35 ) and (5.36 ).
.The following result connects Eqs. (5.35 ) and (5.36 ).
Furthermore, because ![]() is a probability vector,
is a probability vector, ![]() and
and ![]() satisfy
satisfy
The formulation of Eq. (5.36) that minimizes the interference load thus provides a connection (by choosing ![]() to be proportional to the subgradient of the utility function) between the general utility maximization problem in Eq. (5.8) and its special case of egalitarian SINR fairness optimization in Eq. (5.16). An interesting interpretation of Lemma 5.3 is that the optimal SINR in the general utility maximization can be scaled relative to the optimal SINR achieved under the egalitarian SINR fairness. Figure 5.4 illustrates the geometric interpretation of the connection between Problems (5.35) and (5.36) by an example using
to be proportional to the subgradient of the utility function) between the general utility maximization problem in Eq. (5.8) and its special case of egalitarian SINR fairness optimization in Eq. (5.16). An interesting interpretation of Lemma 5.3 is that the optimal SINR in the general utility maximization can be scaled relative to the optimal SINR achieved under the egalitarian SINR fairness. Figure 5.4 illustrates the geometric interpretation of the connection between Problems (5.35) and (5.36) by an example using ![]() with a positive
with a positive ![]() .
.

Figure 5.4 Illustration of the connection between Eqs. (5.35) and (5.36). Achievable region for a two-user example with objective function  . The channel gains are given by
. The channel gains are given by  ,
,  ,
,  , and
, and  and the weight is
and the weight is  . The maximum power and interference temperature for users are
. The maximum power and interference temperature for users are  W and
W and  W, respectively. The noise powers for both users are 1 W. The intersection point of the direction
W, respectively. The noise powers for both users are 1 W. The intersection point of the direction  and achievable region is the optimal solution. Moreover, the minimization of Problem (5.36) also intersects with the optimal solution of Eq. (5.35) at the boundary of the feasible region.
and achievable region is the optimal solution. Moreover, the minimization of Problem (5.36) also intersects with the optimal solution of Eq. (5.35) at the boundary of the feasible region.
5.3.6 Utility Maximization Algorithm
In Eq. (5.36), we have shown that it is possible to find a scaling factor that connects the SINR assignment in problem (5.35) (which is related to Eq. (5.14) through a Taylor's series first-order approximation) with the egalitarian SINR fairness. This means that Eq. (5.35) can be first solved by considering Eq. (5.36) to find the scaling factor and then to scale the optimal solution of Eq. (5.36) to finally obtain the solution of Eq. (5.14).
We use the projected subgradient method to solve Eq. (5.36). The parameter ![]() in Eq. (5.36) is updated iteratively. In particular, at the
in Eq. (5.36) is updated iteratively. In particular, at the ![]() th iteration, we update
th iteration, we update ![]() as the subgradient of
as the subgradient of ![]() at
at ![]() . Thus, instead of solving Eq. (5.14) directly, we replace the objective function of Eq. (5.14) in a neighborhood of a feasible point
. Thus, instead of solving Eq. (5.14) directly, we replace the objective function of Eq. (5.14) in a neighborhood of a feasible point ![]() by its Taylor series (cf. proof of Theorem 5.3), which is a successive convex approximation technique. Meanwhile, the algorithm iterates according to the subgradient of both the objective function and the constraint functions. However, computing the gradient of the spectral radius functions, that is, the Schur product of the Perron right and left eigenvectors, requires centralized computation in general. This Schur product is the shadow price of the SINR assignment for utility maximization.
by its Taylor series (cf. proof of Theorem 5.3), which is a successive convex approximation technique. Meanwhile, the algorithm iterates according to the subgradient of both the objective function and the constraint functions. However, computing the gradient of the spectral radius functions, that is, the Schur product of the Perron right and left eigenvectors, requires centralized computation in general. This Schur product is the shadow price of the SINR assignment for utility maximization.
However, by exploiting the wireless network duality, this task can be made distributed. Making use of the results in Section 5.3.4, we can then obtain a distributed algorithm to solve Eq. (5.14). Observe that the gradient ![]() of
of ![]() and
and ![]() in terms of
in terms of ![]() ,
, ![]() ,
, ![]() , and
, and ![]() are, respectively, given by (cf. Lemma 5.2)
are, respectively, given by (cf. Lemma 5.2)
and
normalized such that ![]() . Furthermore, Eqs.(5.38) and (5.39) can be rewritten, respectively, as
. Furthermore, Eqs.(5.38) and (5.39) can be rewritten, respectively, as
and
Now, in Eqs. (5.40) and (5.41), the respective variables ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() can be locally obtained, thus making the gradient computation distributed. We next use Eqs. (5.40) and (5.41) to obtain a distributed algorithm based on the projected subgradient method to solve Eq. (5.8).
can be locally obtained, thus making the gradient computation distributed. We next use Eqs. (5.40) and (5.41) to obtain a distributed algorithm based on the projected subgradient method to solve Eq. (5.8).
Furthermore, if a constant step size is used in Step 4, Algorithm 5.2 is guaranteed to converge to a neighborhood of the optimal solution.
5.3.7 A Software Implementation
The spectral radius function is an important feature that characterizes the optimal wireless network utility. We next discuss how to compute this function numerically when it is used in optimization problems. Our spectral radius function is implemented as a Matlab routine using the cvx software. The cvx software tool in Reference 44 is a Matlab toolbox software for rapid definition, manipulation, and solution of convex optimization problems and is freely available for download. This cvx software solves optimization problems that are appropriately modeled using a set of libraries known as atom library in cvx. The modularity of the atom library software facilitates new functionalities that are specific to some optimization problems with unique features by adding new (user-defined) cvx atoms in cvx. In addition, new cvx atoms need to follow the disciplined convex programming ruleset (DCP ruleset for short), which are drawn from basic principles of convex optimization. This means that a violation of a set of modeling rules can lead to parsing software error.
We now discuss how the convex spectral radius function used in the previous sections given by
can conform to the cvx DCP ruleset, thereby facilitating its cvx implementation to solve optimization problems. A trick to numerically evaluate Eq. (5.42) is an application of the Perron–Frobenius theorem to rewrite Eq. (5.42) as
where ![]() is an (auxiliary) optimization variable. Thus, Eq. (5.42) can be evaluated numerically by solving a geometric program (a special class of convex optimization problems). Using the
is an (auxiliary) optimization variable. Thus, Eq. (5.42) can be evaluated numerically by solving a geometric program (a special class of convex optimization problems). Using the cvx software, the implementation of the spectral radius function in cvx is given by
function cvx_optval = spectral_radius( x, B )
s = size( B, 1 );
cvx_begin gp
variables rho z( s )
minimize( rho );
subject to
diag( exp(x) ) * B * z <= rho * z;
cvx_end
The above function cvx_optval is then put into a subdirectory named as @cvx in the cvx software package, and Matlab can automatically recognize the function call of spectral_radius whenever it is used in the constraints or objectives of a convex optimization problem that follows the cvx DCP ruleset. This cvx software implementation can be useful for verifying the solution computed by the distributed dual algorithms and the nonlinear Perron–Frobenius-theory-based fixed-point algorithm in the previous sections.
5.3.8 Connection between Dual Algorithm and Pricing Function in Game Theory
There are several approaches in the literature to solving the wireless utility maximization problem. A well-studied approach to maximize the utility using distributed power control is to design a noncooperative power control game where users maximize their utility. The outcome of the game results in a Nash equilibrium that is often inefficient.
In the seminal work [11], pricing of transmit powers was introduced to obtain Pareto improvement of the noncooperative power control game, that is, to obtain improvements in user utilities relative to the case with no pricing. In particular, the lth user solves a local utility maximization problem given by
where ![]() is a general pricing function, which is not restricted to any particular form. In Eq. (5.43 ), the lth user treats the transmit powers of other users as fixed and only optimizes its own transmit power. In Reference 11, the pricing function is linearly proportional to the transmit powers in Eq. (5.43), that is,
is a general pricing function, which is not restricted to any particular form. In Eq. (5.43 ), the lth user treats the transmit powers of other users as fixed and only optimizes its own transmit power. In Reference 11, the pricing function is linearly proportional to the transmit powers in Eq. (5.43), that is, ![]() , where c and
, where c and ![]() are positive scalars. Clearly, this pricing function imposes a price that increases with the transmit power of the user. The pricing factor, that is, c, is a common parameter shared by all the users in the game. It is important to note that c has to be appropriately tuned (possibly by a centralized controller through multiple rounds of the noncooperative power control game) such that user's self-interest leads to best possible improvement in overall utility maximization.
are positive scalars. Clearly, this pricing function imposes a price that increases with the transmit power of the user. The pricing factor, that is, c, is a common parameter shared by all the users in the game. It is important to note that c has to be appropriately tuned (possibly by a centralized controller through multiple rounds of the noncooperative power control game) such that user's self-interest leads to best possible improvement in overall utility maximization.
Saraydar et al. [11] also explored the noncooperative game equilibrium of equalizing the SINR (called the equal-SIR equilibrium in Reference 11), which is equivalent to solve the max–min SINR fairness optimization in Eq. (5.16 ). It is interesting to note that the max–min SINR fairness optimization (when used appropriately as an iterative computational submodule) can achieve the social optimum in terms of utility maximization (as used in our dual algorithms). In the following, we state a result that establishes a connection between our dual algorithms for solving Eq. (5.8) in the previous sections and the noncooperative game-theoretic pricing function introduced in Reference 11.
5.4 Numerical Examples
In this section, we provide numerical examples to illustrate the performance of Algorithm 5.1 in Section 5.3.3 and Algorithm 5.2 in Section 5.3.6, illustrating the convergence properties of Algorithms 5.1 and 5.2. Recall that an optimization problem having two different utility functions can be constructed to yield the same optimal solution for egalitarian SINR fairness (cf. (5.23) in Section 5.3.3). By setting the weight of Eq. (5.23) appropriately, and applying Algorithms 5.1 and 5.2 to solve the max–min SINR and the weighted sum of logarithmic SINR utility, respectively, we evaluate the numerical convergence of the power and interference temperature iterates.
We use the following channel gain matrix

and the following weights for the power constraints:

We set ![]() W and
W and ![]() W. The noise power of each user is 1 W.
W. The noise power of each user is 1 W.

Figure 5.5 Illustration of the convergence of Algorithm 5.1 with randomly chosen initial  . We plot the trajectory of power for each of the three users in (a) and the trajectory of interference temperature for each of the three users in (b). We can observe from the figures that the convergence of Algorithm 5.1 is geometrically fast.
. We plot the trajectory of power for each of the three users in (a) and the trajectory of interference temperature for each of the three users in (b). We can observe from the figures that the convergence of Algorithm 5.1 is geometrically fast.

Figure 5.6 Illustration of the convergence of Algorithm 5.2 with randomly chosen initial  . Algorithm 5.2 is a distributed algorithm.
. Algorithm 5.2 is a distributed algorithm.  and
and  are obtained from Step 2, which terminates when
are obtained from Step 2, which terminates when 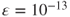 . The number of iterations in the figure corresponds to the outer loop (slower time scale). We plot the trajectory of power for each of the three users in (a) and the trajectory of interference temperature for each of the three users in (b).
. The number of iterations in the figure corresponds to the outer loop (slower time scale). We plot the trajectory of power for each of the three users in (a) and the trajectory of interference temperature for each of the three users in (b).

Figure 5.7 An illustration of Algorithm 5.2. All the other parameters are the same as Figure 5.6 except that  .
.
Figure 5.5 plots the evolution of the power and interference temperature for three users that run Algorithm 5.1 with ![]() equal to
equal to ![]() . We set the initial power vector to
. We set the initial power vector to ![]() W and run Algorithm 5.1 for 10 iterations before it terminates. Figure 5.5 shows that Algorithm 5.1 converges geometrically fast to the optimal solution (verifying Theorem 5.2). The optimal
W and run Algorithm 5.1 for 10 iterations before it terminates. Figure 5.5 shows that Algorithm 5.1 converges geometrically fast to the optimal solution (verifying Theorem 5.2). The optimal ![]() is
is ![]() (verifying Lemma 5.1).
(verifying Lemma 5.1).
Figure 5.6 plots the evolution of the power and interference temperature for three users that run Algorithm 5.2. The objective function that we use in this numerical example is ![]() , where
, where ![]() is
is ![]() . The sum of weighted logarithmic SINR satisfies Assumption 5.2. We set the initial
. The sum of weighted logarithmic SINR satisfies Assumption 5.2. We set the initial ![]() to
to ![]() and run Algorithm 5.2 for 700 iterations and run Algorithm 5.1 as an inner loop. The stopping criterion for the inner loop is
and run Algorithm 5.2 for 700 iterations and run Algorithm 5.1 as an inner loop. The stopping criterion for the inner loop is ![]() . We use a constant step size, that is,
. We use a constant step size, that is, ![]() for all k. Figure 5.6 shows that Algorithm 5.2 converges to the optimal solution (verifying Theorem 5.3). The optimal
for all k. Figure 5.6 shows that Algorithm 5.2 converges to the optimal solution (verifying Theorem 5.3). The optimal ![]() is
is ![]() W and the optimal
W and the optimal ![]() is
is ![]() W so that
W so that ![]() is equal to
is equal to ![]() (verifying Theorem 5.2). We also adjust the value of
(verifying Theorem 5.2). We also adjust the value of ![]() to verify the robustness of our algorithm. Figure 5.7 shows the evolution of the power and interference temperature when the inner loop of Algorithm 5.2, that is, Algorithm 5.1, terminates with
to verify the robustness of our algorithm. Figure 5.7 shows the evolution of the power and interference temperature when the inner loop of Algorithm 5.2, that is, Algorithm 5.1, terminates with ![]() keeping all the other parameters the same as those used in Figure 5.6. Furthermore, we also run Algorithm 5.2 with a suitably large number of primary and secondary users. Figure 5.8 shows the evolution of the power and interference temperature for 5 users out of 30 users.
keeping all the other parameters the same as those used in Figure 5.6. Furthermore, we also run Algorithm 5.2 with a suitably large number of primary and secondary users. Figure 5.8 shows the evolution of the power and interference temperature for 5 users out of 30 users.

Figure 5.8 An illustration of Algorithm 5.1 for 30 users. In this figure, we show the power and interference temperature evolution for only five users.

Figure 5.9 Performance comparison of Algorithms 5.1 and 5.2 by solving two equivalent problems, namely, Eqs. (5.16) and (5.9) with a utility given by Eq. (5.23). (a) and (b) show the trajectories of the power and the interference temperature iterates, respectively, for User 1. The number of iterations in the figure corresponds to the inner loop (faster time scale). With the weight  chosen as in Eq. (5.23), these two algorithms converge to the same solution. As shown, Algorithm 5.1 converges much faster than Algorithm 5.2.
chosen as in Eq. (5.23), these two algorithms converge to the same solution. As shown, Algorithm 5.1 converges much faster than Algorithm 5.2.
Next, we compare the convergence of the power and interference temperature in two different problems that have the same optimal solution. From the second numerical example, we already know in advance that the second power constraint is tight at optimality. Thus, we can set ![]() . Although the solution of these two different problems are the same, Figure 5.9 shows that Algorithm 5.1 converges faster than Algorithm 5.2.
. Although the solution of these two different problems are the same, Figure 5.9 shows that Algorithm 5.1 converges faster than Algorithm 5.2.
To illustrate, we list down the cvx Matlab routine to solve the following utility maximization problem example using the cvx atom mentioned in Section 5.3.7:
Using the software atom developed for the spectral radius function in Section 5.3.7, the cvx code to solve Eq. (5.47) numerically is given by
cvx_begin
variables gamma_tilde(3)
maximize( w' * gamma_tilde );
subject to
log( spectral_radius( gamma_tilde, B1 ) ) <= 0;
log( spectral_radius( gamma_tilde, B2 ) ) <= 0;
log( spectral_radius( gamma_tilde, B3 ) ) <= 0;
cvx_end
In the above, the matrices B1, B2, and B3 are evaluated using Eq. (5.17), and they contain the problem parameters, that is, the channel gains, the weight and weighted power constraints, and so on.
5.5 Conclusion
We studied the network utility maximization in a wireless network with both power budget constraints and interference temperature constraints in this chapter. We first reformulated the problem as one in the SINR domain that has appropriately constructed spectral radius constraints. The advantages of our reformulation were that, firstly, it captured the entire feasible SINR region and, secondly, it decoupled the SINR assignment for primary and secondary users from power and interference temperature control. We also studied a special case of egalitarian fairness utility, which is the max–min weighted SINR problem using the nonlinear Perron–Frobenius theory, and a geometrically fast convergent (with no parameter tuning) algorithm was proposed to solve this max–min weighted SINR problem. Then, we developed a wireless network duality and established its connection to the gradient of the spectral radius function as shadow prices for SINR assignment in the general utility maximization problem. We leveraged the wireless network duality and an interference load minimization problem, which interestingly is related to the max–min weighted SINR problem, to develop a distributed algorithm to solve the utility maximization problem. Extensive numerical examples demonstrated the good performance of our algorithms, particularly the flexibility, the fast convergence time, and the robustness to different numbers of primary and secondary users. We also discussed a connection between this shadow price dual algorithm approach for utility maximization with a noncooperative power control game in obtaining improvements in user utilities relative to the case with no pricing.
References
- 1. S. Ha, S. Sen, C. Joe-Wong, Y. Im, and M. Chiang.
 : time-dependent pricing for mobile data. In Proceedings of ACM SIGCOMM, 2012.
: time-dependent pricing for mobile data. In Proceedings of ACM SIGCOMM, 2012. - 2. C. Joe-Wong, S. Ha, and M. Chiang. Time dependent broadband pricing: feasibility and benefits. In Proceedings of IEEE ICDCS, 2011.
- 3. S. Sorooshyari, C. W. Tan, and M. Chiang. “Power control for cognitive radio networks: axioms, algorithms, and analysis,” IEEE/ACM Transactions on Networking, 20(3), 2012, 878–891.
- 4. S. Ren and M. van der Schaar. “Data demand dynamics in wireless communications markets,” IEEE Transactions on Signal Processing, 60(4), 2012, 1986–2000.
- 5. Y. Cui, T. Ma, and X. Cheng. Multi-hop access pricing in public area
 s. In Proceedings of IEEE INFOCOM, 2011.
s. In Proceedings of IEEE INFOCOM, 2011. - 6. P. Hande, M. Chiang, R. Calderbank, and S. Rangan. Network pricing and rate allocation with content provider participation. In Proceedings of IEEE INFOCOM, 2009.
- 7. P. Hande, M. Chiang, R. Calderbank, and J. Zhang. Pricing under constraints in access networks: revenue maximization and congestion management. In Proceedings of IEEE INFOCOM, 2010.
- 8. E. Altman, P. Bernhard, S. Caron, G. Kesidis, J. Rojas-Mora, and S. Wong. “A model of network neutrality with usage-based prices,” Telecommunication Systems, 52(2), 2011, 1–9.
- 9. S. Caron, G. Kesidis, and E. Altman. “Application neutrality and a paradox of side payments,” In Proc. ACM ReARCH, 2010.
- 10. S. Ren, J. Park, and M. van der Schaar. “Entry and spectrum sharing scheme selection in femtocell communications markets,” IEEE/ACM Transactions on Networking, 21(1), 2012, 218–232.
- 11. C. U. Saraydar, N. B. Mandayam, and D. J. Goodman. “Efficient power control via pricing in wireless data networks,” IEEE Transactions on Communications, 50(2), 2002, 291–303.
- 12. S. Shakkottai and R. Srikant. “Economics of network pricing with multiple
 s,” IEEE/ACM Transactions on Networking, 14(6), 2006, 1233–1245.
s,” IEEE/ACM Transactions on Networking, 14(6), 2006, 1233–1245. - 13. S. Shakkottai, R. Srikant, A. Ozdaglar, and D. Acemoglu. “The price of simplicity,” IEEE Journal on Selected Areas in Communications, 26(7), 2008, 1269–1276.
- 14. T. Basar and R. Srikant. Revenue-maximizing pricing and capacity expansion in a many-users regime. In Proceedings of IEEE INFOCOM, vol. 1, 2002.
- 15. S. Shakkottai and R. Srikant. “Network optimization and control,” NOW Monograph in Foundations and Trends in Networking, 2(3), 2007, 271–379.
- 16. M. Chiang, P. Hande, T. Lan, and C. W. Tan. “Power control in wireless cellular networks,” NOW Monograph in Foundations and Trends in Networking, 2(4), 2008, 381–533.
- 17. P. Hande, S. Rangan, M. Chiang, and X. Wu. “Distributed uplink power control for optimal
 assignment in cellular data networks,” IEEE/ACM Transactions on Networking, 16(6), 2008, 1420–1433.
assignment in cellular data networks,” IEEE/ACM Transactions on Networking, 16(6), 2008, 1420–1433. - 18. S. Huang, X. Liu, and Z. Ding. “Decentralized cognitive radio control based on inference from primary link control information,” IEEE Journal on Selected Areas in Communications, 29(2), 2011, 394–406.
- 19. M. Lotfinezhad, L. Ben, and E. S. Sousa. Optimal control of constrained cognitive radio networks with dynamic population size. In Proceedings of IEEE INFOCOM, 2010.
- 20. S. Rangan and R. Madan. “Belief propagation methods for intercell interference coordination in femtocell networks,” IEEE Journal on Selected Areas in Communications, 30(3), 2012, 631–640.
- 21. A. L. Stolyar and H. Viswanathan. Self-organizing dynamic fractional frequency reuse for best-effort traffic through distributed inter-cell coordination. In Proceedings of IEEE INFOCOM, 2009.
- 22. A. L. Stolyar and H. Viswanathan. Self-organizing dynamic fractional frequency reuse in
 systems. In Proceedings of IEEE INFOCOM, 2008.
systems. In Proceedings of IEEE INFOCOM, 2008. - 23. K. R. Krishnan and H. Luss. Power selection for maximizing
 in femtocells for specified
in femtocells for specified  in macrocell. In Proceedings of IEEE WCNC, 2011.
in macrocell. In Proceedings of IEEE WCNC, 2011. - 24. C. W. Tan, M. Chiang, and R. Srikant. “Fast algorithms and performance bounds for sum rate maximization in wireless networks,” IEEE/ACM Transactions on Networking, 21(3), 2012, 706–719.
- 25. L. Zheng and C. W. Tan. “Cognitive radio network duality and algorithms for utility maximization,” IEEE Journal on Selected Areas in Communications, 31(3), 2013, 500–513.
- 26. C. W. Tan, M. Chiang, and R. Srikant. “Maximizing sum rate and minimizing
 on multiuser downlink: optimality, fast algorithms and equivalence via max–min
on multiuser downlink: optimality, fast algorithms and equivalence via max–min  ,” IEEE Transactions on Signal Processing, 59(12), 2011, 6127–6143.
,” IEEE Transactions on Signal Processing, 59(12), 2011, 6127–6143. - 27. C. W. Tan, S. Friedland, and S. H. Low. “Nonnegative matrix inequalities and their application to nonconvex power control optimization,” SIAM Journal on Matrix Analysis and Applications, 32(3), 2011, 1030–1055.
- 28. C. W. Tan, S. Friedland, and S. H. Low. “Spectrum management in multiuser cognitive wireless networks: optimality and algorithm,” IEEE Journal on Selected Areas in Communications, 29(2), 2011, 421–430.
- 29. J. Mo and J. Walrand. “Fair end-to-end window-based congestion control,” IEEE/ACM Transactions on Networking, 8(5), 2000, 556–567.
- 30. J. F. C. Kingman. “A convexity property of positive matrices,” Proceedings of the American Mathematical Society, 12(2), 1961, 283–284.
- 31. S. Boyd and L. Vanderberghe. Convex Optimization. Cambridge University Press, Cambridge, U.K, 2004.
- 32. P. Viswanath and D. N. C. Tse. “Sum capacity of the vector Gaussian broadcast channel and uplink–downlink duality,” IEEE Transactions on Information Theory, 49(8), 2003, 1912–1921.
- 33. W. Yu. “Uplink–downlink duality via minimax duality,” IEEE Transactions on Information Theory, 52(2), 2006, 361–374.
- 34. F. Rashid-Farrokhi, K. J. Ray Liu, and L. Tassiulas. “Transmit beamforming and power control for cellular wireless systems,” IEEE Journal on Selected Areas in Communications, 16(8), 1998, 1437–1449.
- 35. B. Song, R. L. Cruz, and B. D. Rao. “Network duality for multiuser
 beamforming networks and applications,” IEEE Transactions on Communication, 55(3), 2007, 618–630.
beamforming networks and applications,” IEEE Transactions on Communication, 55(3), 2007, 618–630. - 36. D. W. H. Cai, T. Quek, and C. W. Tan. “A unified analysis of max–min weighted SINR for MIMO downlink system,” IEEE Transactions on Signal Processing, 59(8), 2011, 3850–3862.
- 37. D. W. H. Cai, T. Quek, C. W. Tan, and S. H. Low. “Max–min SINR coordinated multipoint downlink transmission - duality and algorithms,” IEEE Transactions on Signal Processing, 60(10), 2012, 5384–5395.
- 38. C. W. Tan, D. P. Palomar, and M. Chiang. “Energy-robustness tradeoff in cellular network power control,” IEEE/ACM Transactions on Networking, 17(3), 2009, 912–925.
- 39. U. Krause. “Concave
 theory and applications,” Nonlinear Analysis, 47(2001), 2001, 1457–1466.
theory and applications,” Nonlinear Analysis, 47(2001), 2001, 1457–1466. - 40. D. P. Bertsekas. Nonlinear Programming. Athena Scientific, Belmont, MA, USA, 2nd edition, 2003.
- 41. G. J. Foschini and Z. Miljanic. “A simple distributed autonomous power control algorithm and its convergence,” IEEE Transactions on Vehicular Technology, 42(4), 1993, 641–646.
- 42. S. Boyd, A. Ghosh, and D. Shah. “Randomized gossip algorithms,” IEEE Transactions on Information Theory, 52(6), 2006, 2508–2530.
- 43. S. Friedland and S. Karlin. “Some inequalities for the spectral radius of non-negative matrices and applications,” Duke Mathematical Journal, 42(3), 1975, 459–490.
- 44. M. Grant and S. Boyd.
 : Matlab software for disciplined convex programming, version 1.21, 2011. http://cvxr.com/cvx.
: Matlab software for disciplined convex programming, version 1.21, 2011. http://cvxr.com/cvx.










