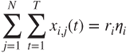Chapter 18
Smart Pricing of Cloud Resources
YU XIANG and TIAN LAN
Large investments have been made in recent years in data centers and cloud computing. A survey by KPMG International [1] in February 2012 shows that more than 50% of senior executives find the most important impact of cloud computing to their business models to be its cost benefits. Accordingly, much research has been focused on demystifying various economic issues in data center and cloud computing, for example, economic and pricing models, cost-optimization techniques, tariff and charging structures, and business objectives.
As in today's clouds the demand for resources in clouds are dynamically fluctuating because of many factors, thus offering fixed resources to all the users regardless of their demands may either not be able to meets some users’ demand or leave some resources wasted. Therefore, one thing attracts most attention in today's Cloud computing is the idea of optimizing the utilization of computing resources among all cloud users, so that the computing resources can be distributed in the most effective manner and restrict the underutilization to a certain level. The intuitive idea to deal with this is that the resources should be regulated by the law of supply and demand, that is, when demand rises but supply remains the same, the price of types of virtual machines (VMs) should go up, and when demand drops, then prices should fall accordingly.
To implement this idea, cloud providers such as Amazon EC2 [2, 3] employs this sort of market-driven resource allocation for unused capacity. In Amazon EC2's spot markets, instead of renting a server for fixed price per hour for each hour that the server runs, users can make a bid for a certain number of hours of a certain type of server. The spot price is set by the cloud provider, which fluctuates in real time according to spot instances supply and demand. When the bid exceed the spot price, the instance will run until the spot price exceed the bid, in which case the instance will be terminated without notice. To use spot instances, users shall place a request that specifies the instance type, the availability zone desired, the number of spot instances desired, and the bidding price per instance hour. Amazon EC2 API provides the spot price history for the past 90 days to help customers decide their bids [4], as shown in Figure18.1.
Cloud resources can be dynamically allocated not only based on just the demand and supply such as in the case of spot instances but also based on service level agreement (SLA), that is, the providers has to ensure users can get certain service level when dynamically allocating resources based on demand and supply to maximize revenue. SLA is a critical bridge between cloudproviders and customers, as in clouds, the providers aim to obtain the revenues by leasing the resources and users rent these resources to meet their application requirements. SLA provides a platform for users to indicate their required quality of service (QoS) [5], which specifies responsibilities, guarantees, warranties, performance levels in terms of availability, response time, and so on. Owing to the fast-growing power consumption and application heterogeneity of data centers, cost optimization and smart service pricing are also becoming ever more urgent and important. In contrast to the adoption of low power devices and energy saving solutions in References [6] and [7], a cost-optimization approach in References [8] and [9] exploits the diversities of electricity prices over time and geographic regions. In particular, a load-balancing algorithm is proposed in Reference [9] to coordinate cloud computing workload with electricity prices at distributed data centers, in order to achieve the goal of minimizing the total electricity cost while guaranteeing the average service delay experienced by all jobs.

Figure 18.1 Amazon EC2 VM spot instance price History: price of a m1.large linux spot instance in US Southeast-1a from May 17 to May 23, 2012 [4].
These queuing-based models for price data center services based on an average service delay may be unsatisfactory to cloud users, not only because they may have heterogeneous job requirements and spending budgets but also because of a fundamental limitation of the average delay approach—individual job completion times are still randomly scattered over a wide range of values. Delayed response may frustrate users and, consequently, result in revenue loss. Therefore, the ability to deliver according to predefined job deadlines increasingly becomes a competitive requirement [10, 11]. Cloud providers and users can negotiate individual job deadlines to determine costs and penalties based on the desired performance and budget. This presents an opportunity to offer deadline-dependent pricing, which generates an additional source of revenue for cloud providers. It immediately raises the following question: How to jointly optimize both electricity cost of distributed data centers and total revenue from deadline-dependent pricing, in order to maximize the net profit cloud providers receive? Wang et al. [12] studied the problem of data center net profit optimization (NPO), which aims to maximize the difference between the total revenue from deadline-dependent pricing and the electricity cost of distributed data centers.
This chapter studies cloud resources allocation based on three types of pricing models, that is, to find out the optimal resource allocation that maximizes the total revenue, where the revenue function depends on various pricing models we employed; for instances, as we discussed earlier, price of cloud resource can be determined by three major factors such as demand and supply in current markets, the SLA level cloud servers provided, and the predefined job deadline users required. We proposed the detailed pricing model with respect to these three factors separately in the following sections and then obtain the optimal cloud resource allocation to maximize the revenue function formulated by these pricing models, an comparison of overall revenue with heuristic static pricing scheme is shown for each pricing model.
18.1 Data Center VM Instance Pricing
Amazon's spot instances mechanism can be described as a continuous seal-bid uniform price auction, where VMs of the same type are sold at identical price and the providers assigns resources to bidders in decreasing order of their bids until all available resources have been allocated, and the spot price may be adjusted when there are no instances running at the current spot price [13]. In this section, we formulate the problem of dynamic resource allocation for simultaneous spot markets, and here the goal is to allocate unused data center resources to each spot market in a timely manner that maximize the total revenue, subject to the capacity constraints of individual machines. In the rest of this section, we shall present our solution approach to achieve this goal for both fixed pricing scheme, where price of a VM type is fixed and thus is independent from market situation, and the uniform pricing scheme,where the price of a VM type is adjustable according to market demand and supply.
18.1.1 Dynamic Scheduling and Server Consolidation for Fixed Pricing Scheme
In the fixed pricing scheme, each VM type has a fixed price that does not fluctuate with the current supply and demand situation. Hence, the virtual machine revenue maximization problem (VRMP) can be modeled as a multiple knapsack problem (MKP) as follows: given a set of machines ![]() and
and ![]() resource types (differed in CPU, memory, and disk), where each machine
resource types (differed in CPU, memory, and disk), where each machine ![]() has a capacity
has a capacity ![]() for each type of VM
for each type of VM ![]() . The set of VMs to be scheduled is
. The set of VMs to be scheduled is ![]() and each VM
and each VM ![]() has a size
has a size ![]() for each
for each ![]() and a value
and a value ![]() . To formulate the optimization problem, we would first choose the optimization variable (which is the VM scheduling parameter
. To formulate the optimization problem, we would first choose the optimization variable (which is the VM scheduling parameter ![]() ), then define the objective and constraints. As we mentioned earlier, the objective is to maximize the total value, which is the summation of all of the chosen VMs(for a chosen VM,
), then define the objective and constraints. As we mentioned earlier, the objective is to maximize the total value, which is the summation of all of the chosen VMs(for a chosen VM, ![]() ; for an abandoned VM,
; for an abandoned VM, ![]() ), which is
), which is ![]() . While the constraints for this goal is the machine capacity, that is, the summation of the size of all chosen VMs should be smaller than or equal to
. While the constraints for this goal is the machine capacity, that is, the summation of the size of all chosen VMs should be smaller than or equal to ![]() . On the basis of the intuition above, the problem can be formulated as
. On the basis of the intuition above, the problem can be formulated as

It can be noticed that this MKP formulation is an NP-hard combinatorial optimization problem, we propose a ![]() local search algorithm [14] that can approximate the optimal solutions, which is specified by Algorithm 18.1. In this algorithm,
local search algorithm [14] that can approximate the optimal solutions, which is specified by Algorithm 18.1. In this algorithm, ![]() is the current set of VMs on machine
is the current set of VMs on machine ![]() ,
, ![]() is the set of VMs chosen to maximize the total value, and
is the set of VMs chosen to maximize the total value, and ![]() isthe value of VM
isthe value of VM ![]() . As it is depicted, the algorithm proceeds in rounds. For each round, first maximize the total revenue among pending requests and current running VMs on machine
. As it is depicted, the algorithm proceeds in rounds. For each round, first maximize the total revenue among pending requests and current running VMs on machine ![]() ; then if there is a potential new configuration for
; then if there is a potential new configuration for ![]() by scheduling, first try to schedule all VMs using available free capacity and then preempt and migrate VMs when the total demand is reaching capacity. To achieve fast convergence rate, we require each local search operation to improve solution quality for each machine
by scheduling, first try to schedule all VMs using available free capacity and then preempt and migrate VMs when the total demand is reaching capacity. To achieve fast convergence rate, we require each local search operation to improve solution quality for each machine ![]() by at least
by at least ![]() .
.
18.1.2 Price Estimation for the Uniform Pricing Scheme
We now consider the case in which the price of each instance vary with the demand–supply curve and the resource availability. In this scenario, above all, we need to periodically analyzes the market situation and predict the demand and supply curves, on which the price of instances depend. The prediction of the demand curves can be constructed by capturing the relationship between the quantity of acceptable requests and the bidding price(as shown in Figure 18.2) over time period ![]() at sampling interval
at sampling interval ![]() , where
, where ![]() denotes the current time and
denotes the current time and ![]() denotes the prediction period. Then we can decide the expected price for each type of VM in each market based on the prediction. Finally, we will be able to make online scheduling decisions for revenue maximization.
denotes the prediction period. Then we can decide the expected price for each type of VM in each market based on the prediction. Finally, we will be able to make online scheduling decisions for revenue maximization.

Figure 18.2 Example demand curve at time  and over time.
and over time.
Let ![]() denote the
denote the ![]() th bidding price in decreasing order,
th bidding price in decreasing order, ![]() denote the demand that bids at price
denote the demand that bids at price ![]() , and
, and ![]() denote the demand that bids at price at least
denote the demand that bids at price at least ![]() at time
at time ![]() . As the spot instances mechanism allows requests with bidding prices higher than or equal to the spot price
. As the spot instances mechanism allows requests with bidding prices higher than or equal to the spot price ![]() to be accepted, then when
to be accepted, then when ![]() equals
equals ![]() , we can schedule
, we can schedule ![]() VM requests. (Demand curve as shown in Fig. 18.2.) As the bidding price of each individual VM request is independent of the current market situation, we can model the demand quantity to
VM requests. (Demand curve as shown in Fig. 18.2.) As the bidding price of each individual VM request is independent of the current market situation, we can model the demand quantity to ![]() independently for each
independently for each ![]() to predict the expected demand curve. Then we are able to predict the future demand
to predict the expected demand curve. Then we are able to predict the future demand ![]() for each
for each ![]() from
from ![]() to
to ![]() . Our approach to do this is to adopt an autoregressive (AR) model [15] that estimates
. Our approach to do this is to adopt an autoregressive (AR) model [15] that estimates ![]() from the historical values
from the historical values ![]() as
as

where ![]() with
with ![]() is the set of parameters of the historical values and
is the set of parameters of the historical values and ![]() is uncorrelated white noise with mean 0 and standard deviation
is uncorrelated white noise with mean 0 and standard deviation ![]() , and all these parameters can be obtained from historical demand data. This is an appropriate model because it is not only lightweight and easy to implement but also capable of capturing short-term trends to let us compute the expected demand curve.
, and all these parameters can be obtained from historical demand data. This is an appropriate model because it is not only lightweight and easy to implement but also capable of capturing short-term trends to let us compute the expected demand curve.
Now we have the demand and supply curve, our objective is now to schedule requests of each spot market to maximize the expected revenue over the next prediction period. This dynamic revenue maximization with variable price (DRMVP) problem is identical to the former VRMP except that price of individual VMs is determined by the estimated demand curve ![]() . Again to formulate the optimization problem, first, we choose the same optimization variable as in Section 18.1.1, which is the scheduling vector of VMs. The difference is this time the variable varies with time because the price varies with time based on the demand curve, so it is defined as
. Again to formulate the optimization problem, first, we choose the same optimization variable as in Section 18.1.1, which is the scheduling vector of VMs. The difference is this time the variable varies with time because the price varies with time based on the demand curve, so it is defined as ![]() . And the objective is the sum of the revenue over demand prediction period
. And the objective is the sum of the revenue over demand prediction period ![]() , subject to the constraints that the total VMs scheduled during time
, subject to the constraints that the total VMs scheduled during time ![]() should be smaller than or equal to the total number of VM requests in
should be smaller than or equal to the total number of VM requests in ![]() , and the total size of all chosen VMs should not exceed the machine capacity
, and the total size of all chosen VMs should not exceed the machine capacity![]() , noticed that each VM size
, noticed that each VM size ![]() here also varies with time because of demand curve prediction. Now we can model this problem as follows:
here also varies with time because of demand curve prediction. Now we can model this problem as follows:

As the objective function of this optimization problem is nonlinear, the problem is even more difficult to solve that of the fixed priced case; however, the revenue function ![]() for a single VM type is a piecewise linear function, and it can be observed from the
for a single VM type is a piecewise linear function, and it can be observed from the ![]() using examples in Figure 18.2. In some situations, scheduling a VM can cause the current market price to be lowered, resulting in a sharp drop in total revenue. Thus motivated by similar work on market clearing algorithms for piecewise linear objective functions, our approach to deal with this issue is to approximate
using examples in Figure 18.2. In some situations, scheduling a VM can cause the current market price to be lowered, resulting in a sharp drop in total revenue. Thus motivated by similar work on market clearing algorithms for piecewise linear objective functions, our approach to deal with this issue is to approximate ![]() using a concave envelope function
using a concave envelope function ![]() , which is computed by constructing a upper convex hull using the extreme points in
, which is computed by constructing a upper convex hull using the extreme points in ![]() .
. ![]() has the following property.
has the following property.
Table 18.2 Average Revenue Achieved by Different Policies
| Policy | Metric | Income | Revenue Loss | Net Income |
| Static | Mean | 67,030.44 | 0399.01 | 66,631.43 |
| Standard deviation | 13,573.32 | 0172.45 | 13,400.87 | |
| Dynamic | Mean | 78,026.33 | 3398.36 | 74,627.97 |
| Standard deviation | 15,173.28 | 1083.63 | 14,089.65 |
18.2 Data Center SLA-Based Pricing
Cloud resources can not only be dynamically allocated based on just the demand and supply such as in the case of spot instances but also based on SLA, that is, the providers has to ensure users can get certain service level when dynamically allocating resources based on demand and supply to maximize revenue. SLA is a critical bridge between cloud providers and customers, as in clouds, the providers aim to obtain the revenues by leasing the resources and users rent these resources to meet their application requirements. SLA provides a platform for users to indicate their required QoS [5], which specifies responsibilities, guarantees, warranties, performance levels in terms of availability, response time, and so on. Usually, cloud providers charge users according to their requirement level for their tasks. For example, Amazon EC2 offers spot instances at a much lower price than that of reserved resources. Service instances (including the user and the VMs he/she rented for service) may have different attributes such as arrival rate, execution time, and pricing mechanism. The challenge here is how much resources must be distributed to a VM to maintain the promised performance in SLAs when trying to maximize the total revenue. Allocate more resources to those who have high arrival rate and high price will certainly ensure revenue, but in practice, there are cases when users have low arrival rate but high price and vice versa.
Our goal in this section is to maximize the SLA-based revenues [16] by proper resource allocation, that is, to schedule resources among different service instances in an adaptive manner based on the dynamic situation. For the rest of the section, first, we formulate the resource allocation problem based on the queuing theory to model user's requirement using parameters such as resource quantity, request arrival, service time, and pricing models. Then we propose our optimal SLA-based resource allocation algorithms, by which providers can maximize their revenues.
In order to find how many servers should be assigned for each service instance in order to achieve maximum revenue for a pricing model, we first formulate our mathematical model for this as follows: A data center consists of ![]() homogeneous servers that are grouped into clusters dynamically; each cluster is virtualized as a single machine. The provider signs SLAs with
homogeneous servers that are grouped into clusters dynamically; each cluster is virtualized as a single machine. The provider signs SLAs with ![]() users, the number of servers allocated to each service instance is
users, the number of servers allocated to each service instance is ![]() , we assume that the more servers assigned, the more powerful the virtual machine is. We also assume that the requests from users are Poisson distributed with arrival rate
, we assume that the more servers assigned, the more powerful the virtual machine is. We also assume that the requests from users are Poisson distributed with arrival rate ![]() and service rate
and service rate ![]() , thus the average service time is exponentially distributed with mean
, thus the average service time is exponentially distributed with mean ![]() , and the service rate of a VM with
, and the service rate of a VM with ![]() servers is
servers is ![]() . Thus based on the above description, each service instance can be modeled as a FIFO(first in, first out) M/M/1 queue. Here we define service intensity
. Thus based on the above description, each service instance can be modeled as a FIFO(first in, first out) M/M/1 queue. Here we define service intensity ![]() as the ratio of arrival rate to service throughput of one server:
as the ratio of arrival rate to service throughput of one server:
The pricing mechanism specifies how service requests are charged, mostly provider oriented. Here we propose two user-oriented pricing mechanisms MRT (mean response time) and IRT (instant response time), in which users are charged according to achieved performance in terms of MRT, which is the mean of the time interval between a request arrives at the system and the instant at which the service is completed. Usually providers divide time into time slots, and we calculate the mean response time of every time slot. For the MRT pricing model, let ![]() be an offset factor of the actual response time to benchmark, which is defined as
be an offset factor of the actual response time to benchmark, which is defined as
where ![]() is the measured average response time during a time slot and
is the measured average response time during a time slot and ![]() is a benchmark of response time defined in SLA, which determines by users’ requirement. Then the pricing mechanism can be formulated as
is a benchmark of response time defined in SLA, which determines by users’ requirement. Then the pricing mechanism can be formulated as
where ![]() is the price of each service provision and
is the price of each service provision and ![]() is the price constant. As shown in Figure 18.3a,
is the price constant. As shown in Figure 18.3a, ![]() is the linear function of
is the linear function of ![]() and when
and when ![]() , the provider will be penalized, also
, the provider will be penalized, also ![]() is the slope of the price function,
is the slope of the price function,

Figure 18.3 Price models. (a) Price model in terms of MRT and (b) price model in terms of IRT.
As MRT is of less practical value as a performance metric when response time varies quite a lot, we propose the IRT pricing model, where request is charged according to measured response time. That is,

The pricing model can be illustrated as in Figure 18.3b, in which the charge under this model is determined by the number of service provisions with response time within required ![]() .
.
Now we are ready to study the optimal allocation based on MRT and IRT. On the basis of some mathematical background of the most popular M/M/1 model in queuing theory, the average response time ![]() of service instance
of service instance ![]() at the steady system state is
at the steady system state is
and the service performance level is
The mean revenue ![]() is calculated as
is calculated as
The overall revenues during a time slot from service instance ![]() is
is
Then the optimization problem can be formulated as

This optimization problem can be solved using Lagrange method. The Lagrange composite function can be constructed as

where ![]() is the Lagrange multiplier constant. Letting
is the Lagrange multiplier constant. Letting ![]() , with
, with ![]() ,
,

then substituting this into the constraint of the optimization problem, we have

Then we yield the final answer, which is the number of servers used for each service instance,

This holds when the request arrival rate of each service instance is less than the service processing rate according to M/M/1 queuing model, otherwise the length of request queue will not converge. Thus our result only holds when
Thus we have
What is more, Figure 18.3 shows that the providers would be penalized once mean response time cannot meet the requirement in SLA, which is ![]() ; hence, our results ensures that
; hence, our results ensures that
Finally, we have the lower bound of resources that can be assigned for each service instance:
Next we will consider the optimal solution for IRT pricing model, the sojourn time probability distribution is
Assuming that service instance ![]() is allocated to
is allocated to ![]() servers, then the mean revenue brought by a service provision is
servers, then the mean revenue brought by a service provision is
Then the overall mean revenue from service instance ![]() during a time slot is
during a time slot is
Thus our optimization problem can be formulated as

Constructing Lagrange composite function

Letting ![]() , where
, where ![]() ,
,

Then we have

Finally, we get

And bounds should be obtained similarly as for the MRT case.
Experiments have been run on a C-based simulator we developed, and events been simulated include arrival, departure, resource allocation for both the MRT and IRT pricing models with the synthetic dataset, and the traced data set. Experimental results for both MRT and IRT shown in Figure 18.4 proved that our algorithms outperform heuristic method.

Figure 18.4 Evolution of revenue during 5 min over time with traces.
18.3 Data Center TIME-DEPENDENT Pricing
In this section, we consider the problem of data center NPO, which aims to maximize the difference between the total revenue from deadline-dependent pricing and the electricity cost of distributed data centers [12]. Time-dependent pricing, which charges users based on not only how much resources are consumed but also when they are consumed, has been widely studied in the electricity industry [17–20] and the Internet service provider (ISP) industry [21–23] as an effective solution to even out resource consumption peaks and reduce operating costs. However, the problem for data center pricing is largely different because the prices are determined by job deadlines (i.e., completion times), whereas job duration or progress are irrelevant.
The goal here is to maximize the data center net profit through job scheduling. It requires (i) to maximize the total revenue as a function of individual job completion deadlines, (ii) to minimize the electricity cost by scheduling jobs to different time and locations, and (iii) to satisfy a capacity constraint at each distributed data center. We formulate this problem as a constrained optimization [12], whose solutions characterizes an interesting trade-off between delay and cost—while completing a job earlier generates a higher revenue, it restricts the set of feasible scheduling decisions, causing higher electricity cost. While being a complex, mixed-integer optimization due to the scheduling formulation, the NPO problem remains to be hard because of the coupling of scheduling decisions and job completion deadlines. There is no closed-form, differentiable function that computes job completion deadlines by scheduling decisions, which is often necessary if standard optimization techniques are to be applied.
As we mentioned earlier, deadline-dependent pricing charges users based on both the amount and the instance time at which the resources are consumed. Suppose that a cloud computing service consists of a set of ![]() distributed data centers and that its billing cycle is divided into
distributed data centers and that its billing cycle is divided into ![]() periods. Let
periods. Let ![]() be the total number of jobs submitted for the next cycle. To enable deadline-dependent SLA and pricing, each user request
be the total number of jobs submitted for the next cycle. To enable deadline-dependent SLA and pricing, each user request ![]() not only contains the number of demanded VM instances (i.e.,
not only contains the number of demanded VM instances (i.e., ![]() ) and the total subscription time (i.e.,
) and the total subscription time (i.e., ![]() ) but is also associated with a bid function
) but is also associated with a bid function ![]() , which measures the payment user
, which measures the payment user ![]() is willing to make if his/her job is accepted and scheduled to complete by period
is willing to make if his/her job is accepted and scheduled to complete by period ![]() . For example, a bid function is flat when a user is indifferent to job deadlines, whereas it becomes strictly decreasing when a user is willing to pay more to get his/her job completed early.
. For example, a bid function is flat when a user is indifferent to job deadlines, whereas it becomes strictly decreasing when a user is willing to pay more to get his/her job completed early.
18.3.1 Electricity Cost
In the electricity market of North America, Regional Transmission Organization (RTO) is responsible for transmit electricity over large interstate areas and electricity prices are regionally different. Electricity prices remain the same for a relatively long period in some regions, whereas they may change every hour, even 15 min in the regions who have wholesale electricity markets [9, 17, 18]. In this paper, we consider cloud computing services consisting of distributed regional data centers, which are subject to different electricity prices. When servers at each data center are homogeneous, the total electricity consumption at each data center ![]() over period
over period ![]() can be calculated directly by multiplying the number of active servers
can be calculated directly by multiplying the number of active servers ![]() and the electricity consumption per server
and the electricity consumption per server ![]() . Let
. Let ![]() be the electricity price of data center
be the electricity price of data center ![]() at time
at time ![]() . We also assume that
. We also assume that ![]() for
for ![]() is known noncausally at the beginning of each billing cycle. In practice, this can be achieved by stochastic modeling of electricity prices [24, 25] or by purchasing forward electricity contracts in the whole sale market [26, 27]. Thus the total electricity cost for
is known noncausally at the beginning of each billing cycle. In practice, this can be achieved by stochastic modeling of electricity prices [24, 25] or by purchasing forward electricity contracts in the whole sale market [26, 27]. Thus the total electricity cost for ![]() data centers over the next cycle is given as
data centers over the next cycle is given as

18.3.2 Workload Constraints
We denote the number of VM instances received by job ![]() from data center
from data center ![]() at period
at period ![]() as
as ![]() . We consider two types of jobs: divisible jobs and indivisible jobs. An indivisible job that requires
. We consider two types of jobs: divisible jobs and indivisible jobs. An indivisible job that requires ![]() VM instances and a subscription time
VM instances and a subscription time ![]() cannot be interrupted and must have
cannot be interrupted and must have ![]() VM running continuously for
VM running continuously for ![]() periods, whereas a divisible job can be partitionedarbitrarily into any number of portions, as long as the total VM instance hour is equal to the demand
periods, whereas a divisible job can be partitionedarbitrarily into any number of portions, as long as the total VM instance hour is equal to the demand ![]() . Each portion of a divisible job can run independently from other portions. Examples of applications that satisfy this divisibility property include image processing, database search, Monte Carlo simulations, computational fluid dynamics, and matrix computations [28]. Given the scheduling decisions
. Each portion of a divisible job can run independently from other portions. Examples of applications that satisfy this divisibility property include image processing, database search, Monte Carlo simulations, computational fluid dynamics, and matrix computations [28]. Given the scheduling decisions ![]() of all jobs, the aggregate workload for each regional data center must satisfy a service rate constraint
of all jobs, the aggregate workload for each regional data center must satisfy a service rate constraint

where ![]() is the service rate per server at regional data center
is the service rate per server at regional data center ![]() and
and ![]() is the number of active server at time
is the number of active server at time ![]() . There is also a limitation on the number of servers at each location. Therefore, we have
. There is also a limitation on the number of servers at each location. Therefore, we have
All user requests for the next cycle are collectively handled by a job scheduler, which decides the location and time for each job to be processed in a judiciary manner. This scheme can be viewed as a generalization of existing on-spot VM instances in Amazon EC2, which allows users to bid for multiple periods and different job deadlines (or job completion times). The system model is illustrated in Figure 18.5. Let ![]() denote the scheduled completiontime of job
denote the scheduled completiontime of job ![]() , the total revenue received by the cloud provider over the next cycle is given as
, the total revenue received by the cloud provider over the next cycle is given as

The goal of this paper is to design a job scheduler that maximizes the net profit ![]() over feasible scheduling decisions
over feasible scheduling decisions ![]() , subject to the workload constraints. For a given job completion time
, subject to the workload constraints. For a given job completion time ![]() , we denote the set of all feasible job scheduling decisions by a set
, we denote the set of all feasible job scheduling decisions by a set ![]() . In particular, for a divisible job, a user is only concerned with the total VM instance hour received before time
. In particular, for a divisible job, a user is only concerned with the total VM instance hour received before time ![]() . This implies
. This implies

where ![]() is the total demand of job
is the total demand of job ![]() . On the other hand, an indivisible job must be assigned to a single regional data center and run continuously before completion. It will have a feasible scheduling set as
. On the other hand, an indivisible job must be assigned to a single regional data center and run continuously before completion. It will have a feasible scheduling set as
where ![]() is an indicator function and equals to 1 if
is an indicator function and equals to 1 if ![]() belongs to the scheduled execution interval
belongs to the scheduled execution interval ![]() and 0 otherwise. We suppress the positivity constraints of
and 0 otherwise. We suppress the positivity constraints of ![]() for simplicity of expressions.
for simplicity of expressions.

Figure 18.5 An illustration of our system model. Four jobs with different parameters are submitted to a front-end server, where a job scheduler decides the location and time for each job to be processed, by maximizing the net profit that a data center operator receives.
We formulate the data center NPO problem as follows:


The above problem can be looked at graphically as illustrated in Figure 18.5. It requires a joint optimization of revenue and electricity cost, which is a mixed-integer optimization because the scheduling decisions ![]() are discrete for indivisible jobs. Further, because of our deadline-dependent pricing mechanism, the maximization of revenue over completion time
are discrete for indivisible jobs. Further, because of our deadline-dependent pricing mechanism, the maximization of revenue over completion time ![]() is coupled with the minimization of electricity cost over feasible scheduling decisions
is coupled with the minimization of electricity cost over feasible scheduling decisions ![]() . However, there is no closed-form, differentiable function that represents
. However, there is no closed-form, differentiable function that represents ![]() by
by ![]() . Therefore, off-the-shelf optimization algorithms cannot be directly applied.
. Therefore, off-the-shelf optimization algorithms cannot be directly applied.
It is worth noticing that our formulation of Problem NPO in Eq. (18.12 ) also incorporates sharp job deadlines. For instance, if job ![]() must be completed before time
must be completed before time ![]() , we can impose a utility function with
, we can impose a utility function with ![]() , for all
, for all ![]() , so that scheduling decisions with a completion time later than
, so that scheduling decisions with a completion time later than ![]() becomes infeasible in Problem NPO.
becomes infeasible in Problem NPO.
Problem NPO is a complex joint optimization over both revenue and electricity cost, whose optimization variables; scheduling decisions ![]() and job completion time
and job completion time ![]() are not independent of each other. There is no closed-form, differentiable function that relates the two optimization variables. Let
are not independent of each other. There is no closed-form, differentiable function that relates the two optimization variables. Let ![]() be the aggregate service rate received by job
be the aggregate service rate received by job ![]() at time
at time ![]() . For given scheduling decisions
. For given scheduling decisions ![]() , we could have replaced constraint (18.15 ) by a supremum
, we could have replaced constraint (18.15 ) by a supremum
where ![]() is the total demand of job
is the total demand of job ![]() . However, it still requires evaluating supremum and inequalities and, therefore, does not yield a differentiable function to represent
. However, it still requires evaluating supremum and inequalities and, therefore, does not yield a differentiable function to represent ![]() by scheduling decisions
by scheduling decisions ![]() .
.
To overcome this difficulty, an approximation of the job completion time function in Eq. (18.17 ) by a differentiable function is proposed in Reference [12]:
where ![]() is a positive constant and
is a positive constant and ![]() normalizes the service rate
normalizes the service rate ![]() . The accuracy of this approximation is given as follows.
. The accuracy of this approximation is given as follows.
By the approximation in Eq. (18.18 ), we obtain a closed-form, differentiable expression for ![]() , which guarantees an approximated completion of job
, which guarantees an approximated completion of job ![]() off by a logarithmic term
off by a logarithmic term ![]() in the worst case. The approximation becomes exact as
in the worst case. The approximation becomes exact as ![]() approaches infinity. However, often there are practical constraints or overhead concerns on using large
approaches infinity. However, often there are practical constraints or overhead concerns on using large ![]() . We choose an appropriate
. We choose an appropriate ![]() such that the resulting optimality gap is sufficiently small.
such that the resulting optimality gap is sufficiently small.
An algorithmic solution for Problem NPO with divisible jobs is derived in Reference [12]. The problem has a feasible set:
In order to solve the problem, we leverage the approximation of job completion time in Eq. (18.18) to obtain an approximated version of Problem NPO. The resulting problem has an easy-to-handle analytical structure and is convex for certain choices of ![]() functions. Further, when the problem is nonconvex, we then convert it into a sequence of linear programming and solve it using an efficient algorithm. It provides useful insights for solving Problem NPO with indivisible jobs.
functions. Further, when the problem is nonconvex, we then convert it into a sequence of linear programming and solve it using an efficient algorithm. It provides useful insights for solving Problem NPO with indivisible jobs.
Rewriting Eq. (18.15 ) in Problem NPO using the approximation in Eq. (18.18 ) and the feasible set in Eq. (18.20 ), we obtain a net profit optimization problem for divisible jobs (named Problem NPOD) as follows:
where completion time becomes a differentiable function of ![]() . The optimization variables in Problem NPOD may still be integer variables, that is, the number of active servers
. The optimization variables in Problem NPOD may still be integer variables, that is, the number of active servers ![]() and the number of demanded VM instances
and the number of demanded VM instances ![]() . We can leverage rounding techniques (e.g., [29]) to relax Problem NPOD so that its optimization variables become continuous.
. We can leverage rounding techniques (e.g., [29]) to relax Problem NPOD so that its optimization variables become continuous.

Figure 18.6 Algorithmic solution for Problem NPOD.
As inequality constraints in Eqs. (18.23 ), (18.24 ), and (18.26 ) are linear, we investigate the convexity of the optimization objective in Eq. (18.22 ), which is a function of ![]() and
and ![]() , by plugging in the equality constraint (18.25 ). It is shown [12] that for
, by plugging in the equality constraint (18.25 ). It is shown [12] that for ![]() in Eq. (18.25 ) and a positive differentiable
in Eq. (18.25 ) and a positive differentiable ![]() , the objective function of Problem NPOD is convex if
, the objective function of Problem NPOD is convex if ![]() for all
for all ![]() and concave if
and concave if ![]() for all
for all ![]() . The two conditions of
. The two conditions of ![]() capture a wide range of functions in practice. Let
capture a wide range of functions in practice. Let ![]() and
and ![]() be arbitrary constants. Examples of
be arbitrary constants. Examples of ![]() that result in a concave objective function include certain exponential and logarithmic functions. Examples that result in a convex objective function include linear
that result in a concave objective function include certain exponential and logarithmic functions. Examples that result in a convex objective function include linear ![]() and logarithm
and logarithm ![]() . We remark that when
. We remark that when ![]() for all
for all ![]() , Problem NPOD is a concave maximization. It can be solved efficiently by off-the-shelf convex optimization algorithms, for example, primal-dual algorithm and interior point algorithm [30].
, Problem NPOD is a concave maximization. It can be solved efficiently by off-the-shelf convex optimization algorithms, for example, primal-dual algorithm and interior point algorithm [30].
On the other hand, when Problem NPOD maximizes a convex objective, an iterative solution based on difference of convex programming is proposed [12]. Relying on a linearization of the objective, the following iterative algorithm is used to solve Problem NPOD via a sequence of linear programming. It starts at some random initial point ![]() , solves the linear programming with
, solves the linear programming with ![]() , and, therefore, generates a sequence
, and, therefore, generates a sequence ![]() . This procedure is indeed a special case of the difference of convex programming and has been extensively used in solving many nonconvex programs of similar forms in machine learning [31]. It is shown that the sequence
. This procedure is indeed a special case of the difference of convex programming and has been extensively used in solving many nonconvex programs of similar forms in machine learning [31]. It is shown that the sequence ![]() converges to a local minimum or a saddle of Problem NPOD, as in Theorem 18.2. We further apply a primal-dual algorithm [30] to obtain a distributed solution to each linear programming. The algorithm is summarized in Fig. 18.6.
converges to a local minimum or a saddle of Problem NPOD, as in Theorem 18.2. We further apply a primal-dual algorithm [30] to obtain a distributed solution to each linear programming. The algorithm is summarized in Fig. 18.6.
Finally, we evaluate our algorithmic solution for Problem NPOD over a 24-h cycle, divided into ![]() 10-min periods. The goal is to obtain empirically validated insights about the feasibility/efficiency of our solution using synthesized data from a recent study [9]. We construct
10-min periods. The goal is to obtain empirically validated insights about the feasibility/efficiency of our solution using synthesized data from a recent study [9]. We construct ![]() regional data centers, which reside in different electricity markets and have electricity prices
regional data centers, which reside in different electricity markets and have electricity prices ![]() $
$ ![]() ,
, ![]() $
$ ![]() , and
, and ![]() $
$ ![]() . The data centers host
. The data centers host ![]() ,
, ![]() , and
, and ![]() servers. Each server is operating at
servers. Each server is operating at ![]() W with
W with ![]() VMs per server for
VMs per server for ![]() .
.
We construct two types of jobs: elephant jobs that subscribes ![]() VMs for
VMs for ![]() periods and mice jobs that subscribes
periods and mice jobs that subscribes ![]() VMs for
VMs for ![]() periods. In our simulations, both
periods. In our simulations, both ![]() and
and ![]() areuniformly randomly generated from their ranges. We fix the total workload to be
areuniformly randomly generated from their ranges. We fix the total workload to be ![]() jobs, each being an elephant job with probability
jobs, each being an elephant job with probability ![]() and a mice job with probability
and a mice job with probability ![]() . Job
. Job ![]() is associated with a nonlinear bid function, given by
is associated with a nonlinear bid function, given by
where ![]() and
and ![]() are uniformly distributed. Using this nonlinear bid function, the approximation of job completion time will result in a convex objective function in Eqs. (18.12 ) and (18.22 ). All numerical results shown in this section are averaged over five realizations of random parameters.
are uniformly distributed. Using this nonlinear bid function, the approximation of job completion time will result in a convex objective function in Eqs. (18.12 ) and (18.22 ). All numerical results shown in this section are averaged over five realizations of random parameters.

Figure 18.7 A comparison of optimized net profit of NPOD, NPOI, and LJF.
To provide benchmarks for our evaluations, we also implement a greedy algorithm that sequentially schedules all jobs with a largest job first (LJF) policy and a heuristic algorithm NPOI (net profit optimization problem for indivisible jobs) by assuming indivisible jobs in problem NPOI. Figure 18.7 compares the optimized net profit of NPOD, NPOI, and LJF algorithms. When jobs are indivisible, our NPOI algorithm improves the net profit by ![]() over the baseline LJF algorithm (from $1868 to $2095), while an additional
over the baseline LJF algorithm (from $1868 to $2095), while an additional ![]() increment (to $2394) can be achieved by NPOD if all jobs are divisible. We also notice that our NPOI algorithm is able to simultaneously improve total revenue and cut down electricity cost, compared to the baseline LJF algorithm. This is achieved by the joint optimization over job completion time
increment (to $2394) can be achieved by NPOD if all jobs are divisible. We also notice that our NPOI algorithm is able to simultaneously improve total revenue and cut down electricity cost, compared to the baseline LJF algorithm. This is achieved by the joint optimization over job completion time ![]() and scheduling decisions
and scheduling decisions ![]() .
.
18.4 Conclusion and Future Work
This chapter discussed three different approaches on smart pricing of cloud services and resources: VM-based pricing, SLA-based pricing, and time-dependent pricing. There is a large number of open problems on topics discussed in this chapter. Many of them are due to the delicate trade-off between operators’ goal of profit maximization and users’ demand for individual performance optimization. In a multiuser environment, while maximizing their total revenue, cloud operators may need to consider establishing a social scheduling policy that would prevent “poor” users from being entirely deprived of resources. Algorithmic solutions to the nonconvex problem of job scheduling and NPO has not been found. Further, to analyze different pricing policies, user payment models must be constructed to reflect not only users’ satisfaction and willingness to pay but also their budget and financial means. Further challenges will arise as stochastic arrivals/departures of users’ demand and cloud resources are incorporated.
References
- 1. KPMG International. “Clarity in the Cloud”, Online technical report at http://www.kpmg.com/, Nov. 2011.
- 2. N. Chohan. See spot run: using spot instances for mapreduce workflows. In USENIX HotCloud Workshop, 2010.
- 3. S. Yi, D. Kondo, and A. Andrzejak. Reducing costs of spot instances via checkpointing in the amazon elastic compute cloud. IEEE International Conference on Cloud Computing, 2010.
- 4. Amazon Elastic Compute Cloud User Guide. Getting Started with Spot Instances. docs.amazonwebservices.com/AWSEC2, Oct. 2008.
- 5. R. Buyya, Cs. Yeo, J. Broberg, and I. Brandic. “Cloud computing and emerging IT platforms: vision, hype, and reality for delivering computing as the 5th utility,” Future Generation Computer Systems, 25, 2009, 599–616.
- 6. X. Fan, W. Weber, and L. A. Barroso. Power provisioning for a warehouse sized computer. In Proceedings of the 34th Annual International Symposium on Computer Architecture, 2007.
- 7. S. Nedevschi, L. Popal, G. Iannaccone, S. Ratnasamy, and D. Wetherall. Reducing network energy consumption via sleeping and rate-adaptation. In Proceedings of the 5th USENIX Symposium on Networked Systems Design & Implementations (NSDI), 2008.
- 8. L. Parolini, B. Sinopoli, and B. Krogh. Reducing data center energy consumption via coordinated cooling and load management. In Proceedings of ACM Workshop on Power Aware Computing and Systems, 2008.
- 9. L. Rao, X. Liu, L. Xie, and W. Liu. Minimizing electricity cost: optimization of distributed internet data centers in a multi-electricity market environment. In Procedings of IEEE Infocom, 2010.
- 10. P. Patel, A. Ranabahu, and A. Sheth. Service level agreement in cloud computing. In Proceedings of the Workshop on Best Practices in Cloud Computing, 2009.
- 11. C. Wilson, H. Ballani, T. Karagiannis, and A. Rowstron. Better never than late, meeting deadlines in data center networks. In Proceedings of SIGCOMM, 2011.
- 12. W. Wang, P. Zhang, T. Lan, and V. Aggarwal. Data center net profit optimization with individual job deadlines. In Proceedings of CISS 2012 (Invited paper), March 2012.
- 13. A. Danak and S. Mannor. Resource allocation with supply adjust- ment in distributed computing systems. In International Conference on Distributed Computing Systems (ICDCS), 2010.
- 14. L. Fleischer. Tight approximation algorithms for maximum general assignment problems. In ACM Symposium on Discrete Algorithms, 2006.
- 15. W. W. S. Wei. Time Series Analysis: Univariate and Multivariate Methods. Addison Wesley, Reading, MA, 1990.
- 16. C. Gong, J. Liu, Q. Zhang, H. Chen, and Z. Gong. The characteristics of cloud computing. 39th International Conference on Parallel Processing Workshops, pp.275–279, 2010.
- 17. S. Littlechild. Wholesale spot price pass-through. Journal of Regulatory Economics, 23(1), 2003, 61–91.
- 18. S. Borenstein. “The long-run efficiency of real-time electricity pricing,” The Energy Journal, 26(3), 2005, 93–116.
- 19. K. Herter. “Residential implementation of critical-peak pricing of electricity,” Energy Policy, 35(4), 2007, 2121–2130.
- 20. A. Faruqui, R. Hledik, and S. Sergici, “Piloting the smart grid,” Electricity Journal, 22(7), 2009, 55–69.
- 21. H. Chao. “Peak load pricing and capacity planning with demand and supply uncertainty,” Bell Journal of Economics, 14(1), 1983, 179–190.
- 22. G. Brunekreeft. Price Capping and Peak-Load-Pricing in Network Industries. Diskussionsbeitrage des Instituts fur Verkehrswissenschaft und Regionalpolitik, Universitat Freiburg, vol. 73, Freiburg, Germany, 2000.
- 23. H. Sangtae, S. Soumya, J. Carlee, I. Youngbin, and C. Mung. “TUBE: time-dependent pricing for mobile data,” In Procedings of ACM SIGCOMM 2012 Conference on Applications, Technologies, Architectures, and Protocols for Computer Communication, SIGCOMM ’12, pp. 247–258, 2012.
- 24. P. Skantze, M. D. Ilic, and J. Chapman. Stochastic modeling of electric power prices in a mult-market environment. IEEE Power Engineering Society Winter Meeting, 2000.
- 25. S. Fleten and J. Lemming, “Constructing forward price curves in electricity markets,” Energy Economics, 25, 2007, 409–424.
- 26. C. K. Woo, I. Horowitz, and K. Hoang. “Cross hedging and value at risk: wholesale electricity forward contracts,” Advances in Investment Analysis and Portfolio Management, 8, 2001, 283–301.
- 27. R. Weber. Cutting the electric bill for Internet-scale systems. In Proceedings of SIGCOMM, pp. 123–134, 2009.
- 28. B. Veeravalli and W. H. Min. “Scheduling divisible loads on heterogeneous linear daisy chain networks with arbitrary processor release times,” IEEE Transactions on Parallel and Distributed Systems, 15, 2010, 273–288.
- 29. A. Neumaier and O. Shcherbina. “Safe bounds in linear and mixed-integer linear programming,” Mathematical Programming, 99, 2004, 283–296.
- 30. S. Boyd and L. Vandenberghe. Convex Optimization. Cambridge University Press, Cambridge, United Kingdom, 2004.
- 31. B. K. Sriperumbudur and G. R. G. Lanckriet. “On the Convergence of the Concave-Convex Procedure”, Online technical report at http://cosmal.ucsd.edu/~gert/papers/nips_cccp.pdf, 2009.