Chapter 8
Usage-Based Pricing Differentiation for Communication Networks: Incomplete Information and Limited Pricing Choices*
SHUQIN LI and JIANWEI HUANG
8.1 Introduction
Pricing is important for the design, operation, and management of communication networks. Pricing has been used with two different meanings in the area of communication networks. One is the “optimization-oriented” pricing for network resource allocation: it is made popular by Kelly's seminal work on network congestion control [2, 3]. For example, the Transmission Control Protocol (TCP) has been successfully reverse engineered as a congestion-pricing-based solution to a network optimization problem [4, 5]. A more general framework of network utility maximization (NUM) was subsequently developed to forward-engineer many new network protocols (see a recent survey in Reference [6]). In various NUM formulations, the “optimization-oriented” prices often represent the Lagrangian multipliers of various resource constraints and are used to coordinate different network entities to achieve the maximum system performance in a distributed manner. The other is the “economics-based” pricing, which is used by a network service provider to various objectives including revenue maximization. The proper design of such a pricing becomes particularly challenging today because of the exponential growth of data volume and applications in both wireline and wireless networks. In this chapter, we focus on studying the “economics-based” pricing schemes for managing communication networks.
Economists have proposed many sophisticated pricing mechanisms to extract surpluses from the consumers and maximize revenue (or profits) for the providers. A typical example is the optimal nonlinear pricing (e.g., [7, 8]). In practice,however, we often observe simple pricing schemes deployed by the service providers. Typical examples include flat-fee pricing and (piecewise) linear usage-based pricing. One potential reason behind the gap between “theory” and “practice” is that the optimal pricing schemes derived in economics often has a high implementational complexity. Besides a higher maintenance cost, complex pricing schemes are not “customer friendly” and discourage customers from using the services [9, 10]. Furthermore, achieving the highest possible revenue with complicated pricing schemes requires knowing the information (identity and preference) of each customer, which can be challenging in large-scale communication networks. It is then natural to ask the following two questions:
- How to design simple pricing schemes to achieve the best trade-off between complexity and performance?
- How does the network information structure impact the design of pricing schemes?
This chapter tries to answer the above two questions with some stylized communication network models. Different from some previous work that considered a flat-fee pricing scheme in which the payment does not depend on the resource consumption (e.g., [9, 11, 12]), here we study the revenue maximization problem with the linear usage-based pricing schemes, where a user's total payment is linearly proportional to allocated resource. In wireless communication networks, the usage-based pricing scheme has become increasingly popular because of the rapid growth of wireless data traffic. In June 2010, AT
T in the United States switched from the flat-free-based pricing (i.e., unlimited data for a fixed fee) to the usage-based pricing schemes for 3G wireless data [13]. Verizon followed up with similar plans in July 2011. Similar usage-based pricing plans have been adopted by major Chinese wireless service providers including China Mobile and China UniCom. Thus, the research on the usage-based pricing is of great practical importance.
In this chapter, we consider the revenue maximization problem of a monopolist service provider facing multiple groups of users. Each user determines its optimal resource demand to maximize the surplus, which is the difference between its utility and payment. The service provider chooses the pricing schemes to maximize his/her revenue, subject to a limited resource. We consider both complete information and incomplete information scenarios and design different pricing schemes with different implementational complexity levels.
Our main contributions are as follows.
- Complete Network Information. We propose a polynomial algorithm tocompute the optimal solution of the partial price differentiation problem, which includes the complete price differentiation scheme and the single pricing scheme as special cases. The optimal solution has a threshold structure, which allocates positive resources with priorities to users with high willingness to pay.
- Revenue Gain under Complete Network Information. Compared to the single pricing scheme, we identify the two important factors behind the revenue increase of the (complete and partial) price differentiation schemes: the differentiation gain and the effective market size. The revenue gain is the most significant when users with high willingness to pay are minority among the whole population and total resource is limited but not too small.
- Incomplete Network Information. We design an incentive-compatible scheme with the goal to achieve the same maximum revenue that can be achieved with the complete information. We find that if the differences of willingness to pays of users are larger than some thresholds, this incentive-compatible scheme can achieve the same maximum revenue. We further characterize the necessary and sufficient condition for the thresholds.
8.1.1 Related Work
It is often quite challenging to design a practical pricing schemes in communication networks. The main difficulties including dealing with the incomplete information structure and limiting the implementational complexity. Under incomplete network information, customers have the private information that is unknown by the service providers. The study of incomplete information is a significant part of microeconomics, especially in several important branches, such as incentive theory [14], information economics [15], organization theory [16], and contract theory [17]. In particular, there exists a rich body of literature on monopoly revenue maximization with incomplete information, for example, [7, 8, 18–26]. Mussa and Rosen in Reference [7] and Maskin and Riley in Reference [8] proposed the optimal price differentiation strategies based on product qualities and quantities, respectively. Armstrong in Reference [22], Bakos and Brynjolfsson in Reference [23], and Geng et al. in Reference [24] studied the optimal multiproduct bundling schemes. Stokey Reference [18], Baron and Besanko in [19], Hart and Tirole in Reference [20], and Acquisti and Varian in Reference [21] focused on multistage price differentiation. Cabral et al. in Reference [25] and Aoyagi in Reference [26] studied the pricing and revenue maximization problem with network externalities. Although these existing results on pricing provide theoretical optimal solutions under incomplete information, they are seldom directly applied in practice, mainly because of their highimplementational complexity. In a practical system, a service provider often needs to constrain the number of pricing choices for the customers, either due to implementation complexity constraint or users’ aversion to too many choices [27].
However, the issue of optimal pricing design subject to complexity constraint is less understood in the literature. One related analytical result is Reference [9], where the authors discussed complexity issue in flat-fee pricing. To the best of our knowledge, our study about partial price differentiation is the first result about the optimal design of limited price choices in usage-based pricing schemes. It is interesting to compare our results on partial price differentiation with results in References [9] and [28]. Shakkottai et al. in Reference [9] showed that the revenue gain of price differentiation is small with a flat entry-fee-based Paris Metro Pricing (e.g., [29]), and a complicated differentiation strategy may not be worthwhile. Chau et al. [28] further derived the sufficient conditions of congestion functions that guarantee the viability of these Paris Metro Pricing schemes. By contrast, our results show that the revenue gain of price differentiation can be substantial for a usage-based pricing system.
Some recent work of usage-based pricing and revenue management in communication network includes References [30–38]. Basar and Srikant in Reference [30] investigated the bandwidth allocation problem in a single-link network with the single pricing scheme. Shen and Basar in Reference [31] extended the study to a more general nonlinear pricing case with the incomplete network information scenario. They discussed the single pricing scheme under incomplete information with a continuum distribution of users’ types. In contrast, our study on the incomplete information focuses on the linear pricing with a discrete setting of users’ types. We also show that, besides the single pricing scheme, it is also possible to design differentiation pricing schemes under incomplete information. Daoud et al. [32] studied an uplink power allocation problem in a CDMA system, where the interference among users are the key constraint instead of the limited total resource considered in this chapter. Jiang et al. in Reference [33], Hande et al. in Reference [34], and Ha et al. in Reference [35] focused on the study of the time-dependent pricing. He and Walrand in Reference [36], Shakkottai and Srikant in Reference [37], and Gajic et al. in Reference [38] focused on the interaction between different service providers embodied in the pricing strategies, rather than the design of the pricing mechanism. Besides, none of the related work considered the partial differential pricing as in this chapter.
8.2 System Model
We consider a network with a total amount of S limited resource (which can be in the form of rate, bandwidth, power, time slot, etc.). The resource is allocated by a monopolistic service provider to a set 
of user groups. Each group 
has Ni homogeneous users1 with the same utility function
where si is the allocated resource to one user in group i and 
represents the willingness to pay of group i. The logarithmic utility function is commonly used to model the proportionally fair resource allocation in communication networks (see Reference [30] for detailed explanations). The analysis of the complete information case can also be extended to more general utility functions (see Appendix 8.A.1). Without the loss of generality, we assume that 
. In other words, group 
contains users with the highest valuation, and group I contains users with the lowest valuation.
We consider two types of information structures:
- 1. Complete Information. The service provider knows each user's utility function. Although the complete information is a very strong assumption, it is the most frequently studied scenario in the network pricing literature [30–34, 36–38]. The significance of studying the complete information is twofold. It serves as the benchmark of practical designs and provides important insights for the incomplete information analysis.
- 2. Incomplete Information. The service provider knows the total number of groups I, the number of users in each group
, and the utility function of each group 
. It does not know which user belongs to which group. Such assumption in our discrete setting is analogous to that the service provider knows only the users’ type distribution in a continuum case. Such statistical information can be obtained through long-term observations of a stationary user population.
The interaction between the service provider and users can be characterized as a two-stage Stackelberg model shown in Figure 8.1.
Figure 8.1 A two-stage Stackelberg model.
The service provider publishes the pricing scheme in Stage 1, and users respond with their demands in Stage 2. The users want to maximize their surpluses by optimizing their demands according to the pricing scheme. The service provider wants to maximize its revenue by setting the right pricing scheme to induce desirable demands from users. As the service provider has a limited total resource, it must guarantee that the total demand from users is no larger than what it can supply.
The details of pricing schemes depend on the information structure of the service provider. Under complete information, because the service provider can distinguish different groups of users, it announces the pricing and the admission control decisions to different groups of users. It can choose from the complete price differentiation scheme, the single pricing scheme, and the partial price differentiation scheme to realize a desired trade-off between the implementational complexity and the total revenue. Under incomplete information, it publishes a common price menu to all users and allows users to freely choose a particular price option in this menu. All these pricing schemes are discussed one by one in the following sections.
8.3 Complete Price Differentiation Under Complete Information
We first consider the complete information case. As the service provider knows the utility and the identity of each user, it is possible to maximize the revenue by charging a different price to each group of users. The analysis will be based on backward induction, starting from Stage 2 and then moving to Stage 1.
8.3.1 User's Surplus Maximization Problem in Stage 2
If a user in group i has been admitted into the network and offered a linear price pi in Stage 1, then it solves the following surplus maximization problem,
which leads to the following unique optimal demand
8.3.2 Service Provider's Pricing and Admission Control Problem in Stage 1
In Stage 1, the service provider maximizes its revenue by choosing the price pi and the number of admitted users ni for each group i subject to the limited total resource S. The key idea is to perform a complete price differentiation (CP) scheme, that is, charging each group with a different price.
where 
, 
, and 
. We use bold symbols to denote vectors in the sequel. Constraint (8.5 ) is the solution of the Stage 2 user surplus maximization problem in Eq. (8.3 ). Constraint (8.6 ) denotes the admission control decision, and constraint (8.7 ) represents the total limited resource in the network.
The CP problem is not straightforward to solve, because it is a nonconvex optimization problem with a nonconvex objective function (summation of products of 
and 
), a coupled constraint (8.7 ), and integer variables 
. However, it is possible to convert it into an equivalent convex formulation through a series of transformations, and thus the problem can be solved efficiently.
First, we can remove the 
sign in constraint (8.5 ) by realizing the fact that there is no need to set pi higher than 
for users in group i; users in group i already demand zero resource and generate zero revenue when 
. This means that we can rewrite constraint (8.5 ) as
Plugging Eq. (8.8 ) into Eq. (8.4 ), the objective function becomes 
. We can further decompose the CP problem in the following two subproblems:
- 1. Resource Allocation. For a fixed admission control decision
, solve for the optimal resource allocation 
.
Denote the solution of
as 
. We further maximize the revenue of the integer admission control variables 
. - 2. Admission Control.
Let us first solve the 
subproblem in 
. Note that it is a convex optimization problem. By using Lagrange multiplier technique, we can get the first-order necessary and sufficient condition:
where 
is the Lagrange multiplier corresponding to the resource constraint (8.9 ).
Meanwhile, we note the resource constraint (8.9 ) must hold with equality, because the objective is a strictly increasing function in 
. Thus, by plugging Eq. (8.11 ) into (8.9 ), we have
This weighted water-filling problem (where 
can be viewed as the water level) in general has no closed-form solution for 
. However, we can efficiently determine the optimal solution 
by exploiting the special structure of our problem. Note that because 
, then 
must satisfy the following condition:
for a group index threshold value 
satisfying
In other words, only groups with index no larger than 
will be allocated the positive resource. This property leads to the following simple Algorithm 8.1 to compute 
and group index threshold 
: we start by assuming 
and compute 
. If Eq. (8.14 ) is not satisfied, we decrease
by one and recompute 
until Eq. (8.14 ) is satisfied.
As 
, Algorithm 8.1 always converges and returns the unique values of 
and 
. The complexity is 
, that is, linear in the number of user groups (not the number of users).
With 
and 
, the solution of the resource allocation problem can be written as
For the ease of discussion, we introduce a new notion of the effective market, which denotes all the groups allocated nonzero resource. For resource allocation subproblem 
, the threshold 
describes the size of the effective market. All groups with indices no larger than 
are effective groups, and users in these groups as effective users. An example of the effective market is illustrated in Figure 8.2.
Figure 8.2 A six-group example for effective market: the willingness to pays decrease from group 1 to group 6. The effective market threshold can be obtained by Algorithm 8.1 and is four in this example.
Now let us solve the admission control subproblem 
. Denote the objective Eq. (8.10 ) as 
, by Eq. (8.15 ), then 
. We first relax the integer domain constraint of ni as 
. As Eq. (8.13 ), by taking the derivative of the objective function 
with respect to ni, we have
Also from Eq (8.13 ), we have 
, thus 
, for 
, and 
, for 
. This means that the objective 
is strictly increasing in ni for all 
, thus it is optimal to admit all users in the effective market. The admission decisions for groups not in the effective market are irrelevant to the optimization, because those users consume zero resource. Therefore, one of the optimal solutions of the 
subproblem is 
for all 
. Solving 
and 
subproblems leads to the optimal solution of the CP problem:
Theorem 8.1 provides the right economic intuition: the service provider maximizes its revenue by charging a higher price to users with a higher willingness to pay. It is easy to check that 
for any 
. The users with low willingness to pay are excluded from the markets.
8.3.3 Properties
Here we summarize some interesting properties of the optimal complete price differentiation scheme:
8.3.3.1 Threshold Structure
The threshold-based resource allocation means that higher willingness to pay groups have higher priories of obtaining the resource at the optimal solution.
To see this clearly, assume the effective market size is 
under parameters 
and S. Here the superscript (1) denotes the first parameter set. Now consider another set of parameters 
and S, where 
for each group i and the new effective market size is 
. By Eq. (8.13 ), we can see that 
. Furthermore, we can show that if some high willingness to pay group has many more users under the latter system parameters, that is, 
is much larger than 
for some 
, then the effective size will be strictly decreased, that is, 
. In other words, the increase of high willingness to pay users will drive the low willingness to pay users out of the effective market.
8.3.3.2 Admission Control with Pricing
Theorem 8.1 shows the explicit admission control is not necessary at the optimal solution. Also from Theorem 8.1, we can see that when the number of users in any effective group increases, the price, 
, for all 
increases and resource, 
, for all 
decreases. The prices serve as the indications of the scarcity of the resources and will automatically prevent the low willingness to pay users to consume the network resource.
8.4 Single Pricing Scheme
In Section 8.3, we showed that the CP scheme is the optimal pricing scheme to maximize the revenue under complete information. However, such a complicated pricing scheme is of high implementational complexity. In this section, we study the single pricing scheme. It is clear that the scheme will in general suffer a revenue loss comparing with the CP scheme. We will try to characterize the impact of various system parameters on such revenue loss.
8.4.1 Problem Formulation and Solution
Let us first formulate the single pricing (SP) problem.
Comparing with the CP problem in Section 8.3, here the service provider charges a single price p to all groups of users. After a similar transformation as in Section 8.3, we can show that the optimal single price satisfies the following weighted water-filling condition
Thus we can obtain the following solution that shares a similar structure as complete price differentiation.
8.4.2 Properties
The SP scheme shares several similar properties as the CP scheme (Section 8.3.3), including the threshold structure and admission control with pricing. Similarly, we can define the effective market for the SP scheme.
It is more interesting to notice the differences between these two schemes. To distinguish solutions, we use the superscript “cp” for the CP scheme, and “sp” for the SP scheme.
The proof is given in Appendix 8.A.2. An illustrative example is shown in Figures 8.3 and 8.4.
Figure 8.3 Comparison of prices between the CP scheme and the SP scheme.
Figure 8.4 Comparison of resource allocation between the CP scheme and the SP scheme.
It is easy to understand that the SP scheme makes less revenue, because it is a feasible solution to the CP problem. A little bit more computation sheds more light on this comparison. We introduce the following notations to streamline the comparison:
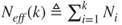: the number of effective users, where k is the size of the effective market.
, 
: the fraction of group i's users in the effective market.
: the average resource per an effective user.
: the average willingness to pay per an effective user.
On the basis of Theorem 8.1, the revenue of the CP scheme is
where
On the basis of Theorem 8.1, the revenue of the SP scheme is
From Eqs. (8.17 ) and (8.19 ), it is clear to see that 
because of two factors: one is the nonnegative term in Eq. (8.18 ) and the other is 
: a higher level of differentiation implies a no smaller effective market. Let us further discuss them in the following two cases:
- If
, then the additional term of Eq. (8.18 ) in Eq. (8.17 ) means that 
. The equality holds if and only if 
, in which case 
. Note that in this case, the CP scheme degenerates to the SP scheme. We name the nonnegative term 
in Eq. (8.18 ) as price differentiation gain, as it measures the average price difference between any effective users in the CP scheme. The larger the price difference, the larger the gain. When there is no differentiation in the degenerating case (
), the gain is zero. - If
, because the common part of two revenue 
is a strictly increasing function of 
, price differentiation makes more revenue even if the positive differentiation gain 
is not taken into consideration. The result that more consumers with purchasing power always mean more revenue in the service provider's pocket is intuitive.
Finally, we note that the CP scheme in Section 8.3 requires the complete network information. The SP scheme here, on the other hand, works in the incomplete information case as well. This distinction becomes important in Section 8.6.
8.5 Partial Price Differentiation Under Complete Information
For a service provider facing thousands of user types, it is often impractical to design a price choice for each user type. The reasons behind this, as discussed in Reference [10], are mainly high system overheads and customers’ aversion. However, as we have shown in Section 8.4, the single pricing scheme may suffer a considerable revenue loss. How to achieve a good trade-off between the implementational complexity and the total revenue? In reality, we usually see that the service provider offers only a few pricing plans for the entire users population; we term it as the partial price differentiation scheme. In this section, we answer the following question: if the service provider is constrained to maintain a limited number of prices, 
, 
, then what is the optimal pricing strategy and the maximum revenue? Concretely, the partial price differentiation (PP) problem is formulated as follows.
Here 
denotes the set 
. As we consider the complete information scenario in this section, the service provider can choose the price charged to each group, thus constraints (8.20 )–(8.22 ) are the same as in the CP problem. Constraints (8.23 ) and (8.24 ) mean that pi charged to each group i is one of J choices from the set 
. For convenience, we define cluster 
, which is a set of groups charged with the same price 
. We use superscript j to denote clusters and subscript i to denote groups through this section. We term the binary variables 
as the partition, which determines which cluster each group belongs to.
The PP problem is a combinatorial optimization problem and is more difficult than the previous CP and SP problems. On the other hand, we notice that this PP problem formulation includes the CP scheme (
) and the SP scheme scenario (
) as special cases. The insights we obtained from solving these two special cases in Sections 8.3 and 8.4 will be helpful to solve the general PP problem.
8.5.1 Three-Level Decomposition
To solve the PP problem, we decompose and tackle it in three levels. In the lowest level 3, we determine the pricing and resource allocation for each cluster, given a fixed partition and fixed resource allocation among clusters. In level 2, we compute the optimal resource allocation among clusters, given a fixed partition. In level 1, we optimize the partition among groups.
Figure 8.5 An illustrative example of level 3: the cluster contains four groups, group 4–7; and the effective market contains groups 4 and 5, thus 
.
8.5.1.1 Level 3: Pricing and Resource Allocation in Each Cluster
For a fix partition 
and a cluster resource allocation 
, we focus the pricing and resource allocation problems within each cluster 
, 
:
The level-3 subproblem coincides with the SP scheme discussed in Section 8.4, because all groups within the same cluster 
are charged with a single price 
. We can then directly apply the results in Algorithm 8.2 to solve the level-3 problem. We denote the effective market threshold2 for cluster 
as 
, which can be computed in Algorithm 8.2. An illustrative example is shown in Figure 8.5, where the cluster contains four groups (groups 4–7), and the effective market contains groups 4 and 5, thus 
. The service provider obtains the following maximum revenue obtained from cluster 
:
8.5.1.2 Level 2: Resource Allocation among Clusters
For a fix partition 
, we then consider the resource allocation among clusters.
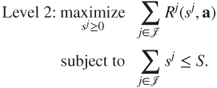
We will show in Section 8.5.2 that subproblems in level 2 and level 3 can be transformed into a complete price differentiation problem under proper technique conditions. Let us denote its optimal value as 
.
Table 8.1 Numerical Examples for Feasible Set Size of the Partition Problem in Level 1
| Number of Groups |  |
 |
 |
||
 |
 |
 |
|||
| Number of Prices |  |
 |
 |
 |
 |
 |
511 | 9330 |  |
 |
 |
 |
9 | 36 | 99 | 4851 | 999 |
8.5.1.3 Level 1: Cluster Partition
Finally, we solve the cluster partition problem.
This partition problem is a combinatorial optimization problem. The size of its feasible set is 
, Stirling number of the second kind [39, Chap.13], where 
is the binomial coefficient. Some numerical examples are given in the third row of Table 8.1. If the number of prices J is given, the feasible set size is exponential in the total number of groups I. For our problem, however, it is possible to reduce the size of the feasible set by exploiting the special problem structure. More specifically, the group indices in each cluster should be consecutive at the optimum. This means that the size of the feasible set is 
as shown in the last row of Table 8.1 and thus is much smaller than 
.
Next we discuss how to solve the three-level subproblems. A route map for the whole solution process is given in Figure 8.6.
Figure 8.6 Decomposition and simplification of the general PP problem: The three-level decomposition structure of the PP problem is shown in the left-hand side (LHS). After simplifications in Sections 8.5.2 and 8.5.3, the problem will be reduced to structure in right-hand side (RHS).
8.5.2 Solving Level 2 and Level 3
The optimal solution (8.25 ) of the level-3 problem can be equivalently written as
The equality (a) in Eq. (8.26 ) means that each cluster 
can be equivalently treated as a group with 
homogeneous users with the same willings to pay 
. We name this equivalent group as a super group (SG). We summarize the above result as the following lemma.
On the basis of Lemma 8.1, the level-2 and level-3 subproblems together can be viewed as the CP problem for SGs. As a cluster and its SG from a one-to-one mapping, we will use the two words interchangeably in the sequel.
However, simply combining Theorems 8.1 and 8.2 to solve level-2 and level-3 subproblems for a fixed partition 
can result in a very high complexity. This is because the effective markets within each SG and between SGs are coupled together. An illustrative example of this coupling effective market is shown in Figure 8.7, where 
is the threshold between clusters and has three possible positions (i.e., between group 2 and group 3, between group 5 and group 6, or after group 6); and 
and 
are thresholds within cluster 
and 
, which have two or three possible positions, respectively. Thus, there are 
possible thresholds possibilities in total.
Figure 8.7 An example of coupling thresholds.
The key idea resolving this coupling issue is to show that the situation in Figure 8.7 cannot be an optimal solution of the PP problem. The results in Sections 8.3 and 8.4 show that there is a unified threshold at the optimum in both the CP and SP cases, for example, Figure 8.2. Next we will show that a unified single threshold also exists in the PP case.
The proof of Lemma 8.2 can be found in Appendix 8.A.3. The intuition is that the resource should be always allocated to high willingness to pay users at the optimum. Thus, it is not possible to have Figure 8.7 at an optimal solution, where high willingness to pay users in group 2 are allocated zero resource while low willingness to pay users in group 3 are allocated positive resources.
On the basis of Lemma 8.2, we know that there is a unified effective market threshold for the PP problem, denoted as 
. As all groups with indices larger than 
make zero contribution to the revenue, we can ignore them and only consider the partition problem for the first 
groups. Given a partition that divides the 
groups into J clusters (SGs), we can apply the CP result in Section 8.3 to compute the optimal revenue in the level 2 based on Theorem 8.1.
8.5.3 Solving Level 1
8.5.3.1 With a Given Effective Market Threshold 
On the basis of the previous results, we first simplify the level-1 subproblem and prove the following theorem.
The level-1 subproblem is still a combinatorial optimization problem with a large feasible set of 
(similar to the original level 1). The following result can help us to reduce the size of the feasible set.
The proof of Theorem 8.4 is given in Appendix 8.A.4. We first prove that this result is true for the level-1 subproblem without constraint (8.29 ) and further show that this result will not be affected by Eq. (8.29 ). The intuition is that high willingness to pay users should be allocated positive resources with priority. It implies that groups with similar willingness to pays should be partitioned in the same cluster, instead of several far away clusters. Or equivalently, the group indices within each cluster should be consecutive.
We define 
as the set of all partitions with consecutive group indices within each cluster, and 
is the value of objective of the level-1 subproblem for a partition 
. Algorithm 8.3 finds the optimal solution of the level-1 subproblem. The main idea for this algorithm is to enumerate every possible partition in set 
, and then check whether the threshold condition (8.29 ) can be satisfied. The main part of this algorithm is to enumerate all partitions in set 
of 
feasible partitions. Thus the complexity of Algorithm 8.3 is no more than 
.
8.5.3.2 Search the Optimal Effective Market Threshold 
We know the optimal market threshold 
is upper bounded, that is, 
. Thus we can first run Algorithm 8.1 to calculate the effective market size for the CP scheme 
. Then, we search the optimal 
iteratively using Algorithm 8.3 as an inner loop. We start by letting 
and run Algorithm 8.3. If there is no solution, we decrease 
by one and run Algorithm 8.3 again. The algorithm will terminate once we find an effective market threshold where Algorithm 8.3 has an optimal solution. Once the optimal threshold and the partition of the clusters are determined, we can further run Algorithm 8.1 to solve the joint optimal resource allocation and pricing scheme. The pseudo-code is given in Algorithm 8.4 as follows.
In Algorithm 8.4, it invokes two functions: Resource-Allocation-CP (
, S) as described in Algorithm 8.1 and Level-1 (
) as in Algorithm 8.3.
The above analysis leads to the following theorem.
Next we discuss the complexity of Algorithm 8.4. The complexity of Algorithm 8.1 is 
, and we run it twice in Algorithm 8.4. The worst case complexity of Algorithm 8.3 is 
, and we run it no more than 
times. Thus the whole complexity of Algorithm 8.4 is no more than 
, which is polynomial of I.