8.6 Price Differentiation Under Incomplete Information
In Sections 8.3–8.5, we discuss various pricing schemes with different implementational complexity level under complete information, the revenues of which can be viewed as the benchmark of practical pricing designs. In this section, we further study the incomplete information scenario, where the service provider does not know the group association of each user. The challenge for pricing in this case is that the service provider needs to provide the right incentive so that a group i user does not want to pretend to be a user in a different group. It is clear that the CP scheme in Section 8.3 and the PP scheme in Section 8.5 cannot be directly applied here. The SP scheme in Section 8.4 is a special case, because it does not require the user-group association information in the first place and thus can be applied in the incomplete information scenario directly. On the other hand, we know that the SP scheme may suffer a considerable revenue loss compared with the CP scheme. Thus it is natural to ask whether it is possible to design an incentive-compatible differentiation scheme under incomplete information. In this section, we design a quantity-based price menu to incentivize users to make the right self-selection and to achieve the same maximum revenue of the CP scheme under complete information with proper technical conditions. We name it the incentive-compatible complete price (ICCP) differentiation scheme.
In the ICCP scheme, the service provider publishes a quantity-based price menu, which consists of several step functions of resource quantities. Users are allowed to freely choose their quantities. The aim of this price menu is to make the users self-differentiated, so that to mimic the same result (the same prices and resource allocations) of the CP scheme under complete information. On the basis of Theorem 8.1, there are only K (without confusion, we remove the superscript “cp” to simplify the notation) effective groups of users receiving nonzero resource allocations, thus there are K steps of unit prices, ![]() in the price menu. These prices are exactly the same optimal prices that the service provider would charge for K effective groups as in Theorem 8.1. Note that for the
in the price menu. These prices are exactly the same optimal prices that the service provider would charge for K effective groups as in Theorem 8.1. Note that for the ![]() groups, all the prices in the menu are too high for them, then they will still demand zero resource. The quantity is divided into K intervals by
groups, all the prices in the menu are too high for them, then they will still demand zero resource. The quantity is divided into K intervals by ![]() thresholds,
thresholds, ![]() . The ICCP scheme can be specified as follows:
. The ICCP scheme can be specified as follows:
A four-group example is shown in Figure 8.8.

Figure 8.8 A four-group example of the ICCP scheme, where the prices 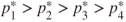 are the same as the CP scheme. To mimic the same resource allocation as under the CP scheme, one necessary (but not sufficient) condition is
are the same as the CP scheme. To mimic the same resource allocation as under the CP scheme, one necessary (but not sufficient) condition is  for all j, where
for all j, where  is the optimal resource allocation of the CP scheme.
is the optimal resource allocation of the CP scheme.
Note that in contrast to the usual “volume discount,” here the price is nondecreasing in quantity. This is motivated by the resource allocation in Theorem 8.1, in which a user with a higher ![]() is charged a higher price for a larger resource allocation. Thus the observable quantity can be viewed as an indication of the unobservable users’ willingness to pay and helps to realize price differentiation under incomplete information.
is charged a higher price for a larger resource allocation. Thus the observable quantity can be viewed as an indication of the unobservable users’ willingness to pay and helps to realize price differentiation under incomplete information.
The key challenge in the ICCP scheme is to properly set the quantity thresholds so that users are perfectly segmented through self-differentiation. This is, however, not always possible. Next we derive the necessary and sufficient conditions to guarantee the perfect segmentation.
Let us first study the self-selection problem between two groups: group i and group q with ![]() . Later on, we will generalize the results to multiple groups. Here group i has a higher willingness to pay and will be charged with a higher price
. Later on, we will generalize the results to multiple groups. Here group i has a higher willingness to pay and will be charged with a higher price ![]() in the CP case. The incentive-compatible constraint is that a high willingness to pay user cannot get more surplus by pretending to be a low willingness to pay user, that is,
in the CP case. The incentive-compatible constraint is that a high willingness to pay user cannot get more surplus by pretending to be a low willingness to pay user, that is, ![]() where
where ![]() is the surplus of a group i user when it is charged with price p.
is the surplus of a group i user when it is charged with price p.
Without confusion, we still use ![]() to denote the optimal resource allocation under the optimal prices in Theorem 8.1, that is,
to denote the optimal resource allocation under the optimal prices in Theorem 8.1, that is, ![]() We define
We define ![]() as the quantity satisfying
as the quantity satisfying
In other words, when a group i user is charged with a lower price ![]() and demands resource quantity
and demands resource quantity ![]() , it achieves the same as the maximum surplus under the optimal price of the CP scheme
, it achieves the same as the maximum surplus under the optimal price of the CP scheme ![]() , as showed in Figure 8.9. As there are two solutions of the first equation of Eq. (8.31 ), we constraint
, as showed in Figure 8.9. As there are two solutions of the first equation of Eq. (8.31 ), we constraint ![]() to be the one that is smaller than
to be the one that is smaller than ![]() .
.

Figure 8.9 When the threshold  , the group i user cannot obtain
, the group i user cannot obtain  if it chooses the lower price pq at a quantity less than
if it chooses the lower price pq at a quantity less than  . Therefore, it will automatically choose the high price
. Therefore, it will automatically choose the high price  to maximize its surplus.
to maximize its surplus.
To maintain the group i users’ incentive to choose the higher price ![]() instead of
instead of ![]() , we must have
, we must have ![]() , which means a group i user cannot obtain
, which means a group i user cannot obtain ![]() if it chooses a quantity less than
if it chooses a quantity less than ![]() . In other words, it will automatically choose the higher (and the desirable) price
. In other words, it will automatically choose the higher (and the desirable) price ![]() to maximize its surplus. On the other hand, we must have
to maximize its surplus. On the other hand, we must have ![]() in order to maintain the optimal resource allocation and allow a group q user to choose the right quantity-price combination (illustrated in Fig. 8.8).
in order to maintain the optimal resource allocation and allow a group q user to choose the right quantity-price combination (illustrated in Fig. 8.8).
Therefore, it is clear that the necessary and sufficient condition that the ICCP scheme under incomplete information achieves the same maximum revenue of the CP scheme under complete information is
By solving these inequalities, we can obtain the following theorem (detailed proof in Appendix 8.A.5).
We want to mention that the condition in Theorem 8.6 is necessary and sufficient for the case of ![]() effective groups.3 For
effective groups.3 For ![]() , Theorem 8.6 is sufficient but not necessary. The intuition of Theorem 8.6 is that users need to be sufficiently different to achieve the maximum revenue.
, Theorem 8.6 is sufficient but not necessary. The intuition of Theorem 8.6 is that users need to be sufficiently different to achieve the maximum revenue.
The following result immediately follows Theorem 8.6.
The Corollary 8.1 means that the users do not need to be extremely different to achieve the maximum revenue.
When the conditions in Theorem 8.6 are not satisfied, there may be revenue loss by using the pricing menu in Eq. (8.30 ). As it is difficult to explicitly solve the parameterized transcend equation (8.31 ), we are not able to characterize the loss in a closed form yet.
8.6.1 Extensions to Partial Price Differentiation under Incomplete Information
For any given system parameters, we can numerically check whether a partial price differentiation scheme can achieve the same maximum revenue under both the complete and incomplete information scenarios. The idea is similar as we described in this section. As the PP problem can be viewed as the CP problem for all effective SGs, then we can check the ICCP bound in Theorem 8.6 for SGs (once the SG partition is determined by the searching using Algorithm 8.4). Deriving an analytical sufficient condition (as in Theorem 8.6) for an incentive-compatible partial price differentiation scheme, however, is highly nontrivial and is part of our future study.
8.7 Connections With the Classical Price Differentiation Taxonomy
In economics, price differentiation is often categorized by the first/second/third-degree price differentiation taxonomy [40]. This taxonomy is often used in the context of unlimited resources and general pricing functions. The proposed schemes in this chapter have several key differences from these standard concepts, mainly because ofthe assumption of limited total resources and the choice of linear usage-based pricing.
In the first-degree price differentiation, each user is charged a price based on its willingness to pay. Such a scheme is also called the perfect price differentiation, as it captures users’ entire surpluses (i.e., leaving users with zero payoffs). For the complete price differentiation scheme under complete information in Section 8.3, the service provider does not extract all surpluses from users, mainly because of the choice of linear price functions. All effective users obtain positive payoffs.
In the second-degree price differentiation, prices are set according to quantities sold (e.g., the volume discount). The pricing scheme under incomplete information in Section 8.6 has a similar flavor of quantity-based charging. However, our proposed pricing scheme charges a higher unit price for a larger quantity purchase, which is opposite to the usual practice of volume discount. This is due to our motivation of mimicking the optimal pricing differentiation scheme under the complete information. Our focus is to characterize the sufficient conditions, under which the revenue loss owing to incomplete information (also called information rent [14, 41]) is zero.
In the third-degree price differentiation, prices are set according to some customer segmentation. The segmentation is usually made based on users’ certain attributes such as ages, occupations, and genders. The partial price differentiation scheme in Section 8.5 is analogous to the third-degree price differentiation, but here the user segmentation is still based on users’ willingness to pay. The motivation of our scheme is to reduce the implementational complexity.
8.8 Numerical Results
We provide numerical examples to quantitatively study several key properties of price differentiation strategies in this section.
8.8.1 When is Price Differentiation Most Beneficial?
In this subsection, we study the revenue gain of the CP scheme, that is, ![]() , where
, where ![]() denotes the number of users in each groups,
denotes the number of users in each groups, ![]() denotes their willingness to pays, and S is the total resource. Notice that this gain is the maximum possible differentiation gain among all PP schemes.
denotes their willingness to pays, and S is the total resource. Notice that this gain is the maximum possible differentiation gain among all PP schemes.
We first study a simple two-group case. According to Theorems 8.1 and 8.2, the revenue under the SP scheme and the CP scheme can be calculated as follows:

and

where ![]() .
.
The revenue gain will depend on five parameters, S, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() . To simplify notations, let
. To simplify notations, let ![]() be the total number of the users,
be the total number of the users, ![]() the percentage of group 1 users, and
the percentage of group 1 users, and ![]() the level of normalized available resource. Thus the revenue gain can be expressed as
the level of normalized available resource. Thus the revenue gain can be expressed as

Next we discuss the impact of each parameter.
One example is showed in Figure 8.10.

Figure 8.10 One example of the revenue gain  for the CP scheme. It is clear that the revenue gain can be divided into three regions. Region (1), increasing region, where
for the CP scheme. It is clear that the revenue gain can be divided into three regions. Region (1), increasing region, where  and the revenue gain comes from the differentiation gain. Region (2), decreasing region, where
and the revenue gain comes from the differentiation gain. Region (2), decreasing region, where  ,
,  , and the revenue gain comes from larger effective market and differentiation gain. Region (3), zero region, where
, and the revenue gain comes from larger effective market and differentiation gain. Region (3), zero region, where  and is a degenerating case where two pricing scheme coincide.
and is a degenerating case where two pricing scheme coincide.
It is clear that the revenue gain is not monotonic in the willingness to pay ratio. Its behavior can be divided into three regions: the increasing Region (1) with ![]() , the decreasing Region (2) with
, the decreasing Region (2) with ![]() , and the zero Region (3) with
, and the zero Region (3) with ![]() .
.
It is also interesting to note that three regions are closed related to the effective market sizes: ![]() in Region (1);
in Region (1); ![]() and
and ![]() in Region (2); and
in Region (2); and ![]() in Region (3) where the CP scheme degenerates to the SP scheme. The peak point of the revenue gain correspond to the place where the effective market of the SP Scheme changes.
in Region (3) where the CP scheme degenerates to the SP scheme. The peak point of the revenue gain correspond to the place where the effective market of the SP Scheme changes.
Intuitively, the CP scheme increases the revenue by charging the high willingness groups with high prices, thus the revenue gain increases first when the difference of willingness to pays increase. However, when the difference of willingness to pay is very large, the CP scheme obtains most revenue from the high willingness to pay users, while the SP scheme declines the low willingness to pay users butserves the high willingness to pays only. Both schemes lead to similar resource allocation in this region, and thus the revenue gain decreases as the difference of willingness to pays increases.
Figure 8.10 shows the revenue gain under usage-based pricing can be very high in some scenario, for example, over ![]() in this example. We can define this peak revenue gain as
in this example. We can define this peak revenue gain as

Figure 8.11 is shown how ![]() changes in
changes in ![]() with different parameters
with different parameters ![]() .
.

Figure 8.11 For a fixed  ,
,  monotonically increases in
monotonically increases in  . For a fixed
. For a fixed  ,
,  first increases in
first increases in  and then decreases in
and then decreases in  .
.
When ![]() is small, which means high willingness to pay users are minorities in the effective market, the advantage of price differentiation is very evident. As shown in Figure 8.11, when
is small, which means high willingness to pay users are minorities in the effective market, the advantage of price differentiation is very evident. As shown in Figure 8.11, when ![]() , the maximum possible revenue gain can be over than
, the maximum possible revenue gain can be over than ![]() ; and when
; and when ![]() , this gain can be even higher than
, this gain can be even higher than ![]() . However, when high willingness to pay users are majority, the price differentiation gain is very limited, for example, the gain is no larger than
. However, when high willingness to pay users are majority, the price differentiation gain is very limited, for example, the gain is no larger than ![]() and
and ![]() for
for ![]() and 0.9, respectively.
and 0.9, respectively.
Intuitively, high willingness to pay users is the most profitable users in the market. Ignoring them is detrimental in terms of revenue even if they only occupy a small fraction of the population. As the SP scheme is set based on the average willingness to pay of the effective market, the high willingness to pay users will be ignored (in the sense of not charging the desirable high price) when ![]() is small. In contrast, ignoring the low willingness to pay users when
is small. In contrast, ignoring the low willingness to pay users when ![]() is large is not a big issue.
is large is not a big issue.
Small ![]() means that resource is very limited, and both schemes allocates the resource to high willingness to pay users (see the discussion of the threshold structure in Sections 8.3 and 8.4), and thus there is not much difference between two pricing schemes. While
means that resource is very limited, and both schemes allocates the resource to high willingness to pay users (see the discussion of the threshold structure in Sections 8.3 and 8.4), and thus there is not much difference between two pricing schemes. While ![]() is very large, that is, the resource is abundant, the prices and the resource allocation with or without differentiation become similar (which can be easily checked from formulations in Theorems 8.1 and 8.2). In these two scenarios, similar resource allocations lead to similar revenues. These explains the bell shape for parameter
is very large, that is, the resource is abundant, the prices and the resource allocation with or without differentiation become similar (which can be easily checked from formulations in Theorems 8.1 and 8.2). In these two scenarios, similar resource allocations lead to similar revenues. These explains the bell shape for parameter ![]() .
.
We find that the revenue gain can be very high under two conditions based on the above observations. First, the high willingness to pay users is minorities in the effective market. Second, the total resource is comparatively limited.
For cases with three or more groups, the analytical study becomes much more challenging because of many more parameters. Moreover, the complex threshold structure of the effective market makes the problem even complicated. We will present some numerical studies to illustrate some interesting insights.
For illustration convenience, we choose a three-group example and three different sets of parameters as shown in Table 8.2. To limit the dimension of the problem, we set the parameters such that the total number of users and the averagewillingness to pay (i.e., ![]() ) of all users are the same across three different parameter settings. This ensures that the SP scheme achieves the same revenue in three different cases when resource is abundant. Figure 8.12 illustrates how the differentiation gain changing changes in resource S.
) of all users are the same across three different parameter settings. This ensures that the SP scheme achieves the same revenue in three different cases when resource is abundant. Figure 8.12 illustrates how the differentiation gain changing changes in resource S.
Table 8.2 Parameter Settings of a Three-Group Example
| Case 1 | 9 | 10 | 3 | 10 | 1 | 80 | 2 |
| Case 2 | 3 | 33 | 2 | 33 | 1 | 34 | 2 |
| Case 3 | 2.2 | 80 | 1.5 | 10 | 1 | 10 | 2 |

Figure 8.12 An example of the revenue gain of the three-group market with the same average willingness to pay.
Similar to the analytical study of the two-group case, Figure 8.12 shows that the revenue gain is large only when the high willingness to pay users are minorities (e.g., case 1) in the effective market and the resource is limited but not too small (![]() in all three cases). When resource S is large enough (e.g.,
in all three cases). When resource S is large enough (e.g., ![]() ), the gain will gradually diminish to zero as the resource increases. For each curve in Figure 8.12, there are two peak points. Each peak point represents a change of the effective market threshold in the SP scheme, that is, when the resource allocation to a group becomes zero. In numerical studies of networks with
), the gain will gradually diminish to zero as the resource increases. For each curve in Figure 8.12, there are two peak points. Each peak point represents a change of the effective market threshold in the SP scheme, that is, when the resource allocation to a group becomes zero. In numerical studies of networks with ![]() groups (not shown in this chapter), we have observed the similar conditions for achieving a large differentiation gain and the phenomenon of
groups (not shown in this chapter), we have observed the similar conditions for achieving a large differentiation gain and the phenomenon of ![]() peak points.
peak points.
8.8.2 What is the Best Trade-Off of Partial Price Differentiation?
In Section 8.5, we design Algorithm 8.4 that optimally solves the PP problem with a polynomial complexity. Here we study the trade-off between total revenue and implementational complexity.
To illustrate the trade-off, we consider a five-group example with parameters shown in Table 8.3. Note that high willingness to pay users is minorities here. Figure 8.13 shows the revenue gain G as a function of total resource S under different PP schemes (including CP scheme as a special case), and Figure 8.14 shows how the effective market thresholds change with the total resource.
Table 8.3 Parameter Setting of a Five-Group Example
| Group Index i | 1 | 2 | 3 | 4 | 5 |
| 16 | 8 | 4 | 2 | 1 | |
| 2 | 3 | 5 | 10 | 80 |
We enlarge Figures 8.13 and 8.14 within the range of ![]() , which is the most complex and interesting part because of several peak points. Similar to Figure 8.12, we observe
, which is the most complex and interesting part because of several peak points. Similar to Figure 8.12, we observe ![]() peak points for each curve in Figure 8.13. Each peak point again represents a change of effective market threshold of the single pricing scheme, as we can easily verify by comparing Figure 8.14 with Figure 8.13.
peak points for each curve in Figure 8.13. Each peak point again represents a change of effective market threshold of the single pricing scheme, as we can easily verify by comparing Figure 8.14 with Figure 8.13.

Figure 8.13 Revenue gain of a five-group example under different price differentiation schemes.

Figure 8.14 Corresponding thresholds of effective markets of Figure 8.13's Example.
As the resource S increases from ![]() , all gains in Figure 8.13 first overlap with each other, then the two-price scheme separates from the others at
, all gains in Figure 8.13 first overlap with each other, then the two-price scheme separates from the others at ![]() , after that the three-price scheme separates at
, after that the three-price scheme separates at ![]() , and finally the four-price scheme separates at near
, and finally the four-price scheme separates at near ![]() . These phenomena are due to the threshold structure of the PP scheme. When the resource is very limited, the effective markets under all pricing scheme include only one group with the highest willingness to pay and all pricing schemes coincide with the SP scheme. As the resource increases, the effective market enlarges from two groups to finally five groups. The change of the effective market threshold can be directly observed in Figure 8.14. Comparing across different curves in Figure 8.14, we find that the effective market size is nondecreasing with the number of prices for the same resource S. This agrees with our intuition in Section 8.4.2, which states that the size of effective market indicates the degree of differentiation.
. These phenomena are due to the threshold structure of the PP scheme. When the resource is very limited, the effective markets under all pricing scheme include only one group with the highest willingness to pay and all pricing schemes coincide with the SP scheme. As the resource increases, the effective market enlarges from two groups to finally five groups. The change of the effective market threshold can be directly observed in Figure 8.14. Comparing across different curves in Figure 8.14, we find that the effective market size is nondecreasing with the number of prices for the same resource S. This agrees with our intuition in Section 8.4.2, which states that the size of effective market indicates the degree of differentiation.
Figure 8.13 provides the service provider a global picture of choosing the most proper pricing scheme according to achieve the desirable financial target under a certain parameter setting. For example, if the total resource ![]() , the two-price scheme seems to be a sweet spot, as it achieves a differential gain of
, the two-price scheme seems to be a sweet spot, as it achieves a differential gain of ![]() compared to the SP scheme and is only
compared to the SP scheme and is only ![]() worser than the CP scheme with five prices.
worser than the CP scheme with five prices.
8.9 Conclusion
In this chapter, we study the revenue-maximizing problem for a monopoly service provider under both complete and incomplete network information. Under complete information, our focus is to investigate the trade-off between the total revenue and the implementational complexity (measured in the number of pricing choices available for users). Among the three pricing differentiation schemes we proposed (i.e., complete, single, and partial), the partial price differentiation is the most general one and includes the other two as special cases. By exploiting the unique problem structure, we designed an algorithm that computes the optimal partial pricing scheme in polynomial time and numerically quantizes the trade-off between implementational complexity and total revenue. Under incomplete information, designing an incentive-compatible differentiation pricing scheme is difficult in general. We show that when the users are significantly different, it is possible to design a quantity-based pricing scheme that achieves the same maximum revenue as under complete information.
Appendix 8.A
8.A.1 Complete Price Differentiation Under Complete Information With General Utility Functions
In this section, we extend the solution of complete price differentiation problem to general form of increasing and concave utility functions ![]() . We denote
. We denote ![]() as the revenue collected from one user in group i. On the basis of the Stackelberg model, the prices satisfy
as the revenue collected from one user in group i. On the basis of the Stackelberg model, the prices satisfy ![]() ,
, ![]()
![]() , thus
, thus
Therefore, we can rewrite the complete price differentiation problem with general utility function (CPG) as follows.

By similar solving technique in Section 8.3, we can solve CPG Problem by decomposing it into two subproblems: resource allocation subproblem ![]() and admission control subproblem
and admission control subproblem ![]() . In subproblem
. In subproblem ![]() , for given
, for given ![]() , we solve
, we solve

After solving the optimal resource allocation ![]() ,
, ![]() , we further solve admission control subproblem:
, we further solve admission control subproblem:

We are especially interested in the case that constraint (8.A.3 ) is active in CPG Problem, which means the resource bound is tight in the considered problem; otherwise, CPG problem degenerates to a revenuemaximization without any bounded resource constraint. We can prove the following results.
Proposition 8.A.1 points out that when the resource constraint (8.A.3 ) is active, the CPG problem can be greatly simplified: its solution can be obtained by solving CPG subproblem with parameters ![]() ,
, ![]() . The following proposition provides a sufficient condition that the resource constraint (8.A.3 ) is active.
. The following proposition provides a sufficient condition that the resource constraint (8.A.3 ) is active.
Next, let us discuss how to calculate the optimal solution. To guarantee uniqueness resource allocation solution, we assume that the revenue is a strictly concave function of the demand,4 that is, ![]() ,
, ![]() . Thus we have the following theorem.
. Thus we have the following theorem.
In Algorithm 8.A.1, we use notation ![]() denotes its inverse function and rearrange the group index satisfying
denotes its inverse function and rearrange the group index satisfying ![]() .
.
8.A.2 Proof of Proposition 8.1
8.A.3 Proof of Lemma 8.2
We can first prove the following lemma.
By the above Lemma 8.A.1, we further prove Lemma 8.2.
8.A.4 Proof of Theorem 8.4
For convenience, we use the notation ![]() to denote a partition with the groups between bars connected with “
to denote a partition with the groups between bars connected with “![]() ” representing a cluster, for example, three partitions for
” representing a cluster, for example, three partitions for ![]() are
are ![]() ,
, ![]() , and
, and ![]() . In addition, we introduce the compound group to simplify the notation of complex clusters with multiple groups. A cluster containing group i can be simply represented as
. In addition, we introduce the compound group to simplify the notation of complex clusters with multiple groups. A cluster containing group i can be simply represented as ![]() , where
, where ![]() (or
(or ![]() ) refers as a compound group composing of all the groups with willingness to pay larger (or smaller) than that of group i in the cluster. Note that the compound groups can be empty in certain cases.
) refers as a compound group composing of all the groups with willingness to pay larger (or smaller) than that of group i in the cluster. Note that the compound groups can be empty in certain cases.
Before we prove the general case in Theorem 8.4, we first prove the results is true for the following two special cases in Lemmas 8.A.2 and 8.A.3.
Further, based on Lemma 8.A.2, we prove another simple special case.
Now Let us prove Theorem 8.4. For convenience, we introduce the notation Compound group, such as ![]() or
or ![]() , which represents some part of a cluster with ordered group indices. For a group i in some cluster,
, which represents some part of a cluster with ordered group indices. For a group i in some cluster, ![]() (or
(or ![]() ) refers to a compound group composing of all the groups with willingness to pay larger (or smaller) than that of group i. For example, in a cluster
) refers to a compound group composing of all the groups with willingness to pay larger (or smaller) than that of group i. For example, in a cluster ![]() ,
, ![]() ,
, ![]() . Note that compound groups can be empty, denoted as
. Note that compound groups can be empty, denoted as ![]() . In the last example,
. In the last example, ![]() . As all the groups within the compound group belong to one cluster, we can apply Lemma 8.2.For example, with the previous cluster setting,
. As all the groups within the compound group belong to one cluster, we can apply Lemma 8.2.For example, with the previous cluster setting, ![]() , and
, and ![]() . By this equivalence rule, a compound group actually has not much difference with one original group. The conclusions of Lemmas 8.A.2 and 8.A.3 can be easily extended to compound groups.
. By this equivalence rule, a compound group actually has not much difference with one original group. The conclusions of Lemmas 8.A.2 and 8.A.3 can be easily extended to compound groups.
8.A.5 Proof of Theorem 8.6
References
- 1. S. Li, J. Huang, and S. Li. Revenue maximization for communication networks with usage-based pricing. In Proceedings of the IEEE Global Telecommunications Conference, pp. 1–6, 2009.
- 2. F. Kelly. Charging and rate control for elastic traffic. In European Transactions on Telecommunications, 1997.
- 3. F. Kelly, A. Maulloo, and D. Tan. “Rate control for communication networks: shadow prices, proportional fairness and stability,” Journal of the Operational Research Society, 49, 1998, 237–252.
- 4. S. Low and D. Lapsley. “Optimization flow control: basic algorithm and convergence,” IEEE/ACM Transactions on Networking (TON), 7(6), 1999, 861–874.
- 5. S. Kunniyur and R. Srikant. “End-to-end congestion control schemes: utility functions, random losses and ecn marks,” IEEE/ACM Transactions on Networking (TON), 11(5), 2003, 702.
- 6. M. Chiang, S. Low, A. Calderbank, and J. Doyle. “Layering as optimization decomposition: a mathematical theory of network architectures,” Proceedings of the IEEE, 95, 2007, 255–312.
- 7. M. Mussa and S. Rosen. “Monopoly and product quality,” Journal of Economic Theory, 18(2), 1978, 301–317.
- 8. E. Maskin and J. Riley. “Monopoly with incomplete information,” RAND Journal of Economics, 15, 1984, 171–196.
- 9. S. Shakkottai, R. Srikant, A. Ozdaglar, and D. Acemoglu. “The price of simplicity,” IEEE Journal on Selected Areas in Communications, 26(7), 2008, 1269–1276.
- 10. V. Valancius, C. Lumezanu, N. Feamster, R. Johari, and V. Vazirani. “How many tiers? Pricing in the internet transit market,” SIGCOMM-Computer Communication Review, 41(4), 2011, 194.
- 11. D. Acemoglu, A. Ozdaglar, and R. Srikant. The marginal user principle for resource allocation in wireless networks. In Proceedings of IEEE Conference on Decision and Control, vol. 2, 2004, pp. 1544–1549.
- 12. R. Gibbens, R. Mason, and R. Steinberg. “Internet service classes under competition,” IEEE Journal on Selected Areas in Communications, 18(12), 2000, 2490–2498.
- 13. John Cox “AT&T shifts to usage-based wireless data plan,” Network World Available online: http://www.networkworld.com/news/2010/060210-att-ends-unlimited-wireless-offering.html?source=nww rss.
- 14. J.-J. Laffont and D. Martmort. The Theory of Incentives: The Principal Agent Modle. Princeton University Press, Princeton, HJ, 2002.
- 15. J. Arrow. Collected Papers of Kenneth J. Arrow, Volume 4: The Economics of Information. Harvard University Press, Cambridge, MA, 1984.
- 16. J. Tirole. The Theory of Industrial Organization. MIT Press, Cambridge, MA, 1988.
- 17. P. Bolton and M. Dewatripont. Contract Theory. MIT Press, Cambridge, MA, 2005.
- 18. N. Stokey. “Intertemporal price discrimination,” Quarterly Journal of Economics, 93(3), 1979, 355–371.
- 19. D. Baron and D. Besanko. “Regulation and information in a continuing relationship,” Information Economics and Policy, 1(4), 1984, 267–302.
- 20. O. Hart and J. Tirole. “Contract renegotiation and coasian dynamics,” Review of Economic Studies, 55(4), 1988, 509–540.
- 21. A. Acquisti and H. Varian. “Conditioning prices on purchase history,” Marketing Sciences, 24(3), 2005, 367–381.
- 22. M. Armstrong. “Price discrimination by a many-product firm,” Review of Economic Studies, 66(1), 1999, 151–168.
- 23. Y. Bakos and E. Brynjolfsson. “Bundling information goods: pricing, profits, and efficiency,” Management Science, 45(12), 1999, 1613–1630.
- 24. X. Geng, M. Stinchcombe, and A. Winston. “Bundling information goods of decreasing value,” Magagement Science, 51(4), 2005, 662–667.
- 25. L. Cabral, D. Salant, and G. Woroch. “Monopoly pricing with network externalities,” International Journal of Industrial Oranization, 17, 1999, 199–214.
- 26. M. Aoyagi. “Coordinating adoption decisions under externalities and incomplete information,” Games and Economic Behavior, 77(1), 2013, 77–89.
- 27. B. Schwartz. The Paradox of Choice: Why More is Less. Harper Perennial, New York, 2005.
- 28. C. Chau, Q. Wang, and D. Chiu. On the viability of paris metro pricing for communication and service networks. In Proceedings of IEEE INFOCOM, 2010, pp. 1–9.
- 29. A. Odlyzko. “Paris metro pricing for the internet. In Proceedings of the 1st ACM Conference on Electronic Commerce, 1999, pp. 140–147.
- 30. T. Basar and R. Srikant. Revenue-maximizing pricing and capacity expansion in a many-users regime. In Proceedings of IEEE INFOCOM, vol. 1, 2002, pp. 294–301.
- 31. H. Shen and T. Basar. “Optimal nonlinear pricing for a monopolistic network service provider with complete and incomplete information,” IEEE Journal on Selected Areas in Communications, 25(6), 2007, 1216–1223.
- 32. A. Daoud, T. Alpcan, S. Agarwal, and M. Alanyali. A stackelberg game for pricing uplink power in wide-band cognitive radio networks. In Proceedings of IEEE Conference on Decision and Control, 2008, pp. 1422–1427.
- 33. L. Jiang, S. Parekh, and J. Walrand. Time-dependent network pricing and bandwidth trading. In Proceedings of IEEE Network Operations and Management Symposium Workshops, 2008, pp. 193–200.
- 34. P. Hande, M. Chiang, R. Calderbank, and J. Zhang. Pricing under constraints in access networks: Revenue maximization and congestion management. In Proceedings of IEEE INFOCOM, 2010.
- 35. S. Ha, S. Sen, C. Joe-Wong, Y. Im, and M. Chiang. Tube: time-dependent pricing for mobile data. In Proceedings of ACM SIGCOMM, Helsinki, Finland, 2012.
- 36. L. He and J. Walrand. Pricing and revenue sharing strategies for internet service providers. In Proceedings IEEE INFOCOM, vol. 1, 2005.
- 37. S. Shakkottai and R. Srikant. “Economics of network pricing with multiple ISPs,” IEEE/ACM Transactions on Networking (TON), 14(6), 2006, 1233–1245.
- 38. V. Gajic, J. Huang, and B. Rimoldi. Competition of wireless providers for atomic users: equilibrium and social optimality. In Proceedings of 47th Allerton Conference on Communication, Control, and Computing, Urbana-Champaign, IL, 2009.
- 39. J. van Lint and R. Wilson. A Course in Combinatorics. Cambridge University Press, 2001.
- 40. B. Pashigian. Price Theory and Applications. McGraw-Hill, New York, 1995.
- 41. A. Mas-Colell, M. Whinston, and J. Green. Microeconomic Theory. Oxford University Press, 1995.
- 42. K. Talluri and G. Van Ryzin. The Theory and Practice of Revenue Management. Springer-Verlag, 2005.

