4.1 Overcoming the tyranny of fixed storage size

Ivan Sutherland talks about “the tyranny of the clock,” referring to the way traditional computer design requires operations to fit into clock cycles instead of letting operations go as fast as possible. There is a similar tyranny in the way we are currently forced to use a fixed storage size for numbers, instead of letting them fit in as small a space as they can. The two concepts go hand-in-hand; smaller numbers should be allowed to do arithmetic as quickly as possible, and larger numbers should be allowed more time to complete their calculations.

In doing arithmetic using pencil-and-paper, it is natural to increase and decrease the number of digits as needed. Computer designers find it more convenient to have fixed sizes, usually a number of bits that is a power of two. They get very uncomfortable with the idea that a numeric value could have a variable number of bits. They accept that a program might declare a type, which means supporting different instructions for different types, like byte, short, real, double, etc. Yet, most of the computer data that processors work with has variable size: Strings, data files, programs, network messages, graphics commands, and so on.

Strings are some number of bytes (characters) long, and files in mass storage are some number of “blocks” long, but the techniques for managing variable-size data are independent of the size of the units that the data is made out of. There are many libraries for extended-precision arithmetic that use software to build operations out of lists of fixed-precision numbers. Why not go all the way down to a single bit as the unit building block for numerical storage?

Suppose written English used the fixed-size tyranny we now have with numbers and required, say, that every word fit into a sixteen-letter allocated space.

Perhaps someone designing word processors would argue that it is much easier and faster to do typesetting if every word is always sixteen letters long. Since the average word length is much less than sixteen letters, this wastes a lot of space. Also, since some English words are more than sixteen letters long, writers have to watch out for “overflow” and use a thesaurus to substitute shorter words.

Morse code is a binary form of communication that is flexible down to the single bit level. It was designed at a time when every bit counted, since sending messages across the country in 1836 was no small feat. Morse estimated the ranking of most common letters and assigned those the shortest dot-dash sequences. In contrast, the ASCII character set makes every character occupy eight bits, and actually uses more bits of information to send English text than does Morse code.

We will later discuss in more detail how to actually build a computer that uses a variable-length format, and that unpacks variable-length numbers into fixed-length storage that is easier and faster to work with. But for now, consider one last point: Hardware designers have to create instructions for half, single, and double precision floats, so they are already coping with variable data sizes.

4.2 The IEEE Standard float formats

We have been using such tiny bit strings to represent numbers, it is almost a shock to see the sizes used for modern floating point math. The IEEE Standard defines four standard sizes for binary floats: 16, 32, 64, and 128 bits long. It also defines the number of exponent and fraction bits for each size:

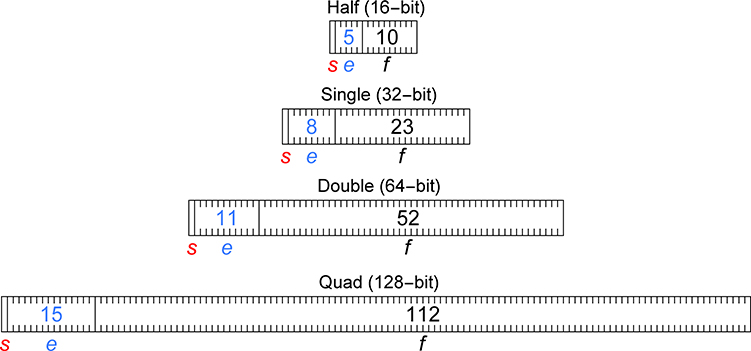
The first thing you might wonder is, why are those the “right” number of bits for the exponent and fraction? Is there a mathematical basis for the number of exponent bits? There is not. They were chosen by committee. One of the influences on the committee was that it is much easier to build exponent hardware than fraction hardware, so the exponents allow dynamic ranges vastly larger than usually required in real-world computations.

One can only imagine the long and contentious arguments in the 1980s about whether a particular size float should have a particular number of bits in its exponent. The sub-field sizes were artistically selected, not mathematically determined. Another argument for large exponents might have been that underflow and overflow are usually bigger disasters than rounding error, so better to use plenty of exponent bits and fewer fraction bits.

The scale factor of a number (like a fixed point number) was originally kept separate from the digits of the number and applied to all the numbers in a computation. Eventually designers realized that each number needed its own individual scale factor, so they attached an exponent field to a fraction field and called it a floating point number. We have the same situation today at the next level up: A block of numbers is specified as all being a particular precision, even though each number needs its own individual exponent size and fraction size. The next logical step, then, is similar to what was done with the scale factor: What if a number were made selfdescriptive about its exponent size and fraction size, with that information as part of its format?

Before exploring that idea further, here is a general description of the state of the four IEEE Standard sizes, at the time of this writing:

• Half precision, 16 bits, is relatively new as a standard size. It was promoted starting around 2002 by graphics and motion picture companies as a format that could store visual quantities like light intensity, with a reasonable coverage of the accuracy and dynamic range of the human eye. It can represent all the integers from –2048 to +2048 exactly. The largest magnitude numbers it can represent are ±65,520, and the smallest magnitude numbers it can represent are about 6×10^-8. It has about three significant decimals of accuracy. Only recently have chip designers started to support the format as a way to store numbers, and existing processors do not perform native arithmetic in half precision; they promote to single precision internally and then demote the final result.

• Single precision is 32 bits total. With an 8-bit exponent, the dynamic range is about 10⁴⁵ to 10³⁸ (subnormal) and 10³⁸ to 10³⁸ (normal) . To put this dynamic range in perspective, the ratio of the size of the known universe to the size of a proton is about 10⁴⁰, so single precision covers this range with about 43 orders of magnitude to spare. The 23-bit fraction provides about seven decimals of accuracy. Single precision floats are often used in imaging and audio applications (medical scans, seismic measurements, video games) where their accuracy and range is more than sufficient.

• Double precision is 64 bits total, and since the late 1970s has become the de facto size for serious computing involving physics simulations. It has about fifteen decimals of accuracy and a vast dynamic range: About 10^-324 to 10^-308 (subnormal) and about 10³⁰⁸ to 10⁺³⁰⁸ (normal). Double precision and single precision are the most common sizes built into processor chips as fast, hard-wired data types.

• Quad precision, 128 bits, is mainly available through software libraries at the time of this writing, with no mainstream commercial processor chips designed to do native arithmetic on such large bit strings. The most common demand for quad precision is when a programmer has discovered that the double precision result is very different from the single precision result, and wants assurance that the double precision result is adequate. A quad precision number has 34 decimals in its fraction and a dynamic range of almost 10⁵⁰⁰⁰ to 10⁺⁵⁰⁰⁰. Because quad precision arithmetic is typically executed with software instead of native hardware, it is about twenty times slower than double precision. Despite its impressive accuracy and dynamic range, quad precision is every bit as capable of making disastrous mathematical errors as its lower-precision kin. And, of course, it is even more wasteful of memory, bandwidth, energy, and power than double precision.

4.3 Unum format: Flexible range and precision

The final step to achieving a “universal number” format is to attach two more self-descriptive fields: The exponent size (es) field and the fraction size (fs) field. They go to the right of the ubit, and we color them green and gray for clarity. sign

Sometimes such fields are called “metadata,” that is, data describing data. How big should the new fields be? That is, how many bits are needed to specify the exponent size and the fraction size?

Suppose we store, in binary, the number of exponent bits in each IEEE float type. The exponent sizes 5, 8, 11, and 15 become 101, 1000, 1011, and 1111 in binary, so four bits suffice to cover all the IEEE cases for the exponent size. But we can be more clever by noticing that there is always at least one exponent bit, so we bias the binary string (treated as if it were a counting number) upward by one. The four exponent sizes can be represented with 100, 111, 1010, and 1110 in binary. Four bits would be the most we would need to specify every exponent size from a single bit (representations that act exactly like fixed point format) to 16 (which is even more exponent bits than used in IEEE quad precision). That is why the exponent size field is marked as storing the value es - 1 instead of es in the above diagram.

Similarly, the four IEEE fraction sizes 10, 23, 52, and 112 become 1010, 10111, 110100, and 1110000 in binary, so seven bits suffice to cover all the IEEE cases. But we similarly can require at least one fraction bit, so the binary counting number stored in the fs field is actually one less than the number of bits in the fraction field. With a seven-bit fs field, we can have fraction sizes that range anywhere from one bit to 2⁷ = 128 bits. The es and fs values can thus be customized based on the needs of the application and the user, not set by committee.

It is possible to have esizesize be as small as zero, which means there is no bit field, and the number of exponent bits is exactly 2⁰ = 1. Similarly for fsizesize. The reason for putting them to the right of the ubit is so that all of the new fields are together and can be stripped away easily if you just want the float part of the number. The reason the ubit is where it is was shown previously; it is an extension of the fraction by one more bit, and creates a monotone sequence of values just like the positional bits in the fraction.

It looks odd to see “size” twice in esizesize and fsizesize, but they are the size of a size, so that is the logical name for them. It is like taking the logarithm of a logarithm, which is why esizesize and fsizesize are usually small, single-digit numbers. For example, suppose we have

• Fraction value = 110101011 in binary; then

• Fraction size = 9 bits, which is 1001 in binary, and

• Fraction size size = 4 bits (number of bits needed to express a fraction size of 9).

The utag is the “tax” we pay for flexibility, compactness, and exactness information, just as having exponents embedded in a number is the “tax” that floating point numbers pay for describing their individual scale factor. The additional self-descriptive information is why unums are to floating point numbers what floating point numbers are to integers.

4.4 How can appending extra bits save storage?

The size of the “tax” is important enough that it deserves a name: utagsize.

If we want to create a superset of all the IEEE floats, utagsize will be 1 + 4 + 7 = 12 bits. Besides the utag bits, there is always a sign bit, at least one exponent bit, and at least one fraction bit, so the minimum number of bits a unum can occupy is utagsize + 3. The maximum possible number of bits also has a name: maxubits.

You might wonder: How is the unum approach going to help reduce memory and energy demands compared to floats, if it adds more bits to the format?

The principal reason is that it frequently allows us to use far fewer bits for the exponent and fraction than a “one-size-fits-all” precision choice. Experiments that show this are in chapters yet to come, but for now it might seem plausible that most calculations use far fewer exponent bits than the 8 and 11 bits allocated for single and double precision floats (dynamic ranges of about 83 and 632 orders of magnitude, not exactly your typical engineering problem).

In the example where all English words had to fill 16-character spaces, the paragraph took up far more space than if every word was simply as long as it needed to be. Similarly, the fraction and the exponent size of a unum increases and decreases as needed, and the average size is so much less than the worst case size of an IEEE float that the savings is more than enough to pay for the utag. Remember the case of Avogadro’s number in the very beginning? Annotating a number with scaling information saved a lot of space compared to storing it as a gigantic integer. The next question might be, does the programmer then have to manage the variable fraction and exponent sizes?

No. That can be done automatically by the computer. Automatic range and precision adjustment is inherent in the unum approach, the same way float arithmetic automatically adjusts the exponent. The key is the ubit, since it tells us what the level of certainty or uncertainty is in a value. The exponent size and fraction size change the meaning of an ULP, so the three fields together provide the computer with what it needs, at last, to automate the control of accuracy loss. If you add only one of any of the three fields in the utag, you will not get a very satisfactory number system.

There is something called “significance arithmetic,” for example, that annotates each value with the number of significant figures. That approach is like a utag that only has a field for the number of bits in the fraction and that assumes every answer is inexact. After only a few operations, a significance arithmetic scheme typically gives even more pessimistic assessments than interval arithmetic, and incorrectly declares that all significance has been lost.

Imagine never having to specify what type of floating point number to use for variables, but instead simply say that a variable is a real number, and let the computer do the rest. There are symbolic programming environments that can do this (Mathematica and Maple, for example), but to do so they use very large data structures that use far more bits than IEEE floats. We will demonstrate that unums get better answers than floats but do it with fewer bits than IEEE floats, even after including the cost of having a utag on every value.

4.5 Ludicrous precision? The vast range of unums

If we use esizesize = 4 and fsizesize = 7, we call that “a {4, 7} environment” for short, or say that a unum uses “a {4, 7 } utag.” While a computer can manage its own environment sizes by detecting unsatisfactory results and recalculating with a bigger utag, the programmer might want some control over this for improved efficiency. It is usually easy for a programmer to make a good estimate of the overall accuracy needs of an application, which still leaves the heavy lifting (dynamically figuring out the precision requirements of each operation) to the computer.

For example, the {3, 4 } unum environment looks appropriate for graphics and other low-precision demands; it provides for an exponent up to 2³ = 8 bits long and a fraction up to 2⁴ = 16 bits long. Therefore, its maximum dynamic range matches that of a 32-bit float and its fraction has more than five decimals of accuracy, yet it cannot require more than 33 bits of total storage (and usually takes far less than that). Using a {3, 4 } environment instead of a {4, 7} environment reduces the utag length to 8 instead of 12, a small but welcome savings of storage.

A surprising amount of very useful computation (for seismic signal processing, say) can be done with a {2, 2 } environment, because of the absence of rounding, overflow, and underflow errors. There is such a thing as a {0, 0 } environment, and it is so useful it will receive its own discussion in Chapter 7. The interesting thing about {0, 0 } unums is that they are all the same size: Four bits.

At the other extreme, unums can easily go well beyond the limits of human comprehension for dynamic range and precision. The number represented in decimal by one followed by a hundred zeros is called a “googol”: 10¹⁰⁰. The number represented by one followed by a googol zeros is called a “googolplex,” or 10¹⁰¹⁰⁰. How big a utag would we need to represent all the integers up to a googol, scaled by a dynamic range of a googolplex?

It works out to only 9 bits each for fsizesize and esizesize, a total utag size of 19 bits! With just a handful of bits, we can create a unum with ludicrous precision. While it seems very unlikely that anyone can justify the use of such precision for a real-world engineering problem, the unum format is certainly up to the task if anyone demands it. Furthermore, such numbers are well within the computing abilities of even the most modest computer. The maximum size of a unum with such a utag is only 1044 bits, about the same amount of storage as 16 double-precision floats.

There are practical problems that demand ultrahigh precision, like e-commerce encryption security that currently requires integers that have hundreds of digits. Even a cell phone uses very large integers for encryption and decryption of data. The need for large integer multiplication for public-key encryption means, incidentally, that hardware designers have already been unwittingly working toward building the type of circuitry needed for fast unum calculations. Computational scientist David H. Bailey has collected many examples where very high precision is needed either to solve a problem, or to figure out that it is unsolvable.

4.6 Changing environment settings within a computing task

The environment can be changed in the middle of a computation, and this actually is a very useful thing to do. For example, the computer might decide higher precision is needed for some task, and temporarily increase fsizesize, resetting it to where it was when finished. In that case, there is no need for a programmer to do anything to the values that have already been calculated.

It can also happen that previously computed unums will be needed in an environment that has different settings. In that case, The program has to know to promote or demote the previously computed unums to the new size, just as one would promote single-precision floats to double precision. It is good practice to annotate a block of unums with their {esizesize, fsizesize } value if they are archived or communicated to another program. Doing so should take only one 8-bit byte, since it is hard to imagine either esizesize or fsizesize taking up more than four bits.

With fixed-size floats, you tend to think of loading or storing all their bits at once. With unums, you have a two-step process like you would have reading character strings of variable length. Based on the environment settings, the computer loads the bits of the es and fs fields, which point to where the sign bit, exponent, and fraction must be to the left of the utag. It then loads the rest of the unum and points to the next unum. This is why esizesize and fsizesize are like processor control values; they tell the processor how to interpret bit strings. A collection of unums are packed together exactly the way the words in this paragraph are packed together. As long as a set of unums is of substantial length, there is little waste in using conventional power-oftwo sizes to move the unum data in blocks, such as cache lines or pages of memory. Only the last block is “ragged” in general, that is, only partly full. Blocking the set of unums can also make it easier to do random access into the set.

These are all classic data management problems, no different than the problem of organizing records on a disk drive. To use the vocabulary of data structures, packed unums form a singly linked list. Each value contains a pointer to where the next value begins, since the utag specifies the total length of the bit string. Chapter 7 will show how unums can be unpacked into a fixed-size form that is actually faster to work with than floats. That restores the ability to use indexed arrays, the way floats are often stored.

In summary, there is no difficulty dealing with multiple environment settings within a calculation, or with multiple unum lengths within a set of unums that are loaded or stored at any particular setting. These are problems that have been solved for many decades, and the solutions are part of every operating system. They simply need to be applied to unums as they have been to many other kinds of variable-sized data.

4.7 The reference prototype

The text you have been reading was not created with a word processor or conventional text editor. Everything you have been reading is the input, output, or comments of a computer program.

The graphics shown here are computed output, as are the numerical examples. This book is a “notebook” written in Mathematica. This has the advantage of eliminating many sources of errors, and making it easier to make changes and additions. The code contained here is the reference prototype of the unum computing environment.

While much of the discussion so far has been conceptual, the unum concept has been reduced to practice, and this book is that reduction. The prototype contains a collection of tools for interactively working with unums and many other ideas. In explaining how the tools work, there are two challenges: One is that we risk sounding like some user’s manual instead of a book about a completely new approach to numerical computing. The other is that it is difficult to shield the reader from seeing some computer code. The example of Section 3.3 had a code snippet that took the square root of a starting value until it “converged” to 1. That resulting series of values was actually computed, not typed in.

Sections of code have a light green background to make it easier to skip them if you (like most people) do not enjoy reading computer code written by others. Most of them are short, like the following command to set the computing environment:

The setenv function sets up the environment for specified settings of esizesize and fsizesize. It takes the desired {esizesize, fsizesize } pair as its argument. It computes all the useful pointers and bit combinations that are used to pull apart and interpret any given unum as a value. The full description of what setenv does is shown in a code listing in Appendix C.1. The line of code shown above just set the unum environment to a maximum exponent size of 2³ bits and a maximum fraction size of 2⁴ bits, and also created all the useful constants that go along with the environment, like maxreal and utagsize. Just as we use this typeface to indicate computerese like binary numbers, functions that are displayed like setenv also indicate that a function exists in the prototype. A value like maxreal becomes maxreal when it actually has to participate in a calculation. Whereas defined concepts like maxreal are listed in the Glossary, defined computer variables and functions are listed in the Appendices for those interested in that level of detail.

One of the things setenv computes is bit masks. When you need to extract a set of bits from a number, you “AND” each bit with a string that has 1 values in just those bits. For instance, if you “AND” a number with 000110 in binary, you will get just the values of the bits in the fourth and fifth position, and all other bits will always be zero. Here are some bit masks that will be useful in writing software for unum arithmetic: ubitmask picks out the ubit, fsizemask selects the bits that indicate the number of fraction bits, and esizemask selects the bits that indicate the number of exponent bits. We also will find combinations handy: efsizemask for both exponent and fraction size fields, and utagmask selects the entire utag. For clarity, we show the three bit fields of the utag, with annotations under each field as a reminder for what the contents of each field represent. The first field, the ubit, is annotated with “…” if there are more bits after the last fraction bit, but “↓” if the fraction is exact. The second and third fields hold binary counting numbers that are one less than the fraction and exponent sizes es and fs.

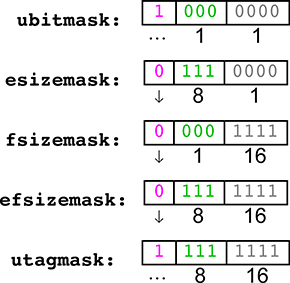
With floats, the ULP bit is the rightmost bit of the number. With unums, the ULP bit is the bit just to the left of the utag. A unum value can have a range of ULP sizes, since the number of bits in the fraction is allowed to vary. The ULP bit mask in a unum is easily computed by shifting a 1 bit left by the number of bits in the utag, utagsize. The value the ULP bit represents depends on the utag bits. The represented real value is an ULP, but the unum mask for it we call ulpu. As a general rule, the names of variables that are unums and functions that produce unums will end in the letter u. Since we currently are in a {3, 5 } environment, the utag is nine bits long and ulpu will be a 1 bit followed by the nine empty bits of the utag, or 1 0 000 00000 in binary. Besides color-coding the bits for clarity, notice that we use a convention that the sign, exponent, and fraction bits are in boldface but the utag bits are not.

Here is a visual way to compare unums and float formats: A grid of dots that shows the possible exponent bits (horizontal) and fraction bits (vertical), color-coded for size comparison with IEEE floats. This diagram shows when a unum has greater fraction accuracy than a standard float type (above a horizontal line), or when a unum has greater dynamic range (to the right of a vertical line).

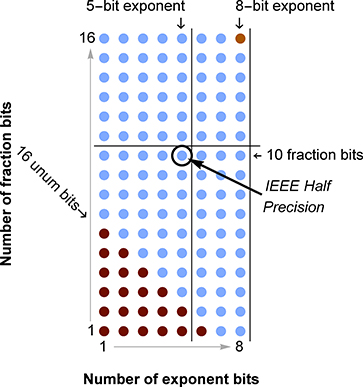
This is the diagram for a {3, 4} environment. As mentioned above, it looks robust enough for graphics and other low-precision demands. The size of the utag is just 8 bits, and it includes half-precision IEEE floats but also has the dynamic range of a 32-bit float and a couple more decimals of precision than 16-bit floats.

The blue dots indicate unums that take more space than a half precision float, but no more than required for single precision. Dark red dots show unums that are as small as a half precision float or smaller. The dark orange dot is the only unum size in a {3, 4} environment that takes more space than IEEE single precision; the largest {3, 4} unum takes 33 bits. The smallest one takes only 11 bits.

The diagram for a {4, 7} environment is so tall that it barely fits on a page. At the top right corner, the largest unum has a larger dynamic range and precision than IEEE quad format. There are

24⋅27=2048

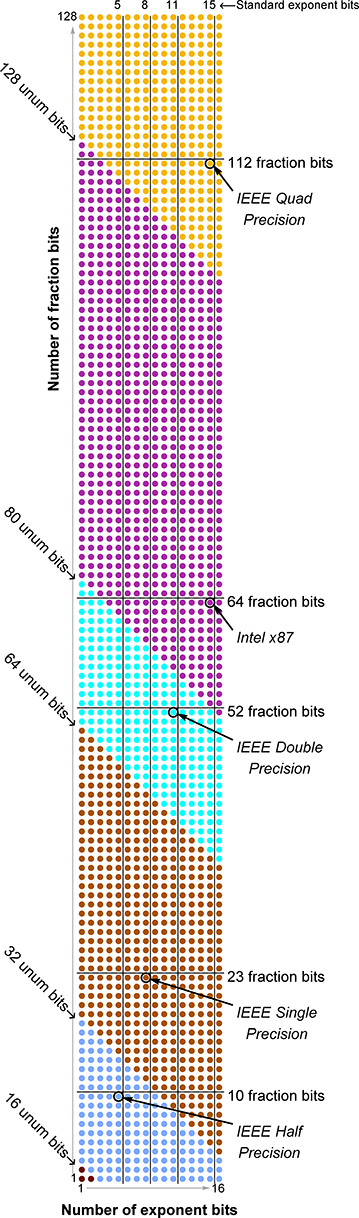
possible combinations for the sizes of the exponent and fraction, four of which match IEEE Standard binary floats, and one of which matches the format used in the original Intel math coprocessors (sometimes called “extended double”). In the 1980s, Intel introduced a coprocessor called the i8087 that internally used 64 bits of fraction and 15 bits of exponent, for a total size of 80 bits. It had successor versions with product numbers ending in 87, so here that format is called “Intel x87.” The 80-bit float was initially one of the IEEE Standard sizes, but exposed an interesting technical-social issue: Most users wanted consistent results from all computers, not results that were more accurate on one vendor’s computers! Using the extra size of the x87 for scratch results reduced rounding error and occurrences of underflow/overflow, but the results then differed mysteriously from those using double precision floats. We will show a general solution for this problem in the next chapter.

There has been much hand-wringing by floating point hardware designers over how many exponent bits and how many fraction bits to allocate. Imagine instead always being able to select the right size as needed.

Note: Be careful when requesting the exponent field size. Even casually asking for an esizesize of 6 can launch you into the land of the outrageous. The prototype environment in particular is not designed to handle such huge numbers.

A unum with this {4, 7} utag can take as few as 15 bits, which is even more compact than a half-precision float. In the bottom left corner is the minimal unum format, with just three bits of float to the left of the utag.

4.8 Special values in a flexible precision environment

For floats with just a ubit appended, we can use the maximum exponent and fraction fields (all bits set to 1) to represent infinity (ubit = 0) or NaN (ubit = 1). With flexible precision unums, the largest magnitude number happens only when we are using the largest possible exponent field and the largest possible fraction field. There is no need to waste bit patterns with multiple ways to represent infinities and NaNs for each possible combination of es and fs. Unum bit strings represent real numbers (or ULP-wide open intervals) unless the es and fs are at maximum, corresponding to the extreme top right-hand corner dot of the two preceding diagrams, which means they represent infinities or NaNs.

Our convention is that unum variable names end in “u” so we do not confuse bit strings with the real values they represent. For instance, maxreal is the largest real value, but the unum that represents it in a particular environment is maxrealu.

The function big ] returns the biggest real value representable by a unum with an es and fs matching that of a unum u. The function bigu [u ] returns the unum bit string that represents that value; unless the es and fs fields are at their maximum, bigu ] is the unum with all 1s in the exponent and fraction fields. If the es and fs fields are at their maximum (all 1 bits), then we have to back off by one ULP, since that bit pattern is reserved for ±∞. In that case, big[u] is the same as maxreal. Think of maxreal as “biggest of the big.” (It was tempting to call the big function mightybig because of the way mightybig ] would be pronounced.)

A set of values is calculated whenever setenv is called. The following table shows the names of special unums and approximate decimal versions of the maxreal and smallsubnormal real values computed when the environment is set to {3, 2 }. The unum for smallsubnormal, like maxreal, occurs when es and fs are at their maximum:

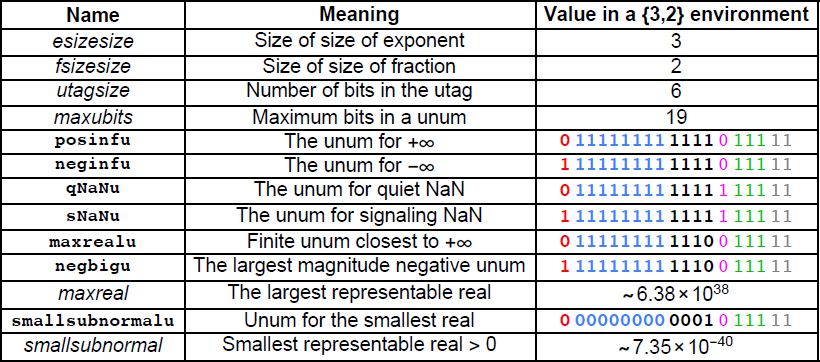
Larger exponents extend expressible magnitudes in both directions, so the largest exponent field expresses the smallest magnitude number. The representation of smallsubnormal has just one bit set to 1 in the fraction, the ULP bit in the last place; all other bits to the left are 0. The tabled values, and others computed by setenv, are mainly of interest if you want to write low-level programs with unums. If there is ever any question about what the current environment is, simply look at the values of esizesize and fsizesize. In the prototype, here is one way to show those values:

In this book, most computed output is in this typeface (Courier plain, not bold).

4.9 Converting exact unums to real numbers

We need a way to convert the floating point part of a unum into its mathematical value. First we use the self-descriptive bits in the utag to determine the fraction and exponent sizes. Then we can extract the sign, exponent, and fraction bits using bit masks. From those values we build a function that converts the part of unum number left of the utag into a real number using IEEE binary float rules. When the ubit is 0, the formula for a unum value is exact. sign

The formula looks very much like the formula for a float (not the strict IEEE float, but the improved one that does not waste huge numbers of bit patterns on NaN).

The code version of this is u2f [u] (“unum to float”) where u is a unum. The code is in Appendix C.3.

To reinforce the connection between unums and floats, here is a utag for IEEE single precision (8 bits of exponent, 23 bits of fraction) in a {3, 5 } environment:

If you put 32 bits to the left of that utag, it will express the same values as an IEEE single precision float, except that it avoids clipping the maximum exponent to NaN.

Similarly, here is a utag for IEEE half precision in a {3, 4} environment:

The utagview [ut] function displays the utags as shown above, where ut is a utag. It can be used even if the environment is {0, 0 }, with no bits for es and fs. It does not have a way of showing a nonexistent bit so it draws the last two squares anyway, empty; es and fs are always zero. The only thing left in the utag is the ubit:

It is easy to convert an exact unum to an IEEE Standard float (at least for unums with exponent and fraction sizes no larger than the largest IEEE type, quad precision). To do that, you find the smallest size IEEE float with fields large enough for the unum exponent and fraction, and pad the unum with extra bits to match the worst-case size allotment in the float. If the exponent is all 1 bits and represents a finite value, you discard all the fraction information and replace it with 0 bits, to represent infinity in the style of the IEEE Standard. There are no NaN values to convert, since a unum NaN is not exact; its ubit is set to 1. And, of course, you strip off the utag. For example, with a unum tag for IEEE half precision,

the largest expressible real number is 131 008. (We can write the binary string for that unum as 0 11111 1111111111 0 100 1001. Using boldface for the float part but not for the utag helps make such long bit strings more readable.) The half precision IEEE Standard only allows values half as large as this: 65 504. Every bit pattern larger than that means either infinity or NaN. The decision to have a vast number of NaN types looks particularly dubious when the precision or dynamic range is small.

You might think, “Wait, all the bits are set to 1 in that unum. Doesn’t that mean it has to express infinity, since we reserve that largest number for infinity?” No, because it is not the largest number possible in the unum environment. With the same size utag, we could also have es and fs values as large as 8 and 16, which permits expression of a much larger dynamic range and precision:

allows 680 554 349 248 159 857 271 492 153 870 877 982 720 as the largest finite number! (About 6.8 × 10³⁸, twice as large as maxreal in IEEE single precision since we do not waste bit patterns on a plethora of NaNs.)

4.10 A complete exact unum set for a small utag

If we set the environment to a small utag, say {2, 2}, the set of possible exact unum values is so small that we can list all of them. Here are the non-negative values:

The unum bit strings for these numbers require from eight to fourteen bits, total. Unums have more than one way to represent exact numbers, so we use one that requires the fewest bits. Even that does not make a unum unique; sometimes there is more than one way to represent an exact number with the minimum number of bits.

Instead of fixing the utag contents, we can also limit the total number of exponent and fraction bits, since that determines the total number of bits of storage. The total additional bits cannot be less than two, since we always have at least one exponent bit and one fraction bit. There are 66 non-negative exact numbers expressible with just two to five bits in addition to the five-bit utag and the sign bit:

Some of those 66 numbers have more than one unum representation. Many of the duplications are like fractions that have not been reduced to lowest terms; there is no need for exact representations like 128 and 64 when 32 means the same thing and requires fewer bits to store. This is one reason unums are more concise than floats. There are 34 values in the preceding set that have more than one representation:

The distribution of the logarithm of possible numbers shows that for a given bit-length budget, the closer the numbers are to 1 in magnitude, the higher the precision. This seems like a practical choice that saves storage. This differs from floats in that it dedicates more bits for precision for numbers near 1 and more bits for dynamic range for the largest and smallest numbers, whereas floats give equal precision to all values. If we sort the values generated above and plot the logarithm of their value, the curve is less steep in the middle, indicating more precision for numbers that are neither huge nor tiny. This allows us to cover almost five orders of magnitude with only a handful of bits, yet have about one decimal of accuracy for numbers near unity.

When people write application programs, they select units of measurement that make the numbers easy to grasp, which means not too many orders of magnitude away from small counting numbers. Pharmacists uses milligrams, cosmologists use light years, chip designers use microns, and chemists measure reaction times in femtoseconds (10¹⁵ second). Floats are designed to treat, say, the numerical range 10³⁰⁶ to 10³⁰⁷ as if it were just as deserving of precision bits as the numbers one to ten, which ignores the human factor. As with Morse code, unums make the more common data expressible with fewer bits.

4.11 Inexact unums

A unum that has its ubit set to 1 indicates a range of values strictly between two exact values, that is, an open bound. An “inexact” unum is not the same thing as a rounded floating point number. In fact, it is the opposite, since IEEE floats return inexact calculations as exact (incorrect) numbers.

The formula for the value should be simple, but we do need to be careful of the values that express infinity and maxreal, and remember that if we go “beyond infinity” by setting the ubit, we get a NaN. Also, if the number is an inexact zero, then the direction “farther from zero” is determined by checking the sign bit.

Recall that in the prototype, u2f (unum to float) is the function that converts a unum into the real number represented by its float parts, and ulpu is the unum bit string with a 1 bit in the last bit of the fraction and zero for its other bits. Occasionally we want to change a unum to the one representing the exact value closer to zero; exact [u ] does just that. If u is already exact, the function leaves it as is. Also, inexQ ] is a Boolean test of whether a unum u is inexact; it returns True if it is and False if it is exact. Just for completeness, exQ [u] does the reverse, to reduce the number of “not” symbols in the program.

Here is the kind of picture you should keep in your head when thinking about inexact unums, where rounded shapes help remind us that the endpoint is not included in the bound. For positive unums:

The way to test if a unum is positive or negative in the prototype is sign [u], which returns the sign bit: 0 if positive, 1 if negative. Adding an ULP always makes the number farther from zero, so for negative unums, adding an ULP makes the represented value more negative:

So u2f [u] handles the case of an exact unum u, and the above figures show how to handle inexact cases. We also need to convert unum strings for signaling and quiet NaN values, sNaNu and qNaNu. In the prototype, we use exact [u], big [u], bigu [u], sign [u ] to express the general conversion function (where signmask [u], signmask [u] is a 1 bit where the sign bit of u is and all 0 bits elsewhere):

Computer logic might first test if all the e, f, es, and fs bits are set to 1, and if they are, sort out the four possible special cases of signaling NaN, quiet NaN, – ∞, and + ∞. The next thing to test is for ±bigu [u] because those are the only cases where adding ulpu would cause integer overflow of the combined exponent and fraction fields, treated as a binary counting number. With all those cases taken care of, we can find the open interval between floats as shown in the two preceding illustrations of the real number line. Notice that the last two lines in the above function take care to express the open interval the way mathematicians usually write open intervals: (a, b), sorted so a < b. Also notice that the first two lines express floats, but the last four are open intervals that will require a new internal data structure; that is the subject of Chapter 5.

4.12 A visualizer for unum strings

The reader is not expected to learn to interpret unum bit strings! That is what computers are for. Understanding the bit strings that represent floats is already difficult enough. Recall that we can view the utag using the utagview [u] function, like this one (which describes an IEEE quad-precision float):

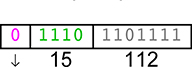
The unumview [u] function similarly annotates each field of a unum u, when we want to see all the machinery in operation. It shows the exponent used in scaling (accounting for the bias) and the value of the hidden bit. It also shows the represented value as both a fraction and a decimal, whenever the two forms are different. Sometimes decimals are easier to read, and sometimes the fraction is easier. The decimals shown are always exact, since a fraction with a power of 2 in the denominator always can be expressed with a finite decimal.

For example, here is how unum format represents π in a {1, 4 } environment:

You expect irrational numbers like π to use the maximum number of fraction bits, and they will always set the ubit to show that the value lies within an ULP-wide range. Expressing π required 18 bits to the left of the utag.

On the other hand, expressing –1 never requires more than three bits to the left of the utag:

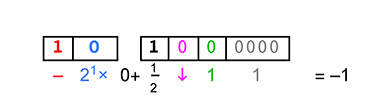
Notice that the hidden bit is 0 in this case since the exponent is zero. The number to add to the fraction is therefore 0 instead of 1, shown under the gap between the boxes. Just think about how often certain floats like –1 and 2 are used in computer programs; the ultra-concise way they can be expressed with unums starts to hint at how much storage and bandwidth they can save.

We need unums for inexact “positive zero” and inexact “negative zero” to fill in the gap between -smallsubnormal and smallsubnormal. The ubit gives us a reason to have “negative zero” representations. Here are two examples of open intervals next to zero in a {2, 3} environment. Using the maximum possible values for exponent size and fraction size with an inexact zero expresses the smallest possible ULP.

Here are the two bit strings that unum arithmetic uses instead of underflowing to zero:

The largest possible ULP next to zero is when the exponent size and fraction size are as small as possible (one bit each):

Unums provide a rich vocabulary for expressing the concept that a number is “small” even when it is not expressible as an exact number.