8.1.1 Conceptual definition of ordering for general intervals

The easiest operations to write for unums are comparisons. They are different from comparisons of floats, since unums and ubounds can represent ranges of numbers and thus overlap completely, partially, or not at all.

For most operations with unums and ubounds, the hardware approach is to move from the u-layer to the g-layer, perform the operation there, and convert the result back to the u-layer. The unpacked form of a ubound discussed in Chapter 7 provides a concrete example of a hardware approach for operations described here.

For a ubound u to be less than a ubound v, the maximum of u must be less than the minimum of v. This gets subtle, however, because endpoints can be closed or open. The maximum of u could equal the minimum of v if either endpoint is open, yet u would still be strictly less than v. The following type of construct comes up a lot when writing the logic for ubound operations:

In the prototype, the ltuQ [u, v] function (where the name comes from “less-than, u-layer Question”) returns a Boolean True if u represents a numerical range strictly less than the numerical range represented by v. In all other cases, including ones where either ubound represents NaN, it returns False. Similarly, we have a greater-than comparison gtuQ [u, v ]. The code for both functions is in Appendix C.8. Notice that these are “strictly less than” and “strictly greater than” functions; any overlap, even just an endpoint, makes the result False.

For example, the prototype command to find out if

It returns False because the intervals both include the exact number 3. However, testing if [1, 3 ] < (3, 100] returns True, because one endpoint is open. Floats and traditional interval arithmetic cannot make this important distinction:

The comparisons are performed by converting the u-layer arguments to general intervals (using u2g) and using the g-layer function ltgQ. This closely resembles the way hardware would do it. The “greater than” test is exactly like the “less than” test with the input endpoints interchanged. The prototype functions for the greater-than test are gtgQ in the g-layer and gtuQ in the u-layer.

With many operations on unums and ubounds, the prototype defines operators that resemble their mathematical equivalents, to make expressions look more like conventional math. The “less than” test for ubounds is “≺”, a slightly curvy less-than symbol, so the test “-2 < -1” in the u-layer can be written in unum math as

Similarly, the “≻” symbol can be used to make expressions easier to read than writing “gtuQ”:

8.1.2 Hardware design for “less than” and “greater than” tests

Recall what a gbound looks like, the scratchpad version of a ubound or unum. Suppose we have both u and v in the scratchpad and wish to test if u is less than v.

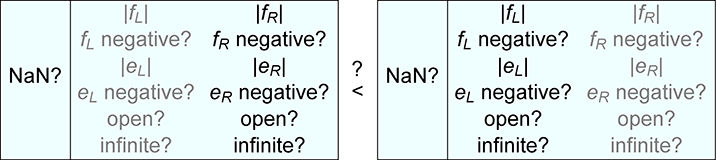
We can ignore all the data shown in gray, since we just need to know if the right endpoint of u is less than the left endpoint of v. The “less than” comparison operation requires peeling away bits in the gbound in order of importance. The gbound parts are tested in the following order, breaking out with a “Done” as soon as a “less than” conclusion of True or False can be drawn:

• NaN? bits

• f negative? bits

• infinite? bits (with tie-breaking using the open? bits)

• Integer values of f after scaling by the difference in e values

• open? bits

If either value is NaN, a less-than or greater-than test returns False. Done. (A better answer might be “Unknown,” but that is not in the vocabulary of a comparison test. There is some logic in answering “Is NaN less than 2?” with “No” since only numbers can be “less than” or “greater than” other numbers.)

Are the “f negative?” bits the same? If not, the decision is easy. If the left one is negative and the right one positive, the less-than test is True, otherwise False. Done. Otherwise, the comparison is between endpoints that have the same sign. Is just one of the “infinite?” bits set? That determines the ordering, done. Are both of the “infinite?” bits set? Then the “open?” bits need to be checked, since (x, ∞) < ∞ and -∞ < (-∞, x) give a True result, else False; done.

With exception testing dispensed with, the next step is more like arithmetic than bit-testing. The e values are integers; subtract them. Use the difference to shift one f value left and reduce its e value, so that both values have the same e value. In other words, line up the binary points, just as you would do for floating point addition and subtraction. Comparison of the scaled f values is then straightforward, but depends on how variable length is implemented. If there is a dedicated location that stores the length of f, then the different lengths quickly break the tie, done. Otherwise, the bit lengths match; go through bits from most significant to least significant until a tie-breaker bit is found. If one is found, done.

After all that, if the values are still tied (identical), then the open-closed flags are checked. If either one is open, then the less-than test is True; if both are closed, the less-than test returns False because u and v touch at that exact point. All it takes is one equal point to spoil a strictly less-than comparison.

A clever hardware designer will notice shortcuts that work directly on u-layer data for a comparison operation, instead of first converting u and v to gbounds. In particular, it is easy to compare two unums that have the same esize and fsize values just by treating the other bits (including the ubit) as signed integers. The trick is to be able to promote the exponent and fraction lengths of each value until they match, taking care not to change the value of inexact (open) endpoints used in the comparison. The prototype includes a function promote [{u, v}] that does this (Appendix D.1).

8.2.1 Conceptual definition of “equal” for general intervals

Less than and greater than relationships are easy to understand even when the numbers are ranges instead of precise point values. A trickier proposition is to define “equal” when talking about ranges of real numbers. What does it mean to say two general intervals are “equal”?

Ubounds or unums are equal if they represent the same gbound. They must have the same endpoints and the same open-closed endpoint properties. The prototype command sameuQ [u, v ] returns True only if those conditions are met. It also returns True if both u-layer inputs represent NaN, since we will have occasions where we need to test if a calculation has lost all validity. That is the only comparison involving NaN that can return a True result; sameuQ tests for “identical,” numeric or not. The “≡” symbol is another way to write sameuQ [u, v] in the prototype: u ≡ v.

However, there is another level of equality that is typically the more useful one in calculations, and it may take some getting used to. It is the level we have to use in the u-layer as opposed to the scratchpad g-layer. Instead of thinking of “ne” as an abbreviation for “not equal,” think of it as “nowhere equal”: Two unums or ubounds are “nowhere equal” if one is strictly greater than or strictly less than another, by the rules in the previous section: disjoint ranges of numbers. The prototype comparison function nequQ [u, v ] returns True if u ≺ v or u ≻ v, and False for all other cases (including when either input is a NaN). There is actually an obscure math symbol for “less than or greater than”: ≶, but we will generally write out nequQ here, for “not equal u-layer Question,” or use this infix symbol: “≉”. Its version in the g-layer is neqgQ. However, nequQ is not the logical opposite of the equality test, sameuQ.

When the general intervals represented by the inputs overlap, we say they are not nowhere equal, which almost sounds like something a hillbilly would say. “Them ain’t nowhere equal!” Here is a test of two ubounds that do not overlap:

But here is one where they do overlap, which means equality cannot be ruled out for all points in the two ranges. The “nowhere equal” test correctly returns False:

While “equal” means identical endpoints and identical open-closed qualities, “not nowhere equal” means the two intervals have some overlap and could represent the same result. If we use “not nowhere equal” where floats would use “equal” or “within some epsilon of each other,” we can preserve mathematical rigor within the accuracy concessions of the u-layer. The prototype test for not nowhere equal in the u-layer is nnequQ [u, v ], and the test is so useful that we also define the operator “≈” to represent it. Do not confuse “≈” (as it is used here) with “approximately equal,” which that symbol is sometimes used to mean.

A more explicit symbol is “≸”, meaning “not less than and not greater than,” but “ ≸” looks too different from an equals sign “=” or the common “==” equality test used in programming languages. Philosophically, “≈” means equal within the expressiveness of the current u-layer computing environment. If comparing unums or ubounds, u ≈ v means the same test as nnequQ [u, v]]; True if u overlaps v, and False if they are disjoint ranges.

Here are a couple of examples of using “≈” to test if u-layer values have elements in common. An exact number is distinct from the ULP-wide range adjacent to it:

For the example where there was overlap between the ubounds, the “≈” test returns True.

The code for all comparison tests mentioned so far is in Appendix C.8.

Algorithms that use floats often need to test when an answer has converged. Writing the stopping condition for an iterative method that uses floats is risky business. For procedures that look like “x_new = f (x_old) until (stop condition),” if you use “when the iteration is no longer changing” for the stop condition, that is, when x_new = x_old, you can still be quite far from the correct answer because the calculation is caught on the zigzag stair step of reals, rounded to floats. That is, the iteration cannot change the answer by more than an ULP, so it keeps rounding it back to where it was.

If the goal is to find solutions to F (x) = y iteratively and you compute the residual as the absolute value of F(x) - y, then an obvious condition for stopping is “when the residual is zero.” But the residual might never get to zero, again because of rounding error. That’s when programmers set an “epsilon” of error tolerance, like “Stop when the residual is less than 0.001.” But, why 0.001? What is the right number to use for epsilon? And should it be an absolute error, or a relative error?

With unums, expressing a stopping condition is far less prone to such errors and difficult choices. An iteration can stop when the ubound residual is “not nowhere equal” to zero, that is, includes zero. You also cannot get “stuck on a stair step” without seeing that the ubound is wide, indicating that more environment precision is needed to tighten the bound. Unum arithmetic automatically promotes precision up to the maximum set by fsizesize, so the algorithm can start with very storage-efficient approximate guesses, and the computer will escalate its efforts as needed. Later we will show ways the computer can adjust its own fsizesize automatically.

The not nowhere equal test says that two general intervals or ubounds intersect. Sometimes we want to know exactly what the intersection is, because that can be used to tighten a bound. If there are different ways to compute something, and we get different ubound answers, then the correct answer lies in their intersection. That can be used to improve the accuracy of the answer; the refined answer is that intersection. If the intersection is empty, that mathematically proves the two methods are not computing the same thing, which can be used to detect program bugs. Or flaws in the mathematical or physical theories. Or a reliability problem in the computing hardware, like a cosmic ray disrupting a memory bit.

This intersection refinement property is partly true for traditional interval arithmetic as well, but traditional intervals cannot detect, say, that 1.0 is disjoint from (1, 1.125). The example of pressing a calculator square root button repeatedly until the answer erroneously “equals” 1 can still happen with interval arithmetic, but not with unums. If you write a program to “Replace u with u until u ≈ ,” it will run forever, which is the correct thing to do since the operation can never produce an exact 1. It gets to (1, 1 + ULP) using the smallest possible ULP, and stays there.

8.2.2 Hardware approach for equal and “not nowhere equal”

Different unum strings can represent the same value, but the gbound form is unique. To test if u-layer items represent identical values, the efficient approach is to see if both represent NaN, and if not, translate to the g-layer and compare bit-for-bit. The comparison can stop the instant a difference is found. If execution speed is favored over power efficiency, then all the bits can be checked in parallel and the results reduced with a fan-in tree to a single bit. If power efficiency is favored, then the best approach is to check, sequentially, the bits in the gbound in the same order as for the “less-than” and “greater-than” operations: Negative? Infinite? Different extended precision length? Different precision bits? Different open-closed bits? Only in the case where values are identical for every bit will the maximum time and energy be expended. Any difference that is detected along the way can save the effort of any remaining work. Those are the two extremes in the design, and many compromises are possible at the discretion of the hardware engineer, based on the application.