The computational cost of finding the largest value in an unsorted list is O(n). Any deterministic algorithm will require O(n) effort to determine the maximum value. However, in scenarios where time is essence, and n is very large, approximation algorithms are used, which, instead of finding the actual solution, determine the solution that is closer to the actual solution. Randomized algorithms can be classified into the following based on their goals:

The cost of randomized algorithms is based on expected bounds and high probability bounds. Expected bounds consists of the average outcomes captured using all random choices, whereas high probability bounds provide information on the upper bound of correctness, usually represented in terms of sampling size. Let's consider an example of finding the largest values from an n size array. The probabilistic algorithms could be very effective in a scenario where n is very large. The approach involves randomly picking an m element from the n size array, and deciding the max value, as demonstrated in Figure 9.8:

Figure 9.8: Randomized algorithm for max value evaluation

As we keep increasing m, the probability that we will get the max value keeps increasing. For large n, if we use m ≈ log₂(n), then the results are pretty good. Let's evaluate the performance of m ≈ log₂(n) using simulation. For example, with n=1,000,000, the number of random sampling done is 20. Splitting the whole data into ventiles (20 blocks), the probability of having a 5% error is , which is equal to is 0.64, and the solution will be in the first two quantiles representing a 10% error, that is 0.87. Let's conduct a simulation to get an error distribution using Monte Carlo simulation for n=10,000,000 and m selected as 24 with 10,000 iterations. The error distribution is shown in Figure 9.9:

Figure 9.9: Error distribution with log m randomized sampling

A similar approach can be applied to other problem statements, such as picking a number from the upper half of n numbers. The probability of a number being in the upper half, when the greater of two number (n₁ and n₂) is picked, will be 3/4 as there are four situations:

The accuracy can be further improved by increasing sampling, with the probability of getting the right solution being represented as , where k is the sample picked from n.

Skip lists are probabilistic data structures developed in 1990 by Bill Pugh. It was developed to address search limitations in link lists and arrays. Skip lists provide an alternative to binary search trees (BST) and similar tree-based data structures, which tend to get unbalanced. The 2-3 tree discussed in Chapter 8, Graphs, guarantees balancing with insertion and deletion; however, it is complicated to implement. Skip lists are easier to implement than a tree-based data structure. However, they do not guarantee optimal performance, as they use randomization in arranging entries so that the search and update time is O(log n) on average, where n is the number of entries in the dictionary. The average time in a skip list is independent of the distribution of keys and input. Instead, it only depends on the randomization seed selected during operations such as insertion. It is a good example of a compromise between implementation complexity and algorithm performance.

A skip list can be considered as an extension of the sorted link list. A sorted link list can be defined as a linked list in which nodes are arranged in sorted order. An example of a sorted linked list is shown in Figure 9.10:

Figure 9.10: An example of a sorted link list

Any insertion or search operation in a sorted link list will require scanning the list with O(n) computational effort in an average case. The skip list is an extension that allows skipping nodes of a sorted link list. An example of a skip list is shown in Figure 9.11:

Figure 9.11: An example of a first order skip list

Figure 9.10 shows an example of a first order skip list, where there are two links: S₀, which connects each node, and S₁, connecting each alternate node of the sorted link list. The node of the skip list can be represented as shown in the following R script:

skListNode<-function(val, height=1){ 
  # function to create empty environment 
  create_emptyenv = function() { 
    emptyenv() 
  } 
  # Create skiplist node 
  skiplist <- new.env(parent=create_emptyenv()) 
  skiplist$element <- val 
  skiplist$nextnode<-rep(list(NULL), height) 
  class(skiplist) <- "skiplist" 
  skiplist 
}

The nextnode in the skipListNode node function can be of variable length depending on the order of the skip list. A skip list can be of n^th order; an example of a second order skip list is shown in Figure 9.11:

Figure 9.11: An example of a second order skip list

The higher order allows a larger jump in the skip list, which, in turn, helps to reduce the execution time of operations such as searching, insertion, and deletion. An example of a search operation for value 101 within a skip list is shown in Figure 9.12:

Figure 9.12: An example of search in a skip list

The dotted line in the graph shows the path that will be followed while searching for the value 101 in the skip list.

The script for searching a value in a skip list is shown next:

# Function to find a value in skip list 
findvalue<-function(skiplist, searchkey){ 
  for (i in level:1){ 
    skiplist<-skiplist$nextnode[[i]] # head values 
    while(!is.null(node) && node$element>searchkey){ 
      skiplist<-skiplist$nextnode[[i]] 
    } 
    skiplist = skiplist$nextnode[0] 
    if(!is.null(skiplist) && searchkey==skiplist$element){ 
      return(skiplist$element) # Return element 
    } else 
    { 
      return(NULL) # Element not found 
    } 
  } 
}

The skip list is stored as an array of environment in nextnode. The search operation starts with the highest level s₂ in case of example shown in Figure 9.12. The while loop keeps moving from the head to 31 and then to 117 before exiting the while loop. The search operation then switches to the s₁ level, and the search moves from 31 -> 99 -> 117. At 117, the nodes again exit the while loop, the pointer is set at node 99, and height is adjusted to s₀. The node goes to 117 before exiting and comparing with searchkey to stop at 101.

The preceding examples of skip lists fall into ideal skip lists where the s₀ layer connects n nodes, s₁ connects 1/2 nodes, and the layer s_k connects  nodes. The distances are equally spaced and they are called a perfectly balanced skip list. However, maintaining this balance is an expensive process, especially during insertion and deletion operations, as all connections need to be updated accordingly to ensure a balanced skip list. To address the issue, a randomized skip list is created, which assigns a random level to the node.

Let S represent a randomized skip list with height h for a dataset D consisting of the series {s₀, s₁, ..., s_h}. List s_i maps to the subset of entries of D in a sorted order, starting at the head and ending at the tail of D. Also, S should satisfy following properties:

An example of a randomized skip list is shown in Figure 9.13:

Figure 9.13: An example of a randomized skip list

The search algorithm holds for randomized skip lists. The operation for the Insertion of a node also uses randomization to decide the height of the new node. The search operation can be used to determine the place where the node is to be inserted. The search strategy is similar to the findvalue function to determine the insertion position. The connections are updated based on backward and forward scanning for randomized height. An example of the insertion operation is shown in Figure 9.14:

Figure 9.14: An insertion example of a node with value 30 in a randomized skip list with height 2. The dashed lines shows a new connection inserted into an already existing skip list

The randomized height is adjusted to a maximum value to ensure that any random value is not picked. The approach of having a fixed height to make it as a function of n such as h = max(l0, 2logn) or any other distribution constrained at maximum value. The deletion algorithm follows a structure similar to insertion, and is quite simple to implement, as the value will be removed and the incoming input is linked to the outgoing node.

An example of deletion is shown in Figure 9.15:

Figure 9.15: An example of the deletion of node 19 in a randomized skip list. The dashed line in the figure shows the connection removed and curved lines are extended to the closest node

Skip lists are very simple to implement. However, skip lists may not be the best data structure in a scenario where insertion is not prevented from going above the specified maximum height, as it will lead to an infinite loop. Let's consider a scenario of a skip list with height h, and n entries. Then, the worst case scenario for insertion, deletion, and search operations is O(n+h). The worst case scenario for a skip list is quite inferior to other implementations discussed in this book. However, this is highly overestimated, because operations are randomized. Thus, the analysis requires probability to get a better estimate for the computational effort required for insertion, deletion, and search operations.

The probability that an entry can be reached at height k is  where k>1. In case of n entries probability P_k of an entry reaching k height is   . The probability that the height h of the skip list is greater than k is equal to the probability that the k^th level has at least one position that is no greater than P_k, that is, h is larger than 3logn with the probability given as follows:

The preceding equation can be generalized for any constant c as follows:

For a skip list with 10,000 entries, the probability would be one in 100 million. Thus, with very high probability, the height of skiplist is O(log n). Similarly, as time spent in scanning any height in a skip list is O(1), and a skip list would have O(log n) levels, which is high probability, the search is expected to take O(log n) computational effort.

As we have shown, the expected number of entries at position k is  , which can be used to evaluate the space required for a skip list with n entries:

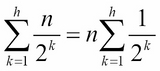
The preceding equation can be reduced using geometric summation as follows:

Thus, the expected space requirement is O(n).