Consider a vector V of numeric elements which needs to be sorted in ascending order. The most intuitive way is to iterate through the vector of elements and then perform element insertions at relevant positions within the vector, satisfying the ordering criterion. This kind of ordering based on a series of insertions is termed insertion sorting. The following Figure 5.1 illustrates the approach for insertion sorting in which each row represents the modified vector for the corresponding ith iteration. The sorting operation is indicated by the arrows:

Figure 5.1: Illustration of insertion sort

The following is the code in R which performs insertion sorting to arrange a vector in increasing order:

Insertion_Sort <- function(V,n) 
{ 
  if(n==0) stop("No elements to sort") 
  for(i in 2:(length(V))) 
  { 
    val <- V[i] 
    j <- i - 1 
    while (j >= 1 && val <= V[j]) 
    { 
      V[j+1] <- V[j] 
      j <- j-1 
    } 
    V[j+1] <- val 
  } 
  return(V) 
}

Let's analyze the code for best-, worst-, and average-case scenarios using the metric as the number of comparisons (val < V[j]).

Worst-case: Assume a vector of n elements in decreasing order. The number of comparisons using the first for loop is one, second for loop is two, and so on till n-1. Thus, the total number of comparisons for the complete execution of sorting is given as follows:

Best-case: Assume a vector of n elements already sorted. The number of comparisons for each of the ­n-1 for loops is one, as the while condition fails for each iteration. Thus, the total number of comparisons for complete execution of sorting is given as:

Average-case: Assume a vector of n elements in any order. For the sake of simplicity, consider the first half of the elements to be sorted, and the remaining as unsorted. Then, the first half would require only  comparisons, while the second half would require  comparisons. Thus, the functional form of system runtime for an average-case scenario is θ(n²). So, the average-case scenario is similar to the worst-case scenario asymptotically.

Similar to the number of comparisons, the number of swaps (V[j+1] <- V[j]) within the while loop is also a measure of an algorithm's performance in assessing its computation runtime. The while conditional loop comprises both comparisons and swaps, wherein the number of swaps is one less than the number of comparisons, as the while loop condition fails for every last iteration of comparison. Thus, the total number of swaps is n-1 less than the total number of comparisons for the complete execution of sorting. Thereby, the functional form of system runtime remains the same for both worst-and average-case scenarios (θ(n²)), whereas it becomes 0 for the best-case scenario.

Unlike insertion sort, bubble sort is non-intuitive, tougher to comprehend, and has poor performance even for the best-case scenario. In every iteration, each element within the vector is compared with the rest of the elements, and the smaller (or larger) element amongst all is pushed toward the first (or last) position, just as a water bubble pops out on the water surface; hence, the algorithm is named as bubble sort. It is a step-by-step approach of comparing adjacent elements and swapping key values.

The following is the R code which performs bubble sorting. The code is implemented in an adaptive format, and performs iterations differently. This is explained in detail below the code along with an illustration (Figure 5.2):

Bubble_Sort <- function(V,n) { 
  if(n==0) stop("No elements to sort") 
  for(i in 1:length(V)) { 
    flag <- 0 
    for(j in 1:(length(V)-i)) { 
      if ( V[j] > V[j+1] ) { 
        val <- V[j] 
        V[j] <- V[j+1] 
        V[j+1] <- val 
        flag <- 1 
      }  
    } 
    if(!flag) break 
  } 
  return(V) 
}

As seen in the preceding code, bubble sort comprises two for loops along with a flag condition to keep a check on the swapping condition to avoid any redundant iterations. The inner for loop is meant to check all adjacent element comparisons and undergo the required swapping operations. If the lower-indexed key value is greater than its higher-indexed key value, then the elements within the vector are swapped. Therefore, the highest key value element is pushed toward the end, and the subsequent lower key value elements are pushed toward the start. As the highest value is pushed right-most, the second iteration of the inner for loop does not consider the last key value for comparison with the second-last key value:

Figure: 5.2: Illustration of bubble sort

Subsequently, iterations are performed using the outer for loop, barring each key value one less than the preceding iteration. The flag condition helps in avoiding redundant loops once the vector is intermediately sorted, as can be seen in the preceding illustrated example.

Let's analyze the code for best, worst, and average-case scenarios for a number of comparisons (V[j] > V[j+1]) without considering the flag condition. Then we can observe that for any order of input vector V, the number of comparisons using both the for loops increases with a factor of 1 for each iteration. Therefore, the asymptote of system runtime using a number of comparisons as an evaluation metric for all the three cases is θ(n²).

Similar to the number of comparisons, the number of swaps can also be considered as an evaluation metric of an algorithm's system runtime. The number of element swaps in a bubble sort depends on the adjacent values within the vector. Assuming half the number of elements to be unsorted for an average-case scenario, the asymptote would be θ(n²), estimated using the number of required swaps.

Again, consider a numeric vector which is to be sorted in ascending order. Another intuitive approach for sorting the vector is to first select the smallest element and place it in the first position, then select the second smallest and place it in the second position, and so on. This kind of select and sort approach is termed selection sort. Selection sort follows an iii principle, that is, in the i^th iteration, select the i^th order element from the vector, and place it in the i^th position. This approach boils down to a unique feature wherein in the number of swaps required in each iteration is only one unlike what was observed in bubble sort. In other words, for a vector of length n, only n-1 swaps are required for a complete execution of sorting; however, the number of comparisons are similar to the bubble sort algorithm. In selection sort, the position of the smallest element is first remembered, and then swapped accordingly. Figure 5.3 further illustrates the selection sort for a numeric vector:

Figure 5.3: Illustration of selection sort

The following R code performs selection sorting. This current raw code is implemented using the for loop:

Selection_Sort_loop <- function(V,n) { 
  if(n==0) stop("No elements to sort") 
  keys <- seq_along(V) 
  for(i in keys) { 
    small_pos <- (i - 1) + which.min(V[i:length(V)]) 
    temp <- V[i] 
    V[i] <- V[small_pos] 
    V[small_pos] <-temp 
  } 
  return(V) 
}

As the number of comparisons is similar to the bubble sort, the function form of system runtime is θ(n²) for all three cases. However, we have seen till now that the swapping operations are much lower. This is advantageous in scenarios where the cost of swaps is higher than the cost of comparisons, such as vectors with large elements or long strings.

Also, selection sort performs very well in vectors with a large number of elements. This is because the swap operations exchange only the position keys (or pointers) instead of position key values (or elements). Thus, additional space is required to store the position keys (or pointers); however, the return of swapping is much faster. The following illustration shows an example of swapping position keys. Consider a numeric vector with four elements. Fig (a) in Figure 5.4 shows the pre-swapped position keys (pointers) along with values, and Fig (b) in Figure 5.4 shows the post-swapped position keys (pointers) along with values:

Figure 5.4: Example of swapping pointers toward key values

Nevertheless, there is a caveat in the implementation of selection sort. The swapping operation is performed even when the position and order of an element is the same. That is to say, even if the i^th order element is present at the i^th position, the swapping operation will continue. This can be avoided using a test condition. However, in general, the cost incurred due to the test condition is higher than the cost saved by avoiding swaps. Thus, the functional form of the system runtime based on the number of swaps is θ(n) for all three cases.

Insertion sort, bubble sort, and selection sort are three typical sorting algorithms which are costly to execute for large size vectors and a large number of recurrent vectors. The reasons pertaining to their higher cost of execution are as follows:

The swapping of adjacent elements is called an exchange; hence, these three algorithms are also called exchange sorts. The cost of execution of these exchange sorts is the total number of cell-to-cell movements (also known as number of inversions) by each element before forming into a right-order vector.

Consider a vector of length n. Then, the total number of exchanges or inversions possible is equal to the total number of available pairs, that is, 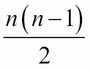. On average, the total number of inversions possible is equivalent to  per vector. Thus, we can comment with certainty that any sorting algorithm performing adjacent pair comparisons (and swaps) will have an associated cost of at least  ~ Ω(n²) for the average-case scenario.

The following Table 5.1 summarizes the system runtime asymptotes for all the three case scenarios (best, worst, and average) using the number of comparisons and number of swaps for insertion sort, bubble sort, and selection sort algorithms. The system runtime of insertion sort and bubble sort is θ(n²) across both average and worst-case scenarios:

Table 5.1: Comparison of asymptotic complexities using different evaluation metrics

Let's continue with other sorting algorithms, which show considerably better performance as compared to the three exchange-sort algorithms.