6.1 Introduction

Let be a random sample from an underlying cumulative distribution function (CDF) . If we assume that is known, we can easily estimate the sampling distribution of any estimator of an unknown parameter through the use of a Monte Carlo simulation, described in the following algorithm:

1. S1.  For ,
   1. S1.1  generate random samples ,
   2. S1.2  and compute .
2. S2.  On the basis of the output , after the 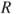iterations in Step S1, use such a sample to estimate the sampling distribution of , through either the associated empirical distribution function or any kernel estimate, among others.

If goes to infinity, something not achievable in practice, we should then get a perfect match to the theoretical calculation, if available, that is, the Monte Carlo error should disappear. But is usually unknown. How to proceed? The use of the bootstrap methodology is a possible way.

Bootstrapping (Efron, 1979) is essentially a computer-based and computer-intensive method for assigning measures of accuracy to sample estimates (see Efron and Tibshirani, 1994; Davison and Hinkley, 1997, among others). Concomitantly, this technique also allows estimation of the sampling distribution of almost any statistic using only very simple resampling methods, based on the observed value of the empirical distribution function, given by

6.1

We can replace in the previously sketched algorithm by , the empirical distribution function associated with the original observed data, , which puts mass on each of the , generating with replacement , in Step S1.1 of the algorithm in the preceding text, computing , , in Step S1.2, and using next such a sample in Step S2.

The main goal of this chapter is to enhance the role of the bootstrap methodology in the field of statistics of univariate extremes, where the bootstrap has been commonly used in the choice of the number of top order statistics or of the optimal sample fraction, , to be taken in the semiparametric estimation of a parameter of extreme events. For an asymptotically consistent choice of the threshold to use in the adaptive estimation of a positive extreme value index (EVI), , the primary parameter in statistics of extremes, we suggest and discuss a double-bootstrap algorithm. In such algorithm, apart from the classical Hill (1975) and peaks over random threshold (PORT)-Hill EVI estimators (Araújo Santos et al., 2006), we consider a class of minimum-variance reduced-bias (MVRB), the simplest one in Caeiroet al. (2005), and associated PORT-MVRB (Gomes et al., 2011a, 2013) EVI estimators. Other bootstrap methods for the choice of can be found in Hall (1990), Longin (1995), Caers et al. (1999), Draisma et al. (1999), Danielsson et al. (2001), and Gomes and Oliveira (2001), among others. For a recent comparison between the simple-bootstrap and the double-bootstrap methodology, see Caeiro and Gomes (2014b), where an improved version of Hall's bootstrap methodology was introduced.

After providing, in Section 6.2, a few technical details in the area of extreme value theory (EVT), related to the EVI estimators under consideration in this chapter, we shall briefly discuss, in Section 6.3, the main ideas behind the bootstrap methodology and optimal sample fraction estimation. In the lines of Gomes et al. (2011b–2012, 2015a), we propose an algorithm for the adaptive consistent estimation of a positive EVI, through the use of resampling computer-intensive methods. The Algorithm is described for the Hill EVI estimator and associated PORT-Hill, MVRB, and PORT-MVRB EVI estimators, but it can work similarly for the estimation of other parameters of extreme events, like a high quantile, the probability of exceedance, or the return period of a high level. The associated code in R language for the adaptive EVI estimation is available upon request. Section 6.4 is entirely dedicated to the application of the Algorithm to three simulated samples. Finally, in Section 6.5, we draw some overall conclusions.

6.2 A Few Details on EVT

The key results obtained by Fisher and Tippett (1928) on the possible limiting laws of the sample maxima, formalized by Gnedenko (1943), and used by Gumbel (1958) for applications of EVT in engineering subjects are some of the key tools that led to the way statistical EVT has been exploding in the last decades. In this chapter, we focus on the behavior of extreme values of a data set, dealing with maximum values and other top order statistics in a univariate framework, working thus in the field of statistics of extremes.

Let us assume that we have access to a random sample of independent, identically distributed, or possibly stationary and weakly dependent random variables from an underlying model , and let us denote by the sample of associated ascending order statistics. As usual, let us further assume that it is possible to linearly normalize the sequence of maximum values, , so that we get a nondegenerate limit. Then (Gnedenko, 1943), that limiting random variable has a CDF of the type of the extreme value distribution, given by

6.2

and is the so-called EVI, the primary parameter in statistics of extremes. We then say that is in the max-domain of attraction of , in (6.2), and use the notation . The EVI measures essentially the weight of the right tail function, . If , the right tail is short and light, since has compulsory a finite right end point, that is, is finite. If , the right tail is heavy and of a negative polynomial type, and has an infinite right end point. A positive EVI is also often called tail index. If , the right tail is of an exponential type, and the right end point can then be either finite or infinite.

Slightly more restrictively than the full max-domain of attraction of the extreme value distribution, we now consider a positive EVI, that is, we work with heavy-tailed models in . Heavy-tailed models appear often in practice in fields like bibliometrics, biostatistics, finance, insurance, and telecommunications. Power laws, such as the Pareto distribution and Zipf's law, have been observed a few decades ago in some important phenomena in economics and biology and have seriously attracted scientists in recent years. As usual, we shall further use the notations for the generalized inverse function of and for the class of regularly varying functions at infinity with an index of regular variation , that is, positive Borel measurable functions such that , as , for all (see Bingham et al., 1987, for details on regular variation). Let us further use the notation for the tail quantile function. For heavy-tailed models we have the validity of the following first-order conditions:

6.3

The first necessary and sufficient condition in the preceding text, related to the right tail function behavior, was proved by Gnedenko (1943), and the second one, related to the tail quantile function behavior, was proved by de Haan (1984).

For these heavy-tailed models, and given a sample , the classical EVI estimators are Hill estimators (Hill, 1975), with the functional expression

6.4

They are thus the average of the log-excesses, , above the random level or threshold . To have consistency of Hill EVI estimators, we need to have , and such a random threshold needs further to be an intermediate order statistic, that is, we need to have

6.5

if we want to have consistent EVI estimation in the whole . Indeed, under any of the first-order frameworks in (6.3), the log-excesses, , are approximately the order statistics of an exponential sample of size , with mean value , hence the reason for the EVI estimators in (6.4).

Under adequate second-order conditions that rule the rate of convergence in any of the first-order conditions in (6.3), Hill estimators, , have usually a high asymptotic bias, and recently, several authors have considered different ways of reducing bias (see the overviews in Gomes et al., 2007b, Chapter 6 of Reiss and Thomas, 2007; Gomes et al., 2008a; Beirlant et al., 2012; Gomes and Guillou, 2015). A simple class of MVRB EVI estimators is the class studied in Caeiro et al. (2005), to be introduced in Section 6.2.2. These MVRB EVI estimators depend on the adequate estimation of second-order parameters, and the kind of second-order parameter estimation that enables the building of MVRB EVI estimators, that is, EVI estimators that outperform the Hill estimator for all , is sketched in Sections 6.2.1 and 6.2.2.

Both Hill and MVRB EVI estimators are invariant to changes in scale but not invariant to changes in location. And particularly the Hill EVI estimators can suffer drastic changes when we induce an arbitrary shift in the data, as can be seen in Figure 6.1.

Indeed, even if a Hill plot (a function of vs ) looks stable, as happens in Figure 6.1, with the sample path, where data, , , come from a unit standard Pareto CDF, , for ), we easily come to the so-called Hill horror plots, a terminology used in Resnick (1997), when we induce a shift to the data. This can be seen also in Figure 6.1 (look now at ), where we present the Hill plot associated with the shifted sample , from the CDF , now for . This led Araújo Santos et al. (2006) to introduce the so-called PORT methodology, to be sketched in Section 6.2.3. The asymptotic behavior of the EVI estimators under consideration is discussed in Section 6.2.4.

6.2.1 Second-Order Reduced-Bias EVI Estimation

For consistent semiparametric EVI estimation, in the whole , we have already noticed that we merely need to work with adequate functionals, dependent on an intermediate tuning or control parameter , the number of top order statistics involved in the estimation, that is, (6.5) should hold. To obtain full information on the nondegenerate asymptotic behavior of semiparametric EVI estimators, we often need to further assume a second-order condition, ruling the rate of convergence in any of the first-order conditions, in (6.3). It is often assumed that there exists a function , such that

6.6

Then, we have . Moreover, if the limit in the left-hand side of (6.6) exists, we can choose so that such a limit is compulsory equal to the previously defined function (Geluk and de Haan, 1987).

Whenever dealing with reduced-bias estimators of parameters of extreme events, and essentially due to technical reasons, it is common to slightly restrict the domain of attraction, , and to consider a Pareto-type class of models, assuming that, with , , , and as ,

6.7

The class in (6.7) is however a wide class of models that contains most of the heavy-tailed parents useful in applications, like the Fréchet, the generalized Pareto, and the Student-, with degrees of freedom. For Fréchet parents, we get and in (6.7). For a generalized Pareto distribution, , with given in (6.2), we get and . For Student- parents, we get and . For further details and an explicit expression of as a function of , see Caeiro and Gomes (2008), among others. Note that the validity of (6.6) with is equivalent to (6.7). To obtain information on the bias of MVRB EVI estimators, it is even common to slightly restrict the class of models in (6.7), further assuming the following third-order condition:

6.8

as , with . All the aforementioned models still belong to this class. Slightly more generally, we could have assumed a general third-order condition, ruling now the rate of convergence in the second-order condition in (6.6), which guarantees that, for all ,

6.9

where must then be in . Equation (6.8) is equivalent to equation (6.9) with . Further details on the topic can be found in de Haan and Ferreira (2006).

Provided that (6.5) and (6.6) hold, Hill EVI estimators, , have usually a high asymptotic bias. The adequate accommodation of this bias has recently been extensively addressed. Among the pioneering papers, we mention Peng (1998), Beirlant et al. (1999), Feuerverger and Hall (1999), and Gomes et al. (2000). In these papers, authors are led to reduced-bias EVI estimators, with asymptotic variances larger than or equal to , where is the aforementioned “shape” second-order parameter in (6.6). Recently, as sketched in Section 6.2.2, Caeiro et al. (2005) and Gomes et al. (2007a, 2008c) have been able to reduce the bias without increasing the asymptotic variance, kept at , just as happens with the Hill EVI estimator.

6.2.2 MVRB EVI Estimation

To reduce bias, keeping the asymptotic variance at the same level, we merely need to use an adequate “external” and a bit more than consistent estimation of the pair of second-order parameters, , in (6.7). The MVRB EVI estimators outperform the classical Hill EVI estimators for all , and among them, we now consider the simplest class by Caeiro et al. (2005), used for value-at-risk (VaR) estimation by Gomes and Pestana (2007b). Such a class, denoted by , has the functional form

6.10

where is an adequate consistent estimator of , with and based on a number of top order statistics usually of a higher order than the number of top order statistics used in the EVI estimation, as explained in Sections 6.2.1 and 6.2.2. For different algorithms for the estimation of , see Gomes and Pestana (2007a,b).

6.2.2.1 Estimation of the “shape” Second-order Parameter

We consider the most commonly used -estimators, the ones studied by Fraga Alves et al. (2003), briefly introduced in the sequel. Given the sample , the -estimators by Fraga Alves et al. (2003) are dependent on the statistics

6.11

defined for any tuning parameter and where

Under mild restrictions on , that is, if (6.5) holds and , with the function in (6.7), the statistics in (6.11) converge toward , independently of the tuning parameter , and we can consequently consider the class of admissible -estimators:

6.12

Under adequate general conditions, and for an appropriate tuning parameter , the -estimators in (6.12) show highly stable sample paths as functions of , the number of top order statistics used, for a range of large -values. Again, it is sensible to advise practitioners not to choose blindly the value of in (6.12). Sample paths of , as functions of , for a few values of , should be drawn, in order to elect the value of , which provides higher stability for large , by means of any stability criterion. For the most common stability criterion, see Gomes and Pestana (2007b) and Remark 6.6. The value , considered in the description of the Algorithm in Section 6.3.2, has revealed to be the most adequate choice whenever we are in the region , a common region in applications, and the region where bias reduction is indeed needed. Distributional properties of the estimators in (6.12) can be found in Fraga Alves et al. (2003). Interesting alternative classes of -estimators have recently been introduced by Goegebeur et al. (2008, 2010), Ciuperca and Mercadier (2010), and Caeiro and Gomes (2014a, 2015).

6.2.2.2 Estimation of the “scale” Second-order Parameter

For the estimation of the scale second-order parameter , on the basis of

we shall consider the estimator in Gomes and Martins (2002):

6.13

dependent on an adequate -estimator, . It has been advised the computation of these second-order parameter estimators at a -value given by

6.14

The estimator , to be plugged in (6.13), is thus , with and given in (6.12) and (6.14), respectively.

Details on the distributional behavior of the estimator in (6.13) can be found in Gomes and Martins (2002) and more recently in Gomes et al. (2008c) and Caeiro et al. (2009). Again, consistency is achieved for models in (6.7) and -values such that (6.5) holds and , as . Alternative estimators of can be found in Caeiro and Gomes (2006) and Gomes et al. (2010). Due to the fact that and , with , , and given in (6.12)–(6.14), respectively, depending on , we often use the notation . But when we work with only, as happens in Section 6.3.2, we shall not use the subscript . Note however that the Algorithm in Section 3.2 can also be used for another fixed choice of , as well as for a data-driven choice of provided by any of the algorithms in Gomes and Pestana (2007a,b), among others.

6.2.3 PORT EVI Estimation

The estimators in (6.4) and (6.10) are scale invariant but not location invariant. In order to achieve location invariance for a class of modified Hill EVI estimators and adequate properties for VaR estimators, Araújo Santos et al. (2006) introduced the so-called PORT methodology. The estimators are then functionals of a sample of excesses over a random level , , that is, functionals of the sample

6.15

Generally, we can have , for any (the random level is an empirical quantile). If the underlying model has a finite left end point, , we can also use (the random level can then be the minimum).

If we think, for instance, on Hill EVI estimators, in (6.4), the new classes of PORT-Hill EVI estimators, theoretically studied in Araújo Santos et al. (2006), and for finite samples in Gomes et al. (2008b), are given by

6.16

Similarly, if we think on the MVRB EVI estimators, in (6.10), the new classes of PORT-MVRB EVI estimators, studied for finite samples in Gomes et al. (2011a, 2013), are given by

6.17

with in (6.16), and any adequate estimator of , the vector of second-order parameters associated with the shifted model, based on the sample , in (6.15).

These PORT EVI estimators are thus dependent on a tuning parameter , 0⩽q<1, that makes them highly flexible. Moreover, they are invariant to changes in both location and scale. Just as in Gomes et al. (2013, 2015a), we shall further include in the algorithm the value , so that with , , , and , given in (6.4), (6.10), (6.16), and (6.17), respectively, we can consider that and for (with the notations , , so that , , ).

Further applications of the PORT methodology can be found in Henriques-Rodrigues et al. (2014, 2015), Caeiro et al. (2016) and Gomes et al. (2016), among others.

6.2.4 Asymptotic Properties of the EVI Estimators

The Hill estimator reveals usually a high asymptotic bias. Indeed, from the results of de Haan and Peng (1998), and with denoting a normal random variable with mean value and variance , there exists such that

6.20

where the bias under condition (6.8) can be very large, moderate, or small, going, respectively, to , a nonnull constant, or 0, as . This nonnull asymptotic bias, together with a rate of convergence of the order of , leads to sample paths with a high variance for small , a high bias for large , and a very sharp mean square error (MSE) pattern, as a function of . Under the same conditions as before, is asymptotically normal with variance also equal to but with a null mean value. Indeed, under the validity of the aforementioned third-order condition in (6.8), related to Pareto-type class of models, we can adequately estimate the vector of second-order parameters so that outperforms for all . Indeed, and for an adequate , computed by Caeiro et al. (2009), we can write

6.21

We can further summarize the aforementioned results in the following theorem.

For the asymptotic behavior of the PORT-Hill EVI estimators, we refer to Araújo Santos et al. (2006). The full asymptotic behavior of the PORT-MVRB EVI estimators is still under development. It is known that the rate of convergence and asymptotic variance do not change. There are however big changes in the bias but for adequate -values the PORT-MVRB EVI estimators are indeed MVRB EVI estimators. Contrarily to what has been done by Gomes et al. (2015a), we shall thus consider for them the same double-bootstrap Algorithm we used for the MVRB EVI estimation.

6.3 The Bootstrap Methodology in Statistics of Univariate Extremes

The use of bootstrap resampling methodologies has revealed to be promising in the choice of the nuisance tuning or control parameter or equivalently of the optimal sample fraction, , in the semiparametric estimation of any parameter of extreme events. If we ask how to choose the tuning parameter in the EVI estimation, either through or or or , , generally denoted , we usually consider the estimation of

6.22

To obtain estimates of , one can use the so-called double-bootstrap method based on two related bootstrap samples of size and . Such a method is applied to an adequate auxiliary statistic like

6.23

which tends to the well-known value zero and has an asymptotic behavior similar to the one of (see Gomes and Oliveira, 2001, among others, for the estimation through and Gomes et al., 2012, for the estimation through ). See also Gomes et al. (2015a,b) and Section 6.3.2.

On the basis of (6.20) and (6.21), and with AMSE standing for “asymptotic MSE,” the sum of the asymptotic variance and the squared dominant component of the bias, we get

6.24

with defined in (6.22). See Theorem 1 of Draisma et al. (1999), for a proof of this result, in the case of . The proof is similar for the cases of , as already mentioned by Gomes et al. (2012). Things work more intricately for the PORT-MVRB EVI estimators, and as mentioned in the preceding text, we shall consider an algorithm similar to the one devised for the MVRB EVI estimators in case we are working with , , since we are interested in the possible specific value of that makes these PORT estimators MVRB EVI estimators. The bootstrap methodology enables us to estimate , in (6.22), in a way similar to the one used for the classical EVI estimators, on the basis of a consistent estimator of , in (6.24), and now through the use of an auxiliary statistic like the one in (6.23), a method detailed in Gomes et al. (2011b–2012) for the MVRB EVI estimation. For the sake of simplicity, we shall next describe the methodology for , but similar formulas work for provided that we replace by , . Indeed, under the aforementioned third-order framework in (6.8),

with asymptotically standard normal.

Consequently, denoting , we have

6.25

6.3.1 The Resampling Methodology in Action

How does the resampling methodology then work? Given the sample from an unknown model , and the functional in (6.23), , , consider for any , , the bootstrap sample

from , in (6.1), the empirical distribution function associated with the available random sample, .

Next, associate with the bootstrap sample the corresponding bootstrap auxiliary statistic, , . Then, with ,

Consequently, for another sample size , and for every ,

It is then enough to choose , in order to have independence of . If we consider , that is, , we have

6.26

On the basis of (6.26), we are now able to consistently estimate and next through (6.25), on the basis of any estimate of the second-order parameter . With denoting the sample counterpart of and , an adequate -estimate, we thus have the estimate

6.27

with

The adaptive estimate of is then given by

6.4 Applications to Simulated Data

To enhance the importance of the PORT-Hill and PORT-MVRB EVI estimation in the field of finance, we refer to Gomes and Pestana (2007b) and Gomes et al. (2013), where, respectively, the MVRB and the PORT-MVRB EVI estimation have been applied to log returns associated with a few sets of financial data. Due to the specificity of such real data sets and to the fact that log returns have often been modeled by a Student- or its skewed versions (see Jones and Faddy, 2003, among others), we have simulated a random sample of size , from a Student's model with degrees of freedom ( and ). Due to the specificity of the data (infinite left end point), we have considered for both the PORT-Hill and the PORT-MVRB EVI estimation -values from 0.15 to 1, with step 0.05. When , we elect the Hill or the MVRB EVI estimates. If , the PORT methodology is elected. We have further considered , with from 0.950 to 0.995, with step 0.0025, and .

Figure 6.3 is related to the Student- generated sample, and we there present as an illustration of the obtained results the PORT-Hill/Hill and PORT-MVRB/MVRB EVI estimates (a), the -estimates (b), and the RMSE estimates (c). The notation PORT •/• means that we are playing with both the PORT-• and the • EVI estimators. We have however been led to a PORT estimator, that is, to -estimates smaller than 1.

6.5 Concluding Remarks

• For the previous simulated sample, we know the true value of and the value 0.25, and we can easily assess the reliability of the estimates provided by the Algorithm in Section 6.3.2, immediately coming to the conclusion that, as expected, the PORT-MVRB methodology provides the more reliable EVI estimation.
• It is clear that, similarly to what usually happens with the Hill EVI estimators, even the PORT-Hill EVI estimation leads to an overestimation of the EVI. The adaptive PORT-MVRB are generally closer to the target.
• Moreover, the RMSE estimates associated with the adaptive PORT-MVRB EVI estimates are always below the RMSE estimates associated with the adaptive PORT-Hill, another point in favor of the PORT-MVRB methodology.
• The performed case studies, including the one used here for illustration, claim obviously for a simulation study of the Algorithm and its application to real data sets. These are however topics out of the scope of this chapter.
• As a general conclusion, we advise the use of the PORT-MVRB methodology for the estimation of a heavy right tail function.

Acknowledgments

Research partially supported by national funds through FCT—Fundação para a Ciência e a Tecnologia, projects UID/MAT/UI0006/2013 (CEA/UL) and UID/MAT/0297/2013 (CMA/UNL) and postdoc grants SFRH/BPD/77319/2011 and SFRH/BPD/72184/2010.

References

1. Araújo Santos, P., Fraga Alves, M.I., Gomes, M.I. Peaks over random threshold methodology for tail index and quantile estimation. Revstat 2006;4(3):227–247.
2. Beirlant, J., Dierckx, G., Goegebeur, Y., Matthys, G. Tail index estimation and an exponential regression model. Extremes 1999;2:177–200.
3. Beirlant, J., Caeiro, F., Gomes, M.I. An overview and open research topics in the field of statistics of univariate extremes. Revstat 2012;10(1):1–31.
4. Bingham, N.H., Goldie, C.M., Teugels, J.L. Regular Variation. Cambridge: Cambridge University Press; 1987.
5. Caeiro, F., Gomes, M.I. A new class of estimators of a “scale” second order parameter. Extremes 2006;9:193–211, 2007.
6. Caeiro, F., Gomes, M.I. Minimum-variance reduced-bias tail index and high quantile estimation. Revstat 2008;6(1):1–20.
7. Caeiro, F., Gomes, M.I. A semi-parametric estimator of a shape second order parameter. In: Pacheco, A., Oliveira, M.R., Santos, R., Paulino, C.D., editors. New Advances in Statistical Modeling and Application, Studies in Theoretical and Applied Statistics, Selected Papers of the Statistical Societies. Berlin and Heidelberg: Springer-Verlag; 2014a. 137–144.
8. Caeiro, F., Gomes, M.I. On the bootstrap methodology for the estimation of the tail sample fraction. In: Gilli, M., Gonzalez-Rodriguez, G., Nieto-Reyes, A., editors. Proceedings of COMPSTAT 2014. Genéva, Switzerland; The International Statistical Institute/International Association for Statistical Computing 2014b. 545–552.
9. Caeiro, F., Gomes, M.I. Bias reduction in the estimation of a shape second-order parameter of a heavy tailed model. J. Stat Comput Simul 2015;85(17):3405–3419.
10. Caeiro, F., Gomes, M.I., Henriques-Rodrigues, L. Reduced-bias tail index estimators under a third order framework. Commun Stat Theory Methods 2009;38(7):1019–1040.
11. Caeiro, F., Gomes, M.I., Pestana, D. Direct reduction of bias of the classical Hill estimator. Revstat 2005;3(2):111–136.
12. Caeiro, F., Gomes, M.I., Henriques-Rodrigues, L. A location invariant probability weighted moment EVI estimator. International Journal of Computer Mathematics 2016;93(4):676–695.
13. Caers, J., Beirlant, J., Maes, M.A. Statistics for modeling heavy tailed distributions in geology: Part I. Methodology. Math Geol 1999;31:391–410.
14. Ciuperca, G., Mercadier, C. Semi-parametric estimation for heavy tailed distributions. Extremes 2010;13(1):55–87.
15. Danielsson, J., de Haan, L., Peng, L., de Vries, C.G. Using a bootstrap method to choose the sample fraction in tail index estimation. Journal of Multivariate Analysis 2001;76:226–248.
16. Davison, A., Hinkley, D.V. Bootstrap Methods and their Application. Cambridge: Cambridge University Press; 1997.
17. de Haan, L. Slow variation and characterization of domains of attraction. In: de Oliveira, T., editor. Statistical Extremes and Applications. Dordrecht: D. Reidel; 1984. 31–48.
18. de Haan, L., Ferreira, A. Extreme Value Theory: An Introduction. New York: Springer Science+Business Media, LLC; 2006.
19. de Haan, L., Peng, L. Comparison of tail index estimators. Stat Neerl 1998;52:60–70.
20. Draisma, G., de Haan, L., Peng, L., Pereira, M.T. A bootstrap-based method to achieve optimality in estimating the extreme value index. Extremes 1999;2(4):367–404.
21. Efron, B. Bootstrap methods: another look at the jackknife. Ann Stat 1979;7(1):1–26.
22. Efron, B., Tibshirani, R.J. An Introduction to the Bootstrap. Boca Raton (FL): CRC Press; 1994.
23. Feuerverger, A., Hall, P. Estimating a tail exponent by modelling departure from a Pareto distribution. Ann Stat 1999;27:760–781.
24. Fisher, R.A., Tippett, L.H.C. Limiting forms of the frequency of the largest or smallest member of a sample. Proc Cambridge Philos Soc 1928;24:180–190.
25. Fraga Alves, M.I., Gomes, M.I., de Haan, L. A new class of semi-parametric estimators of the second order parameter. Portugaliae Mathematica 2003;60(2):194–213.
26. Geluk, J., de Haan, L. Regular Variation, Extensions and Tauberian Theorems. Amsterdam, Netherlands: CWI Tract 40, Center for Mathematics and Computer Science; 1987.
27. Gnedenko, B.V. Sur la distribution limite du terme maximum d'une série aléatoire. Ann Math 1943;44:423–453.
28. Goegebeur, Y., Beirlant, J., de Wet, T. Linking Pareto-tail kernel goodness-of-fit statistics with tail index at optimal threshold and second order estimation. Revstat 2008;6(1):51–69.
29. Goegebeur, Y., Beirlant, J., de Wet, T. Kernel estimators for the second order parameter in extreme value statistics. J Stat Plann Inference 2010;140(9):2632–2652.
30. Gomes, M.I., Guillou, A. Extreme value theory and statistics of univariate extremes: a review. Int Stat Rev 2015;83(2):263–292.
31. Gomes, M.I., Martins, M.J. “Asymptotically unbiased” estimators of the tail index based on external estimation of the second order parameter. Extremes 2002;5(1):5–31.
32. Gomes, M.I., Oliveira, O. The bootstrap methodology in Statistical Extremes—choice of the optimal sample fraction. Extremes 2001;4(4):331–358.
33. Gomes, M.I., Pestana, D. A simple second order reduced-bias' tail index estimator. J Stat Comput Simul 2007a;77(6):487–504.
34. Gomes, M.I., Pestana, D. A sturdy reduced-bias extreme quantile (VaR) estimator. J Am Stat Assoc 2007b;102(477):280–292.
35. Gomes, M.I., Martins, M.J., Neves, M.M. Alternatives to a semi-parametric estimator of parameters of rare events—the Jackknife methodology. Extremes 2000;3(3):207–229.
36. Gomes, M.I., Martins, M.J., Neves, M.M. Improving second order reduced-bias tail index estimation. Revstat 2007a;5(2):177–207.
37. Gomes, M.I., Reiss, R.-D., Thomas, M. Reduced-bias estimation. In: Reiss, R.-D., Thomas, M., editors. Statistical Analysis of Extreme Values with Applications to Insurance, Finance, Hydrology and Other Fields. 3rd ed., Chapter 6. Basel, Boston (MA), Berlin: Birkhäuser Verlag; 2007b. p 189–204.
38. Gomes, M.I., Canto e Castro, L., Fraga Alves, M.I., Pestana, D. Statistics of extremes for IID data and breakthroughs in the estimation of the extreme value index: Laurens de Haan leading contributions. Extremes 2008a;11(1):3–34.
39. Gomes, M.I., Fraga Alves, M.I., Araújo Santos, P. PORT hill and moment estimators for heavy-tailed models. Commun Stat Simul Comput 2008b;37:1281–1306.
40. Gomes, M.I., de Haan, L., Henriques-Rodrigues, L. Tail index estimation for heavy-tailed models: accommodation of bias in weighted log-excesses. J R Stat Soc B 2008c;70(1):31–52.
41. Gomes, M.I., Pestana, D., Caeiro, F. A note on the asymptotic variance at optimal levels of a bias-corrected Hill estimator. Stat Probab Lett 2009;79:295–303.
42. Gomes, M.I., Henriques-Rodrigues, L., Pereira, H., Pestana, D. Tail index and second order parameters' semi-parametric estimation based on the log-excesses. J Stat Comput Simul 2010;80(6):653–666.
43. Gomes, M.I., Henriques-Rodrigues, L., Miranda, C. Reduced-bias location-invariant extreme value index estimation: a simulation study. Commun Stat Simul Comput 2011a;40(3):424–447.
44. Gomes, M.I., Mendonça, S., Pestana, D. Adaptive reduced-bias tail index and VaR estimation via the bootstrap methodology. Commun Stat Theory Methods 2011b;40(16):2946–2968.
45. Gomes, M.I., Figueiredo, F., Neves, M.M. Adaptive estimation of heavy right tails: resampling-based methods in action. Extremes 2012;15:463–489.
46. Gomes, M.I., Henriques-Rodrigues, L., Fraga Alves, M.I., Manjunath, B.G. Adaptive PORT-MVRB estimation: an empirical comparison of two heuristic algorithms. J Stat Comput Simul 2013;83(6):1129–1144.
47. Gomes, M.I., Henriques-Rodrigues, L., Figueiredo, F. Resampling-based methodologies in statistics of extremes: environmental and financial applications. In: Bourguignon, J.-P., Jeltsch, R., Adrega Pinto, A., Viana, M., editors. Mathematics of Planet Earth: Energy and Climate, CIM Series in Mathematical Sciences, Chapter 8. Switzerland: Springer-Verlag; 2015a. p 197–215.
48. Gomes, M.I., Figueiredo, F., Martins, M.J., Neves, M.M. Resampling methodologies and reliable tail estimation. S Afr Stat J 2015b;49:1–20.
49. Gomes, M.I., Henriques-Rodrigues, L., Manjunath, B.L. Mean-of-order-p location-invariant extreme value index estimation. Revstat 2016;14(3):273–296.
50. Gumbel, E.J. Statistics of Extremes. New York: Columbia University Press; 1958.
51. Hall, P. Using the bootstrap to estimate mean squared error and select smoothing parameter in nonparametric problems. J Multivariate Anal 1990;32:177–203.
52. Hill, B.M. A simple general approach to inference about the tail of a distribution. Ann Stat 1975;3:1163–1174.
53. Henriques-Rodrigues, L., Gomes, M.I., Fraga Alves, M.I., Neves, C. PORT estimation of a shape second-order parameter. Revstat 2014;12(3):299–328.
54. Henriques-Rodrigues, L., Gomes, M.I., Manjunath, B.G. Estimation of a scale second-order parameter related to the PORT methodology. Journal of Statistical Theory and Practice 2015;9(3):571–599.
55. Jones, M.C., Faddy, M.J. A skew extension of the -distribution, with applications. J R Stat Soc B 2003;65(1):159–174.
56. Longin, F. Le choix de la loi des rentabilités d'actifs financiers: les valeurs extrémes peuvent aider. Finance 1995;16:25–47.
57. Peng, L. Asymptotically unbiased estimator for the extreme-value index. Stat Probab Lett 1998;38(2):107–115.
58. Peng, L., Qi, Y. Estimating the first and second order parameters of a heavy tailed distribution. Aust N Z J Stat 2004;46:305–312.
59. Reiss, R.-D., Thomas, M. Statistical Analysis of Extreme Values with Applications to Insurance, Finance, Hydrology and Other Fields. 3rd ed. Basel, Boston (MA), Berlin: Birkhäuser Verlag; 2007.
60. Resnick, S. Heavy tail modelling and teletraffic data. Ann Stat 1997;25(5):1805–1869.
61. Weissman, I. Estimation of parameters and large quantiles based on the largest observations. J Am Stat Assoc 1978;73:812–815.